A Novel Two-Stage 3D-Printed Halbach Array-Based Device for Magneto-Mechanical Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Apparatus (Design/Manufacture)
2.2. Computational Modelling (Simulation)
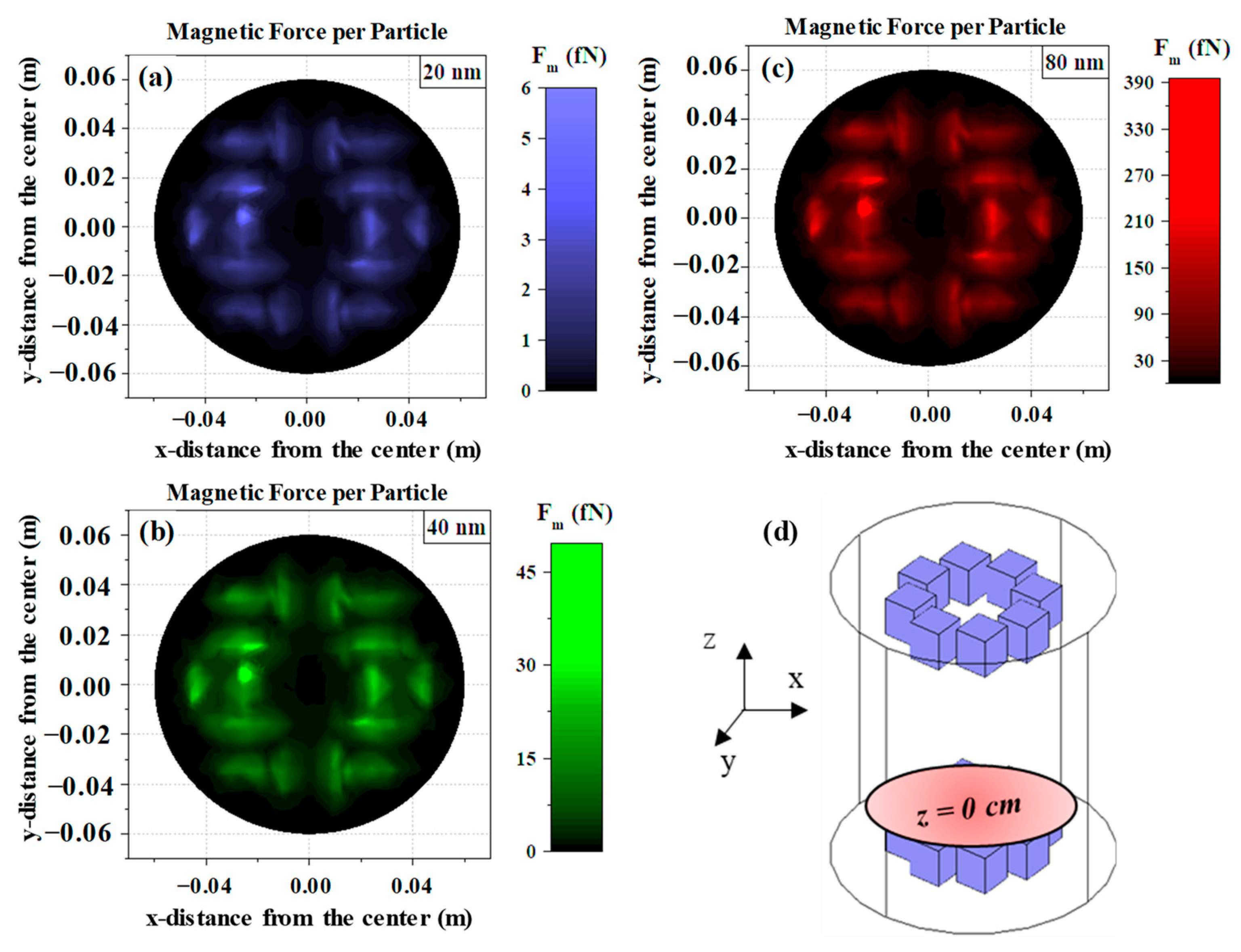
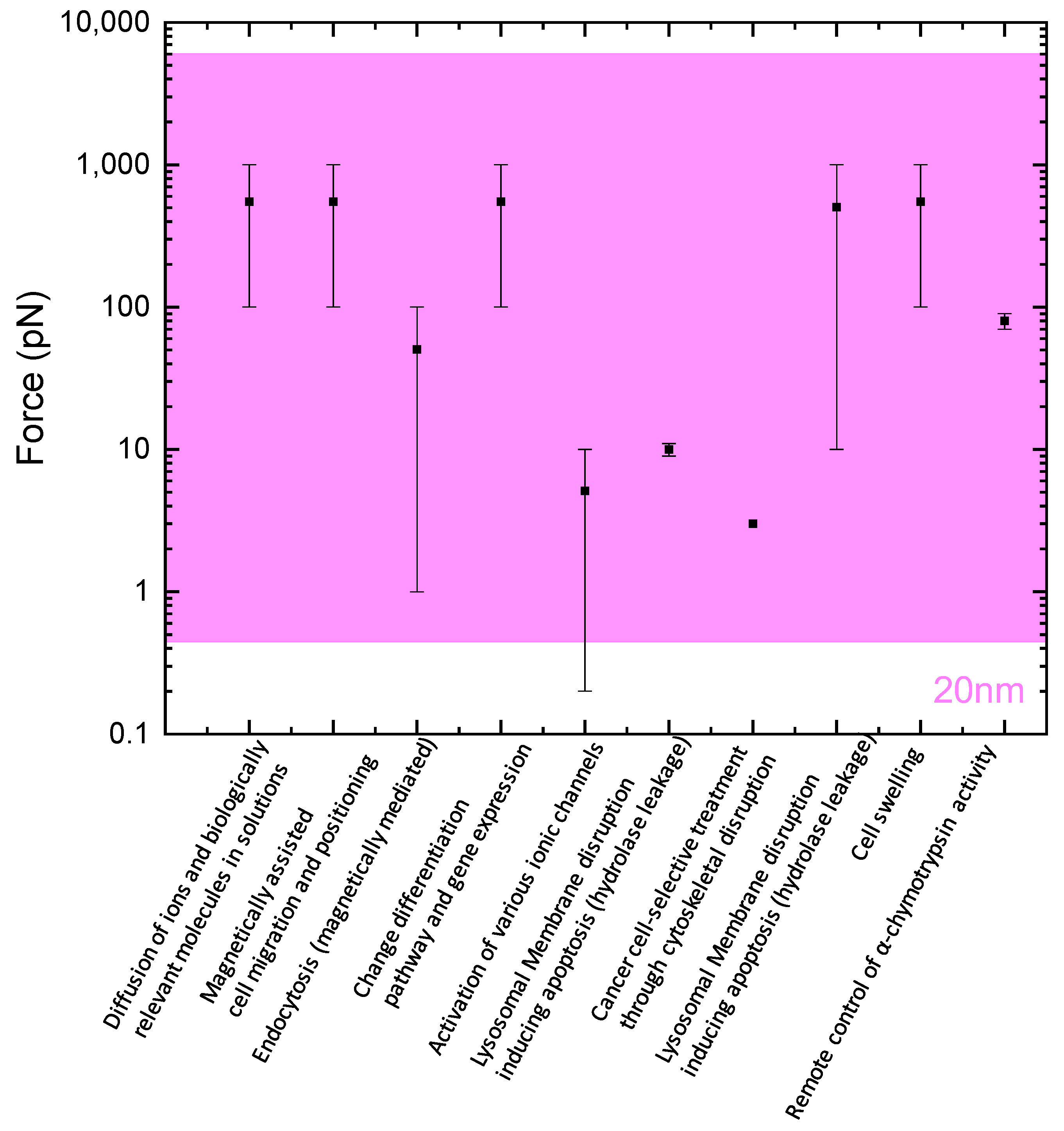
2.3. Force Estimation
2.4. Computational Steps
3. Results and Discussion
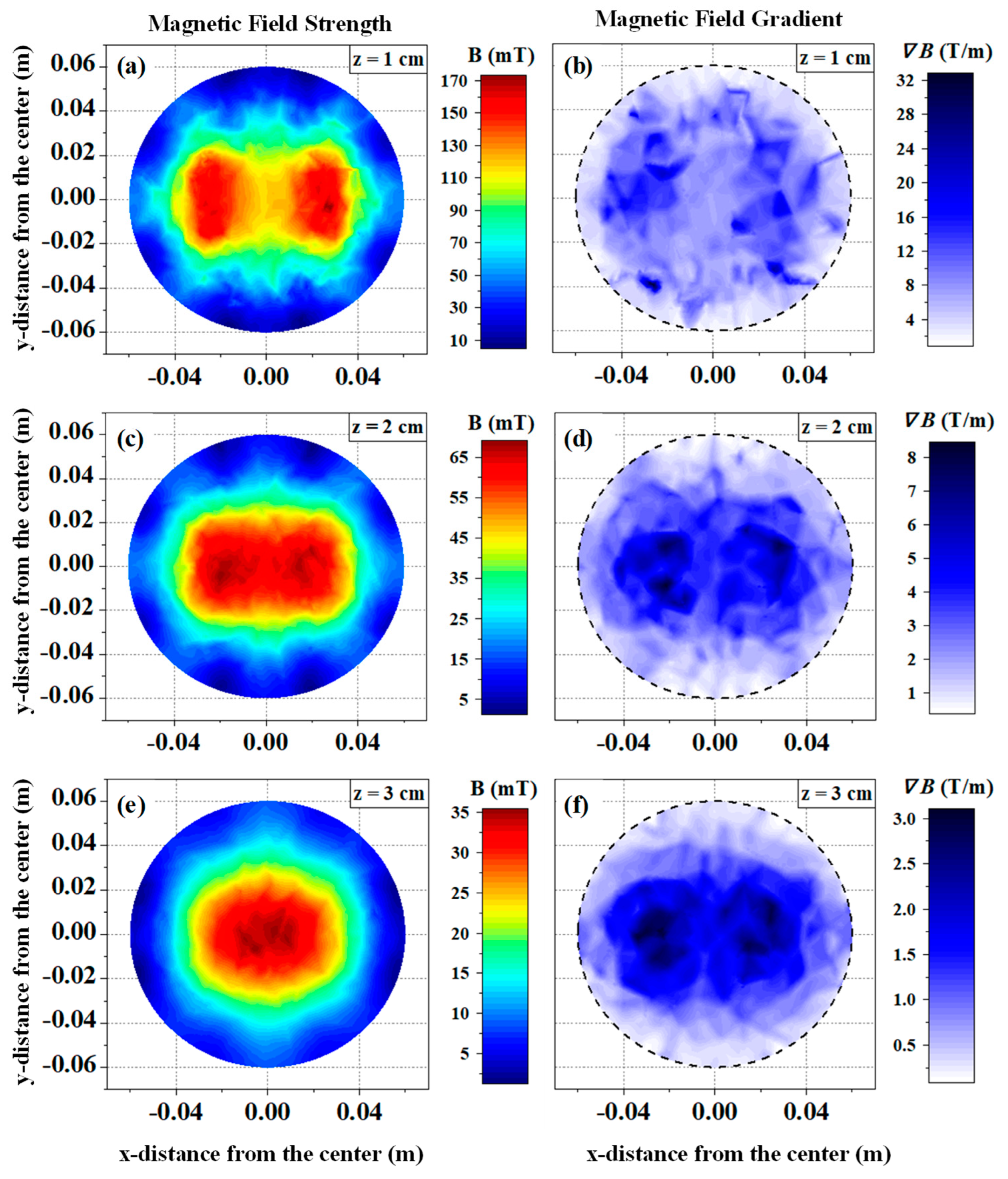
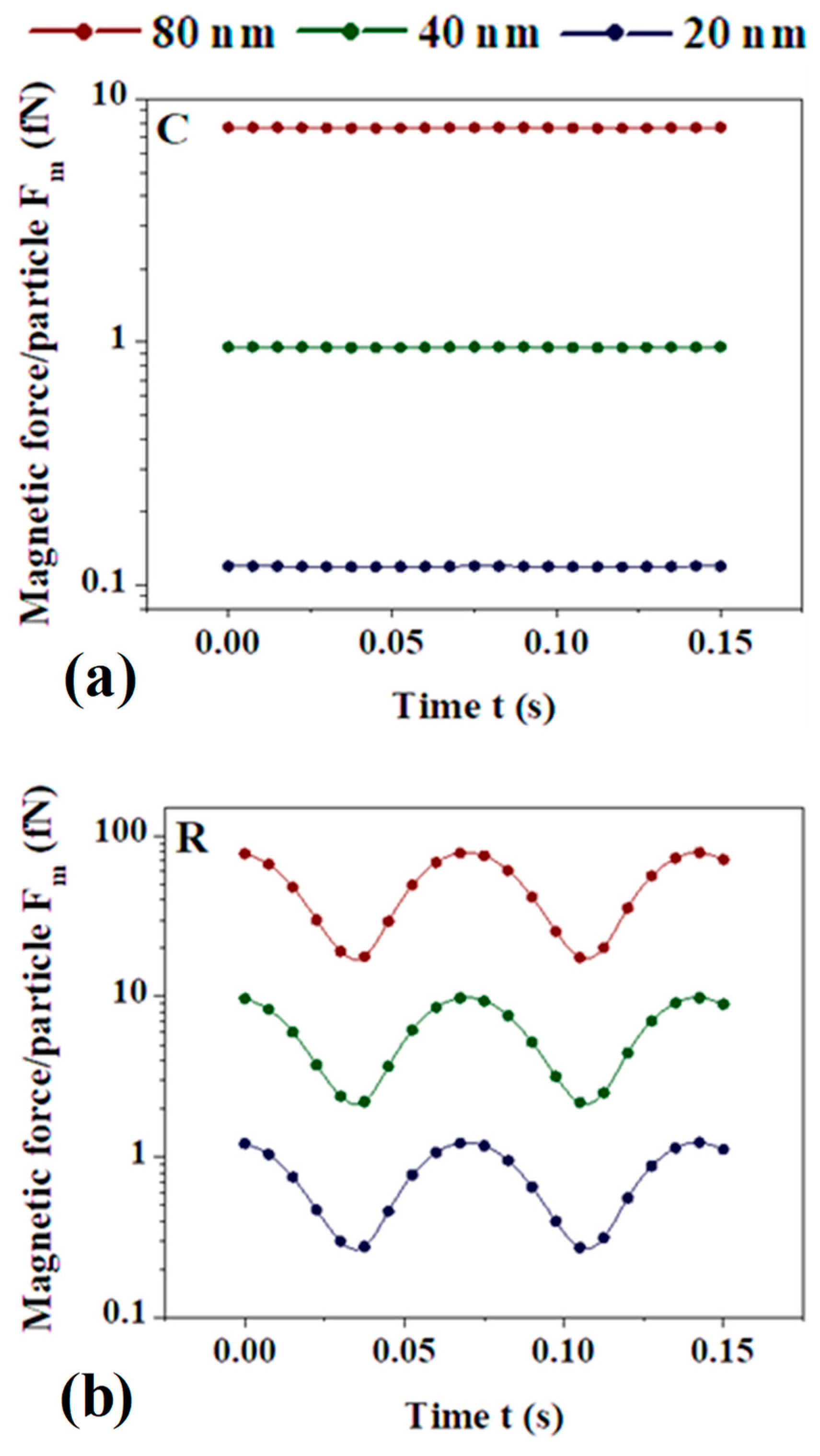
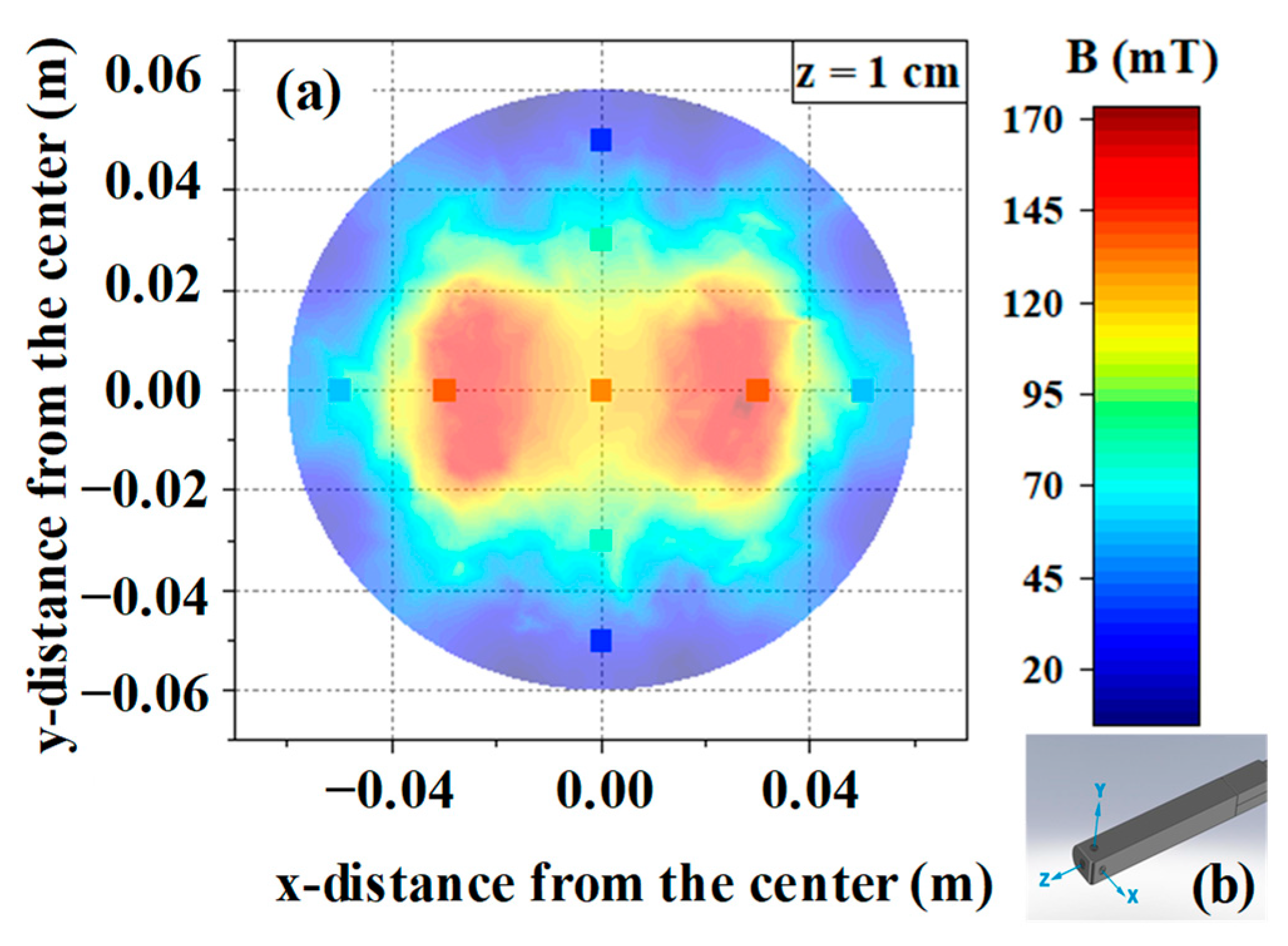
3.1. Static Study
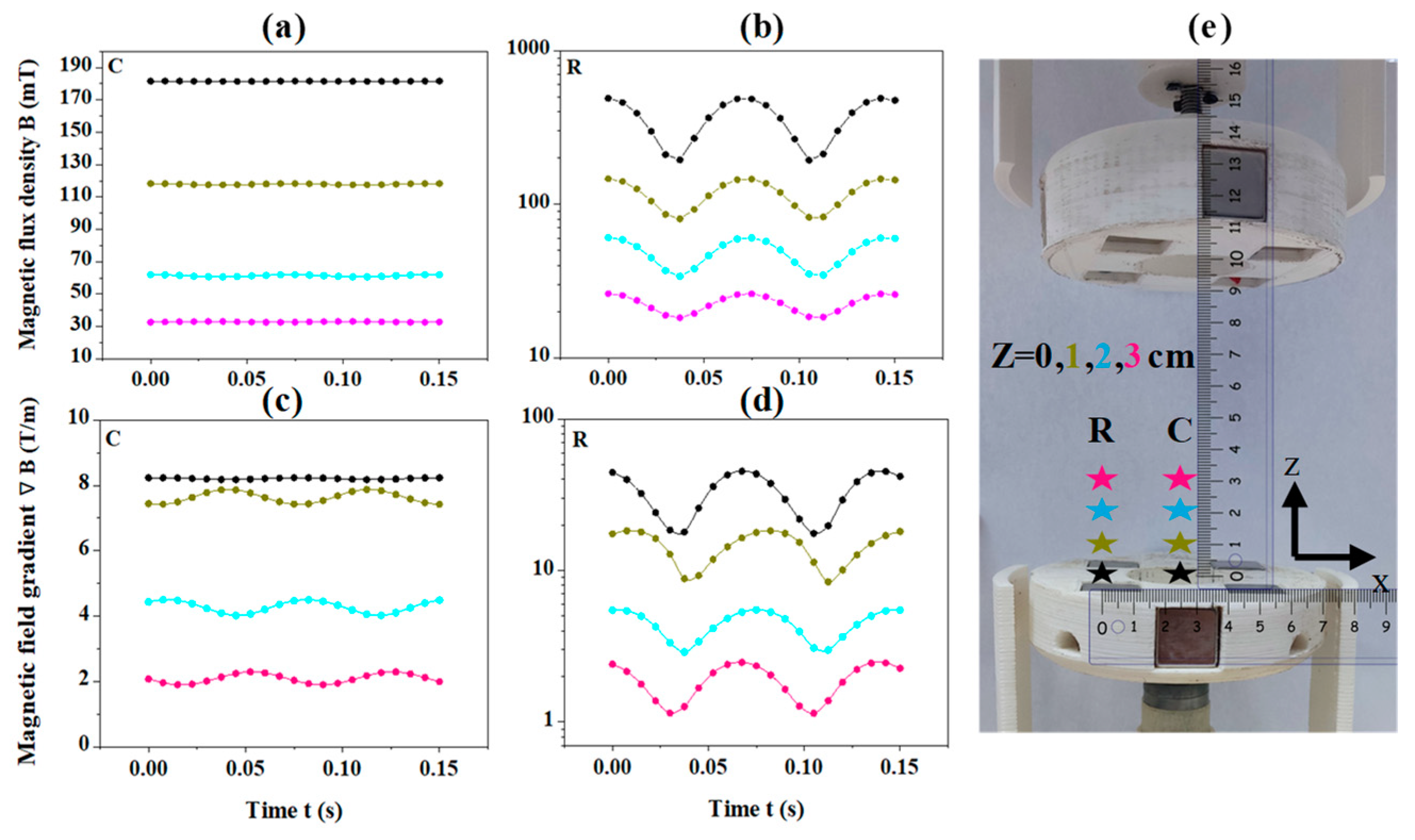
3.2. Rotational Study
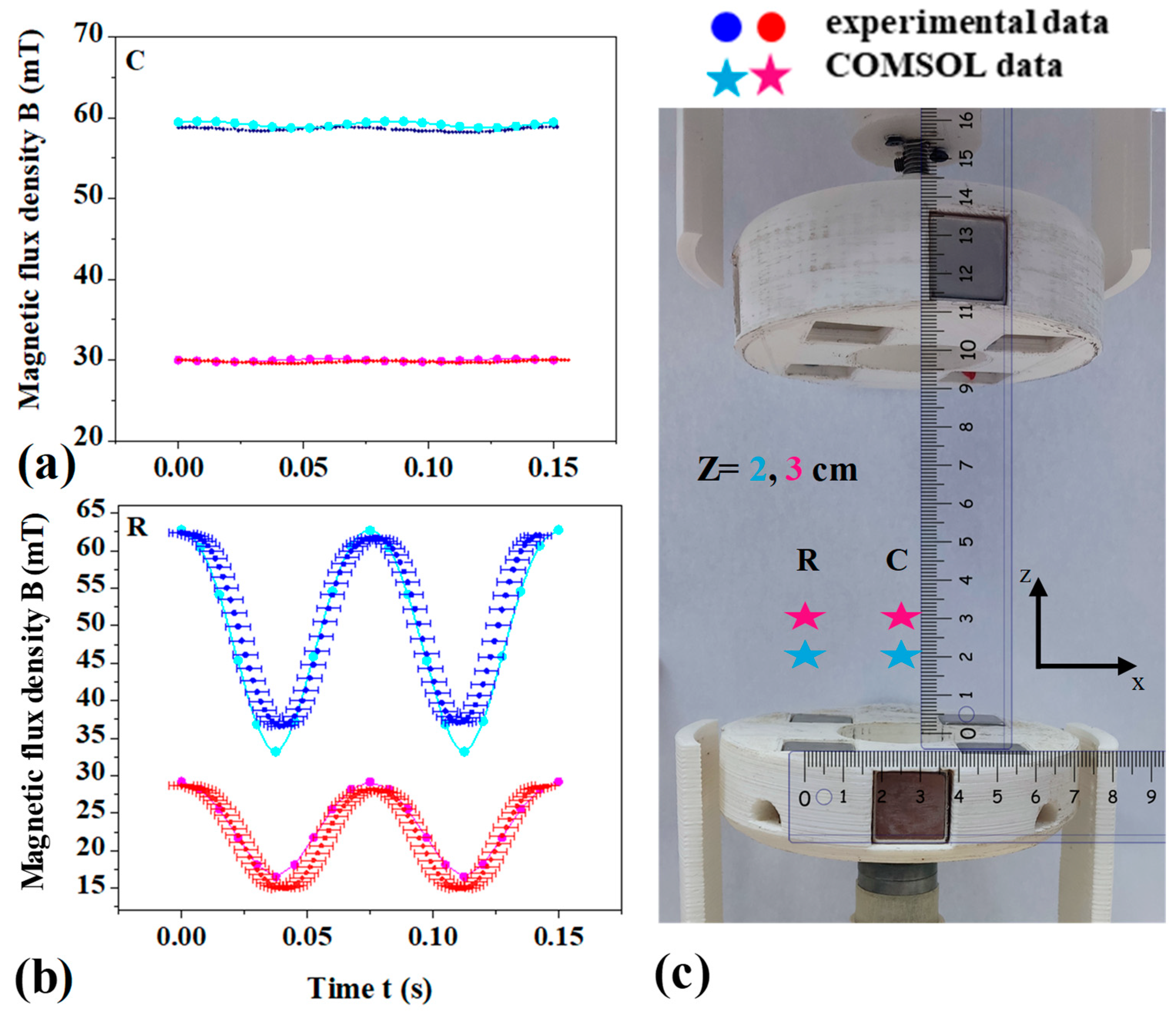
3.3. Experimental Validation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barinec, P.; Krafčík, A.; Babincová, M.; Rosenecker, J. Dynamics of magnetic particles in cylindrical Halbach array: Implications for magnetic cell separation and drug targeting. Med. Biol. Eng. Comput. 2010, 48, 745–753. [Google Scholar] [CrossRef] [PubMed]
- Pankhurst, Q.A.; Thanh NT, K.; Jones, S.K.; Dobson, J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2009, 42, 224001. [Google Scholar] [CrossRef]
- Berry, C.C.; Curtis, A.S.G. Functionalisation of magnetic nanoparticles for applications in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R198. [Google Scholar] [CrossRef]
- Makridis, A.; Kazeli, K.; Kyriazopoulos, P.; Maniotis, N.; Samaras, T.; Angelakeris, M. An accurate standardization protocol for heating efficiency determination of 3D printed magnetic bone scaffolds. J. Phys. D Appl. Phys. 2022, 55, 435002. [Google Scholar] [CrossRef]
- Vergallo, C.; Ahmadi, M.; Mobasheri, H.; Dini, L. Impact of inhomogeneous static magnetic field (31.7–232.0 mT) exposure on human neuroblastoma SH-SY5Y cells during cisplatin administration. PLoS ONE 2014, 9, e113530. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.A.; Semelka, R.C. MRI: Basic Principles and Applications; Wiley-Liss: New York, NY, USA, 1999. [Google Scholar]
- Tao, C.; Chen, Y.; Wang, D.; Cai, Y.; Zheng, Q.; An, L.; Lin, J.; Tian, Q.; Yang, S. Macromolecules with Different Charges, Lengths, and Coordination Groups for the Coprecipitation Synthesis of Magnetic Iron Oxide Nanoparticles as T 1 MRI Contrast Agents. Nanomaterials 2019, 9, 699. [Google Scholar] [CrossRef] [PubMed]
- Makridis, A.; Okkalidis, N.; Trygoniaris, D.; Kazeli, K.; Angelakeris, M. Composite magnetic 3D-printing filament fabrication protocol opens new perspectives in magnetic hyperthermia. J. Phys. D Appl. Phys. 2023, 56, 285002. [Google Scholar] [CrossRef]
- Phadatare Manisha, R.; Meshram, J.V.; Gurav, K.V.; Kim, J.H.; Pawar, S.H. Enhancement of specific absorption rate by exchange coupling of the core–shell structure of magnetic nanoparticles for magnetic hyperthermia. J. Phys. D Appl. Phys. 2016, 49, 095004. [Google Scholar] [CrossRef]
- Kianfar, E. Magnetic nanoparticles in targeted drug delivery: A review. J. Supercond. Nov. Magn. 2021, 34, 1709–1735. [Google Scholar] [CrossRef]
- Kharat, P.B.; Somvanshi, S.B.; Jadhav, K.M. Multifunctional magnetic nano-platforms for advanced biomedical applications: A brief review. J. Phys. Conf. Ser. 2020, 1644, 012036. [Google Scholar] [CrossRef]
- Mitchell, M.J.; Billingsley, M.M.; Haley, R.M.; Wechsler, M.E.; Peppas, N.A.; Langer, R. Engineering precision nanoparticles for drug delivery. Nat. Rev. Drug Discov. 2021, 20, 101–124. [Google Scholar] [CrossRef] [PubMed]
- Angelakeris, M. Magnetic nanoparticles: A multifunctional vehicle for modern theranostics. Biochim. Biophys. Acta BBA 2017, 1861, 1642–1651. [Google Scholar] [CrossRef]
- Nikitin, A.A.; Ivanova, A.V.; Semkina, A.S.; Lazareva, P.A.; Abakumov, M.A. Magneto-mechanical approach in biomedicine: Benefits, challenges, and future perspectives. Int. J. Mol. Sci. 2022, 23, 11134. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; El Haj, A.J.; Dobson, J. Receptor-targeted, magneto-mechanical stimulation of osteogenic differentiation of human bone marrow-derived mesenchymal stem cells. Int. J. Mol. Sci. 2013, 14, 19276–19293. [Google Scholar] [CrossRef] [PubMed]
- Golovin, Y.I.; Gribanovsky, S.L.; Golovin, D.Y.; Klyachko, N.L.; Majouga, A.G.; Master, A.M.; Sokolsky, M.; Kabanov, A.V. Towards nanomedicines of the future: Remote magneto-mechanical actuation of nanomedicines by alternating magnetic fields. J. Control. Release 2015, 219, 43–60. [Google Scholar] [CrossRef]
- Veselov, M.M.; Uporov, I.V.; Efremova, M.V.; Le-Deygen, I.M.; Prusov, A.N.; Shchetinin, I.V.; Savchenko, A.G.; Golovin, Y.I.; Kabanov, A.V.; Klyachko, N.L. Modulation of α-Chymotrypsin Conjugated to Magnetic Nanoparticles by the Non-Heating Low-Frequency Magnetic Field: Molecular Dynamics, Reaction Kinetics, and Spectroscopy Analysis. ACS Omega 2022, 7, 20644–20655. [Google Scholar]
- Thalmayer, A.S.; Zeising, S.; Fischer, G.; Kirchner, J. Steering magnetic nanoparticles by utilizing an adjustable linear Halbach array. In Proceedings of the 2021 Kleinheubach Conference, Miltengerg, Germany, 28–30 September 2021; pp. 1–4. [Google Scholar]
- Rana, S.M.S.; Salauddin, M.; Sharifuzzaman; Lee, S.H.; Shin, Y.D.; Song, H.; Jeong, S.H.; Bhatta, T.; Shrestha, K.; Park, J.Y. Ultrahigh-Output Triboelectric and Electromagnetic Hybrid Generator for Self-Powered Smart Electronics and Biomedical Applications. Adv. Energy Mater. 2022, 12, 2202238. [Google Scholar] [CrossRef]
- Gibson, G.; Hailing, F.U. Wireless Power Transfer Using A Halbach Array and A Magnetically Plucked Piezoelectric Transducer for Medical Implants. In Proceedings of the 21st International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS), Salt Lake City, UT, USA, 12–15 December 2022; pp. 50–53. [Google Scholar]
- Halbach, K. Design of permanent multipole magnets with oriented rare earth cobalt material. Nucl. Instrum. Methods 1980, 169, 3605–3608. [Google Scholar] [CrossRef]
- Post, R.F.; Ryutov, D.D. The inductrack: A simpler approach to magnetic levitation. IEEE Trans. Appl. Supercond. 2000, 10, 901–904. [Google Scholar] [CrossRef]
- Fuwa, Y.; Takayanagi, T.; Iwashita, Y. Development of Combined-Function Multipole Permanent Magnet for High-Intensity Beam Transportation. IEEE Trans. Appl. Supercond. 2022, 32, 4006705. [Google Scholar] [CrossRef]
- Xue, M.; Xiang, A.; Guo, Y.; Wang, L.; Wang, R.; Wang, W.; Ji, G.; Lu, Z. Dynamic Halbach array magnet integrated microfluidic system for the continuous-flow separation of rare tumor cells. RSC Adv. 2019, 9, 38496–38504. [Google Scholar] [CrossRef]
- Zablotskii, V.; Lunov, O.; Novotná, B.; Churpita, O.; Trošan, P.; Holáň, V.; Syková, E.; Dejneka, A.; Kubinová, Š. Down-regulation of adipogenesis of mesenchymal stem cells by oscillating high-gradient magnetic fields and mechanical vibration. Appl. Phys. Lett. 2014, 105, 103702. [Google Scholar] [CrossRef]
- Maniotis, N.; Makridis, A.; Myrovali, E.; Theopoulos, A.; Samaras, T.; Angelakeris, M. Magneto-mechanical action of multimodal field configurations on magnetic nanoparticle environments. J. Magn. Magn. Mater. 2019, 470, 6–11. [Google Scholar] [CrossRef]
- Spyridopoulou, K.; Makridis, A.; Maniotis, N.; Karypidou, N.; Myrovali, E.; Samaras, T.; Angelakeris, M.; Chlichlia, K.; Kalogirou, O. Effect of low frequency magnetic fields on the growth of MNP-treated HT29 colon cancer cells. Nanotechnology 2018, 29, 175101. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Furlani, E.J.; Furlani, E.P. A model for predicting magnetic targeting of multifunctional particles in the microvasculature. J. Magn. Magn. Mater. 2007, 312, 187–193. [Google Scholar] [CrossRef]
- Maniotis, N.; Kalaitzidou, K.; Asimoulas, E.; Simeonidis, K. A rotary magnetic separator integrating nanoparticle-assisted water purification: Simulation and laboratory validation. J. Water Process Eng. 2023, 53, 103825. [Google Scholar] [CrossRef]
- Master, A.M.; Williams, P.N.; Pothayee, N.; Pothayee, N.; Zhang, R.; Vishwasrao, H.M.; Golovin, Y.I.; Riffle, J.S.; Sokolsky, M.; Kabanov, A.V. Remote actuation of magnetic nanoparticles for cancer cell selective treatment through cytoskeletal disruption. Sci. Rep. 2016, 6, 33560. [Google Scholar] [CrossRef] [PubMed]
- Tran, H.B.; Matsushita, Y.I. Temperature and size dependence of energy barrier for magnetic flips in L10 FePt nanoparticles: A theoretical study. Scr. Mater. 2024, 242, 115947. [Google Scholar] [CrossRef]
- Moghanizadeh, A.; Ashrafizadeh, F.; Varshosaz, J.; Ferreira, A. RETRACTED ARTICLE: Study the effect of static magnetic field intensity on drug delivery by magnetic nanoparticles. Sci. Rep. 2021, 11, 18056. [Google Scholar] [CrossRef]
- Sandhu, A.; Handa, H. Magnetic Nanoparticles for Medical Diagnostics; IOP Publishing: Bristol, UK, 2018. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makridis, A.; Maniotis, N.; Papadopoulos, D.; Kyriazopoulos, P.; Angelakeris, M. A Novel Two-Stage 3D-Printed Halbach Array-Based Device for Magneto-Mechanical Applications. Magnetochemistry 2024, 10, 21. https://doi.org/10.3390/magnetochemistry10040021
Makridis A, Maniotis N, Papadopoulos D, Kyriazopoulos P, Angelakeris M. A Novel Two-Stage 3D-Printed Halbach Array-Based Device for Magneto-Mechanical Applications. Magnetochemistry. 2024; 10(4):21. https://doi.org/10.3390/magnetochemistry10040021
Chicago/Turabian StyleMakridis, Antonios, Nikolaos Maniotis, Dimitrios Papadopoulos, Pavlos Kyriazopoulos, and Makis Angelakeris. 2024. "A Novel Two-Stage 3D-Printed Halbach Array-Based Device for Magneto-Mechanical Applications" Magnetochemistry 10, no. 4: 21. https://doi.org/10.3390/magnetochemistry10040021
APA StyleMakridis, A., Maniotis, N., Papadopoulos, D., Kyriazopoulos, P., & Angelakeris, M. (2024). A Novel Two-Stage 3D-Printed Halbach Array-Based Device for Magneto-Mechanical Applications. Magnetochemistry, 10(4), 21. https://doi.org/10.3390/magnetochemistry10040021







