Theoretical Hints to Optimize Energy Dissipation and Cell–Cell Response in Quantum Cellular Automata Based on Tetrameric and Bidimeric Cells †
Abstract
1. Introduction
2. Description of the Molecular Cells within the Vibronic Approach
2.1. Hamiltonians of the Bidimeric and Tetrameric Working Cells
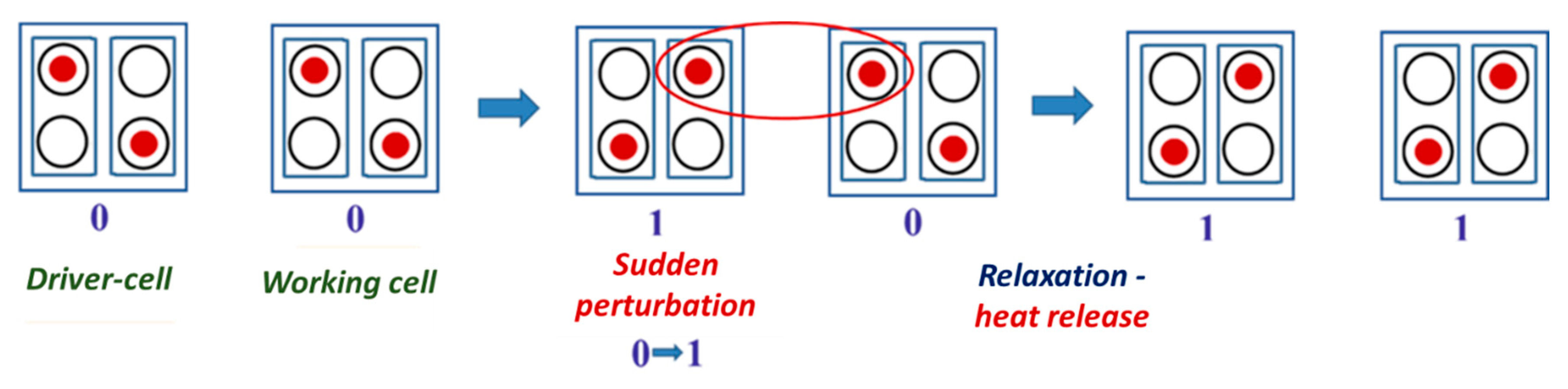
2.2. Quantum-Mechanical Vibronic Approach: Evaluation of Cell–Cell Response
2.3. Quantum–Mechanical Vibronic Approach: Evaluation of Specific Heat Release
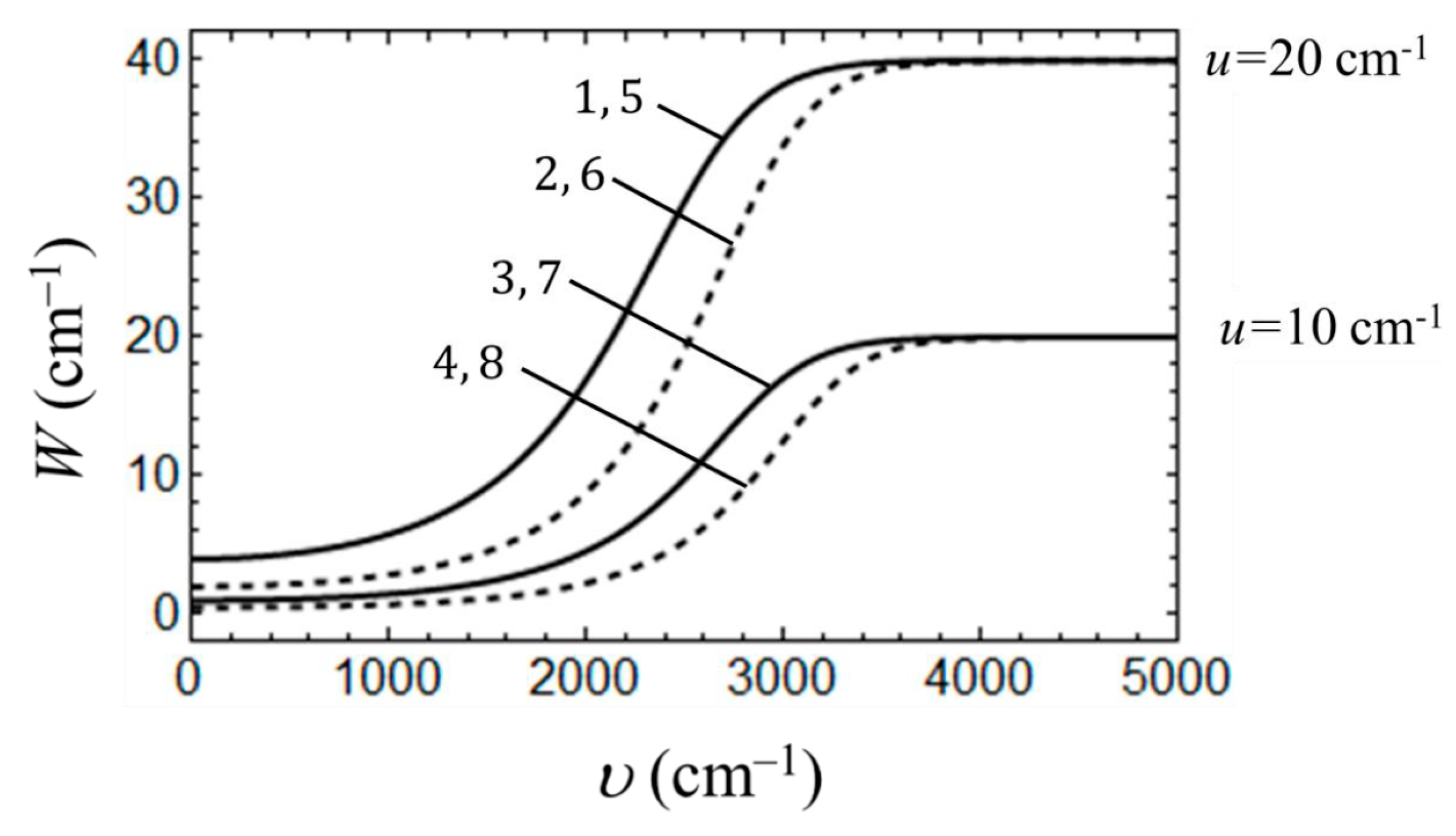
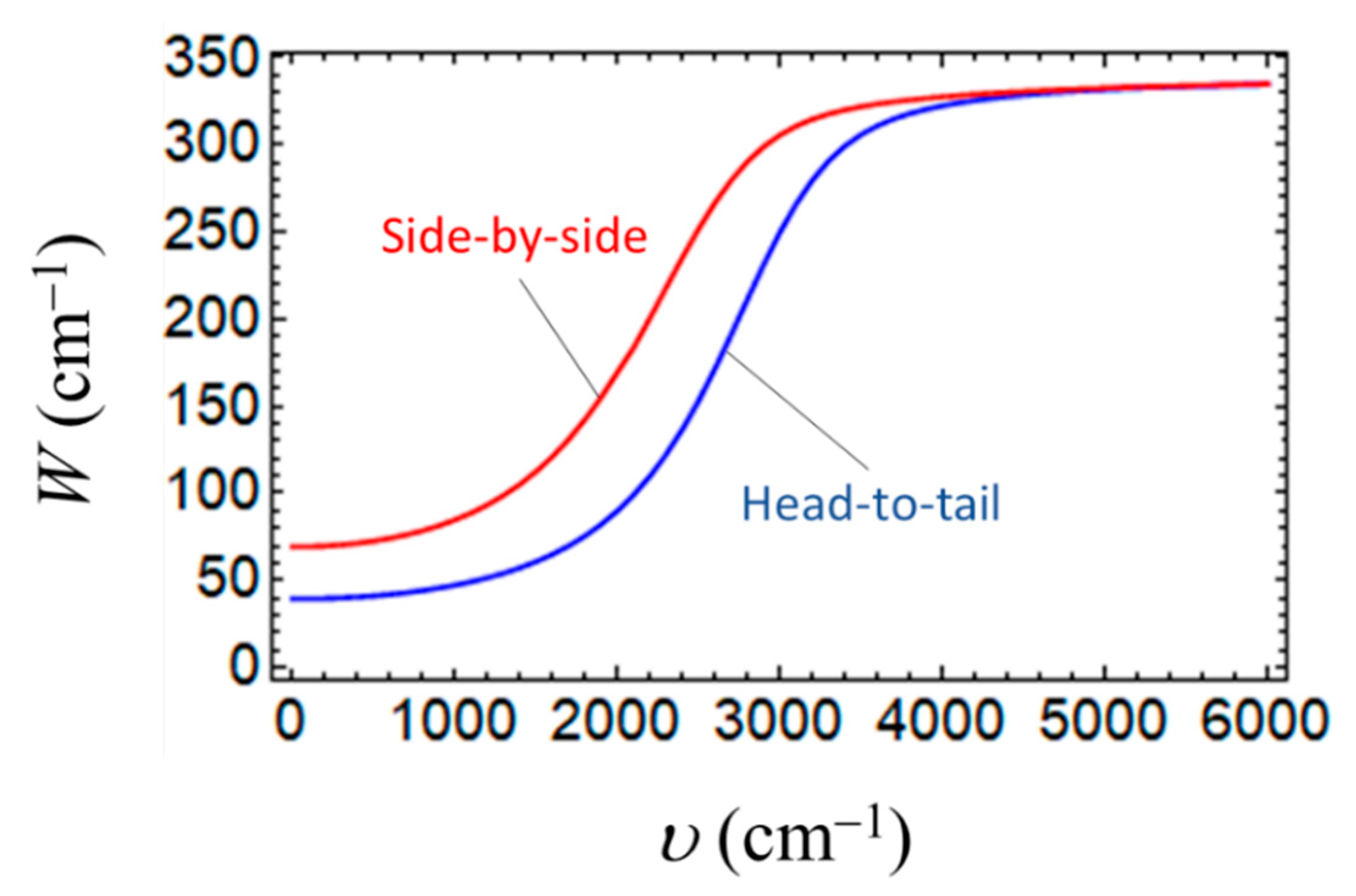
3. Results and Discussion
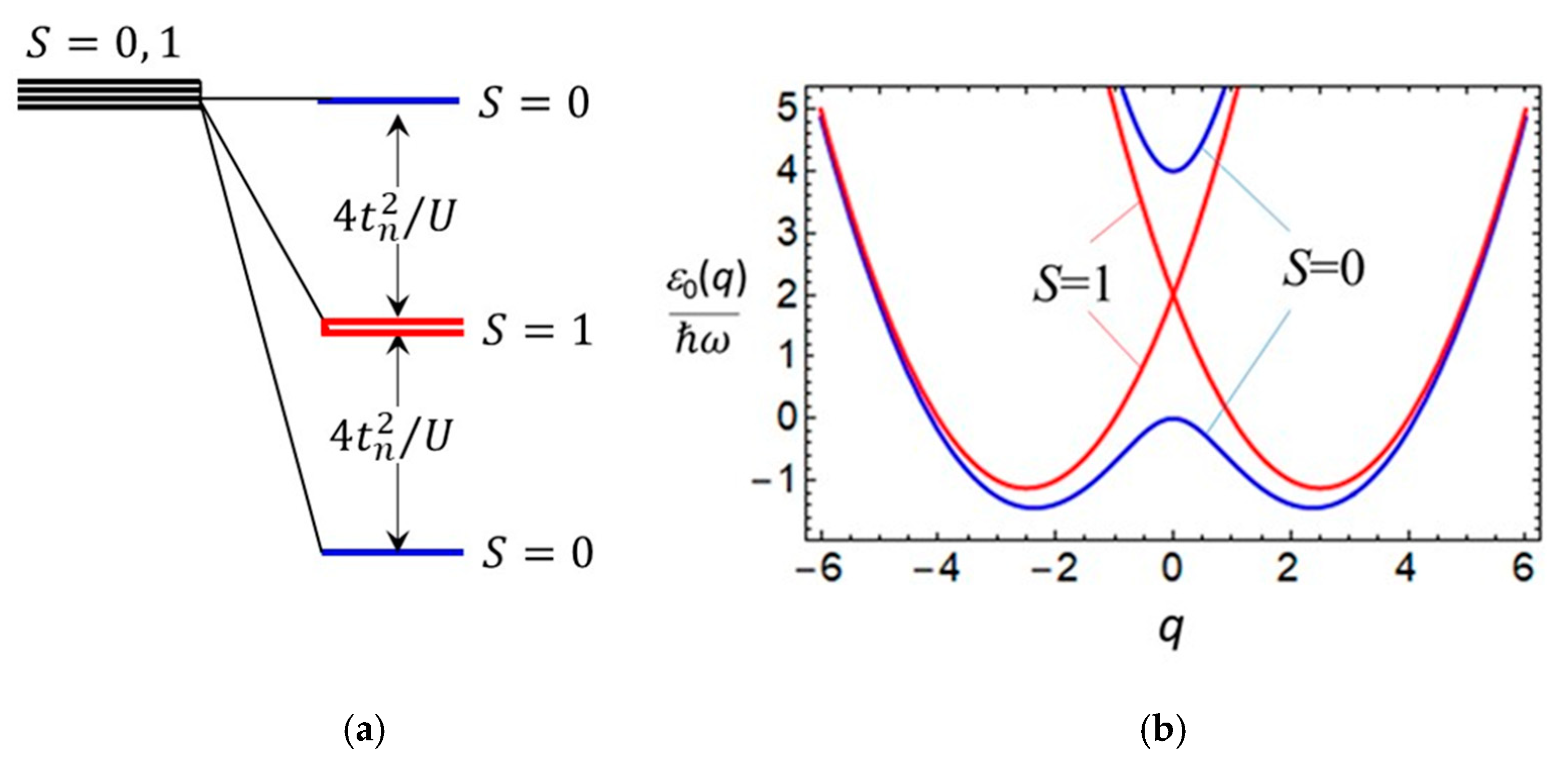
3.1. Consideration of Bidimeric and Tetrameric Cells: Limit of Strong Coulomb Repulsion
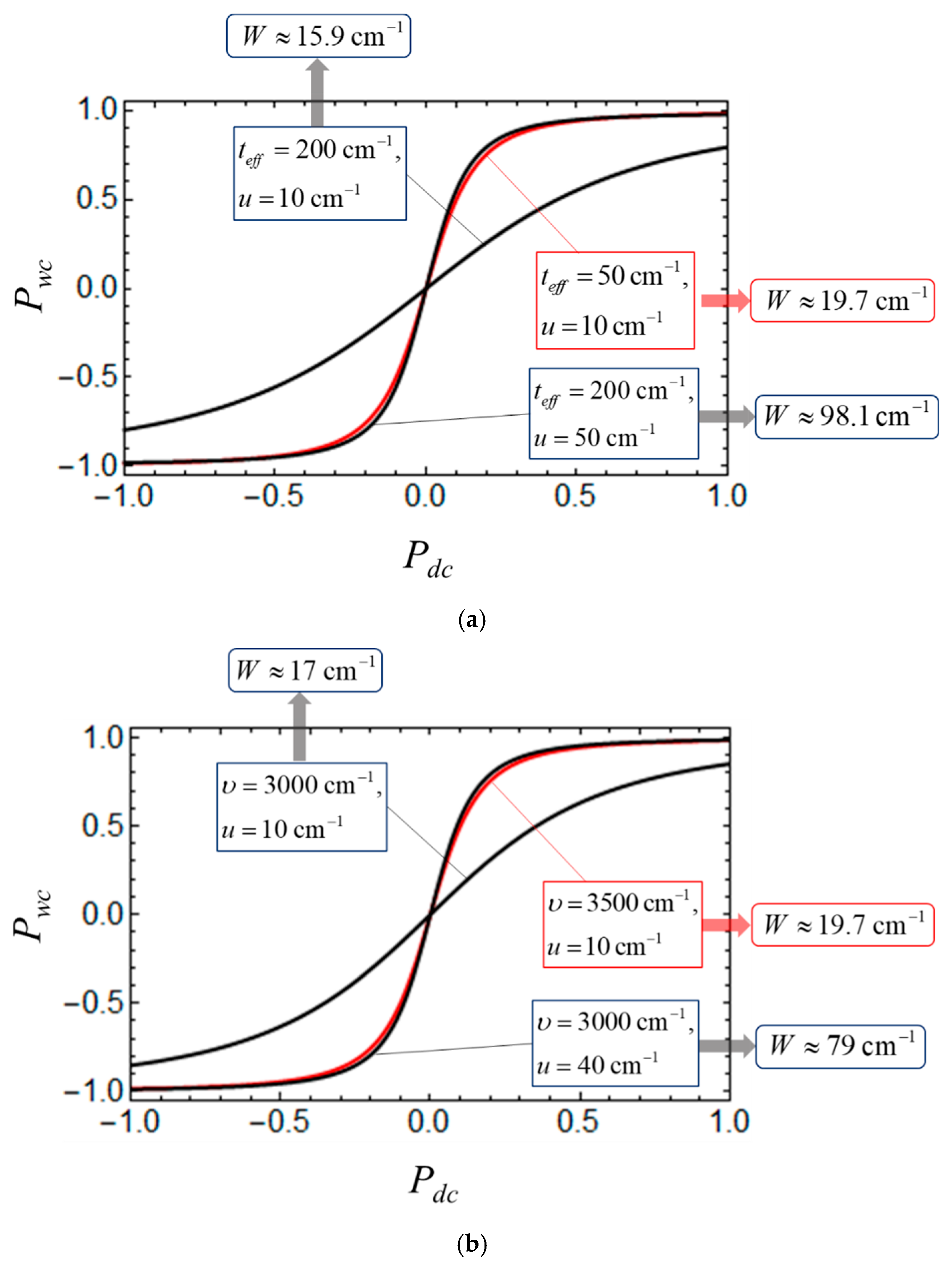
3.2. Consideration of Bidimeric and Tetrameric Cells: Common Case of Arbitrary Coulomb Interaction
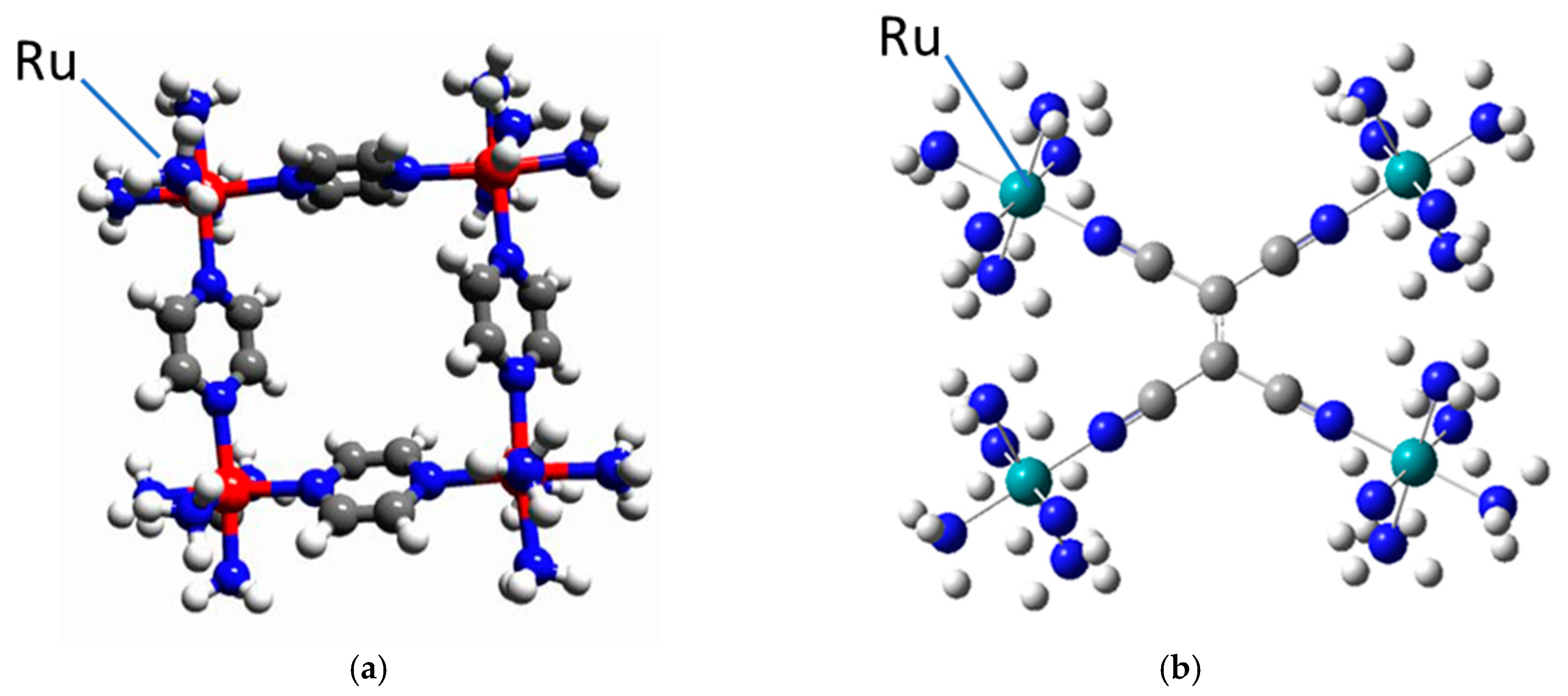
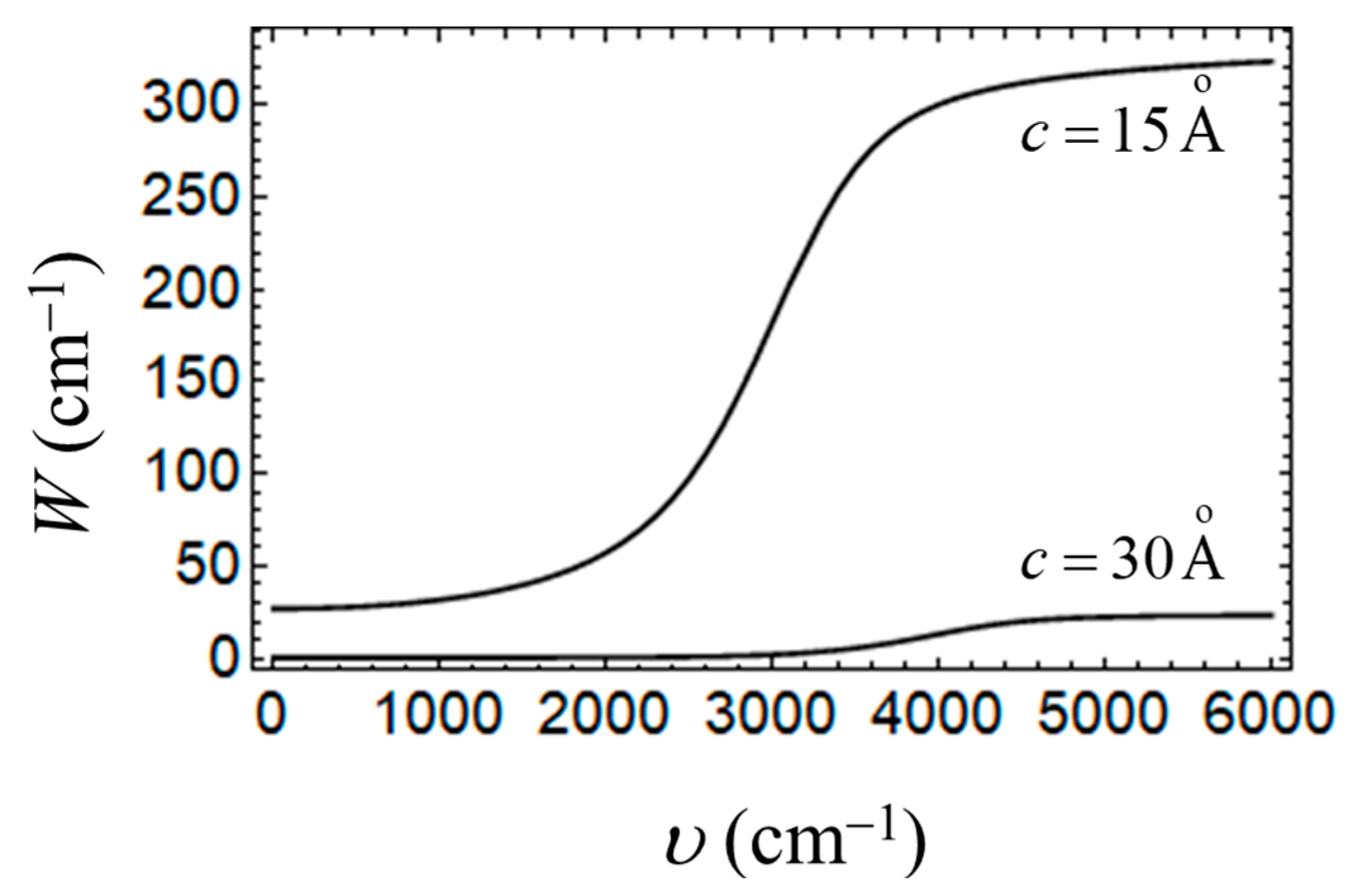
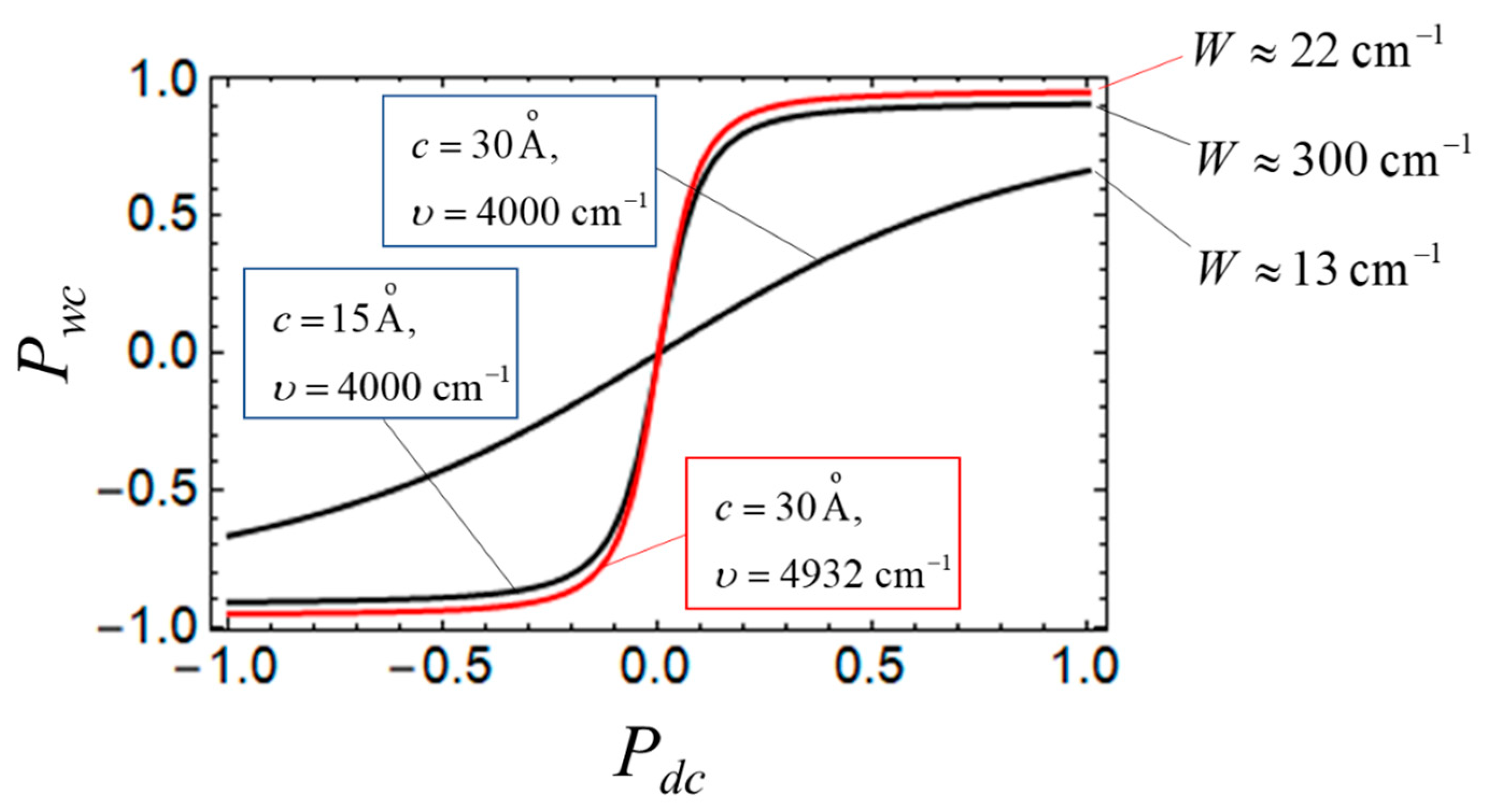
4. Some Relevant Ab Initio Results and Possibility of Controlling the Key Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lent, C.S. Bypassing the transistor paradigm. Science 2000, 288, 1597–1599. [Google Scholar] [CrossRef]
- Lieberman, M.; Chellamma, S.; Varughese, B.; Wang, Y.; Lent, C.; Bernstein, G.H.; Snider, G.; Peiris, F.C. Quantum-dot cellular automata at a molecular scale. Ann. N. Y. Acad. Sci. 2002, 960, 225–239. [Google Scholar] [CrossRef]
- Lent, C.S.; Isaksen, B.; Lieberman, M. Molecular quantum-dot cellular automata. J. Am. Chem. Soc. 2003, 125, 1056–1063. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Long, G.J.; Grandjean, F.; Beatty, A.M.; Fehlner, T.P. Building Blocks for the Molecular Expression of Quantum Cellular Automata. Isolation and Characterization of a Covalently Bonded Square Array of Two Ferrocenium and Two Ferrocene Complexes. J. Am. Chem. Soc. 2003, 125, 7522–7523. [Google Scholar] [CrossRef]
- Li, Z.; Beatty, A.M.; Fehlner, T.P. Molecular QCA Cells. 1. Structure and Functionalization of an Unsymmetrical Dinuclear Mixed-Valence Complex for Surface Binding. Inorg. Chem. 2003, 42, 5707–5714. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Fehlner, T.P. Molecular QCA Cells. 2. Characterization of an Unsymmetrical Dinuclear Mixed-Valence Complex Bound to a Au Surface by an Organic Linker. Inorg. Chem. 2003, 42, 5715–5721. [Google Scholar] [CrossRef]
- Qi, H.; Sharma, S.; Li, Z.; Snider, G.L.; Orlov, A.O.; Lent, C.S.; Fehlner, T.P. Molecular Quantum Cellular Automata Cells. Electric Field Driven Switching of a Silicon Surface Bound Array of Vertically Oriented Two-Dot Molecular Quantum Cellular Automata. J. Am. Chem. Soc. 2003, 125, 15250–15259. [Google Scholar] [CrossRef]
- Braun-Sand, S.B.; Wiest, O. Theoretical Studies of Mixed Valence Transition Metal Complexes for Molecular Computing. J. Phys. Chem. A 2003, 107, 285–291. [Google Scholar] [CrossRef]
- Braun-Sand, S.B.; Wiest, O. Biasing Mixed-Valence Transition Metal Complexes in Search of Bistable Complexes for Molecular Computing. J. Phys. Chem. B 2003, 107, 9624–9628. [Google Scholar] [CrossRef]
- Qi, H.; Gupta, A.; Noll, B.C.; Snider, G.L.; Lu, Y.; Lent, C.; Fehlner, T.P. Dependence of Field Switched Ordered Arrays of Dinuclear Mixed-Valence Complexes on the Distance between the Redox Centers and the Size of the Counterions. J. Am. Chem. Soc. 2005, 127, 15218–15227. [Google Scholar] [CrossRef]
- Jiao, J.; Long, G.J.; Rebbouh, L.; Grandjean, F.; Beatty, A.M.; Fehlner, T.P. Properties of a Mixed-Valence (FeII)2(FeIII)2 Square Cell for Utilization in the Quantum Cellular Automata Paradigm for Molecular Electronics. J. Am. Chem. Soc. 2005, 127, 17819–17831. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Lent, C.S. Theoretical Study of Molecular Quantum Dot Cellular Automata. J. Comput. Electron. 2005, 4, 115–118. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, D.; Liu, Y.; He, C.; Duan, C. A Mixed-Valence (FeII)2(FeIII)2 Square for Molecular Expression of Quantum Cellular Automata. Chem. Commun. 2008, 5725–5727. [Google Scholar] [CrossRef] [PubMed]
- Nemykin, V.N.; Rohde, G.T.; Barrett, C.D.; Hadt, R.G.; Bizzarri, C.; Galloni, P.; Floris, B.; Nowik, I.; Herber, R.H.; Marrani, A.G.; et al. Electron-Transfer Processes in Metal-Free Tetraferrocenylporphyrin. Understanding Internal Interactions to Access Mixed Valence States Potentially Useful for Quantum Cellular Automata. J. Am. Chem. Soc. 2009, 131, 14969–14978. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Lent, C. Self-doping of molecular quantum-dot cellular automata: Mixed valence zwitterions. Phys. Chem. Chem. Phys. 2011, 13, 14928–14936. [Google Scholar] [CrossRef]
- Lu, Y.; Lent, C.S. Counterion-free molecular quantum-dot cellular automata using mixed valence zwitterions—A double-dot derivative of the [closo-1-CB9H10]− cluster. Chem. Phys. Lett. 2013, 582, 86–89. [Google Scholar] [CrossRef]
- Christie, A.; Forrest, R.P.; Corcelli, S.A.; Wasio, N.A.; Quardokus, R.C.; Brown, R.; Kandel, S.A.; Lu, Y.; Lent, C.S.; Henderson, K.W. Synthesis of a neutral mixed-valence diferrocenyl carborane for molecular quantum-dot cellular automata applications. Angew. Chem. 2015, 127, 15668–15671. [Google Scholar] [CrossRef]
- Wang, X.; Yu, L.; Inakollu, V.S.S.; Pan, X.; Ma, J.; Yu, H. Molecular Quantum-Dot Cellular Automata Based on Diboryl Radical Anions. J. Phys. Chem. C 2018, 122, 2454–2460. [Google Scholar] [CrossRef]
- Macrae, R.M. Mixed-valence realizations of quantum dot cellular automata. J. Phys. Chem. Solids 2023, 177, 111303. [Google Scholar] [CrossRef]
- Aviram, A. Molecules for Memory, Logic, and Amplification. J. Am. Chem. Soc. 1988, 125, 5687–5692. [Google Scholar] [CrossRef]
- Creutz, C.; Taube, H. Binuclear complexes of ruthenium ammines. J. Am. Chem. Soc. 1973, 95, 1086–1094. [Google Scholar] [CrossRef]
- Timler, J.; Lent, C.S. Power gain and dissipation in quantum-dot cellular automata. J. Appl. Phys. 2002, 91, 823–831. [Google Scholar] [CrossRef]
- Rahimi, E. Energy dissipation of quantum-dot cellular automata logic gates. Micro Nano Lett. 2016, 11, 369–371. [Google Scholar] [CrossRef]
- Rahimi, E.; Reimers, J.R. Molecular quantum cellular automata cell design trade-offs: Latching vs. power dissipation. Phys. Chem. Chem. Phys. 2018, 20, 17881–17888. [Google Scholar] [CrossRef]
- Pidaparthi, S.S.; Lent, C.S. Molecular reorganization energy in quantum-dot cellular automata switching. J. Appl. Phys. 2022, 131, 044502. [Google Scholar] [CrossRef]
- Palii, A.; Belonovich, V.; Tsukerblat, B. In quest of optimal parametric regime of nonadiabatic switching ensuring low heat release in conjunction with high polarizability of mixed-valence molecular dimer. Phys. Chem. Chem. Phys. 2023, 25, 17526–17534. [Google Scholar] [CrossRef]
- Palii, A.; Belonovich, V.; Aldoshin, S.; Zilberg, S.; Tsukerblat, B. Mixed-Valence Bridged Norbornylogous Compounds as Switchable Cells for Molecular Quantum Cellular Automata: A Compromise between High Polarizability and Low Power Dissipation. J. Phys. Chem. A 2023, 127, 9030–9039. [Google Scholar] [CrossRef]
- Lent, C.S.; Tougaw, P.; Porod, W. Bistable saturation in coupled quantum dots for quantum cellular automata. Appl. Phys. Lett. 1993, 62, 714–716. [Google Scholar] [CrossRef]
- Lent, C.S.; Tougaw, P.D. Lines of interacting quantum dot cells: A binary wire. J. Appl. Phys. 1993, 74, 6227–6233. [Google Scholar] [CrossRef]
- Tougaw, P.; Lent, C. Logical Devices Implemented Using Quantum Cellular Automata. J. Appl. Phys. 1994, 75, 1818–1825. [Google Scholar] [CrossRef]
- Lent, C.S.; Tougaw, P.D. A device architecture for computing with quantum dots. Proc. IEEE 1997, 85, 541–557. [Google Scholar] [CrossRef]
- Porod, W.; Lent, C.S.; Bernstein, G.H.; Orlov, A.O.; Amlani, I.; Snider, G.L.; Merz, J.L. Quantum-dot cellular automata: Computing with coupled quantum dots. Int. J. Electron. 1999, 86, 549–590. [Google Scholar]
- Tsukerblat, B.; Palii, A.; Clemente-Juan, J.M.; Coronado, E. Mixed-Valence Molecular Four-Dot Unit for Quantum Cellular Automata: Vibronic Self-Trapping and Cell-Cell Response. J. Chem. Phys. 2015, 143, 134307. [Google Scholar] [CrossRef] [PubMed]
- Palii, A.; Zilberg, S.; Rybakov, A.; Tsukerblat, B. Double-Dimeric Versus Tetrameric Cells for Quantum Cellular Automata: A Semiempirical Approach to Evaluation of Cell−Cell Responses Combined with Quantum-Chemical Modeling of Molecular Structures. J. Phys. Chem. C 2019, 123, 22614–22623. [Google Scholar] [CrossRef]
- Palii, A.; Aldoshin, S.; Tsukerblat, B. Towards the design of molecular cells for quantum cellular automata: Critical reconsideration of the parameter regime for achieving functionality. Dalton Trans. 2022, 51, 286–302. [Google Scholar] [CrossRef]
- Palii, A.; Aldoshin, S.; Tsukerblat, B. Functional Properties of Tetrameric Molecular Cells for Quantum Cellular Automata: A Quantum-Mechanical Treatment Extended to the Range of Arbitrary Coulomb Repulsion. Magnetochemistry 2022, 8, 92. [Google Scholar] [CrossRef]
- Tsukerblat, B.; Palii, A.; Zilberg, S.; Korchagin, D.; Aldoshin, S.; Clemente-Juan, J.M. Vibronic recovering of functionality of quantum cellular automata based on bi-dimeric square cells with violated condition of strong Coulomb repulsion. J. Chem. Phys. 2022, 157, 074308. [Google Scholar] [CrossRef]
- Piepho, S.B.; Krausz, E.R.; Schatz, P.N. Vibronic coupling model for calculation of mixed valence absorption profiles. J. Am. Chem. Soc. 1978, 100, 2996–3005. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics (Non-Relativistic Theory), 3rd ed.; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Tsukerblat, B.; Palii, A.; Clemente-Juan, J.M. Self-trapping of charge polarized states in four-dot molecular quantum cellular automata: Bi-electronic tetrameric mixed-valence species. Pure Appl. Chem. 2015, 87, 271–282. [Google Scholar] [CrossRef]
- Zilberg, S.; Stekolshik, Y.; Palii, A.; Tsukerblat, B. Controllable Electron Transfer in Mixed-Valence Bridged Norbornylogous Compounds: Ab Initio Calculation Combined with a Parametric Model and Through-Bond and Through-Space Interpretation. J. Phys. Chem. A 2022, 126, 2855–2878. [Google Scholar] [CrossRef]
- Roos, B.O. The Complete Active Space Self-Consistent Field Method and its Applications in Electronic Structure Calculations. Adv. Chem. Phys. 1987, 69, 399–445. [Google Scholar]
- Busch, T.; Degli Esposti, A.; Werner, H.-J. Analytical Energy Gradients for Multiconfiguration Self-Consistent Field Wave Functions with Frozen Core Orbitals. J. Chem. Phys. 1991, 94, 6708–6715. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.J.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Gordon, M.S.; Schmidt, M.W. Advances in Electronic Structure Theory: GAMESS a Decade Later. In Theory and Applications of Computational Chemistry, The First Forty Years; Dykstra, C.E., Frenking, G., Kim, K.S., Scuseria, G.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; Chapter 41; p. 1167. Available online: http://www.msg.chem.iastate.edu/GAMESS/GAMESS.html (accessed on 25 September 2024).
- Zilberg, S.; Tsukerblat, B.; Palii, A. Polaronic Mechanism of Vibronic Localization in Mixed-Valence Cation Radicals with a Non-Conjugated Chromophore on the Bridge. J. Phys. Chem. A 2023, 127, 3281−3292. [Google Scholar] [CrossRef]
- Lent, C.S.; Isaksen, B. Clocked Molecular Quantum-Dot Cellular Automata. IEEE Trans. Electron Devices 2003, 50, 1890–1896. [Google Scholar] [CrossRef]
- Blair, E.; Lent, C. Clock Topologies for Molecular Quantum-Dot Cellular Automata. J. Low Power Electron. Appl. 2018, 8, 31–44. [Google Scholar] [CrossRef]
- Hennessy, K.; Lent, C.S. Clocking of molecular quantum-dot cellular automata. J. Vac. Sci. Technol. B 2001, 19, 1752–1755. [Google Scholar] [CrossRef]
- Toth, G.; Lent, C. Quasiadiabatic switching for metal-island quantum-dot cellular automata. J. Appl. Phys. 1999, 85, 2977–2984. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, M.; Lent, C.S. Molecular quantum-dot cellular automata: From molecular structure to circuit dynamics. J. Appl. Phys. 2007, 102, 034311. [Google Scholar] [CrossRef]
- Lent, C.S.; Liu, M.; Lu, Y. Bennett clocking of quantum-dot cellular automata and the limits to binary logic scaling. Nanotechnology 2006, 17, 4240–4251. [Google Scholar] [CrossRef]
- Palii, A.; Aldoshin, S.; Tsukerblat, B. Theoretical insight into clocking in a molecular mixed valence cell of quantum cellular automata through the vibronic approach. J. Chem. Phys. 2024, 160, 014302. [Google Scholar] [CrossRef] [PubMed]
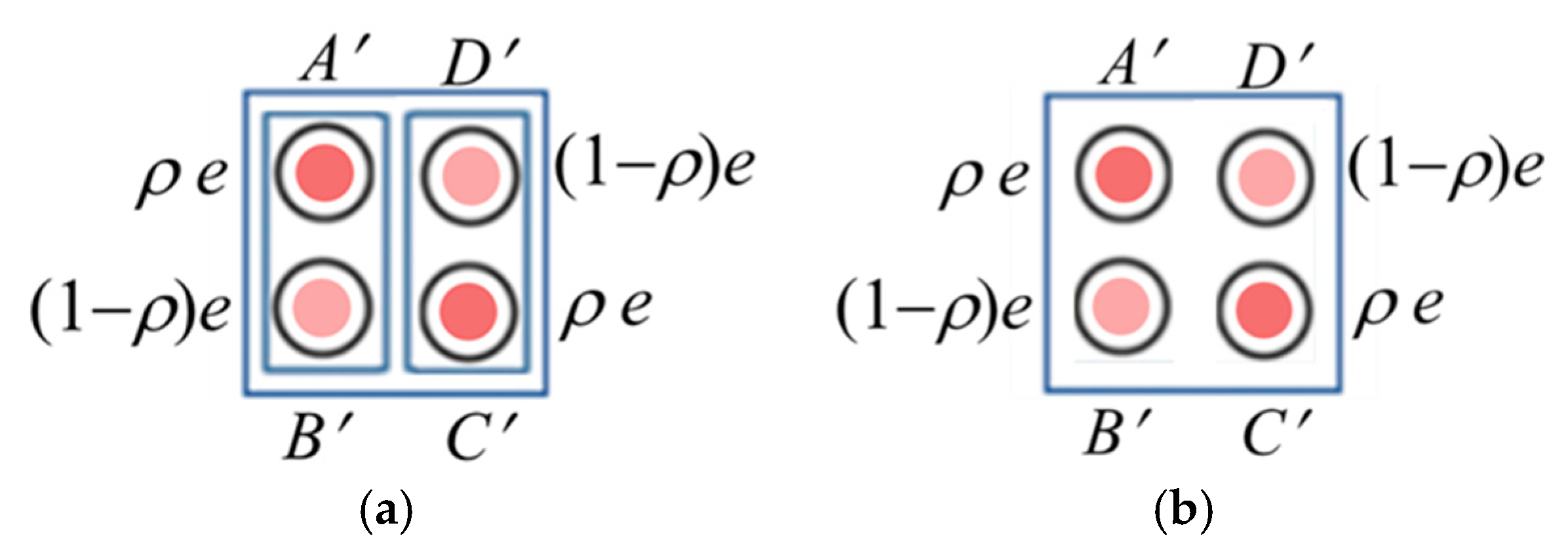


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palii, A.; Zilberg, S.; Tsukerblat, B. Theoretical Hints to Optimize Energy Dissipation and Cell–Cell Response in Quantum Cellular Automata Based on Tetrameric and Bidimeric Cells. Magnetochemistry 2024, 10, 73. https://doi.org/10.3390/magnetochemistry10100073
Palii A, Zilberg S, Tsukerblat B. Theoretical Hints to Optimize Energy Dissipation and Cell–Cell Response in Quantum Cellular Automata Based on Tetrameric and Bidimeric Cells. Magnetochemistry. 2024; 10(10):73. https://doi.org/10.3390/magnetochemistry10100073
Chicago/Turabian StylePalii, Andrew, Shmuel Zilberg, and Boris Tsukerblat. 2024. "Theoretical Hints to Optimize Energy Dissipation and Cell–Cell Response in Quantum Cellular Automata Based on Tetrameric and Bidimeric Cells" Magnetochemistry 10, no. 10: 73. https://doi.org/10.3390/magnetochemistry10100073
APA StylePalii, A., Zilberg, S., & Tsukerblat, B. (2024). Theoretical Hints to Optimize Energy Dissipation and Cell–Cell Response in Quantum Cellular Automata Based on Tetrameric and Bidimeric Cells. Magnetochemistry, 10(10), 73. https://doi.org/10.3390/magnetochemistry10100073









