Study on the Mechanism of Rootstock Damage during Clamping in Watermelon Grafting
Abstract
:1. Introduction
2. Materials and Methods
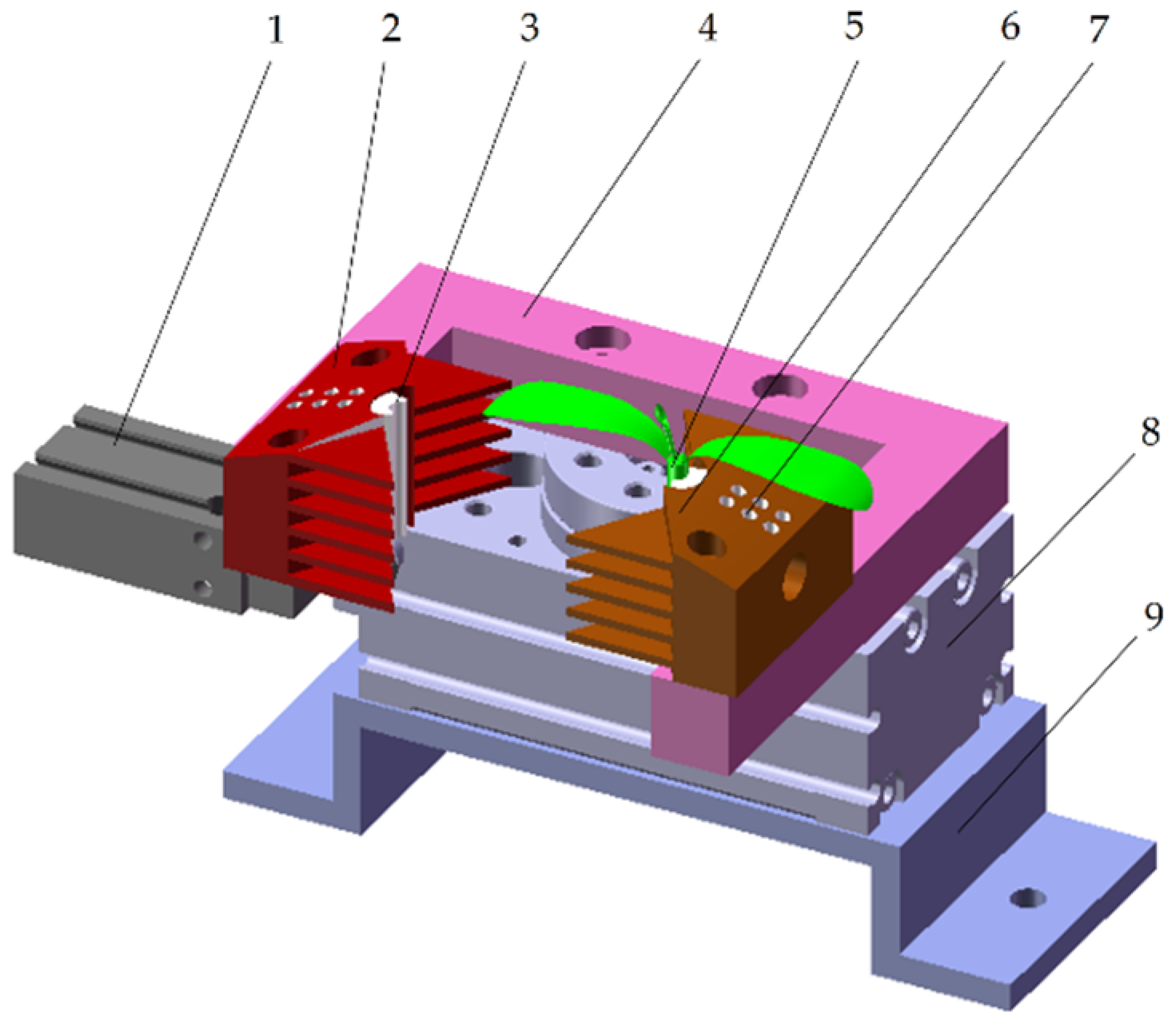
2.1. Rootstock Clamping Mechanism Model
2.1.1. Rootstock Clamping Mechanism
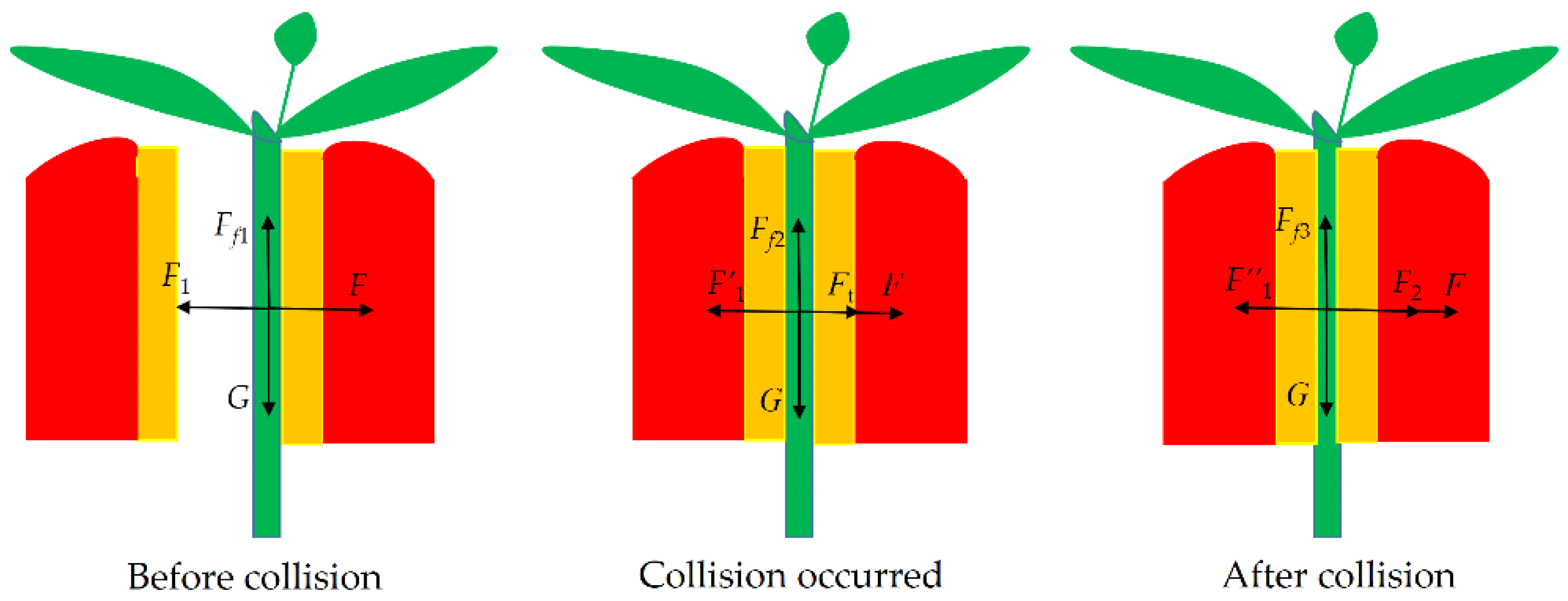
2.1.2. Clamping Process Analysis
- (a)
- Before collision: the cylinder drove clamping block ‘a’ to move toward clamping block ‘b’ at a certain velocity, which is the acceleration stage. At this time, the rootstock stem was closely attached to the inner side of the silicone rubber under the external suction action. The force equation is as follows.
- F1—The supporting force of silicone rubber to the stem, N;
- F—The external suction force, N;
- Ff1—The friction force between silicone rubber and the stem, N;
- G—The rootstock seedlings gravity, N.
- (b)
- Collision occurred: clamping block ‘a’ started to come into contact with the rootstock stem and continued to squeeze, and the silicone rubber deformed under pressure. Silicone rubber is an elastic composite material with nonlinear characteristics, and thus, the force F′1 is a nonuniform variation value. When clamping block ‘a’ collided with clamping block ‘b’, the movement stopped. At this stage, the acceleration of clamping block ‘a’ gradually decreased, and the velocity first increased and then decreased. To prevent damage to the stem under pressure, the stress of the stem should be less than the yield stress of the stem. The force equation on the stem can be expressed asThen,
- Ft—The driving force of the cylinder over time, N;
- S—The contact area between silicone rubber and the stem, m2;
- S0—The contact area between air hole and the stem, m2;
- G—The rootstock seedlings gravity, N;
- σe—Yield stress of the stem, Pa;
- m—Mass of silicone rubber and clamping block ‘a’, kg;
- a—Acceleration of silicone rubber and clamping block ‘a’, m/s2;
- P—Negative pressure, Pa.
- (c)
- After collision: the clamping collision was completed, and the deformation of silicone rubbers reached a stable state. At this time, the force equation is presented below.
- F″1—The supporting force of right silicone rubber to the stem, N;
- F2—The force of left silicone rubber to the stem, N;
- Ff3—The friction force between silicone rubbers and the stem, N.
2.2. Plant Material
2.3. Finite Element Modeling
2.3.1. Geometric Model of Clamping Mechanism
2.3.2. Settings of the Element Type and Material Properties
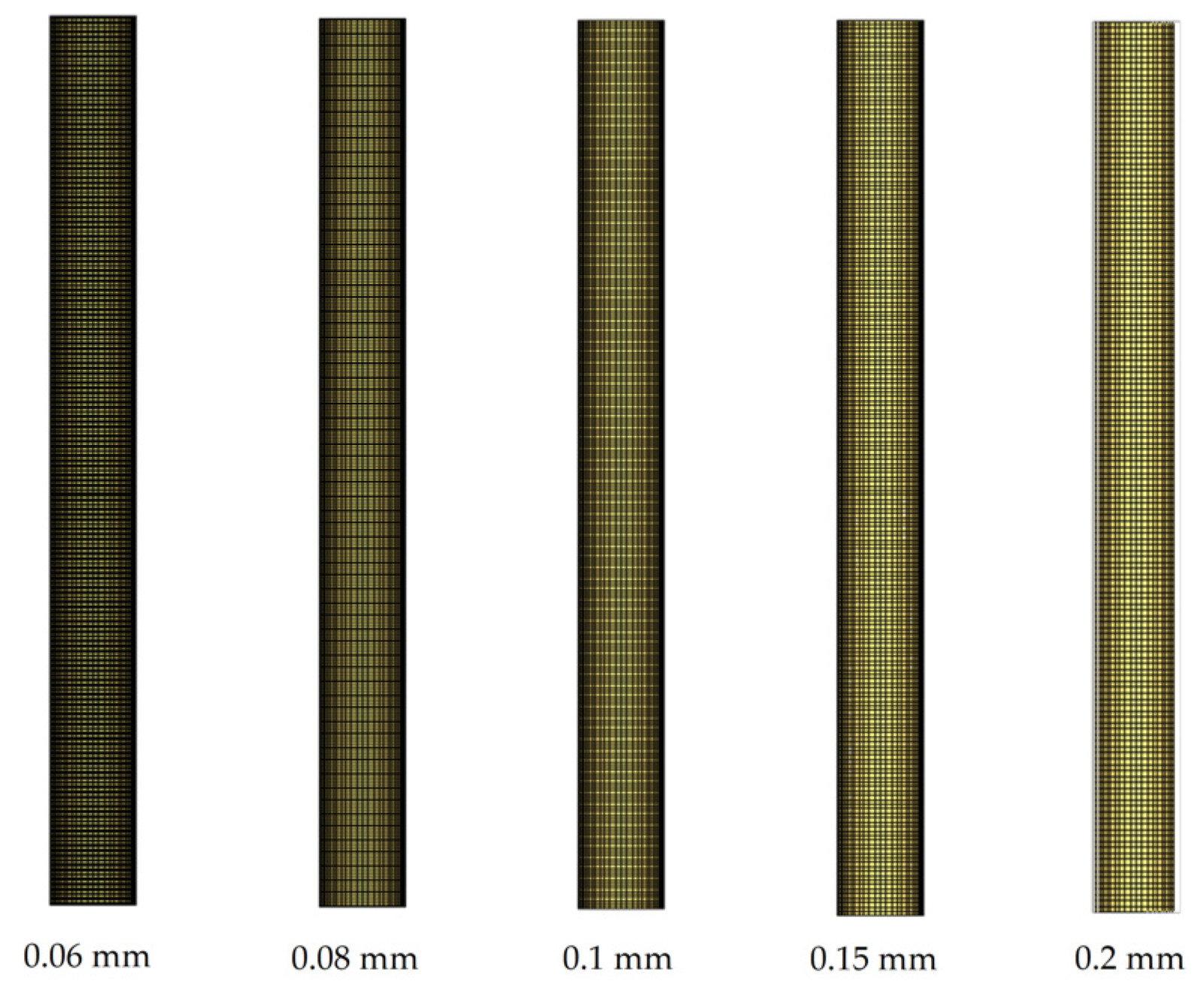
2.3.3. Grid Division
2.3.4. Contact Settings of the Element Type and Material Properties
3. Results and Discussion
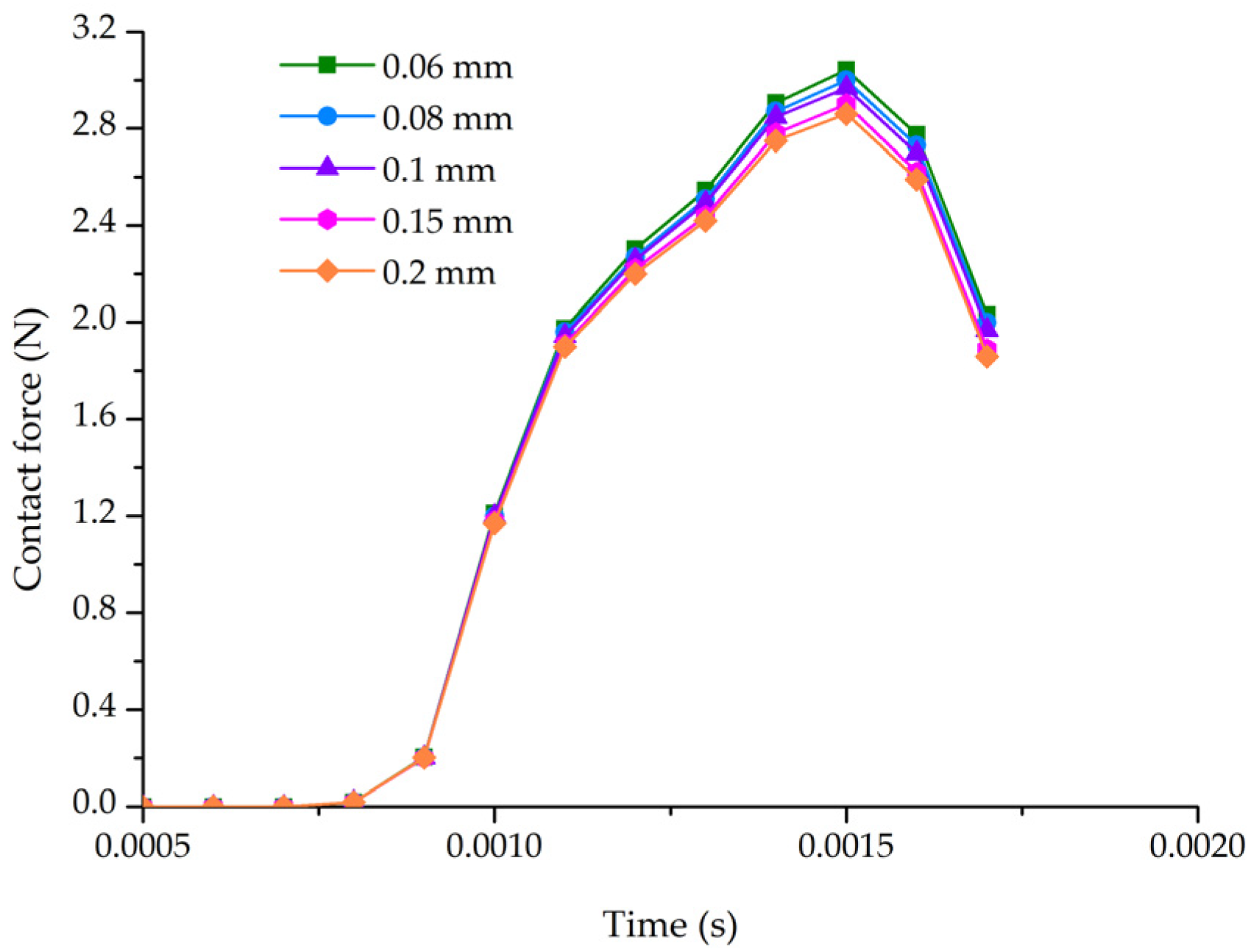
3.1. Grid Independence Validation
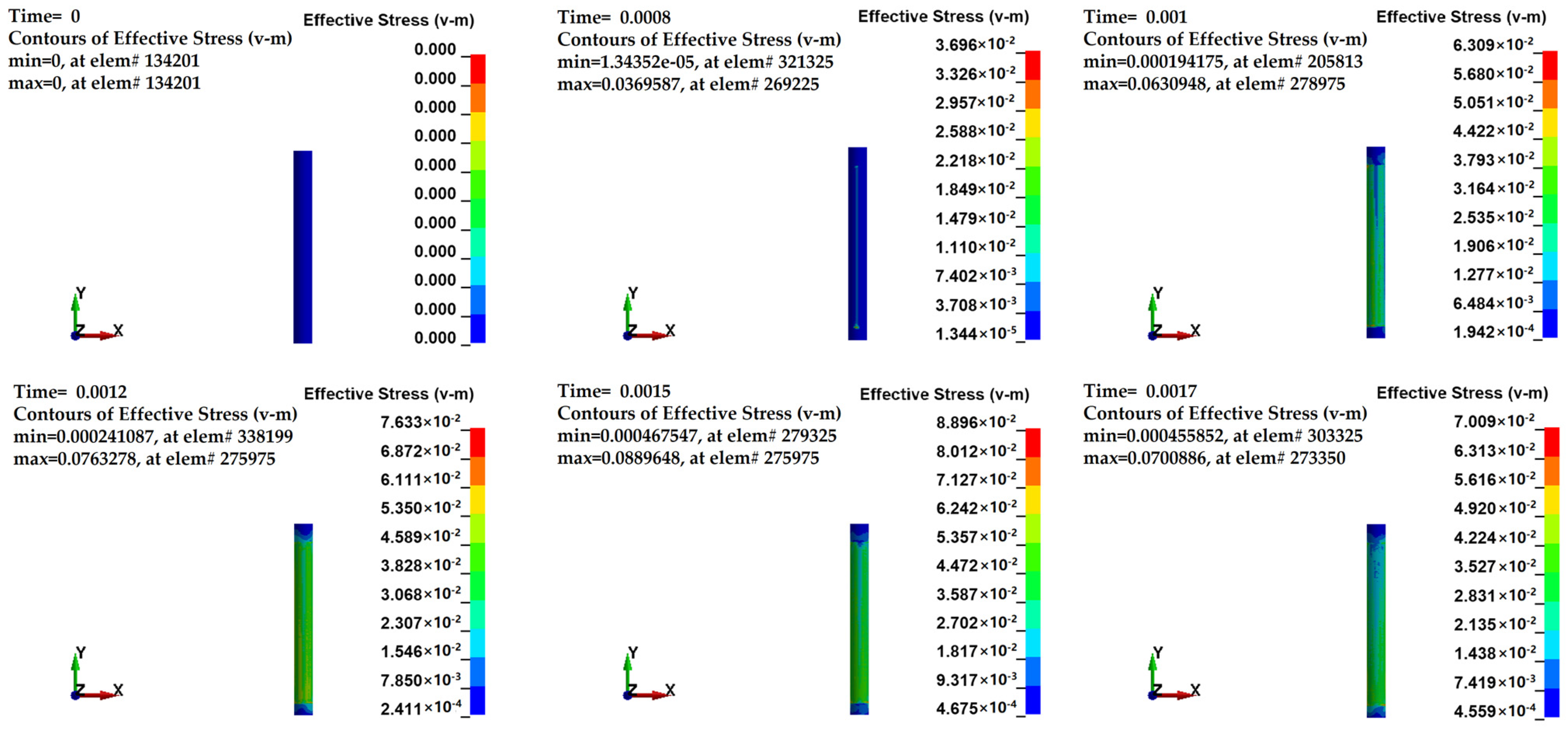
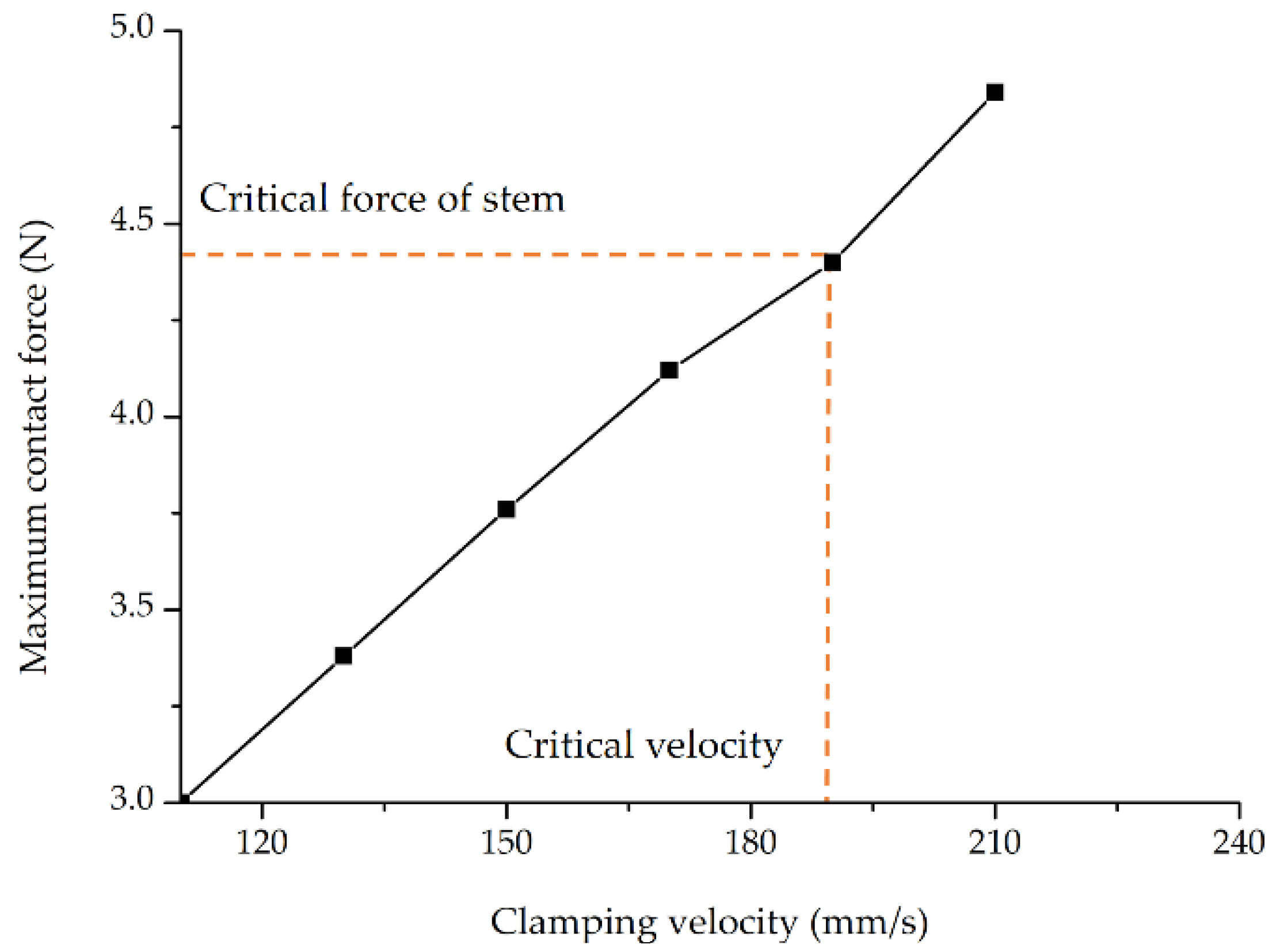
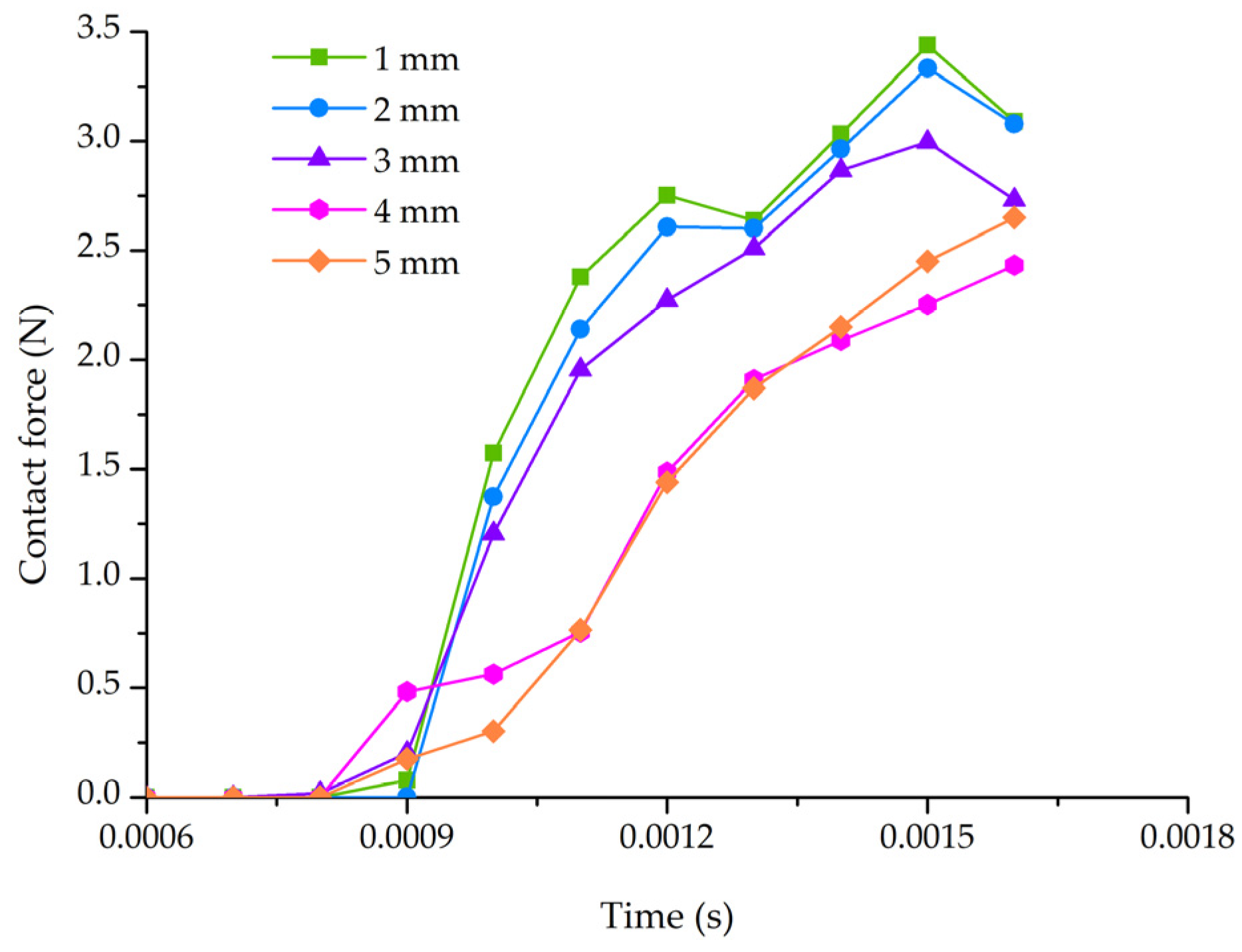
3.2. FE Simulation Results and Discussion
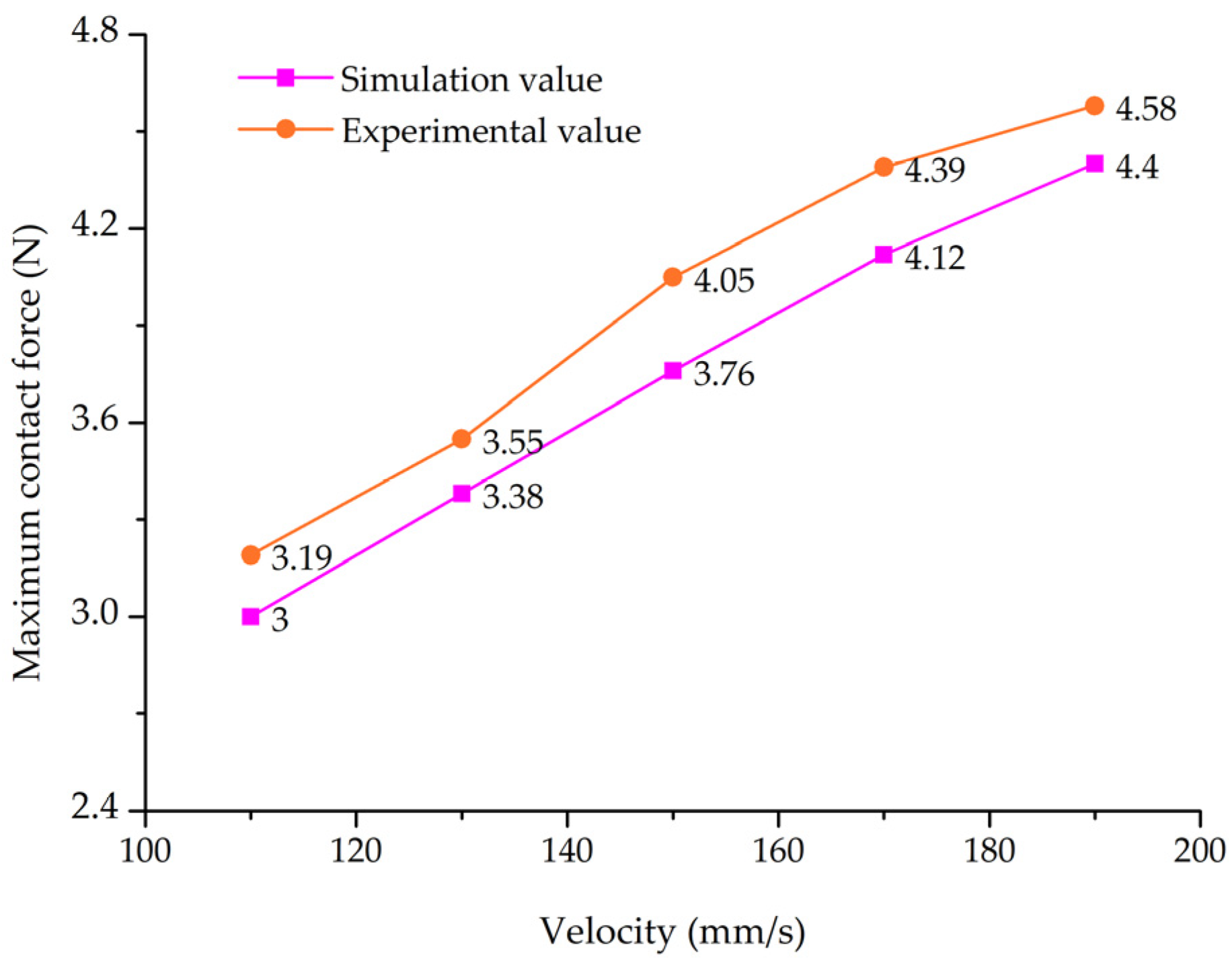
3.3. Test Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aslam, A.; Zhao, S.; Azam, M.; Lu, X.; He, N.; Li, B.; Dou, J.; Zhu, H.; Liu, W. Comparative analysis of primary metabolites and transcriptome changes between ungrafted and pumpkin-grafted watermelon during fruit development. PeerJ 2020, 8, e8259. [Google Scholar] [CrossRef] [PubMed]
- Food and Agriculture Organization (FAO). STAT. 2020. Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 30 December 2021).
- Michielse, C.B.; Rep, M. Pathogen profile update: Fusarium oxysporum. Mol. Plant Pathol. 2009, 10, 311–324. [Google Scholar] [CrossRef] [PubMed]
- Netzer, D.; Weintall, C. Inheritance of resistance in watermelon to race 1 of Fusarium oxysporum f. sp. niveum. Plant Dis. 1980, 64, 853–854. [Google Scholar] [CrossRef]
- Martyn, R.D.; Netzer, D. Resistance to races 0, 1, and 2 of Fusarium wilt of watermelon in Citrullus sp. PI-296341-FR. HortScience 1991, 26, 429–432. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.; Lin, Y.; Wan, Y.; Chen, K.; Huang, J.; Chang, P. Degenerated virulence and irregular development of Fusarium oxysporum f. sp. niveum induced by successive subculture. J. Fungi 2020, 6, 382. [Google Scholar] [CrossRef]
- Rouphael, Y.; Venema, J.; Edelstein, M.; Savvas, D.; Colla, G.; Ntatsi, G.; Ben-Hur, M.; Kumar, P.; Schwarz, D. Grafting as a Tool for Tolerance of Abiotic Stress. Vegetable Grafting: Principles and Practices; Colla, G., Perez-Alfocea, F., Schwarz, D., Eds.; CAB International: Wallingford, UK, 2017; pp. 171–215. [Google Scholar] [CrossRef]
- Aloni, B.; Cohen, R.; Karni, L.; Aktas, H.; Edelstein, M. Hormonal signaling in rootstock scion interactions. Sci. Hortic. 2010, 127, 119–126. [Google Scholar] [CrossRef]
- Zhang, K.; Chu, J.; Zhang, T.; Yin, Q.; Kong, Y.; Liu, Z. Development status and analysis of automatic grafting technology for vegetables. Trans. CSAM 2017, 48, 1–10. [Google Scholar] [CrossRef]
- Lou, J.Z.; Wu, K.; Chen, J.Y.; Ma, G.; Li, J.P. Design and test of self-adaptive stock cotyledons pressing and clamping mechanism for oblique inserted grafting of cucurbitaceous vegetables. Trans. CSAE 2018, 34, 76–82. [Google Scholar] [CrossRef]
- Jiang, K.; Chen, L.; Zhang, Q.; Feng, Q.; Guo, W.; Cao, L. Design and experiment on flexible clamping and conveying mechanism of vegetable grafting robot. Trans. CSAM 2020, 51, 63–71. [Google Scholar] [CrossRef]
- Chu, J.; Zhang, L.; Zhang, T.; Zhang, W.; Wang, L.; Liu, Z. Design and experiment of grafting robot operated by one person for cucurbitaceous seedlings cultivated in plug trays. Trans. CSAM 2017, 48, 7–13. [Google Scholar] [CrossRef]
- Nikara, S.; Ahmadi, E.; Nia, A.A. Finite element simulation of the micromechanical changes of the tissue and cells of potato response to impact test during storage by scanning electron microscopy. Postharvest Biol. Technol. 2020, 164, 111153. [Google Scholar] [CrossRef]
- Lu, R.; Chen, Y. Characterization of nonlinear elastic properties of beef products under large deformation. Trans. ASAE 1998, 41, 163–171. [Google Scholar] [CrossRef]
- Chen, H.; Baerdemaeker, J.D. Modal analysis of the dynamic behavior of pineapples and its relation to fruit firmness. Trans. ASAE 1993, 36, 1439e144. [Google Scholar] [CrossRef]
- Yousefi, S.; Farsi, H.; Kheiralipour, K. Drop test of pear fruit: Experimental measurement and finite element modelling. Biosyst. Eng. 2016, 147, 17–25. [Google Scholar] [CrossRef]
- Li, Z.; Li, P.; Yang, H.; Liu, J. Internal mechanical damage prediction in tomato compression using multiscale finite element models. Int. J. Food Eng. 2013, 116, 639e647. [Google Scholar] [CrossRef]
- Sadrnia, H.; Rajabipour, A.; Jafari, A.; Javadi, A.; Mostofi, Y.; Kafashan, J.; Dintwa, E.; Baerdemaeker, J.D. Internal bruising prediction in watermelon compression using nonlinear models. Int. J. Food Eng. 2008, 86, 272–280. [Google Scholar] [CrossRef]
- Cui, H.; Shen, H. Modeling and simulation of buckling and postbuckling of plant stems under combined loading conditions. Int. J. Appl. Mech. 2011, 3, 119–130. [Google Scholar] [CrossRef]
- Celik, H.K.; Cinar, R.; Yilmaz, D.; Ulmeanu, M.E.; Rennie, A.W.; Akinci, I. Mechanical collision simulation of potato tubers. J. Food Process Eng. 2019, 42, e13078. [Google Scholar] [CrossRef]
- Dintwa, E.; Van, Z.M.; Ramon, H.; Tijskens, E. Finite element analysis of the dynamic collision of apple fruit. Postharvest Biol. Technol. 2008, 49, 260–276. [Google Scholar] [CrossRef]
- Zajaczkowska, U.; Kucharski, S.; Nowak, Z.; Grabowska, K. Morphometric and mechanical characteristics of Equisetum hyemale stem enhance its vibration. Planta 2017, 245, 835–848. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Lou, J.Z.; Li, C.; Li, J.Z. Experimental evaluation of rootstock clamping device for inclined inserted grafting of melons. Agriculture 2021, 11, 736. [Google Scholar] [CrossRef]
- Liu, J.; Bai, X.; Li, P.; Mao, H. Complex collision model in high-speed gripping of fruit. Trans. CSAM 2014, 45, 49–54. [Google Scholar] [CrossRef]
- Carlone, P.; Palazzo, G.S. Finite element analysis of the thermoforming manufacturing process using the hyperelastic Mooney-Rivlin model. In Proceedings of the 6th international conference on Computational Science and Its Applications, Glasgow, UK, 8–11 May 2006. [Google Scholar] [CrossRef]
- Keerthiwansa, R.; Javorik, J.; Kledrowetz, J.; Nekoksa, P. Elastomer testing: The risk of using only uniaxial data for fitting the Mooney-Rivlin hyperelastic-material model. Mater. Tehnol. 2018, 52, 3–8. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Ma, Z.; Zhao, Z.; Wang, C. Theoretical analysis and finite element simulation of a rice kernel obliquely impacted by a threshing tooth. Biosyst. Eng. 2013, 114, 146–156. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Du, D.D. Finite element analysis of dynamic impact damage process of maize kernel based on HyperMesh and LS-DYNA. J. Zhejiang Univ. (Agric. Life Sci.) 2018, 44, 465–475. [Google Scholar] [CrossRef]
- Celik, H.K. Determination of bruise susceptibility of pears (Ankara variety) to impact load by means of FEM-based explicit dynamics simulation. Postharvest Biol. Technol. 2017, 128, 83–97. [Google Scholar] [CrossRef]
- Li, S.; Deng, R. Dynamic simulation and application of colliding process of cam and rolling bearing in circuit breaker. High. Volt. Apparat. 2008, 6, 497e500. [Google Scholar]
- Azimi, N.H.; Karparvarfard, H.; Naderi, B.M.; Rahmanian, K.H. Combined finite element and statistical models for predicting force components on a cylindrical mouldboard plough. Biosyst. Eng. 2019, 186, 168–181. [Google Scholar] [CrossRef]
- Wu, K.; Lou, J.Z.; Li, C.; Luo, W.; Li, C.C.; Li, J.P. Study on the mechanism of rootstock holding damage in watermelon grafting. Agriculture 2021, 11, 1266. [Google Scholar] [CrossRef]
- Zakeri, R.; Moghaddas Tafreshi, S.N.; Dawson, A.R.; Baidya, D.K. Influence of rubber sheet on dynamic response of machine foundations. Constr. Build. Mater. 2020, 274, 121788. [Google Scholar] [CrossRef]
- Chen, X.; Ding, M.; Wang, S.; Luo, Z.; Yang, D. Modeling and analysis on the elastic performance of SMT silicone rubber keypad. In Proceedings of the 18th International Conference on Electronic Packaging Technology (ICEPT), Harbin, China, 16–19 August 2017. [Google Scholar] [CrossRef]



| Density | Poisson Ratio | C01 (Constant) | C10 (Constant) | |
|---|---|---|---|---|
| Silicone rubber | 1380 kg/m3 | 0.49 | 2.04 | −0.38 |
| Density | Modulus of Elasticity | Poisson Ratio | |
|---|---|---|---|
| Clamping block | 1250 kg/m3 | 902.48 MPa | 0.42 |
| Rootstock stem | 1970 kg/m3 | 10.29 MPa | 0.3 |
| Grid Size | 0.06 | 0.08 | 0.1 | 0.15 | 0.2 |
|---|---|---|---|---|---|
| Element amount | 480,000 | 270,000 | 180,000 | 72,000 | 45,000 |
| Node amount | 511,020 | 293,280 | 198,660 | 84,420 | 54,360 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Significant |
|---|---|---|---|---|---|---|
| Velocity | 3.016 | 5 | 0.603 | 12065.286 | 0.007 | Yes |
| Thickness | 0.958 | 4 | 0.240 | 4792.167 | 0.011 | Yes |
| Error | 5 × 10−5 | 1 | ||||
| Total | 138.201 | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Lou, J.; Li, C.; Luo, W.; Li, C.; Li, J. Study on the Mechanism of Rootstock Damage during Clamping in Watermelon Grafting. Horticulturae 2022, 8, 617. https://doi.org/10.3390/horticulturae8070617
Wu K, Lou J, Li C, Luo W, Li C, Li J. Study on the Mechanism of Rootstock Damage during Clamping in Watermelon Grafting. Horticulturae. 2022; 8(7):617. https://doi.org/10.3390/horticulturae8070617
Chicago/Turabian StyleWu, Kang, Jianzhong Lou, Chen Li, Wei Luo, Congcong Li, and Jianping Li. 2022. "Study on the Mechanism of Rootstock Damage during Clamping in Watermelon Grafting" Horticulturae 8, no. 7: 617. https://doi.org/10.3390/horticulturae8070617
APA StyleWu, K., Lou, J., Li, C., Luo, W., Li, C., & Li, J. (2022). Study on the Mechanism of Rootstock Damage during Clamping in Watermelon Grafting. Horticulturae, 8(7), 617. https://doi.org/10.3390/horticulturae8070617






