Abstract
The current mechanical harvesting methods of Lycium barbarum L. are labor intensive and cause too much damage, but vibrating and comb-brushing harvesting can increase the efficiency while minimizing the damage. However, optimizing the main factors and their parameter values of vibrating and comb-brushing harvesting is challenging. To achieve the high-efficiency and low-damage harvesting of L. barbarum, firstly, the mechanical models of the materials used in the experiments were established based on the physical tests. Then, the vibrating and comb-brushing harvesting simulations were conducted based on FEM to acquire the ranges of the parameter values. The effects of the rotating speed, material, and amplitude on the harvesting rate of ripe fruit and harvesting rate of unripe fruit, as well as the damage rate of ripe fruit were determined based on RSM. Finally, the optimized parameters were obtained and verified using the field experiments. The field experiments showed that the harvesting rate of ripe fruit was 85.8%, the harvesting rate of unripe fruit was 10.5%, and the damage rate of ripe fruit was 9.7%. The findings provided the optimal parameter values, which were a design basis for the vibrating and comb-brushing harvesters of L. barbarum.
1. Introduction
Lycium barbarum L. (L. barbarum) is a deciduous shrub [1,2], which is grown as a commercial crop with high economic value [3,4]. Its ripe fruit, when dried, are called goji berries [5]. Goji berries are highly popular due to the health benefits related to their high concentrations of polysaccharides [6]. But the price of goji berries has remained high because of the high cost of harvesting [7]. Therefore, it is necessary to design and develop an efficient L. barbarum harvester [8,9]. Various prototype harvesters have been previously designed for L. barbarum. In total, four types of L. barbarum harvesters have been proposed, i.e., the vibrating [10,11,12,13,14,15,16,17], comb-brushing [1,18,19], shearing [7], and air-flowing harvesters [7]. Based on the field experiments, the vibrating harvester was the most efficient one, but it also caused the most damage [9,14,15,16]. By contrast, the comb-brushing harvester had the lowest efficiency and lowest damage [1,19]. The shearing harvester was both inefficient and difficult to mechanize [7,19]. Similarly, the air-flowing harvester had not overcome the problems relating to the air-flow stability and field passability [7,19]. Combining methods to efficiently harvest L. barbarum have also been tried, taking the advantage of high efficiency of vibrating and low damage of comb-brushing. Recently, Xu et al. and Chen et al. tried to design a vibrating and comb-brushing harvester and optimized the mechanical structural parameters, respectively. Their efforts demonstrated that the combined harvesting approach did indeed improve the overall harvesting performance (i.e., high-efficiency and low-damage harvesting L. barbarum), and they suggested that the principle parameters not affected by changing the mechanical structure should be optimized. To ensure that the overall harvesting performance is optimized, it is necessary to identify the main factors affecting the vibrating and comb-brushing harvesting process and determine their parameter values. This effort would provide a design on which future research and development of the vibrating and comb-brushing harvester of L. barbarum could be based.
In this study, to optimize the vibrating and comb-brushing harvesting, its main factors and their parameter values were obtained based on the finite element method (FEM) and response surface methodology (RSM). The mechanical models of the materials used in the experiments were established based on the physical tests. The vibrating and comb-brushing harvesting simulations were conducted based on FEM to acquire the ranges of the parameter values. Then, based on RSM, the effects of the rotating speed, material, and amplitude on the harvesting rate of ripe fruit, harvesting rate of unripe fruit, and damage rate of ripe fruit were determined. The optimized parameters were obtained and verified using the field experiments. Such findings could provide the optimal parameter values, which were a design basis for the vibrating and comb-brushing harvesters of L. barbarum.
2. Materials and Methods
2.1. Physical Tests Using the Universal Testing Machine
The vibrating and comb-brushing harvesting simulations were conducted before the parameter optimization experiments so that suitable ranges of the parameter values could be obtained. This allowed the number of experiments to be greatly reduced. The mechanical properties (i.e., the density, elastic (shear) modulus, and Poisson’s ratio) were essential for the simulations. However, the mechanical properties of different materials are different. Therefore, establishing the mechanical models of the materials (i.e., the fruit branch, fruit stem, fruit, and rods) used in the experiments was fundamental. The mechanical properties of the fruit stem and fruit were obtained from the previous studies [5,20], so only the mechanical properties of the fruit branch and rods needed to be measured. The densities were calculated by measuring the masses and volumes. An electronic scale (type: SA-120; manufactured by Shinko Denshi Co., Ltd., Tokyo, Japan) was used to measure the masses. An electronic vernier caliper (type: CD-15APX; manufactured by Mitutoyo Corporation, Kanagawa, Japan) was used to obtain the measurements required to calculate the volumes. The Poisson’s ratios were obtained from the relevant references [9,21]. However, the moduli should be calculated from the stress–strain curves obtained from the physical tests. Hence, an electronic universal testing machine (type: AG-1; manufactured by Shimadzu Corporation, Kyoto, Japan) was used to perform all physical tests. A simplified elastic model was used to represent the rods, and one of the essential parameters of the rods was the elastic moduli. Nevertheless, there are nine engineering constants for the orthotropic materials [21]. Because the fruit branch is transverse isotropic [22], there are five independent engineering constants, and these constants could be calculated based on the references [21,22,23].
The size of the fruit branch should be processed to comply with the requirements according to the references [9,24,25]. The deflection increment of the endpoint was calculated based on the reference [9]. Additionally, all cutting surfaces were honed and polished before the tests. To obtain the accurate stress–strain curves, 1 mm/min was selected as the speed of the compression tests and 0.5 mm/min was selected as the speed of the three-point bend tests. To eliminate random errors, five fruit branches were tested. According to the standard deviation analysis, the differences among the five fruit branches were small. Therefore, the mean values of the test results of the five fruit branches were used as the mechanical properties in the simulations.
2.2. Vibrating and Comb-Brushing Harvesting Simulations Based on FEM
The vibrating and comb-brushing harvesting simulations based on FEM were performed in the Abaqus software to acquire the theoretically suitable ranges of the parameter values based on the obtained mechanical properties. The three-dimensional (3D) models of the fruit branch, fruit stem, fruit, and rods were constructed and assembled in the CATIA version-5 software. The assembled 3D models were imported into the Part module. The mechanical properties of the materials were imported into the Property module. The gravitational acceleration was applied to the 3D models in the Load module with the head of the fruit branch held stationary. The 3D models were meshed in the Mesh module, as shown in Figure 1.
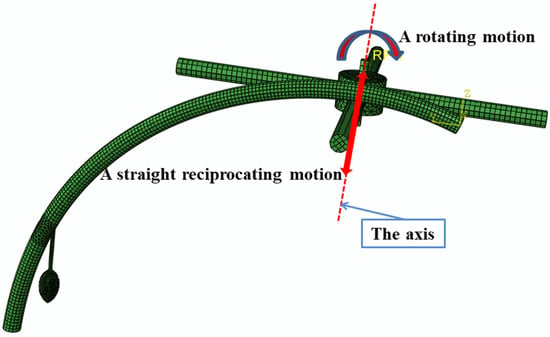
Figure 1.
The meshed 3D models.
According to the previous studies, the resonance of the branch would occur at the vibrating frequency of 2 Hz [9]. Thus, the vibrating frequency of 2 Hz was selected for the simulations. Based on the pre-tests, the three factors (i.e., the rotating speed, material, and amplitude) all significantly affected the overall vibrating and comb-brushing harvesting performance. As shown in Figure 1, the mechanism was applied by a rotating motion around the axis and a straight reciprocating motion along the axis. It was expected that the fruit could fall off when the mechanism hit the fruit branch. For this reason, the simulations were repeated with different parameter values for each of the three factors. The result of one simulation (the rotating speed was 180 r/min, the material was the silica gel, and the amplitude was 20 mm) is shown in Figure 2.
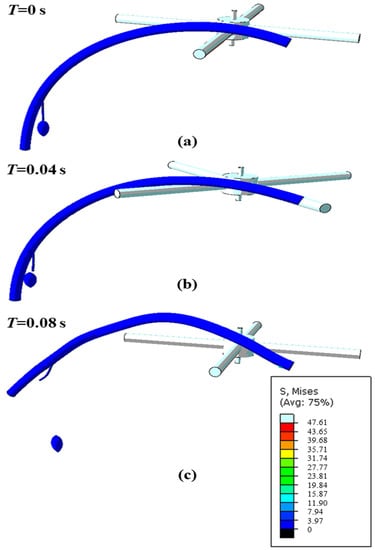
Figure 2.
The result of one simulation (the rotating speed was 180 r/min, the material was the silica gel, and the amplitude was 20 mm) at 0 s (a), 0.04 s (b), and 0.08 s (c).
After completing all the simulations, the results indicated that the fruit could fall off at rotating speeds ranging from 120 to 240 r/min and amplitudes between 10 and 30 mm, and using the wood, silica gel, or polypropylene materials.
2.3. Parameter Optimization Experiments
The simulations provided the following suitable ranges for the three factors: 120–240 r/min for the rotating speed (X1), the wood, silica gel, or polypropylene for the material (X2), and 10–30 mm for the amplitude (X3). For the identification, the wood, silica gel, and polypropylene materials were denoted 1, 2, and 3, respectively. Experiments were then conducted to further optimize the parameter values within these ranges using a vibrating and comb-brushing harvesting device, which is shown in Figure 3.

Figure 3.
The vibrating and comb-brushing harvesting device.
The rotating speed was controlled by the motor and measured with the tachometer (type: DT2236B; manufactured by Shenzhen Sanpo Instrument Co., Ltd., Shenzhen, China). The amplitude was adjusted by changing the stroke of the slider-crank mechanism and measured with the electronic vernier caliper. The goal while harvesting L. barbarum is to maximize the amount of harvested ripe fruit while minimizing the damage. Furthermore, the harvesting of unripe fruit should be minimized to avoid impacting the yield. Therefore, based on the references [16,19], the harvesting rate of ripe fruit (Y1), harvesting rate of unripe fruit (Y2), and damage rate of ripe fruit (Y3) were selected as the evaluation indexes for the experiments and calculated according to the following three Equations (1)–(3).
where N1 is the amount of harvested ripe fruit; N2 is the amount of unharvested ripe fruit; N3 is the amount of harvested unripe fruit; N4 is the amount of unharvested unripe fruit; and N5 is the amount of damaged harvested ripe fruit.
A quadratic orthogonal rotation design with three factors and three levels was used in the experiments. The experimental designs were created, and analyses were performed using the Design-expert software. The codes of the factors are listed in Table 1 and the experimental schemes and results are shown in Table 2. Seventeen tests were performed in the experiments. Considering the harvesting efficiency, the harvesting time of each test was 10 s.

Table 1.
The codes of the factors.

Table 2.
The experimental schemes and results.
3. Results
3.1. Establishing the Mechanical Models
3.1.1. Densities
According to the definition of density, the densities of the materials used in the experiments were calculated and are listed in Table 3 and Table 4.

Table 3.
The mechanical properties of the fruit branch.

Table 4.
The mechanical properties of the fruit stem, fruit, and rods.
3.1.2. Elastic Moduli
The elastic moduli of the rods were directly obtained from the stress–strain curves. The stresses and strains were calculated based on the following two Equations (4) and (5) and references [5,26].
where σ is the stress of the sample, MPa; F is the load of the test, N; A0 is the cross-sectional area of the sample, mm2; ε is the strain of the sample, mm·mm−1; and ∆l is the length change of the sample, mm.
The elastic modulus was determined based on the following Equation (6) and references [20,27].
Based on the compression tests and references [20,26,27], the stress–strain curves of the fruit branch and rods were determined. Based on the Equations (4)–(6), the elastic moduli of the rods were calculated and are listed in Table 4. Meanwhile, the radial elastic modulus and axial elastic modulus of the fruit branch were also calculated. The results are shown in Table 3.
3.1.3. Shear Moduli
According to the obtained radial elastic modulus, the axial shear modulus of the fruit branch was calculated. To obtain the radial shear modulus of the fruit branch, the three-point bend tests of the fruit branch were conducted, which provided the load–displacement curves of the fruit branch according to the test method [21,25]. The radial shear modulus of the fruit branch was then calculated according to the reference [9]. The results are listed in Table 3.
3.1.4. Poisson’s Ratios
According to the reference [21], the Poisson’s ratio of the rods and Poisson’s ratio in the XY plane of the fruit branch were assumed to be 0.3. The Poisson’s ratios in the YZ and XZ plane of the fruit branch were then calculated and are listed in Table 3.
3.2. Regression Analyses
To determine the effects of the three factors on the evaluation indexes, the regression analyses of the experimental results were conducted using the Design-expert software. The regression model of the harvesting rate of ripe fruit (response) using the codes of the factors as the variables is as follows.
The analysis of variance (ANOVA) of the harvesting rate of ripe fruit was performed, as shown in Table 5. The model was significant (p = 0.0001), and X1, X2, X3, X12, and X22 all had the significant effects on the harvesting rate of ripe fruit (p < 0.05). The lack-of-fit was not significant (p = 0.2415), indicating that none of the factors were irrelevant.

Table 5.
ANOVA of the harvesting rate of ripe fruit.
The regression model of the harvesting rate of unripe fruit (response) using the codes of the factors as the variables is as follows.
The ANOVA of the harvesting rate of unripe fruit was performed, as shown in Table 6. The model was significant (p = 0.0001), and X1, X2, X3, X12, X22, and X32 all had the significant effects on the harvesting rate of unripe fruit (p < 0.05). The lack-of-fit was not significant (p = 0.8284), indicating that none of the factors were irrelevant.

Table 6.
ANOVA of the harvesting rate of unripe fruit.
The regression model of the damage rate of ripe fruit (response) using the codes of the factors as the variables is as follows.
The ANOVA of the damage rate of ripe fruit was performed, as shown in Table 7. The model was significant (p = 0.0378), and X2 and X3 both had the significant effects on the damage rate of ripe fruit (p < 0.05). The lack-of-fit was not significant (p = 0.9719), indicating that none of the factors were irrelevant.

Table 7.
ANOVA of the damage rate of unripe fruit.
3.3. Response Surface Analyses
RSM was a common tool to analyze the effects of each factor on the evaluation indexes and also used in this study [2,5,16,19]. The horizontal and vertical coordinates represented one factor, respectively. The depth of the color represented the size of one evaluation index value. The response surfaces of the harvesting rate of ripe fruit affected by the factors are shown in Figure 4. As shown in Table 5, the rotating speed and material were equal in having the largest effect on the harvesting rate of ripe fruit, while the effect of the amplitude was the smallest. None of the interaction effects between combinations of the factors had the significant effect on the harvesting rate of ripe fruit. As the rotating speed increased, the harvesting rate of ripe fruit initially increased rapidly, but at a certain point, the increase slowed (Figure 4a). As the amplitude increased, the harvesting rate of ripe fruit slowly increased (Figure 4b). As for materials, the wood returned the lowest of the harvesting rate of ripe fruit, while the silica gel and polypropylene were almost equal (Figure 4c).
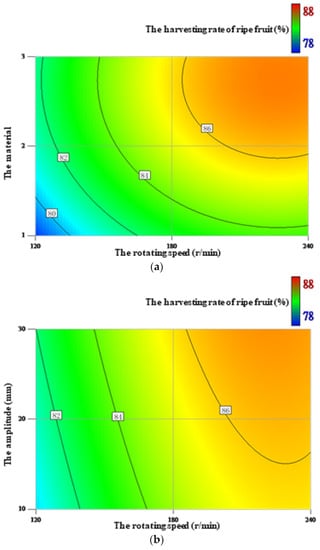
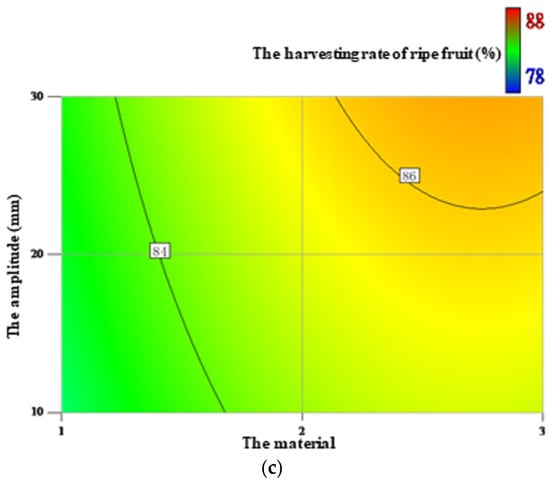
Figure 4.
The response surfaces of the harvesting rate of ripe fruit affected by the rotating speed and material (a), the rotating speed and amplitude (b), and the material and amplitude (c).
The response surfaces of the harvesting rate of unripe fruit affected by the factors are shown in Figure 5. As shown in Table 6, the rotating speed and material were equal in having the biggest effect on the harvesting rate of unripe fruit, while the amplitude had the smallest effect. The interactions between each combination of the factors did not significantly affect the harvesting rate of unripe fruit. Figure 5a shows that, as the rotating speed increased, the harvesting rate of unripe fruit initially increased slowly, but then increased rapidly at higher speeds. Similarly, as shown in Figure 5b, as the amplitude increased, the harvesting rate of unripe fruit initially increased slowly and then increased rapidly. Finally, as seen in Figure 5c, the harvesting rate of unripe fruit was highest with the polypropylene material, while the harvesting rate of unripe fruit using the wood and silica gel were nearly the same.
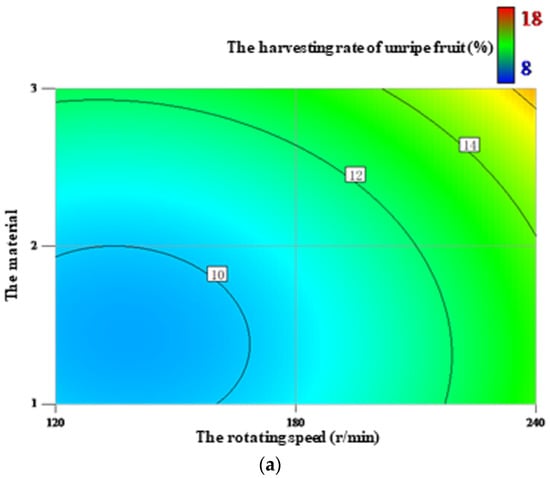
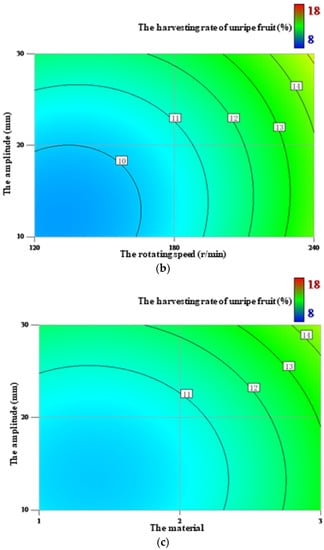
Figure 5.
The response surfaces of the harvesting rate of unripe fruit affected by the rotating speed and material (a), the rotating speed and amplitude (b), and the material and amplitude (c).
The response surfaces of the damage rate of ripe fruit affected by the factors are shown in Figure 6. As shown in Table 7, the material had the largest influence on the damage rate of ripe fruit, followed by the amplitude and rotating speed, in that order. The interactions between each combination of the factors did not significantly influence the damage rate of ripe fruit. As shown in Figure 6a, as the rotating speed increased, the damage rate of ripe fruit initially remained unchanged, but then increased rapidly. Figure 6b shows that, as the amplitude increased, the damage rate of ripe fruit decreased slowly at first, but then increased rapidly. Finally, as shown in Figure 6c, the damage rate of ripe fruit was highest when the polypropylene was used, followed by the silica gel and wood.
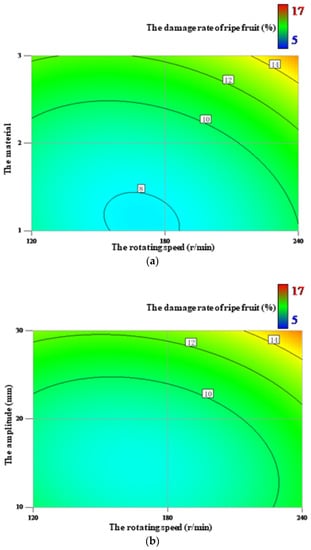
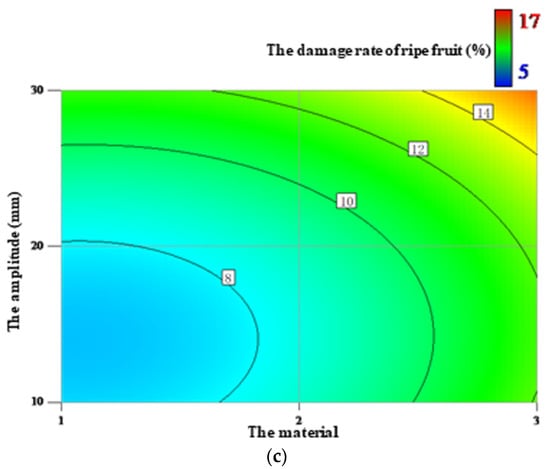
Figure 6.
The response surfaces of the damage rate of ripe fruit affected by the rotating speed and material (a), the rotating speed and amplitude (b), and the material and amplitude (c).
With the goal of maximizing the harvesting rate of ripe fruit while minimizing the harvesting rate of unripe fruit and damage rate of ripe fruit, these experiments showed that the optimal parameters were a rotating speed of 180 r/min, using the silica gel, an amplitude of 15 mm.
3.4. Verification Using the Field Experiments
The field experiments, as shown in Figure 7, were conducted to verify that the optimized parameters were indeed the best. The fruit branch before harvesting and fruit branch after harvesting were shown in Figure 7a and Figure 7b, respectively. The harvested fruit was shown in Figure 7c. All experimental tests were repeated 10 times to reduce the impact of random errors. The field experiments showed that the harvesting rate of ripe fruit was 85.8%, the harvesting rate of unripe fruit was 10.5%, and the damage rate of ripe fruit was 9.7%.

Figure 7.
The field experiment before harvesting (a) and after harvesting (b) and the harvested fruit (c).
4. Discussion
For this method of harvesting L. barbarum by vibrating and comb-brushing, only Xu et al. and Chen et al. have conducted relevant experiments. Xu et al. found that the best combination was a comb brush speed of 80 r/min, disc rotation speed of 100 r/min, and vibration amplitude of 80 mm for their vibrating and comb-brushing harvester. The harvest efficiency was 13.12 kg/h using this harvester. Chen et al. proposed that the best combination was determined to be a revolving speed of comb brush of 64.52 r/min, revolving speed of cam of 29.68 r/min, and with the straight tooth as the style of comb brush. Using the equivalent substitution, it was seen that the values of their factors were consistent with the results obtained in this study in terms of magnitude. In addition, in both cases, the harvesting rate of ripe fruit was more than 80%, and both the harvesting rate of unripe fruit and damage rate of ripe fruit were less than 15%. These field experiments indicated that the high-efficiency and low-damage harvesting of L. barbarum could be achieved using the vibrating and comb-brushing harvesting. However, the parameters obtained in the previous studies were those of mechanical structure. They would be changed due to the change of mechanical structure. For this study, the parameters that were optimized here were principle parameters, meaning they are not affected by changing mechanical structure. Our study indicated that the key design parameters of a vibrating and comb-brushing harvester of L. barbarum could be determined before designing. The obtained results in this study provided the optimal parameter values, which were a design basis for the vibrating and comb-brushing harvesters of L. barbarum. In the future, a vibrating and comb-brushing harvester of L. barbarum will be designed based on the optimal parameter values (i.e., a rotating speed of 180 r/min, using the silica gel, with an amplitude of 15 mm) to achieve the goal of high-efficiency and low-damage harvesting of L. barbarum.
5. Conclusions
In this study, to optimize the vibrating and comb-brushing harvesting, its main factors and their parameter values were obtained based on the FEM and RSM. The mechanical models of the materials used in the experiments were established based on the physical tests. The vibrating and comb-brushing harvesting simulations were conducted based on FEM, and the results indicated that the fruit could fall off at rotating speeds ranging from 120 to 240 r/min and amplitudes between 10 and 30 mm, and using the wood, silica gel, or polypropylene materials. Furthermore, the optimized parameters, i.e., a rotating speed of 180 r/min, using the silica gel, an amplitude of 15 mm, were obtained based on RSM and verified using the field experiments. The field experiments showed that the harvesting rate of ripe fruit was 85.8%, the harvesting rate of unripe fruit was 10.5%, and the damage rate of ripe fruit was 9.7%. The findings provided the optimal parameter values, which were a design basis for the vibrating and comb-brushing harvesters of L. barbarum. Using the knowledge earned in this study, our future work will focus on designing a vibrating and comb-brushing harvester of L. barbarum with high efficiency and low damage.
Author Contributions
Conceptualization, J.Z. (Jian Zhao), T.M., T.I., S.T. and J.C.; methodology, J.Z. (Jian Zhao), T.M., Y.C., Q.C. and Z.G.; software, J.Z. (Jian Zhao) and G.H.; validation, J.Z. (Jian Zhao), Z.W., J.Z. (Jianguo Zhou) and M.W.; investigation, J.Z. (Jian Zhao), T.M., T.I., S.T. and J.C.; writing—original draft preparation, J.Z. (Jian Zhao); writing—review and editing, T.M., T.I., S.T. and J.C.; visualization, J.Z. (Jian Zhao), T.M. and T.I.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research and APC were funded by the National Key Research and Development Program of China, grant number 2018YFD0701102. The authors also appreciate the financial support provided by the China Scholarship Council.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, L.; Chen, J.; Wu, G.; Yuan, Q.; Ma, S.; Yu, C.; Duan, Z.; Xing, J.; Liu, X. Design and operating parameter optimization of comb brush vibratory harvesting device for wolfberry. Trans. CSAE 2018, 34, 75–82. [Google Scholar] [CrossRef]
- Zhao, J.; Sugirbay, A.; Liu, F.; Chen, Y.; Hu, G.; Zhang, E.; Chen, J. Parameter optimization of winnowing equipment for machine-harvested Lycium barbarum L. Span. J. Agric. Res. 2019, 17, e0203. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Zhao, J.; Chen, J. Recognition of the position of Chinese wolfberry branches under the artificial background. IFAC-PapersOnLine 2018, 51, 321–325. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, W.; Qureshi, W.S.; Gao, C.; Zhang, C.; Li, W. Autonomous navigation for a wolfberry picking robot using visual cues and fuzzy control. Inf. Process. Agric. 2020, 8, 15–26. [Google Scholar] [CrossRef]
- Zhao, J.; Sugirbay, A.; Chen, Y.; Zhang, S.; Liu, F.; Bu, L.; Wang, Z.; Chen, J. FEM explicit dynamics simulation and NIR hyperspectral reflectance imaging for determination of impact bruises of Lycium barbarum L. Postharvest Biol. Technol. 2019, 155, 102–110. [Google Scholar] [CrossRef]
- Amagase, H.; Farnsworth, N.R. A review of botanical characteristics, phytochemistry, clinical relevance in efficacy and safety of Lycium barbarum fruit (Goji). Food Res. Int. 2011, 44, 1702–1717. [Google Scholar] [CrossRef]
- Wang, J.; Meng, S.; Xiao, H.; Zhao, Y.; Zhou, H. Research on Mechanized Harvesting Methods of Lycium barbarum Fruit. IFAC-PapersOnLine 2018, 51, 223–226. [Google Scholar] [CrossRef]
- Zhou, B.; He, J. Design of simulate hand wolfberry picking machine. Trans. CSAE 2010, 26 (Supp. 1), 13–17. [Google Scholar] [CrossRef]
- Zhao, J.; Tsuchikawa, S.; Ma, T.; Hu, G.; Chen, Y.; Wang, Z.; Chen, Q.; Gao, Z.; Chen, J. Modal Analysis and Experiment of a Lycium barbarum L. Shrub for Efficient Vibration Harvesting of Fruit. Agriculture 2021, 11, 519. [Google Scholar] [CrossRef]
- So, J.D. Vibration Characteristics of Boxthorn (Lycium chinense Mill) Branches. Appl. Eng. Agric. 2001, 17, 755–760. [Google Scholar] [CrossRef]
- So, J.D. Vibratory Harvesting Machine for Boxthorn (Lycium chinense Mill) Berries. Trans. ASAE 2003, 46, 211–221. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, H.; Ding, W.; Mei, S. Machanism simulation analysis and prototype experiment of Lycium barbarum harvest by vibration mode. Trans. CSAE 2015, 31, 20–28. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, M.; Zhang, J.; Li, W. Design and experiment of vibrating wolfberry harvester. Trans. CSAM 2018, 49, 97–102. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Han, B.; Chen, J. Research on laws of wolfberry dropping based on high-speed camera. J. Agric. Mech. Res. 2018, 40, 166–170. [Google Scholar] [CrossRef]
- Wang, Y. Research on Key Technology of Wolfberry Vibration Harvest. Master’s Thesis, Northwest A&F University, Yangling, China, 2018. [Google Scholar]
- Zhao, J.; Chen, Y.; Wang, Y.; Chen, J. Experimental research on parameter optimization of portable vibrating and harvesting device of Chinese wolfberry. J. Agric. Mech. Res. 2019, 41, 176–182. [Google Scholar] [CrossRef]
- He, M.; Kan, Z.; Li, C.; Wang, L.; Yang, L.; Wang, Z. Mechanism analysis and experiment on vibration harvesting of wolfberry. Trans. CSAE 2017, 33, 47–53. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Tan, Y.; Li, W. Optimal design and experiment on variable pacing combing brush picking device for Lycium barbarum. Trans. CSAM 2018, 49, 83–90. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, J.; Chen, Y.; Bu, L.; Hu, G.; Zhang, E. Design and experiment on vibrating and comb brushing harvester for Lycium barbarum. Trans. CSAM 2019, 50, 152–161. [Google Scholar] [CrossRef]
- Zhao, J.; Ma, T.; Inagaki, T.; Chen, Q.; Gao, Z.; Sun, L.; Cai, H.; Chen, C.; Li, C.; Zhang, S.; et al. Finite Element Method Simulations and Experiments of Detachments of Lycium barbarum L. Forests 2021, 12, 699. [Google Scholar] [CrossRef]
- Shen, C.; Li, X.; Tian, K.; Zhang, B.; Huang, J.; Chen, Q. Experimental analysis on mechanical model of ramie stalk. Trans. CSAE 2015, 31, 26–33. [Google Scholar] [CrossRef]
- Wang, Y. Abaqus Analysis User’s Guide: Materials Volume, 1st ed.; China Machine Press: Beijing, China, 2018; pp. 27–28. [Google Scholar]
- Shi, N. Peeling Method of Cotton Stalk and Development of Rubbing Peeling Machine. Ph.D. Thesis, Northwest A&F University, Yangling, China, 2018. [Google Scholar]
- Wu, J.; Huang, Y.; Wang, Y.; Wang, W. Study on axial compression properties of cotton stalks. J. Agric. Mech. Res. 2004, 26, 148–149, 152. [Google Scholar] [CrossRef]
- The State General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China; China National Standardization Administration Commission. Test Method for Flexural Properties of Sandwich Constructions; National Standards of the People’s Republic of China: Beijing, China, 2005; pp. 1–9. [Google Scholar]
- Celik, H.K. Determination of bruise susceptibility of pears (Ankara variety) to impact load by means of FEM-based explicit dynamics simulation. Postharvest Biol. Technol. 2017, 128, 83–97. [Google Scholar] [CrossRef]
- Shen, C.; Chen, Q.; Li, X.; Zhang, B.; Huang, J.; Tian, K. Test and analysis of axial compressive mechanical properties for ramie stalk. Acta Agric. Univ. Zhejiangensis 2016, 28, 688–692. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).