Advances in Growing Degree Days Models for Flowering to Harvest: Optimizing Crop Management with Methods of Precision Horticulture—A Review

Abstract

Temperature plays a vital role in plant metabolism, and effective crop temperature appears to be influenced by variables related to climate change. While extreme weather events are widely discussed, the effects of moderate temperature changes pose consistent yet underexplored challenges for farmers. The “growing degree days” (GDD) also termed “heat unit”, is the most widely used approach in agricultural and ecological studies to quantify the relationship between temperature and plant development. This review provides a comprehensive examination of GDD methodology as applied to horticultural crop production, specifically from initial fruit development to fruit maturity, and postharvest. It is the first integrated synthesis of the conceptual evolution, methodological refinement, and broad application of GDD, thereby highlighting the need to optimize GDD approaches in light of emerging technological tools. While the GDD model is valuable for predicting crop development based on heat accumulation, it has limitations in capturing the effects of other environmental factors. Additionally, air temperature may not provide precise data on each plant organ. Recent advances in remote sensing, such as the integration of thermal imaging, RGB cameras, and lidar have enabled the measurement of spatially resolved temperature distribution within crop canopies, including fruit surface temperature. Recent advances, highlighted in the literature, suggest that integrating sensor innovations with machine learning approaches holds high potential for improving the precision of modeling temperature-dependent growth responses and their interactions with other environmental variables. By addressing these challenges and expanding its applications, GDD can continue to serve as an essential tool in promoting sustainable horticultural practices and adapting to global warming.

1. Introduction

Climate change is one of the biggest challenges that global agriculture is facing in the 21st century. Under projected climate scenarios, the air temperature is expected to rise, potentially shifting growing seasons—either shortening, extending, or altering their onset and end [1,2]. Global radiation, temperature, and precipitation are the main climatic factors that affect plant phenology; and temperature is considered the most important element, influencing the growth and development of crops [3,4]. Climate change is directly or indirectly linked to other indicators such as soil temperature, photoperiod, and apparent solar radiation [5]. Changes in ambient temperature, whether moderate or extreme, affect virtually every aspect of plant physiology simultaneously, creating a complex web of interconnected responses, through a cascade of cellular, biochemical, and molecular mechanisms, including enzyme kinetics, hormone synthesis [6], and membrane fluidity [7]. A moderate increase in temperature can enhance enzymatic reaction rates by increasing molecular collisions and lowering activation energy barriers. This acceleration benefits various metabolic processes such as photosynthesis, respiration, and nitrogen assimilation [8]. For example, under moderate temperature increases, Calvin cycle enzymes, particularly ribulose-1,5-bisphosphate carboxylase/oxygenase (RuBisCO), the primary carbon-fixing enzyme, exhibit heightened catalytic activity, leading to improved carbon fixation rates [9,10]. Respiratory enzymes also show considerable temperature dependencies that influence plant energy metabolism and growth rates. The citric acid cycle enzymes, electron transport chain components, and ATP synthase all exhibit distinct temperature response curves that collectively determine respiratory capacity across different thermal conditions [11,12]. The temperature sensitivity of respiratory processes often exceeds that of photosynthesis, leading to changes in the photosynthesis-to-respiration ratio with temperature that can affect plant carbon balance and growth [13]. Moreover, membrane fluidity is highly temperature-dependent. It becomes more rigid under cold conditions and more fluid at elevated temperature, which in turn modulates the activity of embedded proteins and signaling complexes [14,15]. These temperature-mediated alterations in membrane dynamics and transport efficiency influence hormone distribution, sugar loading, and nutrient uptake, all of which being crucial for flower initiation, fruit development, and quality [16].

While extreme temperature events often receive primary attention in climate change discussions, moderate temperature increase, typically within 0.5–4 °C of historical averages, create equally important, but more subtle impacts throughout the horticultural production process [17,18]. These moderate increases represent the most common temperature scenario under current climate projections and warrant detailed examination of their effects on plant growth and product quality. For the purpose of this review, the term high temperature or temperature stress will only be limited to moderate increase in temperature.

One of the key metrics for understanding temperature-plant interactions is the concept of Growing Degree Days (GDD), a fundamental tool that quantifies thermal energy accumulation for predicting the timing of various plant development stages [19,20]. The GDD or approach was for the first time introduced by the French scientist Rene A. F. de Réaumur as “degré de chaleur moyenne” [21]. He suggested that the duration of a particular growth stage is directly related to temperature and that this duration for a particular species could be predicted using the sum of mean daily air temperature, ${\overline{T}}_{air}$ [22,23]. Various terminologies are related or used interchangeably with the term GDD in the literature; such as “heat unit”, “degree day”, “heat requirement” [24,25], “thermal time” [26,27], “heat accumulation” [19,28], and “heat summation” [29]. Although the terminology may differ, the concept is grounded in the observation that temperature can be used to monitor or predict the development of an organism at each growth stage in its life cycle [30,31]. The GDD is generally calculated by summing the daily ${\overline{T}}_{air}$ above a base threshold, representing the minimum temperature needed for plant growth. The GDD methodology extends across multiple agricultural domains, enabling optimization of planting schedules [32], precise timing of harvest operations [33,34], monitoring of pest life cycles [35], and strategic scheduling of fertilizer and pesticide applications [36,37]. It provides valuable insights into how temperature variations affect the physiological growth of plants, aiding in the prediction of crop yield potential and the timing of important agricultural tasks, hence, potentially optimizing economic returns and minimizing environmental impacts [38,39]. However, there has been no recent critical analysis or review of the existing knowledge regarding this valuable tool for agricultural production and management.

The relationship between GDD, temperature, and plant growth is fundamental for vice versa understanding how temperature affects horticultural crops. As temperatures rise and GDD values increase, plants experience accelerated development. This may not always result in increased productivity or optimum quality of produce. If temperatures surpass optimal growth ranges, the benefits of higher GDD can be offset by high temperature stress. The latter disrupts optimum plant development and potentially causes irreversible damage in the field [40] or even affects storability of fresh produce [41]. High-temperature stress, moderate temperature, and cold are essential information used in crop management and, consistently, to frame GDD. However, the number of high temperature events are expected to increase under future climate scenarios, potentially causing growing seasons to shift, shorten or even be extended [1,2] depending on species, cultivar-specific traits, and region. Therefore, development of adaptive strategies based on field or even fruit data are vital for maintaining horticultural productivity and ensuring food security.

During the flowering to fruit maturation phase, the accumulation of GDD plays a pivotal role in determining synchronization of flowering with optimal pollination conditions as well as the length of time required for fruit ripening [42,43]. Changes in temperature can advance or delay flowering and/or fruiting by speeding or slowing heat accumulation [44]. Likewise, a rise in temperature may increase fruit growth rate and shorten the duration of fruit development [45,46]. However, rapid developmental phases may compromise final fruit quality attributes, as reduced developmental time limits dry matter accumulation, and biochemical compound synthesis and thus affecting sensory and nutritional quality attributes [46,47]. Understanding this dynamic allows farmers to make more informed decisions about crop management practices in the field and anticipate high temperature stress events that may disrupt plant growth. The knowledge is also relevant in decision-making, choosing the most suitable varieties for their region, adjusting planting times, and net or sprinkler installations.

Estimating GDD from flower bud to fruit maturity is not without challenges. Traditional GDD estimation faces inherent limitations including uncertainties in base temperature selection, optimal starting date determination, and temperature measurement accuracy—all factors that considerably influence prediction reliability [48]. Furthermore, the assumption of linear temperature-development relationships often oversimplifies complex biological responses, while environmental interactions involving soil moisture, quality and intensity of light, and humidity patterns further complicate predictive accuracy [49]. Recent studies confirm that nonlinear heat accumulation methods can substantially reduce prediction errors [50]. Standard GDD-based models often exhibit limited generalizability across climates and cultivars; for instance, multi-site evaluations of apple phenology revealed considerable shortcomings in model transferability between contrasting environmental settings [41]. Despite these challenges, recent advancements in technology, including precision temperature monitoring, remote sensing, the Internet of Things (IoT), and machine learning are transforming the information gaining on how agricultural systems respond to environmental stressors like increase in air temperature. With the ability to collect high amounts of data in real time and processing with these technologies, the accuracy and reliability of GDD models can be improved. This allows their adaptation to diverse geographic regions and growing conditions [51,52]. Additionally, it could allow for early detection or prediction of high temperature stress by identifying subtle changes in plant physiology before they are visible to the human eye and thus call for possible remedial action by farmers.

This study aims to summarize previous research on the relationship between temperature increase and GDD, highlighting the use of GDD method as a tool to monitor or predict the influence of increased temperature on flowering, fruit development, harvest maturity, and product quality. Furthermore, various modifications and extensions of the GDD model that have been proposed to enhance its precision and applicability across different geographic regions and plant species are discussed. Ultimately, this review lays a theoretical foundation for future work on how GDD can be optimized, particularly in light of emerging technological tools, to support predictions that are more accurate in fruit crop production.

2. Methodology

A literature search was conducted to identify relevant studies on the concept and applications of growing degree days (GDD). The search was performed across major scientific databases, including the Web of Science Core Collection, Science Direct, Scopus, PubMed, and the state library Berlin (Germany); and include literature from 1949 to 2025. A variety of keywords were employed, such as “growing degree days”, and its various variations “thermal unit”, “heat accumulation,” and “thermal time”, as well as application-specific terms like “phenology,” “temperature and flowering” “and “temperature, fruit development and quality”. The results were further refined by restricting the search to the fields of agricultural, plant, and environmental sciences. Thus, studies that focused on degree day concepts unrelated to growing degree days were systematically excluded from the review to ensure relevance and specificity in the literature selection process. Studies with a main focus on heat stress were also excluded. Duplicates were checked manually by the authors and excluded. The results indicate an increasing interest in understanding the impact of temperature on plant behavior (Figure 1), a trend likely driven by concerns over the continuous rise in global temperatures due to climate change.

3. Growing Degree Days Model

3.1. Concept

The use of calendar days to predict plant development for management decision is an old practice. However, calendar days can be misleading due to local weather conditions and particularly in time of increased climate variability and unpredictability. Furthermore, the change in temperature can alter plant physiology and phenology and those modifications, e.g., plants grow faster during warm weather than in cold weather, cannot be captured by calendar days. Thus, measuring the temperature accumulated over time provides a more accurate approach [53]. The unit of GDD is mostly reported as °C. Some authors refer to degree days (°d), while Kelvin (K) would be the unit for temperature differences according to SI. The quantity reported by the three units is the same; therefore, this review follows the majority of authors and reports in °C. According to the GDD concept, if GDD = 1000 °C required for maturity, the plant should reach maturity by the number of days on which 1000 °C has been accumulated [22], which is directly accessible by the farmer. The original heat unit concept uses the simple daily average [54]. When the $T_{air}$ is below a threshold, the development rates are assumed insignificant [55]. For example, according to the GDD concept, if a plant has a base temperature ($T^b$) of 1 °C and the mean temperature ($\overline{T}$) of this day is 10 °C, the difference for that day (in this example, 9 °C) is phrased “degree days” or “heat units”. The GDD is calculated as

$$GDD={\sum }_{\mathrm{d}=1}^{\mathrm{D}}{\displaystyle \frac{\left({}^{max}T+{}^{min}T\right)}{2}}-T^b$$

(1)

• d: day
• D: end of growing stage

where the maximum (${}^{max}T$) and minimum (${}^{min}T$) (typically air) temperature and base temperature ($T^b$) are considered.

The model has evolved since its inception (

Table 1. Methods of base temperature determination (adapted from [55,63]).

Method	Variants of Base Temperature, ${\mathit{T}}^{\mathit{b}}$ in °C	Criteria, Minimized to Select ${\mathit{T}}^{\mathit{b}}$ for GDD Calculation
Least standard deviation in GDD	$T_{{SD}_{GDD}}^b={\displaystyle \frac{({\sum }_{i=1}^N{\overline{T}}_i{d}_i{\sum }_{i=1}^N{d}_i-N{\sum }_{i=1}^N{d}_i^2{\overline{T}}_i)}{{({\sum }_{i=1}^N{d}_i)}^2-N{\sum }_{i=1}^N{d}_i^2}}$ (2) N: number of plantings per year	${SD}_{GDD}=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^N{\left({GDD}_{i-}\overline{GDD}\right)}^2}{N-1}}}$ (3) GDDi: GDD of the observed timing of the phenological stage for i plantings $\overline{GDD}$: overall mean GDD of the phenological event across all plantings N: number of plantings/years. ${SD}_{GDD}$ is given in °C
Least standard deviation in days	$T_{{SD}_d}^b=\overline{T}-{\displaystyle \frac{{({\sum }_{i=1}^N{\overline{T}}_i{d}_i)}^2-N{\sum }_{i=1}^N{\overline{T}}_i^2{d}_i^{,2}}{N{\sum }_{i=1}^N{d}_i^2{\overline{T}}_i-{\sum }_{i=1}^N{d}_i{\overline{T}}_i{\sum }_{i=1}^N{d}_i}}$ (4) , where ${\overline{T}}_i=\overline{T}-\overline{T}$ ${\overline{T}}_i:$ overall mean of temperature in all plantings $\overline{T}$: mean temperature of ith planting/year	${SD}_d={\displaystyle \frac{{SD}_{GDD}}{({}^{max}T-T_{SDd}^b)}}$ (5) ${SD}_{GDD}$: standard deviation in GDD $\overline{T}$: overall mean temperature of the developmental period of all years or all plantings ${SD}_d$ is given in days
Coefficient of variation in days	$T_{CV}^b={\displaystyle \frac{{\sum }_{i=1}^N{{\overline{T}}_{i}d}_i^2{\sum }_{i=1}^N{\overline{T}}_i{d}_i-{\sum }_{i=1}^N{d}_i{\sum }_{i=1}^N{\overline{T}}_i^2{d}_i^2}{{\sum }_{i=1}^N{d}_i^2{\sum }_{i=1}^N{\overline{T}}_i{d}_i-{\sum }_{i=1}^N{n}_i{\sum }_{i=1}^N{\overline{T}}_i{d}_i^2}}$ (6)	${CV}_d={\displaystyle \frac{{SD}_d}{\overline{d}}}\times 100$ (7) Mean d is the number of days observed to reach the phenological stage across all plantings ${CV}_d$ is given as percentage
Linear regression	$T_r^b={\displaystyle \frac{{\sum }_{i=1}^N{\overline{T}}_i{\sum }_{i=1}^N{\overline{T}}_i{d}_i-N{\sum }_{i=1}^N{d}_i{\overline{T}}_i^2}{{\sum }_{i=1}^N{\overline{T}}_i{\sum }_{i=1}^N{\overline{T}}_i-N{\sum }_{i=1}^N{d}_i{\overline{T}}_i}}$ (8)	$RMSE=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^N{(n_i^p-n_i^o)}^2}{N}}}$ (9) $n_i^p$: Predicted number of d in the ith year. $n_1^0$: Observed number of d in the ith year

), with advancements enhancing its accuracy and applicability across various domains. The modifications include: the use of different base temperatures [48,56]; more precise integrations of the upper and lower threshold temperature [19,57]; the inclusion of a day length factor [56,58]; and the use of a temperature index as opposed to time as the divisor in growth analysis functions [23]. The simple average [54], sine wave [19], the triangulation methods [59] and their variants [35,60,61] are classified as linear models. While nonlinear developmental rate models are common, linear-based degree day models have been shown to provide a better predictive capability in the field for some cases [50,62].

3.2. Starting Date

In cultivated annual plants, phenological events are typically traced and dated back to the first visible phenophases, most commonly the initial germination, and occasionally from the date of sowing [48]. For perennial plants, the starting dates, also known as biofix, for growth and development can differ substantially among species, ecotypes, and plant age [64,65]. Identifying optimal starting dates for physiological processes in perennial plants is often challenging. In the 1900s, the 1st of January was used as the biofix date for phenological studies in temperate regions [66,67], which proved problematic, especially in northern temperate areas, where the growing season may commence in March or later [48]. The timing of flowering can vary widely based on local climate conditions, even within a single region [68]. This variability complicates the selection of an appropriate starting date, potentially leading to inaccurate predictions of subsequent developmental stages or mismanagement of agricultural practices.

Furthermore, the definition of “flowering” “further contributes to inconsistencies among studies, as it depends on both crop type and modeling objectives. Most past and recent studies refer to the “first flowering date” when discussing flower phenology [69,70,71]. However, there is some ambiguity regarding what represents the “first flowering date,” even across Europe, as the BBCH scale is not crop specific [72]. Phenological datasets may be recorded from the day the first flower is spotted [71,73] or later, when it is assumed that approximately 10% of the plants are in bloom, particularly in fruit trees [74,75]. Some studies initiate monitoring when 20–25% of blossoms have opened [76,77] or at 50% [78,79]. The BBCH scale suggests six secondary stages, namely first flower, 10%, 30%, and 50% flower open, flowering finishing, and visible fruit set [72,80]. Conversely, some studies consider three secondary stages: first flowering (25%), peak flowering (50%), and last flowering (75% faded) [81], or first flowering (10% open), full flower (80% open), and petal fall (90% fallen) [74]. Regardless of percentages, determination of flowering date through visual observation can be subjective, adding to variability. In some instances, early flowers may not fully develop or may drop before maturity, resulting in discrepancies between the observed “start” of flowering and the actual growth processes that affect development [82]. Furthermore, some flowers may wither or fall off, while others bloom within the same period [74]. Relying solely on the date of first flowering may overestimate shifts in peak flowering and fail to predict changes in subsequent growth stages, making it difficult to detect responses to climate change [83]. Additionally, variations in population size can lead to earlier or later first flowering dates [71].

3.3. Base Temperature

Just as the starting date is crucial, the selection of a threshold temperature and the accuracy of calculations are vital to ensure that GDD models are adjusted to local farming conditions. Typically, the base temperature is determined by the minimum temperature required for crop development, below which the biological processes of interest do not progress [30]. The base temperature, $T^b$, is not universally fixed. It can be species-specific for each phase of a crop and may depend on environmental conditions and the objectives of the study [31,84]. Environmental factors that influence the $T^b$ include soil characteristics, day length, general air and soil temperatures, water conditions, and light quality and quantity [22,85]. In the 1800s, only heat units above 0 °C were typically summed as the threshold temperature [48]. By the 1900s, a $T^b$ of 5–6 °C became the most commonly used standard for cold-season crops, particularly in agriculture [57,86,87]. In warm-season crops, such as corn and soybean, higher $T^b$ (8–10 °C) were considered [30,88]. The mid-20th century marked a more systematic effort to define and calculate base temperatures. Experimental approaches became prevalent, with greater emphasis placed on the biological status of the plant rather than solely relying on historical growth data or previous observations [19].

The value of estimated $T^b$ may also vary considerably with methodologies used to determine thresholds [54] and GDD model [30]. The most common mathematical formula for calculating the base temperature for GDD are the least standard deviation in GDD, ${SD}_{GDD}$ (Equation (2), Table 1) [89,90]; the least standard deviation in days, ${SD}_d$ (Equation (4), Table 1) [54]; the coefficient of variation in days, ${CV}_d$ (Equation (6), Table 1) [91]; and the regression coefficient (Equation (8), Table 1 and

Table 2. Example data comparing three methods standard deviation for setting the base temperature, $T^b$, and resulting degree days given in parenthesis, calculated between flowering and fruit harvest maturity, for apricot [75] and cherry [55]. Terms refer to least standard deviation ($T_{{SD}_{GDD}}^b$), least coefficient of variation ($T_{CV}^b$), linear regression ($T_r^b$). The unit °C has been used as synonym for degree days (°d) or Kelvin.

Crop	Cultivar	${\mathit{T}}_{{\mathit{S}\mathit{D}}_{\mathit{G}\mathit{D}\mathit{D}}}^{\mathit{b}}$ in °C	${\mathit{T}}_{\mathit{C}\mathit{V}}^{\mathit{b}}$ in °C	${\mathit{T}}_{\mathit{r}}^{\mathit{b}}$ in °C
Apricot	Harcot	6.4 (925)	3.0 (1248)	4.3 (1117)
	Bergeron	5.0 (1311	2.6 (1578)	3.7 (1472)
	Stella	3.5 (1280)	2.0 (1417)	2.5 (1367)
Cherry	Burlat C1	−3 (887)	-	1 (650)
	Burlat	1 (649)	-	4 (475)
	Forli	2 (673)	-	3 (585)

) [92].

These empirical methods seek to determine the $T^b$ that best aligns with the growth patterns observed in a particular species by minimizing the standard deviation, coefficient of variation, and root mean square error in the prediction of plant phenological events, such as flowering or fruit ripening. The $T^b$ is usually set across multiple years. GDD is calculated using a series of candidate base temperatures, each one resulting in a set of GDDs and standard deviations. The temperature that generates GDDs with the smallest standard deviation is selected as the base temperature [56,75]. In annual crops, it is usually selected using a series of plantings [93]. The ${SD}_{GDD}$ focuses on minimizing the variability in the total GDD accumulation or heat unit for predicting a phenological event, while the ${SD}_d$ approach aims to minimize variation between calendar days. The ${CV}_{GDD/d}$ aims to calculate the relative magnitudes of the variation in days, as this is relevant for practical application [56]. Another method that uses Equation (1) for $T^b$ determination is the iteration method [55]. The iteration model minimizes the root mean square error (RMSE, Equation (9), Table 1) between the observed and predicted number of days in development period. Similar to the least standard deviation, in the iteration approach, adjustments of the base temperature are performed until it no longer results in meaningful improvements in the accuracy of the predictions. The regression coefficient model assumes that GDD is a constant for crop development and can be expressed as a function of the threshold temperature, $T^b$ (Table 2) [56,92]. For a series of base temperatures, regression equations are computed, the resulting GDD values are plotted versus $\overline{T}$, and the correct $T^b$ appears where the regression equation equals zero. That is until the plant no longer accumulates enough heat for meaningful growth.

The upper threshold is less well defined, while it is considered as the temperature at which the rate of growth or development begins to decrease or stop [22,94]. Determining a consistent upper threshold is difficult. Often, they are unavailable for use in phenology models and may occur at higher temperatures than the one recorded in the study site [53]. Some authors have even argued that upper thresholds do not sufficiently increase the accuracy of the prediction for growth or development [19,95]. The introduction of the upper threshold led to an increase in the coefficient of variation in GDD when determining the heat requirement from blooming to maturing in apricot cultivars [95]. However, it is likely that the upper threshold will become more crucial in the future due to enhanced number of heat (wave) events.

3.4. Simple Average Method

A straightforward model has been used since the 1800s, and remains relevant for farmers, extension workers, and parts of the scientific community. It is computed directly by averaging the daily maximum and minimum temperatures, then subtracting a base temperature specific to the organism or the growth stage over the specified period (Equation (1), [54,96,97]). This method assumes a linear relationship between the heat units accumulated and daily extremes temperatures and does not account for upper temperature threshold [19]. Ignoring intra-day temperature patterns can result in inaccuracies during periods of rapid temperature changes, leading to underestimate/overestimate heat accumulation [29,98,99]. To overcome this challenge, GDD is frequently calculated with the growing degree hour (GDH) [100,101] if hourly temperatures are available. When considering hourly data, GDD is determined by first calculating degree-hours for each hour of the day, followed by the summation of the degree-hours over the 24 h day and dividing the total by 24 [62,94]. In a comparative study, it was found that if temperatures exceed the base temperature during part of the day, while the daily mean remains at or below the base temperature, then the accumulated growing degree using GDH method is meaningful [29]. In comparison, GDD may lead to an underestimation of heat summation. Few authors recommended using GDH estimates for more accurate heat summation, a conclusion supported by other researchers [3,102,103].

3.5. Sine Wave Approximation (Baskerville-Emin Method)

This mathematical approach employs a sinusoidal curve to model daily temperature and estimates GDD by calculating using the area above the base temperature [19,98]. The method allows for both upper and lower threshold. The GDD is estimated by integrating the area under the sine curve using one or more of four cases (

Table 3. Calculating growing degree days (GDD) by the single sine method. Accumulated degree days are shaded areas of diagrams [19,35].

	Diagram	Equation
1		GDD = $\sum {\displaystyle \frac{\left({}^{max}T+{}^{min}T\right)}{2}}-T^b$
2		GDD = ${\displaystyle \frac{1}{\pi }}$ [(${\displaystyle \frac{\left({}^{max}T+{}^{min}T\right)}{2}}-T^b$)$(\pi /2-{\theta }_1)+\propto \cos \left({\theta }_1\right)$] ${\theta }_1={\sin }^{-1}⌊(T^b-{\displaystyle \frac{{}^{max}T+{}^{min}T}{2}} )÷\propto ⌋$
3		GDD = ${\displaystyle \frac{1}{\pi }}${$({\displaystyle \frac{\left({}^{max}T+{}^{min}T\right)}{2}}-T^b)$$({\theta }_2+$π/2$)+\left(T^u-T^b\right)\left({\displaystyle \frac{\pi }{2}}-{\theta }_2\right)- [\propto \cos \left({\theta }_1\right)]$} ${\theta }_2={\sin }^{-1}⌊(T^u-{\displaystyle \frac{{}^{max}T+{}^{min}T}{2}} )÷\propto ⌋$ $T^u$: upper threshhold
4		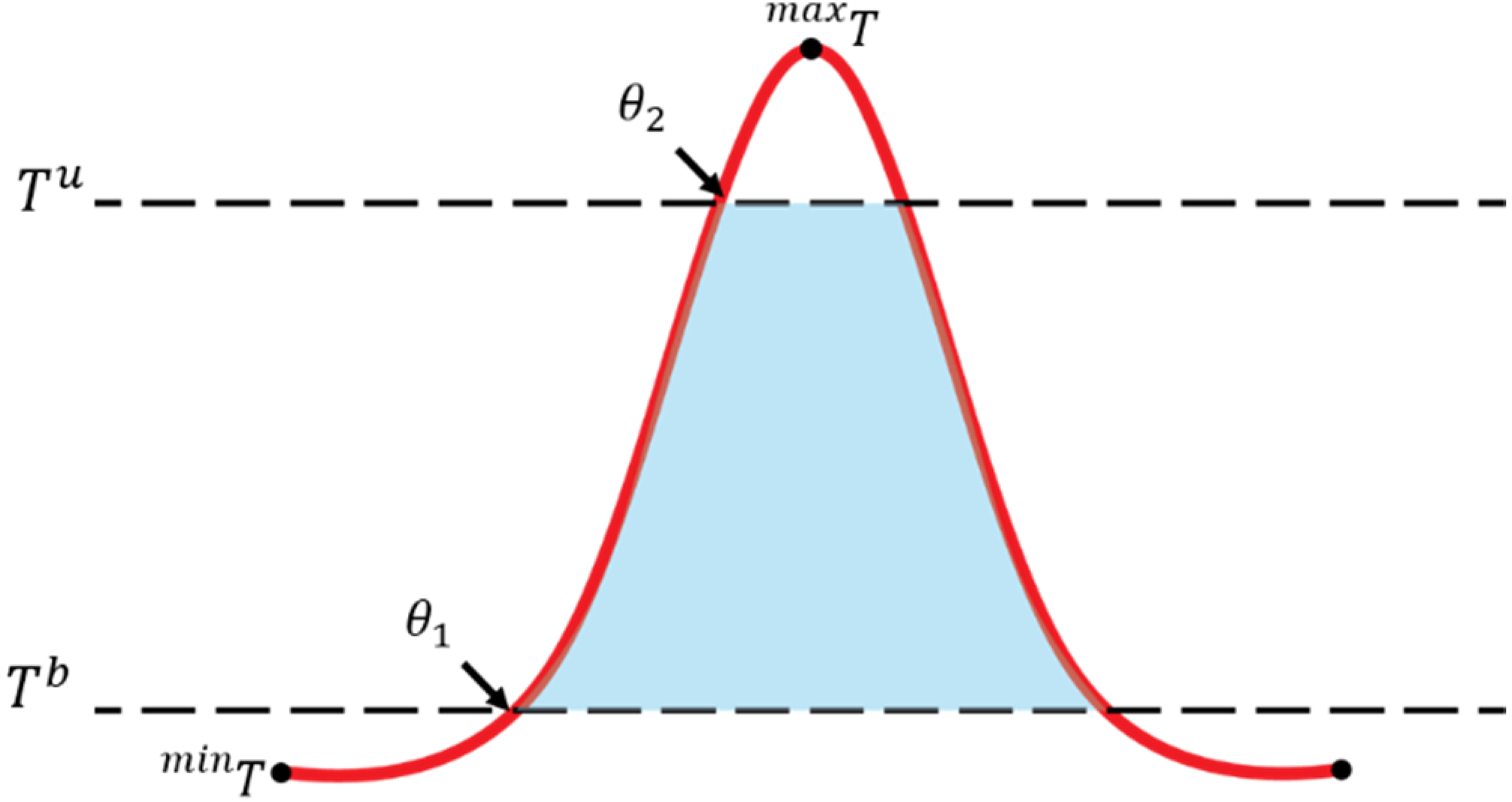GDD = ${\displaystyle \frac{1}{\pi }}${$({\displaystyle \frac{\left({}^{max}T+t_{min}\right)}{2}}-T^b)$$({\theta }_2-{\theta }_1)+\propto [\cos \left({\theta }_1\right)-\cos \left({\theta }_2\right)]+\left(T^u-T^b\right)\left({\displaystyle \frac{\mathsf{\pi }}{2}}-{\theta }_2\right)$} ${\theta }_1={\sin }^{-1}⌊(T^b-{\displaystyle \frac{{}^{max}T+{}^{min}T}{2}} )÷\propto ⌋$ ${\theta }_2={\sin }^{-1}⌊(T^u-{\displaystyle \frac{{}^{max}T+{}^{min}T}{2}} )÷\propto ⌋$

Case 1: The daily minimum temperature is above the single threshold temperature. The GDD is calculated following the simple average method. Case 2: The daily minimum temperature is below a single threshold temperature. Degree days are calculated by integrating the curve to receive the area under the sine curve above the base temperature. Case 3 and Case 4: There are both upper and base threshold temperatures. Degree days are calculated as the difference considering the area above the base and below the upper threshold temperatures under the sine curve.

, [19,62]). Advancement of the sine-wave method was approached by calculating degree days from half-day curves. This approach was published as double sine method [98]. The single sine method fits a sine curve through the day’s minimum and the maximum temperature, while the double sine method uses separate sine curves for the maximum temperature period of the day and the minimum temperature of the following day [98]. This approach can be particularly useful in climates with extreme day–night temperature variation [35]. While some researchers prefer the double sin method, studies [35,94] indicate that it is more accurate when considering only few days. In contrast, the difference between the two methods becomes negligible over longer observation period. Similar to the sine curve method, the triangulation method utilizes a day’s low and high temperatures to produce an equilateral triangle over a 24 h or 12 h period. Degree days are estimated by calculating the area between the two thresholds enclosed by either the single or the double triangle [60,94].

However, the use of GDD as a tool to monitor or predict when a crop will reach important developmental stages is not without criticism. One of the major concerns is that most models are based on the assumption of a linearity between plant developmental rate and temperature. However, this is not strictly the case, particularly at lower temperatures [66,104] and in events of high temperature spikes that occur outside of typical growth ranges [105]. Secondly, the dependence on only one of the many environmental parameters to explain the variation in biological response [22,106]. There have been attempts to improve GDD models by adding other environmental factors such as the photoperiod [85,107]. It is predicted that, as a response to climatic warming, species with a high sensitivity to temperature and little sensitivity to photoperiod would be expected to undergo noticeable changes in flowering time. In contrast, less change would be observed in species strictly controlled by photoperiod [108]. Thus, a model that estimates the rate of development at this stage of growth must represent the interaction of these factors, to increase the accuracy of GDD [109,110]. The first model of GDD that integrated photoperiod was developed by Nuttonson, based on the observation that the number of degree days from emergence to maturity multiplied by the average day length was more reliable compared on degree days used alone [85]. Several researchers continue to advocate on the importance of either considering GDD model concurrently with (or integrate GDD in) other models for crop growth prediction [111,112,113]. In any application, some progress on using advanced technology may support improved GDD accuracy.

4. Using Growing Degree Days to Guide Harvest and Quality Decisions

4.1. Flowering

In annual crops, which complete their life cycle in a single season, GDD accumulation typically begins from planting, making predictions relatively straightforward [30,31]. In perennial fruit crops, GDD models must consider carry-over effects from the previous season, particularly the accumulation of chilling hours during dormancy. For species of temperate climate, the timing and duration of chilling play a crucial role in determining bud break or bud opening. A specific number of chill hours (or chilling requirements) at low temperatures is required to break endodormancy and prepare for spring growth. Apple and peach trees may require approximately 600 to 1000 chill hours, depending on the variety, before bud break can occur [114]. Several chilling accumulation models have been developed to estimate chill accumulation, including the Chilling Hours Model, the Utah Model [96], the Dynamic Model [115], and Phenoflex [116].

In temperate deciduous fruit trees, flowering is closely related to heat accumulation following dormancy release, and cultivar-specific GDD thresholds allow reliable prediction. Apple cultivars such as ‘Gala’ and ‘Fuji’ differ substantially in their GDD requirements for flowering and harvest, with early cultivars flowering at lower heat sums than late cultivars [117]. Sweet cherry (Prunus avium) exhibits predictable GDD ranges: approximately 100–200 °C for bud break, 300–500 °C for full bloom, and 1200–1800 °C from bloom to harvest depending on cultivar [118]. In Nordic climates, it was confirmed that sweet cherry flowering can be accurately modeled using GDD despite low spring temperatures [119], as opposed to in Mediterranean regions. It was shown that almond (5654–10,201 °C) and apple (7471–9690 °C) cultivars require distinct heat sums for bloom [120]. Subtropical crops such as mango (Mangifera indica) also follow GDD-dependent flowering patterns [121,122], with a cultivar-dependent range of 382–500 °C in India [121], and a yearly variation of 665–714 °C in Brazil [122] from bud swelling to flowering. These differences showcase the broad applicability of GDD-based models across climatic zone, and also the need for adaptation of the models (Table 4).

Warmer summer temperatures often accelerate the accumulation of GDD, speeding up physiological processes such as floral initiation and development in several species, reported for strawberry [123], grape [124], and peach [125]. Budburst, flowering, and veraison occur earlier by an average of 5–7 days, 12–14 days, and 17–19 days, respectively, in various cultivars of grape due to rising temperatures [124]. However, the relationship between temperature and flowering is complex. While earlier onset of flowering is commonly observed with temperature increases, the magnitude and direction of phenological shifts vary between early- and late-flowering crop species or varieties. Crops that flower early in the season (e.g., apricot, plum, peaches) often exhibit stronger advancements in phenology [126,127] compared to those with later flowering periods, e.g., apple, pear [117,128]. Furthermore, increased winter temperatures could delay blooming by reducing chilling hour accumulation, while excessive temperatures may adversely affect flower development, leading to poor pistil development and reduced fruit set [129,130].

GDD modeling for flowering provides actionable guidance for frost protection, pollination scheduling, and labor planning. By using locally calibrated cultivar-specific base temperatures and thermal thresholds, growers can anticipate bloom timing, even under climate variability [131,132].

Table 4. Examples of growing degree day (GDD) requirements, and the base temperature, $T^b$ or flowering prediction across crops and climates. The unit °C has been used as synonym for degree days (°d) or Kelvin.

Crop	Climatic Region	${\mathit{T}}^{\mathit{b}}$$\mathbf{i}\mathbf{n}$°C	Starting Date/Duration	GDD (°C)	Reference
Olive	Mediterranean	5.0	1 January	1434	[133]
Apple	Mediterranean	4.0	February	7471–9690 *	[120]
Sweet cherry	Temperate	2.0	1 March	254	[119]
Sweet cherry	Temperate	4.5	3 Feb–28 March 11 Feb–14 April	3233–4343 * 5444–6988 *	[134]
Sour cherry	Temperate	2.0	1 January	492	[135]
Sour cherry	Temperate	4.0	1 March	125	[38]
Grapevine	Temperate	10.0	1 January	1600–1850	[136]
Grapevine	Temperate	10.0	1 January	318–552	[131]
Mango	Subtropical	10.0	from floral bud swelling-floral opening	623	[122]

* Calculated with growing degree hours model.

Table 4. Examples of growing degree day (GDD) requirements, and the base temperature, $T^b$ or flowering prediction across crops and climates. The unit °C has been used as synonym for degree days (°d) or Kelvin.

Crop	Climatic Region	${\mathit{T}}^{\mathit{b}}$$\mathbf{i}\mathbf{n}$°C	Starting Date/Duration	GDD (°C)	Reference
Olive	Mediterranean	5.0	1 January	1434	[133]
Apple	Mediterranean	4.0	February	7471–9690 *	[120]
Sweet cherry	Temperate	2.0	1 March	254	[119]
Sweet cherry	Temperate	4.5	3 Feb–28 March 11 Feb–14 April	3233–4343 * 5444–6988 *	[134]
Sour cherry	Temperate	2.0	1 January	492	[135]
Sour cherry	Temperate	4.0	1 March	125	[38]
Grapevine	Temperate	10.0	1 January	1600–1850	[136]
Grapevine	Temperate	10.0	1 January	318–552	[131]
Mango	Subtropical	10.0	from floral bud swelling-floral opening	623	[122]

* Calculated with growing degree hours model.

4.2. Fruit Development and Maturity

Once flowering has occurred, GDD accumulation governs fruit development and the timing of harvest (Table 5). Temperature influences fruit development by altering the plant’s metabolic activity. Generally, warmer temperatures speed up biochemical processes, resulting in faster fruit growth and ripening, although this relationship varies across development stages [137]. For every 1 °C increase in average spring temperature, the bloom-to-harvest period shortens by about 3.5 days in temperate fruit trees [138], a trend also observed in Kinnow mandarin (Citrus nobilis Lour × Citrus deliciosa Tenora), where warmer temperatures lead to an increase in GDD accumulation, accelerating fruit set, cell division, and overall maturation [139]. In peaches (Prunus persica), GDD is used alongside chilling requirements to forecast flowering and fruit development, critical for frost management and harvest optimization [96].

Table 5. Growing degree day (GDD) requirements, and the base temperature, $T^b$ for fruit maturity prediction across crops and climates.

Crop	Climatic Region	${\mathit{T}}^{\mathit{b}}$$\mathbf{i}\mathbf{n}$°C	Starting Date/Measurement Duration	GDD (°C)	Reference
Peach	Sub-temperate	7.0	January	814–1894	[140]
Peach	Temperate	7.0	May–August	1651–1826	[141]
Grapevine	Temperate	10.0	April–September	1204–1940	[142]
Grapevine	Temperate	10.0	After bloom	556–800	[131]
Grapevine	Humid continental	10.0	1 April–31 Oct.	1070–1700	[143]
Mango	Tropical	17.9	July–November	1062.71–1309.41	[121]
Mango	Tropical	12.0	Asparagus stage of flower	1740–2185	[144]
Mango	Subtropical	10.0	Floral bud swelling to commercial maturity	2399	[122]
Papaya	Subtropical	15.0	Flowering to harvest	1293–1488	[34]
Orange	Subtropical (Humid)	12.8	9 August	4462–5090	[145]
Eggplant	Subtropical	15.6	June–November	892–1078	[146]

Table 5. Growing degree day (GDD) requirements, and the base temperature, $T^b$ for fruit maturity prediction across crops and climates.

Crop	Climatic Region	${\mathit{T}}^{\mathit{b}}$$\mathbf{i}\mathbf{n}$°C	Starting Date/Measurement Duration	GDD (°C)	Reference
Peach	Sub-temperate	7.0	January	814–1894	[140]
Peach	Temperate	7.0	May–August	1651–1826	[141]
Grapevine	Temperate	10.0	April–September	1204–1940	[142]
Grapevine	Temperate	10.0	After bloom	556–800	[131]
Grapevine	Humid continental	10.0	1 April–31 Oct.	1070–1700	[143]
Mango	Tropical	17.9	July–November	1062.71–1309.41	[121]
Mango	Tropical	12.0	Asparagus stage of flower	1740–2185	[144]
Mango	Subtropical	10.0	Floral bud swelling to commercial maturity	2399	[122]
Papaya	Subtropical	15.0	Flowering to harvest	1293–1488	[34]
Orange	Subtropical (Humid)	12.8	9 August	4462–5090	[145]
Eggplant	Subtropical	15.6	June–November	892–1078	[146]

In peaches, GDD exceeding 494 °C in the first 30 days post-bloom resulted in less than 60% of peaches being classified as large, compared to years with combined GDD of 468 °C or less during the same timeframe [147]. Similarly, strong correlation between GDD and the timing of maturity stages were found in other experiments on peaches, providing a reliable index beyond simple calendar days [140,141]. Grapevines (Vitis vinifera L.) rely heavily on GDD for predicting veraison, and harvest, aiding vineyard zoning and quality forecasting [148,149]. For reported grapevine grown in temperate semi-arid conditions, development from bloom to veraison occurred after accumulating 556–800 °C with a base temperature of 10 °C [131]. In comparison, grapevines cultivated in a humid continental climate required a higher heat accumulation of 1070–1700 °C from April 1 to October 31 to reach harvest [143]. Subtropical oranges (Citrus sinensis) showed even greater thermal requirements, needing 4462–5090 °C from August 9 onward at a base temperature of 12.8 °C [145], illustrating how GDD accumulation varies substantially among species and climatic regions. Modeling the impact of air temperature and cumulated temperature on the duration of fruit developmental stages from flowering to green, white, and turning stages, has been proposed to optimize the harvest date in strawberry [150].

Similarly, in cherries, GDH accumulation closely tracks key developmental stages, including flowering and fruit set, allowing precise phenological predictions. This was demonstrated in sweet cherry under temperate conditions [38], and its importance was subsequently confirmed for sour cherry as well [151]. GDD models are also effective in tropical and subtropical crops. For instance, papaya (Carica papaya L.) requires approximately 293–1488 °C from anthesis to ripening, enabling optimized harvest timing [34]. The relationship between GDD and crop outcomes is also evident in vegetable production. Research on eggplant (Solanum melongena) cultivation, for example, revealed a multifaceted association [145]. The latter authors found that GDD reliably predict the timing of key phenological stages, from flowering to fruit maturity, which directly influences yield potential by affecting the rate of fruit set and development. Furthermore, the study showed that GDD affects marketable quality, finding that sufficient thermal time was necessary to achieve desirable commercial characteristics such as optimal fruit size. An earlier study found that the heat units model was more effective than calendar-day methods for determining optimal harvest time in cucumber production [152].

Beyond predicting phenology, GDD models can evaluate whether new cultivars will reach full maturity within the growing season, as shown in kiwifruit by Kovaleski et al. [153]. In warmer regions, model accuracy can be improved by incorporating both lower and upper temperature thresholds, as demonstrated for mango in Australia [143].

4.3. Fruit Quality

While GDD is primarily used to predict phenological timing, their influence extends deeply into the final quality of harvested fruit (

Table 6. Fruit quality monitoring using growing degree day across crops and climates. Titratable acidity (TA), soluble solids content (SSC).

Crop	Climatic Region	${\mathit{T}}^{\mathit{b}}$$\mathbf{i}\mathbf{n}$°C	Starting Date/Measurement Duration	GDD (°C)	Fruit Quality Attributes Related to GDD	Reference
Mango	Subtropical	12.0	From asparagus stage of flowering	1728–2185	Flesh color, dry matter content, SSC:TA ratio	[144]
Peach	Subtropical	7.0	From full bloom to fruit senescence/harvest	1106–1547	Fruit size and mass, mesocarp cell number	[158]
Grape	Humid continental	10.0	August–October	1330–1500	SSC, timing of ripening	[159]
Apple	Humid continental	10.0	Seasonal accumulation up to harvest (29 Aug–3 Oct. 2012, 11 Sept–26 Sept. 2013)	1444–2406	SSC, TA, starch index, firmness, internal ethylene and soft-scald susceptibility	[160]
Apple	Temperate	7.2	From anthesis to harvest	892	SSC, firmness, diameter	[161]

). The GDD accumulated throughout a growing season directly shapes critical postharvest attributes like flavor, texture, color, and shelf-life, as these traits are intrinsically linked to fruit maturity [154,155]. Achieving an optimal GDD accumulation is essential; insufficient heat results in underdeveloped fruit, while excessive heat can accelerate ripening to the detriment of overall quality [156,157].

In grapevine development, cumulative GDD critically shapes fruit composition, particularly the sugar and acid balance that determines a wine’s quality potential. Several authors [132,136,145] observed that increased GDD accelerates berry ripening by promoting sugar accumulation, while reducing titratable acidity. It was further emphasized that this process could be reliably predicted using cultivar-specific models, highlighting the need to tailor such predictions to different grape varieties [132]. While these compositional changes can enhance stylistic attributes like body and perceived sweetness, they also risk creating imbalances in warmer vintages by advancing ripening too quickly and diminishing acidity below optimal levels. These findings underscore the dual role of GDD: it is both a key predictor of phenological progress and a potential driver of compositional trade-offs that must be managed to preserve wine quality under changing climatic conditions.

In peaches, a strong correlation between GDD thresholds and the onset of physiological maturity has been documented, allowing for more accurate estimation of harvest readiness [142]. Similarly, changes in fruit texture and sugar–acid balance, important determinants of firmness and flavor, has been found to be temporally linked to specific GDD accumulations [141]. Concurrent monitoring of fruit quality variables (firmness, soluble solids content (SSC), and titratable acidity) along with temperature from full bloom to harvest led to the identification of 2469 °C as the optimum harvest date for pears [162]. Generally, warmer conditions tend to decrease fruit firmness and titratable acidity (TA) while increasing SSC. This pattern has been observed in apples grown at warmer temperatures [45] as well as in peaches [163] and plums. In tomatoes, increased heat unit accumulation prior to harvest substantially enhances sugar content but also reduces fruit firmness and increases the risk of cracking [164]. Adding to this complexity, other studies have shown that warmer temperatures raise SSC and acidity, but concurrently decrease levels of lycopene and total carotenoids compounds essential for both fruit color and nutritional quality [165,166].

Collectively, these studies demonstrate that GDD and GDH models are versatile and effective tools for predicting key developmental stages such as flowering, fruit set, and harvest maturity across a wide range of horticultural species and climatic conditions. Their robustness and low cost make GDD-based modeling particularly valuable for practical applications, including frost risk assessment, optimizing pollination timing, irrigation scheduling, thinning, and harvest planning. The accuracy and reliability of these models depend heavily on careful calibration tailored to specific cultivars, phenological stages, and local climate conditions. For deciduous temperate crops, it is crucial to consider the interactions between chilling requirements and heat accumulation to improve model precision. Furthermore, ensuring that input data are precise and representative using accurately calibrated sensors is essential for producing reliable model predictions.

5. Remote Sensing Approaches

In most studies, meteorological data on $T_{air}$ from the closest official weather stations are used for this purpose [167]. The contribution of those studies to scientific knowledge cannot be disputed. Aimed at more precise analysis, the importance of microclimatic temperatures for limiting deviation from actual GDD at the plant and even plant organ scale was highlighted since the late 20 century [62,167,168]. According to Roltsch et al. [62], the most important factor to consider when employing GDD models in the field is “How well do available temperature readings reflect the microclimatic temperatures that an organism actually experiences within the field environment?”. The actual conditions depend on all climate variables, such as global radiation, relative humidity, wind, affected by within-canopy shading and airflow resistance. Sources of error of GDD calculations linked to data collection has been discussed: the temporal resolution of data recorded, collections of data once daily using separate thermometers and the use of $\overline{T}$ calculated using daily maximum and minimum versus the $\overline{T}$ calculated by averaging values recorded every minutes, and the position of the sensors [27]. The latter researcher emphasized the fact that even when temperature sensors are located in the field, the $T_{air}$ at shelter height may differ from the temperature affecting the plant.

A good understanding of changes in flowering phenology requires monitoring from the beginning to the end of the growth stage. Recording flower phenology throughout the full growing seasons using real-time monitoring tools, such as remote sensing, can help mitigate these challenges [169,170]. Automatic image-based monitoring technologies for flower phenology are being progressively explored in ecological studies, yielding promising results [171,172,173,174]. For example, a precision of up to 0.92 in their flower detection model was reported when using automated method to monitor the phenology of two species in the South Greenland [173]. A national flowering map of Southern Beech in Australia was created with overall classification of 90.8% accuracy using a Sentinel-2 Imagery, as fully automated remote sensing system [174].

Consistently, it was shown that degree days calculated from local weather stations, using the single sine method failed to reflect the predicted delay in tomato development and also lead to erratic prediction of ripening rate [167]. Even if it may be reasonable in some research work to assume that $T_{air}$ = $T_{fruit}$, a more accurate measurement would be supportive [175,176]. Furthermore, considering the different mass, absorption coefficients, and heat transfer coefficient [177] when comparing fruit and leaf, a difference between $T_{air}$ and $T_{leaf}$ or $T_{fruit}$ can be reasonably assumed.

Based on weather data and thermodynamic model considering the absorption and emissivity of apple fruit, the fruit surface temperature was modeled [178]. Since the radiative fruit properties are requested in this approach, direct measurements appear as an alternative for analysis of a high number of fruit and implementation in practice: Temperature measurements at the fruit surface in the field were mostly performed by means of thermocouples [176,179] (Figure 2). For this purpose, the probes were inserted under the epidermis. The data are collected by data logger or wireless sensor network. Influencing factors are the penetration depth of the wire, wind conditions, direct exposure to the sun, as well as tissue decay due to the sensor implementation. While only low numbers of fruit can be measured with this approach, the methodology is frequently used as reference for new sensor approaches and machine learning [180].

Thermal imaging has been applied in orchards, initially employed to detect fruit in the canopy, followed by the interest in fruit surface temperature due to global warming. Using a sensor combination of RGB and thermal cameras, $T_{fruit}$ was estimated with a non-contact approach [182,184]. The root mean square error, RMSE, was documented in the range 0.50–1.08 Kelvin (Figure 2, [182]). By means of this approach, data from a higher number of fruit were acquired, compared to fruit readings with thermocouples. Recent studies applied thermal 2D information to study the susceptibility of grape to heat stress [185]. In apple, the $T_{fruit}$ was extracted with 2D spatial resolution, considering a min, max, and mean value [186]. Such data have been applied for the prediction of free water on the fruit surface of sweet cherry [187,188]. Using this range of temperature obtained may also provide valuable input in GDD models. Thermal cameras have the advantage of being precalibrated by the manufacturer capturing environmental variables such as relative humidity. However, the heat emission coefficients of fruit surface are different from the surrounding [177], which results in a certain error in field measurement. Under conditions of free water on the fruit surface due to precipitation, irrigation, condensation as well as dense fog, thermal imaging cannot measure the fruit surface temperature.

Furthermore, measuring spatial temperature distribution in 3D would address individual fruit to capture the large variation between fruit appearing within a canopy, resulting from the microclimate and individual fruit’s radiative properties [176]. The estimation of 3D spatially resolved temperature distribution has recently gained interest in other disciplines such as in building layouts, where linear textures appear [189]. Subsequently, the concept of merging mobile terrestrial light detection and ranging (lidar) sensor and thermal imaging has been introduced in crop production. The methodology has been in an early stage of development, showing the temperature distribution of leafy structures in an apple orchard in Chile [190]. While 3D point clouds obtained by lidar provide 3D information on the geometric structure of tree canopies, the merging with thermal data results in in situ data on the 3D distribution of temperature in the canopy, as shown with high resolution at the fruit level (Figure 2). Temperature information is provided in the x, y, z coordinate system as points, either in local or global coordinate system. The approach of analyzing position and temperature of individual fruit was enabled in a data pipeline. The first step captures the data fusion of lidar and thermal imaging, resulting in T annotated point clouds [191]. As a second step, segmentation of T annotated fruit point clouds from the canopy point cloud is necessary [192]. The entire data pipeline enabled the analysis of $T_{fruit}$ spatially within the canopy (Figure 2) with a documented RMSE of 1.9% [193]. The spatial monitoring of variation in fruit surface temperature, affected by environmental changes, can provide specific information for crop management. Physiological changes observed on fruit could be related to tree architecture and climate change with high density of fruit data. In a study on Gala–Brookfield apples, seasonal and diel courses of $T_{fruit}$ were described [193]. In previous studies, it was proposed that a time gap between air and fruit temperature exists throughout the diel course, which is diminished when working with daily mean temperatures [176]. In diurnal courses measured with the 3D approach, the gap between the course of $T_{air}$ and $T_{fruit}$ was described in the Gala–Brookfield apples [193], which provides new opportunities for 3D GDD modeling. As an addition, this approach allows the assessment of position, fruit size, and distribution of $T_{fruit}$ in canopies, potentially capturing a high number of fruit also for these variables [194]. A low-cost solution, using RGB-D sensors instead of lidar and low-cost thermal cameras, was already approached [195] and tested in apple and grape. However, the methodology of analyzing spatial temperature distribution has been introduced only recently by few workgroups and more research is requested on the implementation of the data as a tool for GDD applications.

Concurrently, there have been recent advancements in fruit maturity identification leveraging radiometric information gained from lidar’s return signal strength intensity [196]. Computer vision and deep learning have greatly enhanced the precision and scalability of automated fruit ripeness assessment. Convolutional neural networks (CNNs) have been pivotal in automating feature extraction from fruit images, enabling accurate classification of maturity stages without manual intervention [197,198]. Notably, the YOLO family, including models like the YOLO-BLBE (combines innovative image enhancement (I-MSRCR) and attention mechanisms) developed for blueberries addressing challenges such as occlusion, variable lighting, and dense fruit clusters [199]. This illustrates the transformative potential of interdisciplinary research, integrating close-range remote sensing, machine learning, and phenological studies potentially in combined models, capturing GDD and maturity analysis for optimized crop management.

6. Conclusions

Growing degree days (GDD) have emerged as a pivotal tool in understanding plant growth and development, offering a quantitative approach to measure the accumulation of heat necessary for crops to progress through their life cycles. It is a simple yet effective approach to understanding temperature-driven biological processes relevant in horticultural production. As the effects of global warming intensify, understanding and adapting to the relationship between GDD and flowering, fruit development, and posthavest quality will be critical for maintaining the standards of fruit production and ensuring sustainability in the face of changing environmental conditions.

Despite its widespread utility, the application of GDD is not without challenges. Considerable effort has been made over years to improve GDD calculation, but there are still limitations in determining appropriate base temperatures, which vary across crops and phenological development. Additionally, GDD models often assume a linear relationship between temperature and development, disregarding the complexities of plant responses to extreme weather, particularly events of heat stress and other environmental factors. Variability in local climate conditions, data availability at the fruit level, and the influence of factors like patterns of rainfall, soil–water potential, carbon dioxide partial pressure, and photoperiod also complicate the accuracy and reliability of GDD models.

Advancements and initial use of satellite data analysis and close-range remote sensing, such as thermal imaging, combining RGB and thermal imaging, or lidar and thermal imaging can enhance the spatially-resolved analysis of temperature distribution in crop canopies at the fruit level. These technologies, along with machine learning algorithms, provide high-density data of potentially all fruit at the tree. In addition, the consideration of dynamic factors has been enabled, e.g., diurnal course of fruit surface temperature ($T_{fruit}$) and the gap between air and fruit temperatures. The new approaches are seen as a new driving force for analyzing the impact of fruit temperature by means of the widely accepted GDD concept. By capturing detailed, 3D temperature data across different spatial scales, these innovations are also predicted to support nonlinear growth responses and interactions with other environmental factors. However, these are research challenges for the future.

In summary, GDD provides an essential framework for understanding and managing plant growth in relation to temperature. While challenges considering the availability of easy-to-use tools remain, advancements in close-range remote sensing technology offer opportunities to enhance the precision and spatial analysis of GDD models. Therefore, GDD can continue to serve as a vital tool in supporting sustainable agricultural practices and adapting to climate change.