Machine Learning Models Using Data Mining for Biomass Production from Yarrowia lipolytica Fermentation
Abstract
1. Introduction
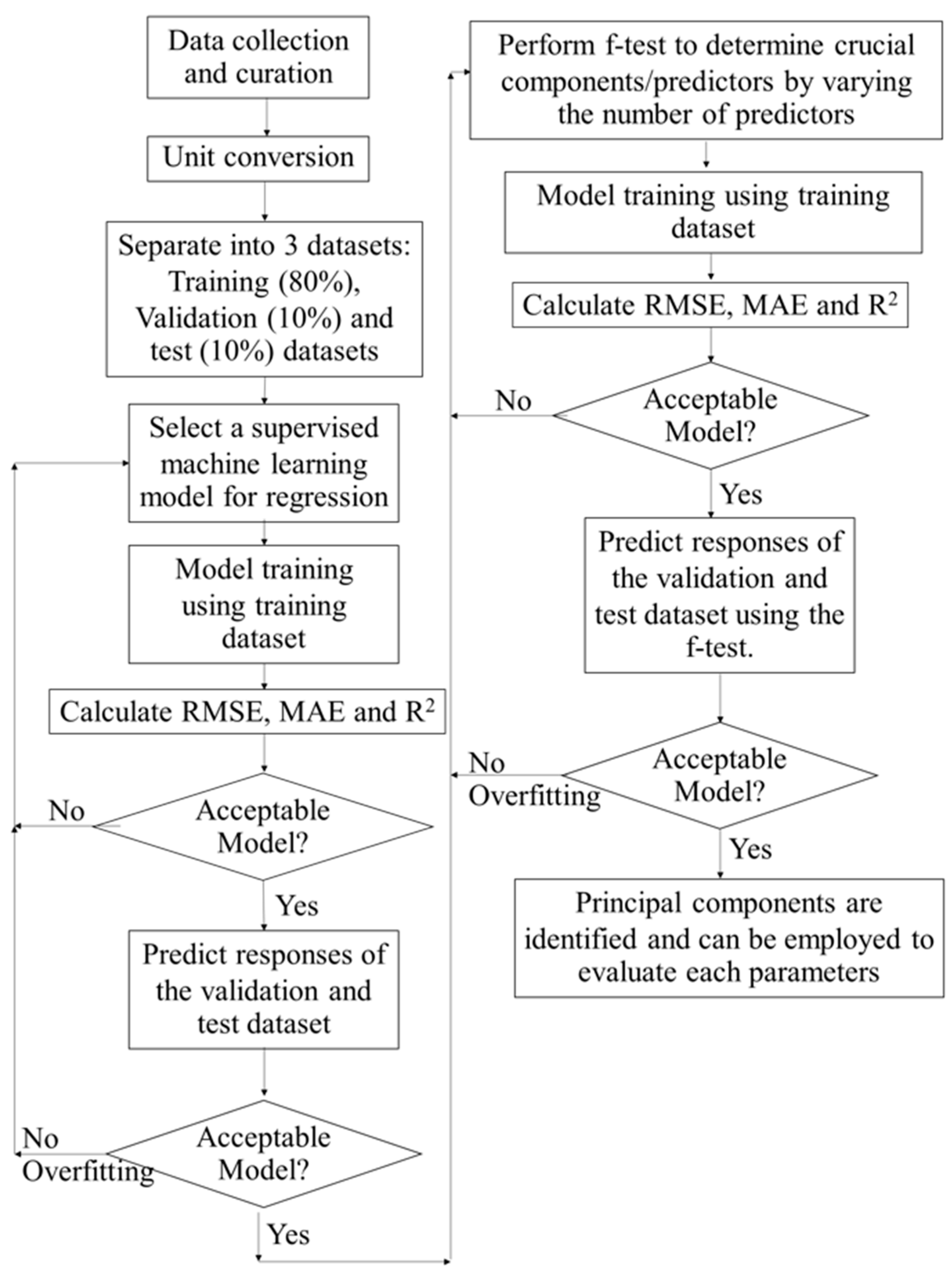
2. Materials and Methods
2.1. Data Collection and Curation
2.2. Supervised Learning for Regression Predicting Biomass Production
2.3. Model Performance Parameters
2.4. Training Dataset, Validation Dataset, and Test Dataset
2.5. Feature Selection Using f-Test
3. Results
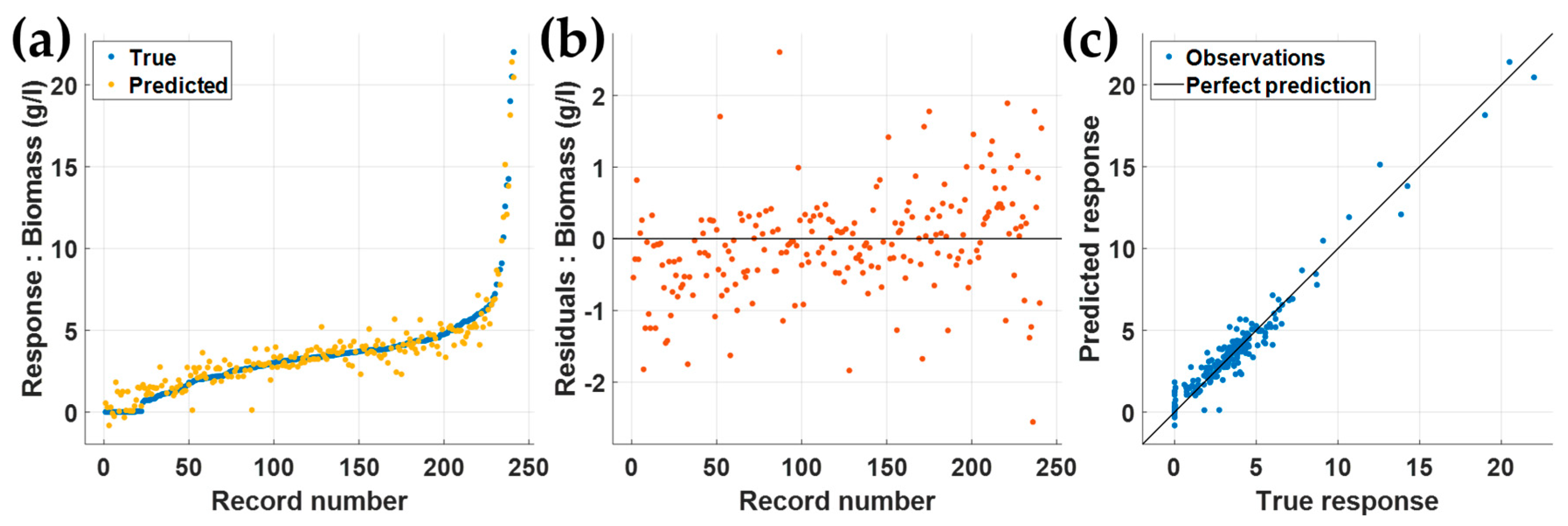
3.1. Machine Learning Model Training Using All 25 Predictors
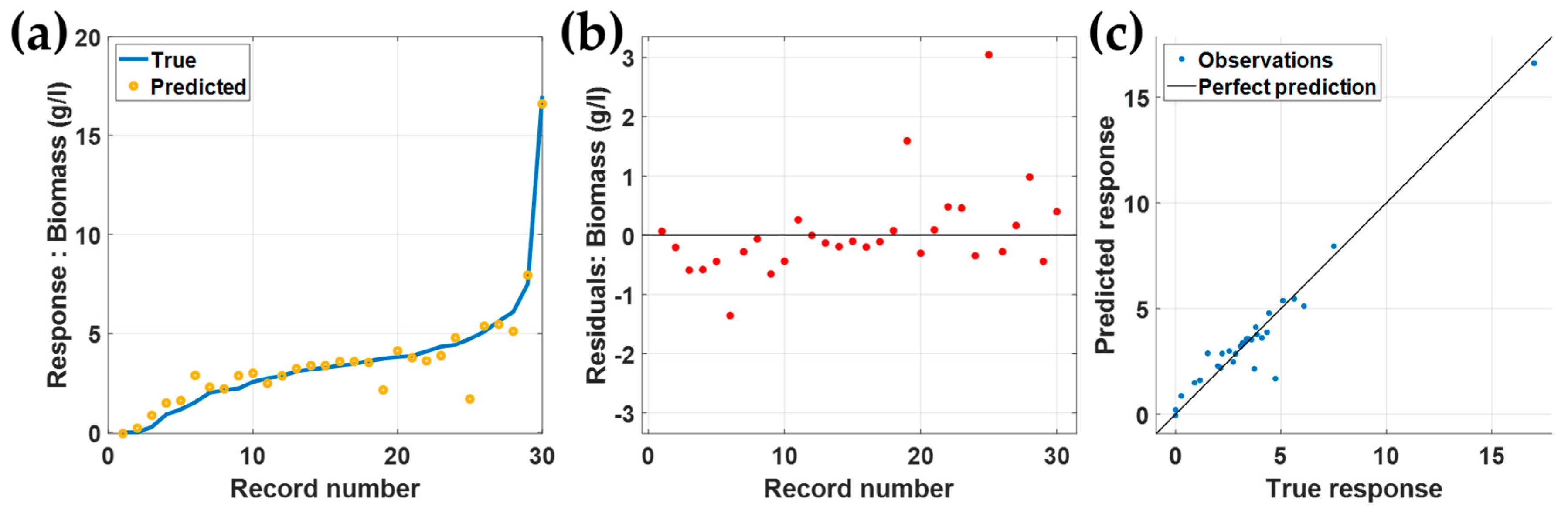
3.2. Validation and Testing Using the Separated 30 Rows
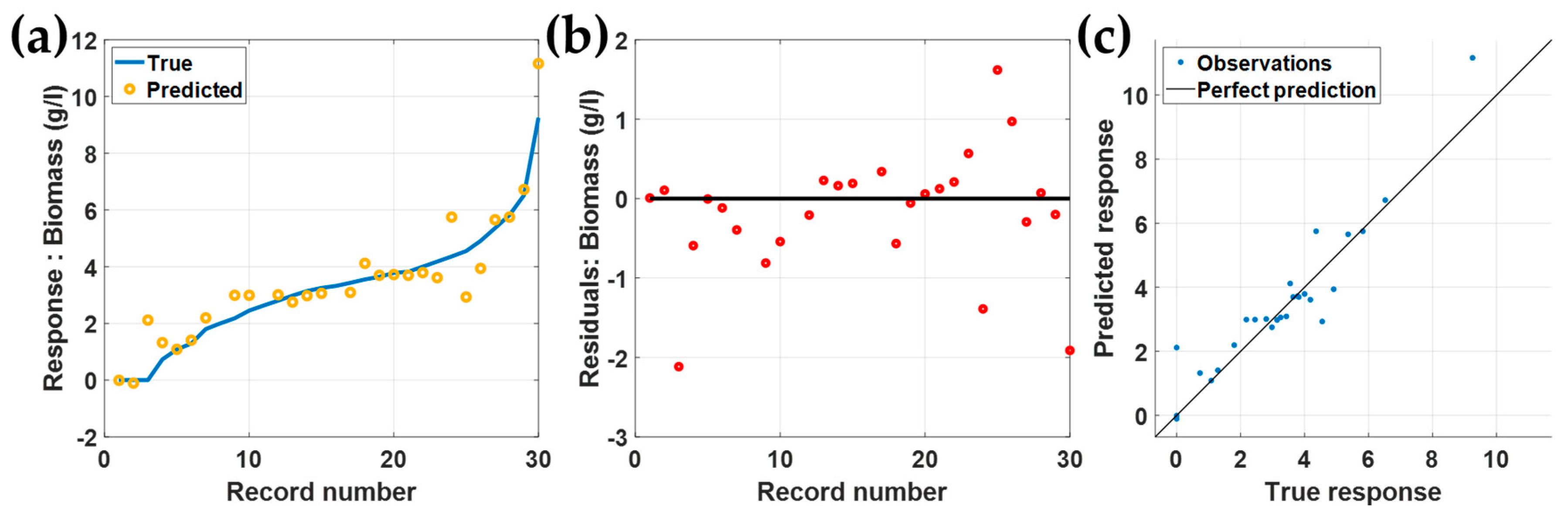
3.3. Testing Using the Separated 30 Rows
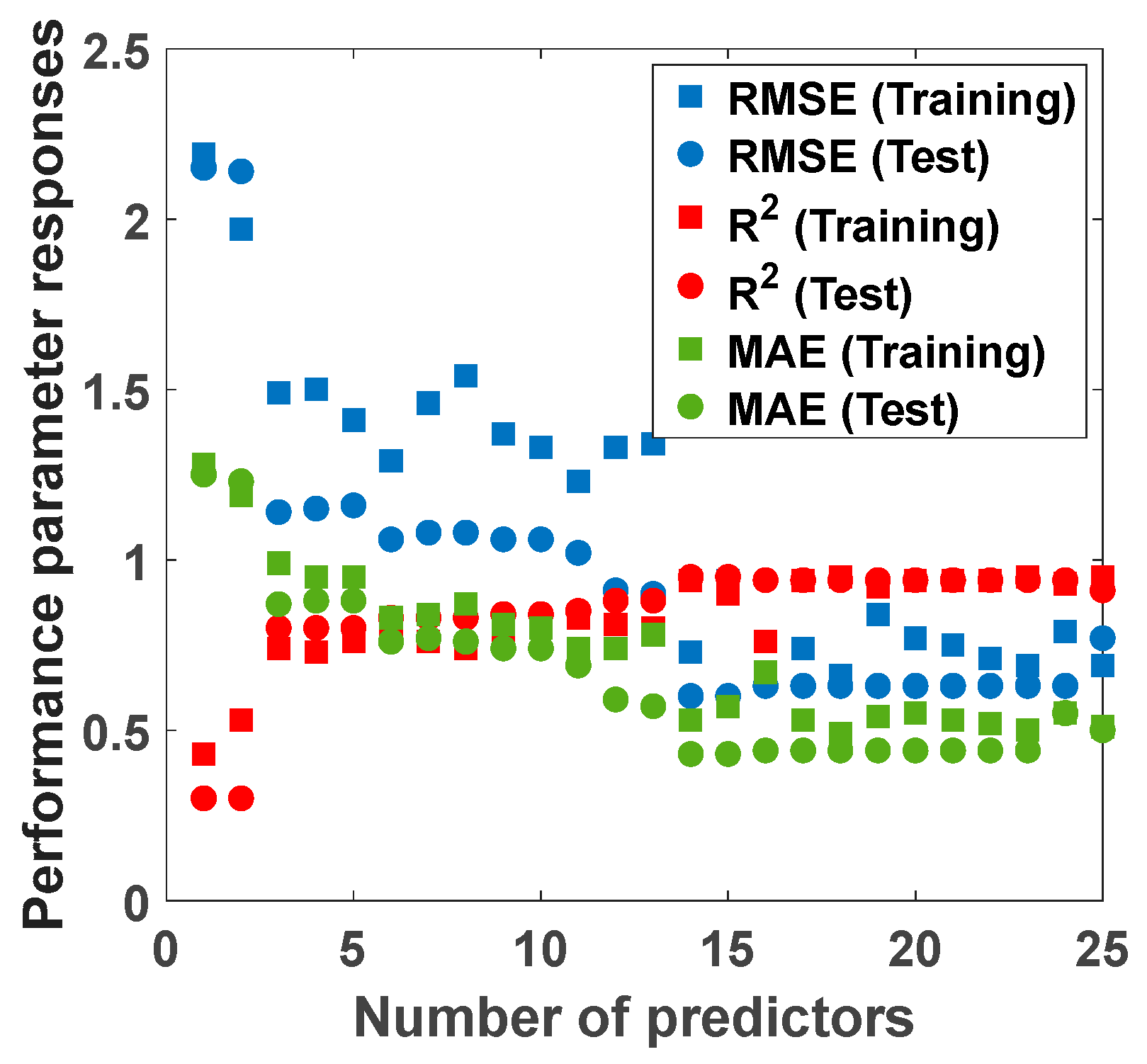
3.4. Predictor Selection Using f-Test
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Song, Y.; Fan, X.; Wang, C.; Lu, X.; Tian, Y. Yarrowia lipolytica as an Oleaginous Platform for the Production of Value-Added Fatty Acid-Based Bioproducts. Front. Microbiol. 2021, 11, 608662. [Google Scholar] [CrossRef] [PubMed]
- Juszczyk, P.; Rymowicz, W.; Kita, A.; Rywińska, A. Biomass production by Yarrowia lipolytica yeast using waste derived from the production of ethyl esters of polyunsaturated fatty acids of flaxseed oil. Ind. Crops Prod. 2019, 138, 111590. [Google Scholar] [CrossRef]
- El Kantar, S.; Koubaa, M. Valorization of Low-Cost Substrates for the Production of Odd Chain Fatty Acids by the Oleaginous Yeast Yarrowia lipolytica. Fermentation 2022, 8, 284. [Google Scholar] [CrossRef]
- Gottardi, D.; Siroli, L.; Braschi, G.; Rossi, S.; Bains, N.; Vannini, L.; Patrignani, F.; Lanciotti, R. Selection of Yarrowia lipolytica Strains as Possible Solution to Valorize Untreated Cheese Whey. Fermentation 2023, 9, 51. [Google Scholar] [CrossRef]
- Gao, R.; Li, Z.; Zhou, X.; Bao, W.; Cheng, S.; Zheng, L. Enhanced lipid production by Yarrowia lipolytica cultured with synthetic and waste-derived high-content volatile fatty acids under alkaline conditions. Biotechnol. Biofuels 2020, 13, 3. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Chevalot, I.; Komaitis, M.; Marc, I.; Aggelis, G. Single cell oil production by Yarrowia lipolytica growing on an industrial derivative of animal fat in batch cultures. Appl. Microbiol. Biotechnol. 2002, 58, 308–312. [Google Scholar] [CrossRef]
- Carreira, A.; Ferreira, L.M.; Loureiro, V. Brown pigments produced by Yarrowia lipolytica result from extracellular accumulation of homogentisic acid. Appl. Environ. Microbiol. 2001, 67, 3463–3468. [Google Scholar] [CrossRef]
- Larroude, M.; Onésime, D.; Rué, O.; Nicaud, J.-M.; Rossignol, T. A Yarrowia lipolytica Strain Engineered for Pyomelanin Production. Microorganisms 2021, 9, 838. [Google Scholar] [CrossRef]
- Bruder, S.; Melcher, F.A.; Zoll, T.; Hackenschmidt, S.; Kabisch, J. Evaluation of a Yarrowia lipolytica Strain Collection for Its Lipid and Carotenoid Production Capabilities. Eur. J. Lipid Sci. Technol. 2020, 122, 1900172. [Google Scholar] [CrossRef]
- Carsanba, E.; Papanikolaou, S.; Fickers, P.; Erten, H. Screening various Yarrowia lipolytica strains for citric acid production. Yeast 2019, 36, 319–327. [Google Scholar] [CrossRef]
- Liu, X.; Lv, J.; Xu, J.; Zhang, T.; Deng, Y.; He, J. Citric Acid Production in Yarrowia lipolytica SWJ-1b Yeast When Grown on Waste Cooking Oil. Appl. Biochem. Biotechnol. 2015, 175, 2347–2356. [Google Scholar] [CrossRef] [PubMed]
- Sayın Börekçi, B.; Kaya, M.; Kaban, G. Citric Acid Production by Yarrowia lipolytica NRRL Y-1094: Optimization of pH, Fermentation Time and Glucose Concentration Using Response Surface Methodology. Fermentation 2022, 8, 731. [Google Scholar] [CrossRef]
- Du, Y.-H.; Wang, M.-Y.; Yang, L.-H.; Tong, L.-L.; Guo, D.-S.; Ji, X.-J. Optimization and Scale-Up of Fermentation Processes Driven by Models. Bioengineering 2022, 9, 473. [Google Scholar] [CrossRef]
- Helleckes, L.M.; Hemmerich, J.; Wiechert, W.; von Lieres, E.; Grünberger, A. Machine learning in bioprocess development: From promise to practice. Trends Biotechnol. 2022. [Google Scholar] [CrossRef]
- Ciliberti, C.; Biundo, A.; Colacicco, M.; Agrimi, G.; Isabella, P. Physiological Characterisation of Yarrowia lipolytica Cultures Grown on Alternative Carbon Sources to Develop Microbial Platforms for Waste Cooking Oils Valorisation. Chem. Eng. Trans. 2022, 93, 241–246. [Google Scholar]
- Hackenschmidt, S.; Bracharz, F.; Daniel, R.; Thürmer, A.; Bruder, S.; Kabisch, J. Effects of a high-cultivation temperature on the physiology of three different Yarrowia lipolytica strains. FEMS Yeast Res. 2019, 19, foz068. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, F.A.; Colen, G.; Takahashi, J.A. Yarrowia lipolytica and its multiple applications in the biotechnological industry. TheScientificWorldJournal 2014, 2014, 476207. [Google Scholar] [CrossRef] [PubMed]
- Mookiah, V.P.; Kasimani, R.; Pandian, S.; Asokan, T. Study on the Effects of Initial pH, Temperature and Agitation Speed on Lipid Production by Yarrowia lipolytica and Chlorella vulgaris using Sago Wastewater as a Substrate. 2020. Available online: https://tierarztliche.com/gallery/v40.53.pdf (accessed on 12 January 2023).
- Mukhtar, H.; Suliman, S.M.; Shabbir, A.; Mumtaz, M.W.; Rashid, U.; Rahimuddin, S.A. Evaluating the Potential of Oleaginous Yeasts as Feedstock for Biodiesel Production. Protein Pept. Lett. 2018, 25, 195–201. [Google Scholar] [CrossRef]
- Czajka, J.J.; Oyetunde, T.; Tang, Y.J. Integrated knowledge mining, genome-scale modeling, and machine learning for predicting Yarrowia lipolytica bioproduction. Metab. Eng. 2021, 67, 227–236. [Google Scholar] [CrossRef]
- Coşgun, A.; Günay, M.E.; Yıldırım, R. Analysis of lipid production from Yarrowia lipolytica for renewable fuel production by machine learning. Fuel 2022, 315, 122817. [Google Scholar] [CrossRef]
- Zhao, C.; Gu, D.; Nambou, K.; Wei, L.; Chen, J.; Imanaka, T.; Hua, Q. Metabolome analysis and pathway abundance profiling of Yarrowia lipolytica cultivated on different carbon sources. J. Biotechnol. 2015, 206, 42–51. [Google Scholar] [CrossRef] [PubMed]
- Golugula, A.; Lee, G.; Madabhushi, A. Evaluating feature selection strategies for high dimensional, small sample size datasets. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 949–952. [Google Scholar]
- Louhasakul, Y.; Cheirsilp, B.; Prasertsan, P. Valorization of Palm Oil Mill Effluent into Lipid and Cell-Bound Lipase by Marine Yeast Yarrowia lipolytica and Their Application in Biodiesel Production. Waste Biomass Valorization 2016, 7, 417–426. [Google Scholar] [CrossRef]
- Intasit, R.; Cheirsilp, B.; Yeesang, J. Selection of Oleaginous Yeasts and their Use for Lipid Production from Oil Palm Sap. In Proceedings of the National and International Graduate Research Conference 2016, Khon Kaen, Thailand, 15 January 2016. [Google Scholar]
- Louhasakul, Y.; Cheirsilp, B. Industrial waste utilization for low-cost production of raw material oil through microbial fermentation. Appl. Biochem. Biotechnol. 2013, 169, 110–122. [Google Scholar] [CrossRef]
- Louhasakul, Y.; Cheirsilp, B.; Treu, L.; Kougias, P.G.; Angelidaki, I. Metagenomic insights into bioaugmentation and biovalorization of oily industrial wastes by lipolytic oleaginous yeast Yarrowia lipolytica during successive batch fermentation. Biotechnol. Appl. Biochem. 2020, 67, 1020–1029. [Google Scholar] [CrossRef] [PubMed]
- Louhasakul, Y.; Cheirsilp, B.; Intasit, R.; Maneerat, S.; Saimmai, A. Enhanced valorization of industrial wastes for biodiesel feedstocks and biocatalyst by lipolytic oleaginous yeast and biosurfactant-producing bacteria. Int. Biodeterior. Biodegrad. 2020, 148, 104911. [Google Scholar] [CrossRef]
- Kebabci, Ö.; Cihangir, N. Comparison of three Yarrowia lipolytica strains for lipase production: NBRC 1658, IFO 1195, and a local strain. Turk. J. Biol. 2012, 36, 15–24. [Google Scholar] [CrossRef]
- Darvishi, F.; Nahvi, I.; Zarkesh-Esfahani, H.; Momenbeik, F. Effect of plant oils upon lipase and citric acid production in Yarrowia lipolytica yeast. J. Biomed. Biotechnol. 2009, 2009, 562943. [Google Scholar] [CrossRef] [PubMed]
- Fickers, P.; Destain, J.; Thonart, P. Improvement of Yarrowia lipolytica lipase production by fed-batch fermentation. J. Basic Microbiol. 2009, 49, 212–215. [Google Scholar] [CrossRef]
- Moftah, O.A.S.; Grbavcic, S.Z.; Moftah, W.A.; Luković, N.D.; Prodanović, O.; Jakovetic, S.M.; Knezevic-Jugović, Z.D. Lipase production by Yarrowia lipolytica using olive oil processing wastes as substrates. J. Serb. Chem. Soc. 2013, 78, 781–794. [Google Scholar] [CrossRef]
- Fickers, P.; Ongena, M.; Destain, J.; Weekers, F.; Thonart, P. Production and down-stream processing of an extracellular lipase from the yeast Yarrowia lipolytica. Enzym. Microb. Technol. 2006, 38, 756–759. [Google Scholar] [CrossRef]
- Gonçalves, F.; Colen, G.; Takahashi, J. Optimization of cultivation conditions for extracellular lipase production by Yarrowia lipolytica using response surface method. Afr. J. Biotechnol. 2013, 12, 2270–2278. [Google Scholar] [CrossRef]
- Magdouli, S.; Guedri, T.; Tarek, R.; Brar, S.K.; Blais, J.F. Valorization of raw glycerol and crustacean waste into value added products by Yarrowia lipolytica. Bioresour. Technol. 2017, 243, 57–68. [Google Scholar] [CrossRef] [PubMed]
- Pereira, A.d.S.; Fontes-Sant’Ana, G.C.; Amaral, P.F. Mango agro-industrial wastes for lipase production from Yarrowia lipolytica and the potential of the fermented solid as a biocatalyst. Food Bioprod. Process. 2019, 115, 68–77. [Google Scholar] [CrossRef]
- Corzo, G.; Revah, S. Production and characteristics of the lipase from Yarrowia lipolytica 681. Bioresour. Technol. 1999, 70, 173–180. [Google Scholar] [CrossRef]
- Nambou, K.; Zhao, C.; Wei, L.; Chen, J.; Imanaka, T.; Hua, Q. Designing of a “cheap to run” fermentation platform for an enhanced production of single cell oil from Yarrowia lipolytica DSM3286 as a potential feedstock for biodiesel. Bioresour. Technol. 2014, 173, 324–333. [Google Scholar] [CrossRef]
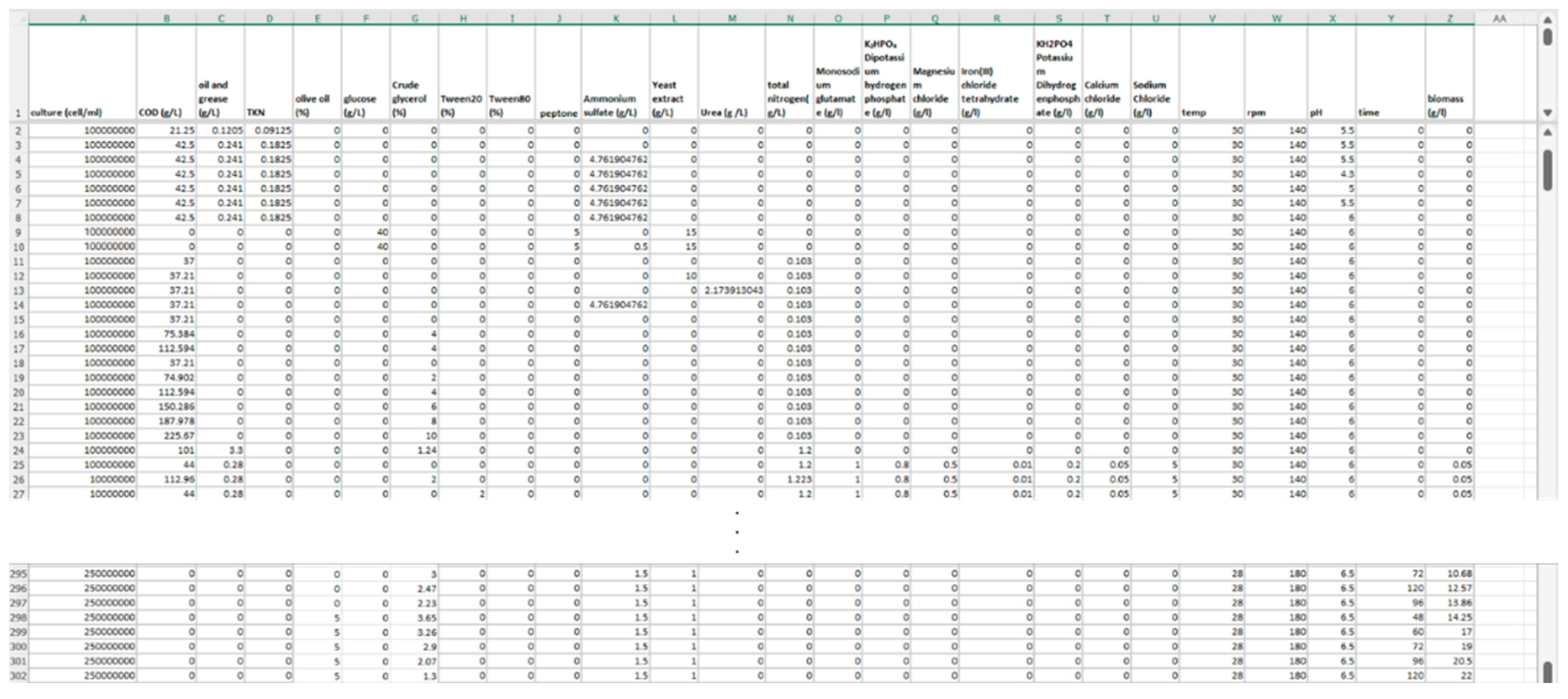
| Attribute No. | Attribute Symbol | Details | Unit | Min | Max | ||
|---|---|---|---|---|---|---|---|
| Predictors | |||||||
| (1) | Inoculum size | cell/mL | 1.07 × 108 | 1.00 × 107 | 2.50 × 108 | 4.02 × 107 | |
| (2) | COD | Chemical oxygen demand | g/L | 70.28 | 0.00 | 225.67 | 48.93 |
| (3) | Oil and grease | g/L | 1.26 | 0.00 | 8.42 | 1.93 | |
| (4) | TKN | Total Kjeldahl nitrogen | g/L | 0.03 | 0.00 | 0.18 | 0.06 |
| (5) | Olive oil | % | 0.15 | 0.00 | 5.00 | 0.85 | |
| (6) | Glucose | C₆H₁₂O₆ | g/L | 1.06 | 0.00 | 40.00 | 6.44 |
| (7) | Crude glycerol | % | 1.58 | 0.00 | 10.00 | 2.26 | |
| (8) | Tween20 | % | 0.05 | 0.00 | 2.00 | 0.30 | |
| (9) | Tween80 | % | 0.05 | 0.00 | 2.00 | 0.30 | |
| (10) | Peptone | g/L | 0.13 | 0.00 | 5.00 | 0.81 | |
| (11) | Ammonium sulfate | g/L | 0.76 | 0.00 | 4.76 | 1.65 | |
| (12) | Yeast extract | g/L | 0.69 | 0.00 | 15.00 | 2.81 | |
| (13) | Urea | g/L | 0.05 | 0.00 | 2.17 | 0.33 | |
| (14) | Total nitrogen | g/L | 0.53 | 0.00 | 1.24 | 0.56 | |
| (15) | Monosodium glutamate | C₅H₈NO₄Na | g/L | 0.11 | 0.00 | 1.00 | 0.31 |
| (16) | Di-potassium hydrogen phosphate | K₂HPO₄ | g/L | 0.09 | 0.00 | 0.80 | 0.25 |
| (17) | Magnesium chloride | MgCl2 | g/L | 0.05 | 0.00 | 0.50 | 0.15 |
| (18) | Iron (III) chloride | FeCl3 | g/L | 0.0011 | 0.00 | 0.0100 | 0.0031 |
| (19) | Potassium dihydrogen phosphate | KH2PO4 | g/L | 0.02 | 0.00 | 0.20 | 0.06 |
| (20) | Calcium chloride | CaCl2 | g/L | 0.01 | 0.00 | 0.05 | 0.02 |
| (21) | Sodium chloride | NaCl | g/L | 0.53 | 0.00 | 5.00 | 1.54 |
| (22) | Temperature | °C | 29.88 | 28.00 | 30.00 | 0.48 | |
| (23) | Shaking rate | rpm | 142.39 | 140.00 | 180.00 | 9.50 | |
| (24) | pH | 5.92 | 4.30 | 6.50 | 0.35 | ||
| (25) | Time | hours | 37.68 | 0.00 | 120.00 | 25.50 | |
| Response (label) | |||||||
| (26) | Biomass | g/L | 3.50 | 0.00 | 22.00 | 2.83 | |
| Model Type | Model Details | 5-Fold Cross-Validation RMSE Calculated from the Training Dataset in (g/L) | 5-Fold Cross-Validation R2 Calculated from the Training Dataset | 5-Fold Cross-Validation MAE Calculated from the Training Dataset in (g/L) |
|---|---|---|---|---|
| Linear regression | Linear | 1.44 | 0.77 | 0.98 |
| Interactions linear | 3.20 | -0.13 | 1.20 | |
| Robust linear | 1.62 | 0.71 | 0.92 | |
| Stepwise linear regression | Stepwise linear | 1.34 | 0.79 | 0.79 |
| Tree | Fine tree | 1.66 | 0.67 | 0.89 |
| Medium tree | 1.92 | 0.56 | 0.94 | |
| Coarse tree | 2.33 | 0.35 | 1.37 | |
| Support vector machine (SVM) | Linear SVM | 1.47 | 0.76 | 0.93 |
| Quadratic SVM | 3.96 | -0.75 | 0.99 | |
| Cubic SVM | 2.69 | 0.20 | 0.95 | |
| Fine Gaussian SVM | 2.34 | 0.39 | 1.01 | |
| Medium Gaussian SVM | 2.03 | 0.54 | 1.15 | |
| Coarse Gaussian SVM | 2.34 | 0.39 | 1.35 | |
| Ensemble | Boosted trees | 1.30 | 0.80 | 0.74 |
| Bagged trees | 1.67 | 0.67 | 0.94 | |
| Gaussian process regression (GPR) | Squared exponential GPR | 0.73 | 0.94 | 0.54 |
| Matern 5/2 GPR | 0.72 | 0.94 | 0.52 | |
| Exponential GPR | 0.77 | 0.93 | 0.54 | |
| Rational quadratic GPR | 0.73 | 0.94 | 0.53 | |
| Neural network | Narrow neural network | 1.19 | 0.84 | 0.68 |
| Medium neural network | 1.18 | 0.85 | 0.74 | |
| Wide neural network | 1.15 | 0.85 | 0.70 | |
| Bilayered neural network | 0.99 | 0.89 | 0.67 | |
| Trilayered neural network | 1.31 | 0.81 | 0.88 | |
| Kernel | SVM kernel | 2.75 | 0.16 | 1.39 |
| Least squares regression kernel | 2.47 | 0.32 | 1.33 |
| Model Type | Model Details | Average RMSE in (g/L) | Average R2 | Average MAE in (g/L) |
|---|---|---|---|---|
| Linear regression | Linear | 1.31 | 0.72 | 0.92 |
| Interactions linear | 5.21 | −5.61 | 1.71 | |
| Robust linear | 1.72 | 0.47 | 0.91 | |
| Stepwise linear regression | Stepwise linear | 1.26 | 0.74 | 0.80 |
| Tree | Fine tree | 1.39 | 0.68 | 0.76 |
| Medium tree | 1.43 | 0.67 | 0.83 | |
| Coarse tree | 1.94 | 0.37 | 1.23 | |
| Support vector machine (SVM) | Linear SVM | 1.36 | 0.70 | 0.87 |
| Quadratic SVM | 2.88 | −0.25 | 0.93 | |
| Cubic SVM | 2.07 | 0.36 | 0.92 | |
| Fine Gaussian SVM | 1.72 | 0.55 | 0.88 | |
| Medium Gaussian SVM | 1.46 | 0.68 | 0.90 | |
| Coarse Gaussian SVM | 1.83 | 0.49 | 1.19 | |
| Ensemble | Boosted trees | 1.12 | 0.79 | 0.69 |
| Bagged trees | 1.23 | 0.75 | 0.79 | |
| Gaussian process regression (GPR) | Squared exponential GPR | 0.80 | 0.88 | 0.56 |
| Matern 5/2 GPR | 0.75 | 0.90 | 0.52 | |
| Exponential GPR | 0.75 | 0.90 | 0.51 | |
| Rational quadratic GPR | 0.76 | 0.90 | 0.53 | |
| Neural network | Narrow neural network | 1.10 | 0.80 | 0.70 |
| Medium neural network | 1.54 | 0.51 | 0.81 | |
| Wide neural network | 1.26 | 0.71 | 0.74 | |
| Bilayered neural network | 0.99 | 0.83 | 0.67 | |
| Trilayered neural network | 1.12 | 0.80 | 0.73 | |
| Kernel | SVM kernel | 2.12 | 0.32 | 1.18 |
| Least squares regression kernel | 2.05 | 0.35 | 1.19 |
| Predictor | f-test |
|---|---|
| Significant parameters | |
| (25) Time | 0.48 |
| (10) Peptone | 0.36 |
| (22) Temperature | 0.36 |
| (4) TKN | 0.36 |
| (23) Shaking rate | 0.22 |
| (14) Total nitrogen | 0.21 |
| (1) Inoculum size | 0.18 |
| (12) Yeast extract | 0.16 |
| (7) Crude glycerol | 0.16 |
| (6) Glucose | 0.13 |
| (3) Oil and grease | 0.12 |
| (24) pH | 0.12 |
| (11) Ammonium sulfate | 0.08 |
| (5) Olive oil | 0.05 |
| Insignificant parameters | |
| (9) Tween80 | 0.04 |
| (19) Potassium di-hydrogen phosphate: KH2PO4 | 0.02 |
| (20) Calcium chloride | 0.02 |
| (21) Sodium chloride | 0.02 |
| (15) Monosodium glutamate | 0.02 |
| (16) Di-potassium hydrogen phosphate: K₂HPO₄ | 0.02 |
| (13) Urea | 0.02 |
| (17) Magnesium chloride | 0.02 |
| (18) Iron (III) chloride tetrahydrate | 0.02 |
| (8) Tween20 | 0.01 |
| (2) COD | 0.00 |
| Number of Predictors | Predictors | Training RMSE (g/L) | Training R2 | Training MAE (g/L) | Test RMSE (g/L) | Test R2 | Test MAE (g/L) |
|---|---|---|---|---|---|---|---|
| 1 | (25) | 2.19 | 0.43 | 1.28 | 2.15 | 0.30 | 1.25 |
| 2 | (25), (10) | 1.97 | 0.53 | 1.19 | 2.14 | 0.30 | 1.23 |
| 3 | (25), (10), (22) | 1.49 | 0.74 | 0.99 | 1.14 | 0.80 | 0.87 |
| 4 | (25), (10), (22), (4) | 1.50 | 0.73 | 0.95 | 1.15 | 0.80 | 0.88 |
| 5 | (25), (10), (22), (4), (23) | 1.41 | 0.76 | 0.95 | 1.16 | 0.80 | 0.88 |
| 6 | (25), (10), (22), (4), (23), (14) | 1.29 | 0.80 | 0.83 | 1.06 | 0.83 | 0.76 |
| 7 | (25), (10), (22), (4), (23), (14), (1) | 1.46 | 0.76 | 0.84 | 1.08 | 0.83 | 0.77 |
| 8 | (25), (10), (22), (4), (23), (14), (1), (12) | 1.54 | 0.74 | 0.87 | 1.08 | 0.83 | 0.76 |
| 9 | (25), (10), (22), (4), (23), (14), (1), (12), (7) | 1.37 | 0.79 | 0.81 | 1.06 | 0.84 | 0.74 |
| 10 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6) | 1.33 | 0.81 | 0.80 | 1.06 | 0.84 | 0.74 |
| 11 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3) | 1.23 | 0.83 | 0.74 | 1.02 | 0.85 | 0.69 |
| 12 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24) | 1.33 | 0.81 | 0.74 | 0.91 | 0.88 | 0.59 |
| 13 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11) | 1.34 | 0.80 | 0.78 | 0.90 | 0.88 | 0.57 |
| 14 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5) | 0.73 | 0.94 | 0.53 | 0.60 | 0.95 | 0.43 |
| 15 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9) | 0.94 | 0.90 | 0.57 | 0.60 | 0.95 | 0.43 |
| 16 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19) | 1.48 | 0.76 | 0.67 | 0.63 | 0.94 | 0.44 |
| 17 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19), (20) | 0.74 | 0.94 | 0.53 | 0.63 | 0.94 | 0.44 |
| 18 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19), (20), (21) | 0.66 | 0.95 | 0.49 | 0.63 | 0.94 | 0.44 |
| 19 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19), (20), (21), (15) | 0.84 | 0.92 | 0.54 | 0.63 | 0.94 | 0.44 |
| 20 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19), (20), (21), (15), (16) | 0.77 | 0.94 | 0.55 | 0.63 | 0.94 | 0.44 |
| 21 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19), (20), (21), (15), (16), (13) | 0.75 | 0.94 | 0.53 | 0.63 | 0.94 | 0.44 |
| 22 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19), (20), (21), (15), (16), (13), (17) | 0.71 | 0.94 | 0.52 | 0.63 | 0.94 | 0.44 |
| 23 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19), (20), (21), (15), (16), (13), (17), (18) | 0.69 | 0.95 | 0.50 | 0.63 | 0.94 | 0.44 |
| 24 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19), (20), (21), (15), (16), (13), (17), (18), (8) | 0.79 | 0.93 | 0.55 | 0.63 | 0.94 | 0.55 |
| 25 | (25), (10), (22), (4), (23), (14), (1), (12), (7), (6), (3), (24), (11), (5), (9), (19), (20), (21), (15), (16), (13), (17), (18), (8), (2) | 0.69 | 0.95 | 0.51 | 0.77 | 0.91 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pensupa, N.; Treebuppachartsakul, T.; Pechprasarn, S. Machine Learning Models Using Data Mining for Biomass Production from Yarrowia lipolytica Fermentation. Fermentation 2023, 9, 239. https://doi.org/10.3390/fermentation9030239
Pensupa N, Treebuppachartsakul T, Pechprasarn S. Machine Learning Models Using Data Mining for Biomass Production from Yarrowia lipolytica Fermentation. Fermentation. 2023; 9(3):239. https://doi.org/10.3390/fermentation9030239
Chicago/Turabian StylePensupa, Nattha, Treesukon Treebuppachartsakul, and Suejit Pechprasarn. 2023. "Machine Learning Models Using Data Mining for Biomass Production from Yarrowia lipolytica Fermentation" Fermentation 9, no. 3: 239. https://doi.org/10.3390/fermentation9030239
APA StylePensupa, N., Treebuppachartsakul, T., & Pechprasarn, S. (2023). Machine Learning Models Using Data Mining for Biomass Production from Yarrowia lipolytica Fermentation. Fermentation, 9(3), 239. https://doi.org/10.3390/fermentation9030239






