Investigating a Stirred Bioreactor: Impact of Evolving Fermentation Broth Pseudoplastic Rheology on Mixing Mechanisms

Abstract

The culture medium in many fermentations is a non-Newtonian fluid. In bacterial alginate batch production, the broth becomes more pseudoplastic as the alginate concentration increases, which impairs the mixing process. This work characterizes the effect of the interaction between changing broth rheology and impeller mixing on a bioreactor fluid dynamics. Experimentally, a fermentation with evolving broth pseudoplastic rheology is reproduced. Three fermentation stages are mimicked using appropriate solutions of water and xanthan gum. Impeller torque measurements are reported. The weakening of the impellers’ interaction over the fermentation process is identified. To overcome the experimental limitations, CFD is applied to study the evolution of the fermentation fluid flow patterns, velocity field, dead zones, and vortical structures. Precessional vortex macro-instabilities are identified as being responsible for the unstable flow patterns identified at the earlier stages of the fermentation. A stable parallel flow pattern accounts for the weakest impellers’ interaction at the final stage. Overall, this work contributes with a complete workflow to adapt CFD models for characterization and aided design of stirred tanks with changing broth pseudoplastic rheology as well as an evolving flow regime.

1. Introduction

Many of the products and services in daily use are the result of the activity of microorganisms grown in bioreactors. In many of those fermentation processes, the culture medium is a non-Newtonian fluid as a result of the content and nature of microorganisms and the presence of solids or polymeric substances. Some examples of such processes are fungi cultivation, wastewater treatment, and the production of extracellular biopolymers [1].

When those bioprocesses are running in batch mode, the rheological properties of the culture medium change over time as the fermentation evolves, such as in the case of microbial alginate production. Alginate is a biopolymer secreted by bacteria, such as Azotobacter vinellandi. It has been reported that the culture medium becomes a non-Newtonian pseudoplastic fluid as the alginate concentration increases over the course of batch fermentation. The broth viscosity, at a shear rate of 12 s⁻¹, can increase from 1 mPa∙s up to about 100 mPa∙s [2]. The alginate production requires aeration, however, the oxygen mass transfer—as well as the mass transfer of other metabolites—is impaired by the highly viscous culture medium, adversely affecting the production of the biopolymer [3].

The mass transfer in a stirred bioreactor depends upon mixing mechanisms at different scales. The macromixing occurs on the scale of the entire reactor and determines the environment for the mixing at the smaller scales. The mesomixing is caused by the turbulent diffusion and the disintegration of large eddies into smaller eddies. The micromixing happens on the smallest scale, the molecular level, such as by molecular diffusion and drops deformation [4,5]. Models have been proposed to predict the volumetric mass transfer coefficient based on the contribution of these mechanisms. However, the effect of the larger-scale mechanisms remains highly unpredictable [6]. That is because the macro and mesomixing depend on the interaction of several factors such as the reactor geometry, the fluid characteristics, and the operating conditions. In particular, the onset of large macro-instability vortices has a significant impact on the mass transfer process. However, their apparition and extent are not easily predictable.

Computational fluid dynamics (CFD) has been widely used to characterize the mixing of stirred bioreactors. Nonetheless, in many of the reported models, the liquid phase properties used were taken as those of water, even when a non-Newtonian fluid was known to develop. This has been the case in several simulations related to anaerobic digestion [7]. More striking is that, to the best of our knowledge, only Hou et al. [8] and Bach et al. [9] have dealt with systems with changing rheological properties by simulating the different stages of the process separately. The former studied the effect of the fluid rheology on the power consumption and mixing time, while the latter analyzed the distribution of the volumetric mass transfer coefficient. However, in both cases, the mixing mechanisms were not explored.

The research group led by Farhad Ein-Mozaffari has several works on CFD modelling of stirred tanks mixing non-Newtonian fluids, mostly related to the study of gas dispersion [10,11,12,13,14,15]. These works address the effect of the mixing on the gas hold-up and power consumption under laminar flow conditions only. Few works have studied mixed tanks with non-Newtonian fluids under turbulent flow conditions [9,16,17,18,19,20]. This is because the turbulence models more widely applied in CFD modelling of bioprocesses were developed to be used with Newtonian fluids, and, therefore, their application with non-Newtonian fluids presents some numerical challenges [18,21]. Thus, the onset of macro-instabilities has not been analyzed for stirred bioreactors mixing fluids with an evolving pseudoplastic behaviour and, least of all, with a changing flow regime.

The purpose of the present work was to characterize the effect of the interaction between the changing rheological properties of the culture medium and the impeller mixing on the fluid dynamics of a baffled bioreactor. The alginate batch production was selected as a study case. An approach combining experimental and computational analysis was applied. Experimentally, the evolution of the rheological properties of the culture medium was characterized. The fermentation broth was mimicked by abiotic systems using appropriate solutions of water and xanthan gum that would represent the fermentation broth at various stages of the process. The fluid dynamics of the fermentation and the abiotic systems were experimentally studied through the impeller torque. CFD was applied to model the mimicked stages, to study the evolution of the fermentation fluid flow patterns, velocity field, dead zones, and vortical structures, which experimentally would be impossible to characterize. The main contribution of this study is to provide validated CFD configurations able to predict the effect of changing rheological properties on the mixing mechanisms of bioprocesses involving stirred reactors. To the best of our knowledge, although many papers have applied CFD to address the fluid dynamics of mixing systems with static fluid properties, this is the first work characterizing the macro-instabilities of a baffled stirred bioreactor with changing broth rheology and an evolving flow regime.

2. Materials and Methods

2.1. Stirred Vessel Configuration

The stirred reactor used in this study was a 5.0 L fermentor (BioFlo 3000, New Brunswick Scientific, Enfield, CT, USA) with a working volume of 4.0 L. The reactor was equipped with dual Rushton turbines, four baffles, four probes, and a sparger. A torsion angle-type torque meter (RWT 421-EE 100 Nm) was attached to the impeller shaft and connected to a computer to record the torque data. The reactor and its dimensions are shown in Figure 1.

2.2. Bacterial Alginate Batch Production

The bacterial alginate batch fermentation was studied in the described bioreactor. Azotobacter vinelandii (ATCC9046) strain was used. Experiments were performed in triplicate as reported in Sadino-Riquelme et al. [22]. During the fermentation, the temperature was maintained at 30 °C, the impeller speed was 400 rpm, and the aeration rate was 4.0 L/min (1 vvm). Samples of 30 mL were withdrawn at different times to analyze the relationship between alginate concentration and the culture medium density and rheology. The alginate concentration was determined gravimetrically. The density was estimated using the mass to volume ratio. The rheological characterization was performed using a cone and plate viscometer (Brookfield DV-II+, UL spindle) with a temperature bath at 30 °C. The spindle rotational speed was varied between 1 and 100 rpm, keeping a torque value between 10 and 99 %. The power-law model parameters, consistency coefficient ($K$) and power-law index ($n$), were fitted from the shear rate ($\dot{\gamma }$) versus shear stress ($\tau$) curve, according to Equation (1).

$$\tau =K{\dot{\gamma }}^n$$

(1)

The torque data were recorded over the whole fermentation. The torque measured for the impeller rotating in the empty tank (blank) was subtracted from the data to eliminate the shaft friction effect.

2.3. Abiotic Systems

Three fluids were chosen to mimic the fluid dynamics of the fermentation broth at the beginning, intermediate and final stages of the alginate production. For that purpose, each fluid had density and rheological parameters similar to the broth in the respective stage. Distilled water was selected because its density and viscosity are similar to that of the culture medium Newtonian properties at time 0 h. In order to mimic the pseudoplastic behaviour that develops in the culture medium when the alginate concentration increases, two solutions were chosen, named Xanthan Sol A and Xanthan Sol B, which were prepared with distilled water and xanthan gum at a concentration of 0.75 and 0.25 mg/mL, respectively. Xanthan Sol A was selected because its viscosity moves between 20 and 100 mPa∙s at low shear rates, as expected for the final stage of the fermentation. Under the same shear rate, Xanthan Sol B has a lower viscosity than Xanthan Sol A, so Xanthan Sol B was used to represent an intermediate stage of the process. Specifically, at a shear rate of 12 s⁻¹, the viscosity of Xanthan Sol A and Xanthan Sol B is 33 and 8 mPa∙s, respectively (see Appendix A). The rheological and physical properties of the fluids, at 30 °C, used for the implementation of the abiotic systems, are described in

Table 1. Characterization of the mimicking fluids used in the abiotic systems.

Fluid Properties	Water	Xanthan Sol B	Xanthan Sol A
Density [kg/m3]	998	1006	1023
Viscosity [Pa·s]	0.001	-	-
Consistency coefficient [Pa·sn]	-	0.0193	0.1173
Power-law index [ ]	-	0.6416	0.4840

. It is important to note that these parameters were defined based on the characterization of the raw broth of the fermentation, so the effect of the alginate and other culture medium components on its properties were incorporated.

For each abiotic system, the reactor was filled with 4.0 L of fluid, and the temperature was controlled at 30 °C. The impellers rotated at 400 rpm, which was the same speed used in the fermentation, however, the abiotic systems were operated without aeration. To double-check that the selected fluids were able to mimic the fluid dynamics of the bioprocess, Xanthan Sol A and Xanthan Sol B were used to implement a system with dynamic rheological properties under operating conditions similar to the fermentation, confirming the suitability of the abiotic systems for the purpose of the present work (see Appendix B).

For each fluid, the torque was recorded for between 10 and 16 min, with the system initially at rest. The time-averaged torque was calculated as the average ($T_{AV{G}_{exp}}$) and standard deviation ($T_{S{D}_{exp}}$) of the experimental torque over the last six minutes of data to characterize the stationary state of each system. The torque measured for the impeller rotating in the empty tank was subtracted from the data to eliminate the shaft friction effect (zeroing). The correctness of the experimental torque data was double-checked against empirically estimated values (see Appendix C).

For further characterization of the abiotic systems, their Reynolds number was estimated. For the case of the Newtonian fluid, the Reynolds number ($\mathrm{Re}$) was calculated using Equation (2). The Reynolds number of the non-Newtonian fluids (${\mathrm{Re}}^{\ast }$) was calculated using Equation (3) [24].

$$\mathrm{Re}=\frac{\rho N{D}^2}{\mu }$$

(2)

$${\mathrm{Re}}^{\ast }=\frac{\rho N^{2-n}{D}^2}{K{k}_s^{n-1}}$$

(3)

where $\rho$, $\mu$, $N$ and $D$ are, respectively, the fluid density, the fluid viscosity, the impeller speed, and the impeller diameter. $k_s$ is the proportionality constant between the mean fluid shear rate and the impeller speed, and its value was assumed equal to 11, based on the evidence provided by Metzner et al. [25]. It is important to mention that Metzner et al. [25] provided experimental evidence that ks could be assumed as constant for systems with flat-bladed turbine impellers with Reynolds numbers between 2 and 1760. However, the ${\mathrm{Re}}^{\ast }$ values estimated for the abiotic systems may be out of that range. Nonetheless, let us consider that the error of this empirical method is already ±20% [25] and, therefore, the error included by using a different value of ks may be negligible when it is compared to the error of the approach itself. Thus, although the validity of the use of this method could be arguable, it provided us a useful reference to analyze the evolution of the flow regimes and impeller torque.

2.4. CFD Modelling of Abiotic Systems

The bioreactor three-dimensional domain was built using Ansys Design Modeler. The domain included the impellers, baffles, probes, and air sparger (See Figure 2a). The mesh was implemented in Ansys Meshing. The hybrid mesh had 2,843,027 nodes (See Figure 2b–d). Details of the implementation and analysis of the geometry and mesh are described in Sadino-Riquelme et al. [23].

The CFD models were adapted in Ansys Fluent (versions 18.2 and 2019R3). The following assumptions were considered to model each abiotic system: it contains only the liquid mimicking the broth properties at a certain fermentation stage, and the liquid-air interface surface is flat. Thus, the described systems were modeled as single-phase. In line with the experimental results, the non-Newtonian fluids were characterized as pseudoplastic, using the power-law model. Therefore, for the models adapted for the abiotic systems with Xanthan Sol A and Xanthan Sol B, the viscosity depends on the rheological parameters and the local shear rates. The rheological parameters and the density of the fluids were considered static and homogeneous. In the case of the system with water, the density, as well as the viscosity, were assumed as static and homogeneous. The fluid properties given in Table 1 were used to model the abiotic systems.

The mixing of a third non-Newtonian pseudoplastic fluid, referred to as Xanthan Sol C, was modeled to evaluate the effect of a higher viscosity on the system fluid dynamics. Xanthan Sol C was characterized with the same properties as Xanthan Sol A, except for the consistency coefficient that was defined as 1.1731 Pa·sⁿ, which is one order of magnitude higher than for Xanthan Sol A.

To set up the non-Newtonian power-law model, the software Ansys Fluent required the specification of viscosity limits. For Xanthan Sol A and Xanthan Sol B, 10⁻⁵ and 1 Pa∙s was used, respectively, as lower and upper limit. For Xanthan Sol C, the lower and upper limits were defined as 0.001 and 300 Pa∙s, respectively. The selection of these values is discussed in Section 3.3.

In order to include the impeller mixing, the sliding mesh transient method was used, with a rotating velocity of 400 rpm for each moving zone. The gravity force was included in all the models.

The system with water was simulated as described in Sadino-Riquelme et al. [23] for the case with the SST k-omega turbulence model. SST k-omega was selected after a comparative analysis against the standard k-epsilon model, where it was proven that the latter model significantly smooths the velocity gradients, thus impairing the torque predictions [23].

In order to model the systems with Xanthan Sol A and Xanthan Sol B, two numerical configurations were evaluated, one with the SST k-omega turbulence model and the other one with the k-kl-omega transition model. In both cases, the simulations were initialized using the standard k-omega model, and after completing two impeller turns, the turbulence model was changed. Additionally, other settings were modified throughout the simulations, such as the discretization methods (except for pressure and gradient) and the time-step size, as detailed in Figure 3. The remaining settings were not modified and were the same for both configurations (see

Table 2. Settings shared by the CFD models of Xanthan Sol A and Xanthan Sol B.

Coupling Scheme	SIMPLE
Iterations	maximum 80 per time step. Iterations stop when all residuals are below 10−5 simultaneously.
Initial conditions	Velocity 0 m/s in all directions (that is, from rest) Turbulence parameters k = 0.1 m2/s2; ω=1 1/s
Boundary conditions	Top wall: symmetry
	Impeller and axis walls: relative velocity to moving zone 0 rpm
	Other walls: no-slip condition
Discretization methods	Gradient: Green Gauss node-based
	Pressure: PRESTO
Under-relaxation factors	Pressure: 0.2
	Density: 0.7
	Body forces: 0.7
	Turbulent viscosity: 0.8
	Others: default value

).

In the case of Xanthan Sol C, anticipating the future need of studying the effect of the aeration, a multi-phase Eulerian model with implicit volume fraction parameters formulation was used. Xanthan Sol C and air were defined as primary and secondary phases, respectively. However, the volume fraction of air was set equal to zero for the whole domain, and the volume fraction equation was disabled. Thus, in practice, a multi-phase model was adapted to represent a single-phase system.

The simulation of Xanthan Sol C was initialized using the standard k-omega model (with low-Re correction, shear flow corrections, and production limiter) with first-order discretization methods (except for pressure and gradient). After completing ten impeller turns, the turbulence model was shifted to laminar and the discretization methods to second-order. The remaining settings were set up as given in

Table 3. Settings used for the CFD model of Xanthan Sol C.

Coupling Scheme	Phase Coupled SIMPLE
Time-step size	0.0004 s
Iterations	maximum 60 per time step. Iterations stop when all residuals are below 10−5 simultaneously.
Initial conditions	Velocity 0 m/s in all directions (that is, from rest) Turbulence parameters k = 0.1 m2/s2; ε = 0.1 m2/s3
Boundary conditions	Top wall: degassing
	Impeller and axis walls: relative velocity to moving zone 0 rpm
	Other walls: no-slip condition
Interphase interactions	Interfacial area: ia-symmetric
	Others: none
Discretization methods	Gradient: Green Gauss node-based
	Pressure: PRESTO
Under-relaxation factors	Pressure: 0.2
	Density: 0.7
	Body forces: 0.5
	Momentum: 0.5
	Turbulent kinetic energy: 0.5
	Specific dissipation rate: 0.5
	Turbulent viscosity: 0.8
	Other: default value

.

The equations of the models can be found in Sadino Riquelme [26].

The decision to change the turbulence model to the k-kl-omega transition model or the laminar model was based on the analysis of the Reynolds number and the turbulent viscosity ratio of each abiotic system, as these parameters indicate whether the fluid flow is in the turbulent, transitional, or laminar regime. This numerical aspect, as well as the suitability of using a turbulence model for the mixing of non-Newtonian fluids, are further discussed in Section 3.3.

All the simulations were solved using double precision and a pressure-based solver with absolute velocity formulation. The discretization methods were used with warped-face gradient correction. The simulations were run on the Compute Canada clusters Graham and Cedar.

For the simulation of each abiotic system, 58 impeller turns were completed to ensure that the last 10 impeller turns were in the stationary state. As in Sadino-Riquelme et al. [23], the impeller torque and the velocity magnitude at different points were recorded after every time step. The monitoring points were located on a vertical central plane (see Appendix D). The data were used to identify the achievement of the stationary state and to discard the appearance of numerical issues. The occurrence of cells with turbulent viscosity ratio exceeding the maximum allowed value (10⁵) was discarded too. At the end of each time step, residuals values below 10⁻⁵ were expected as a convergence criterion.

Hereinafter, for ease of reference of the models, they will be named according to the fluid and the turbulence model used by the CFD configuration. Thus, XSolA-SSTkω and XSolA-kklω correspond to the models for Xanthan Sol A with, respectively, the SST k-omega and the k-kl-omega models. Similarly named are the models for Xanthan Sol B, XSolB-SSTkω, and XSolB-kklω. The models of the systems with water and Xanthan Sol C were named Water-SSTkω and XSolC-lam, respectively.

2.5. Mesh Analysis and Model Validation

A thorough mesh and time-step size analysis was performed for the simulation of the system with water, as reported in Sadino-Riquelme et al. [23]. Therefore, the simulations of the systems with non-Newtonian fluids were assumed to be independent of the mesh and time-step size, as well. To confirm this, we compared the instantaneous torque computed on the impeller (moving walls) versus on the stationary walls for the different abiotic systems.

The system with water was validated in Sadino-Riquelme et al. [23], based on the comparison of the impeller torque and radial velocity profiles with experimental data. Additionally, the models of the systems with the non-Newtonian fluids were validated based on the torque. For each abiotic system, the time-averaged torque was calculated as the average ($T_{AV{G}_{sim}}$) and standard deviation ($T_{S{D}_{sim}}$) of the data simulated over the last 10 impeller turns. For the validation of the models, the comparison error ($E$) between the simulated and experimental torque was estimated, using Equation (4), and compared with the validation uncertainty ($U_V$), as proposed by Coleman and Stern [27].

$$E=\frac{T_{AV{G}_{sim}}-T_{AV{G}_{exp}}}{T_{AV{G}_{exp}}}·100\%$$

(4)

2.6. Analysis of Mixing Mechanisms

In order to investigate the macro and mesomixing mechanisms, the existence of vortical structures was analyzed, based on the simulated data, using the software Tecplot™. The precessing vortex cores were extracted using the method of the velocity gradient eigenmodes. In order to visualize their directionality, streamtraces were drawn from the vortex cores. In addition, the trailing vortices were drawn as iso-surfaces of constant vorticity magnitude at 300, 240, and 180 s⁻¹.

Furthermore, the maximum turbulence length scale ($l$) in each abiotic system was estimated using a user-defined function with Equation (5). Similarly, to investigate the micromixing, the minimum Kolmogorov length scale (${\lambda }_K$) in each abiotic system was estimated, using a user-defined function with Equation (6). For the non-Newtonian fluids, the local viscosities were calculated using Equation (7).

$$l={0.09}^{3/4}·\frac{k^{3/2}}{\epsilon }$$

(5)

$${\lambda }_K={\left(\frac{{\left(\mu /\rho \right)}^3 }{\epsilon }\right)}^{1/4}$$

(6)

$$\mu =\frac{\tau }{\dot{\gamma }}$$

(7)

Additionally, the Schmidt number ($Sc$) of the abiotic systems was calculated with Equation (8). For the viscosity, the instantaneous volume-average value computed with the CFD models was used. The oxygen diffusion coefficient ($\mathcal{D}$) for alginate aqueous solutions was estimated from data reported by Ho et al. [28].

$$Sc=\frac{\mu /\rho }{\mathcal{D}}$$

(8)

3. Results and Discussions

3.1. Fermentation Broth Physical and Rheological Characterization

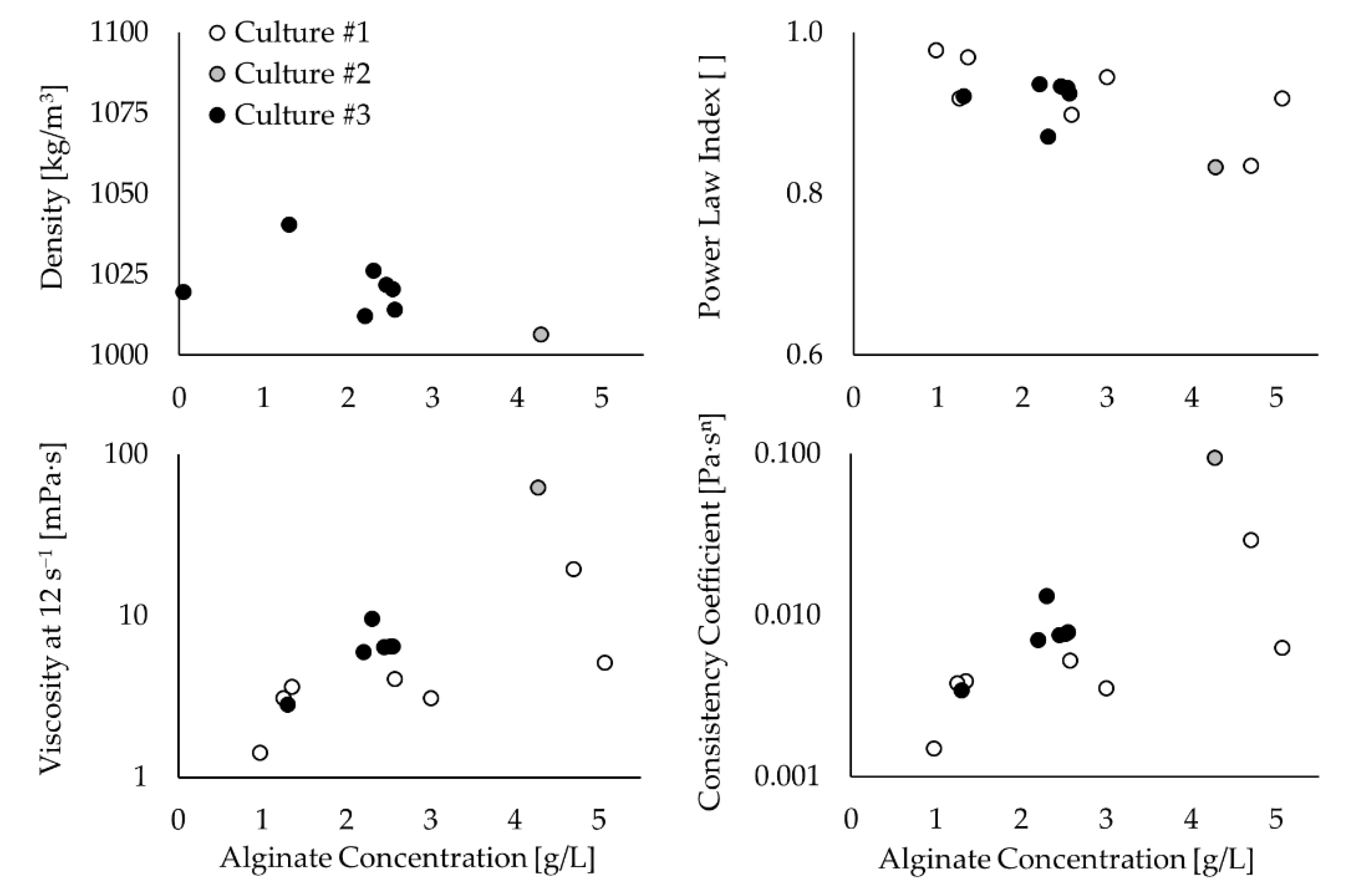
The rheological characterization of the fermentation samples confirmed the non-Newtonian pseudoplastic behaviour of the culture medium because the power-law index decreases below one as the alginate concentration increases (see Figure 4). Exceptions were found at alginate concentrations below 1 g/L when the culture medium behaves as a Newtonian fluid with a viscosity similar to water. On the other hand, the consistency coefficient shows a trend to increase with the alginate concentration but with very dispersed values. The density also shows scattered values but within a narrow range between 1000 kg/m³ and 1040 kg/m³ (see Figure 4).

The highest viscosity of the culture medium was associated with an alginate concentration of around 4.5 g/L, and varied between 19 and 62 mPa∙s (at 12 s⁻¹) among the cultures (see Figure 4). This result is in good agreement with Peña et al. [2], who reported viscosities between 20 and 420 mPa∙s (at 12 s⁻¹) for 4 g/L of alginate produced in a 1.0 L system stirred at 300 rpm by three Rushton turbines, under different controlled DOT values.

It is important to mention that the sampling from the cultures became more difficult as the alginate concentration increased because the mixing close to the sampler probe became poorer, and, therefore, the sample may not represent adequately other parts of the system. Furthermore, despite the existence of a pH control unit, the pH of the culture medium increased during the fermentations. This may also be due to the mixing problems triggered by the high viscosity of alginate. All these operational difficulties and the complex and inherently variable nature of the microorganisms may cause variations in the process itself. Indeed, the characteristics of the alginate aggregates changed during the process. This was observed after the precipitation and resuspension of alginate from the broth samples. For culture #1, the alginate aggregate of the samples at times 30 and 51 h had a disaggregated and a compact look, respectively, while a compact aspect was observed for most of the re-suspended alginate of culture #2 (see Appendix E). Furthermore, large variations in the consistency coefficient of the broth samples were registered among the triplicates. Both facts may respond to a variation in the molecular composition of the alginate that can affect its intrinsic viscosity and gelling properties [29].

3.2. Experimental Torque Characterization

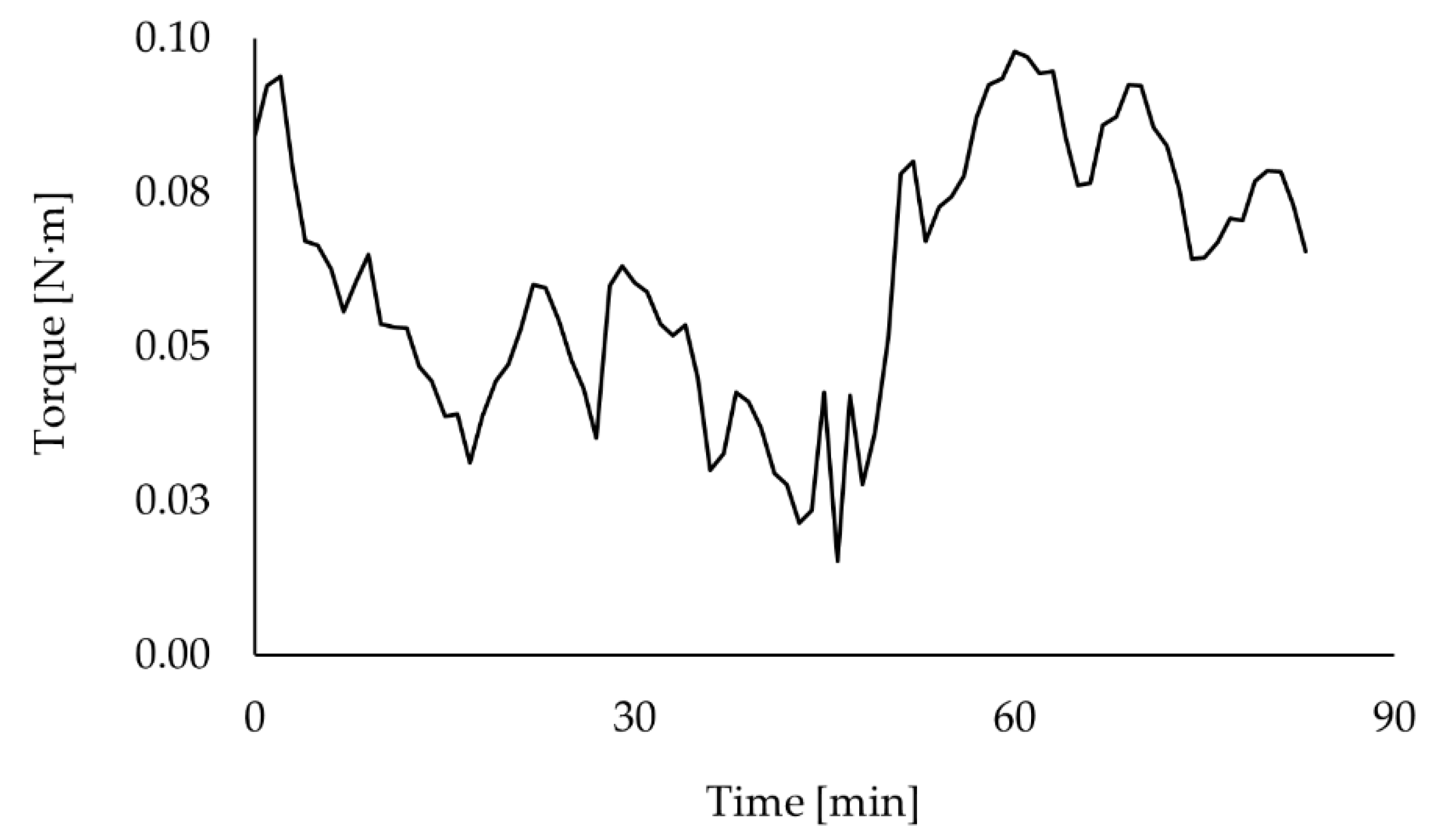
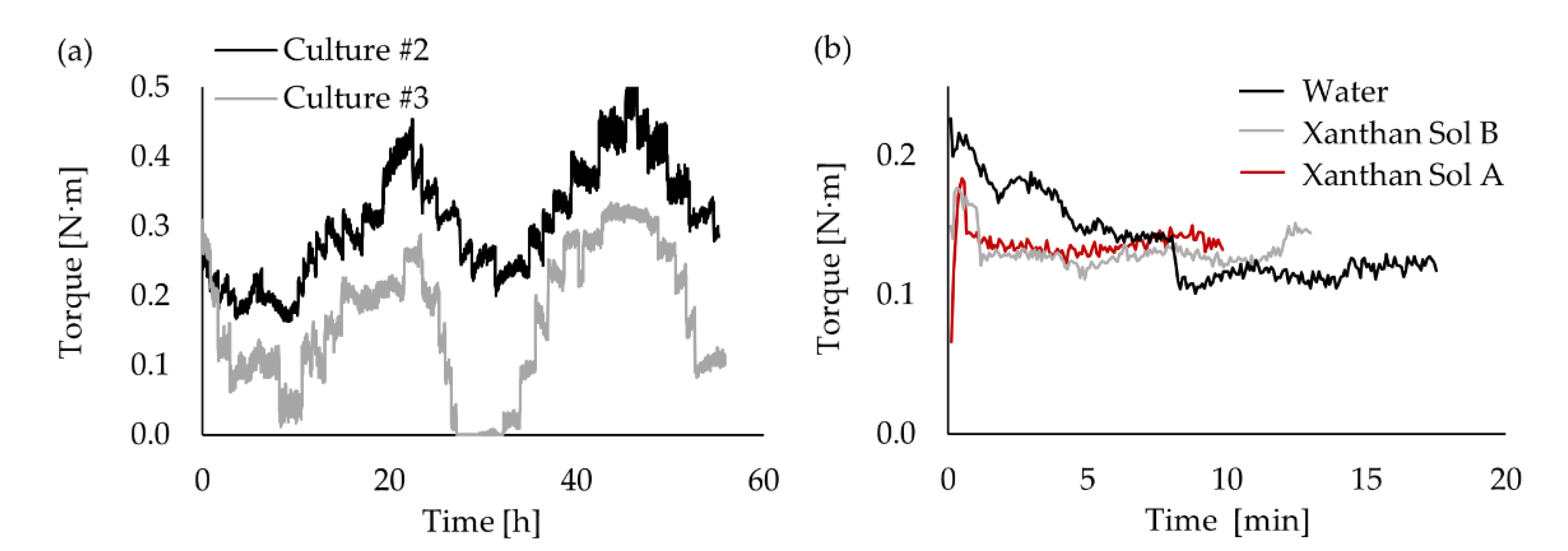
Due to the broth opacity (see Appendix E), the shaft torque measurement was the most suitable technique that could be used to monitor the fluid dynamics over the fermentation. Unfortunately, the torque data registered during culture #1 had to be discarded due to a technical problem. The torque curve shows similar behaviour for cultures #2 and #3 (see Figure 5a). The curves are separated by an almost constant gap, except at around hour 30. That bigger gap was caused by an earthquake (6.7 Mww in Chile [30]) that occurred during culture #3 and affected the performance of the torque meter calibration over a few hours.

Both torque curves have significant small oscillations as part of bigger oscillations. This could be explained by the interaction of different factors, such as mechanical mixing, aeration, and rheological changes. However, due to the complexity of the system, it is difficult to identify how each of these factors contributes to the bioreactor fluid dynamics and, thus, to its torque curve. Therefore, it was necessary to study the abiotic systems to be able to isolate the effect of those factors at different stages of the fermentation process.

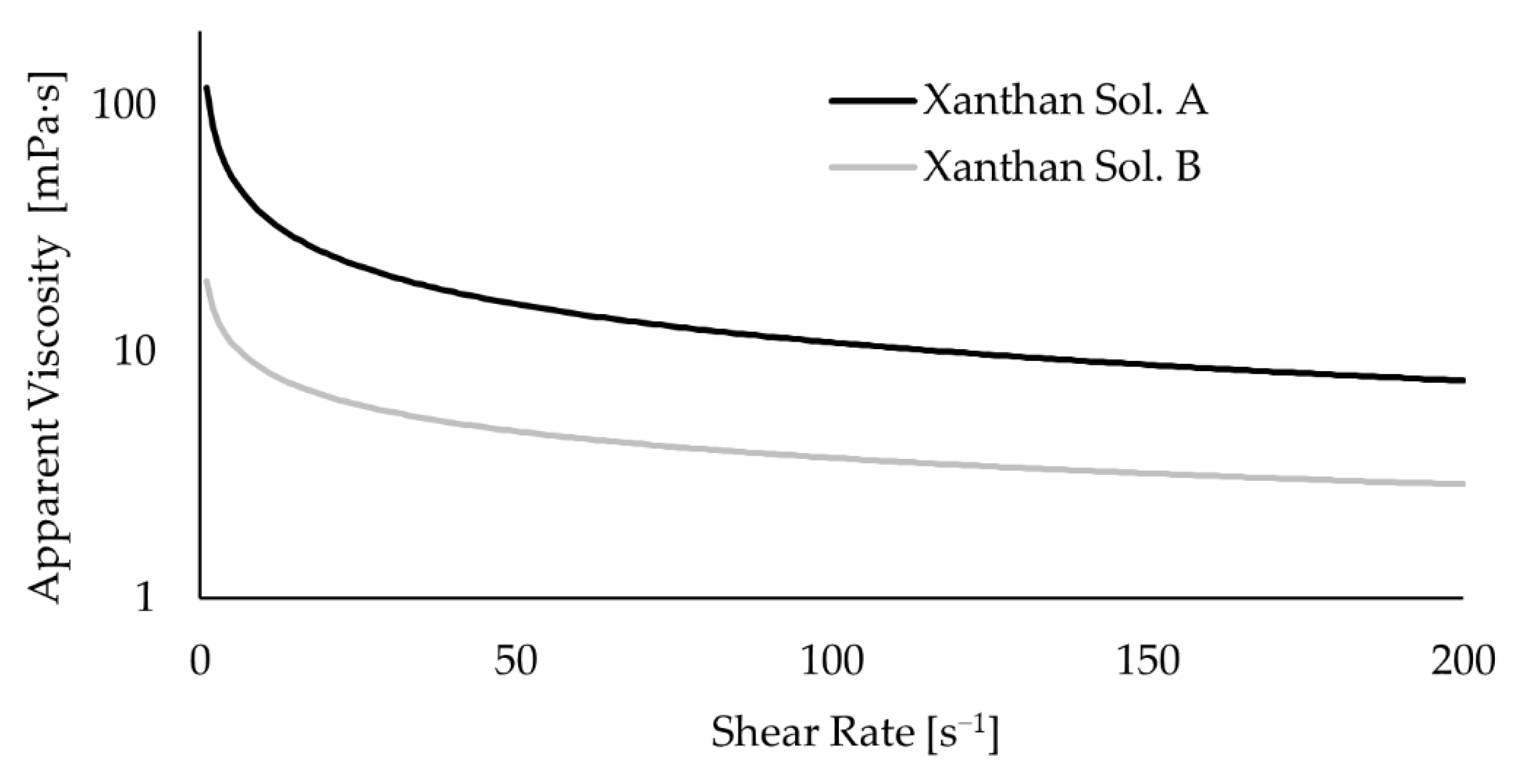
The study of the abiotic systems enabled us to analyze the impact of the mechanical mixing on the torque and how the extent of that impact depends on the rheological characteristics of the fluid (see Figure 5b). The case with water shows more torque oscillations. It may be explained by the onset of vortical macro-instabilities along the impeller shaft, as discussed in Section 3.5 which make the initial stabilization of the system more difficult. On average, the system with water had a lower torque than the cases with xanthan solution and, though a slight difference, Xanthan Sol B had a lower torque than Xanthan Sol A (see

Table 4. Experimental characterization of the abiotic systems.

Model	Reynolds Number [ ]	${\mathit{T}}_{\mathit{A}\mathit{V}{\mathit{G}}_{\mathit{e}\mathit{x}\mathit{p}}}[\mathbf{N}·\mathbf{m}]$	${\mathit{T}}_{\mathit{S}{\mathit{D}}_{\mathit{e}\mathit{x}\mathit{p}}}[\mathbf{N}·\mathbf{m}]$
Water	38,937	0.1172	0.0061
Xanthan Sol B	9474	0.1311	0.0076
Xanthan Sol A	3121	0.1360	0.0056

). That is in agreement with the fluid viscosity differences as, under the same operating conditions, a higher torque was obtained for a fluid with a higher viscosity.

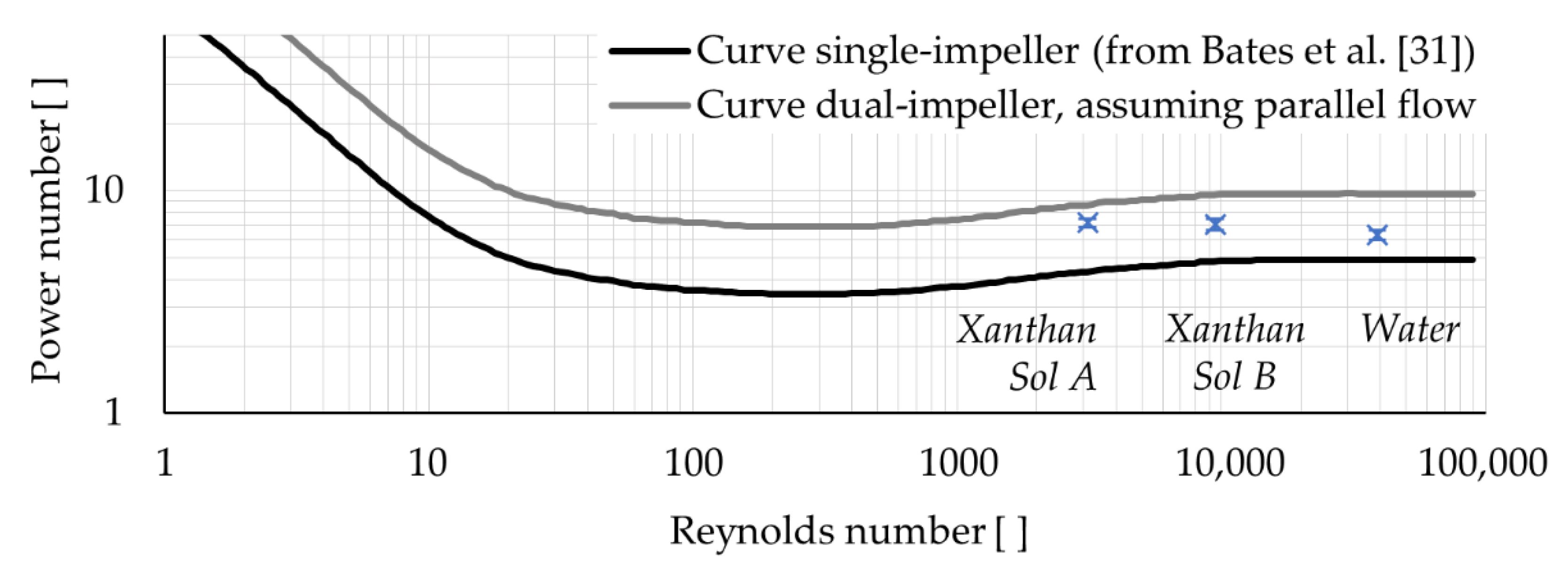
Figure 6 compares the power number experimentally obtained for the abiotic systems versus the one expected for a dual-impellers reactor with a parallel flow (see Appendix C). The Reynolds number of the abiotic systems is given in Table 4, while the power number was estimated from the experimental torque based on equations given in Appendix C. It can be observed that, under the same operating conditions, the system with the highest viscosity (Xanthan Sol A) had a power number more similar to the value expected for dual-impellers with a parallel flow, and the system with the lowest viscosity (water) had a power number more similar to a single-impeller tank, while the other system was in an intermediate situation. Therefore, it is proposed that viscosity had a fundamental role in the flow pattern definition as it determined the level of interaction between the impellers. Particularly, the impeller interaction decreased as the viscosity increased.

3.3. CFD Settings Analysis

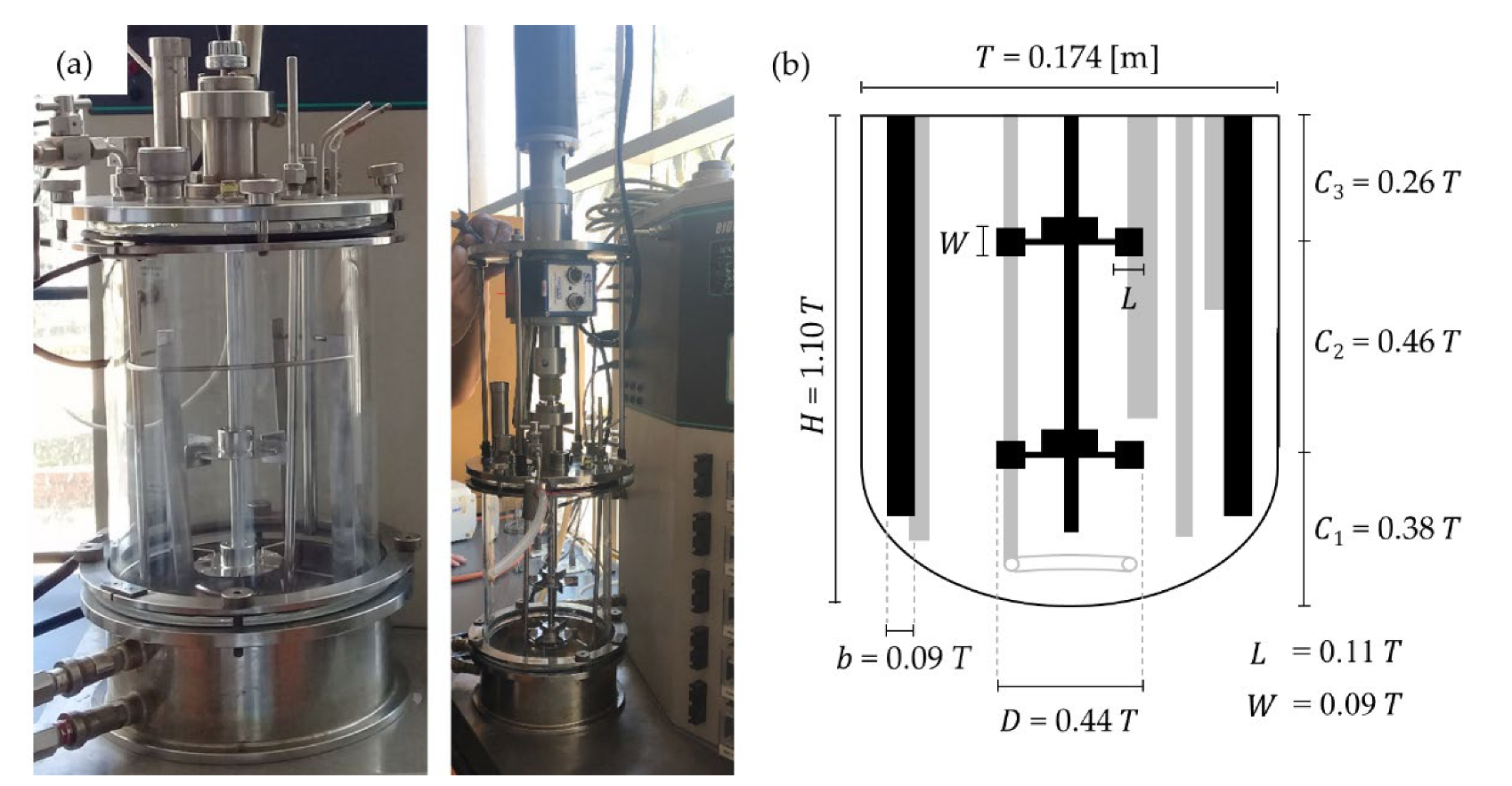
For an accurate simulation of the mixing process, we have included all of the internal elements of the bioreactor in the CFD domain, even the probes that are usually neglected because we have previously proved that they affect the fluid flow patterns [23]. Furthermore, to have an insight into the macro-instabilities, transient simulations are necessary [23,32,33]. All of these factors add to the complexity of the CFD model, requiring a small time-step to achieve a convergent, numerically stable, and time-step size-independent simulation. That is the reason why, with the existing computational capabilities, it is not possible to simulate the evolution of the bioprocess within a reasonable period of time and, therefore, the strategy of simulating the abiotic systems to approach the fermentation process stages remains the only realistic option for now. Indeed, to simulate 0.15 s (one impeller turn) of XSolB-SSTkω, 7.5 h of computation was required using a cluster of 64 CPUs with processors Intel(R) Xeon(R) E5-2683 v4. Thus, using the same computational resources, around1232 years would be required to simulate 60 hr of fermentation. If we consider the continuous computational improvement during that time, however, this estimation would be substantially reduced.

The residual values were verified. In the case of XSolA-SSTkω, initially, the residual for the turbulence parameter ω converged intermittently, to finally stop converging during the simulation of the sixth impeller turn, while all the other residuals were below 10⁻⁵ at every time step. For XSolB-SSTkω, all the residuals were below 10⁻⁵ at every time step, except the residual of the parameter ω in a few time steps (approximately 17 out of 750 time-steps). In the cases of XSolA-SSTkω and XSolB-SSTkω, the parameter ω stabilized around 10⁻⁵ and did not go below. For XSolA-kklω, XSolB-kklω, and XSolC-lam, the residuals values were below 10⁻⁵ at every time step. Furthermore, based on the monitored variables, numerical instabilities were discarded, and it was ensured that the systems were in a stationary state over the last ten impeller turns.

According to the analysis of the Reynolds number, the systems with Xanthan Sol C, Xanthan Sol B, and Xanthan Sol A are all in the transitional flow regime (10 ≤ ${\mathrm{Re}}^{\ast }$≤ 10⁴). However, the analysis of the turbulent viscosity ratio permitted a different conclusion (see Appendix F). For this study, it was accepted, as a rule of thumb, that a turbulent viscosity ratio above 10 and below 5 indicates, respectively, a turbulent and a laminar flow regime, while a value between 5 and 10 corresponds to a transitional regime. Therefore, for Xanthan Sol C, even though ${\mathrm{Re}}^{\ast }$= 312, the flow actually corresponds to a laminar regime based on the turbulent viscosity ratio. In the case of Xanthan Sol A, the turbulent viscosity ratio values have a broader distribution, spanning the three flow regimes, but the zones in the laminar and transitional regimes prevail. As previously described, the simulation XSolA-SSTkω had convergence issues related to the parameter ω, which has been attributed to the use of a turbulent model to characterize a system where the turbulent regime is not predominant. In consequence, the model XSolA-SSTkω was discarded, and only XSolA-kklω was used to study the system Xanthan Sol A. The k-kl-omega model was chosen because it is suitable for systems where the boundary layer transitions between the laminar and turbulent regimes [34], as happens in most of the walls of the tank due to the periodical passage of the blades and the high pseudoplasticity of Xanthan Sol A.

With respect to Xanthan Sol B, the turbulent viscosity ratio values span the three flow regimes as well, but the turbulent regime is more prevalent than for Xanthan Sol A. So much so that the results obtained with XSolB-SSTkω and XSolB-kklω are very similar, in agreement with the fact that the Reynolds number of Xanthan Sol B is very close to the limit between the transitional and turbulent range. As there is not enough information to ensure which one of the models adapted for Xanthan Sol B is better than the other one, the results of both are considered in this study. It is hypothesized that, probably, the real behaviour of the system Xanthan Sol B is at some point in between the predictions of XSolB-SSTkω and XSolB-kklω.

It is important to remark that the RANS turbulence models available in Ansys Fluent were not developed to describe the flow of non-Newtonian fluids. Their inaccuracy relies on the use of the resolved-scale strain rate instead of the local one to compute the apparent viscosity of the fluid. Unfortunately, there are few developments that could be applied for the modelling of turbulent non-Newtonian fluid flows. Gavrilov and Rudyak [35] have proposed a new turbulence model to be used with power-law non-Newtonian fluids, but it has not been validated for stirred tanks. Instead, in recent publications of CFD models in bioprocesses as well as other fields, the traditional RANS equations have been applied to simulate the flow of non-Newtonian fluids with successful experimental validation [9,17,36]. Particularly, for the case of stirred tanks, it has been shown that the SST k-omega model allows an accurate prediction of torque and flow patterns when mixing non-Newtonian fluids in the turbulent flow regime [18,19,20]. However, to our knowledge, the use of k-kl-omega has not been reported for non-Newtonian fluids.

As mentioned before, ANSYS Fluent requires as input a lower and upper viscosity limit for the non-Newtonian power-law model. In other words, a power-law fluid is handled similarly to a Carreau fluid [37]. Therefore, it is important to set up limits that will not artificially influence the simulation of the mixing system. This was evident in the case with Xanthan Sol C, for which preliminarily the upper limit was set as 0.5 Pa·s. However, after the simulation of several impeller turns, the contours at different planes showed that the viscosity reached the maximum allowed value in several zones (see Appendix G). This observation raised the question of whether the applied upper limit was too low. During the experimental characterization of Xanthan Sol A, the maximum measured viscosity was 0.2 Pa∙s at a shear rate of 0.36 s⁻¹, but lower shear rates can be found in the bioreactor and, therefore, higher viscosities. According to the literature, Xanthan solutions can reach viscosities up to 8 and 200 Pa∙s at 0.1 and 0.001 s⁻¹, respectively [38,39]. Based on this, the simulation for Xanthan Sol C was re-started, using 300 Pa∙s as the upper limit. Similar attention was given to the lower viscosity limit. Thus, it was ensured that the applied viscosity limits did not affect the results obtained with the models of the abiotic systems with non-Newtonian fluids. See viscosity contours in Appendix G.

3.4. Mesh Analysis and CFD Model Validation

The mesh independence was thoroughly proven for Water-SSTKω in previous work [23]. So, as the models for the systems with non-Newtonian fluids used the same mesh, only the confirmation of their mesh independence was pending. As expected for grid-independent results, we found small differences between the computed values of the torque on the moving walls versus on the stationary walls responding to the conservation of angular momentum. The highest difference was 4.3%, which is similar to the one obtained for Cortada-Garcia et al. [40] for its optimal grid. The detailed results of this analysis can be found in Appendix H.

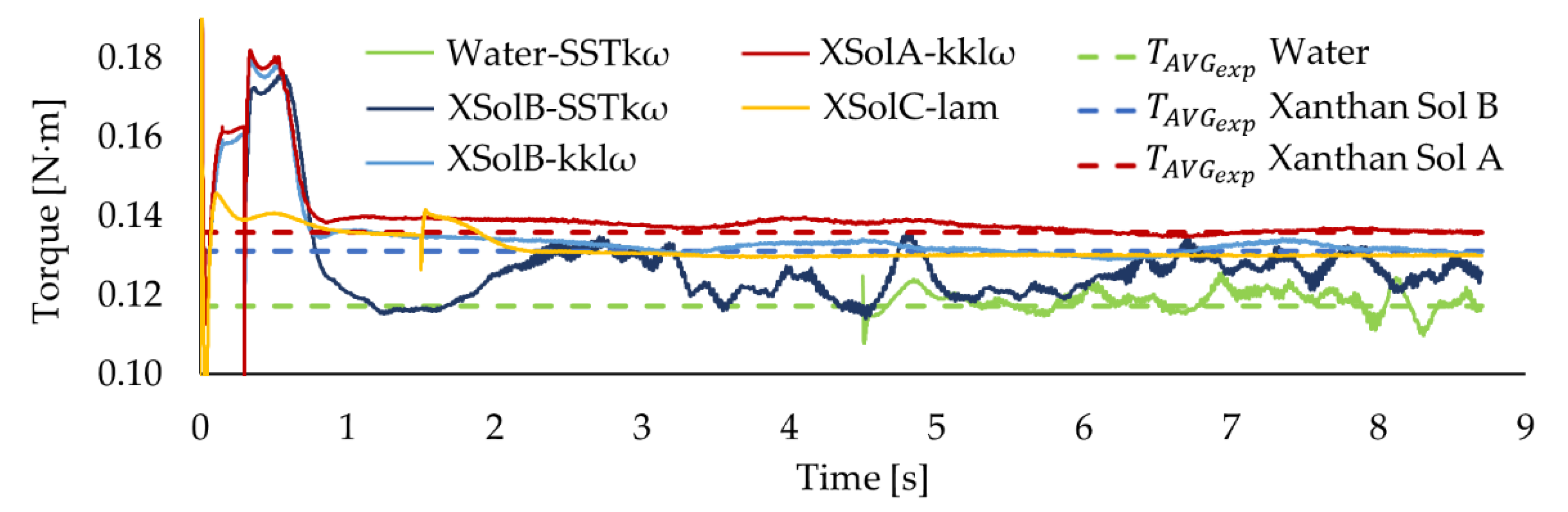
Observing Figure 7, it is apparent that the CFD models successfully predicted the effect that the fluid viscosity has on the torque. In particular, the models XSolA-kklω and XSolB-kklω satisfactorily captured the effect of the fluid rheology on the torque for the non-Newtonian systems in the transitional flow regime. This is a relevant result because, to the best of our knowledge, it is the first time that the k-kl-omega transition model has been evaluated for the simulation of stirred tanks.

The validation analysis of Water-SSTKω can be found in Sadino-Riquelme et al. [23]. In the case of the abiotic system with non-Newtonian fluids, $T_{AV{G}_{sim}}$ was compared with $T_{AV{G}_{exp}}$, obtaining $\left|E\right|$ below 5% (see

Table 5. Computational characterization of the abiotic systems. Torque is given as $T_{AV{G}_{sim}}$ ± $T_{S{D}_{sim}}$ in units of [N∙m], $\left|E\right|$ is given as [%], and the length scales are given in units of [m]. The viscosity and Sc correspond to instantaneous volume-average values. The viscosity is given in units of [Pa·s].

CFD Model	Validation		Length Scales		Viscosity	Sc
	Torque	$\left|\mathit{E}\right|$	Kolmogorov Scale	Turbulence Scale
XSolA-kklω	0.1364 ± 0.0003	0.3	1.85 × 10−5	0.065	0.020	9890
XSolB-kklω	0.1320 ± 0.0011	0.7	1.42 × 10−5	0.060	0.006	2817
XSolB-SSTkω	0.1269 ± 0.0029	3.2	4.06 × 10−6	0.004	0.005	2532
XSolC-lam	0.1301 ± 0.0001	-	-	-	0.207	103,551
Water-SSTkω	0.1185 ± 0.0031	1.1	8.76 × 10−6	0.004	0.001	514

). These are small errors in comparison to the ones obtained by Ebrahimi et al. [41], which vary between 5.7% and 14.9% for the simulations of dual impellers mixing water with $\mathrm{Re}$ between 11,700 and 35,000. It is important to notice that the cited study used power values for validation purposes, which is analogous to using torque, based on their linear relationship.

Previously, for the verification analysis of the model Water-SSTkω, $U_V$ was estimated as equal to 8.2% [23]. Assuming that the validation uncertainty is the same for the abiotic systems with non-Newtonian fluids, and as $\left|E\right|<U_V$ in all the cases, the CFD models for Xanthan Sol A and Xanthan Sol B are successfully validated at an 8.2% uncertainty level.

In the case of XSolC-lam, although not having experimental data to compare with, a higher comparative error related to the use of a multi-phase model with single-phase conditions can be expected. In a preliminary study, the mechanical mixing of water was simulated using the same domain described in this article to compare a single-phase CFD model versus a CFD multi-phase model under single-phase conditions. It was observed that the comparative error estimated for the multi-phase model was between 2-fold and 2.5-fold bigger than for the single-phase model. Additionally, it is interesting to notice that a lower torque was predicted for Xanthan Sol C than for Xanthan Sol A and Xanthan Sol B. Considering that Xanthan Sol C has a significantly higher viscosity than the other fluids, this result may appear erroneous, but it is not. Actually, it is in agreement with the power number curve behaviour, as Xanthan Sol C has ${\mathrm{Re}}^{\ast }$= 236, which corresponds to a power number smaller than for the other systems and, therefore, to a smaller torque (see Figure 6). Thus, the model XSolC-lam is assumed as valid too.

Thus, different single-phase CFD model configurations were successfully adapted to model a stirred tank without aeration, which are able to simulate changing fluid rheology as well as an evolving flow regime.

3.5. Analysis of Mixing Mechanisms

Based on the analysis of the flow regime, it can be expected that the mixing process of the system with Xanthan Sol C will depend more on the micromixing than on the macro or mesomixing scales, contrary to what is predicted for the other systems. A comparative analysis of the turbulence length scale and Kolmogorov scale also supports that hypothesis (see Table 5). Furthermore, the Kolmogorov scale for Xanthan Sol B (as mentioned before, it is hypothesized that the real behaviour of the system Xanthan Sol B is at some point in between the predictions of XsolB-SSTkω and XsolB-kklω), as well as for water, would be around 50% lower than for Xanthan Sol A. This would explain a significantly higher mixing time of the system Xanthan Sol A in comparison to the other systems experimentally studied. It is important to remark that the length scales are not reported for XSolC-lam because this analysis does not apply for laminar flows.

The Schmidt number allows us to compare the viscous diffusion with the molecular diffusion (see Table 5). For alginate aqueous solutions, with alginate concentration between 0.25 and 2% (w/w), the oxygen diffusion coefficient varies only 14%, according to the experimental data reported by Ho et al. [28], with an average value of 1.96∙10⁻⁹ m²/s. Therefore, we could expect a similar value for this parameter over the fermentation process. However, the kinematic viscosity increases 1800% from water to Xanthan Sol A (see Table 5). Thus, even if the oxygen diffusion coefficient increases over the process due to the effect of certain broth compounds, we could still expect that the mixing will be significantly limited by the viscous diffusion.

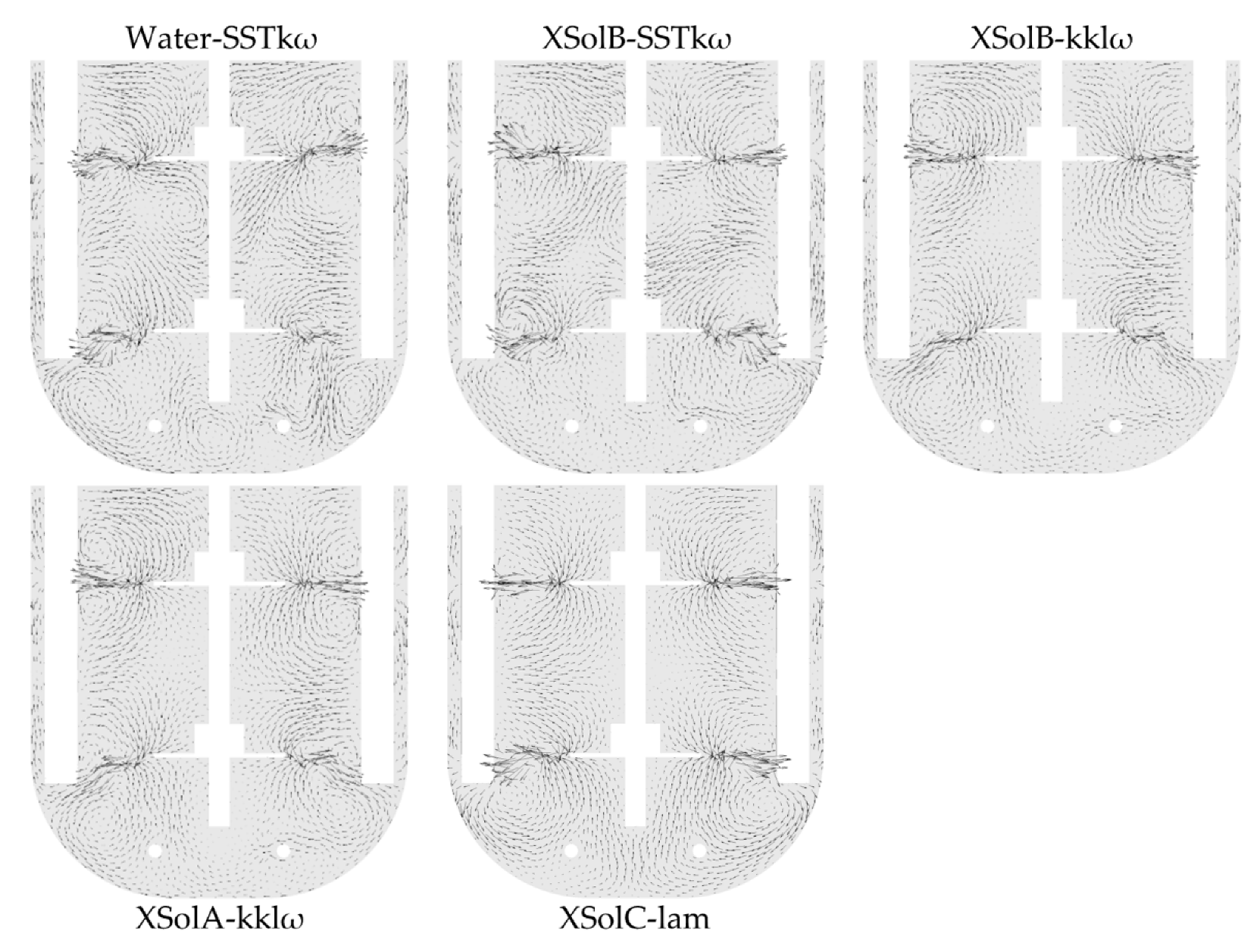
The velocity vectors of the systems were compared with those described by Rutherford et al. [42] for stable flow patterns in a dual-Rushton turbine stirred vessel. Based on the behaviour of the vectors between the impellers and at the bottom of the fermenter, it is concluded that the systems with water and Xanthan Sol B do not have stable flow patterns, while the system with Xanthan Sol C has a parallel stable flow. In the case of Xanthan Sol A, the criterion of a parallel pattern is met by the zone between the impellers but not by the bottom zone (see Figure 8). The flow patterns can also be studied from the examination of the lower and upper impeller torque. Both torque values are expected to be similar in a system with a parallel flow, meaning that the impellers are working independently of each other. As expected, this condition is only fulfilled by Xanthan Sol C (see Appendix I).

The flow patterns are of importance because they affect the mixing time. Among the stable patterns, a parallel flow would have the weakest interchange between the upper and lower zones of the tank, increasing the mixing time [42].

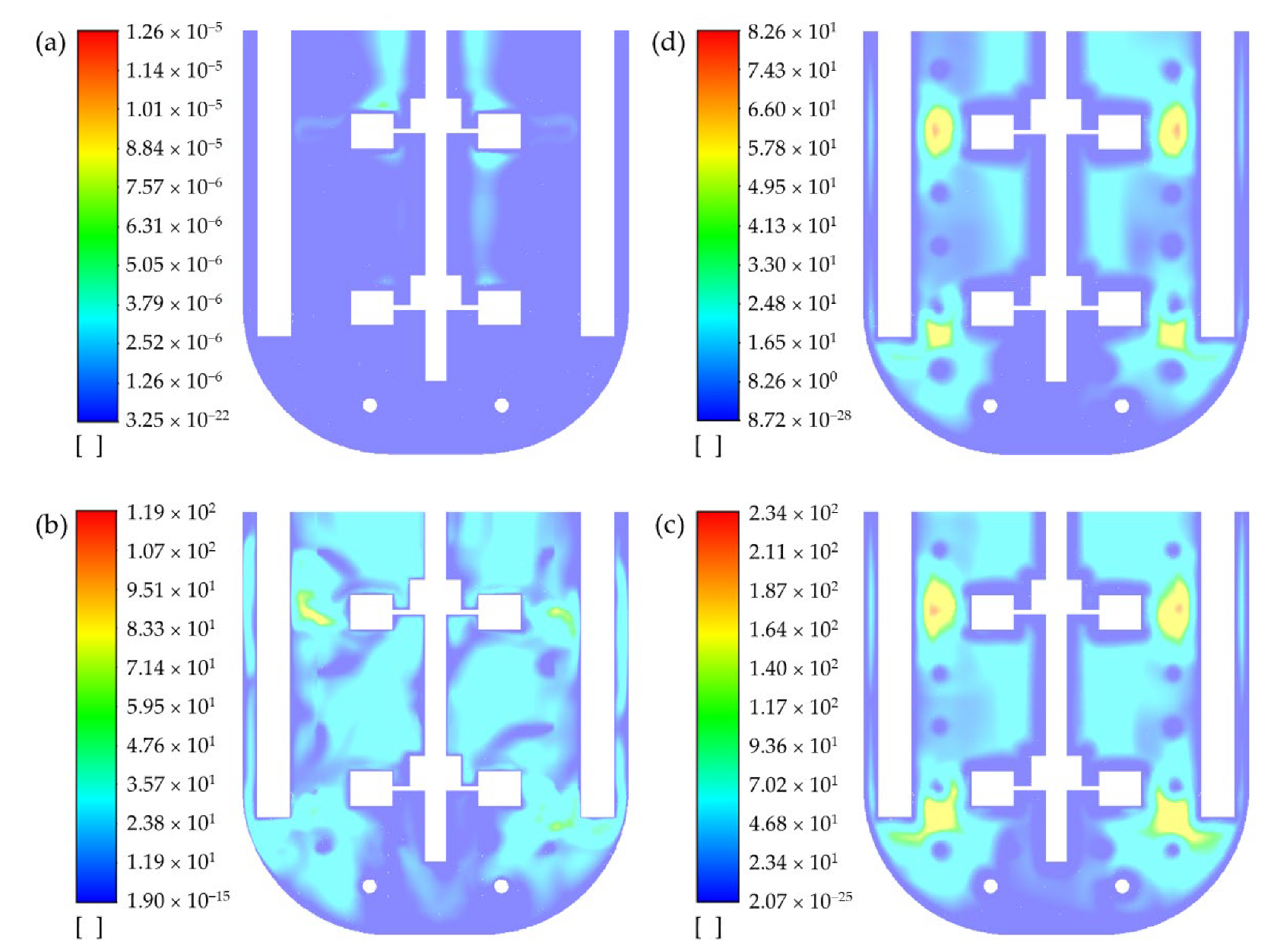
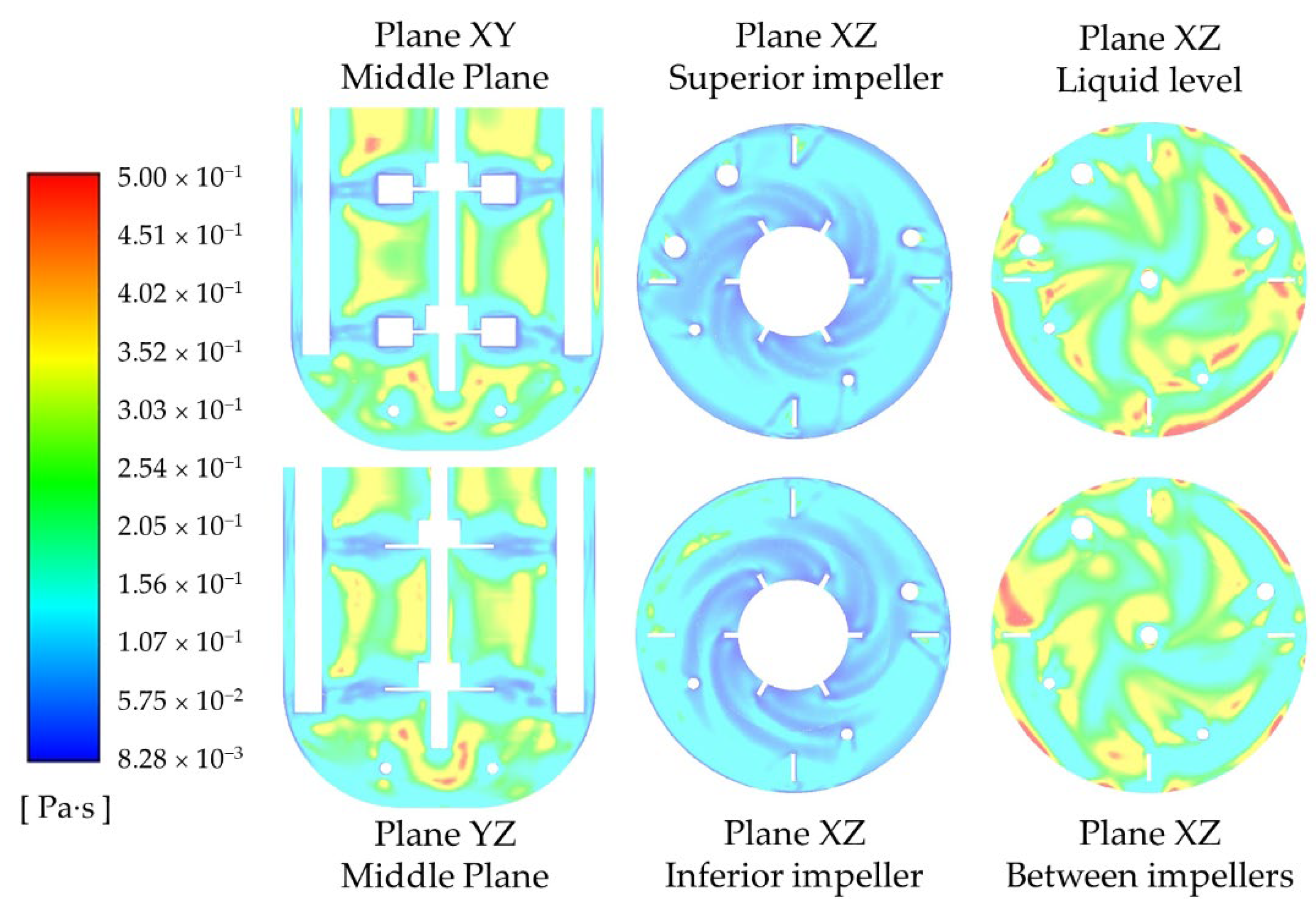
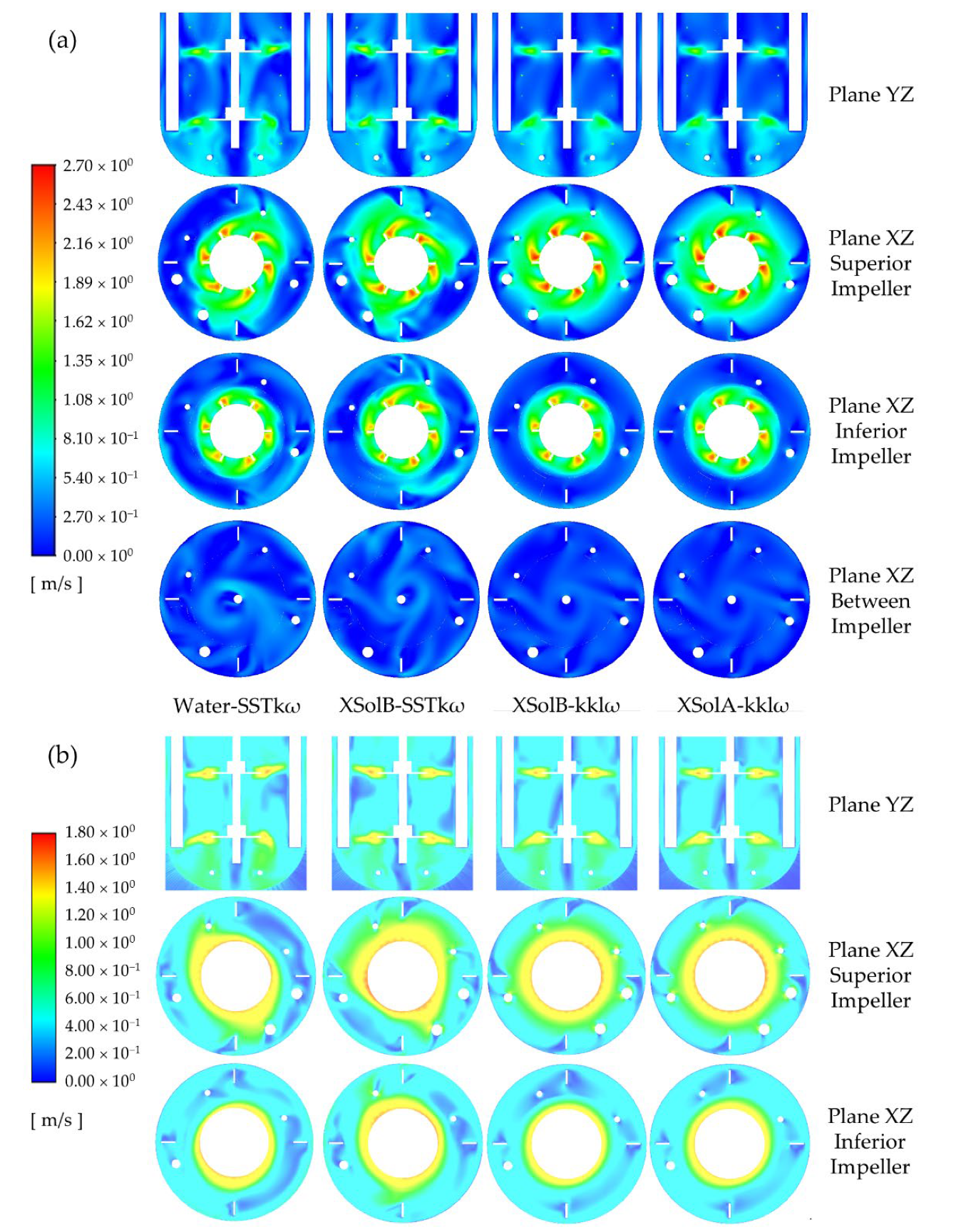
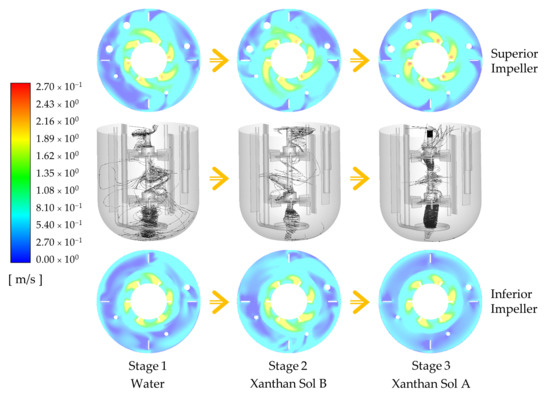
Among the three abiotic systems experimentally studied, the velocity not only changed in direction but also in magnitude. A comparative analysis of the instantaneous velocity magnitude contours shows a significant reduction of the velocity close to the walls, the liquid surface, and between the impellers, as the fluid becomes more pseudoplastic (see Figure 9a); while the time-averaged contours reveal that the higher velocities span less area, but more symmetrically, around the impellers (see Figure 9b). The latter is a consequence of the direction of the impeller discharge stream. The impeller discharge stream for the system with water has axial and radial components, while it is mostly radial for the other fluids.

In terms of the mixing time, that may not be detrimental for the system Xanthan Sol B, but it is a disadvantage for the case with Xanthan Sol A. Adding an axial component to the impeller discharge stream of Xanthan Sol A could help to reduce the stagnant zones and mixing time.

Over the course of the fermentation, an additional factor can impair the homogenization of the system, which is the stagnation of the fluid into dead zones. In this work, the definition of the dead zone used by Vesvikar and Al-Dahhan [43] was applied. This definition considers the zones with velocity magnitude lower than 5% of the maximum velocity magnitude of the system ($V_{max}$). Based on this concept, when the broth properties evolve from water to Xanthan Sol B and Xanthan Sol A, although there is a significant increment of fluid volume with velocities below 20% $V_{max}$, it does not significantly affect the dead zone volume. On the other hand, if the broth properties evolve to Xanthan Sol C, the dead zones span 14% of the system volume, which is almost 5-fold bigger than for water. See graphics in Appendix J.

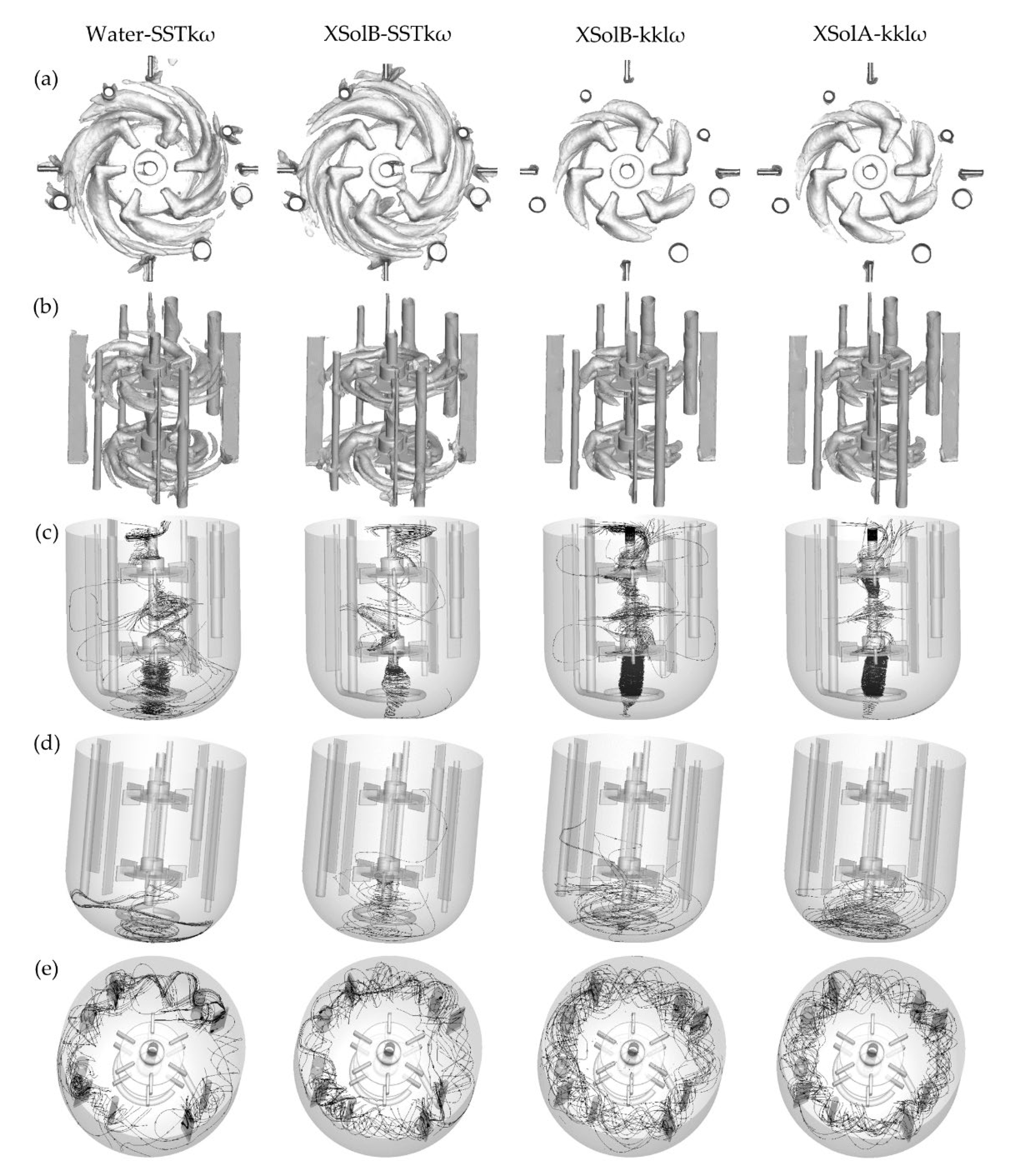
The rotation of the Rushton turbines creates several vortical structures that enhance the mixing process by creating flow instabilities. The trailing vortices are formed just behind the blades and affect the flow due to their periodic passage (see Figure 10a,b). For the systems with Xanthan solutions, the trailing vortices dissipated at a shorter radial distance from the shaft than for the case with water due to the higher viscosities that dissipate the eddies into heat. Moreover, the vertical distance between the trailing vortices of each blade is stretched as higher the pseudoplasticity. Overall, the superior impeller vortices are slightly different from those of the inferior one as an effect of the tank’s internal elements.

An additional vortical structure was found around the impeller axis (see Figure 10c). It is an effect of a phenomenon called the Ekman Layer, where the pressure gradient force, the Coriolis force and the turbulent drag play a fundamental role. The difference between the vorticity in the bulk of the fluid and the tank bottom generates a vertical velocity that, in these systems, pumps the fluid upwards (see Figure 10d). This is called Ekman pumping, and it can be associated with a precessional vortex type of macro-instability [44]. This feature is an advantage when there are particles that need to be suspended, such as the microorganisms inside the bioreactor. Furthermore, the unstable flow patterns of the abiotic systems with water and Xanthan Sol B can be explained by the behaviour of these vortices, especially by its asymmetric shape around the shaft, in the zone between the impellers. Congruently, the parallel flow pattern was related to a symmetric vortex around the impeller axis (see Appendix K). Furthermore, the vortex around the impeller axis would explain the flow pattern differences observed in the tank bottom when comparing the vortex shape Xanthan Sol C with the other abiotic systems.

Other vortical structures are formed around the probes, baffles, and sparger (see Figure 10e). It is important to highlight the existence of these vortices because, most of the time, these elements are not included in the CFD domain. However, as shown here, they play a role in the fluid dynamics at a mesomixing scale.

Based on the experimental and computational results, it is hypothesized that the aeration would modify the trailing vortices and the Ekman pumping by the onset of the air cavities and the modification of the pressure gradients in the bottom zone of the tank, respectively. Currently, the CFD models with aeration are being adapted to study the veracity of these hypotheses.

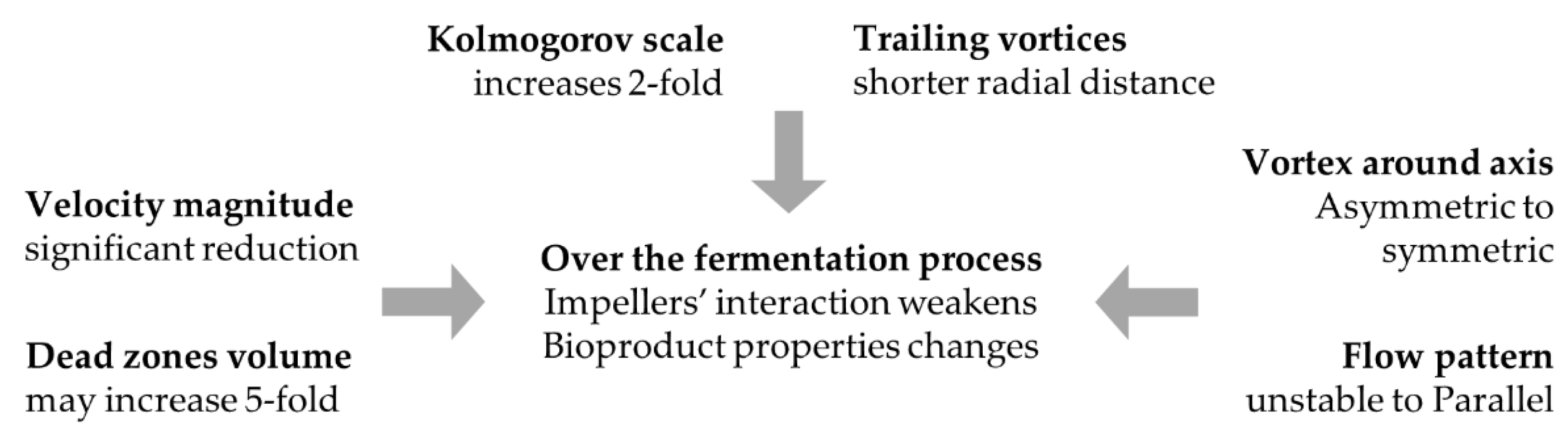
Figure 11 summarizes the modifications that the fluid dynamics of a bioprocess with evolving pseudoplasticity can be subjected to that may impair the fermentation results. Importantly, all these factors were characterized using CFD modelling, which implies that CFD-aided design can be applied to optimize the mixing mechanisms of stirred bioprocesses with changing fluid rheology. For example, the effect of the position of probes, impellers, and air injection on the vortical structures could be studied to identify a tank configuration that improves the mixing times and biomass suspension. Furthermore, the CFD configurations described in this work would allow the study of the optimization of the fluid dynamics based on the specific needs of the different fermentation stages. For example, variable operating conditions could be analyzed in order to counteract the rheology changes.

4. Conclusions

The fluid dynamics of a stirred fermentation with evolving broth pseudoplasticity was experimentally studied through the impeller torque. The weakening of the upper and lower impeller interaction over the course of the bioprocess was identified. CFD modelling was applied to study the bioreactor mixing mechanisms further, overcoming the experimental limitations. The CFD model validation was based on the good agreement between the predicted and measured torque. The computational simulations allowed us to characterize the evolution of the mixing mechanisms impairing the mass transfer as the fermentation proceeds. An analysis of the turbulence length scale and Kolmogorov scale showed that the mixing relies on the macro and mesomixing at the beginning and intermediate stages of the process and on the micromixing at the final stage. Although a reduction of the velocities across the domain was predicted, the total volume of the dead zones could remain almost constant during the fermentation. Furthermore, it was identified that the fluid flow pattern moves from unstable to parallel (stable) over the process. Macro-instabilities as vortical structures were characterized, such as trailing vortices and precessional vortices. The shape of the vortex around the impeller axis is responsible for the unstable flow patterns. It was hypothesized that the aeration would increase the mixing times by the modification of the vortical structures. Based on the findings, the modification of the parallel flow into a merging flow was suggested to improve the mixing times. Overall, along with a detailed analysis of the effect of an evolving broth pseudoplasticity on the mixing mechanisms of a stirred bioprocess, this work contributes with a completed workflow to adapt computational models for the study and CFD aided design of tanks stirring pseudoplastic fluids with changing rheology as well as an evolving flow regime.