1. Introduction
Fermentation is a cornerstone of both traditional and modern biotechnology, serving as a critical biological process for the transformation of organic substrates into valuable products through the metabolic activity of microorganisms. In particular, enzymatic fermentations are biosystems in which enzymes, produced by microorganisms, selectively catalyze biochemical reactions to transform substances [
1].
Enzymes accelerate the chemical reactions that occur during fermentation, such as the breakdown of carbohydrates into simple sugars or the conversion of these sugars into other products. Enzymes are highly specific, meaning that each enzyme catalyzes a particular reaction, allowing for more precise control of the fermentation processes.
The most common types of enzymatic fermentations are lactic fermentation, where lactose is converted into lactic acid, as in the production of yogurt and cheese; alcoholic fermentation, in which sugars are transformed into ethyl alcohol and carbon dioxide, as in the production of beer and wine; additionally, butyric fermentation which produces butyric acid, which can give rise to particular flavors and smells in some fermented foods; and propionic fermentation which produces propionic acid, which is found in cheeses as well as in the manufacture of industrial products such as enzymes for detergents and biofuels [
2].
Recent advances in fermentation technology have focused on improving substrate utilization, microbial strain performance, and downstream processing, with a growing emphasis on sustainability and integration into circular economy frameworks.
Fermentation processes are inherently dynamic systems, often in nonlinear and complex ways, involving oscillatory behavior, steady-state multiplicity and bifurcation phenomena in continuous fermentation systems. Understanding this dynamic behavior is essential for effective process control, optimization, and scale-up in industrial biotechnology [
3,
4,
5,
6,
7,
8].
From the above, the relevance of closed-loop control of biochemical reactors has increased in recent years, under this frame, regulatory control is the main strategy to reach the basic operational requirements, for this reason, the new feedback control designs are an important research topic in industrial and academic areas [
9,
10]. Regulatory control has been performed via classical proportional–integral–derivative (PID) feedback controllers, considering the ease of its practical implementation and satisfactory performance under common industrial practice [
11,
12]; however, high disturbances and nonlinear behaviors can lead to unstable closed-loop operations [
13]. From the above, other feedback controllers have been proposed to improve the dynamic performance of the chemical reactor, between them, the adaptive controllers which can modify some parameters in the control’s structure to keep satisfactory process operation [
14,
15], and some robust controllers designed against input disturbances and noisy measurements have been presented in the open literature over several years, under the frameworks of sliding-mode theory, observed-based I/O linearizing controllers, and optimal controllers, etc. [
16,
17]. In particular, a model based adaptative control for the fermentation of milk in batch bioreactors has been addressed in [
18] and a method for globally stabilizing the control of a continuous ethanol fermentation process, initiating from batch production mode, is presented in [
19].
In addition, by applying thermal effects, the use of a heating device to control the probiotic beverage production in a batch bioreactor is developed in [
20] and novel batch-to-batch optimization control of fed-batch fermentation processes based on a recursively updated learning machine approach is considered in [
21].
Nonlinear feedforward designs have been applied for systems with a large variation in process variables; in addition, a study proposed a hybrid controller for a continuous stirred tank in (bio)chemical reactors, combining inversion-based static nonlinear mapping with a dynamic linear segment designed via pole assignment [
21,
22].
Table 1 resumes the main published results in nonlinear control for continuous chemical reactors.
However, one of the most important drawbacks of the advanced control design is the complexity the practical applications, and the complete understanding for the plant engineers; therefore, the alternative control structures must be simple enough to avoid the above-mentioned drawbacks. Under this focus, this paper has proposed a class of nonlinear controllers with an adaptive-type gain, which can adequately stabilize the operation of a continuous stirred bioreactor with complex dynamic behavior, such as chaotic oscillations, and keeps a simple structure. The stability proof of the closed-loop system is performed using the Lyapunov framework, where an appropriate selection of controller gains guarantees asymptotic stability. Moreover, some numerical experiments show the feasibility of the proposed method via the feedback control of a chaotic continuous-flow enzymatic–fermentative bioreactor.
The rest of the work is divided as follows.
Section 2 describes the fourth-order model of the continuous flow enzymatic–fermentative bioreactor which exhibits chaotic behavior with the given set of initial conditions and parameter values.
Section 2 also includes some comments about the instrumentation in continuous biochemical reactors. In
Section 3, a novel nonlinear controller is designed, based on certain boundedness assumptions.
Section 4 shows some numerical experiments and the corresponding discussions. Finally, in
Section 5, some concluding remarks are mentioned.
2. Continuous Bioreactor Modeling and Instrumentation
Continuous chemical reactors, particularly continuous stirred tank reactors, often exhibit complex and nonlinear dynamic behaviors. A classic example is the emergence of multiple steady states in exothermic biochemical reactions, where a reactor may stabilize at different conversion levels under identical operating conditions. This phenomenon is typically associated with saddle-node bifurcations, which mark the sudden appearance or disappearance of equilibrium points as system parameters vary [
23].
Mathematical nonlinear modeling of the fermentation process, incorporating phenomenological kinetics, provides a powerful framework for describing and predicting the dynamic behavior of microbial systems. These models are based on the fundamental principles of mass and energy balances, coupled with biochemical kinetics, thermodynamic, and transport phenomena governing microbial metabolism [
24]. Unlike empirical models, which simply fit experimental data, phenomenological models aim to reflect the actual mechanisms driving microbial growth, substrate uptake, and product formation. Unlike linear systems, these bioreactors can respond unpredictably to changes in operating parameters such as feed concentration, flow rate, or coolant temperature [
25].
This memory-like behavior of continuous fermentations can be complex in industrial applications, where an operator might unknowingly push the system into an unstable or unsafe regime. Instabilities of this sort are often analyzed using bifurcation diagrams and continuation methods to map out the boundaries of safe operation [
26].
Therefore, here we consider the generic mathematical kinetic model presented by [
27], which is proposed as a four states dynamical system, considering enzymatic biochemical reactions, where some conditions are established, such as that chemical reactions occur in a completely uniform environment within a thoroughly mixed tank reactor that operates at a constant temperature, where all chemical substances participate in self-catalyzing reactions and are described mathematically using models based on the Michaelis–Menten type.
This model is selected as an excellent and challenging example for control purposes, because its mathematical structure can reproduce complex oscillations, including chaos. The model’s structure can predict ethanol fermentation by
Zymomonas mobilis and
Saccharomyces cerevisiae, which has been reported in the open literature [
28,
29,
30,
31]
This kinetic model is included in the mass balance of the continuous stirred tank reactor, considering chaotic behavior. The mathematical model of the chaotic continuous-flow enzymatic–fermentative bioreactor is given by a fourth-order model and represents the dimensionless mass balances for each chemical compound, expressed by the following: dimensionless mass concentrations for substrate , biomass (), product (), and key intermediate ().
Mass balances:
where
,
, …,
, and
K are the corresponding kinetic parameters,
and
are external disturbances that are included to model realistic process functioning,
,
,
, and
are the possible inlet concentrations to the reactor, and
u is considered as the control input. In accordance with common practice for these procedures, the control input is expressed as
u = F/V, where
F represents the volumetric flow entering the the system and
V stands for the reactor’s volume, which is typically regarded as being constant in these types of systems.
With the following set of initial conditions and parameter values, system (1)–(4) exhibits chaotic behavior. The values of the kinetic parameters are fixed as the following:
k1 =
k2 =
k3 = 1,
k4 = 0.25,
k5 = 152.5,
k6 = 1,
k7 = 130,
k8 = 0.001,
k9 = 1,
k10 = 1.051,
k11 = 0.5, and
K = 0.001. The constant disturbances are
d0 = 90 and
d1 = 2.2. The initial conditions are chosen as follows:
129.1,
76.06,
0.5895, and
21.38. The inlet concentrations to the reactor are
,
, and the nominal value of the control input is considered as
u = 0.015. In the numerical experiments of
Section 4, it will be assumed that the mass concentration,
, is obtained by measurement and it is available for feedback; therefore,
will be used to implement the nonlinear control.
To justify the selection of mass concentration as a measured variable for feedback control purposes, it is important to mention the importance related to the instrumentation in continuous biochemical reactors. This point is essential to maintaining precise control over biological processes, as real-time monitoring enables operators to detect possible faults in the operation of fermentation systems [
32].
The assumption of real-time measurements of biomass concentration
can be performed in real-time analysis based on spectroscopy, such as near-infrared (NIR) or mid-infrared (MIR), as well as in-line refractive index or dielectric spectroscopy, which are increasingly used to monitor substrate and product concentrations without sampling delays. These techniques facilitate direct control of nutrient feed, reducing lag times and enhancing productivity. Additionally, soft sensors—computational models driven by multivariate calibration data—are often integrated with spectroscopic data to infer unmeasured variables like biomass or key metabolites [
33,
34].
In addition, flow and mixing instrumentation are also vital, especially when feeding substrates or extracting products continuously. Precision flow meters (e.g., Coriolis and peristaltic pumps with integrated flow feedback) enable tight control of reactor loading and residence time [
35].
3. Control Design
Consider the following nonlinear dynamic system:
Here, is the state vector, , where X is a connected manifold of dimension n, is the vector of affine control inputs, is some open subset, is a bounded vector field, is the vector of linear measurements, is some open subset, and is a constant matrix. The nonlinear vector field satisfies the Lipschitz condition.
Now, let us assume the following boundedness conditions for the control design.
Assumption 1. The nonlinear vector field f is globally Lipschitz bounded, i.e., for all , , is the named regulation error, where xsp is the required set point and is the time derivative of the control error .
The Lipschitz constant,
, is obtained from the Jacobian matrix as follows. Let us consider the Jacobian matrix:
Assumption 2. The vector field g(x) is bounded, i.e., for all .
It is important to mention that Assumptions 1 and 2 are physically realizable for (bio)chemical reacting systems.
Proposition 1. If there exists such that , there exists such that and Assumptions 1 and 2 are fulfilled, then the control input u, given by (7) and (8), can regulate the nonlinear system (5):where m is a positive odd integer. Proof of Proposition 1. Let us substitute control law (7)–(8) on the dynamic equation of the control error defined by Assumption 1, as
Here, can be noticed that the adaptive control gain
k(e), is alternatively represented by the Euclidean norm:
Defining
, for
:
Because
is lower and upper bounded, expression (11) yields to
Then, solving Equation (10), the adaptive-type gain
is obtained in an interval
:
Now, let us consider an interval, , it is a compact (bound and closed) interval and let as a continuous function in I, then h is bounded in I, i.e., exists , such that , then for all .
Therefore,
is continuous integrable, such that:
Consequently, let us define then, in accordance with the above-mentioned, h(e) has an upper bound, therefore .
Now, the Cauchy–Schwarz inequality will be applied, also known as the Cauchy–Bunyakovsky–Schwarz inequality.
Then, under Assumptions 1 and 2, and maximizing Equations (9)–(13), by applying the Cauchy–Schwartz inequality:
or rewriting the inequality (14):
Lyapunov analysis is a powerful mathematical tool used to evaluate the stability and performance of closed-loop control systems, particularly in nonlinear and dynamic environments such as continuous biochemical reactors. These reactors often exhibit complex behaviors due to nonlinear kinetics, time delays, and coupling between biological and chemical processes, making classical linear stability analysis insufficient. In a closed-loop configuration, Lyapunov functions are constructed to assess whether the system trajectories converge to a desired equilibrium point (e.g., steady-state biomass or substrate concentration). If a suitable Lyapunov candidate function can be found—typically a positive-definite function whose time derivative along system trajectories is negative-definite—the closed-loop system is proven to be globally or locally asymptotically stable.
This approach allows control engineers to design and verify nonlinear controllers for biochemical reactors with guaranteed stability properties. Lyapunov-based design also facilitates performance analysis by quantifying convergence rates, robustness to disturbances, and the effect of parameter uncertainties on system behavior. In practice, Lyapunov analysis ensures that the controlled biochemical reactor maintains stable operation, avoids oscillations or washout, and meets productivity and safety constraints under varying conditions.
Now, proposing the following Lyapunov candidate function:
The corresponding time derivative is as follows:
Substituting (15) into Equation (17):
If the control gains are chosen as
or
, and
:
□
Finally, from the stability Lyapunov framework, the system (9) is closed loop asymptotically stable.
Remark 1. From Equation (18), note that the control’s gain can be selected large enough to compensate the nonlinear term represented by the Lipschitz constant such that , therefore and considering that: By defining with as above-mentioned, a closed-loop exponential-type convergence can be reached for system (5) under the proposed controller.
4. Numerical Results and Analysis
To show the performance of the proposed control law (7)–(8), numerical simulations were performed on a PC with an Intel Core i7 processor and ode23s MATLAB
® library for ordinary differential equations was used to solve the system (1)–(4), under the initial conditions indicated in the section on bioreactor modeling. As mentioned, the considered bioreactor model shows sustained complex oscillations in open-loop operations, which is an undesirable condition in industrial practice, such that the industrial plant productivity is hugely affected.
Figure 1 depicts the general diagram for the closed-loop operation of the continuous bioreactor, where the controlled variable corresponds to the
x1 concentration, which is assumed to be online measured, and feedback to the control law, the selected control input is the inlet mass flow to the bioreactor, as usual for this kind of processes.
For our study case, the nonlinear system (5) is represented as
The nonlinear vector field
is given by:
and the vector field
is expressed as
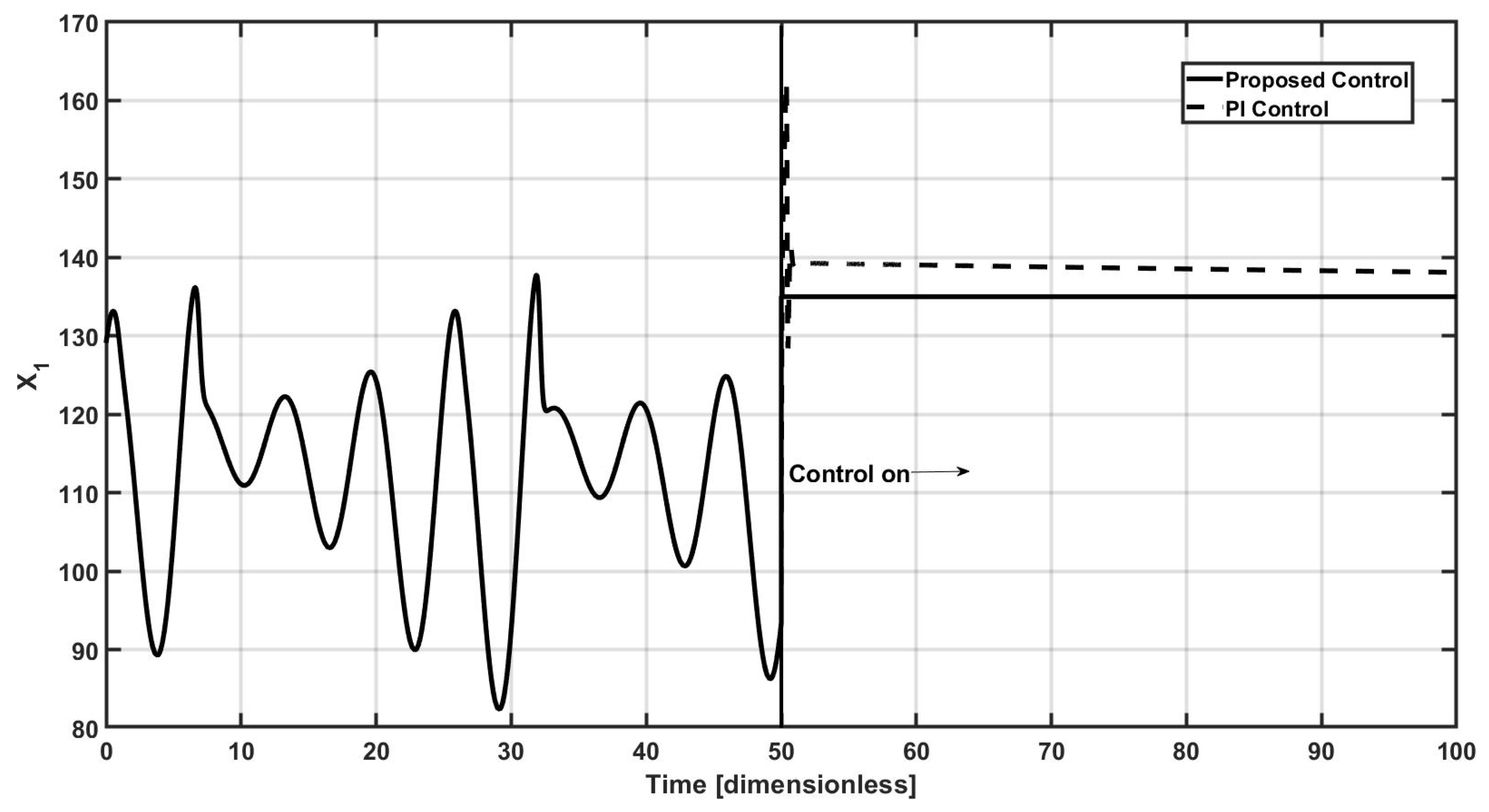
Therefore, a closed-loop strategy must be implemented to avoid the bioreactor’s oscillatory dynamic behavior; the proposed controller turns up at
t = 50 time units, as observed in
Figure 2, and the proposed controller leads the controlled concentration
x1 to the required reference point
x1,sp = 135, almost immediately with a small overshoot and null settling time, without offset, here for comparative purposes a standard proportional–integral (PI) controller is also implemented. Proportional–integral (PI) controllers are widely applied in fermentation processes due to their simplicity and effectiveness in managing slow and nonlinear dynamics regularly found in bioreactors. The performance of PI controllers in fermentation is generally characterized by stable tracking of setpoints and rejection of disturbances, particularly in the presence of moderate process nonlinearity [
36].
However, due to the integrating nature of the fermentation dynamics and the presence of time delays, proper tuning of the PI parameters is critical. In addition, the performance may degrade in highly nonlinear regimes or during phase transitions in microbial growth, where adaptive or gain-scheduled control strategies may outperform fixed-parameter PI controllers. Despite these limitations, PI controllers remain a practical and cost-effective solution in industrial fermentation processes, especially when combined with appropriate filtering and feedforward strategies.
For our study case, it is important to note that identification and tuning gains procedures for the PI controller, given the complex oscillating behavior of the bioreactor, are not possible to realize via the typical procedures as Ziegler–Nichols, Cohen–Coon or IMC methods, for example; so, a trial and error selection of the proportional and integral gains of the PI controller was conducted, where the best obtained closed-loop performance corresponds to
kp = −0.5 and
ki = −0.01, respectively. The selected gains for the proposed controller are
l1 = 1 and
l2 = −1, and
m = 3. As observed in
Figure 2, the PI controller has a notorious overshoot and it presents an offset from the required set point, so the first objective of the proposed controller is reached adequately.
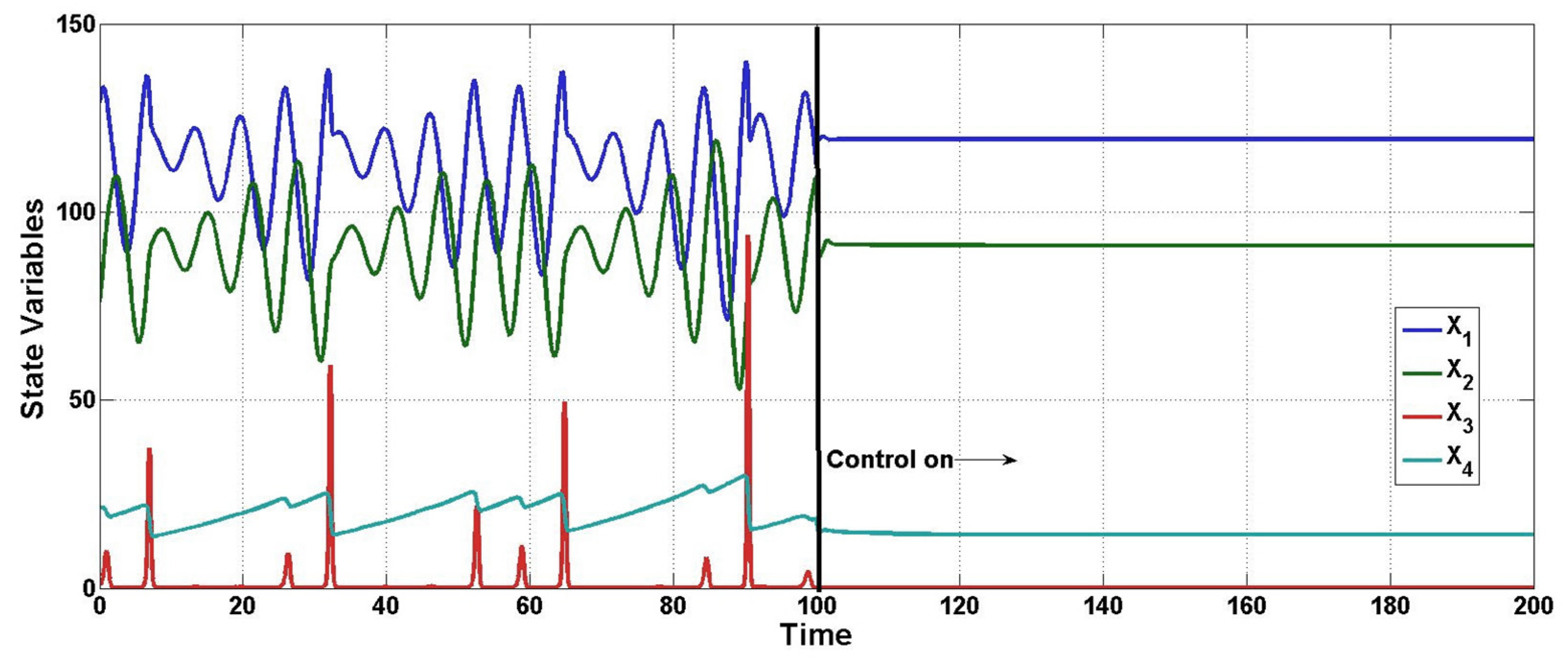
Figure 3 is related to the dynamic behavior of the uncontrolled concentrations from
x2 to
x4, which is named the inner or zero dynamic of the bioreactor, as can be seen, and despite the open-loop oscillatory behavior, the concentration remains in a closed domain by the mass conservation principles, i.e., the mass concentrations cannot reach physically unrealizable values; moreover, when the closed-loop operation is active, the oscillatory behavior disappears. Furthermore,
Figure 4 confirms the above-mentioned, and is a 3D phase portrait with uncontrolled concentrations, here it can be empirically seen as the attractive basin, where the concentrations remain.
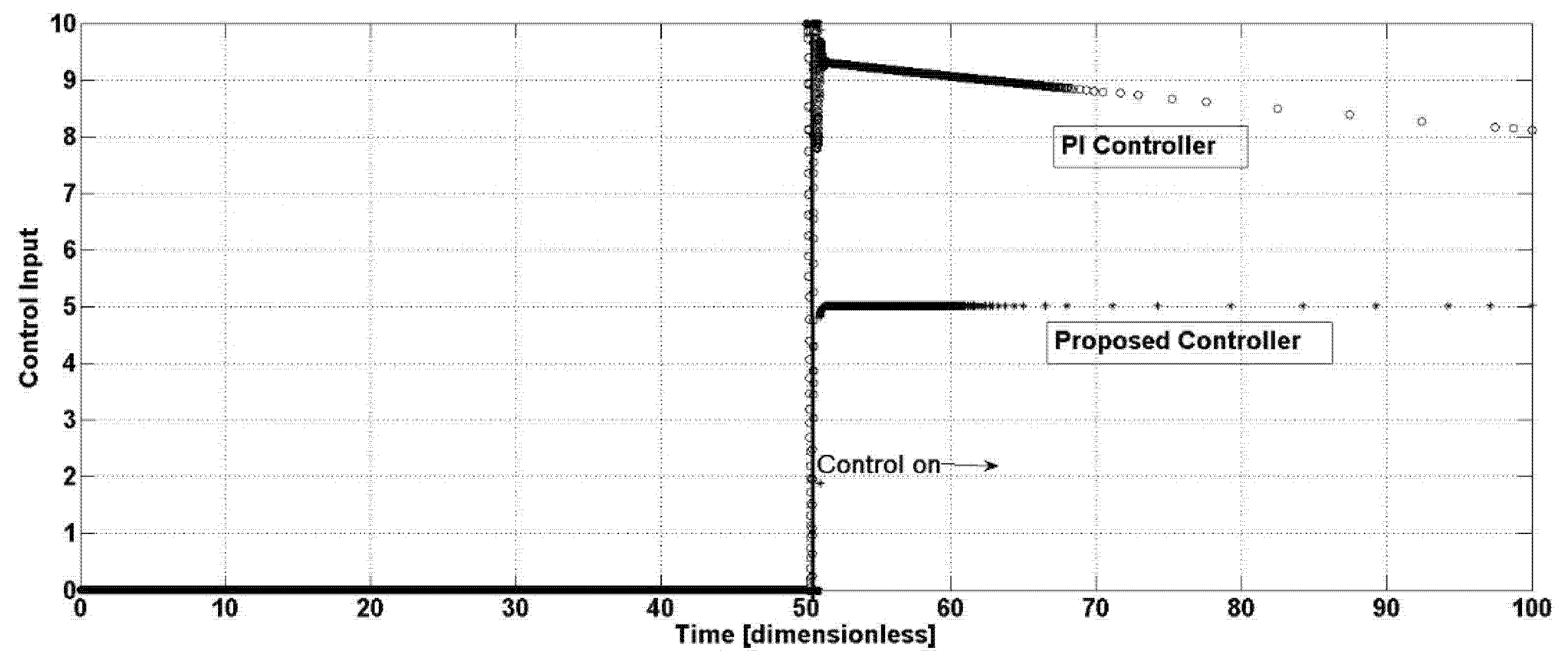
Figure 5 shows the control efforts required by the proposed and the PI controllers.
The closed-loop oscillation suppression is tackled by the proposed feedback control system when it is integrated into the reactor’s operations. The dynamic performance of such a closed-loop system is characterized by its ability to detect deviations from steady-state operation and apply corrective actions in a timely and stable manner. A critical aspect of dynamic performance lies in the speed of response of the control action, i.e., how quickly the controller can suppress oscillations, robustness (its effectiveness under process disturbances and parameter uncertainties), and stability margins related to its ability to maintain control without inducing new oscillations or instability. In biological reactors, where cell metabolism and growth introduce significant time delays and nonlinear responses, the proposed controller tries to accommodate changes in system dynamics over time, such as shifts in microbial population behavior or ensuring changes in environmental conditions are satisfactory, as observed in
Figure 2,
Figure 3 and
Figure 4. The PI controller demands a higher flow, around 60% more than the proposed controller, which reaches a steady-state value of 5 time units, against 8 time units required by the PI control law. A higher value of the input flow provokes a diminishment of the residence time in the bioreactor, in consequence, the chemical reactions have low conversion values, diminishing the concentrations of important product generation, while maintaining a higher volumetric flow; therefore, more energy consumption is needed.
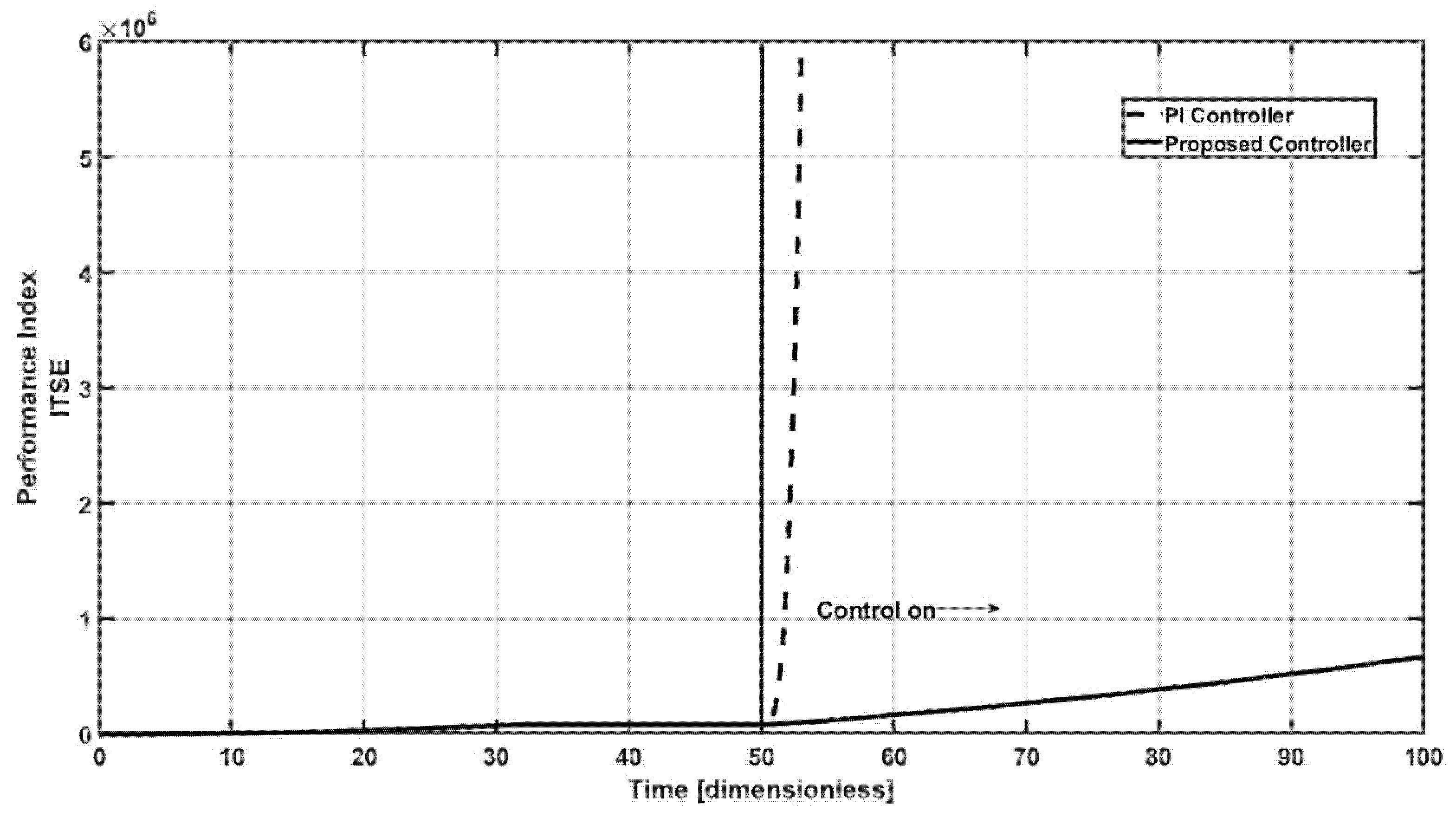
Figure 6 contains the comparative effort of both controllers, via the performance index of the integral time square index (ITSE), where as expected, the PI controller has the worst performance, with the higher value of the index, this result is a consequence of the above mentioned.
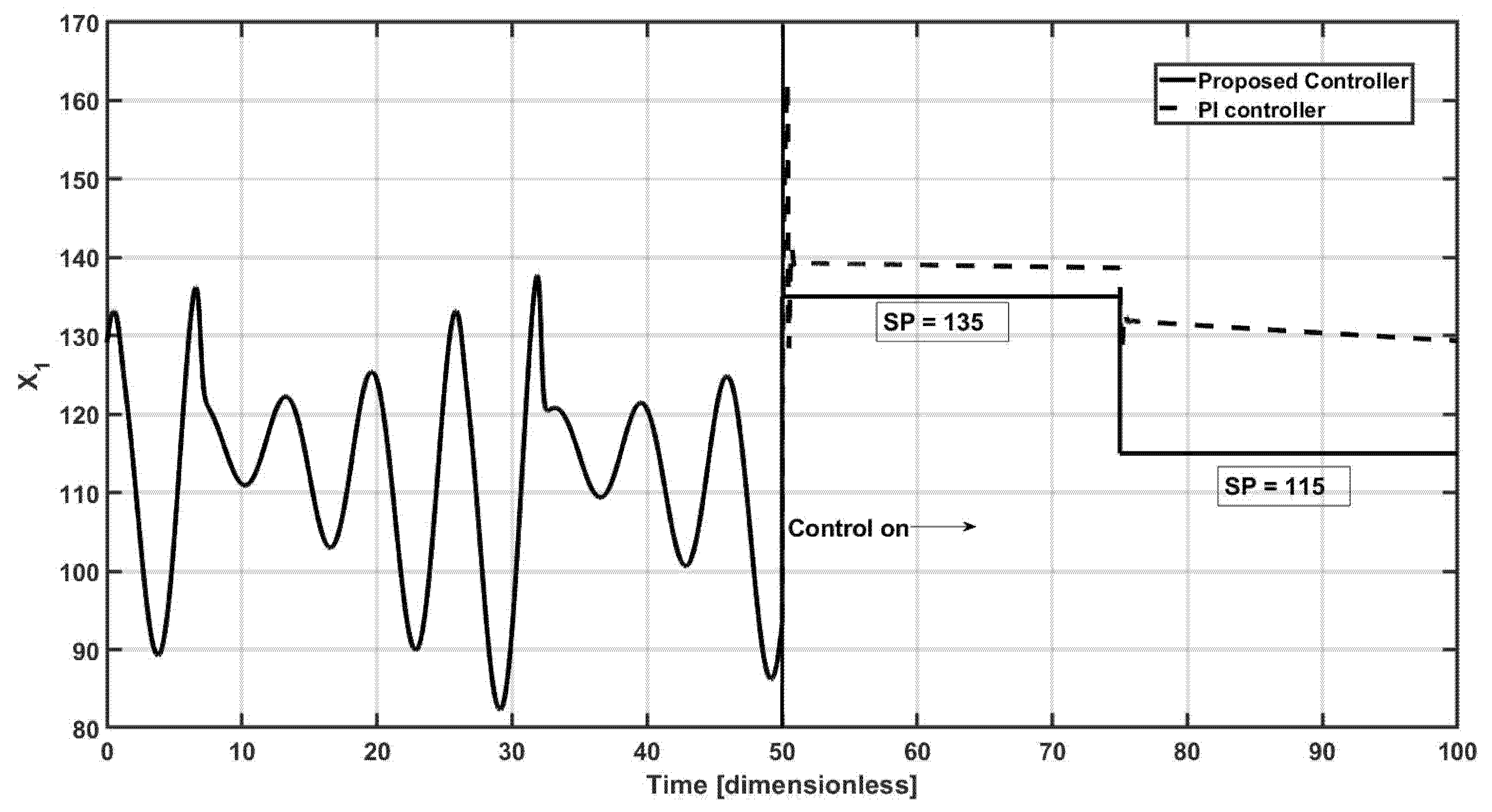
Finally, the performance of the proposed and the PI controllers are shown in
Figure 7, under a set point change, at
t = 75 time units, the first set point is
x1,sp = 135 which changes to
x1,sp = 115. In nonlinear systems, the relationship between input and output varies with operating conditions, this is completely in conflict with the fixed gain structure of linear PI controllers. As a result, the PI controller may perform well near a specific operating point but exhibit reduced stability, slower response, or even induce oscillations when the process deviates from that point. For example, in bioreactors with substrate inhibition or enzyme saturation kinetics, the linear PI controller may fail to compensate adequately for changes in system gain or delay, leading to poor disturbance rejection and steady-state errors. Therefore, as expected, the proposed controllers track the corresponding trajectory without any effort, where no offset, overshoot, and settling time is observed; meanwhile, the PI controller shows that an overshoot and an offset of four concentration units is detected, where the set point changes the PI control law is unable to reach the new required reference and a higher offset, around 15 concentration units are observed, where can be concluded that the PI controller is not able to track the required trajectories.
5. Conclusions
In this proposal, a class of nonlinear control was introduced, with application to a continuous bioreactor, where enzymatic reactions take place, provoking complex oscillatory dynamic behavior. The proposed control law can eliminate the sustained oscillations and impose stable, closed-loop behavior by reaching a fixed set point or tracking the reference trajectory, when the set point is changed to another value, the proposed methodology shows robustness against set point changes; in comparison, a standard PI controller has poor closed-loop performance when a regulation operation is required and is unable to track trajectories when the set point is changed. The stability of the proposed controller was demonstrated via Lyapunov analysis with success. From the above, the applications for real life processes of the proposed control law are possible; therefore, controlling continuous bioreactors offers significant technical advantages that contribute to improved efficiency and product quality in bioprocessing. This stability allows for continuous operation, for example, keeping cells in their exponential growth phase and thereby increasing volumetric productivity compared to batch processes. Well-controlled continuous bioreactors are easier to scale and integrate into automated production systems, making them highly suitable for industrial applications where consistency, scalability, and automation are critical.