Model Identification of E. coli Cultivation Process Applying Hybrid Crow Search Algorithm
Abstract
1. Introduction
- (1)
- A hybrid technique, GA-CSA, that combines the exploration abilities of GA and the exploitation of CSA is proposed.
- (2)
- The GA-CSA hybrid is applied for the model parameter identification of the E. coli BL21(DE3)pPhyt109 fed-batch cultivation process. The obtained mathematical model is successfully verified.
- (3)
- The proposed hybrid model outperforms the pure GA and CSA methods in terms of accuracy while utilizing significantly fewer computational resources, such as computational time and memory. The resource usage is reduced by 8 to 10 times.
- (4)
- The improved performance of the newly proposed hybrid GA-CSA, when compared to the pure CSA and GA in terms of model accuracy, is approved by applying ICrA and several classical statistical tests.
2. Materials and Methods
2.1. Escherichia coli BL21(DE3)pPhyt109 Fed-Batch Cultivation Process
2.1.1. Fed-Batch Cultivation Process
2.1.2. Mathematical Model of E. coli BL21(DE3)pPhyt109 Fed-Batch Cultivation Process
- To simplify the model, all possible effects of mixing the highly concentrated feeds with the cultivation medium are ignored. The bioreactor is completely mixed.
- Throughout the experiment, the viscosity of the suspension in the reactor remains constant.
- Biomass, phytase, and water are the main products of E. coli cultivation.
- The substrate (glucose) is consumed mainly oxidatively.
- The growth conditions are balanced.
- Balanced growth conditions are assumed, meaning that any deviation in the growth rate, substrate consumption, or phytase production is not expected to have a significant impact on the elemental composition of the biomass.
- The production of phytase, for simplicity, is considered to be a one-step enzymatic reaction.
2.2. Metaheuristic Algorithms for Model Parameter Identification
2.2.1. Crow Search Algorithm
2.2.2. Genetic Algorithm
3. Hybrid GA-CSA
| Algorithm 1: Pseudo-code of the hybrid GA-CSA | |
| 1 | Begin |
| 2 | define the GA input parameters: GA operators, NInd, MaxGen, GGAP, , and |
| 3 | define the CSA input parameters: N, MaxIter, fl, AP |
| 4 | problem initialization: number of parameters d, parameters’ bounds, objective function f(x), process model, experimental data |
| 5 | % initialization phase of CSA |
| 6 | for i := 1 to N |
| 7 | generate randomly NInd number of individuals |
| 8 | evaluate the individuals in the population |
| 9 | for j := 1 to MaxGen |
| 10 | select individuals from the current generation |
| 11 | perform crossover on the selected individuals with a probability |
| 12 | perform mutation on each individual with a probability |
| 13 | place the offspring into the new population |
| 14 | evaluate the individuals in the new population |
| 15 | end for |
| 16 | rank the individuals in the population |
| 17 | store the best individual and its estimation |
| 17 | end for |
| 18 | % intrinsic part of CSA |
| 19 | initialize the memory of each crow |
| 20 | for iter := 1 to MaxIter |
| 21 | for i := 1 to N (all crows in the flock) |
| 22 | choose randomly a crow to follow |
| 23 | define an awareness probability |
| 24 | if |
| 25 | change the current position of the |
| 26 | Else |
| 27 | generate a new random position of the |
| 28 | end if |
| 29 | end for |
| 30 | check if all new positions are feasible |
| 31 | evaluate the new positions |
| 32 | update the memory of each crow |
| 33 | end for |
| 34 | rank the position of the crows in the flock |
| 35 | store the best position |
| 36 | End |
4. Numerical Results and Discussion
4.1. Parameters’ Algorithms Tuning
- the population size NInd = 100 (pure GA) and NInd = 25 (hybrid GA-CSA);
- the maximum number of generations MaxGen = 100 (pure GA) and MaxGen = 25 (hybrid GA-CSA);
- the generation gap GGAP = 0.97;
- the crossover probability = 0.7;
- the crossover operator—extended intermediate recombination;
- the mutation rate = 0.1;
- the type of mutation—real-value mutation like Breeder genetic algorithm [73];
- the selection operator—roulette wheel selection.
- the population sizeN = 100 (pure CSA) and N = 25 (hybrid GA-CSA);
- the maximum number of iterationsMaxIter = 100 (pure CSA) and MaxIter = 50 (hybrid GA-CSA);
- the flight length fl = 2;
- the awareness probability AP = 0.1.
4.2. Parameter Identification of E. coli BL21(DE3)pPhyt109 Fed-Batch Cultivation Process
4.2.1. Simulation Setup
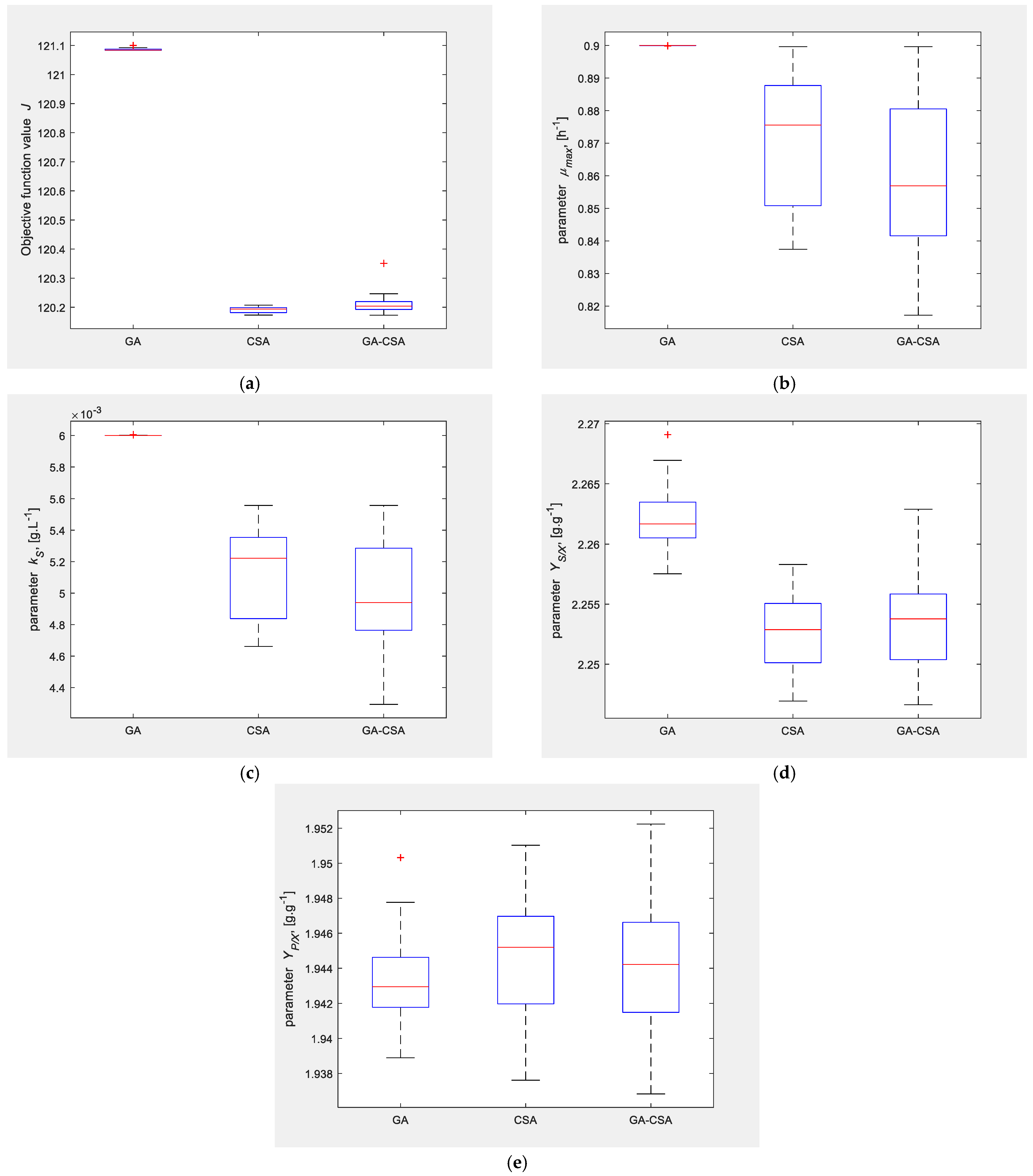
4.2.2. Numerical Results
4.2.3. Interpretation of the Results
InterCriteria Analysis of the Results
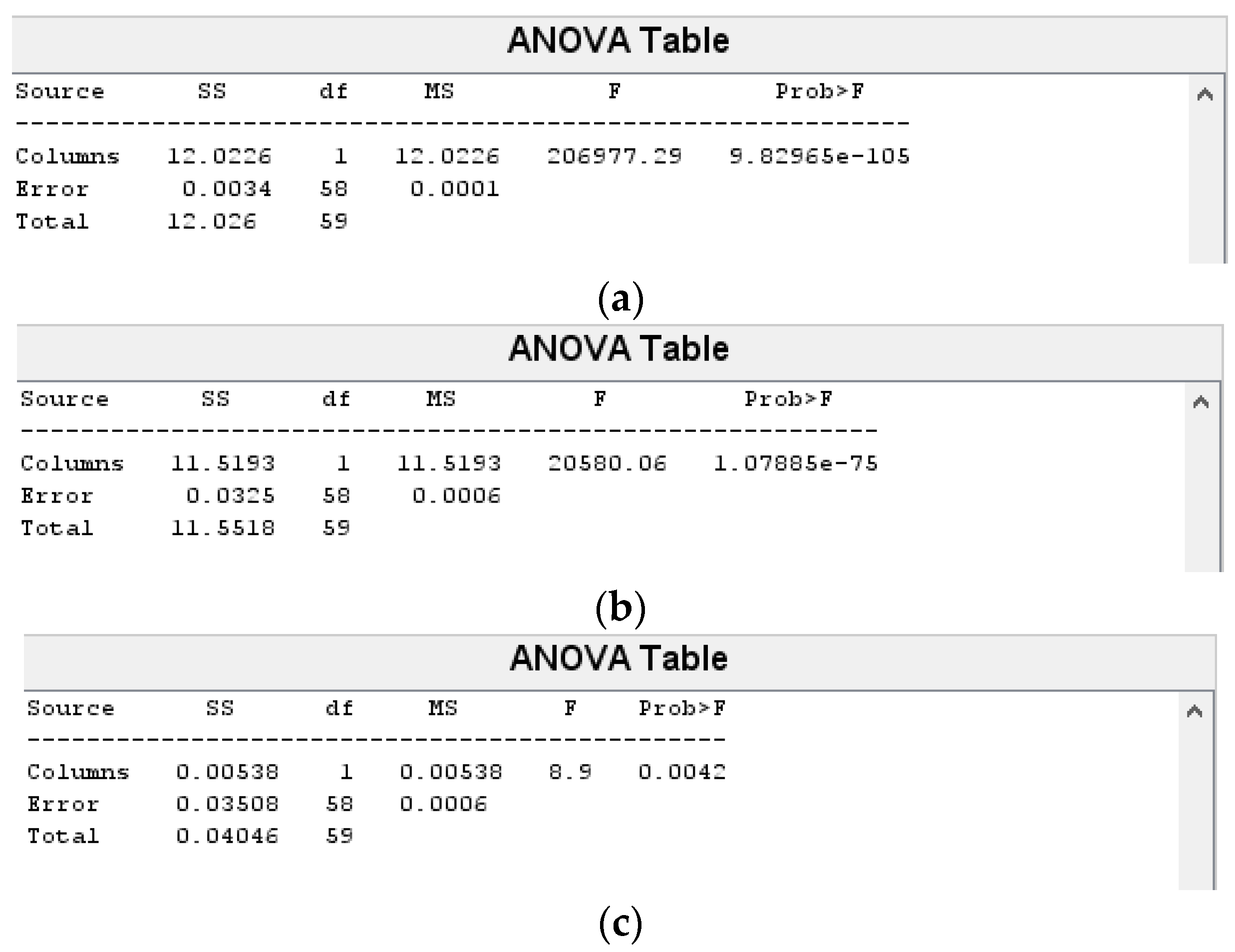
Statistical Analysis of the Results
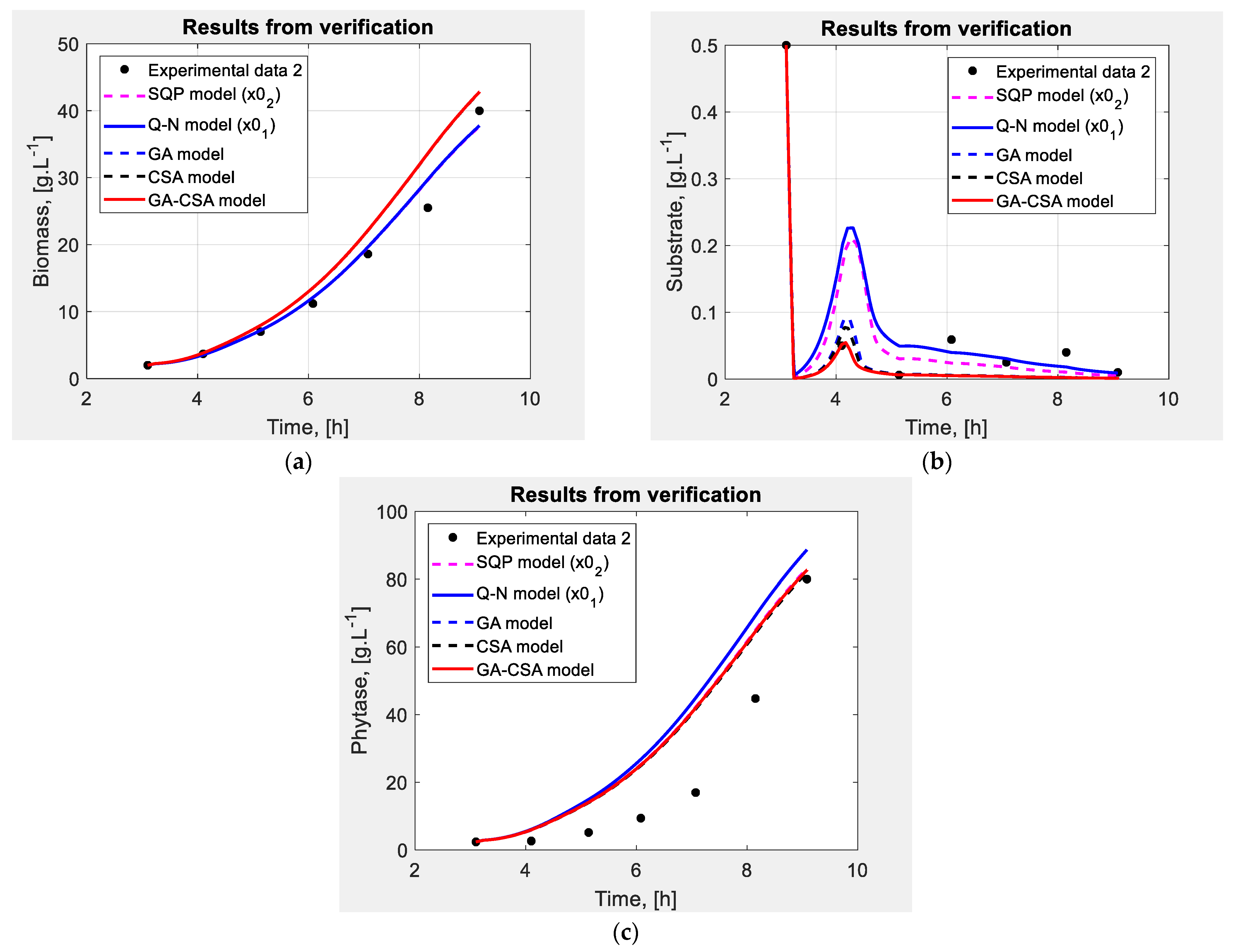
4.3. Verification of the Obtained Mathematical Model of E. coli BL21(DE3)pPhyt109 Fed-Batch Cultivation Process
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hassanien, A.E.; Rizk-Allah, R.M.; Elhoseny, M. A hybrid crow search algorithm based on rough searching scheme for solving engineering optimization problems. J. Ambient Intell. Humaniz. Comput. 2018, 1–25. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-inspired optimization algorithms: Challenges and open problems. J. Comput. Sci. 2020, 46, 101104. [Google Scholar] [CrossRef]
- Hussain, K.; Mohd Salleh, M.N.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Hu, J.; Wu, H.; Zhong, B.; Xiao, R. Swarm intelligence-based optimisation algorithms: An overview and future research issues. Int. J. Autom. Control 2020, 14, 656–693. [Google Scholar] [CrossRef]
- Sharma, P.; Raju, S. Metaheuristic optimization algorithms: A comprehensive overview and classification of benchmark test functions. Soft Comput. 2023, 1–64. [Google Scholar] [CrossRef]
- Pan, J.S.; Hu, P.; Snášel, V.; Chu, S.C. A survey on binary metaheuristic algorithms and their engineering applications. Artif. Intell. Rev. 2023, 56, 6101–6167. [Google Scholar] [CrossRef] [PubMed]
- Kaur, S.; Kumar, Y.; Koul, A.; Kumar Kamboj, S. A systematic review on metaheuristic optimization techniques for feature selections in disease diagnosis: Open issues and challenges. Arch. Comput. Methods Eng. 2023, 30, 1863–1895. [Google Scholar] [CrossRef]
- Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A comparative review on mobile robot path planning: Classical or meta-heuristic methods? Annu. Rev. Control 2020, 50, 233–252. [Google Scholar] [CrossRef]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Review of Metaheuristic Optimization Algorithms for Power Systems Problems. Sustainability 2023, 15, 9434. [Google Scholar] [CrossRef]
- Roeva, O.; Zoteva, D.; Castillo, O. Joint set-up of parameters in genetic algorithms and the artificial bee colony algorithm: An approach for cultivation process modelling. Soft Comput. 2021, 25, 2015–2038. [Google Scholar] [CrossRef]
- Roeva, O.; Zoteva, D.; Roeva, G.; Lyubenova, V. An Efficient Hybrid of an Ant Lion Optimizer and Genetic Algorithm for a Model Parameter Identification Problem. Mathematics 2023, 11, 1292. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Professional: Boston, MA, USA, 1989. [Google Scholar]
- Yang, X.-S.; Deb, S. Cuckoo search via levy flights. In Proceedings of the World Congress on Nature and Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 210–214. [Google Scholar]
- Dorigo, M.; Stutzle, T. Ant Colony Optimization; MIT Press: Cambridge, UK, 2004. [Google Scholar]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Angelova, M.; Roeva, O.; Vassilev, P.; Pencheva, T. Multi-Population Genetic Algorithm and Cuckoo Search Hybrid Technique for Parameter Identification of Fermentation Process Models. Processes 2023, 11, 427. [Google Scholar] [CrossRef]
- Angelova, M.; Vassilev, P.; Pencheva, T. Genetic Algorithm and Cuckoo Search Hybrid Technique for Parameter Identification of Fermentation Process Model. Int. J. Bioaut. 2020, 24, 277–288. [Google Scholar] [CrossRef]
- Sun, Y.; Dai, H.L.; Moayedi, H.; Le, B.N.; Adnan, R.M. Predicting steady-state biogas production from waste using advanced machine learning-metaheuristic approaches. Fuel 2024, 355, 129493. [Google Scholar] [CrossRef]
- Zhao, S.; Jiao, T.; Wang, Z.; Adade, S.Y.S.S.; Wu, X.; Ouyang, Q.; Chen, Q. On-line detecting soluble sugar, total acids, and bacterial concentration during kombucha fermentation based on the visible/near infrared combined meta-heuristic algorithm. J. Food Compos. Anal. 2023, 123, 105653. [Google Scholar] [CrossRef]
- Roeva, O.; Angelova, M.; Zoteva, D.; Pencheva, T. Water cycle algorithm for modelling of fermentation processes. Processes 2020, 8, 920. [Google Scholar] [CrossRef]
- Bouaouda, A.; Sayouti, Y. Hybrid meta-heuristic algorithms for optimal sizing of hybrid renewable energy system: A review of the state-of-the-art. Arch. Comput. Methods Eng. 2022, 29, 4049–4083. [Google Scholar] [CrossRef]
- Hassan, A.; Pillay, N. Hybrid metaheuristics: An automated approach. Expert Syst. Appl. 2019, 130, 132–144. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, P.; Heidari, A.A.; Zhao, X.; Chen, H. Boosted crow search algorithm for handling multi-threshold image problems with application to X-ray images of COVID-19. Expert Syst. Appl. 2023, 213, 119095. [Google Scholar] [CrossRef]
- Singh, H.; Tyagi, S.; Kumar, P. Cloud resource mapping through crow search inspired metaheuristic load balancing technique. Comput. Electr. Eng. 2021, 93, 107221. [Google Scholar] [CrossRef]
- Mohammadi, F.; Abdi, H. A modified crow search algorithm (MCSA) for solving economic load dispatch problem. Appl. Soft Comput. 2018, 71, 51–65. [Google Scholar] [CrossRef]
- Meraihi, Y.; Gabis, A.B.; Ramdane-Cherif, A.; Acheli, D. A comprehensive survey of Crow Search Algorithm and its applications. Artif. Intell. Rev. 2021, 54, 2669–2716. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, C.; He, A.; Dong, W. Overview of Crow Search Algorithm. J. Phys. Conf. Ser. 2022, 2258, 012017. [Google Scholar] [CrossRef]
- Hussien, A.G.; Amin, M.; Wang, M.; Liang, G.; Alsanad, A.; Gumaei, A.; Chen, H. Crow search algorithm: Theory, recent advances, and applications. IEEE Access 2020, 8, 173548–173565. [Google Scholar] [CrossRef]
- Huang, K.W.; Girsang, A.S.; Wu, Z.X.; Chuang, Y.W. A hybrid crow search algorithm for solving permutation flow shop scheduling problems. Appl. Sci. 2019, 9, 1353. [Google Scholar] [CrossRef]
- Cheng, Q.; Huang, H.; Chen, M.A. Novel Crow Search Algorithm Based on Improved Flower Pollination. Hindawi Math. Probl. Eng. 2021, 2021, 1048879. [Google Scholar] [CrossRef]
- Sannasi Chakravarthy, S.R.; Rajaguru, H. A novel improved crow-search algorithm to classify the severity in digital mammograms. Int. J. Imaging Syst. Technol. 2021, 31, 921–954. [Google Scholar] [CrossRef]
- Díaz, P.; Pérez-Cisneros, M.; Cuevas, E.; Avalos, O.; Gálvez, J.; Hinojosa, S.; Zaldivar, D. An improved crow search algorithm applied to energy problems. Energies 2018, 11, 571. [Google Scholar] [CrossRef]
- Lee, D.; Kim, J.; Shon, S.; Lee, S. An Advanced Crow Search Algorithm for Solving Global Optimization Problem. Appl. Sci. 2023, 13, 6628. [Google Scholar] [CrossRef]
- Wijayaningrum, V.N.; Putriwijaya, N.N. An improved crow search algorithm for data clustering. EMITTER Int. J. Eng. Technol. 2020, 8, 86–101. [Google Scholar] [CrossRef]
- Jain, M.; Rani, A.; Singh, V. An improved crow search algorithm for high-dimensional problems. J. Intell. Fuzzy Syst. 2017, 33, 3597–3614. [Google Scholar] [CrossRef]
- Gholami, J.; Mardukhi, F.; Zawbaa, H.M. An improved crow search algorithm for solving numerical optimization functions. Soft Comput. 2021, 25, 9441–9454. [Google Scholar] [CrossRef]
- Cortés-Caicedo, B.; Avellaneda-Gómez, L.S.; Montoya, O.D.; Alvarado-Barrios, L.; Álvarez-Arroyo, C. An improved crow search algorithm applied to the phase swapping problem in asymmetric distribution systems. Symmetry 2021, 13, 1329. [Google Scholar] [CrossRef]
- Huang, H.; Liao, H. An improved crow search algorithm with multi strategy disturbance. In ITM Web of Conferences; EDP Sciences: Evry, France, 2022; Volume 47, p. 02007. [Google Scholar]
- Sharma, M.; Pathik, B. Crow Search Algorithm with Improved Objective Function for Test Case Generation and Optimization. Intell. Autom. Soft Comput. 2022, 32, 1125–1140. [Google Scholar] [CrossRef]
- Shekhawat, S.; Saxena, A. Development and applications of an intelligent crow search algorithm based on opposition based learning. ISA Trans. 2020, 99, 210–230. [Google Scholar] [CrossRef]
- He, J.; Peng, Z.; Zhang, L.; Zuo, L.; Cui, D.; Li, Q. Enhanced crow search algorithm with multi-stage search integration for global optimization problems. Soft Comput. 2023, 27, 14877–14907. [Google Scholar] [CrossRef]
- Javidi, A.; Salajegheh, E.; Salajegheh, J. Enhanced crow search algorithm for optimum design of structures. Appl. Soft Comput. 2019, 77, 274–289. [Google Scholar] [CrossRef]
- Sayed, G.I.; Hassanien, A.E.; Azar, A.T. Feature selection via a novel chaotic crow search algorithm. Neural Comput. Appl. 2019, 31, 171–188. [Google Scholar] [CrossRef]
- Arora, S.; Singh, H.; Sharma, M.; Sharma, S.; Anand, P. A new hybrid algorithm based on grey wolf optimization and crow search algorithm for unconstrained function optimization and feature selection. IEEE Access 2019, 7, 26343–26361. [Google Scholar] [CrossRef]
- El-Ashmawi, W.H.; Ali, A.F.; Slowik, A. Hybrid crow search and uniform crossover algorithm-based clustering for top-N recommendation system. Neural Comput. Appl. 2021, 33, 7145–7164. [Google Scholar] [CrossRef]
- Anter, A.M.; Ali, M. Feature selection strategy based on hybrid crow search optimization algorithm integrated with chaos theory and fuzzy c-means algorithm for medical diagnosis problems. Soft Comput. 2020, 24, 1565–1584. [Google Scholar] [CrossRef]
- Krishnadoss, P.; Pradeep, N.; Ali, J.; Nanjappan, M.; Krishnamoorthy, P.; Kedalu Poornachary, V. CCSA: Hybrid cuckoo crow search algorithm for task scheduling in cloud computing. Int. J. Intell. Eng. Syst. 2021, 14, 241–250. [Google Scholar] [CrossRef]
- Hossain, S.Z.; Sultana, N.; Mohammed, M.E.; Razzak, S.A.; Hossain, M.M. Hybrid support vector regression and crow search algorithm for modeling and multiobjective optimization of microalgae-based wastewater treatment. J. Environ. Manag. 2022, 301, 113783. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.N.; Fred, A.L.; Miriam, L.J.; Padmanabhan, P.; Gulyás, B.; Kumar, A.; Dayana, N. Improved crow search algorithm based on arithmetic crossover—A novel metaheuristic technique for solving engineering optimization problems. In Multi-Objective Combinatorial Optimization Problems and Solution Methods; Academic Press: Cambridge, MA, USA, 2022; pp. 71–91. [Google Scholar]
- Cao, L.; Yue, Y.; Zhang, Y.; Cai, Y. Improved crow search algorithm optimized extreme learning machine based on classification algorithm and application. IEEE Access 2021, 9, 20051–20066. [Google Scholar] [CrossRef]
- Gupta, D.; Sundaram, S.; Khanna, A.; Hassanien, A.E.; De Albuquerque, V.H.C. Improved diagnosis of Parkinson’s disease using optimized crow search algorithm. Comput. Electr. Eng. 2018, 68, 412–424. [Google Scholar] [CrossRef]
- Hamed Alnaish, Z.A.; Algamal, Z.Y. Improving binary crow search algorithm for feature selection. J. Intell. Syst. 2023, 32, 20220228. [Google Scholar] [CrossRef]
- Braik, M.; Al-Zoubi, H.; Ryalat, M.; Sheta, A.; Alzubi, O. Memory based hybrid crow search algorithm for solving numerical and constrained global optimization problems. Artif. Intell. Rev. 2023, 56, 27–99. [Google Scholar] [CrossRef]
- Durgut, R.; Aydin, M.E. Multi Strategy Search with Crow Search Algorithm. In Optimisation Algorithms and Swarm Intelligence; IntechOpen: Rijeka, Croatia, 2022. [Google Scholar]
- Adamu, A.; Abdullahi, M.; Junaidu, S.B.; Hassan, I.H. A hybrid particle swarm optimization with crow search algorithm for feature selection. Mach. Learn. Appl. 2021, 6, 100108. [Google Scholar] [CrossRef]
- Roeva, O.; Pencheva, T.; Tzonkov, S.; Arndt, M.; Hitzmann, B.; Kleist, S.; Miksch, G.; Friehs, K.; Flaschel, E. Multiple model approach to modelling of Escherichia coli fed-batch cultivation extracellular production of bacterial phytase. Electron. J. Biotechnol. 2007, 10, 592–603. [Google Scholar] [CrossRef][Green Version]
- Kleist, S.; Miksch, G.; Hitzmann, B.; Arndt, M.; Freihs, K.; Flaschel, E. Optimization of the extracellular production of a bacterial phytase with Escherichia coli by using different fed-batch fermentation strategies. Appl. Microbiol. Biotechnol. 2003, 61, 456–462. [Google Scholar] [CrossRef] [PubMed]
- Miksch, G.; Kleist, S.; Friehs, K.; Flaschel, E. Overexpression of the phytase from Escherichia coli and its extracellular production in bioreactors. Appl. Microbiol. Biotechnol. 2002, 59, 685–694. [Google Scholar] [CrossRef]
- Atanassov, K.; Mavrov, D.; Atanassova, V. Intercriteria decision making: A new approach for multicriteria decision making, based on index matrices and intuitionistic fuzzy sets. Issues Intuit. Fuzzy Sets Gen. Nets 2014, 11, 1–8. [Google Scholar]
- Zaharieva, B.; Doukovska, L.; Ribagin, S.; Radeva, I. InterCriteria Analysis of Data Obtained from Patients with Behterev’s Disease. Int. J. Bioautom. 2020, 24, 5–14. [Google Scholar] [CrossRef]
- Jekova, I.; Vassilev, P.; Stoyanov, T.; Pencheva, T. InterCriteria analysis: Application for ECG data analysis. Mathematics 2021, 9, 854. [Google Scholar] [CrossRef]
- Atanassov, K.; Pencheva, T. InterCriteria Analysis Approach as a Tool for Promising Decision Making in Physiological Rhythms. In 2019-20 MATRIX Annals; MATRIX Book Series; de Gier, J., Praeger, C.E., Tao, T., Eds.; Springer: Cham, Switzerland, 2021; Volume 4. [Google Scholar] [CrossRef]
- Petrov, M. Modeling and Use of Inter-Criteria Decision Analysis for Selecting Growth Rate Models for Batch Cultivation of Yeast Kluyveromyces marxianus var. lactis MC 5. Fermentation 2021, 7, 163. [Google Scholar] [CrossRef]
- Antonov, A. Analysis and Detection of the Degrees and Direction of Correlations between Key Indicators of Physical Fitness of 10–12-year-old Hockey Players. Int. J. Bioautom. 2019, 23, 303–314. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods and Scientific Inference, 2nd ed.; Hafner Publishing Co.: New York, NY, USA, 1959. [Google Scholar]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of nonparametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC’2005 special session on real parameter optimization. J. Heuristics 2009, 15, 617–644. [Google Scholar] [CrossRef]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Oliva, D.; Hinojosa, S.; Cuevas, E.; Pajares, G.; Avalos, O.; Gálvez, J. Cross entropy based thresholding for magnetic resonance brain images using Crow Search Algorithm. Expert Syst. Appl. 2017, 79, 164–180. [Google Scholar] [CrossRef]
- Velasco, L.; Guerrero, H.; Hospitaler, A. Can the global optimum of a combinatorial optimization problem be reliably estimated through extreme value theory? Swarm Evol. Comput. 2022, 75, 10117. [Google Scholar] [CrossRef]
- Pandey, H.M. 3—State of the Art: Genetic Algorithms and Premature Convergence. In State of the Art on Grammatical Inference Using Evolutionary Method; Hari, M.P., Ed.; Academic Press: Cambridge, MA, USA, 2022; pp. 35–124. [Google Scholar]
- Roeva, O.; Zoteva, D. Knowledge discovery from data: InterCriteria analysis of mutation rate influence. Notes Intuitionistic Fuzzy Sets 2018, 24, 120–130. [Google Scholar] [CrossRef]
- Roeva, O.; Fidanova, S.; Atanassova, V. Hybrid ACO-GA for parameter identification of an E. coli cultivation process model. In International Conference on Large-Scale Scientific Computing; Springer: Berlin/Heidelberg, Germany, 2013; pp. 313–320. Available online: https://link.springer.com/chapter/10.1007/978-3-662-43880-0_35 (accessed on 7 November 2023).
- Mühlenbein, H.; Schlierkamp-Voosen, D. Predictive models for the breeder genetic algorithm I. Continuous parameter optimization. Evol. Comput. 1993, 1, 25–49. [Google Scholar] [CrossRef]
- Atanassov, K.; Szmidt, E.; Kacprzyk, J. On intuitionistic fuzzy pairs. Notes Intuitionistic Fuzzy Sets 2013, 19, 1–13. [Google Scholar]
- Atanassov, K. Intuitionistic Fuzzy Sets. VII ITKR Session, Sofia, 20–23 June 1983. Reprinted. Int. J. Bioautom. 2016, 20, S1–S6. [Google Scholar]
- Atanassov, K.; Atanassova, V.; Gluhchev, G. InterCriteria Analysis: Ideas and problems. Notes Intuitionistic Fuzzy Sets 2015, 21, 81–88. [Google Scholar]
- Ikonomov, N.; Vassilev, P.; Roeva, O. ICrAData—Software for InterCriteria Analysis. Int. J. Bioautom. 2018, 2, 1–10. [Google Scholar] [CrossRef]
- Atanassov, K. On index matrices, Part 1: Standard cases. Adv. Stud. Contemp. Math. 2010, 20, 291–302. [Google Scholar]
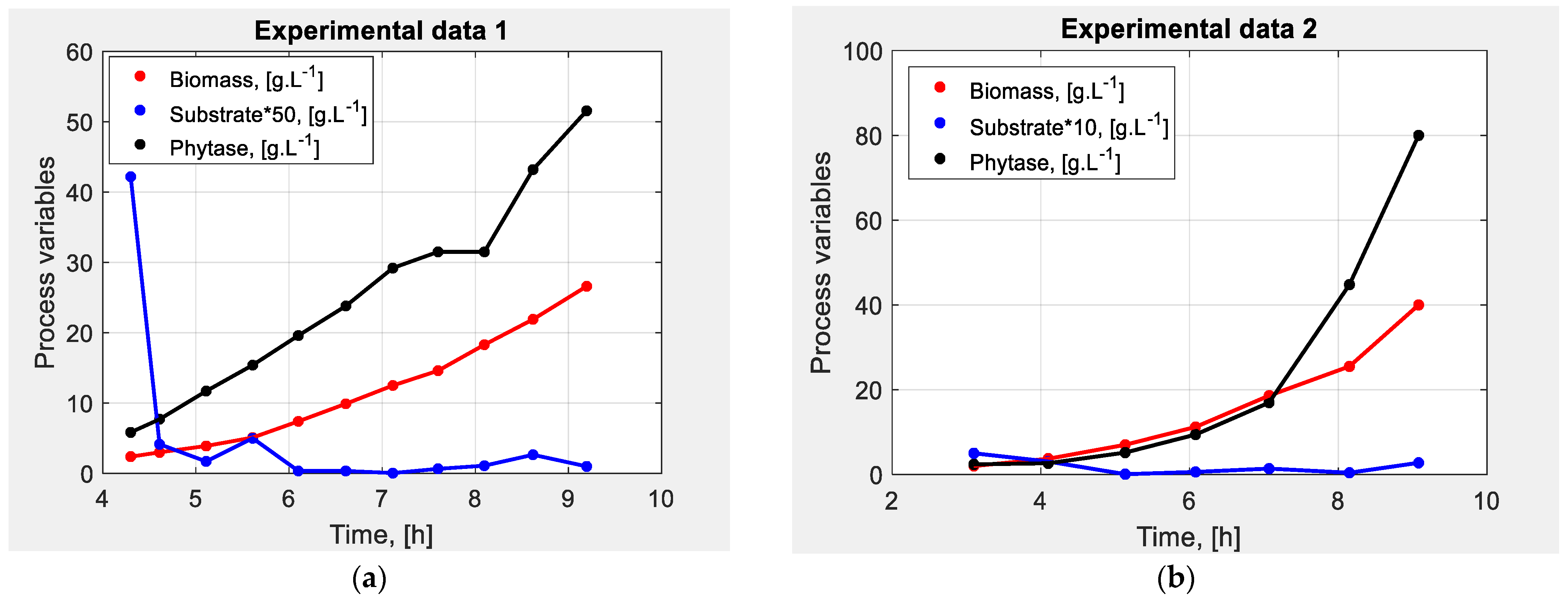
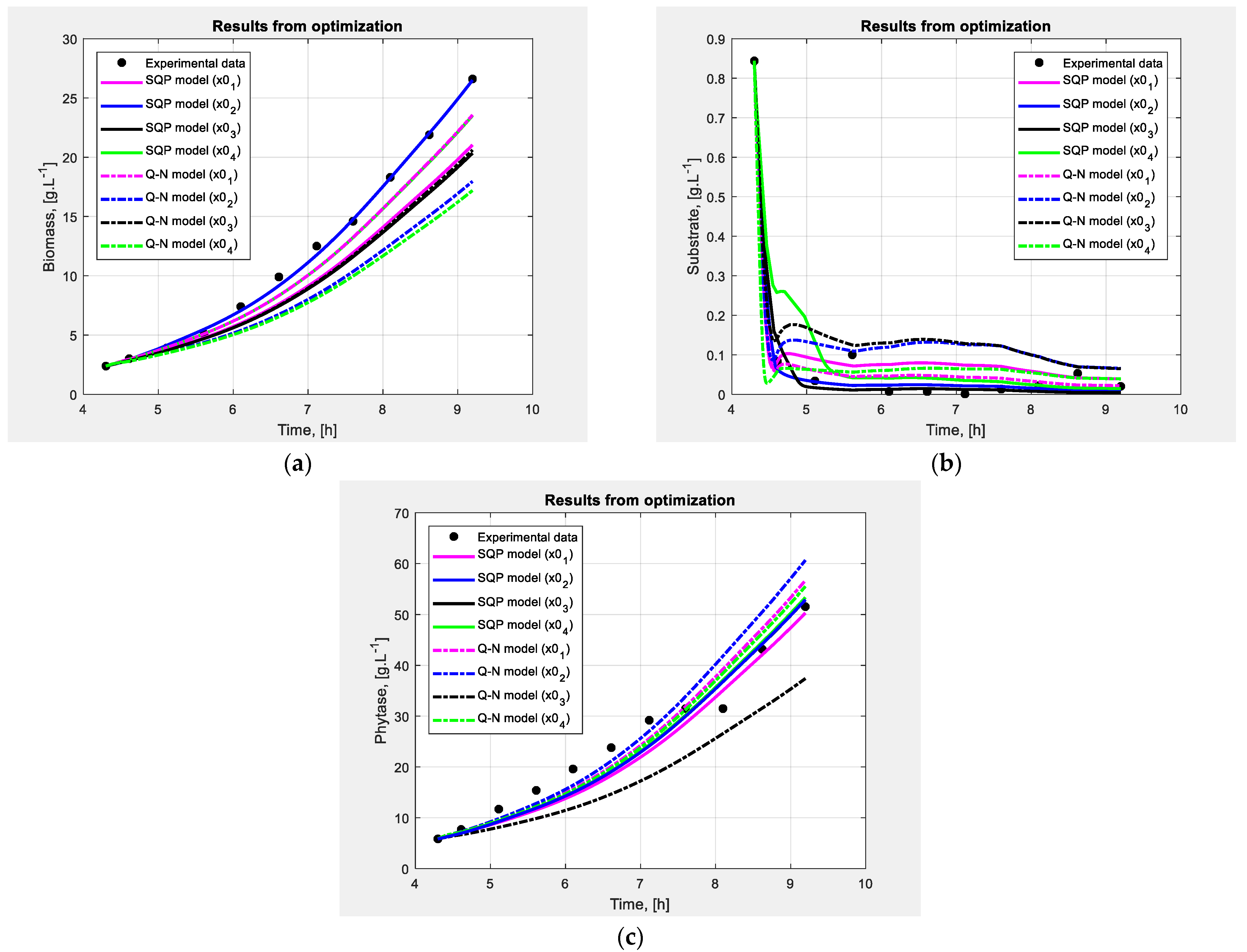

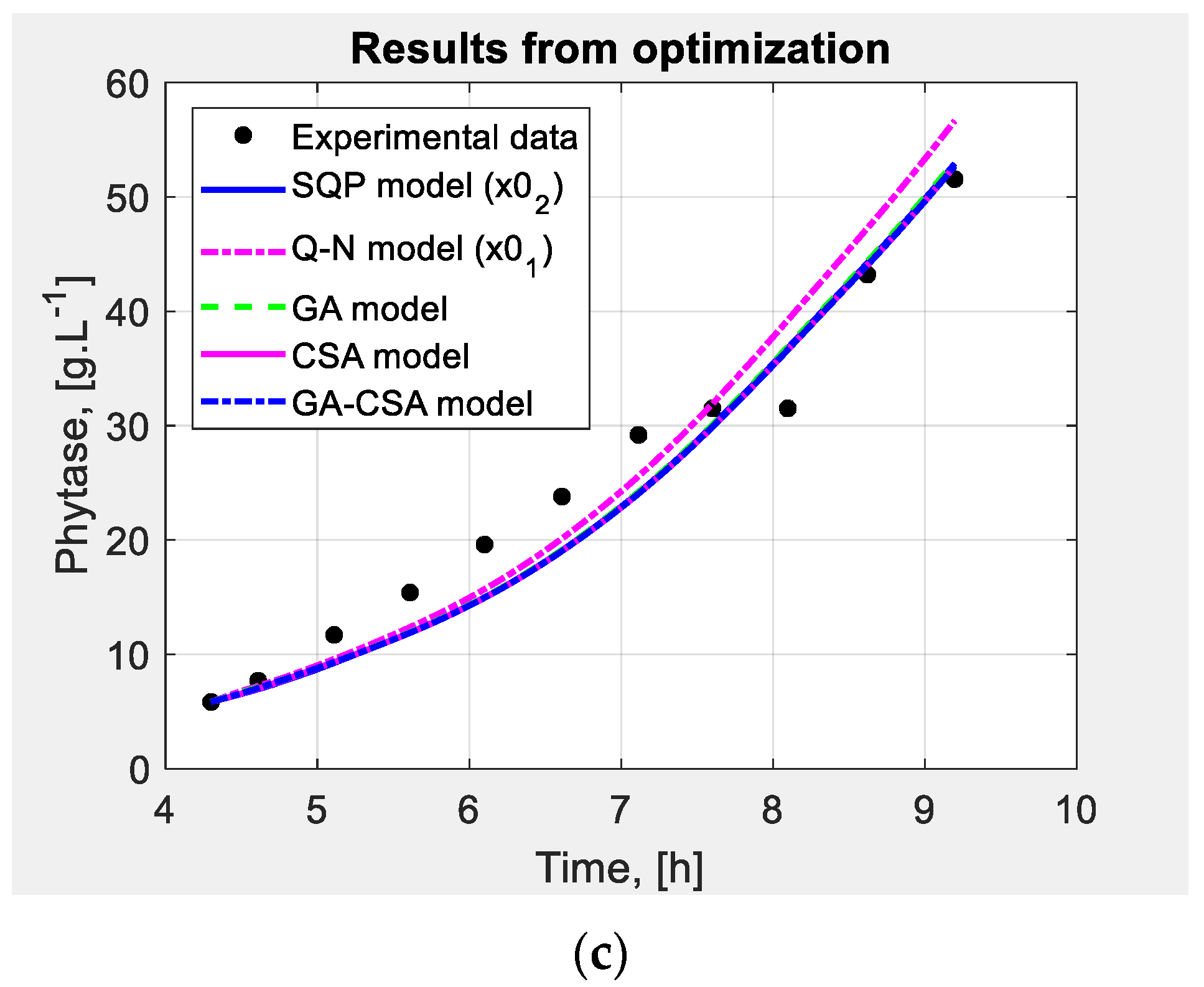
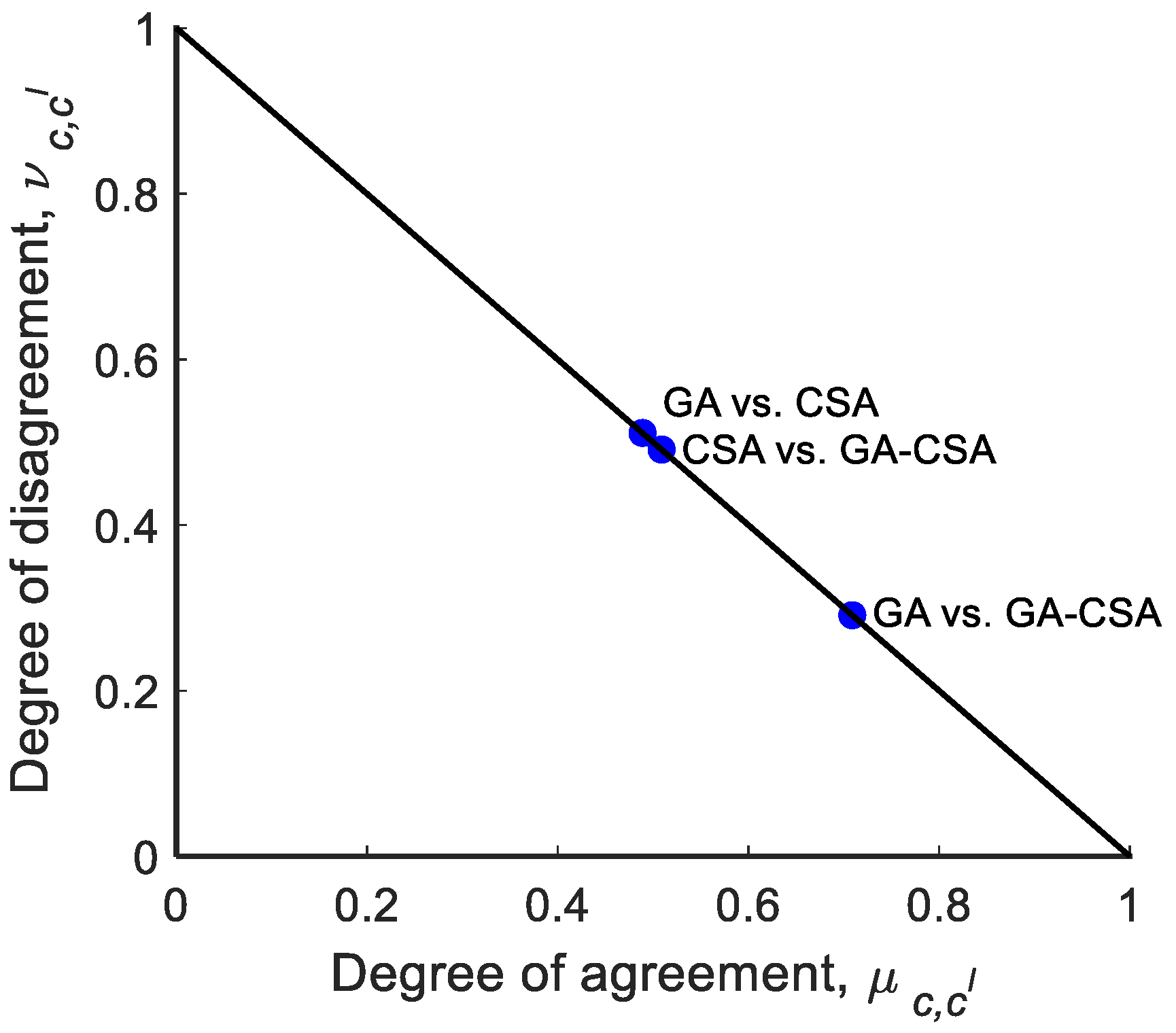

| Algorithm | Reference, Year | Algorithm Parameters | |
|---|---|---|---|
| Flight Length, fl | Awareness Probability, AP | ||
| Crow search algorithm (original) | [15], 2016 | 1.5, 2, 2.5 | 0, 0.05, 0.2 |
| RCSA—CSA with the rough searching scheme | [2], 2018 | dynamic | 0.1 |
| HCSA—CSA with Nawaz–Enscore–Ham heuristic technique and SA combined with the variable neighborhood search | [29], 2019 | 10 | 0.25 |
| IFCSA—CSA based on improved flower pollination algorithm | [30], 2021 | 2 | 0.1 |
| ImCSOA—CSA with chaotic maps | [31], 2021 | 1.8 | 0.1 |
| MCSA—CSA with the innovative selection of the crows and adaptive adjustment of the flight length | [25], 2018 | 1.9, 2 | 0.1 |
| CSA with modified awareness probability and random perturbation | [32], 2018 | 2 | dynamic |
| CSA with dynamic fl and AP | [33], 2023 | dynamic | dynamic |
| Improved CSA with dynamic AP | [34], 2020 | 2, 2.5 | dynamic |
| ICSA—CSA improved by introducing experience factor, adaptive adjustment operator and Lévy flight distribution in position updating mechanism of crows | [35], 2017 | 2 | 0.1 |
| ICSA—improved CSA with a new update mechanism | [36], 2021 | 1.2–1.6 | 0.1 |
| Classical CSA using the VSA evolution mechanism to revise and exploit the solution space | [37], 2021 | 2 | 0.1, 0.5 |
| Improved CSA with multi-strategy disturbance | [38], 2022 | 2 | 0.1 |
| CSA with an improved objective function | [39], 2022 | 0.7 | 0.5 |
| CSA with a cosine function and incorporating the opposition-based learning concept | [40], 2020 | 2 | 0.1 |
| CSA with chaos and multiple opposition-based learning techniques | [41], 2023 | 2 | 0.1 |
| Enhanced CSA with a free-fly mechanism and the personal upper-bound strategy | [42], 2019 | 1.5, 2, 2.5, 3 | 0, 0.1, 0.2 |
| Chaotic CSA (CCSA) | [43], 2019 | 2 | 0.1 |
| GWOCSA—hybrid grey wolf optimization with CSA | [44], 2019 | 2 | 0.1 |
| HCSUC—hybrid CSA and uniform crossover algorithm | [45], 2021 | 2 | 0.1 |
| CFCSA—hybrid CSA algorithm integrated with chaos theory and fuzzy c-means algorithm | [46], 2020 | 2 | 0.1 |
| CCSA—hybrid cuckoo CSA | [47], 2021 | 2 | 0.1 |
| Hybrid support vector regression and CSA | [48], 2022 | 2 | 0.1 |
| Improved CSA based on arithmetic crossover | [49], 2022 | 2 | 0.1 |
| CSA with a particle swarm algorithm search strategy | [50], 2021 | 2 | 0.1 |
| Crow search algorithm for efficient feature selection | [51], 2018 | 0.2 | 0.1 |
| BCSA—hybrid binary CSA based on quasi-oppositional method | [52], 2023 | 1–1.8 | 0.2 |
| MHCSA—memory-based hybrid CSA with particle swarm optimization algorithm | [53], 2023 | - | - |
| CSA with implemented multi-strategy approach with a selection mechanism | [54], 2022 | 2 | 0.1 |
| Enhanced chaotic crow search and particle swarm optimization algorithm | [55], 2021 | 2 | 0.2 |
| Condition | Cultivation Process 1 | Cultivation Process 2 |
|---|---|---|
| growth medium | glucose mineral salt medium | |
| bioreactor working volume | 5 L | |
| bioreactor total volume | 7 L | |
| temperature | 37 °C | |
| airflow | 10 L·min−1 | |
| stirrer speed | 500 rpm | |
| pH | 6.9 # | |
| 4.30 h | 3.10 h | |
| 2.70 L | ||
| 3.20 g/L | ||
| 0.78 g/L | 0.50 g/L | |
| 500 g/L | ||
| 0.2 g/L | 0.1 g/L | |
| Algorithm | Objective Function, J | |||
|---|---|---|---|---|
| Mean | Worst | Best | SD | |
| GA | 121.0858 | 121.1001 | 121.0831 | 0.003546 |
| CSA | 120.1905 | 120.2070 | 120.1731 | 0.009986 |
| GA-CSA | 120.2095 | 120.3507 | 120.1724 | 0.032704 |
| Algorithm | Initial Solution | Objective Function, J |
|---|---|---|
| SQP | [0.85; 0.03; 2.5; 2.5] | 225.3851 |
| Q-N | 185.2192 | |
| SQP | [0.75; 0.08; 3.5; 3.5] | 122.7380 |
| Q-N | 483.1404 | |
| SQP | [0.8; 0.03; 2; 2.5] | 227.5362 |
| Q-N | 860.9834 | |
| SQP | [0.6; 0.05; 3.5; 3.5] | 148.5591 |
| Q-N | 378.2660 |
| Algorithm | Model Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|---|
| , [h−1] | SD | , [g·L−1] | SD | , [g·g−1] | SD | , [g·g−1] | SD | |
| SQP | 0.729 | -- | 0.0156 | -- | 2.276 | -- | 1.957 | -- |
| Q-N | 0.850 | -- | 0.0315 | -- | 2.588 | -- | 2.400 | -- |
| GA | 0.900 | 3.76 × 10−5 | 0.0060 | 1.18E-06 | 2.262 | 0.0025 | 1.943 | 0.0025 |
| CSA | 0.888 | 0.0196 | 0.0054 | 0.00028 | 2.250 | 0.0029 | 1.943 | 0.0035 |
| GA-CSA | 0.892 | 0.0232 | 0.0054 | 0.00033 | 2.251 | 0.0036 | 1.944 | 0.0039 |
| Wilcoxon Test | ||||
|---|---|---|---|---|
| Algorithms | p-Value | H | STATS | |
| Zval | Ranksum | |||
| GA vs. CSA | 3.0199 × 10−11 | 1 | 6.6456 | 1365 |
| GA vs. GA-CSA | 2.9392 × 10−11 | 1 | 5.5268 | 1451 |
| CSA vs. GA-CSA | 0.0047 | 1 | −2.8244 | 723.5 |
| Algorithm | Error, J |
|---|---|
| SQP | 1620,2603 |
| Q-N | 1892,2863 |
| GA | 1408,1104 |
| CSA | 1408,0141 |
| GA-CSA | 1386,9798 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roeva, O.; Zoteva, D. Model Identification of E. coli Cultivation Process Applying Hybrid Crow Search Algorithm. Fermentation 2024, 10, 12. https://doi.org/10.3390/fermentation10010012
Roeva O, Zoteva D. Model Identification of E. coli Cultivation Process Applying Hybrid Crow Search Algorithm. Fermentation. 2024; 10(1):12. https://doi.org/10.3390/fermentation10010012
Chicago/Turabian StyleRoeva, Olympia, and Dafina Zoteva. 2024. "Model Identification of E. coli Cultivation Process Applying Hybrid Crow Search Algorithm" Fermentation 10, no. 1: 12. https://doi.org/10.3390/fermentation10010012
APA StyleRoeva, O., & Zoteva, D. (2024). Model Identification of E. coli Cultivation Process Applying Hybrid Crow Search Algorithm. Fermentation, 10(1), 12. https://doi.org/10.3390/fermentation10010012







