Graphene and Nanoclay as Processing Aid Agents: A Study on Rheological Behavior in Polystyrene
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Processing
2.3. Characterizations
3. Results and Discussion
3.1. Morphology of Graphene Composites
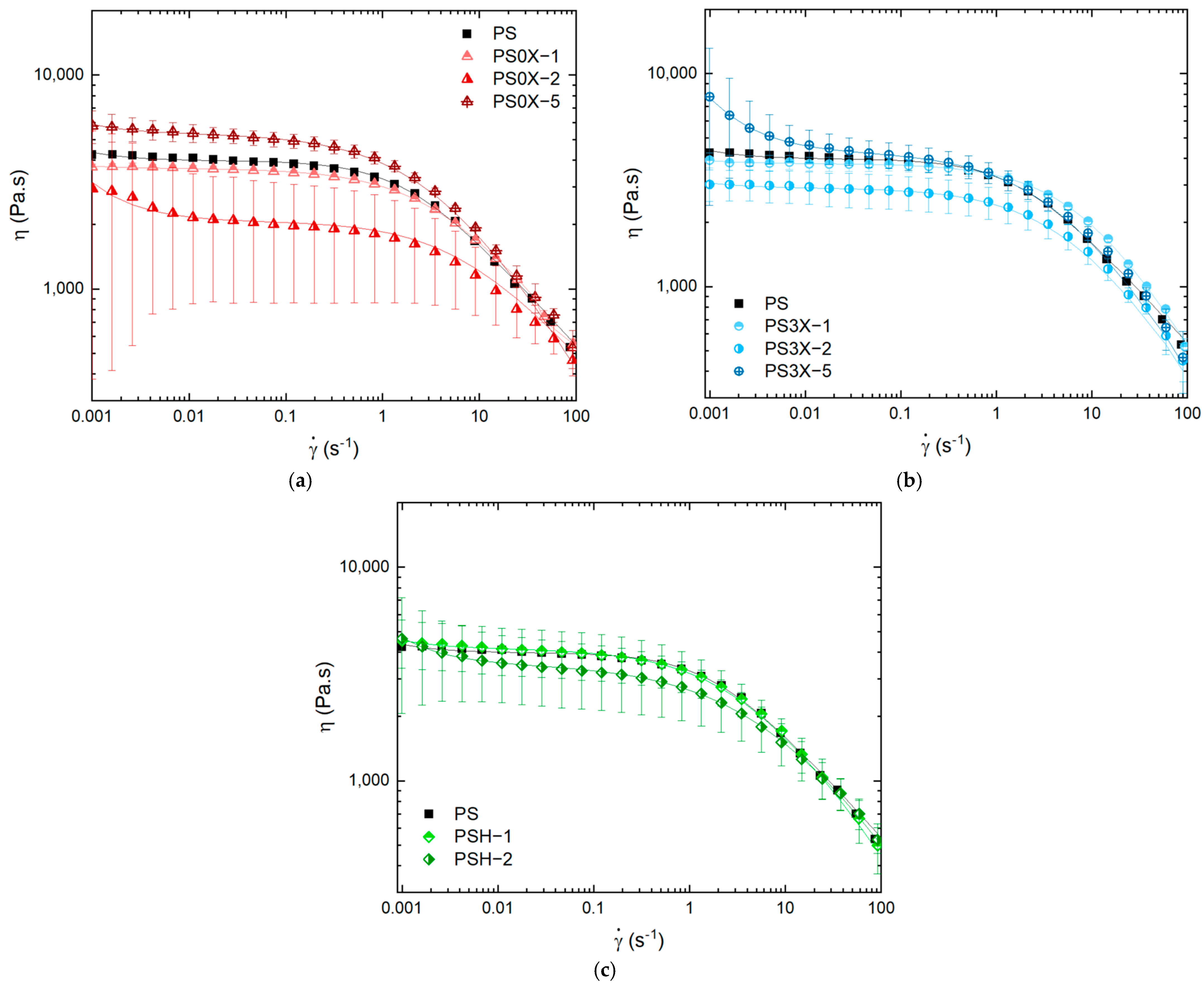
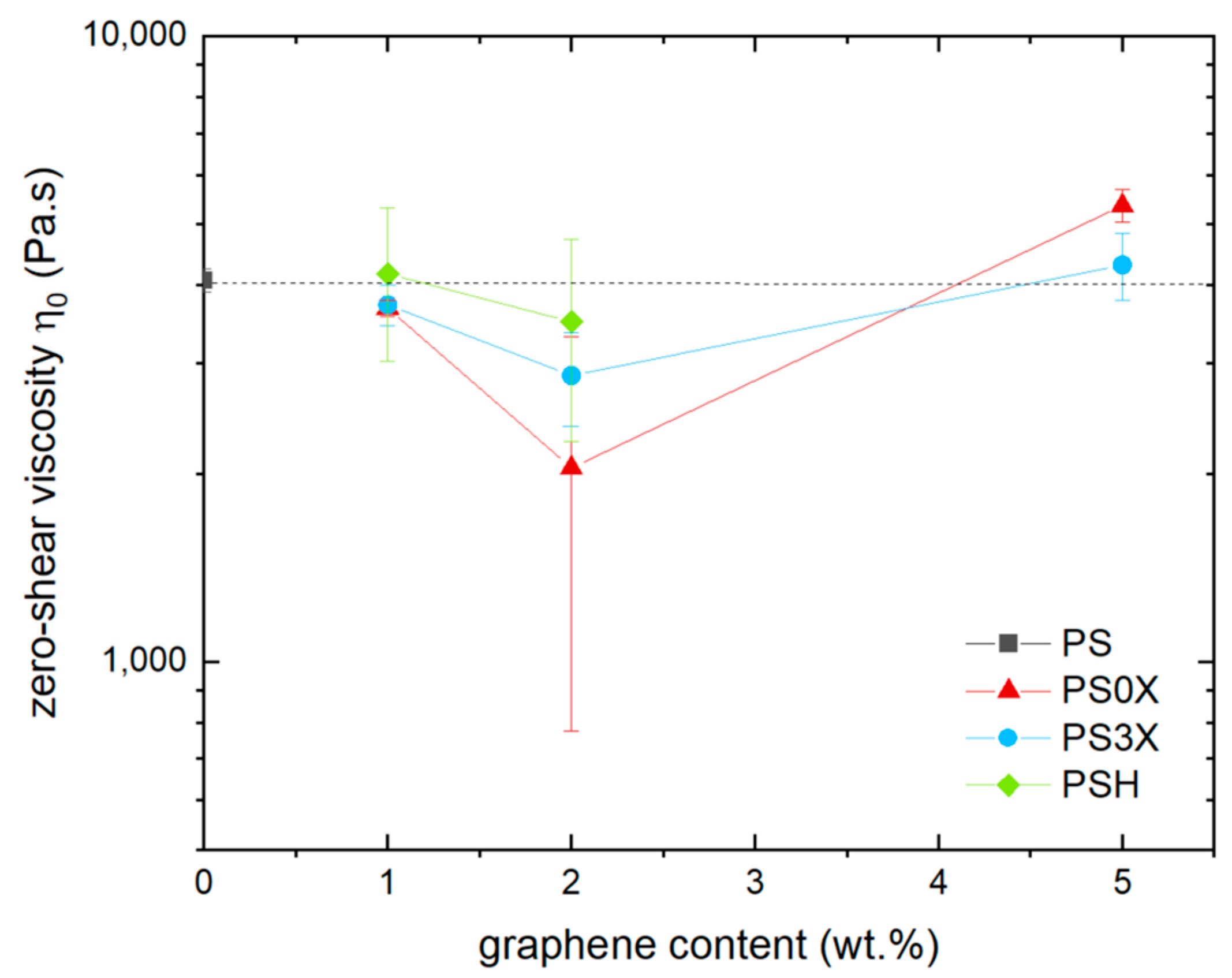
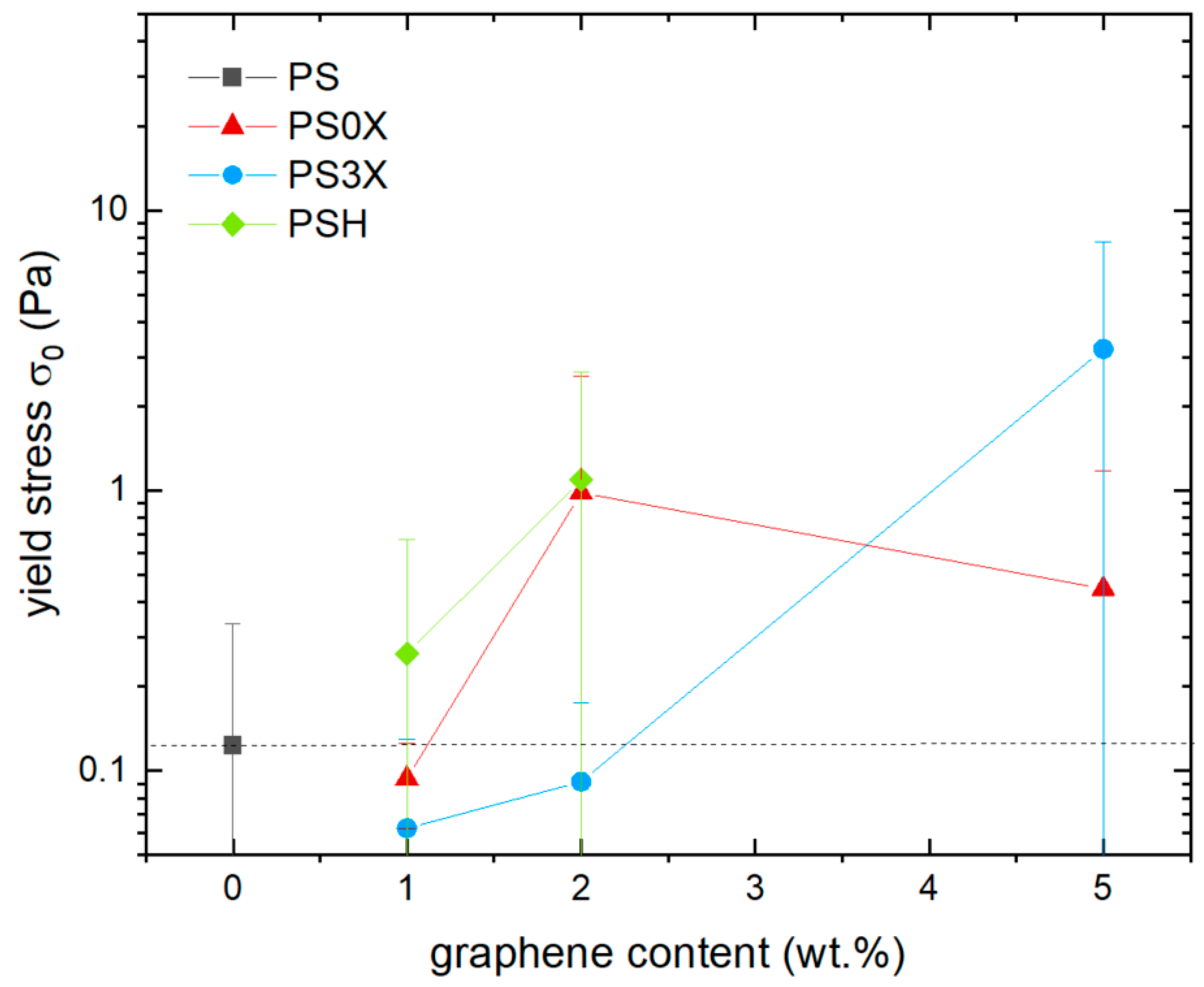
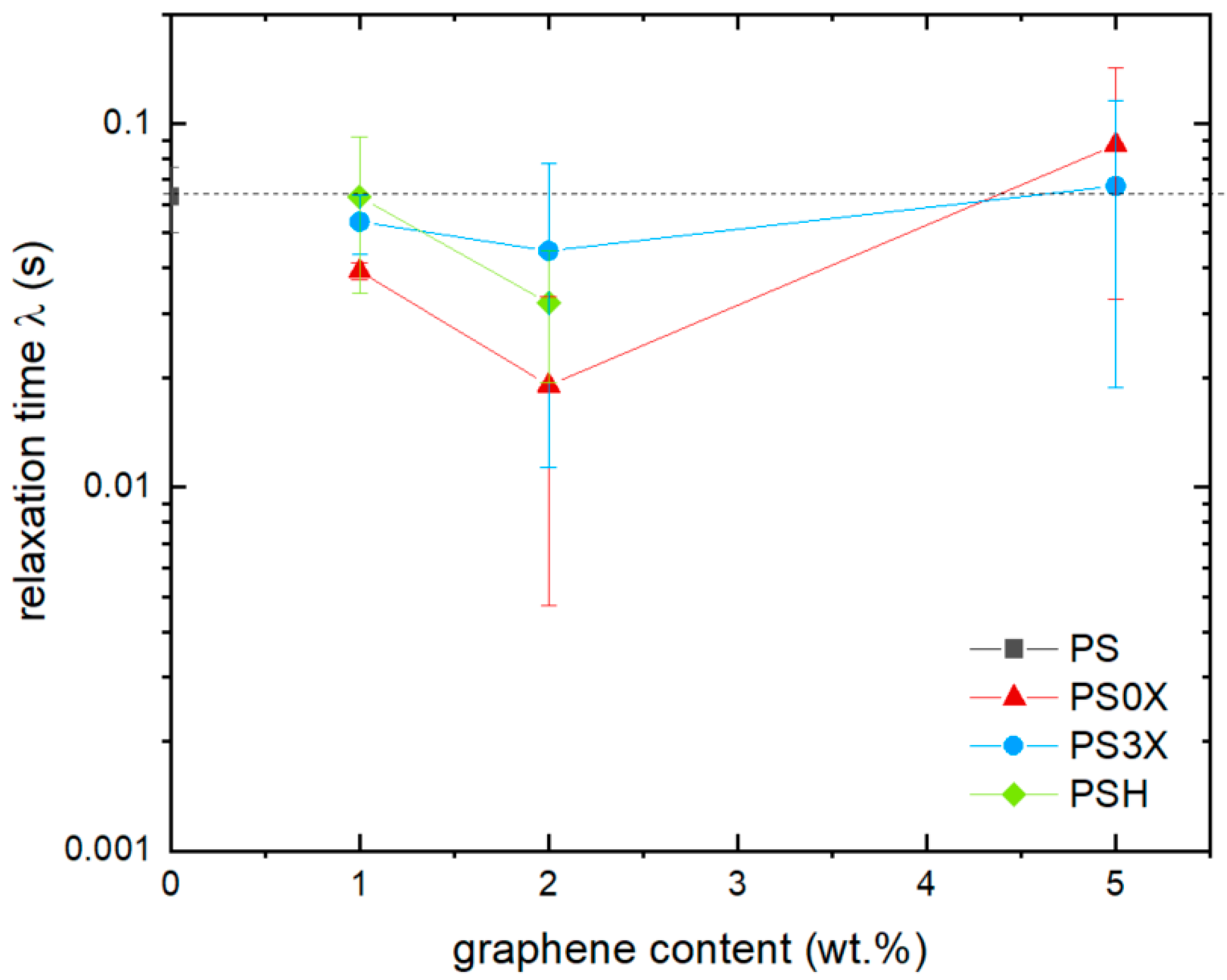
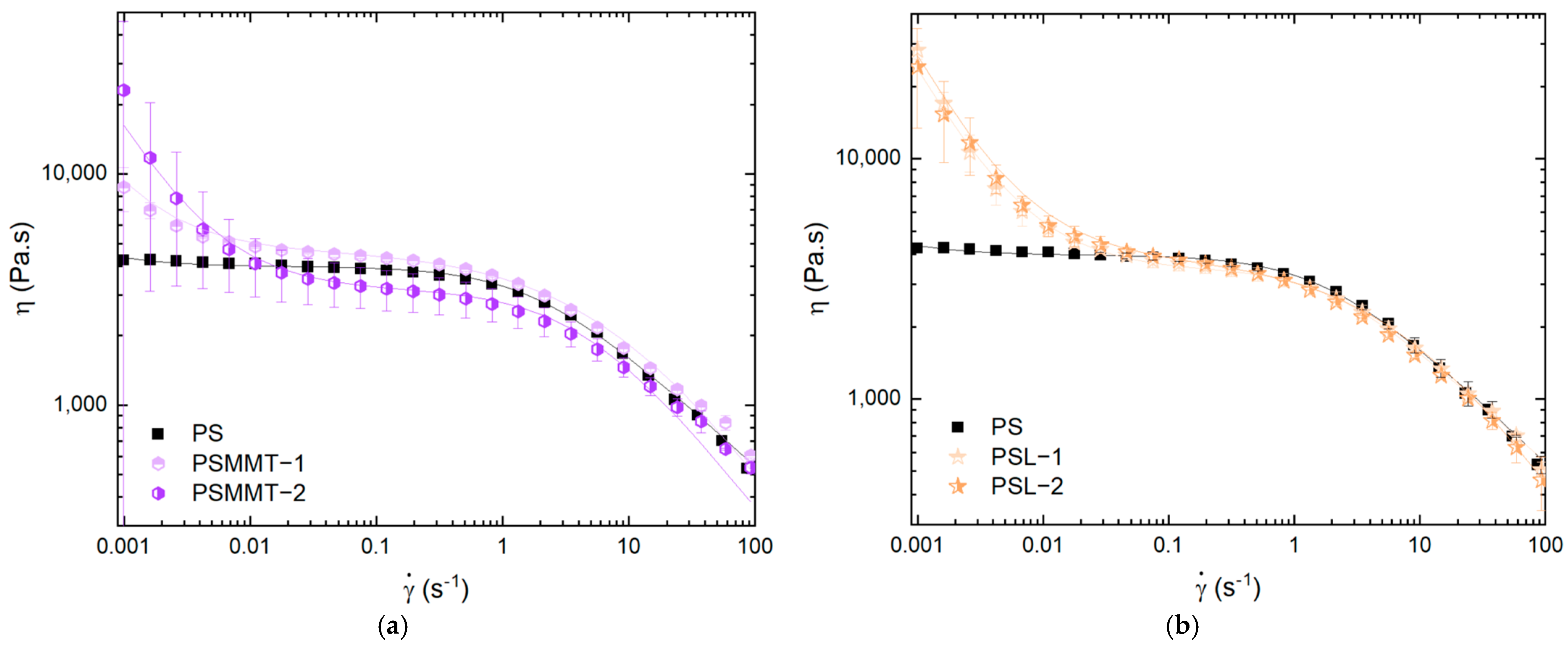
3.2. Effect of Graphene on Shear Viscosity
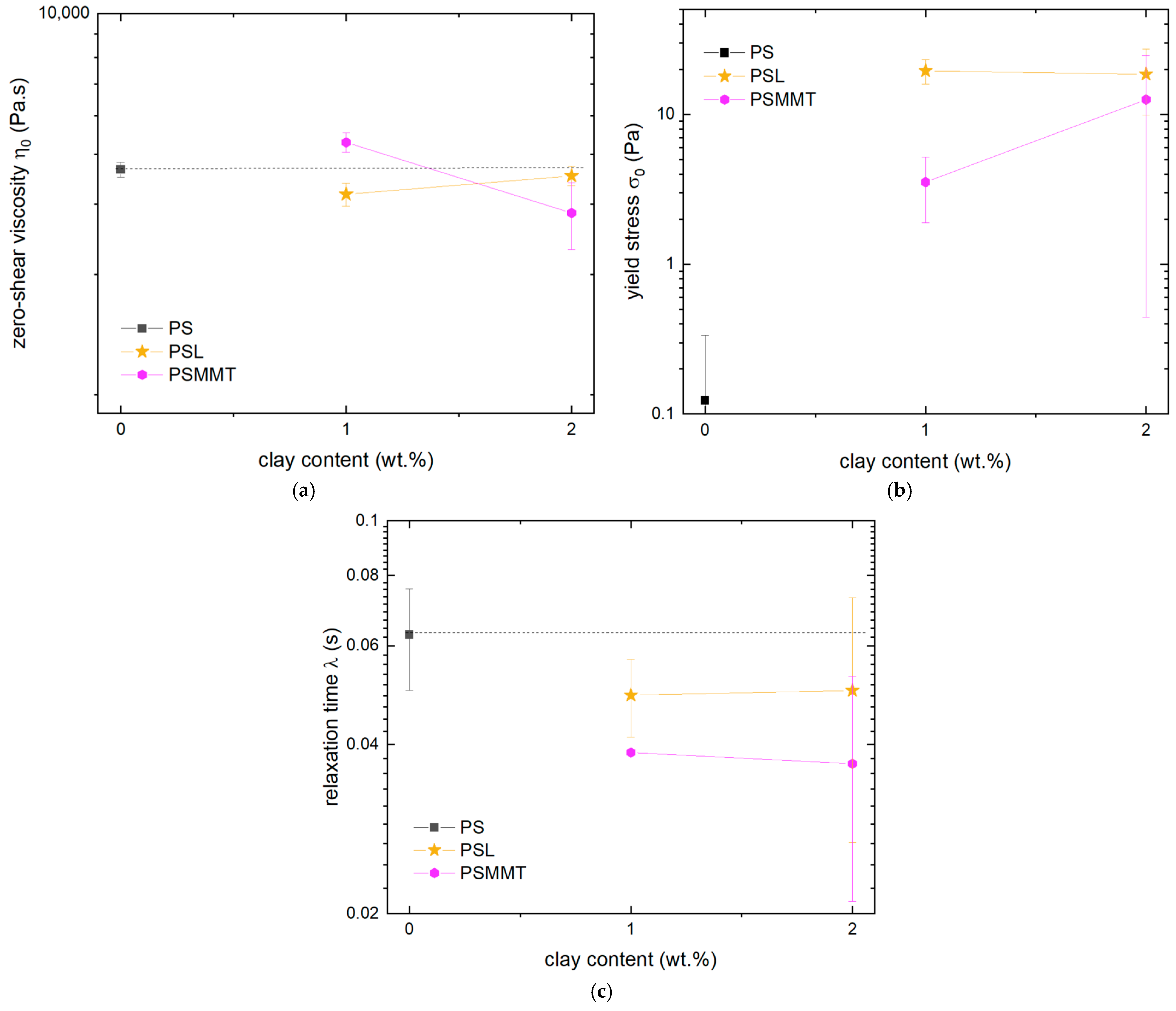
3.3. Effect of Smectic Clays on Shear Viscosity
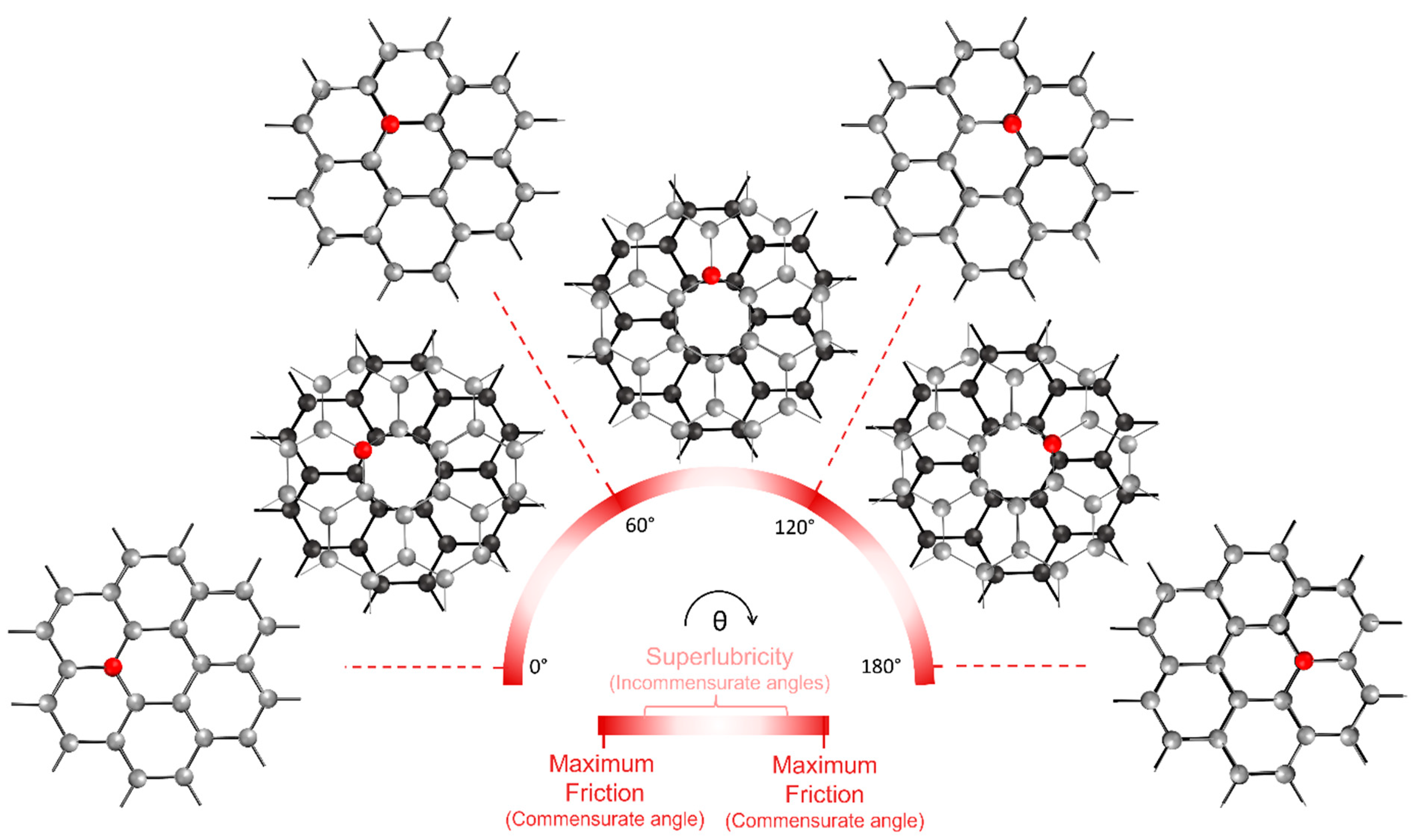
3.4. Comparison of Graphene and Clays
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Achilleos, E.C.; Georgiou, G.; Hatzikiriakos, S.G. Role of processing aids in the extrusion of molten polymers. J. Vinyl Addit. Technol. 2002, 8, 7–24. [Google Scholar] [CrossRef]
- Kazatchkov, I.B.; Yip, F.; Hatzikiriakos, S.G. The effect of boron nitride on the rheology and processing of polyolefins. Rheol. Acta 2000, 39, 583–594. [Google Scholar] [CrossRef]
- Yip, F.; Diraddo, R.; Hatzikiriakos, S.G. Effect of combining boron nitride with fluoroelastomer on the melt fracture of HDPE in extrusion blow molding. J. Vinyl Addit. Technol. 2000, 6, 196–204. [Google Scholar] [CrossRef]
- Adesina, A.A.; Nasser, M.S.; Hussein, I.A. Comparative Analysis of the Effect of Organoclay, Boron Nitride, and Fluoropolymer on the Rheology and Instabilities in the Extrusion of High Density Polyethylene. Int. J. Polym. Sci. 2015, 2015, 190537. [Google Scholar] [CrossRef]
- Gul, S.; Arican, S.; Cansever, M.; Beylergil, B.; Yildiz, M.; Okan, B.S. Design of Highly Thermally Conductive Hexagonal Boron Nitride- Reinforced PEEK Composites with Tailored Heat Conduction Through-Plane and Rheological Behaviors by a Scalable Extrusion. Appl. Polym. Mater. 2023, 5, 329–341. [Google Scholar] [CrossRef]
- Emre Bozkurt, Y.; Yıldız, A.; Turkarslan, O.; Sasal, F.N.; Cebeci, H. Thermally conductive h-BN reinforced PEI composites: The role of processing conditions on dispersion states. Mater. Today Commun. 2021, 29, 102854. [Google Scholar] [CrossRef]
- Çelik, O.N.; Ay, N.; Göncü, Y. Effect of nano hexagonal boron nitride lubricant additives on the friction and wear properties of AISI 4140 steel. Part. Sci. Technol. 2013, 31, 501–506. [Google Scholar] [CrossRef]
- Sagbas, B. Tribological performance of peek with green lubricant enhanced by nano hexagonal boron nitride powder. Ind. Lubr. Tribol. 2020, 72, 203–210. [Google Scholar] [CrossRef]
- Bragg, W. An Introduction to Crystal Analysis. Nature 1928, 122, 915–916. [Google Scholar]
- Liu, L.; Zhou, M.; Jin, L.; Li, L.; Mo, Y.; Su, G.; Tian, Y. Recent advances in friction and lubrication of graphene and other 2D materials: Mechanisms and applications. Friction 2019, 7, 199–216. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, S.M.; Yang, J.R.; YangLiu, J.Z.; Yang, Y.L.; Zheng, Q.S. Interlayer shear strength of single crystalline graphite. Acta Mech. Sin. 2012, 28, 978–982. [Google Scholar] [CrossRef]
- Dienwiebel, M.; Pradeep, N.; Verhoeven, G.S.; Zandbergen, H.W.; Frenken, J.W.M. Model experiments of superlubricity of graphite. Surf. Sci. 2005, 576, 197–211. [Google Scholar] [CrossRef]
- Dienwiebel, M.; Verhoeven, G.S.; Pradeep, N.; Frenken, J.W.M. Superlubricity of Graphite. Phys. Rev. Lett. 2004, 92, 126101. [Google Scholar] [CrossRef]
- Feng, X.; Kwon, S.; Park, J.Y.; Salmeron, M. Superlubric Sliding of Graphene Nano flakes on Graphene. ACS Nano 2013, 7, 1718–1724. [Google Scholar] [CrossRef]
- Karatas, E.; Gul, O.; Karsli, N.G.; Yilmaz, T. Synergetic effect of graphene nanoplatelet, carbon fiber and coupling agent addition on the tribological, mechanical and thermal properties of polyamide 6,6 composites. Compos. Part B Eng. 2019, 163, 730–739. [Google Scholar] [CrossRef]
- Kurusu, R.S.; Helal, E.; Moghimian, N.; David, E.; Demarquette, N. The Role of Selectively Located Commercial Graphene Nanoplatelets in the Electrical Properties, Morphology, and Stability of EVA/LLDPE Blends. Macromol. Mater. Eng. 2018, 303, 1–9. [Google Scholar] [CrossRef]
- Helal, E.; Kurusu, R.S.; Moghimian, N.; Gutierrez, G.; David, E.; Demarquette, N.R. Correlation between morphology, rheological behavior, and electrical behavior of conductive cocontinuous LLDPE/EVA blends containing commercial graphene nanoplatelets. J. Rheol. 2019, 63, 961–976. [Google Scholar] [CrossRef]
- Salari, M.; Sansone, N.D.; Razzaz, Z.; Taromsari, S.M.; Leroux, M.; Park, C.B.; Lee, P.C. Insights into synergy-induced multifunctional property enhancement mechanisms in hybrid graphene nanoplatelet reinforced polymer composites. Chem. Eng. J. 2023, 463, 142406. [Google Scholar] [CrossRef]
- Karimi, S.; Helal, E.; Gutierrez, G.; Moghimian, N.; Madinehei, M.; David, E.; Samara, M.; Demarquette, N.R. A review on graphene’s light stabilizing effects for reduced photodegradation of polymers. Crystals 2021, 11, 3. [Google Scholar] [CrossRef]
- Silibin, M.; Karpinsky, D.; Bystrov, V.; Zhaludkevich, D.; Bazarova, M.; Mirzadeh Vaghefi, P.; Marques, P.A.A.P.; Singh, B.; Bdikin, I. Preparation, Stability and Local Piezoelectrical Properties of P(VDF-TrFE)/Graphene Oxide Composite Fibers. C 2019, 5, 48. [Google Scholar] [CrossRef]
- Diallo, A.K.; Helal, E.; Gutierrez, G.; Madinehei, M.; David, E.; Demarquette, N.; Moghimian, N. Graphene: A multifunctional additive for sustainability. Sustain. Mater. Technol. 2022, 33, e00487. [Google Scholar] [CrossRef]
- Sultana, S.M.N.; Helal, E.; Gutiérrez, G.; David, E.; Moghimian, N.; Demarquette, N.R. Effect of Few-Layer Graphene on the Properties of Mixed Polyolefin Waste Stream. Crystals 2023, 13, 358. [Google Scholar] [CrossRef]
- Moghimian, N.; Nazarpour, S. The future of carbon: An update on graphene’s dermal, inhalation, and gene toxicity. Crystals 2020, 10, 718. [Google Scholar] [CrossRef]
- Bai, Y.; Zhou, S.; Lei, X.; Zou, H.; Liang, M. Enhanced thermal conductivity of polycarbonate-based composites by constructing a dense filler packing structure consisting of hybrid boron nitride and flake graphite. J. Appl. Polym. Sci. 2022, 139, e52895. [Google Scholar] [CrossRef]
- Ferreira, E.H.C.; Andrade, R.J.E.; Fechine, G.J.M. The ‘Superlubricity State’ of Carbonaceous Fillers on Polyethylene-Based Composites in a Molten State. Macromolecules 2019, 52, 9620–9631. [Google Scholar] [CrossRef]
- Muñoz, P.A.R.; de Oliveira, C.F.P.; Amurin, L.G.; Rodriguez, C.L.C.; Nagaoka, D.A.; Tavares, M.I.B.; Domingues, S.H.; Andrade, R.J.E.; Fechine, G.J.M. Novel improvement in processing of polymer nanocomposite based on 2D materials as fillers. Express Polym. Lett. 2018, 12, 930–945. [Google Scholar] [CrossRef]
- Vega, J.F.; Martinez-Salazar, J.; Trujillo, M.; Arnal, M.L.; Muller, A.J.; Bredeau, S.; Dubois, P. Rheology, processing, tensile properties, and crystallization of polyethylene/carbon nanotube nanocomposites. Macromolecules 2009, 42, 4719–4727. [Google Scholar] [CrossRef]
- Hirano, M.; Shinjo, K. Superlubricity and frictional anisotropy. Wear 1993, 168, 121–125. [Google Scholar] [CrossRef]
- Claerbout, V.E.P.; Polcar, T.; Nicolini, P. Superlubricity achieved for commensurate sliding: MoS 2 frictional anisotropy in silico. Comput. Mater. Sci. 2019, 163, 17–23. [Google Scholar] [CrossRef]
- Genoyer, J.; Demarquette, N.R.; Soulestin, J. Effect of clay particles size and location on coalescence in PMMA/PS blends. J. Rheol. 2019, 63, 883–893. [Google Scholar] [CrossRef]
- Seehra, M.S.; Geddam, U.K.; Schwegler-Berry, D.; Stefaniak, A.B. Detection and quantification of 2H and 3R phases in commercial graphene-based materials. Carbon 2015, 95, 818–823. [Google Scholar] [CrossRef]
- Kim, T.H.; Jeon, E.K.; Ko, Y.; Jang, B.Y.; Kim, B.S.; Song, H.K. Enlarging the d-spacing of graphite and polarizing its surface charge for driving lithium ions fast. J. Mater. Chem. A 2014, 2, 7600–7605. [Google Scholar] [CrossRef]
- Low, I.; Albetran, H.M.; Degiorgio, M. Structural Characterization of Commercial Graphite and Graphene Materials. J. Nanotechnol. Nanomater. 2020, 1, 23–30. [Google Scholar]
- Jian, M.Q.; Xie, H.H.; Xia, K.L.; Zhang, Y.Y. Challenge and Opportunities of Carbon Nanotubes. In Industrial Applications of Carbon Nanotubes; Peng, H., Li, Q., Chen, T., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2017; pp. 433–476. [Google Scholar]
- Pérez, E.M.; Martín, N. π-π Interactions in carbon nanostructures. Chem. Soc. Rev. 2015, 44, 6425–6433. [Google Scholar] [CrossRef] [PubMed]
- Georgakilas, V.; Tiwari, K.; Kemp, K.C.; Perman, J.A.; Bourlinos, A.B.; Kim, K.S.; Zboril, R. Noncovalent Functionalization of Graphene and Graphene Oxide for Energy Materials, Biosensing, Catalytic, and Biomedical Applications. Chem. Rev. 2016, 116, 5464–5519. [Google Scholar] [CrossRef] [PubMed]
- Apátiga, J.L.; Del Castillo, R.M.; Del Castillo, L.F.; Calles, A.G.; Espejel-Morales, R.; Favela, J.F.; Compan, V. Non-covalent interactions on polymer-graphene nanocomposites and their effects on the electrical conductivity. Polymers 2021, 13, 1714. [Google Scholar] [CrossRef]
- Macosko, C.W. Rheology: Principles, Measurements, and Applications; Wiley-VCH: New York, NY, USA, 1994. [Google Scholar]
- Vergnes, B. The use of apparent yield stress to characterize exfoliation in Polymer Nanocomposites. Int. Polym. Process. 2011, 26, 229–232. [Google Scholar] [CrossRef]
- Lertwimolnun, W.; Vergnes, B. Influence of compatibilizer and processing conditions on the dispersion of nanoclay in a polypropylene matrix. Polymer 2005, 46, 3462–3471. [Google Scholar] [CrossRef]
- Genoyer, J.; Lentzakis, H.; Demarquette, N.R. Effect of the addition of cellulose filaments on the relaxation behavior of thermoplastics. J. Rheol. 2021, 65, 779–789. [Google Scholar] [CrossRef]
- Mackay, M.E.; Dao, T.T.; Tuteja, A.; Ho, D.L.; Van Horn, B.; Kim, H.; Hawker, C.J. Nanoscale effects leading to non-einstein-like decrease in viscosity. Nat. Mater. 2003, 2, 762–766. [Google Scholar] [CrossRef]
- Ferreira, E.H.C.; de Lima, L.P.; Fechine, G.J.M. The ‘Superlubricity State’ of Carbonaceous Fillers on Polymer Composites. Macromol. Chem. Phys. 2020, 52, 9620–9631. [Google Scholar]
- Dealy, J.M.; Wang, J. Melt Rheology, and Its Applications in the Plastics Industry; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Tuteja, A.; Mackay, M.E.; Hawker, C.J.; Van Horn, B. Effect of ideal, organic nanoparticles on the flow properties of linear polymers: Non-einstein-like behavior. Macromolecules 2005, 38, 8000–8011. [Google Scholar] [CrossRef]
- Brigatti, M.F.; Galán, E.; Theng, B.K.G. Structure and Mineralogy of Clay Minerals. In Developments in Clay Science; Bergaya, F., Lagaly, G., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2013; Volume 5, pp. 21–81. [Google Scholar]



| Type of Particle | Supplier | Grade | Abbreviation | Primary Particle Lateral Size (µm) * |
|---|---|---|---|---|
| Graphene | NanoXplore Inc. | GrapheneBlackTM 3X | 3X | 1–2 |
| GrapheneBlackTM 0X | 0X | 0.5–1 | ||
| XG Sciences Inc. | xGnP H-25 | H | 25 | |
| Montmorillonite | BYK | Cloisite Na+ | MMT | <25 |
| Laponite | Laponite RD | L | 0.030 |
| 2θ (°C) | Interlayer Spacing (nm) | |
|---|---|---|
| PS0X−2 | 30.99 | 0.335 |
| PS3X−2 | 30.99 | 0.335 |
| PSH−2 | 30.94 | 0.335 |
| Sample | D50 (µm) | D90 (µm) |
|---|---|---|
| PS0X-2 | 8.3 * | 15.6 * |
| >22 ** | >55 ** | |
| PS3X-2 | 12.6 | 40.1 |
| PSH-2 | 9.6 | 48.8 |
| Sample | D50 (µm) | D90 (µm) |
|---|---|---|
| PSMMT−2 | 11.8 | 35.2 |
| PSL−2 | 4.0 | 37.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Genoyer, J.; Helal, E.; Gutierrez, G.; Moghimian, N.; David, E.; Demarquette, N.R. Graphene and Nanoclay as Processing Aid Agents: A Study on Rheological Behavior in Polystyrene. C 2023, 9, 96. https://doi.org/10.3390/c9040096
Genoyer J, Helal E, Gutierrez G, Moghimian N, David E, Demarquette NR. Graphene and Nanoclay as Processing Aid Agents: A Study on Rheological Behavior in Polystyrene. C. 2023; 9(4):96. https://doi.org/10.3390/c9040096
Chicago/Turabian StyleGenoyer, Julie, Emna Helal, Giovanna Gutierrez, Nima Moghimian, Eric David, and Nicole R. Demarquette. 2023. "Graphene and Nanoclay as Processing Aid Agents: A Study on Rheological Behavior in Polystyrene" C 9, no. 4: 96. https://doi.org/10.3390/c9040096
APA StyleGenoyer, J., Helal, E., Gutierrez, G., Moghimian, N., David, E., & Demarquette, N. R. (2023). Graphene and Nanoclay as Processing Aid Agents: A Study on Rheological Behavior in Polystyrene. C, 9(4), 96. https://doi.org/10.3390/c9040096








