On the Problem of “Super” Storage of Hydrogen in Graphite Nanofibers
Abstract
1. Introduction
2. Methods
3. Results of the Study of a Number of Experimental Data
3.1. Analysis and Interpretation of TDS and TG Spectra of the Rodriguez and Becker Group for “Irreversible” Hydrogen in GNF
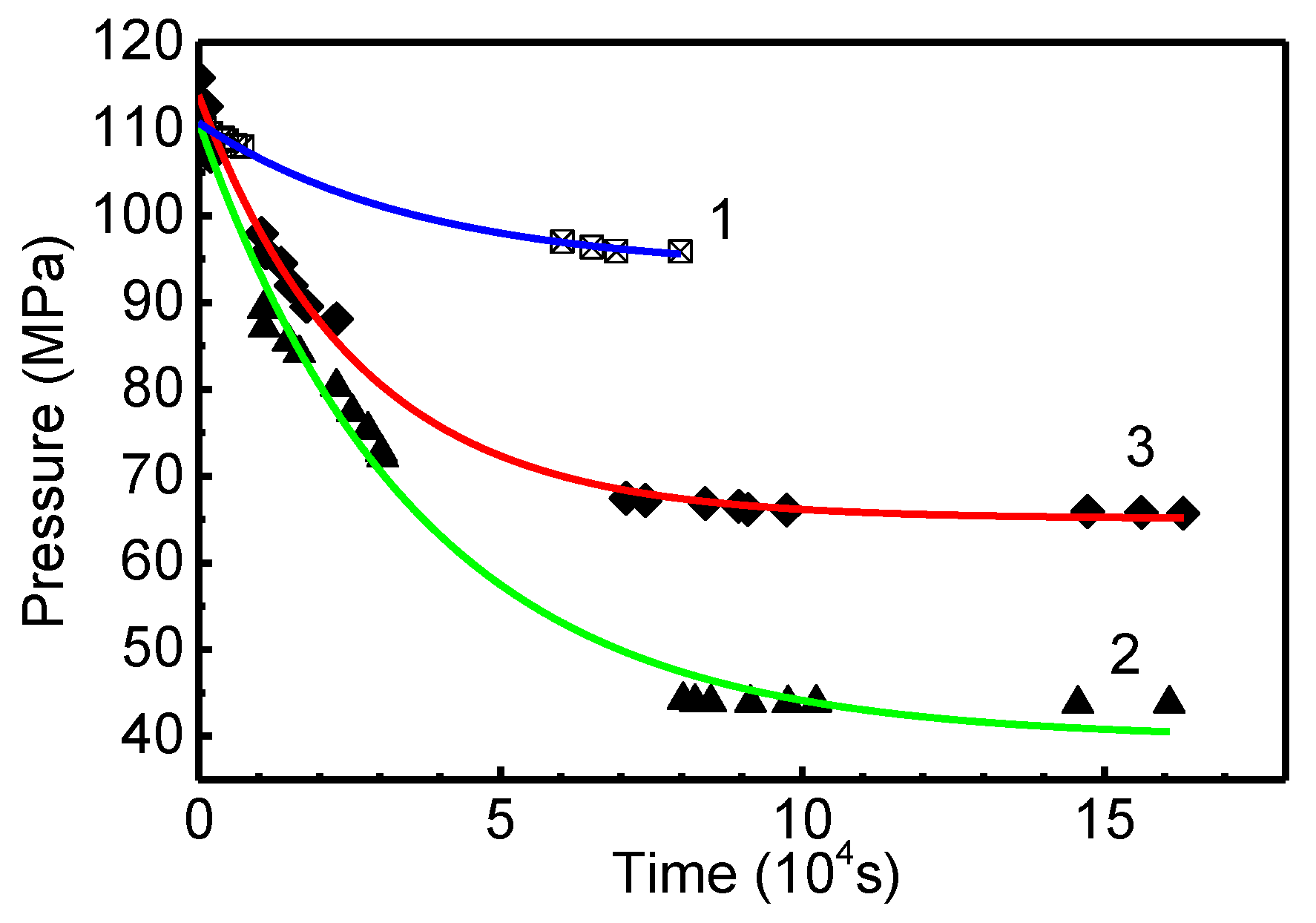
3.2. Analysis and Interpretation of the Kinetic Data of the Rodriguez and Becker Group on the “Super” Sorption of “Reversible” Hydrogen (~30 wt.%) in GNF
3.3. Consideration of the Kinetic Data of the Rodriguez and Becker Group on X-ray Diffraction
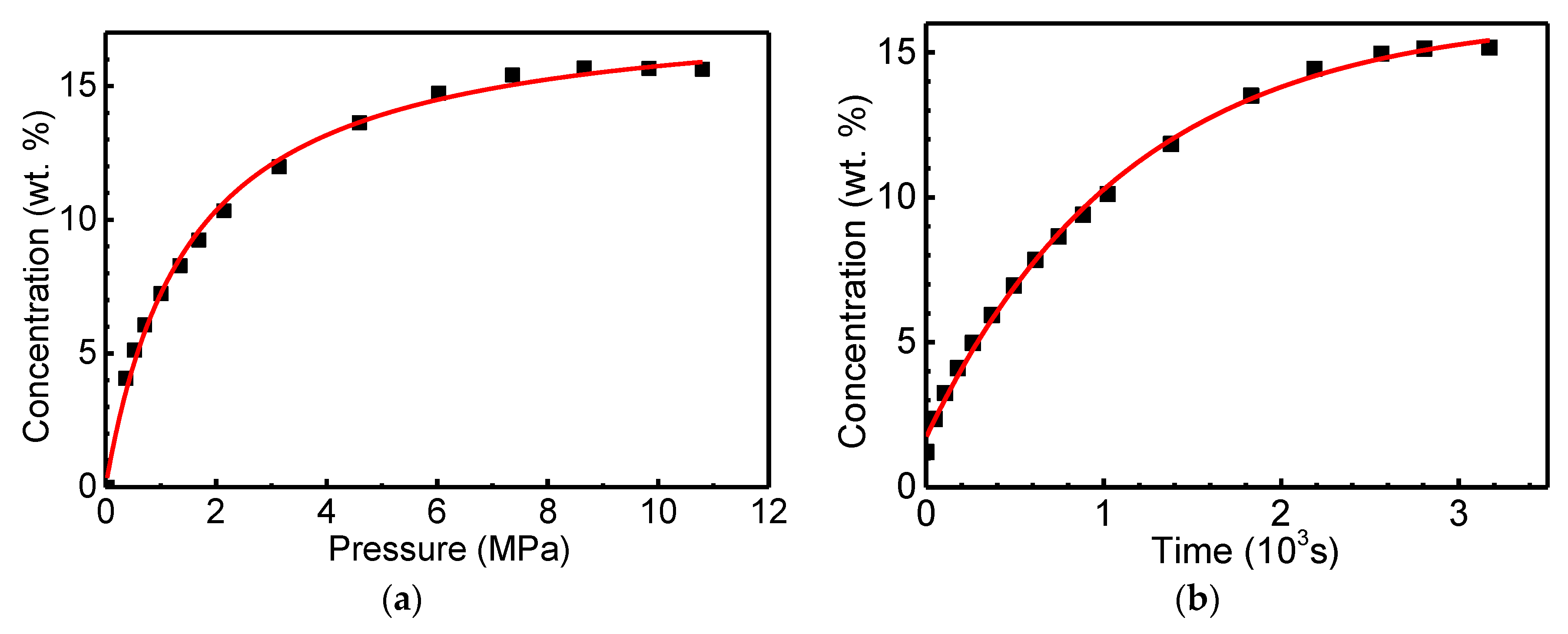
3.4. Consideration of the Results of the Gupta’s Group on the “Super” Sorption of “Reversible” Hydrogen (~17 wt.%) in GNF
3.5. Physics of “Super” Storage of “Reversible” Hydrogen in GNF
4. Analysis of TDS Data for “Irreversible” Hydrogen in GNF
5. Conclusions
- The study carried out in this work (using the methodology and results of [17,18,19,20,21,22,23,24,25]) of a number of kinetic and thermodynamic aspects (fundamentals) related to solving the problem of “super” storage of hydrogen in graphite nanofibers (GNF) [1,2,3] shows that the results obtained in works [5,6,7,8,9,10,11,12], i.e., the extraordinary experimental results (accumulation of about 20–30 wt.% of “reversible” hydrogen and about 7–10 wt.% of “irreversible” hydrogen), are neither a mistake nor a mystification.
- It is shown that the physics of accumulation of ~20–30 wt.% of “reversible” high-density hydrogen intercalated in nanocavities between the base carbon layers in GNF is connected with the Kurdjumov phenomenon and the spillover effect in terms of thermoelastic phase equilibrium.
- The conducted study shows that there is a real possibility of reproducing the earlier extraordinary experimental results [5,6,7,8,9,10,11,12], but only if the details of the technologies used in these works for activating GNF are revealed, which led to the appearance of a type #1 thermal desorption peak in the material (Figure 1a) corresponding to “irreversible” chemisorbed hydrogen (in an amount of ~8 wt.%) with certain kinetic and thermodynamic characteristics.
- In this regard, further experimental and theoretical studies are needed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Cavity Model
References
- Maeland, A.J. The storage of hydrogen for vehicular use—A review and reality check. Int. Sc. J. Altern. Energy Ecol. 2002, 1, 19–29. [Google Scholar]
- Nechaev, Y.S.; Yurum, A.; Tekin, A.; Yavuz, N.K.; Yürüm, Y.; Veziroglu, T.N. Fundamental Open Questions on Engineering of “Super” Hydrogen Sorption in Graphite Nanofibers: Relevance for Clean Energy Applications. Am. J. Anal. Chem. 2014, 5, 1151–1165. [Google Scholar] [CrossRef]
- Nechaev, Y.S.; Makotchenko, V.G.; Shavelkina, M.B.; Nechaev, M.Y.; Veziroglu, A.; Veziroglu, T.N. Comparing of Hydrogen On-Board Storage by the Largest Car Companies, Relevance to Prospects for More Efficient Technologies. Open J. Energy Effic. 2017, 6, 73–79. [Google Scholar] [CrossRef][Green Version]
- Chambers, A.; Park, C.; Baker, R.T.K.; Rodriguez, N.M. Hydrogen Storage in Graphite Nanofibers. J. Phys. Chem. B 1998, 102, 4253–4256. [Google Scholar] [CrossRef]
- Park, C.; Anderson, P.E.; Chambers, A.; Tan, C.D.; Hidalgo, R.; Rodriguez, N.M. Further Studies of the Interaction of Hydrogen with Graphite Nanofibers. J. Phys. Chem. 1999, 103, 10572–10581. [Google Scholar] [CrossRef]
- Rodriguez, N.M.; Baker, R.T.K. Storage of Hydrogen in Layered Nanostructures. U.S. Patent 5653951, 5 August 1997. [Google Scholar]
- Rodriguez, N.M.; Baker, R.T.K. Method for Introducing Hydrogen into Layered Nanostructures. U.S. Patent 6159538, 12 December 2000. [Google Scholar]
- Baker, R.T.K. Encyclopedia of Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2005; 932p. [Google Scholar]
- Gupta, B.K.; Srivastava, O.N. Synthesis and hydrogenation behavior of graphitic nanofibers. Int. J. Hydrogen Energy 2000, 25, 825–830. [Google Scholar] [CrossRef]
- Gupta, B.K.; Srivastava, O.N. Further Studies on Microstructural Characterization and Hydrogenation Behavior of Graphitic Nanofibers. Int. J. Hydrogen Energy 2001, 26, 857–862. [Google Scholar] [CrossRef]
- Gupta, B.K.; Tiwari, R.S.; Srivastava, O.N. Studies on Synthesis and Hydrogenation Behavior of Graphitic Nanofibers Prepared through Palladium Catalyst Assisted Thermal Cracking of Acetylene. J. Alloys Comp. 2004, 381, 301–308. [Google Scholar] [CrossRef]
- Gupta, B.K.; Srivastava, O.N. New carbon variants: Graphitic nanofibers (nano-springs, nano-shoeckers) as hydrogen storage materials. Int. Sci. J. Altern. Energy Ecol. 2006, 5, 63. [Google Scholar]
- Rzepka, M.; Bauer, E.; Reichenauer, G.; Schliermann, T.; Bernhardt, B.; Bohmhammel, K.; Braue, W. Hydrogen Storage Capacity of Catalytically Grown Carbon Nanofibers. J. Phys. Chem. B 2005, 109, 14979–14989. [Google Scholar] [CrossRef]
- Reichenauer, G.; Rzepka, M.; Bauer, E.; Schliermann, T.; Bernhardt, B.; Bohmhammel, K.; Braue, W. Hydrogen storage capacity of catalytically grown carbon nanofibers. In Proceedings of the International Conference on Carbon, Aberdeen, UK, 6–21 July 2006. [Google Scholar]
- Hirscher, M.; Becher, M.; Haluska, M.; Quintel, A.; Skakalova, V.; Choi, Y.-M.; Fink, J. Hydrogen Storage in Carbon Nanostructures. J. Alloys Comp. 2002, 330, 654–658. [Google Scholar] [CrossRef]
- Tibbetts, G.G.; Meisner, G.P.; Olk, C.H. Hydrogen storage capacity of carbon nanotubes, filaments, and vapor-grown fibers. Carbon 2001, 39, 2291–2301. [Google Scholar] [CrossRef]
- Nechaev, Y.S. The nature, kinetics, and ultimate storage capacity of hydrogen sorption by carbon nanostructures. Phys. Usp. 2006, 49, 563–591. [Google Scholar] [CrossRef]
- Nechaev, Y.S.; Veziroglu, T.N. On the hydrogenation-dehydrogenation of graphene-layer-nanostructures: Relevance to the hydrogen on-board storage problem. Int. J. Phys. Sci. 2015, 10, 54–89. [Google Scholar] [CrossRef]
- Nechaev, Y.S.; Alexandrova, N.M.; Shurygina, N.A.; Cheretaeva, A.O.; Kostikova, E.K.; Öchsner, A. On characteristics and physics of processes of thermal desorption of deuterium from isotropic graphite at 700–1700 K. J. Nucl. Mater. 2020, 535, 152162. [Google Scholar] [CrossRef]
- Nechaev, Y.S.; Alexandrova, N.M.; Cheretaeva, A.O.; Kuznetsov, V.L.; Öchsner, A.; Kostikova, E.K.; Zaika, Y.V. Studying the thermal desorption of hydrogen in some carbon nanostructures and graphite. Int. J. Hydrogen Energy 2020, 45, 25030–25042. [Google Scholar] [CrossRef]
- Nechaev, Y.S.; Alexandrova, N.M.; Shurygina, N.A.; Cheretaeva, A.O.; Denisov, E.A.; Kostikova, E.K. Studying the States of Hydrogen in Graphene, Graphite, and Steels. Bull. Russ. Acad. Sci. Phys. 2021, 85, 771–775. [Google Scholar] [CrossRef]
- Nechaev, Y.S.; Denisov, E.A.; Shurygina, N.A.; Cheretaeva, A.O.; Kostikova, E.K.; Davydov, S.Y.; Öchsner, A. Revealing Hydrogen States in Carbon Structures by Analyzing the Thermal Desorption Spectra. C 2022, 8, 6. [Google Scholar] [CrossRef]
- Zaika, Y.V.; Kostikova, E.K.; Nechaev, Y.S. Hydrogen thermal desorption peaks: Modeling and interpretation. Tech. Phys. 2021, 66, 210–220. [Google Scholar] [CrossRef]
- Nechaev, Y.S.; Alexandrova, N.M.; Shurygina, N.A.; Cheretaeva, A.O. On manifestation & physics of the Kurdjumov and spillover effects in carbon nanostructures, under intercalation of high density hydrogen. Fuller. Nanotub. Carbon Nanostruct. 2020, 28, 233–237. [Google Scholar] [CrossRef]
- Nechaev, Y.S.; Denisov, E.A.; Shurygina, N.A.; Cheretaeva, A.O.; Kostikova, E.K.; Davydov, S.Y. On the Physics and Atomic Mechanisms of Molecular Hydrogen Intercalation into Graphite Nanofibers. JETP Lett. 2021, 114, 337–340. [Google Scholar] [CrossRef]
- Yang, R.T.; Wang, Y. Catalyzed Hydrogen Spillover for Hydrogen Storage. J. Am. Chem. Soc. 2009, 131, 4224–4226. [Google Scholar] [CrossRef] [PubMed]
- Zacharia, R.; Rather, S.; Hwang, S.W.; Nahm, K.S. Spillover of physisorbed hydrogen from sputter-deposited arrays of platinum nanoparticles to multi-walled carbon nanotubes. Chem. Phys. Lett. 2007, 434, 286–291. [Google Scholar] [CrossRef]
- Zhou, C.; Wu, J.; Nie, A.; Forrey, R.C.; Tachibana, A.; Cheng, H. On the Sequential Hydrogen Dissociative Chemisorption on Small Platinum Clusters: A Density Functional Theory Study. J. Phys. Chem. C 2007, 111, 12773–12778. [Google Scholar] [CrossRef]
- Zielinski, M.; Wojcieszak, R.; Monteverdi, S.; Mercy, M.; Bettahar, M.M. Hydrogen storage in nickel catalysts supported onactivated carbon. Int. J. Hydrogen Energy 2007, 32, 1024–1032. [Google Scholar] [CrossRef]
- Karim, W.; Spreafico, C.; Kleibert, A.; Gobrecht, J.; VandeVondele, J.; Ekinci, Y.; van Bokhoven, J.A. Catalyst support effects on hydrogen spillover. Nature 2017, 541, 68–71. [Google Scholar] [CrossRef]
- Lobodyuk, V.A.; Estrin, E.I. Martensitic Transformations; Cambridge International Science Publishing: Cambridge, UK, 2014; 538p, ISBN 9781907343995. [Google Scholar]
- Koval’, Y.M. Features of Relaxation Processes During Martensitic Transformation. Usp. Fiz. Met. 2005, 6, 169–196. [Google Scholar] [CrossRef][Green Version]
- Lobo, R.F.M.; Santos, D.M.F.; Sequeira, C.A.C.; Ribeiro, J.H.F. Molecular Beam-Thermal Desorption Spectrometry (MB-TDS) Monitoring of Hydrogen Desorbed from Storage Fuel Cell Anodes. Materials 2012, 5, 248–257. [Google Scholar] [CrossRef]
- Lobo, R.F.M.; Berardo, F.M.V.; Ribeiro, J.H.F. Molecular beam-thermal hydrogen desorption from palladium. Rev. Sci. Instr. 2010, 81, 043103. [Google Scholar] [CrossRef]
- Habenschaden, E.; Küppers, J. Evaluation of flash desorption spectra. Surf. Sci. 1984, 138, L147–L150. [Google Scholar] [CrossRef]
- Wei, F.-G.; Enomoto, M.; Tsuzaki, K. Applicability of the Kissinger’s formula and comparison with the McNabb–Foster model in simulation of thermal desorption spectrum. Comput. Mater. Sci. 2012, 51, 322–330. [Google Scholar] [CrossRef]
- Legrand, E.; Oudriss, A.; Savall, C.; Bouhattate, J.; Feaugas, X. Towards a better understanding of hydrogen measurements obtained by thermal desorption spectroscopy using FEM modelling. Int. J. Hydrogen Energy 2015, 40, 2871–2881. [Google Scholar] [CrossRef]
- Ebihara, K.-I.; Kaburaki, H.; Suzudo, T.; Takai, K. A numerical study on the validity of the local equilibrium hypothesis in modelling hydrogen thermal desorption spectra. ISIJ Int. 2009, 49, 1907–1913. [Google Scholar] [CrossRef]
- Zhao, X.; Outlaw, R.A.; Wang, J.J.; Zhu, M.Y.; Smith, G.D.; Holloway, B.J. Thermal desorption of hydrogen from carbon nanosheets. J. Chem. Phys. 2006, 124, 194704. [Google Scholar] [CrossRef]
- Nayyar, I.; Ginovska, B.; Karkamkar, A.; Gennett, T.; Autrey, T. Physi-Sorption of H2 on Pure and Boron–Doped Graphene Monolayers: A Dispersion–Corrected DFT Study. C 2020, 6, 15. [Google Scholar] [CrossRef]
- Nechaev, Y.S. Characteristics of hydride-like segregates of hydrogen at dislocations in palladium. Phys. Uspekhi 2001, 44, 1189–1198. [Google Scholar] [CrossRef]
- Hu, S.; Lozada-Hidalgo, M.; Wang, F.C.; Mishchenko, A.; Schedin, F.; Nair, R.; Hill, W.; Boukhvalov, D.W.; Katsnelson, M.I.; Dryfe, R.A.W.; et al. Proton transport through one-atom-thick crystals. Nature 2014, 516, 227–230. [Google Scholar] [CrossRef]
- Lueking, A.D.; Yang, R.T.; Rodriguez, N.M.; Baker, R.T.K. Hydrogen Storage in Graphite Nanofibers: Effect of Synthesis Catalyst and Pretreatment Conditions. Langmuir 2004, 20, 714–721. [Google Scholar] [CrossRef]
- Davydov, S.Y.; Sabirova, G.I. Adsorption of hydrogen, alkali metal, and halogen atoms on graphene: Adatom charge calculation. Techn. Phys. Lett. 2011, 37, 515–518. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.Z.; Cheng, Y.; Li, Z.; Wang, L.; Zheng, Q. Interlayer binding energy of graphite: A mesoscopic determination from deformation. Phys. Rev. B 2012, 85, 205418. [Google Scholar] [CrossRef]
- Wang, W.; Dai, S.; Li, X.; Yang, J.; Srolovitz, D.J.; Zheng, Q. Measurement of the cleavage energy of graphite. Nat. Commun. 2015, 6, 7853. [Google Scholar] [CrossRef] [PubMed]
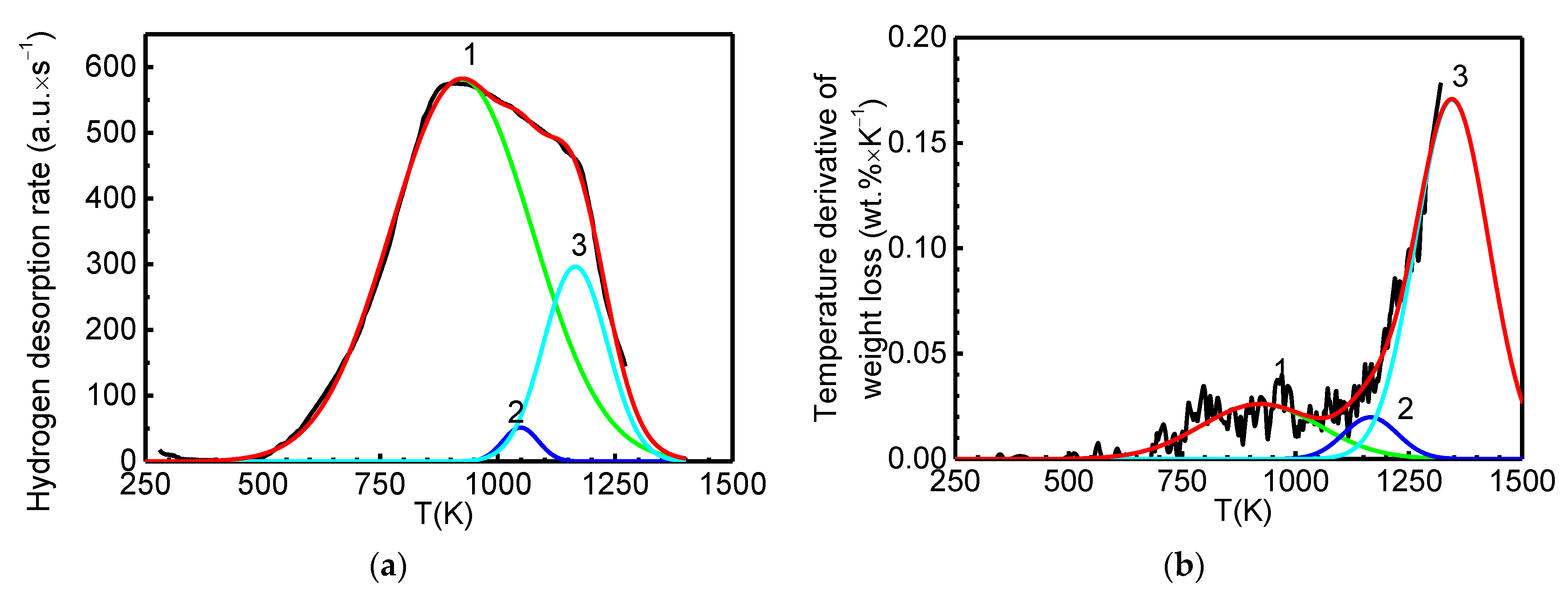


| Peak # | Tmax, K | Reaction Order | Q, kJ mol−1 | K0, s−1 | K(Tmax), s−1 | Q*, kJ mol−1 | γ | CH2, wt.% | (H/C) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 914 | 1 | 39.0 | 1.5 × 10−1 | 9 × 10−4 | 39 | 0.76 | 8.4 | 1.1 |
| 2 | 77.5 | 5.1 × 101 | 2 × 10−3 | 77.5 | |||||
| 2 | 1036 | 1 | 199 | 4.2 × 107 | 4 × 10−3 | 198 | 0.02 | 0.2 | 0.02 |
| 2 | 398 | 8.8 × 1017 | 7 × 10−3 | 396 | |||||
| 3 | 1161 | 1 | 126 | 8.5 × 102 | 2 × 10−3 | 125 | 0.22 | 2.4 | 0.30 |
| 2 | 250 | 7.0 × 108 | 4 × 10−3 | 250 |
| Peak # | Tmax, K | Reaction Order | Q, kJ mol−1 | K0, s−1 | K(Tmax), s−1 | Q*, kJ mol−1 | γ | wt. % | (H/C) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 923 | 1 | 43 | 2.9 × 10−1 | 1 × 10−3 | 43 | 0.23 | 8.5 | 1.1 |
| 2 | 87 | 1.7 × 102 | 2 × 10−3 | 87 | |||||
| 2 | 1165 | 1 | 152 | 1.5 × 104 | 2 × 10−3 | 152 | 0.08 | 2.9 | 0.4 |
| 2 | 304 | 2.0 × 1011 | 4 × 10−3 | 303 | |||||
| 3 | 1345 | 1 | 149 | 1.0 × 103 | 2 × 10−3 | 148 | 0.69 | 26 | |
| 2 | 298 | 1.2 × 109 | 1 × 10−3 | 297 |
| Peak # | Tmax, K | Reaction Order | Q, kJ mol−1 | K0, s−1 | K(Tmax), s−1 | Q*, kJ mol−1 | γ | wt. % | (H/C) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1203 | 1 | 163 | 1.6 × 104 | 1.3 × 10−3 | 162 | 0.96 | 0.08 | 0.010 |
| 2 | 325 | 3.6 × 1011 | 2.7 × 10−3 | 324 | |||||
| 2 | 397 | 1 | 68 | 4.5 × 106 | 5.1 × 10−3 | 67 | 0.04 | 0.02 | 0.002 |
| 2 | 133 | 4.1 × 1015 | 1.0 × 10−3 | 134 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nechaev, Y.S.; Denisov, E.A.; Cheretaeva, A.O.; Shurygina, N.A.; Kostikova, E.K.; Öchsner, A.; Davydov, S.Y. On the Problem of “Super” Storage of Hydrogen in Graphite Nanofibers. C 2022, 8, 23. https://doi.org/10.3390/c8020023
Nechaev YS, Denisov EA, Cheretaeva AO, Shurygina NA, Kostikova EK, Öchsner A, Davydov SY. On the Problem of “Super” Storage of Hydrogen in Graphite Nanofibers. C. 2022; 8(2):23. https://doi.org/10.3390/c8020023
Chicago/Turabian StyleNechaev, Yury S., Evgeny A. Denisov, Alisa O. Cheretaeva, Nadezhda A. Shurygina, Ekaterina K. Kostikova, Andreas Öchsner, and Sergei Yu. Davydov. 2022. "On the Problem of “Super” Storage of Hydrogen in Graphite Nanofibers" C 8, no. 2: 23. https://doi.org/10.3390/c8020023
APA StyleNechaev, Y. S., Denisov, E. A., Cheretaeva, A. O., Shurygina, N. A., Kostikova, E. K., Öchsner, A., & Davydov, S. Y. (2022). On the Problem of “Super” Storage of Hydrogen in Graphite Nanofibers. C, 8(2), 23. https://doi.org/10.3390/c8020023








