Structure and Properties of Chained Carbon: Recent Ab Initio Studies

Abstract

Carbon chains or carbyne-like structures represent the next generation of 1D materials whose properties can be tuned by the chain length, doping, and the type of termination. Currently inaccessible technology of the macroscopic carbyne synthesis and characterization makes theoretical work especially valuable. The state of the art methods being applied in the field are density functional theory and molecular dynamics. This paper provides a review of the current state of research on modeling linear carbon structures and related materials. We show that even though the “static” properties of carbon chains (mechanical strength, thermal conduction, band gaps, and phonon spectra) are extensively described, there are only a few simulations of the synthesis processes that constitute the next challenge in 1D research.

1. Introduction

Carbyne is a one-dimensional chain of carbon atoms containing sp¹-hybridized bonds, thus representing the tiniest nanorope or nanowire [1]. Carbyne-based materials are prospective for multiple applications including miniature electronic circuits, friction-resistant coatings, biocompatible layers or chemical absorbers, to name a few. The design of a functional chained structure requires a profound understanding of its atomic arrangement and its physical and chemical properties at different temperatures and operating environments.

A carbyne chain may exist as either α-phase (polyyne (–С≡С)_n), with alternate single and triple bonds, or β-phase (cumulene (=C=C)_n), with double bonds only. The atomic structure and mechanical characteristics of short carbon chains, up to 21 atoms, were studied numerically by ab initio techniques [2]. However, the precise synthesis conditions, phase-transition pathways, and defect formation remain mostly unexplored [3]. The disadvantage of carbyne is its instability in many environments, which prevents its large-scale synthesis and may negatively affect potential applications [4].

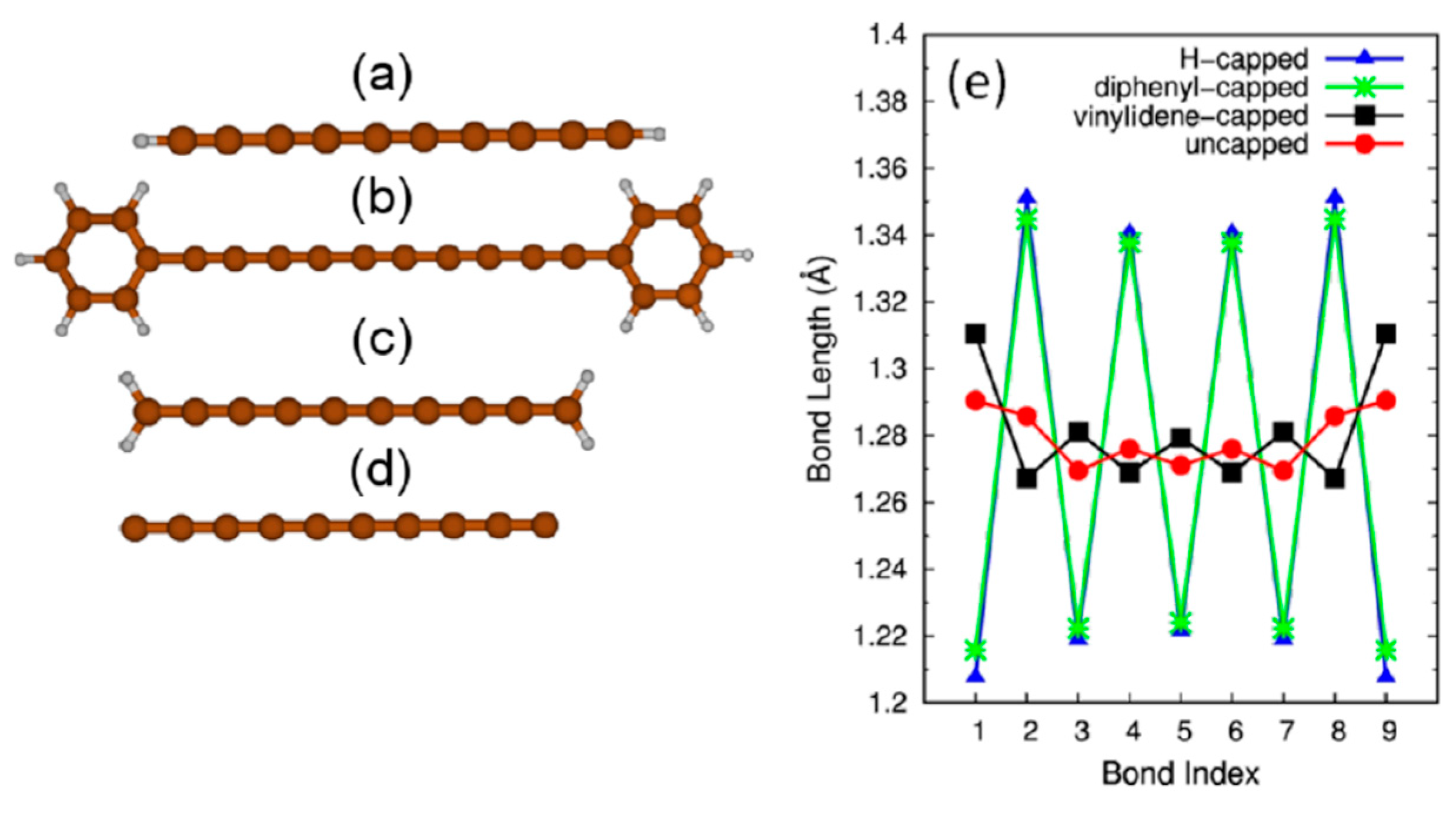
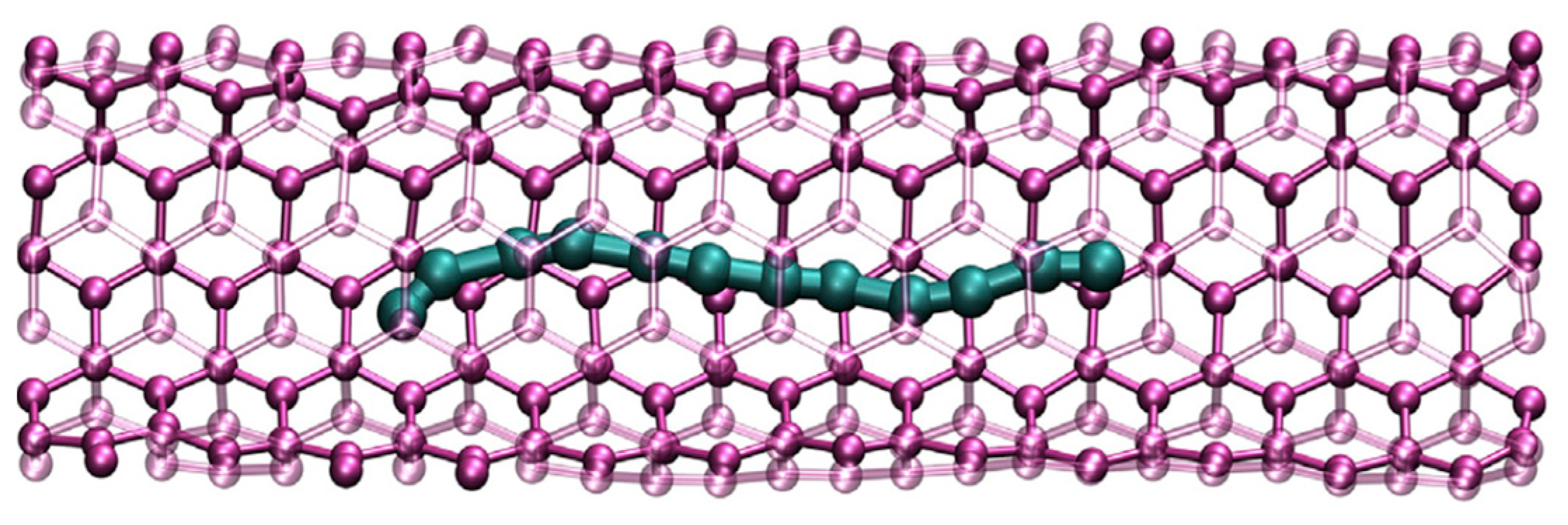
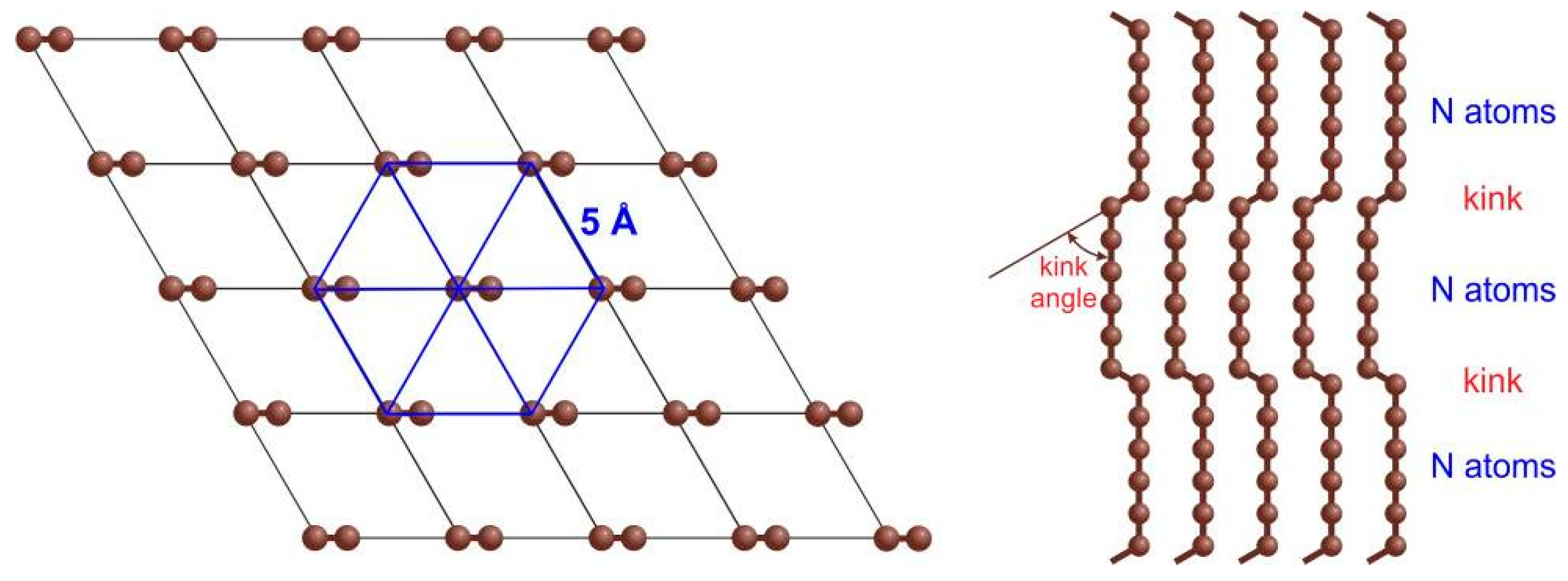
Among the types of chained carbons available experimentally [1], one can name the finite chains terminated by various chemical groups (Figure 1), long chains enclosed in nanotubes (Figure 2), and 2D-crystals of chains called the linear-chained carbon (LCC) or tetracarbon (Figure 3).

For the finite chains, the terminal group effects play a major role: The chemical nature of the end groups influences the structure of the chain, increasing or decreasing the bond length alternation (BLA, see Figure 1e) and, therefore, inducing the energy gap and vibrational properties of the chain [5]. The opportunity of controlling the physical properties, e.g., the conducting character, by proper functionalization is considered a basis for diverse applications [6].

Extremely long carbon chains comprising as many as 6000 atoms have recently been synthesized within double-walled carbon nanotubes (DWCNT) [8]. This achievement shows us a new hopeful way to direct gap 1D-semiconductors [9]. Even though the details of the physical mechanism of the confined chains synthesis are not yet clear, the combination of ab initio calculations and Raman and high-resolution electron microscopy measurements prove their existence and predict possible applications. For example, 1D thermal transport seems valuable, as the heat conduction would be directed along the chain [10].

A prospective advance is the ion-assisted condensation of sp¹-chains, ordered in a hexagonal array with 5 Å distance between 2D–ordered linear-chained carbon (LCC) [12]. Being synthesized from carbon ions and their clusters in the plasma beam, they nevertheless present a material macroscopic in two dimensions. Although it is being already applied; peculiar regimes of the deposition process are yet to be understood theoretically. An additional issue of LCC is the lack of a straightforward characterization method that quickly assesses its structure.

Nowadays it is difficult to synthesize monoatomic carbon chains in any form. It is even more challenging to isolate one from another and to measure specific physical properties, which usually implies attaching/focusing macroscopic or nanoscale probes to an angstrom-sized object. An excellent study of Kaiser et al. [14] succeeded in combining density functional theory (DFT) calculations and atomic force microscopy images of an 18-atom ring in order to prove its polyyne structure. Nevertheless, there are still very few experimental papers on carbyne, so ab initio predictions are of great value. Despite a pronounced interest in the 1D-carbon modifications perceived as a next step of semiconductors downsizing, there are also surprisingly few ab initio simulations that tackle the thermal properties and synthesis of carbyne-related materials. This paper aims to review the recent ab initio studies on carbon chains performed in the last decade.

2. Mechanical Properties

A general analysis of carbyne properties by means of ab initio modeling was performed by Liu et al. [15]. DFT approximation with Perdew-Burke-Ernzerhof (PBE) pseudopotentials was used to calculate the elastic properties and GW-corrections [16] were applied during the band gap determination. It was found that under strain the stiffness of the chained carbon is roughly two times higher than that of diamond. It also has a unique specific strength of 7.5 ×·10⁷ N∙m/kg, with a force of ~10 nN required to break the chain. Amazingly, its torsional stiffness is zero but may be increased by choosing functional groups at the ends. Carbyne self-aggregation was shown to have an activation barrier of 0.6 eV, while the cross-link density for two parallel atomic chains was estimated as 1 cross-link per 17 C atoms [15].

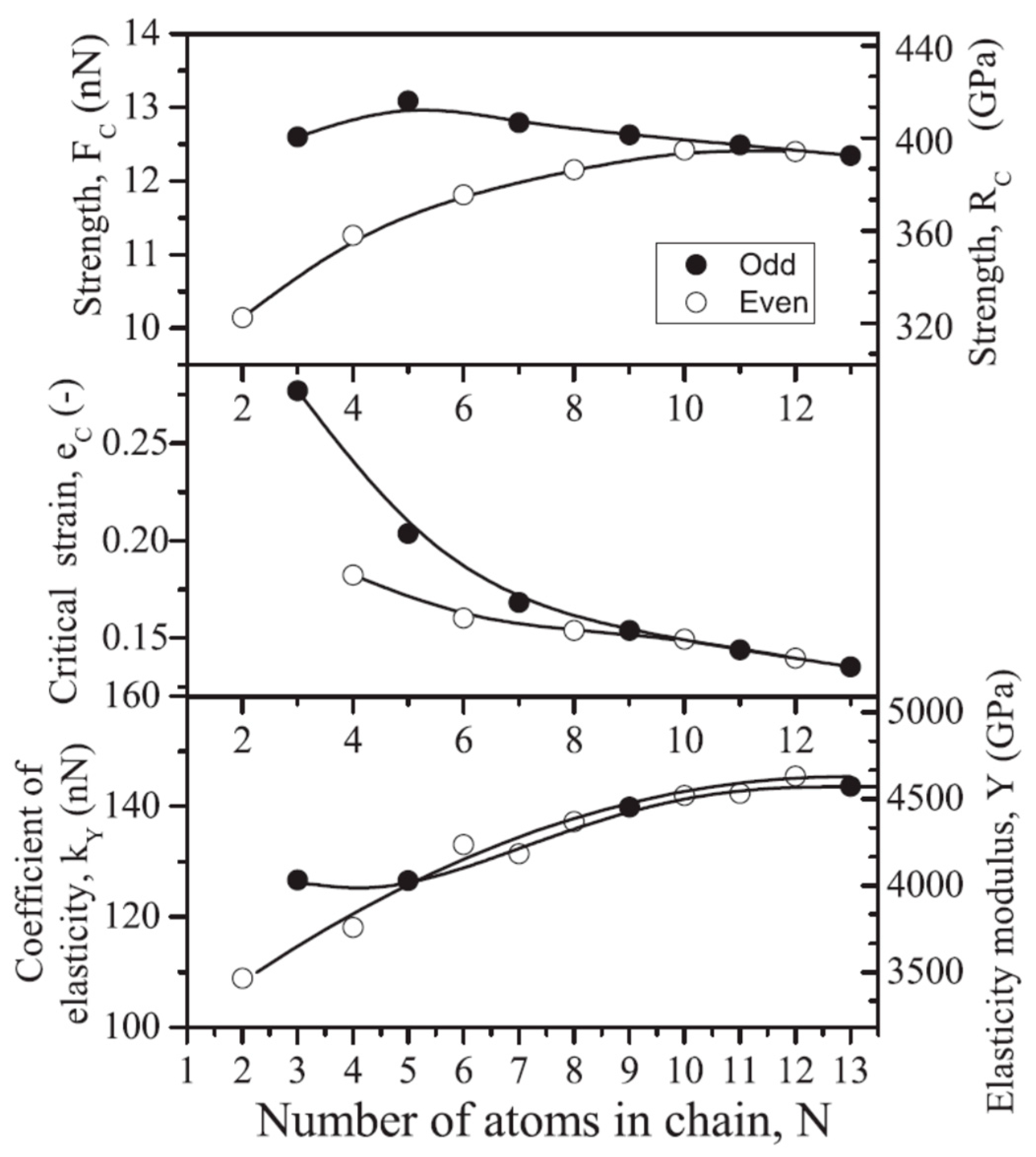
Inspired by the superior strength predicted for carbyne, many investigations were devoted to the mechanical properties of carbon chains. For instance, Timoshevskii et al. [2] used the Vanderbilt pseudopotentials in the framework of the plane-wave DFT approach to model the finite carbon chains up to 21 atoms and predicted a stable cumulene structure in the chains with a length higher than 10 atoms. The calculation of stress-strain diagrams of such chains enabled the determination of their strength, elasticity, and fragility (Figure 4), all of them were shown to demonstrate the scale effect and “even-odd” effect. The maximum strength value was found for the five-atom-long chains [2].

Due to the unaffordable simulation times needed for realistic ab initio calculations of mechanical characteristics, Kocsis et al. [17] chose faster but less accurate classical molecular dynamics (MD) with a ReaxFF force field. The latter is known to demonstrate reliable results for carbon-based materials [18]. While carbyne chains exhibit unique mechanical tension, it was established that its compression stiffness is much lower, due to the buckling under external force. Authors used the effect of confinement to improve the mechanical modulus of a chain in compression. This way, the stiffness can be increased by an order of magnitude from 0.54 kcal mol^-1Ų to 46 kcal mol^-1Ų [17].

Molecular dynamics under a microcanonical ensemble was used by Mirzaeifar et al. [19] to study the strength of carbon chains of different dimensions at a variable temperature. It was found that the presence of H₂O molecules improves the bond stability, resulting in higher values of mechanical strength. In general, it was observed that the basic environment cuts the chain strength, while the stability is moderately raised in acidic solution [19].

An interesting approach was implemented in a recent study of Muller and Nair [4], where DFT was employed to estimate the maximum local stiffness in a composite of carbyne between two nickel (Ni) slabs (Figure 5). It was also shown how charge carriers are distributed within the composite affecting the local specific stiffness. Authors demonstrated that carbyne augments the local specific stiffness by 25% when dielectrically screened by graphene sheets. On the contrary, without proper screening, the stiffness drops by ∼60% compared to the graphene-screened case [4].

Overall, the ab initio studies of the carbon chains confirm earlier predictions of a high specific strength in the stretching regime. However, its weakness in a compression and chemical instability requires some kind of confinement, usually performed with carbon nanotubes or graphene. Experimentally, carbyne appears to be the strongest material [20] having the strength of 251 GPa at 77 K when attached to graphene. A famous 2D-modification of graphene itself has more than two times less value—that of 130 GPа. Ab initio calculations, though, result in an even greater strength of the C-C bonds inside the chain, which is difficult to measure in experiments.

3. Thermal Conductivity

Due to the issues in stability, it is hard to find experimental studies and realistic applications for linear carbyne chains [1]. This problem is even bigger with temperature-dependent processes, which may involve phase transitions [21], chain disassemble, and amorphization. Such phenomena were not studied enough experimentally and are unattainable by a plain DFT approach. In this paragraph, we describe high temperature and/or high pressure investigations performed by various molecular dynamics approaches.

It is known [1] that an infinite carbyne chain may have two structures—cumulene and polyyne —that become equilibrium phases at different temperatures. The crucial point here is the temperature of the phase transition, since the noted phases must have a hugely different electrical and thermal conduction. Liu et al. [3] used molecular dynamics with ReaxFF force fields to calculate the phase β-α transition point at 499 K, while the transition time was as fast as 150 fs. They underline that the cumulene has a considerably higher bending stiffness and Young’s modulus than polyyne, at the level of the toughest natural materials. Cumulene is also a twice better thermal conductor than polyyne, although the defects in bonding can radically drop the thermal conductivity of polyyne [3].

In our recent work [21], we used a new Monte Carlo algorithm for the carbon chains ordered into a hexagonal array. The chemical bonding of such a variant of carbyne was calculated from absolute zero to 1300 K. It was confirmed that the cumulene is more stable at low temperatures but that the system switches into polyyne during heating. The bond softening begins at 500 K. This temperature was shown to be increased by interstitial doping but it does not depend on the length of chains. The elastic modulus of the carbyne was estimated as 1.7 TPa at 5 K and the thermal expansion as +7 × 10⁻⁵ K⁻¹ at 300 K. The heat capacity anomaly initiates around 3800 K, indicating the phase transition across melting point.

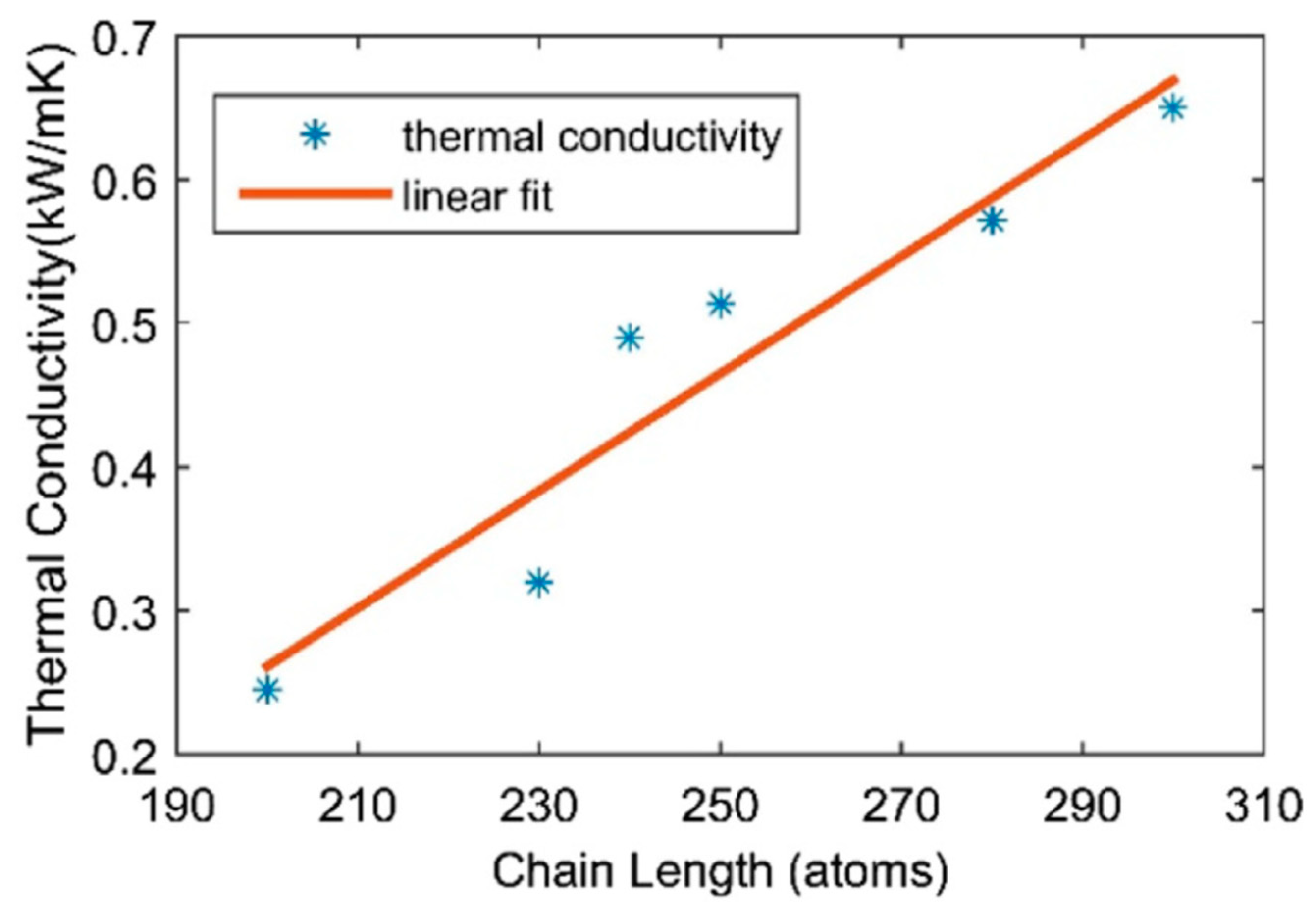
Deng and Cranford [10] studied the thermal conductivity of polyyne chains by means of reverse nonequilibrium molecular dynamics. Müller–Plathe reverse perturbation method [22] was used to calculate the conductivity along the chain direction. For a 40 nm freestanding chain the ultrahigh thermal value was of 0.793 kW/m-K, close to that of carbon nanotubes and graphene. It was shown that the thermal conductivity decreases with strain and increases almost linearly with a growing chain length (Figure 6) [10].

A review of Zhan and Gu [23] gives a perspective of earlier works on thermal conduction of spⁿ-hybridized variants of carbon. As it was established by molecular dynamics studies, κ grows from ∼200 W/mK to 680 W/mK when the chain length extends from 20 to 40 nm. However, a little 3% strain may decrease these values by 70%. The thermal conductivity of carbyne shows a positive temperature dependence at a low temperature range and becomes negative at higher temperatures. At the same time, the α- and β-phases have very dissimilar thermal conduction characteristics. Unlike cumulene, which demonstrates a high phonon-related conductivity, the polyyne shows a much lesser thermal transport [3].

The thermal properties of carbyne are inevitably related to the high temperature synthesis processes. One method of such synthesis was investigated by Deng and Cranford [11] using molecular dynamics with a ReaxFF force field. It exploits the interior of a carbon nanotube as a chemical reactor for chain growth. The authors have found the optimal conditions for growth inside single walled carbon nanotubes (SWCNTs). Inserting the free carbons into an SWCNT, they varied the nanotube diameters, temperature, and chain lengths. It was confirmed that carbyne could positively be synthesized in nanotubes with a diameter not more than 9 Å and at temperatures above 500 K. A correlation plot of the chain length versus nanotube diameter and synthesis temperature was introduced that can facilitate experimental works on the subject [11].

Mazzolari and Manini [24] simulated another route of synthesis—creation of sp¹ carbon by thermal destruction of graphene heated by a hot discharge plasma, using the tight-binding MD. Though no Van-der-Waals interactions were accounted for, this model gives eligible results at a few thousand Kelvin. The authors have found that the carbyne depletion between its generation in the hot part of the plasma and the final deposition can happen at a rate, which depends on the plasma pressure and flux. Quantitative studies are necessary to give precise predictions for an experimental procedure [24].

4. Electronic Properties, Raman Response, and Superconductivity

More studies have been devoted to the properties of carbon chains in relation to their electronic subsystem. Ming et al. [25] investigated the electronic, mechanical, and optical properties of the monatomic carbon chains by DFT using a hybrid density functional. It was found that the material has a direct gap of 2.21 eV and a breaking force of 12 nN, in good accordance with experimental data. The optical absorption showed a single sharp peak below 10 eV and exhibited pronounced anisotropy. Applying elastic strains, the authors managed to tune the band gap from 1.58 to 3.86 eV with the corresponding shift of the absorption band. A genuine graphene-chain device was suggested to apply strains on the chain, which may be used in nano- and optoelectronics devices [25].

It was predicted by theorists that the length of the chains, the end groups, and the environment could tune the carbyne band gap. Nevertheless, various DFT functionals lead to quite dissimilar values of the band gap of infinitely long chains. An excellent paper of Shi et al. [9] applied resonant Raman excitation spectroscopy (Figure 7) to define experimentally the band gap of long carbon chains placed inside double-walled CNTs. The resulting gap has a linear relation with Raman frequency. It was observed that the encapsulation itself leads to a substantial decrease of the band gap due to the contact of the chain and the surrounding CNT [9].

Many experimental and theoretical works were devoted to the Raman fingerprints of carbyne chains (see [1,32] and references therein). In our recent publication [13] the empirical results and first principles modeling were combined to interpret the Raman response of the LCC films. A relation between straight section length, bend angle, and normal modes of LCC were established by means of DFT. High frequency and low frequency modes were identified, taking into account the distribution of LCC structural factors. Clues have been found to suggest a quick attestation technique for carbyne coatings [13]. 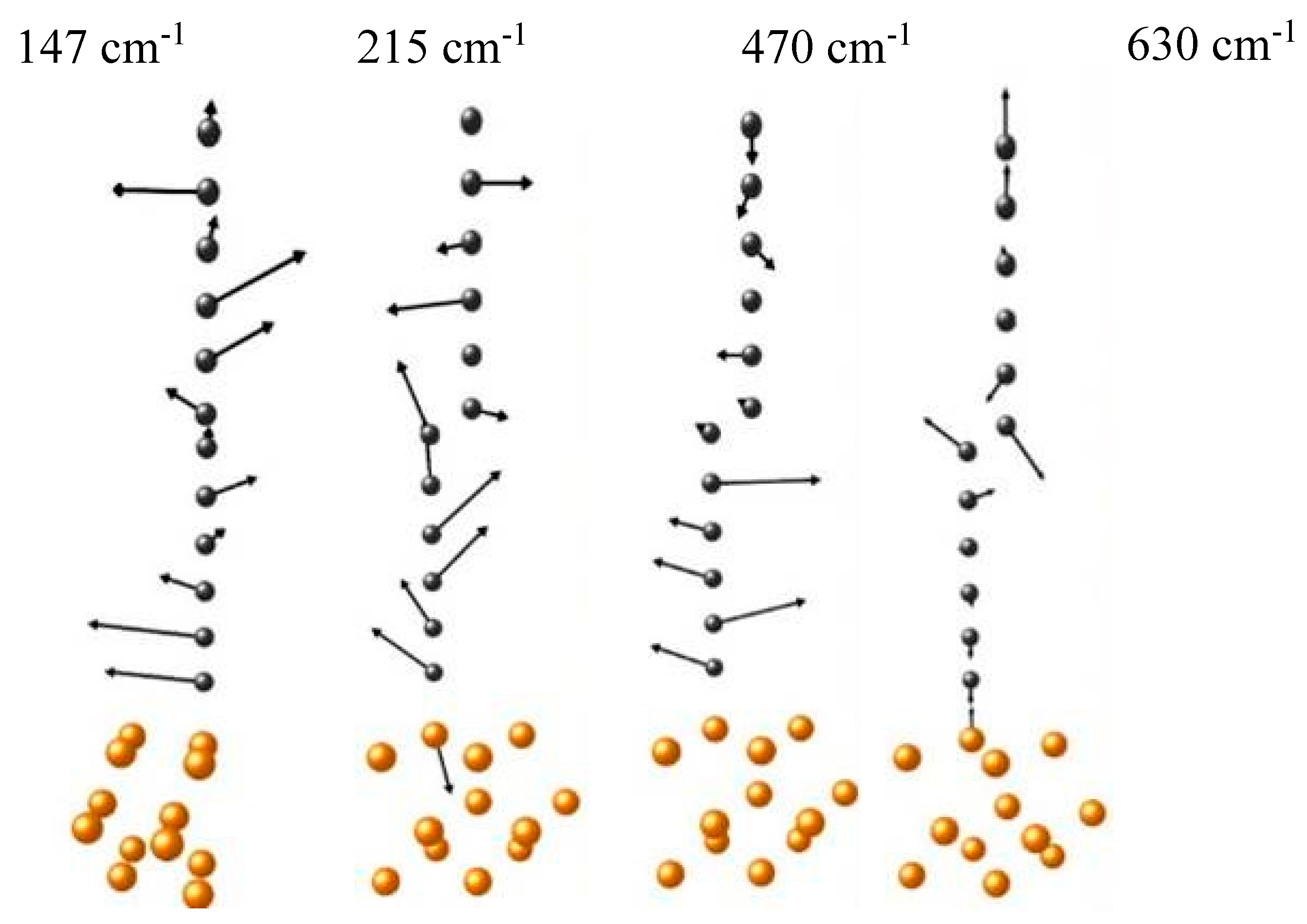Later on, Raman and electron photoemission spectroscopies [33] were utilized to explore the bond types, electron work functions, and band gaps for carbon coatings containing monoatomic chains on metal and semiconductor plates. The spatial distribution of the Raman signal confirmed the heterogeneity of hybridization across the carbon-coated area on polycrystalline copper substrate. More sophisticated models that take into account chain-substrate interactions reveal the eigenvectors of low-frequency vibration modes present in the experimental Raman spectra (Figure 8) [33].

Superconductivity is a long-term desire for researchers in the field of carbon chains. One of possible approaches [34] to obtain the superconductor properties proposed for carbyne by Yu. Prazdnikov [35] is to induce a giant spin-orbit interaction thanks to the specific arrangement of the carbyne crystal. The maximal value of spin-orbit coupling was predicted for low-dimensional systems. Oriented carbyne has been presented as a localized phase of the room-temperature superconductor and the way to gain macroscopic superconductivity was given.

In our paper [36] the superconducting transition temperature is predicted for different thin SWCNT resulting from electron-phonon coupling by an ab initio method, taking into account the effect of radial pressure, chirality, and bond lengths. Optimizing the geometry of the carbon nanotubes, a maximum Tc of 60 K was established. The superconductivity threshold for a LCC inserted in the center of (5,0) SWCNTs was predicted to be even higher: Twice, as compared to the blank (5,0) SWCNTs [36].

Correlated electron systems are not the only option for high-temperature superconductors. Instead, they may occur in the class of phonon-mediated classical superconductors with high Debye temperature and high electronic density of states (DOS) at the Fermi level, in a material with lightweight atoms and covalent bonds. One-dimensional structures seem hopeful because of the Van Hove singularities in their electronic DOS. We used a DFT method to improve quasi-1D superconducting carbon structures (Figure 9). Starting from (4,2) carbon nanotubes we reduced the nanotubes to a loop, opened it to form chains, optimized bond length and bend structure, and formed a new type of closed carbon loop that has a T_c of 115 K [37].

5. Conclusions

Overall, the ab initio studies of the carbon chains confirm earlier predictions of its unique properties, including a high specific strength in the stretching regime, highly tunable thermal conductivity, and even a prospect of superconductivity. Many theoretical papers describe these characteristics in detail. Comparisons with experimental data were attempted, though they are complicated due to difficulties in synthesis and extreme reactivity of monoatomic linear chains.

A more challenging task is to simulate and then optimize a synthesis procedure. A combination of multiple atoms, external fields and ion beams, plasma and high temperatures together with hundreds of picoseconds timescale makes researchers introduce more or less coarse approximations, which makes it hard to use purely ab initio methods. However, the successful examples of numerical simulations describing in detail the high-temperature synthesis of carbon chains gives us hope for a solution to the long-standing problem of carbyne production.