Macroscopic Behavior and Microscopic Factors of Electron Emission from Chained Nanocarbon Coatings
Abstract
1. Introduction
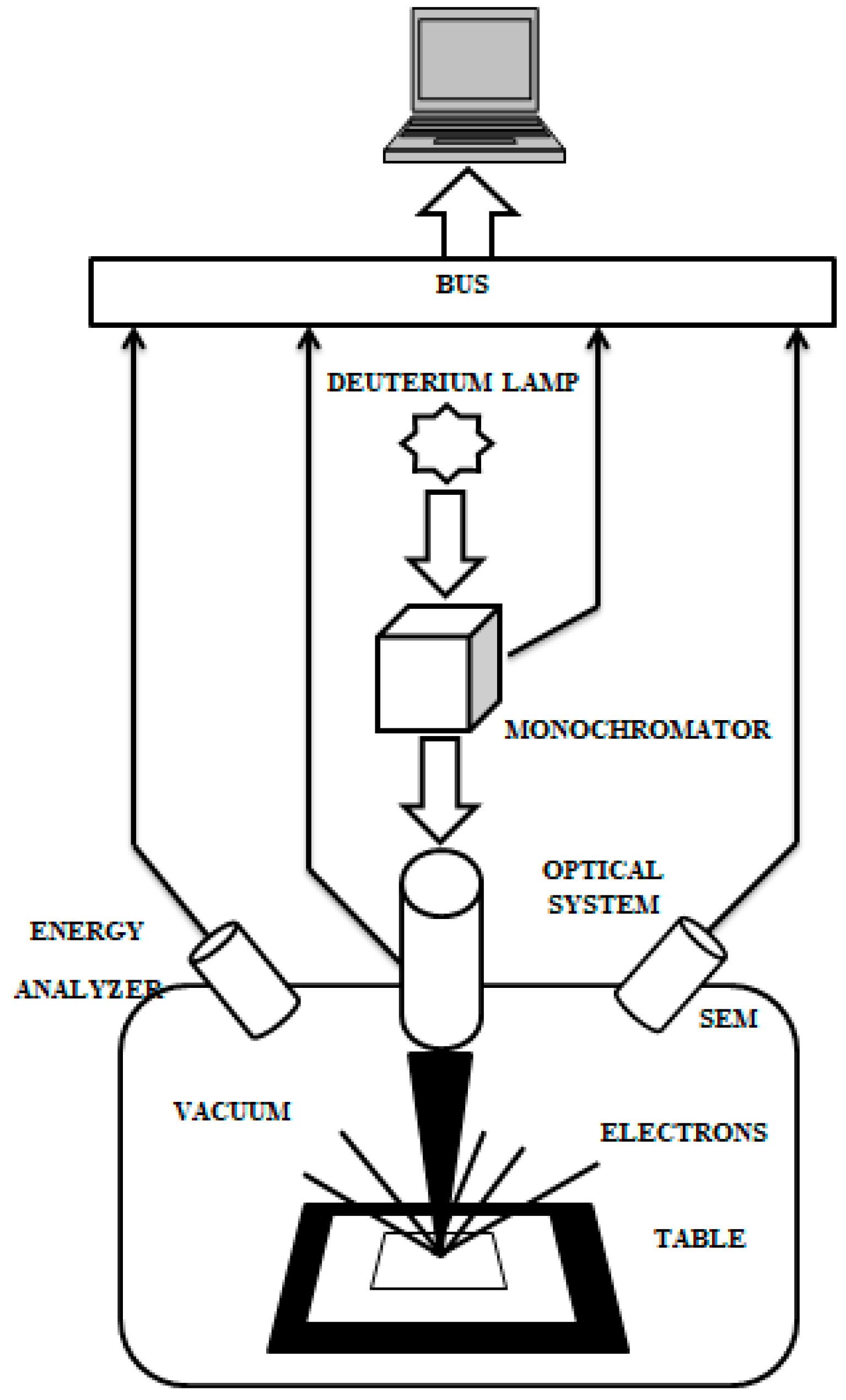
2. Samples and Methods
3. Results and Discussion
3.1. OSEE Measurements
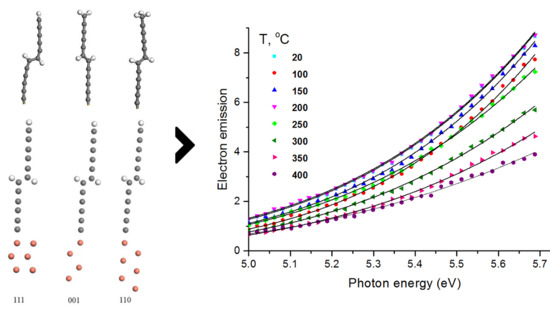
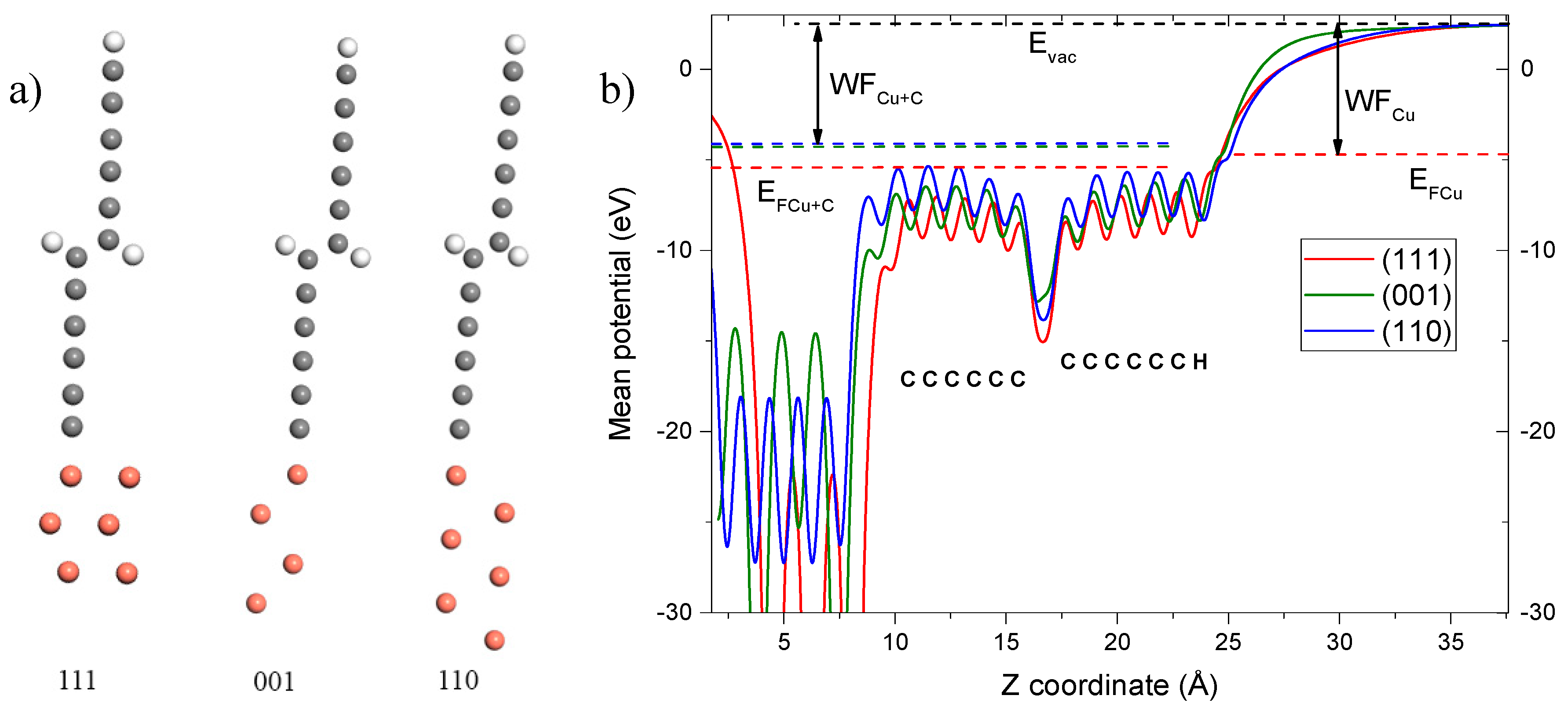
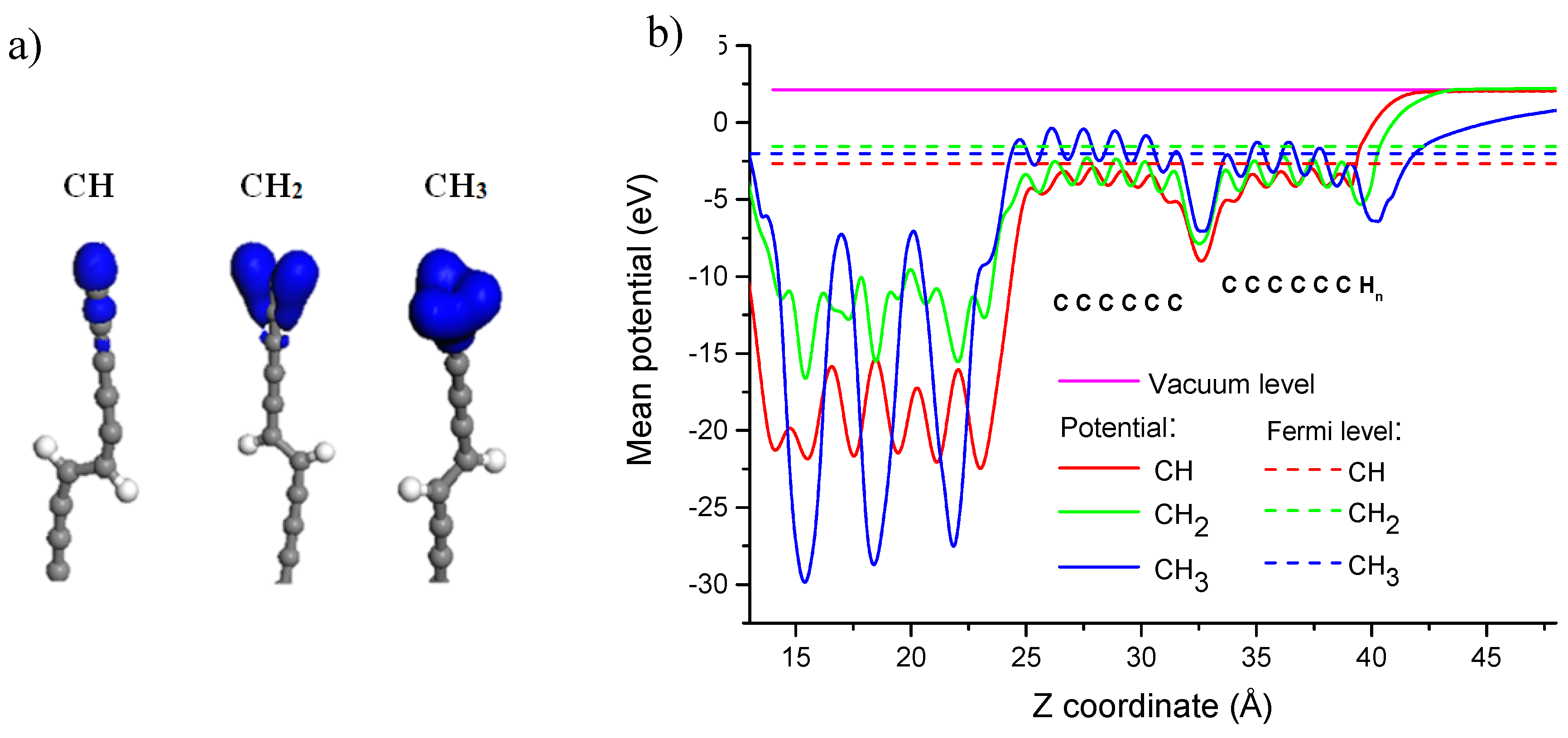
3.2. Density-Functional Theory (DFT) Modeling
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mingjie, L. Carbyne from first principles: Chain of C atoms, a nanorod or a nanorope. ACS Nano 2013, 7, 10075–100082. [Google Scholar]
- Christopher, B.; Goldman, N. Carbyne fiber synthesis within evaporating metallic liquid carbon. J. Phy. Chem. C 2015, 119, 21605–21611. [Google Scholar]
- Bitao, P. Carbyne with finite length: The one-dimensional sp carbon. Sci. Adv. 2015, 1, e1500857. [Google Scholar]
- Sladkov, A.M.; Kasatochkin, V.I.; Korshak, V.V. New crystalline form of carbon - carbyne. USSR Patent No. 107, 7 December 1971. Priority date 4 November 1960. [Google Scholar]
- Pacchioni, G.; Skuja, L.; Griscom, D. Defects in SiO2 and Related Dielectrics: Science and Technology; Springer: Heidelberg, Germany, 2012; p. 624. [Google Scholar]
- Luth, H. Solid Surfaces. In Interfaces and Thin Films; Springer: Heidelberg, Germany, 2010; p. 586. [Google Scholar]
- Buntov, E.A.; Zatsepin, A.F.; Slesarev, A.I.; Shchapova, Y.V.; Challinger, S.; Baikie, I. Effect of thickness and substrate type on the structure and low vacuum photoemission of carbyne-containing films. Carbon 2019, 152, 388–395. [Google Scholar] [CrossRef]
- Kudryavtsev, Y.P.; Guseva, M.B.; Babaev, V.G. Oriented carbyne layers. Carbon 1992, 30, 213–221. [Google Scholar] [CrossRef]
- Zatsepin, A.F.; Biryukov, D.Y.; Kortov, V.S. Taking account of the nonstationarity in analyzing the optically stimulated electron emission of irradiated dielectrics. J. Appl. Spectr. 2005, 72, 671–678. [Google Scholar] [CrossRef]
- Buntov, E.A.; Zatsepin, A.F. OSEE fitter program, registered in the Russian state register of software. No. 2008614289. 11 November 2008. [Google Scholar]
- Smeu, M.; Guo, H.; Ji, W.; Wolkow, R.A. Electronic properties of Si(111)-7 × 7 and related reconstructions: Density functional theory calculations. Phys. Rev. B 2012, 85, 195315. [Google Scholar] [CrossRef]
- Kane, E.O. Theory of Photoelectric Emission from Semiconductors. Phys. Rev. 1962, 127, 131. [Google Scholar] [CrossRef]
- Anderson, P.A. The Work Function of Copper. Phys. Rev. 1949, 76, 388–390. [Google Scholar] [CrossRef]
- Wong, C.H.; Buntov, E.A.; Rychkov, V.N.; Guseva, M.B.; Zatsepin, A.F. Simulation of chemical bond distributions and phase transformation in carbon chains. Carbon 2017, 114, 106–110. [Google Scholar] [CrossRef]
- Ravagnan, L.; Siviero, F.; Lenardi, C.; Piseri, P.; Barborini, E.; Milani, P.; Casari, C.S.; Li Bassi, A.; Bottani, C.E. Cluster-beam deposition and in situ characterization of carbyne-rich carbon films. Phys. Rev. Lett. 2002, 89, 285506. [Google Scholar] [CrossRef]
- Lucotti, A.; Casari, C.S.; Tommasini, M.; Li Bassi, A.; Fazzi, D.; Russo, V.; Del Zoppo, M.; Castiglioni, C.; Cataldo, F.; Bottani, C.E.; et al. Sp Carbon chain interaction with silver nanoparticles probed by Surface Enhanced Raman Scattering. Chem. Phys. Lett. 2009, 478, 45. [Google Scholar] [CrossRef][Green Version]
- Casari, C.S.; Milani, A. Carbyne: From the elusive allotrope to stable carbon atom wires. MRS Commun. 2018, 8, 207–219. [Google Scholar] [CrossRef]
- Allen, F.G.; Cobelli, G.W. Work Function, Photoelectric Threshold and Surface States of Atomically Clean Silicon. Phys. Rev. 1962, 127, 150–158. [Google Scholar] [CrossRef]
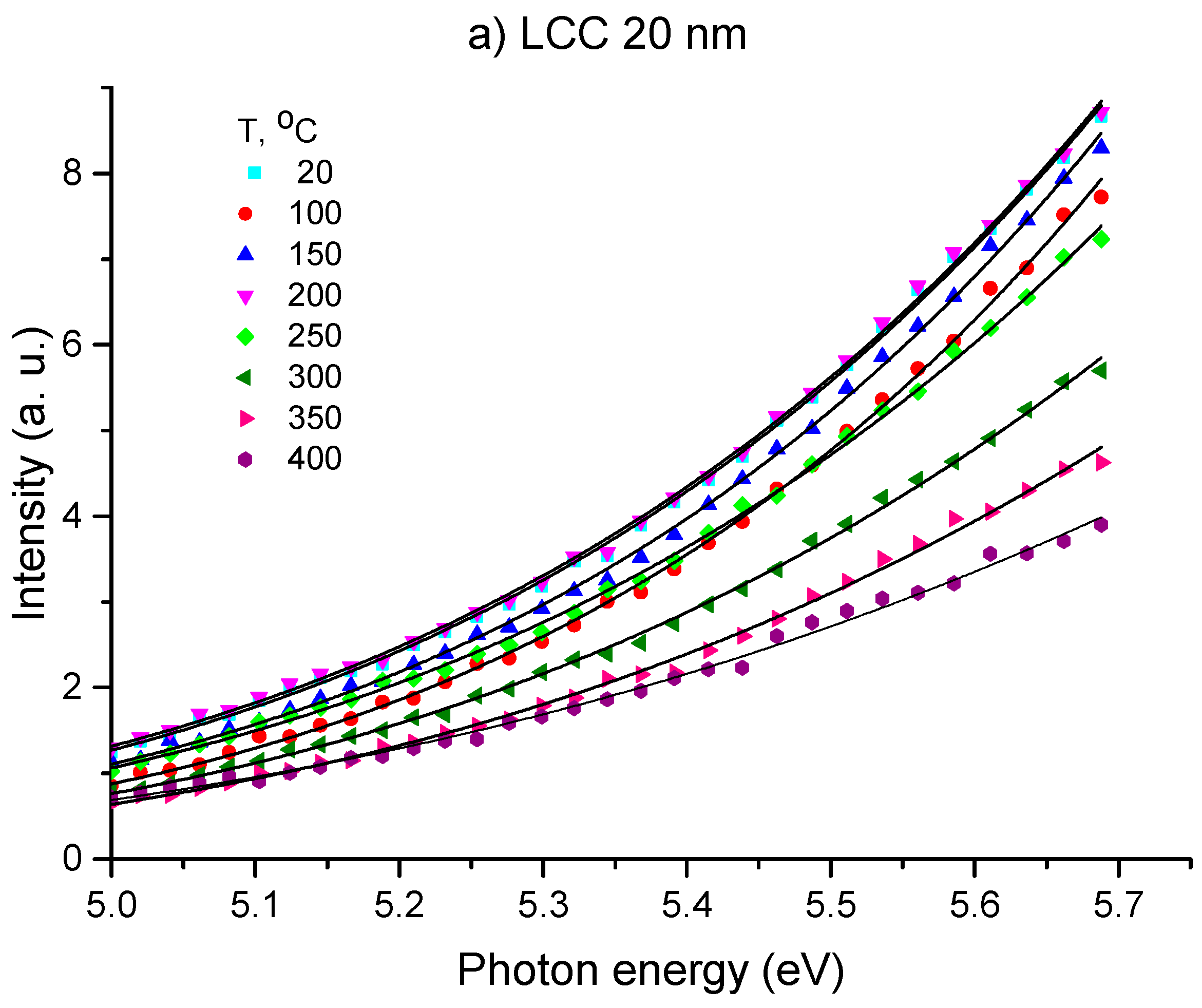
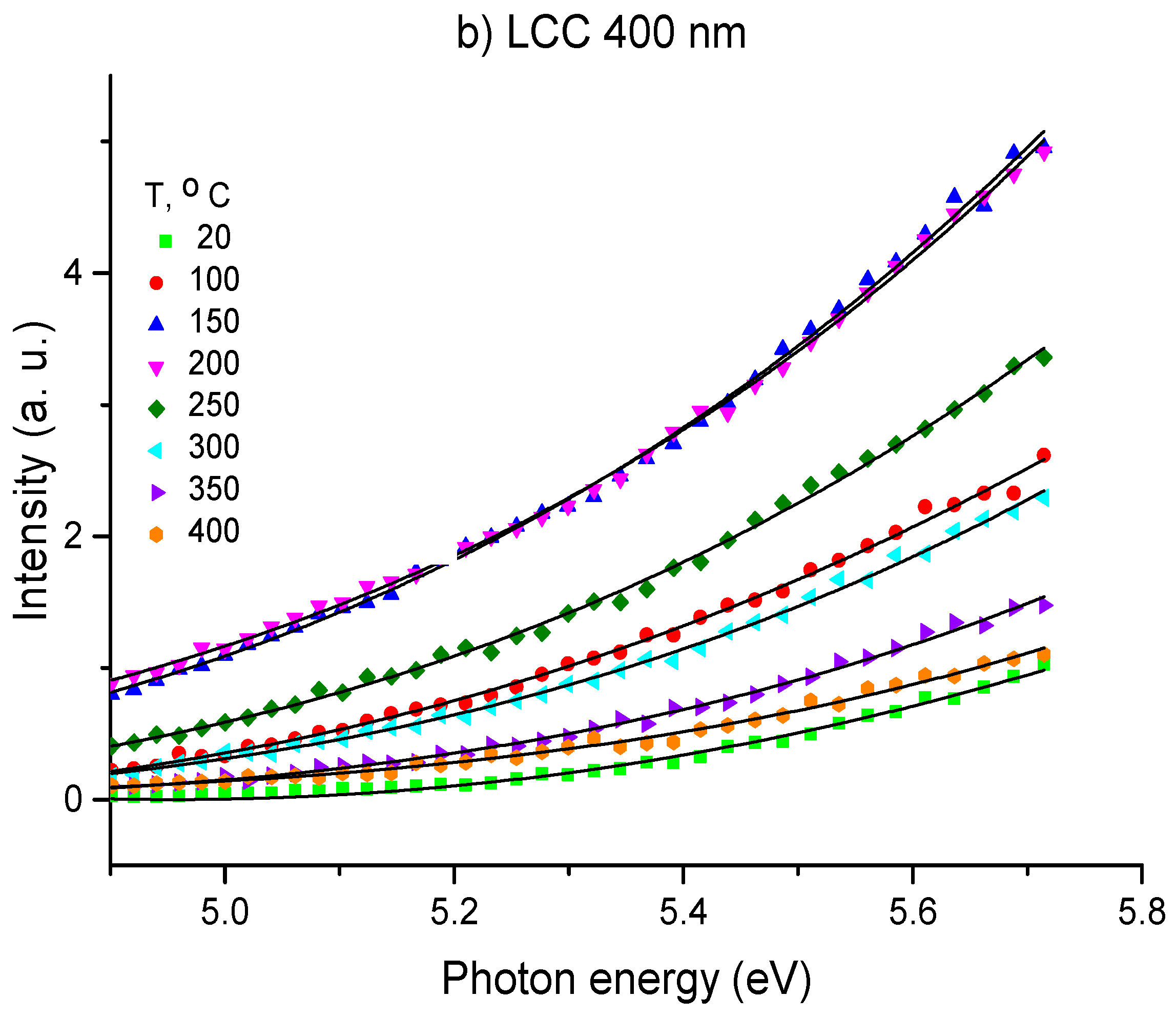
| Temperature, °C | LCC 20 nm Φ, eV | LCC 400 nm Φ, eV |
|---|---|---|
| 20 | 4.26 | 4.50 |
| 100 | 4.14 | 4.53 |
| 150 | 4.36 | 4.03 |
| 200 | 4.30 | 4.03 |
| 250 | 4.24 | 4.19 |
| 300 | 4.35 | 4.27 |
| 350 | 4.47 | 4.47 |
| 400 | 4.10 | 4.47 |
| Orientation of the substrate | Φtheor, eV [10] | EF, eV | Evacuum, eV | Φtheor, eV (calculated) |
|---|---|---|---|---|
| (111) | 7.7 | 5.4 | 2.52 | 7.92 |
| (001) | 8.0 | 4.4 | 2.52 | 6.92 |
| (110) | 6.8 | 4.3 | 2.52 | 6.82 |
| End groups of the LCC | Φteor, eV [18] | EF, eV | Evacuum, eV | Φteor, eV (calculated) |
|---|---|---|---|---|
| CH | 4.83 | −3.13 | 1.65 | 4.78 |
| CH2 | 4.83 | −2.91 | 1.65 | 4.56 |
| CH3 | 4.83 | −1.93 | 1.65 | 3.58 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boqizoda, D.; Zatsepin, A.; Buntov, E.; Slesarev, A.; Osheva, D.; Kitayeva, T. Macroscopic Behavior and Microscopic Factors of Electron Emission from Chained Nanocarbon Coatings. C 2019, 5, 55. https://doi.org/10.3390/c5030055
Boqizoda D, Zatsepin A, Buntov E, Slesarev A, Osheva D, Kitayeva T. Macroscopic Behavior and Microscopic Factors of Electron Emission from Chained Nanocarbon Coatings. C. 2019; 5(3):55. https://doi.org/10.3390/c5030055
Chicago/Turabian StyleBoqizoda, Daleri, Anatoly Zatsepin, Evgeny Buntov, Anatoly Slesarev, Daria Osheva, and Tatiana Kitayeva. 2019. "Macroscopic Behavior and Microscopic Factors of Electron Emission from Chained Nanocarbon Coatings" C 5, no. 3: 55. https://doi.org/10.3390/c5030055
APA StyleBoqizoda, D., Zatsepin, A., Buntov, E., Slesarev, A., Osheva, D., & Kitayeva, T. (2019). Macroscopic Behavior and Microscopic Factors of Electron Emission from Chained Nanocarbon Coatings. C, 5(3), 55. https://doi.org/10.3390/c5030055