Conversion of Carbon Dioxide into Solar Fuels Using MgFe2O4 Thermochemical Redox Chemistry
Abstract
1. Introduction
2. Thermodynamic Model
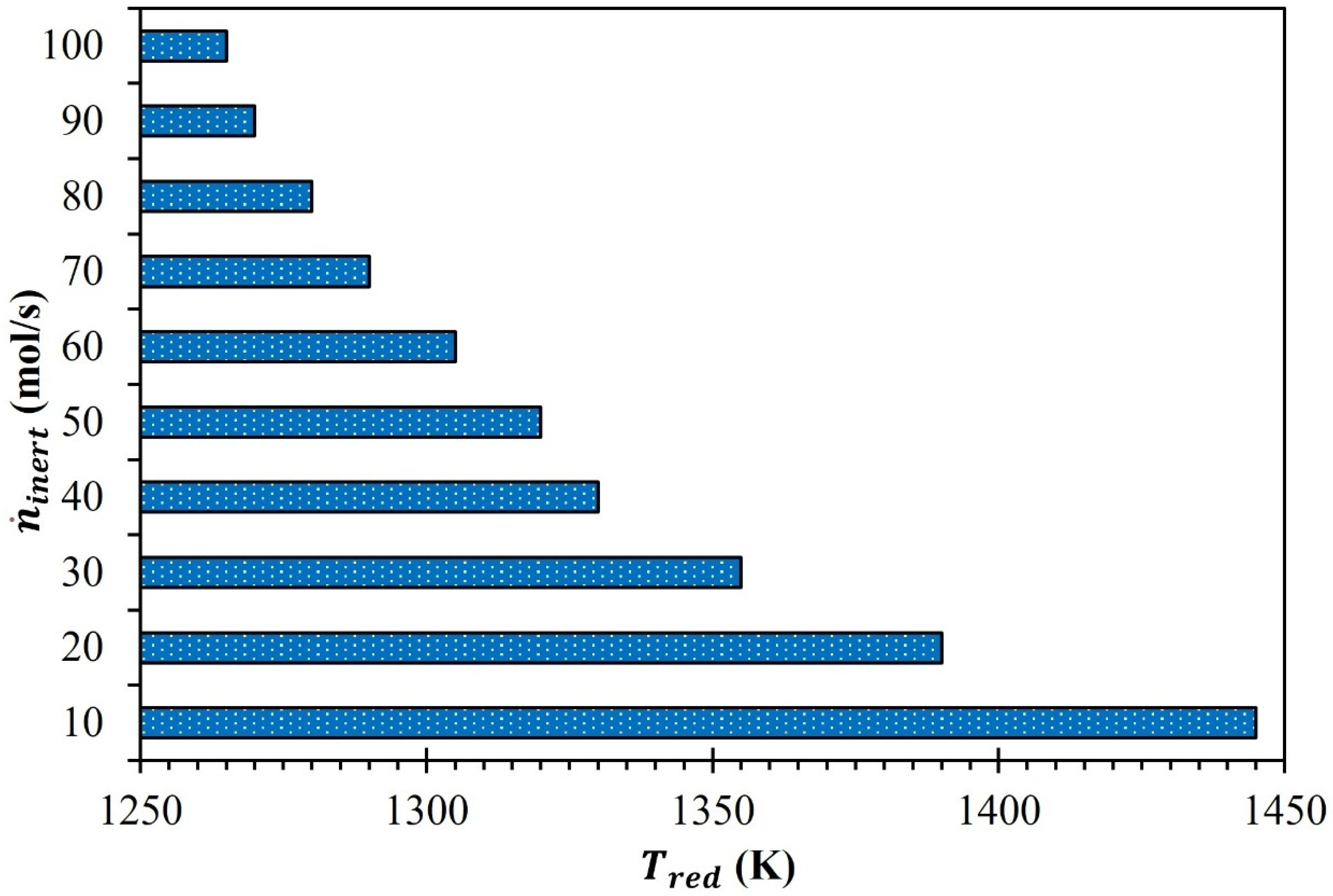
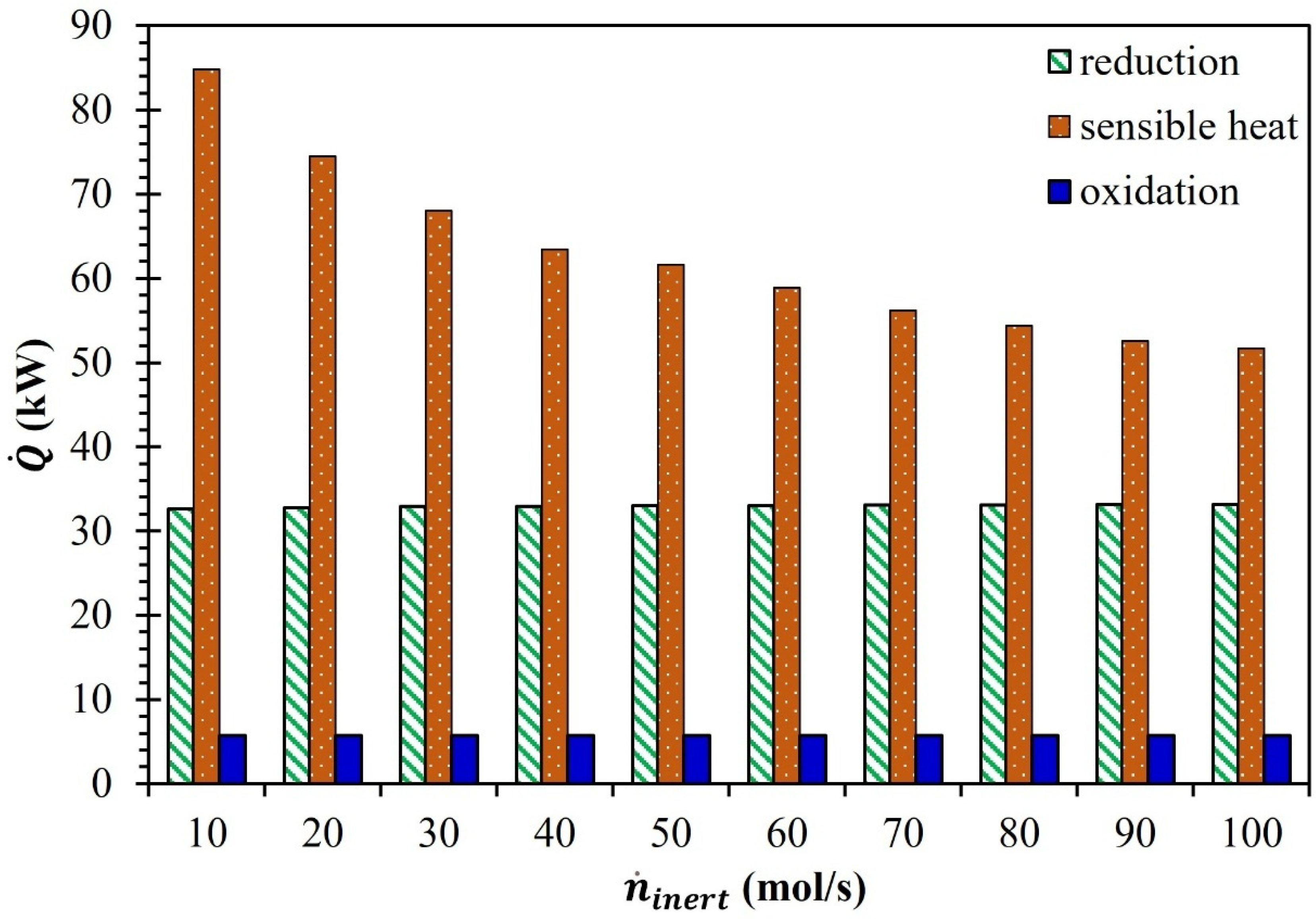
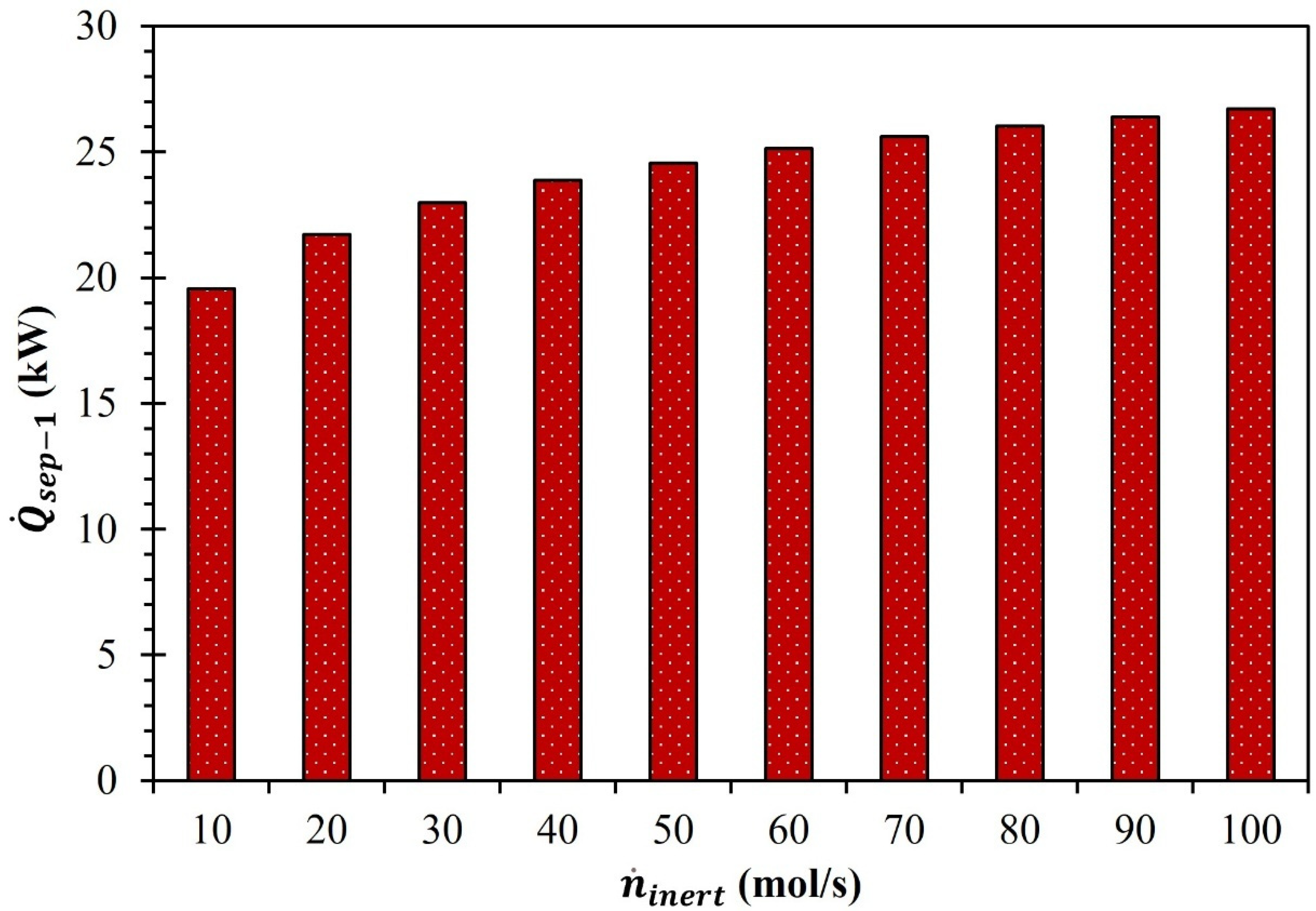
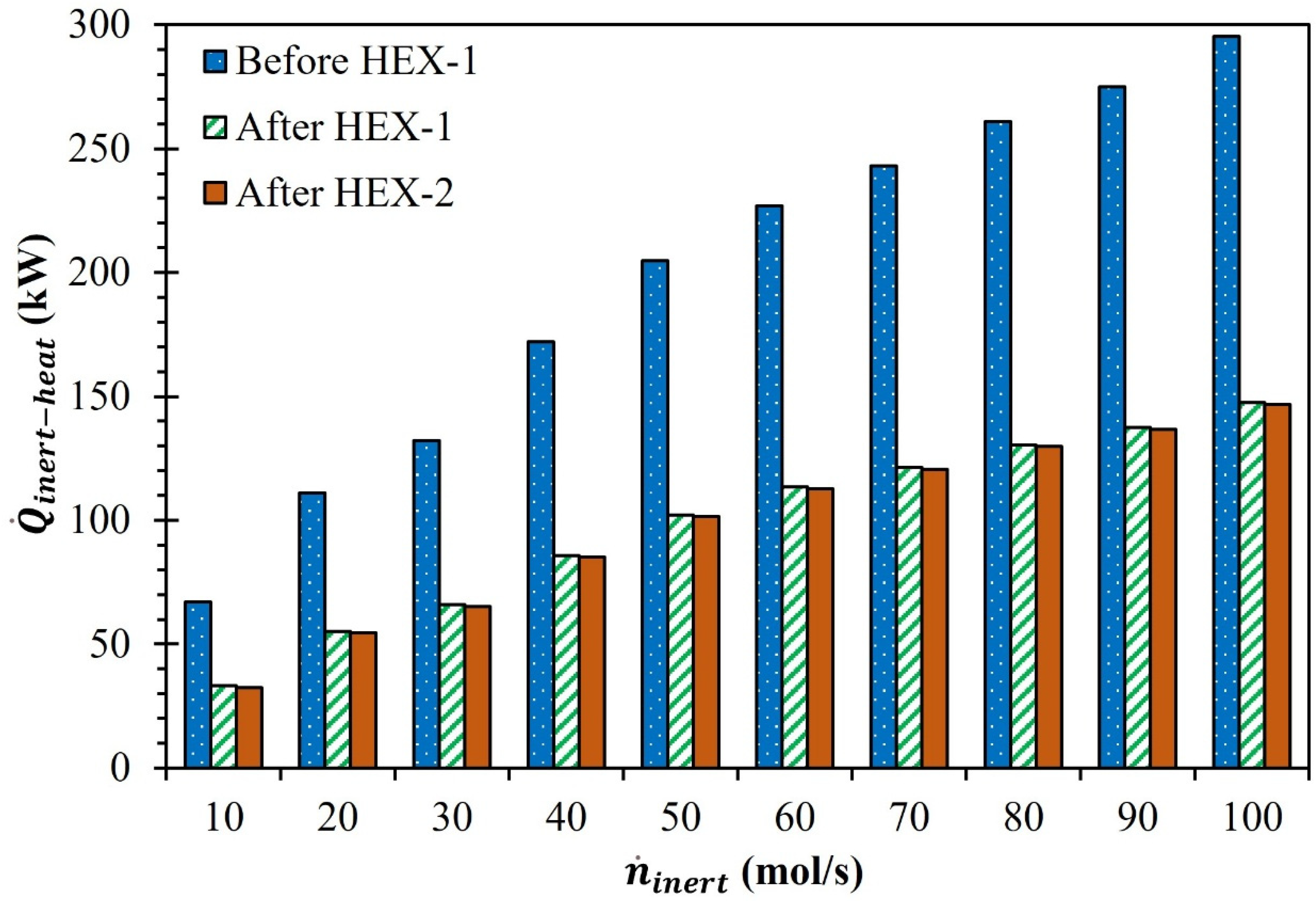
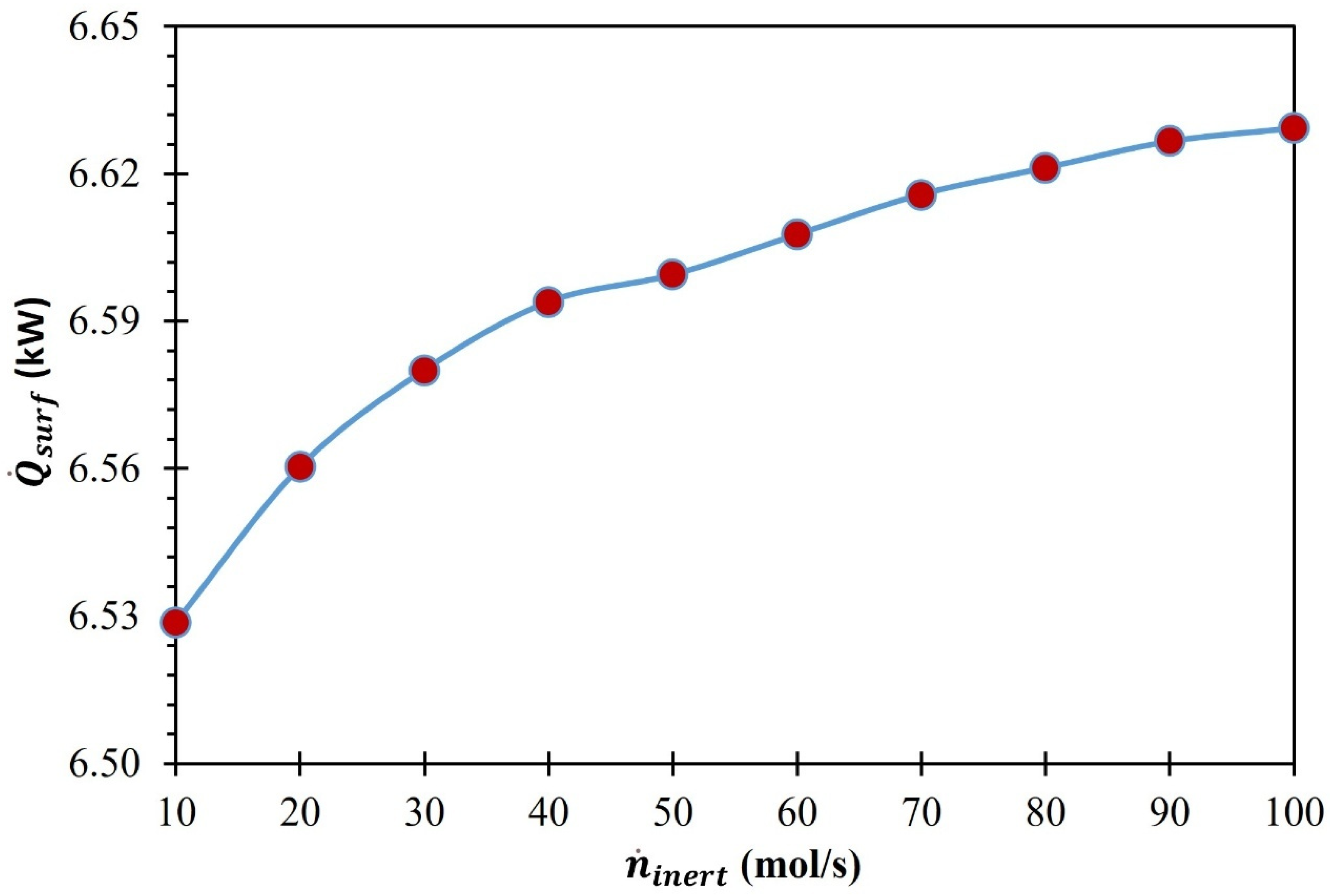
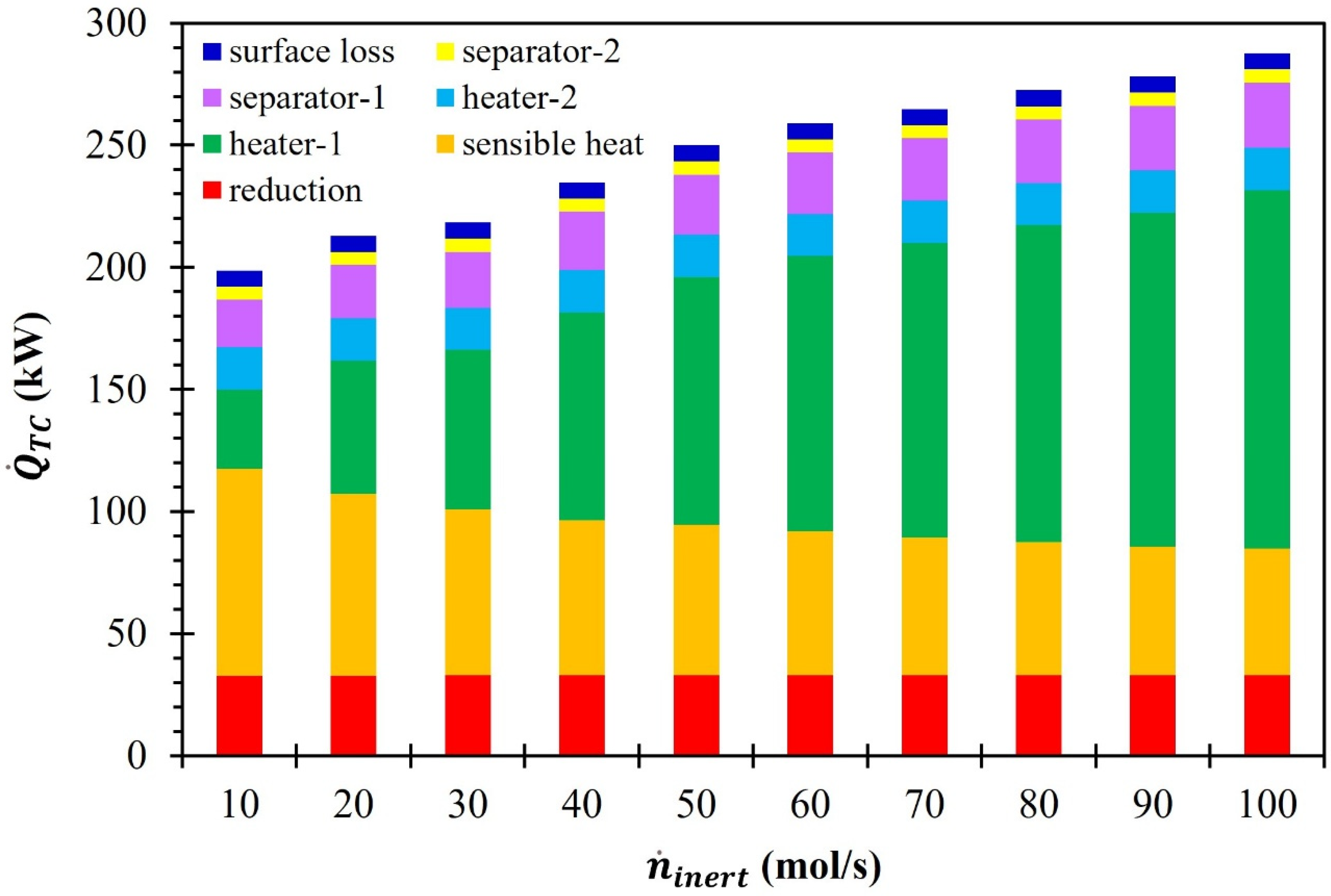
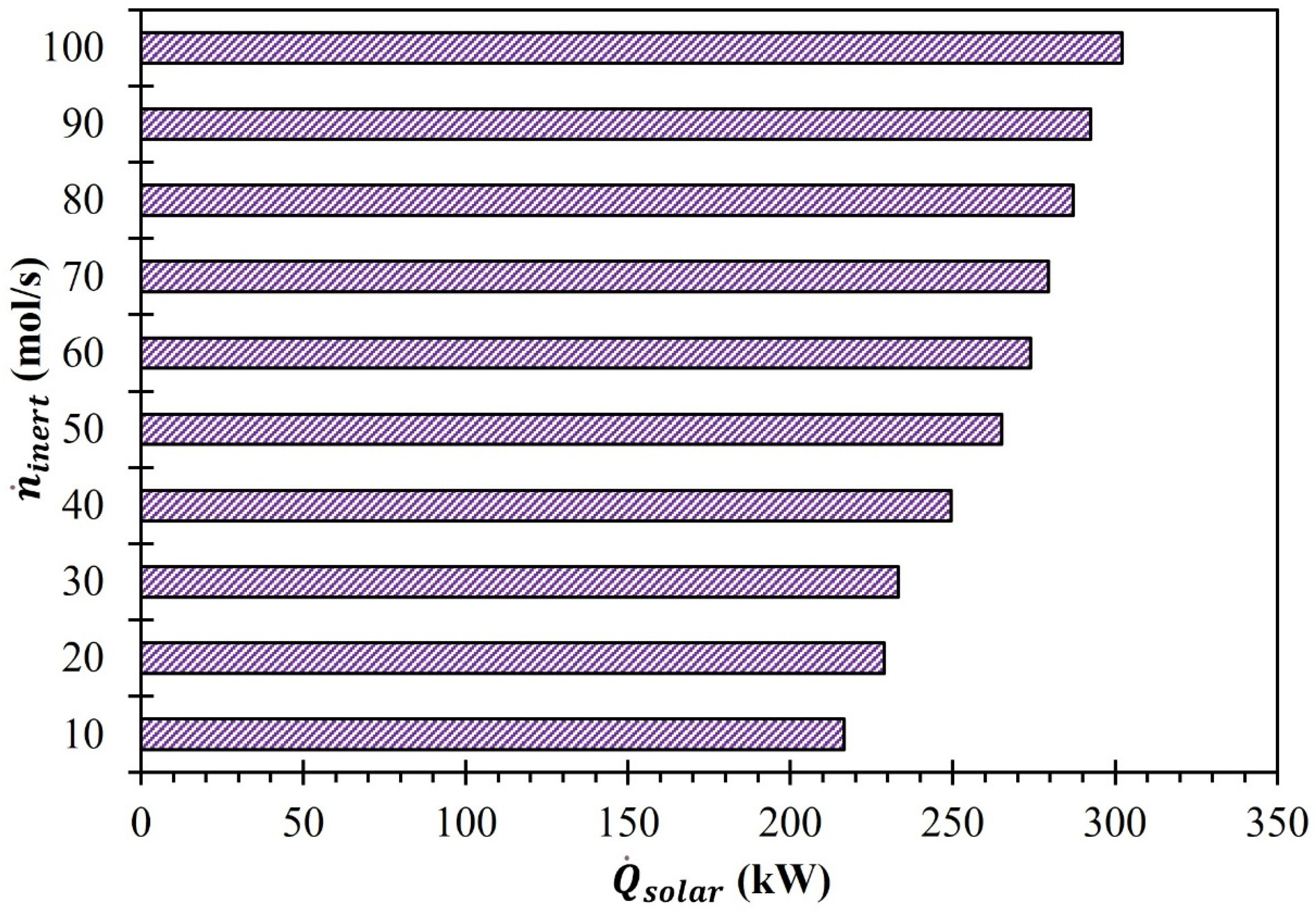
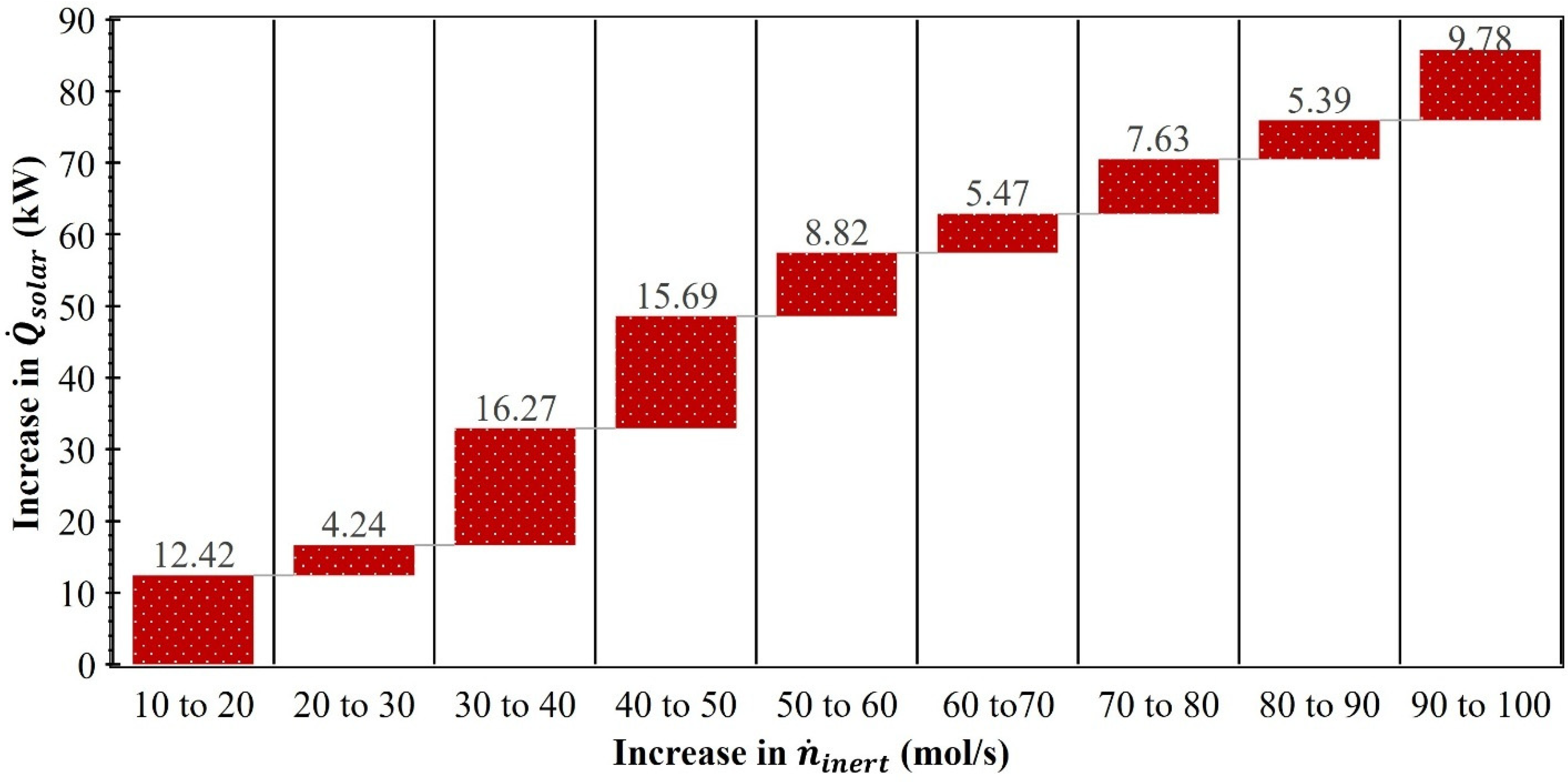
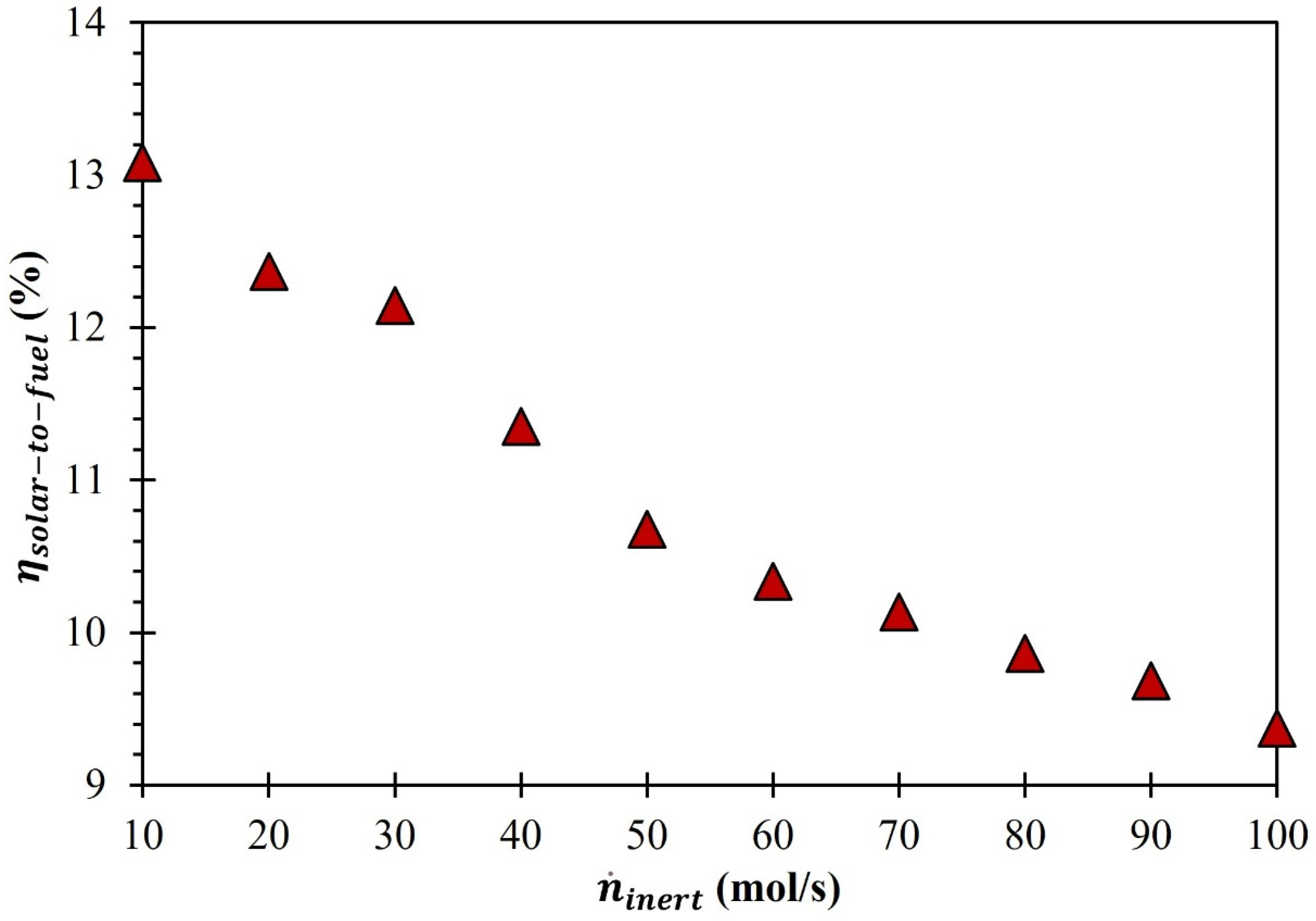
3. Results and Discussion
4. Summary and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| C | Solar flux concentration ratio, suns |
| Higher heating value of CO, kW | |
| HEX-1 | Solid-to-solid heat exchanger 1 |
| HEX-2 | Gas-to-gas heat exchanger 2 |
| HEX-3 | Gas-to-gas heat exchanger 3 |
| HEX-4 | Gas-to-gas heat exchanger 4 |
| I | Normal beam solar insolation, W/m2 |
| MO | Metal oxide |
| Molar amount, mol | |
| , mol | |
| , mol | |
| , mol | |
| , mol | |
| Molar flow rate, mol/s | |
| Molar flow rate of inert, mol/s | |
| , mol/s | |
| Molar flow rate of CO2, mol/s | |
| Molar flow rate of CO, mol/s | |
| Molar flow rate of O2, mol/s | |
| Thermal energy required to heat Ar, kW | |
| Thermal energy released during cooling of inert + O2 gas mixture, kW | |
| Thermal energy released during cooling of CO2 + CO gas mixture, kW | |
| Thermal energy required to heat CO2, kW | |
| Auxiliary thermal energy required to heat Ar, kW | |
| Auxiliary thermal energy required to heat CO2, kW | |
| Thermal energy released during cooling of O2, kW | |
| Solar energy required to run the cycle, kW | |
| Thermal energy required for the operation of separator-1, kW | |
| Thermal energy required for the operation of separator-2, kW | |
| Thermal energy losses over the reduction chamber walls, kW | |
| Thermal energy required to run the cycle, Kw | |
| Thermal energy required for thermal reduction of MgFe2O4, kW | |
| Thermal energy required to heat the MgFe2O4-δred, kW | |
| Thermal energy released during re-oxidation of MgFe2O4-δred, kW | |
| Re-radiation losses from the cycle, kW | |
| Ideal gas constant (8.314 J/mol·K) | |
| Ambient temperature, K | |
| Oxidation (splitting) temperature, K | |
| Reduction temperature, K | |
| Operating temperature of separator-1, K | |
| Operating temperature of separator-2, K | |
| , mol | |
| , mol | |
| , mol | |
| , mol | |
| Solar energy absorption efficiency, % | |
| Efficiency of separator-1, % | |
| Efficiency of separator-2, % | |
| Solar-to-fuel energy conversion efficiency, % | |
| Reduction non-stoichiometry | |
| Gas-to-gas heat recovery effectiveness | |
| Solid-to-solid heat recovery effectiveness | |
| Stefan–Boltzmann constant (5.670 × 10−8 W/m2·K4) |
References
- Carrillo, R.J.; Scheffe, J.R. Advances and trends in redox materials for solar thermochemical fuel production. Solar Energy 2017, 156, 3–20. [Google Scholar] [CrossRef]
- Vaidya, P.D.; Kenig, E.Y. CO2-alkanolamine reaction kinetics: A review of recent studies. Chem. Eng. Technol. 2007, 30, 1467–1474. [Google Scholar] [CrossRef]
- Schäppi, R.; Rutz, D.; Dähler, F.; Muroyama, A.; Haueter, P.; Lilliestam, J.; Patt, A.; Furler, P.; Steinfeld, A. Drop-in fuels from sunlight and air. Nature 2022, 601, 63–68. [Google Scholar] [CrossRef]
- Safari, F.; Dincer, I. A review and comparative evaluation of thermochemical water splitting cycles for hydrogen production. Energy Convers. Manag. 2020, 205, 112182. [Google Scholar] [CrossRef]
- Steinfeld, A. Solar thermochemical production of hydrogen––A review. Solar Energy 2005, 78, 603–615. [Google Scholar] [CrossRef]
- Amar, V.S.; Puszynski, J.A.; Shende, R.V. H2 generation from thermochemical water-splitting using yttria stabilized NiFe2O4 core-shell nanoparticles. J. Renew. Sustain. Energy 2015, 7, 023113. [Google Scholar] [CrossRef]
- Dry, M.E. The Fischer-Tropsch process: 1950–2000. Catal. Today 2002, 71, 227–241. [Google Scholar] [CrossRef]
- Dry, M.E. The fischer-tropsch process—Commercial aspects. Catal. Today 1990, 6, 183–206. [Google Scholar] [CrossRef]
- Steinfeld, A. Solar hydrogen production via a two-step water-splitting thermochemical cycle based on Zn/ZnO redox reactions. Int. J. Hydrogen Energy 2002, 27, 611–619. [Google Scholar] [CrossRef]
- Koepf, E.; Villasmil, W.; Meier, A. Pilot-scale solar reactor operation and characterization for fuel production via the Zn/ZnO thermochemical cycle. Appl. Energy 2016, 165, 1004–1023. [Google Scholar] [CrossRef]
- Loutzenhiser, P.G.; Steinfeld, A. Solar syngas production from CO2 and H2O in a two-step thermochemical cycle via Zn/ZnO redox reactions: Thermodynamic cycle analysis. Int. J. Hydrogen Energy 2011, 36, 12141–12147. [Google Scholar] [CrossRef]
- Chambon, M.; Abanades, S.; Flamant, G. Solar thermal reduction of ZnO and SnO2: Characterization of the recombination reaction with O2. Chem. Eng. Sci. 2010, 65, 3671–3680. [Google Scholar] [CrossRef]
- Bhosale, R.R.; Gupta, R.B.; Shende, R.V. Thermodynamic evaluation of solar assisted ZnO/Zn thermochemical CO2 splitting cycle. Environ. Res. 2022, 212, 113266. [Google Scholar] [CrossRef] [PubMed]
- Abanades, S. CO2 and H2O reduction by solar thermochemical looping using SnO2/SnO redox reactions: Thermogravimetric analysis. Int. J. Hydrogen Energy 2012, 37, 8223–8231. [Google Scholar] [CrossRef]
- Abanades, S.; Charvin, P.; Lemont, F.; Flamant, G. Novel two-step SnO2/SnO water-splitting cycle for solar thermochemical production of hydrogen. Int. J. Hydrogen Energy 2008, 33, 6021–6030. [Google Scholar] [CrossRef]
- Charvin, P.; Abanades, S.; Lemont, F.; Flamant, G. Experimental study of SnO2/SnO/Sn thermochemical systems for solar production of hydrogen. AIChE J. 2008, 54, 2759–2767. [Google Scholar] [CrossRef]
- Scheffe, J.R.; Li, J.; Weimer, A.W. A spinel ferrite/hercynite water-splitting redox cycle. Int. J. Hydrogen Energy 2010, 35, 3333–3340. [Google Scholar] [CrossRef]
- Agrafiotis, C.; Zygogianni, A.; Pagkoura, C.; Kostoglou, M.; Konstandopoulos, A.G. Hydrogen production via solar-aided water splitting thermochemical cycles with nickel ferrite: Experiments and modeling. AIChE J. 2013, 59, 1213–1225. [Google Scholar] [CrossRef]
- Diver, R.B.; Miller, J.E.; Allendorf, M.D.; Siegel, N.P.; Hogan, R.E. Solar Thermochemical Water-Splitting Ferrite-Cycle Heat Engines. J. Sol. Energy Eng. 2008, 130, 041001. [Google Scholar] [CrossRef]
- Tamaura, Y.; Hasegawa, N.; Kojima, M.; Ueda, Y.; Amano, H.; Tsuji, M. Water splitting with the Mn(II)-ferrite–CaO–H2O system at 1273K. Energy 1998, 23, 879–886. [Google Scholar] [CrossRef]
- Scheffe, J.R.; McDaniel, A.H.; Allendorf, M.D.; Weimer, A.W. Kinetics and mechanism of solar-thermochemical H2 production by oxidation of a cobalt ferrite–zirconia composite. Energy Environ. Sci. 2013, 6, 963. [Google Scholar] [CrossRef]
- Kaneko, H.; Gokon, N.; Hasegawa, N.; Tamaura, Y. Solar thermochemical process for hydrogen production using ferrites. Energy 2005, 30, 2171–2178. [Google Scholar] [CrossRef]
- Lougou, B.G.; Geng, B.; Jiang, B.; Zhang, H.; Sun, Q.; Shuai, Y.; Qu, Z.; Zhao, J.; Wang, C.H. Copper ferrite and cobalt oxide two-layer coated macroporous SiC substrate for efficient CO2-splitting and thermochemical energy conversion. J. Colloid. Interface Sci. 2022, 627, 516–531. [Google Scholar] [CrossRef]
- Chueh, W.C.; Falter, C.; Abbott, M.; Scipio, D.; Furler, P.; Haile, S.M.; Steinfeld, A. High-Flux Solar-Driven Thermochemical Dissociation of CO2 and H2O Using Nonstoichiometric Ceria. Science 2010, 330, 1797–1801. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, F.A.; Barreiros, M.A.; Haeussler, A.; Caetano, A.P.; Mouquinho, A.I.; e Silva, P.M.; Novais, R.M.; Pullar, R.C.; Abanades, S. High performance cork-templated ceria for solar thermochemical hydrogen production via two-step water-splitting cycles. Sustain. Energy Fuels 2020, 4, 3077–3089. [Google Scholar] [CrossRef]
- Takalkar, G.; Bhosale, R.R.; Rashid, S.; AlMomani, F.; Shakoor, R.A.; Al Ashraf, A. Application of Li-, Mg-, Ba-, Sr-, Ca-, and Sn-doped ceria for solar-driven thermochemical conversion of carbon dioxide. J. Mater. Sci. 2020, 55, 11797–11807. [Google Scholar] [CrossRef]
- Scheffe, J.R.; Steinfeld, A. Thermodynamic analysis of cerium-based oxides for solar thermochemical fuel production. Energy Fuels 2012, 26, 1928–1936. [Google Scholar] [CrossRef]
- Chen, J.; Ma, J.; Alford, M.B.; Sun, Y.; Tong, J.; Peng, F. Porous Zr-Doped Ceria Microspheres for Thermochemical Splitting of Carbon Dioxide. ACS Appl. Energy Mater. 2021, 4, 10451–10458. [Google Scholar] [CrossRef]
- Hill, C.M.; Hernaiz, E.A.; Furler, P.; Ackermann, S.; Scheffe, J.R. Characterization of Zr-Doped Ceria and Sr-Doped La−Mn Perovskites as Redox Intermediates for Solar Chemical-Looping Reforming of Methane. Energy Technol. 2022, 10. [Google Scholar] [CrossRef]
- Luciani, G.; Landi, G.; Di Benedetto, A. Syngas Production Through H2O/CO2 Thermochemical Splitting Over Doped Ceria-Zirconia Materials. Front. Energy Res. 2020, 8, 204. [Google Scholar] [CrossRef]
- Lee, C.I.; Meng, Q.L.; Kaneko, H.; Tamaura, Y. Solar hydrogen productivity of ceria-scandia solid solution using two-step water-splitting cycle. J. Sol. Energy Eng. Trans. ASME 2013, 135, 011002. [Google Scholar] [CrossRef]
- Mostrou, S.; Büchel, R.; Pratsinis, S.E.; van Bokhoven, J.A. Improving the ceria-mediated water and carbon dioxide splitting through the addition of chromium. Appl. Catal. A Gen. 2017, 537, 40–49. [Google Scholar] [CrossRef]
- Takalkar, G.; Bhosale, R.R. Solar thermocatalytic conversion of CO2 using PrxSr(1−x)MnO3−Δ perovskites. Fuel 2019, 254, 115624. [Google Scholar] [CrossRef]
- Carrillo, R.J.; Scheffe, J.R. Beyond Ceria: Theoretical Investigation of Isothermal and Near-Isothermal Redox Cycling of Perovskites for Solar Thermochemical Fuel Production. Energy Fuels 2019, 33, 12871–12884. [Google Scholar] [CrossRef]
- Haeussler, A.; Abanades, S.; Jouannaux, J.; Julbe, A. Non-Stoichiometric Redox Active Perovskite Materials for Solar Thermochemical Fuel Production: A Review. Catalysts 2018, 8, 611. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhang, H.; Cao, Y.; Hong, H.; Jin, H. Solar hydrogen production via perovskite-based chemical-looping steam methane reforming. Energy Convers. Manag. 2019, 187, 523–536. [Google Scholar] [CrossRef]
- Antipinskaya, E.A.; Politov, B.V.; Petrova, S.A.; Zhukov, V.P.; Chulkov, E.V.; Suntsov, A.Y.; Kozhevnikov, V.L. Reassessment of thermochemical energy storage in perovskite-like manganites at comparative studies of RP SrCa3Mn3O10-δ vs. orthorhombic Sr0.25Ca0.75MnO3-δ. J. Energy Storage 2022, 53, 105175. [Google Scholar] [CrossRef]
- Li, S.; Wheeler, V.M.; Kumar, A.; Venkataraman, M.B.; Muhich, C.L.; Hao, Y.; Lipiński, W. Thermodynamic Guiding Principles for Designing Nonstoichiometric Redox Materials for Solar Thermochemical Fuel Production: Ceria, Perovskites, and Beyond. Energy Technol. 2022, 10, 2000925. [Google Scholar] [CrossRef]
- Bulfin, B.; Vieten, J.; Starr, D.E.; Azarpira, A.; Zachäus, C.; Hävecker, M.; Skorupska, K.; Schmücker, M.; Roeb, M.; Sattler, C. Redox chemistry of CaMnO3 and Ca0.8Sr0.2MnO3 oxygen storage perovskites. J. Mater. Chem. A Mater. 2017, 5, 7912–7919. [Google Scholar] [CrossRef]
- Bayon, A.; de la Calle, A.; Ghose, K.K.; Page, A.; McNaughton, R. Experimental, computational and thermodynamic studies in perovskites metal oxides for thermochemical fuel production: A review. Int. J. Hydrogen Energy 2020, 45, 12653–12679. [Google Scholar] [CrossRef]
- Lorentzou, S.; Agrafiotis, C.C.; Konstandopoulos, A.G. Aerosol spray pyrolysis synthesis of water-splitting ferrites for solar hydrogen production. Granul. Matter 2008, 10, 113–122. [Google Scholar] [CrossRef]
- Bhosale, R.R.; Kumar, A.; Almomani, F.; Alxneit, I. Propylene oxide assisted sol-gel synthesis of zinc ferrite nanoparticles for solar fuel production. Ceram. Int. 2016, 42, 2431–2438. [Google Scholar] [CrossRef]
- Fresno, F.; Fernández-Saavedra, R.; Gómez-Mancebo, M.B.; Vidal, A.; Sánchez, M.; Rucandio, M.I.; Quejido, A.J.; Romero, M. Solar hydrogen production by two-step thermochemical cycles: Evaluation of the activity of commercial ferrites. Int. J. Hydrogen Energy 2009, 34, 2918–2924. [Google Scholar] [CrossRef]
- Bhosale, R.R. Thermodynamic analysis of Ni-ferrite based solar thermochemical H2O splitting cycle for H2 production. Int. J. Hydrogen Energy 2019, 44, 61–71. [Google Scholar] [CrossRef]
- Teknetzi, I.; Nessi, P.; Zaspalis, V.; Nalbandian, L. Ni-ferrite with structural stability for solar thermochemical H2O/CO2 splitting. Int. J. Hydrogen Energy 2017, 42, 26231–26242. [Google Scholar] [CrossRef]
- Goikoetxea, N.B.; Gómez-Mancebo, M.B.; Fernández-Saavedra, R.; Borlaf, F.; García-Pérez, F.; Jiménez, J.A.; Llorente, I.; Rucandio, I.; Quejido, A.J. Understanding water-splitting thermochemical cycles based on nickel and cobalt ferrites for hydrogen production. Int. J. Hydrogen Energy 2019, 44, 17578–17585. [Google Scholar] [CrossRef]
- Takalkar, G.; Bhosale, R.R.; AlMomani, F. Sol-gel synthesized NixFe3−xO4 for thermochemical conversion of CO2. Appl. Surf. Sci. 2019, 489, 693–700. [Google Scholar] [CrossRef]
- Takalkar, G.; Bhosale, R.R.; AlMomani, F.; Khraisheh, M. Thermocatalytic splitting of CO2 using sol-gel synthesized Co-ferrite redox materials. Fuel 2019, 257, 115965. [Google Scholar] [CrossRef]
- Randhir, K.; Rhodes, N.R.; Li, L.; AuYeung, N.; Hahn, D.W.; Mei, R.; Klausner, J.F. Magnesioferrites for solar thermochemical fuel production. Solar Energy 2018, 163, 1–15. [Google Scholar] [CrossRef]
- Takalkar, G.; Bhosale, R.R. Thermochemical CO2 splitting using a sol-gel–synthesized Mg-ferrite–based redox system. Int. J. Energy Res. 2019, 43, 6983–6993. [Google Scholar] [CrossRef]
- Furler, P.; Scheffe, J.; Gorbar, M.; Moes, L.; Vogt, U.; Steinfeld, A. Solar Thermochemical CO 2 Splitting Utilizing a Reticulated Porous Ceria Redox System. Energy Fuels 2012, 26, 7051–7059. [Google Scholar] [CrossRef]
- Bader, R.; Venstrom, L.J.; Davidson, J.H.; Lipiński, W. Thermodynamic analysis of isothermal redox cycling of ceria for solar fuel production. Energy Fuels 2013, 27, 5533–5544. [Google Scholar] [CrossRef]
- Ehrhart, B.D.; Muhich, C.L.; Al-Shankiti, I.; Weimer, A.W. System efficiency for two-step metal oxide solar thermochemical hydrogen production—Part 1: Thermodynamic model and impact of oxidation kinetics. Int. J. Hydrogen Energy 2016, 41, 19881–19893. [Google Scholar] [CrossRef]
- Checchetto, R.; De Angelis, M.G.; Minelli, M. Exploring the membrane-based separation of CO2/CO mixtures for CO2 capture and utilisation processes: Challenges and opportunities. Sep. Purif. Technol. 2024, 346, 127401. [Google Scholar] [CrossRef]
- Dyer, P.N.; Richards, R.E.; Russek, S.L.; Taylor, D.M. Ion transport membrane technology for oxygen separation and syngas production. Solid. State Ion. 2000, 134, 21–33. [Google Scholar] [CrossRef]
- Anderson, L.L.; Armstrong, P.A.; Broekhuis, R.R.; Carolan, M.F.; Chen, J.; Hutcheon, M.D.; Lewinsohn, C.A.; Miller, C.F.; Repasky, J.M.; Taylor, D.M.; et al. Advances in ion transport membrane technology for oxygen and syngas production. Solid. State Ion. 2016, 288, 331–337. [Google Scholar] [CrossRef]
- Scheffe, J.R.; Jacot, R.; Patzke, G.R.; Steinfeld, A. Synthesis, characterization, and thermochemical redox performance of Hf4+, Zr4+, and Sc3+ doped ceria for splitting CO2. J. Phys. Chem. C 2013, 117, 24104–24110. [Google Scholar] [CrossRef]
- Loutzenhiser, P.G.; Elena Gálvez, M.; Hischier, I.; Graf, A.; Steinfeld, A. CO2 splitting in an aerosol flow reactor via the two-step Zn/ZnO solar thermochemical cycle. Chem. Eng. Sci. 2010, 65, 1855–1864. [Google Scholar] [CrossRef]
- Scheffe, J.R.; Steinfeld, A. Oxygen exchange materials for solar thermochemical splitting of H2O and CO2: A review. Mater. Today 2014, 17, 341–348. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, L.; Agrafiotis, C.; Vieten, J.; Roeb, M.; Sattler, C. Solar fuels production: Two-step thermochemical cycles with cerium-based oxides. Prog. Energy Combust. Sci. 2019, 75, 100785. [Google Scholar] [CrossRef]
- Agrafiotis, C.; Tescari, S.; Roeb, M.; Schmücker, M.; Sattler, C. Exploitation of thermochemical cycles based on solid oxide redox systems for thermochemical storage of solar heat. Part 3: Cobalt oxide monolithic porous structures as integrated thermochemical reactors/heat exchangers. Solar Energy 2015, 114, 459–475. [Google Scholar] [CrossRef]
- Abanades, S. Redox Cycles, Active Materials, and Reactors Applied to Water and Carbon Dioxide Splitting for Solar Thermochemical Fuel Production: A Review. Energies 2022, 15, 7061. [Google Scholar] [CrossRef]

| Assumption No. | Assumption Details |
|---|---|
| Assumption 1 | All process operations operated at a steady state |
| Assumption 2 | All process calculations were conducted as per ideal gas behavior |
| Assumption 3 | Reduction cells, as well as oxidation cells, operated isothermally |
| Assumption 4 | MgFe2O4 and the gases involved in the process were in chemical equilibrium |
| Assumption 5 | The working efficiency of the ideal CO2/CO fuel was equal to 100% |
| Assumption 6 | All reactions achieved 100% conversion |
| Assumption 7 | Kinetic and potential energies as well as viscous losses were negligible |
| Assumption 8 | No side reactions |
| Assumption 9 | 20% of the thermal energy supplied to the reduction chamber was dissipated via conduction/convection losses |
| (mol/s) | (kW) | (kW) |
|---|---|---|
| 10 | 66.9 | 30.7 |
| 20 | 111.0 | 52.8 |
| 30 | 132.2 | 63.4 |
| 40 | 172.1 | 83.4 |
| 50 | 204.8 | 99.7 |
| 60 | 227.0 | 110.8 |
| 70 | 243.0 | 118.9 |
| 80 | 261.1 | 127.9 |
| 90 | 275.0 | 134.9 |
| 100 | 295.2 | 145.0 |
| (mol/s) | (%) | (kW) |
|---|---|---|
| 10 | 91.8 | 17.8 |
| 20 | 92.9 | 16.2 |
| 30 | 93.6 | 14.9 |
| 40 | 94.1 | 14.8 |
| 50 | 94.3 | 15.2 |
| 60 | 94.5 | 15.0 |
| 70 | 94.8 | 14.6 |
| 80 | 94.9 | 14.6 |
| 90 | 95.1 | 14.4 |
| 100 | 95.2 | 14.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhosale, R.R. Conversion of Carbon Dioxide into Solar Fuels Using MgFe2O4 Thermochemical Redox Chemistry. C 2025, 11, 25. https://doi.org/10.3390/c11020025
Bhosale RR. Conversion of Carbon Dioxide into Solar Fuels Using MgFe2O4 Thermochemical Redox Chemistry. C. 2025; 11(2):25. https://doi.org/10.3390/c11020025
Chicago/Turabian StyleBhosale, Rahul R. 2025. "Conversion of Carbon Dioxide into Solar Fuels Using MgFe2O4 Thermochemical Redox Chemistry" C 11, no. 2: 25. https://doi.org/10.3390/c11020025
APA StyleBhosale, R. R. (2025). Conversion of Carbon Dioxide into Solar Fuels Using MgFe2O4 Thermochemical Redox Chemistry. C, 11(2), 25. https://doi.org/10.3390/c11020025







