Gate-Tunable Asymmetric Quantum Dots in Graphene-Based Heterostructures: Pure Valley Polarization and Confinement
Abstract
1. Introduction
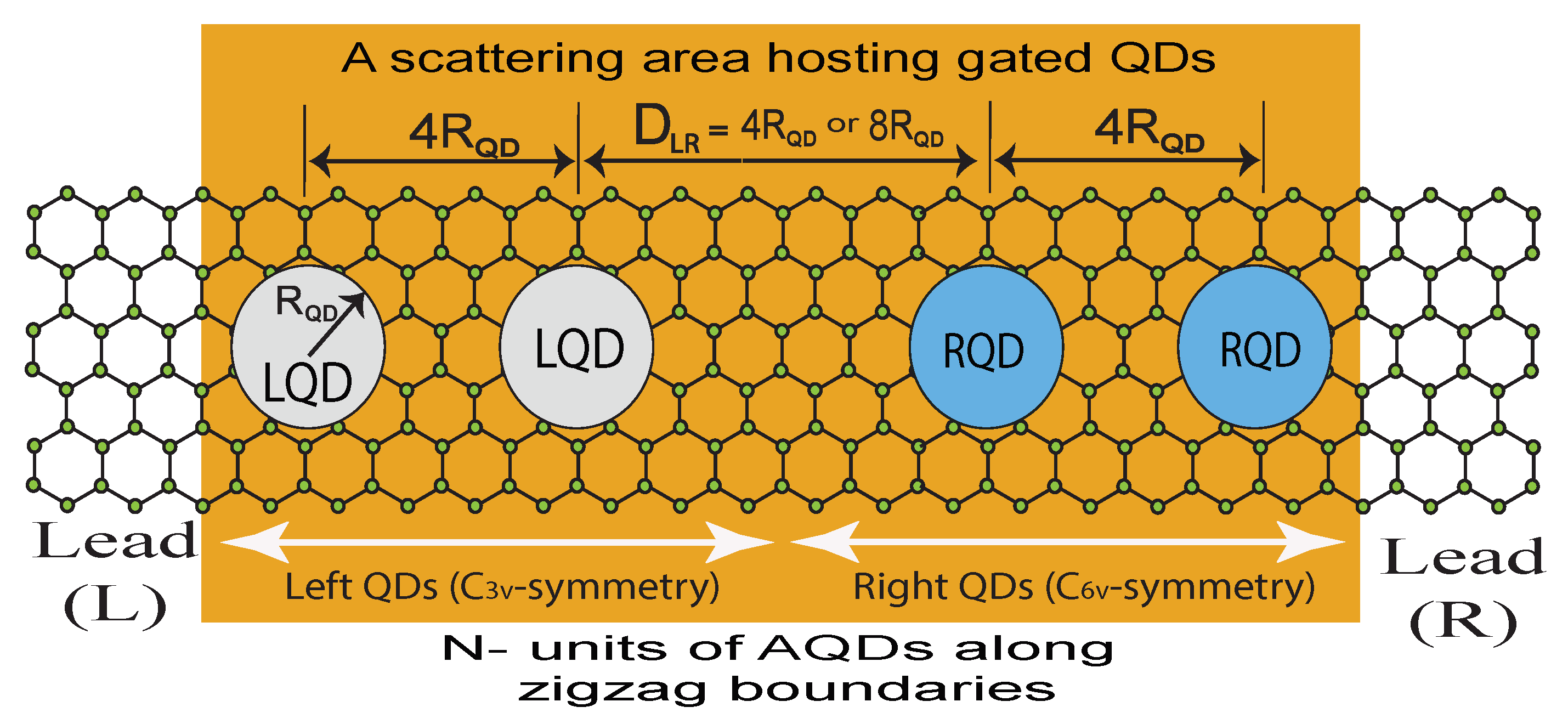
2. Basics of the Model
3. Results and Discussion
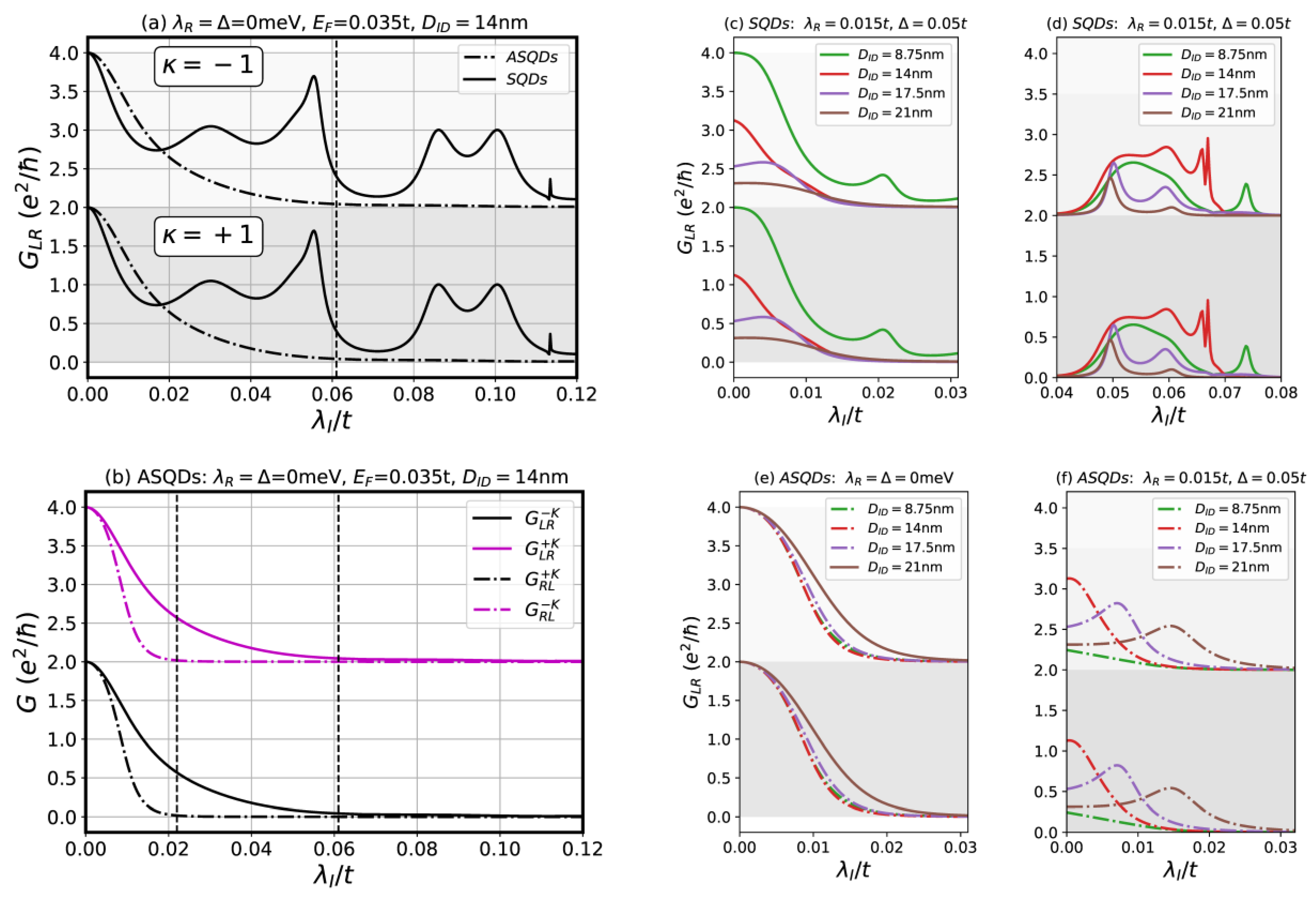
3.1. Valley Dependence in Gated Symmetric or Asymmetric QDs
- At , with the current injected from left to right, valley +K is conducting while valley −K is not. Instead, if the current is injected front the right, the conductance through valley +K vanishes and that from valley −K is finite;
- At , we state that the valley polarization is ensured only in one direction. We highlight the presence of a finite conductance of one valley only (, , in units of . A change in the direction of the current for the same energy does exchange the valleys, as in (1) () but leads to a finite, unpolarized conductance at both valleys (, in units of ).
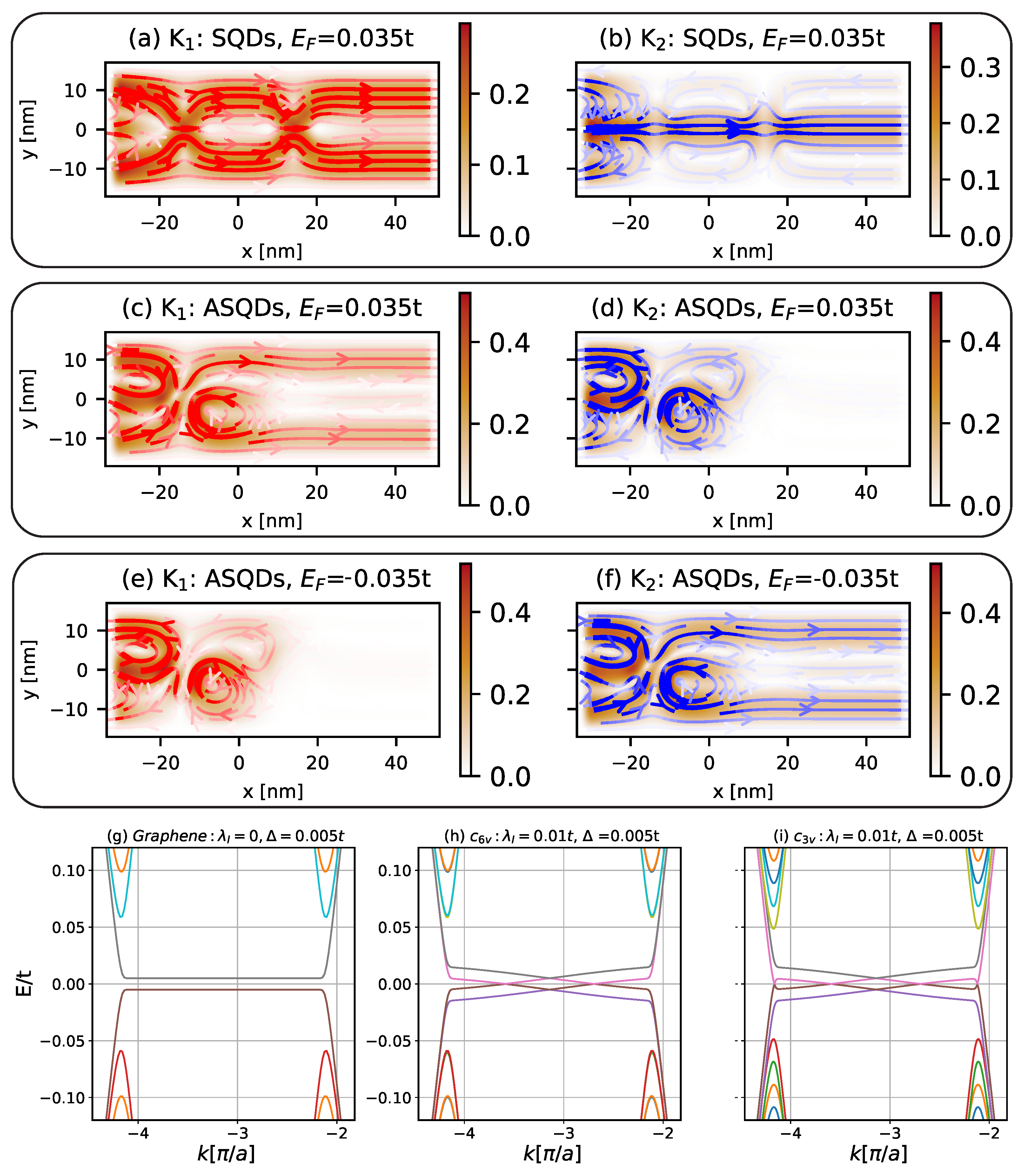
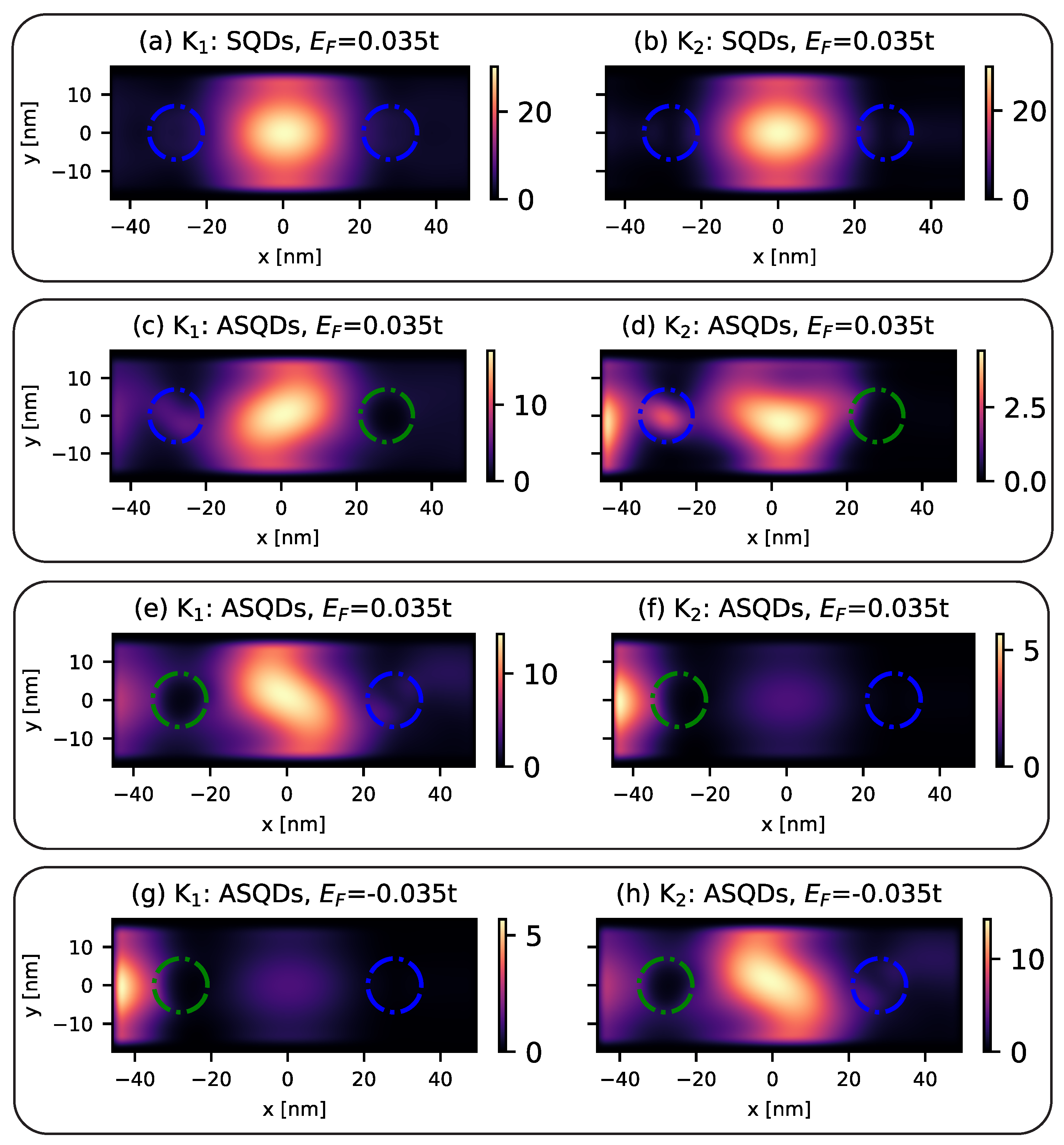
3.2. Valley-Hall Signals and Valley Quasi-Bound States in AQDs
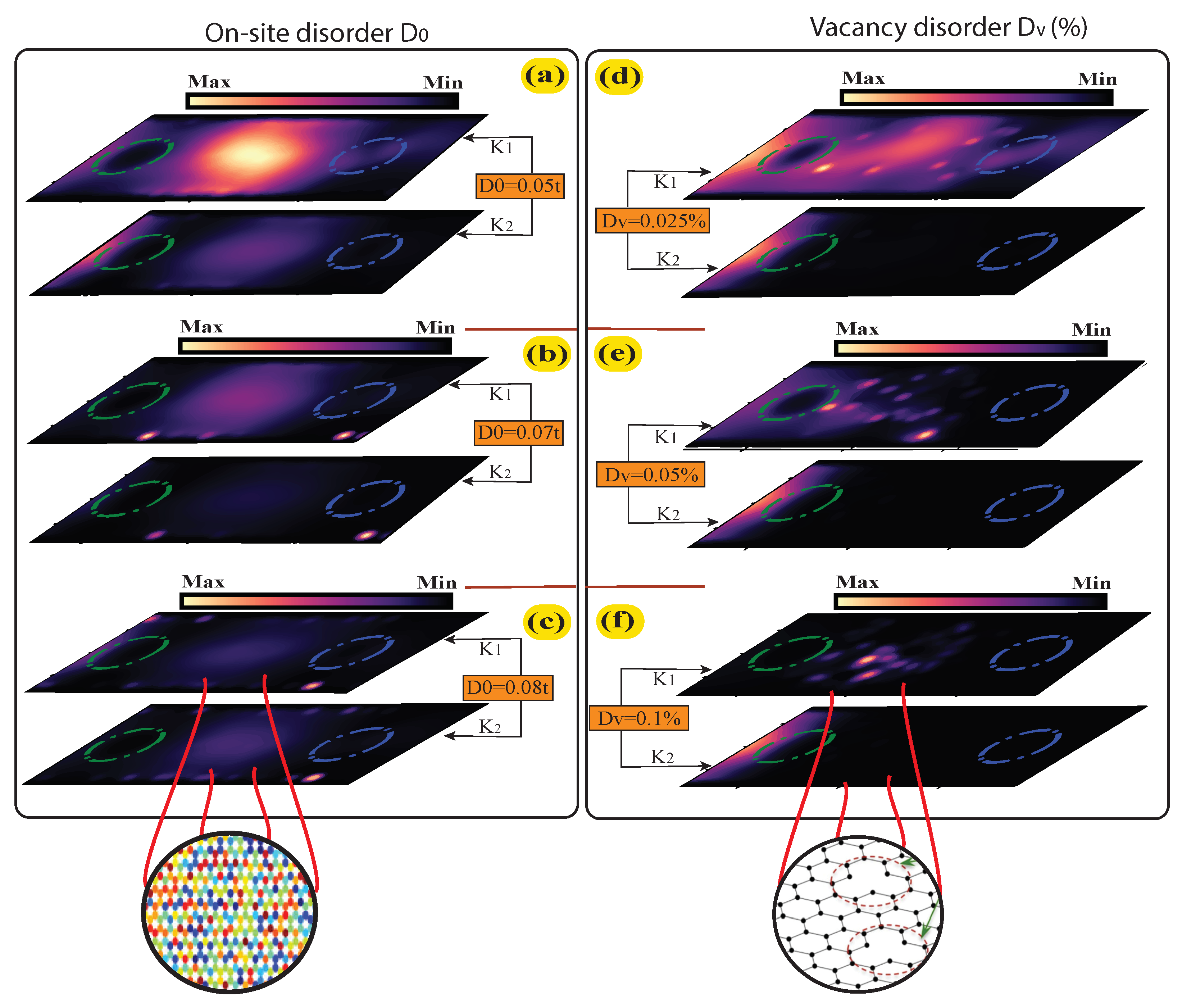
3.3. Disorder and Robustness of the Valley Confined States
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Valley-Dependent Conductance
Appendix B. Valley-Resolved Local Density of States and Current
Appendix C. Disorder in a Tight-Binding Approach
References
- Dean, C.R.; Young, A.F.; Meric, I.; Lee, C.; Wang, L.; Sorgenfrei, S.; Watanabe, K.; Taniguchi, T.; Kim, P.; Shepard, K.L.; et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 2010, 5, 722. [Google Scholar] [CrossRef] [PubMed]
- Fu, W.; Nef, C.; Tarasov, A.; Wipf, M.; Stoop, R.; Knopfmacher, O.; Weiss, M.; Calame, M.; Schönenberger, C. High mobility graphene ion-sensitive field-effect transistors by noncovalent functionalization. Nanoscale 2013, 5, 12104. [Google Scholar] [CrossRef] [PubMed]
- Banszerus, L.; Schmitz, M.; Engels, S.; Dauber, J.; Oellers, M.; Haupt, F.; Watanabe, K.; Taniguchi, T.; Beschoten, B.; Stampfer, C. Ultrahigh-mobility graphene devices from chemical vapor deposition on reusable copper. Sci. Adv. 2015, 1, e1500222. [Google Scholar] [CrossRef] [PubMed]
- Tse, W.K.; Hwang, E.H.; Sarma, S.D. Ballistic hot electron transport in graphene. Appl. Phys. Lett. 2008, 93, 023128. [Google Scholar] [CrossRef]
- Masubuchi, S.; Iguchi, K.; Yamaguchi, T.; Onuki, M.; Arai, M.; Watanabe, K.; Taniguchi, T.; Machida, T. Boundary Scattering in Ballistic Graphene. Phys. Rev. Lett. 2012, 109, 036601. [Google Scholar] [CrossRef]
- Singh, A.K.; Auton, G.; Hill, E.; Song, A. Estimation of intrinsic and extrinsic capacitances of graphene self-switching diode using conformal mapping technique. 2D Mater. 2018, 5, 035023. [Google Scholar]
- Mahmud, M.T.; Sandler, N. Emergence of strain-induced moiré patterns and pseudomagnetic field confined states in graphene. Phys. Rev. B 2020, 102, 235410. [Google Scholar] [CrossRef]
- Mahmud, M.T.; Zhai, D.; Sandler, N. Strain Modulated Superlattices in Graphene. Nano Lett. 2023, 23, 7725. [Google Scholar] [CrossRef] [PubMed]
- Hadadi, N.; Belayadi, A.; AlRabiah, A.; Ly, O.; Akosa, C.A.; Vogl, M.; Bahlouli, H.; Manchon, A.; Abbout, A. Pseudo electric field and pumping valley current in graphene nanobubbles. Phys. Rev. B 2023, 108, 195418. [Google Scholar] [CrossRef]
- Tobias, F.; Petra, H.; Martin, G.; Denis, K.; Jaroslav, F. Protected Pseudohelical Edge States in Z2-Trivial Proximitized Graphene. Phys. Rev. Lett. 2018, 120, 156402. [Google Scholar]
- Petra, H.; Tobias, F.; Zollner, K.; Denis, K.; Martin, G.; Jaroslav, F. Quantum Anomalous Hall Effects in Graphene from Proximity-Induced Uniform and Staggered Spin-Orbit and Exchange Coupling. Phys. Rev. Lett. 2020, 124, 136403. [Google Scholar]
- Belayadi, A.; Vasilopoulos, P. A spin modulating device, tuned by the Fermi energy, in honeycomb-like substrates periodically stubbed with transition-metal-dichalkogenides. Nanotechnology 2023, 34, 085704. [Google Scholar]
- Belayadi, A.; Vasilopoulos, P. Spin-dependent polarization and quantum Hall conductivity in decorated graphene: Influence of locally induced spin–orbit-couplings and impurities. Nanotechnology 2023, 34, 365706. [Google Scholar] [CrossRef]
- Ghiasi, T.S.; Ingla-Aynés, J.; Kaverzin, A.A.; van Wees, B.J. Large Proximity-Induced Spin Lifetime Anisotropy in Transition-Metal Dichalcogenide/Graphene Heterostructures. Nano Lett. 2017, 17, 7528–7532. [Google Scholar] [CrossRef]
- Cummings, A.W.; Garcia, J.H.; Fabian, J.; Roche, S. Giant Spin Lifetime Anisotropy in Graphene Induced by Proximity Effects. Phys. Rev. Lett. 2017, 119, 206601. [Google Scholar] [CrossRef]
- Rohling, N.; Burkard, G. Universal quantum computing with spin and valley states. New J. Phys. 2012, 14, 083008. [Google Scholar] [CrossRef]
- Schaibley, J.R.; Yu, H.; Clark, G.; Rivera, P.; Ross, J.S.; Seyler, K.L.; Yao, W.; Xu, X. Valleytronics in 2D materials. Nat. Rev. Mater. 2016, 1, 16055. [Google Scholar] [CrossRef]
- Szechenyi, G.; Chirolli, L.; Palyi, A. Impurity-assisted electric control of spin-valley qubits in monolayer MoS2. 2D Mater. 2018, 5, 035004. [Google Scholar] [CrossRef]
- Krasnok, A.; Alù, A. Valley-Selective Response of Nanostructures Coupled to 2D Transition-Metal Dichalcogenides. Appl. Sci. 2018, 7, 1157. [Google Scholar] [CrossRef]
- Sharma, S.; Elliott, P.; Shallcross, S. Valley control by linearly polarized laser pulses. Optica 2022, 9, 947. [Google Scholar] [CrossRef]
- Godiksen, R.H.; Wang, S.; Raziman, T.V.; Rivas, J.G.; Curto, A.G. Impact of indirect transitions on valley polarization in WS2 and WSe2. Nanoscale 2022, 14, 17761. [Google Scholar] [CrossRef]
- Qi, J.; Li, X.; Niu, Q.; Feng, J. Giant and tunable valley degeneracy splitting in MoTe2. Phys. Rev. B 2015, 92, 121403. [Google Scholar] [CrossRef]
- Cresti, A.; Nikolic, B.K.; Garcıa, J.H.; Roche, S. Charge, spin and valley Hall effects in disordered graphene. Riv. Del Nuovo Cim. 2016, 39, 587. [Google Scholar]
- Zhang, Z.; Ni, X.; Huang, H.; Hu, L.; Liu, F. Valley splitting in the van der Waals heterostructure WSe2/CrI3: The role of atom superposition. Phys. Rev. B 2019, 99, 115441. [Google Scholar] [CrossRef]
- Wu, Y.; Tong, Q.; Liu, G.-B.; Yu, H.; Yao, W. Spin-valley qubit in nanostructures of monolayer semiconductors: Optical control and hyperfine interaction. Phys. Rev. B 2016, 93, 045313. [Google Scholar] [CrossRef]
- Pawlowski, J. Spin-valley system in a gated MoS2-monolayer quantum dot. New J. Phys. 2019, 21, 123029. [Google Scholar] [CrossRef]
- Behn, W.A.; Krebs, Z.J.; Smith, K.J.; Watanabe, K.; Taniguchi, T.; Brar, V.W. Measuring and Tuning the Potential Landscape of Electrostatically Defined Quantum Dots in Graphene. Nano Lett. 2021, 21, 5013. [Google Scholar] [CrossRef]
- Belayadi, A.; Hadadi, N.; Vasilopoulos, P.; Abbout, A. Valley-dependent tunneling through electrostatically created quantum dots in heterostructures of graphene with hexagonal boron nitride. Phys. Rev. B 2023, 108, 085419. [Google Scholar] [CrossRef]
- Park, H.C.; Son, M.; Lee, S.J.; Myoung, N. A strain-engineered graphene qubit in a nanobubble. J. Korean Phys. Soc. 2021, 78, 1208. [Google Scholar] [CrossRef]
- Li, S.Y.; He, L. Recent progresses of quantum confinement in graphene quantum dots. Front. Phys. 2022, 17, 33201. [Google Scholar] [CrossRef]
- Ren, H.-Y.; Ren, Y.-N.; Zheng, Q.; He, J.-Q.; He, L. Electron-electron interaction and correlation-induced two density waves with different Fermi velocities in graphene quantum dots. Phys. Rev. B 2023, 108, L081408. [Google Scholar] [CrossRef]
- Miravet, D.; Altıntaş, A.; Rodrigues, A.W.; Bieniek, M.; Korkusinski, M.; Hawrylak, P. Interacting holes in gated WSe2 quantum dots. Phys. Rev. B 2023, 108, 195407. [Google Scholar] [CrossRef]
- Boddison-Chouinard, J. Gate-controlled quantum dots in monolayer WSe2. Appl. Phys. Lett. 2021, 119, 133104. [Google Scholar] [CrossRef]
- Zollner, K.; Gmitra, M.; Fabian, J. Heterostructures of graphene and hBN: Electronic, spin-orbit, and spin relaxation properties from first principles. Phys. Rev. B 2019, 99, 125151. [Google Scholar] [CrossRef]
- Groth, C.W.; Wimmer, M.; Akhmerov, A.R.; Waintal, X. Kwant: A software package for quantum transport. New J. Phys 2014, 16, 063065. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Heinisch, R.L.; Bronold, F.X.; Fehske, H. Mie scattering analog in graphene: Lensing, particle confinement, and depletion of Klein tunneling.Mie scattering analog in graphene: Lensing, particle confinement, and depletion of Klein tunneling. Phys. Rev. B 2013, 87, 155409. [Google Scholar] [CrossRef]
- Fehske, H.; Hager, G.; Pieper, A. Electron confinement in graphene with gate-defined quantum dots. Phys. Status Solidi B 2015, 252, 1868. [Google Scholar] [CrossRef]
- Das, K.; Ghorai, K.; Culcer, D.; Agarwal, A. Nonlinear Valley Hall Effect. Phys. Rev. Lett. 2024, 132, 096302. [Google Scholar] [CrossRef] [PubMed]
- Lihm, J.-M.; Park, C.-H. Nonlinear Hall Effect from Long-Lived Valley-Polarizing Relaxons. Phys. Rev. Lett. 2024, 132, 106402. [Google Scholar] [CrossRef] [PubMed]
- Nedell, J.G.; Spector, J.; Abbout, A.; Vogl, M.; Fiete, G.A. Deep learning of deformation-dependent conductance in thin films: Nanobubbles in graphene. Phys. Rev. B 2022, 105, 075425. [Google Scholar] [CrossRef]
- Istas, M.; Groth, C.; Akhmerov, A.R.; Wimmer, M.; Waintal, X. A general algorithm for computing bound states in infinite tight-binding systems. SciPost Phys. 2018, 4, 026. [Google Scholar] [CrossRef]
- Ozaki, T.; Nishio, K.; Kino, H. Efficient implementation of the nonequilibrium Green function method for electronic transport calculations. Phys. Rev. B 2010, 81, 035116. [Google Scholar] [CrossRef]
- Belayadi, A.; Bourahla, B. A theoretical model to compute the localized electronic states at the surface of hexagonal structures with different coupling orbitals. Surf. Sci. 2018, 675, 1–14. [Google Scholar] [CrossRef]
- Belayadi, A.; Bourahla, B.; Mekideche-Chafa, F. Localized electronic surface states in metalic structures. Surf. Rev. Lett. 2018, 25, 1850101. [Google Scholar] [CrossRef]
- Blayadi, A. A phase field matching model to compute the localized electronic bands of a 3D monatomic chain of body-centered cube structure: Investigating the (100), (110) and (111) cutting directions. Physica. B. Condens. Matter 2018, 547, 12–32. [Google Scholar] [CrossRef]
- Ferreira, A.; Mucciolo, E. Critical Delocalization of Chiral Zero Energy Modes in Graphene. Phys. Rev. Lett. 2015, 115, 106601. [Google Scholar] [CrossRef]
- Weibe, A.; Wellein, G.; Alvermann, A.; Fehske, H. Alexander Weiße, Gerhard Wellein, Andreas Alvermann, and Holger Fehske. Critical Delocalization of Chiral Zero Energy Modes in Graphene. Rev. Mod. Phys. 2006, 78, 275. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belayadi, A.; Vasilopoulos, P. Gate-Tunable Asymmetric Quantum Dots in Graphene-Based Heterostructures: Pure Valley Polarization and Confinement. C 2024, 10, 44. https://doi.org/10.3390/c10020044
Belayadi A, Vasilopoulos P. Gate-Tunable Asymmetric Quantum Dots in Graphene-Based Heterostructures: Pure Valley Polarization and Confinement. C. 2024; 10(2):44. https://doi.org/10.3390/c10020044
Chicago/Turabian StyleBelayadi, Adel, and Panagiotis Vasilopoulos. 2024. "Gate-Tunable Asymmetric Quantum Dots in Graphene-Based Heterostructures: Pure Valley Polarization and Confinement" C 10, no. 2: 44. https://doi.org/10.3390/c10020044
APA StyleBelayadi, A., & Vasilopoulos, P. (2024). Gate-Tunable Asymmetric Quantum Dots in Graphene-Based Heterostructures: Pure Valley Polarization and Confinement. C, 10(2), 44. https://doi.org/10.3390/c10020044







