Prediction of Geometrical Characteristics of an Inclined Negatively Buoyant Jet Using Group Method of Data Handling (GMDH) Neural Network
Abstract
1. Introduction
2. Methodology
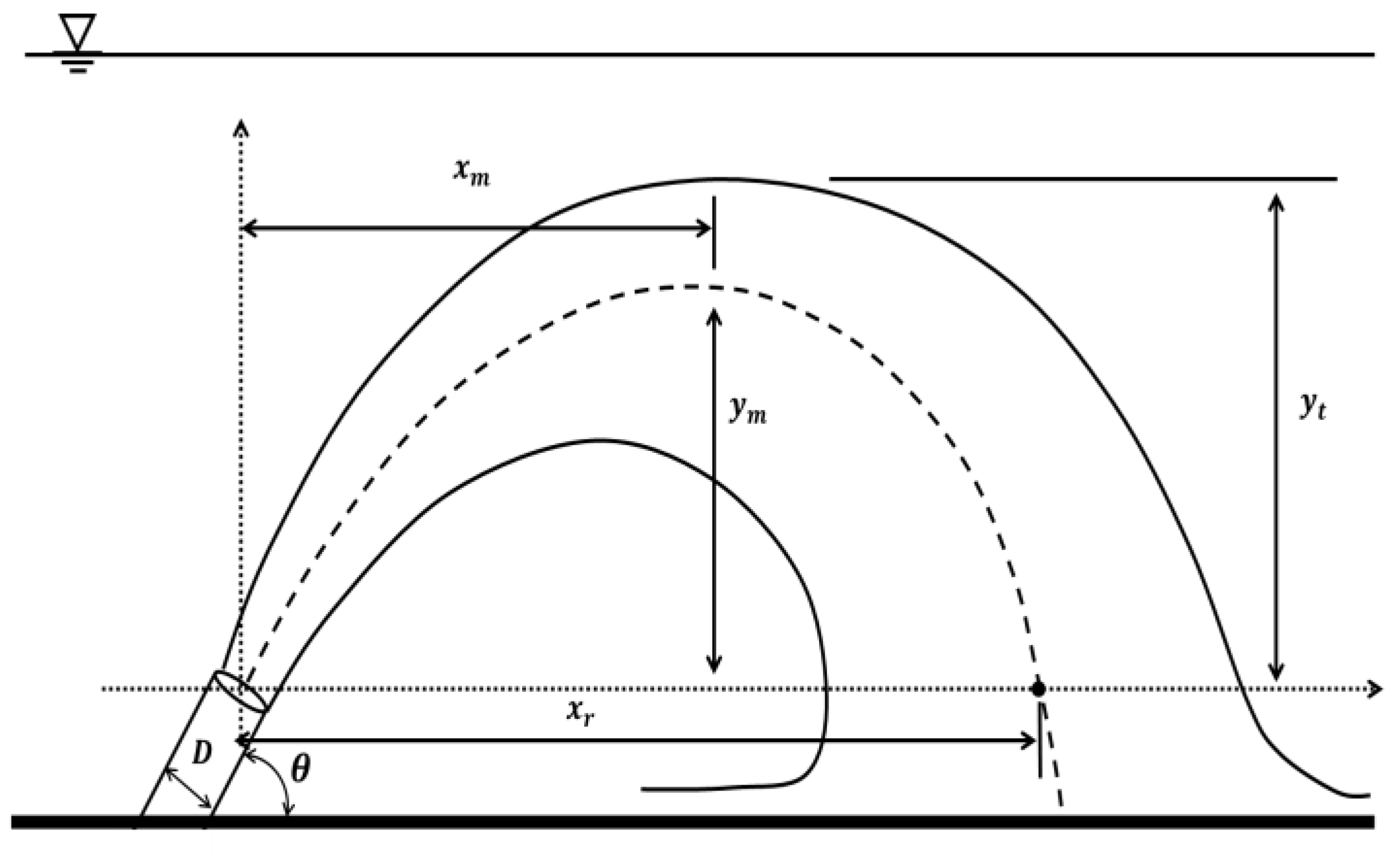
2.1. Analysis of Inclined Negatively Buoyant Jet
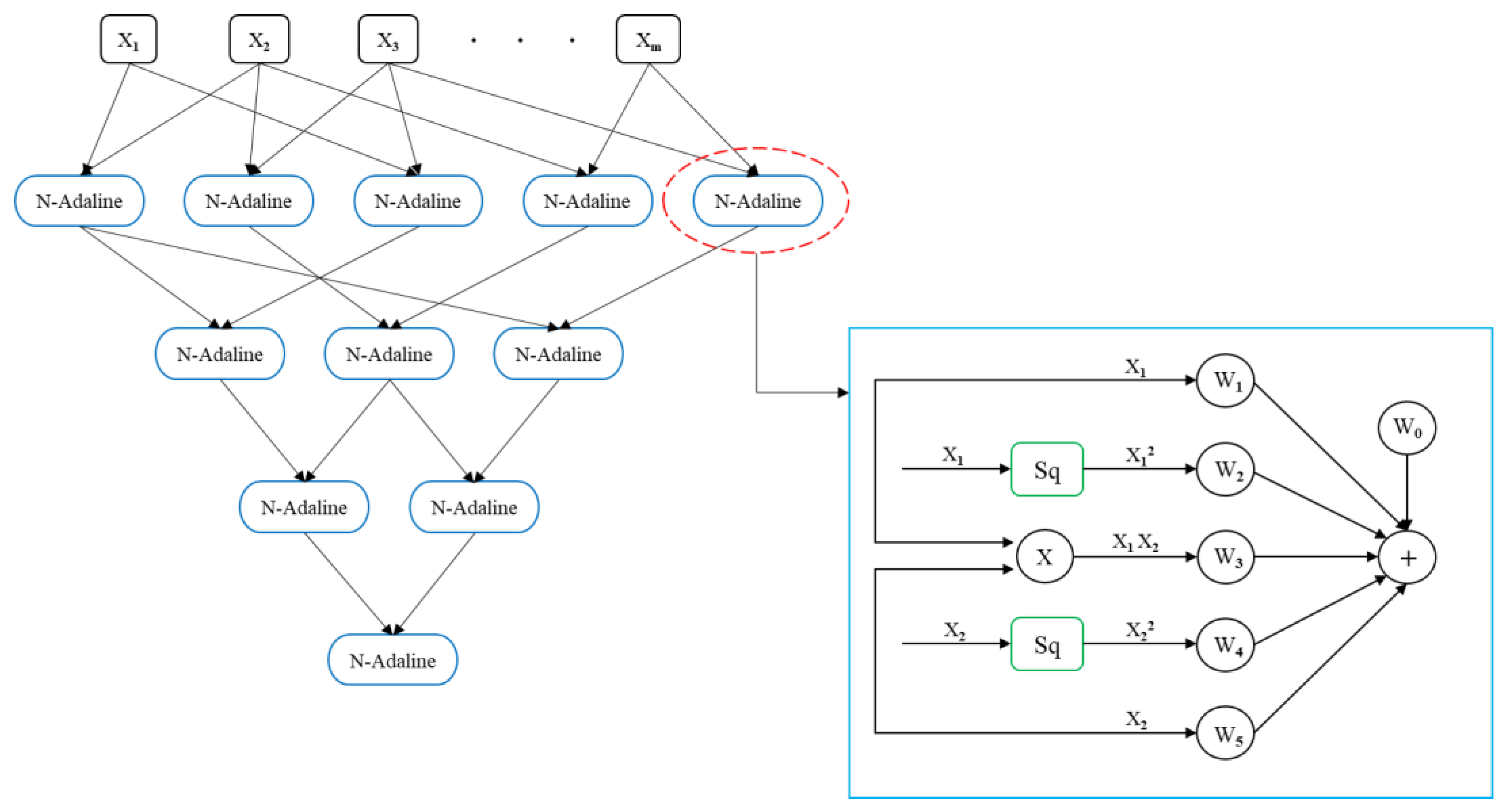
2.2. GMDH Method
GMDH Modeling Setup
3. Results and Discussion
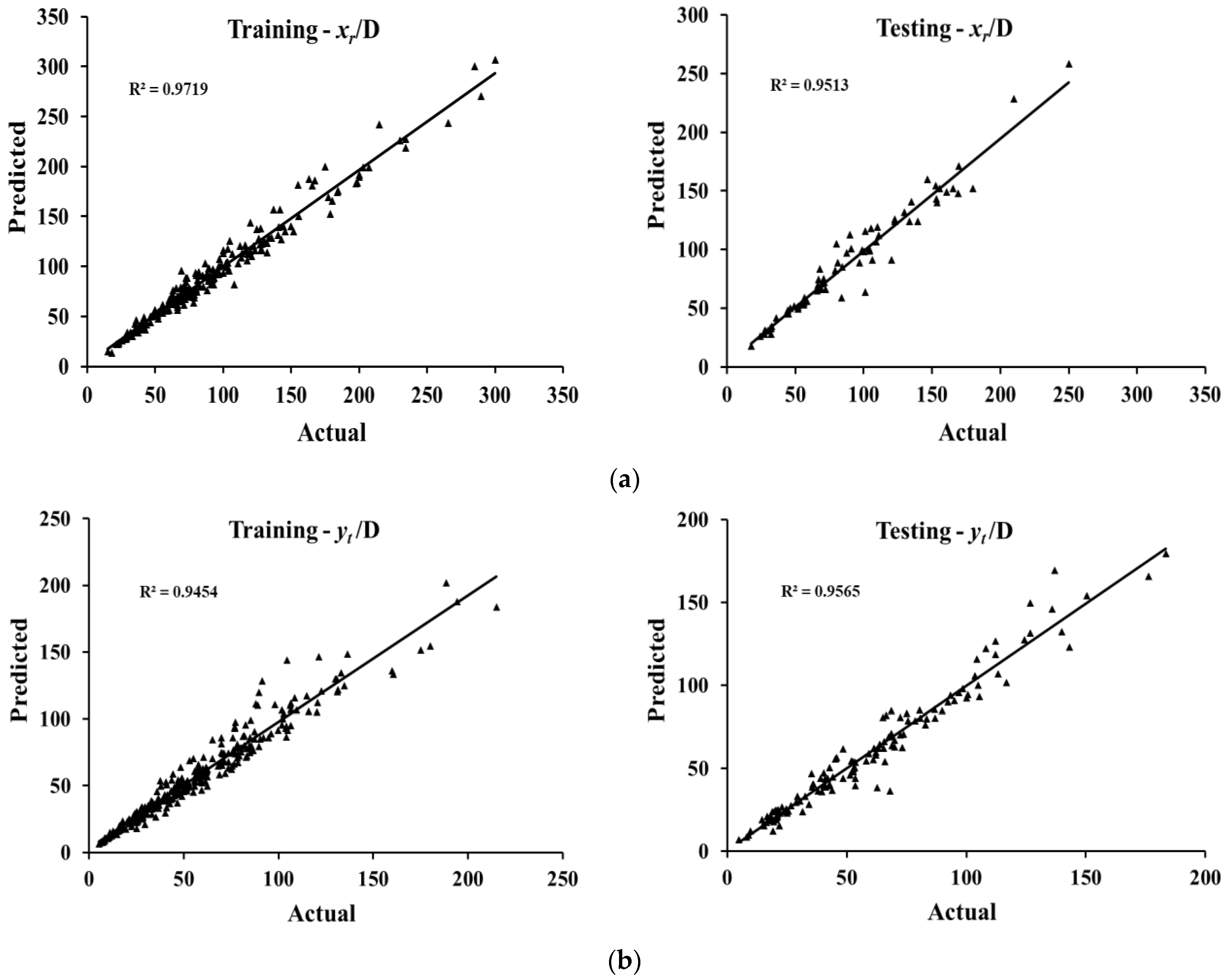
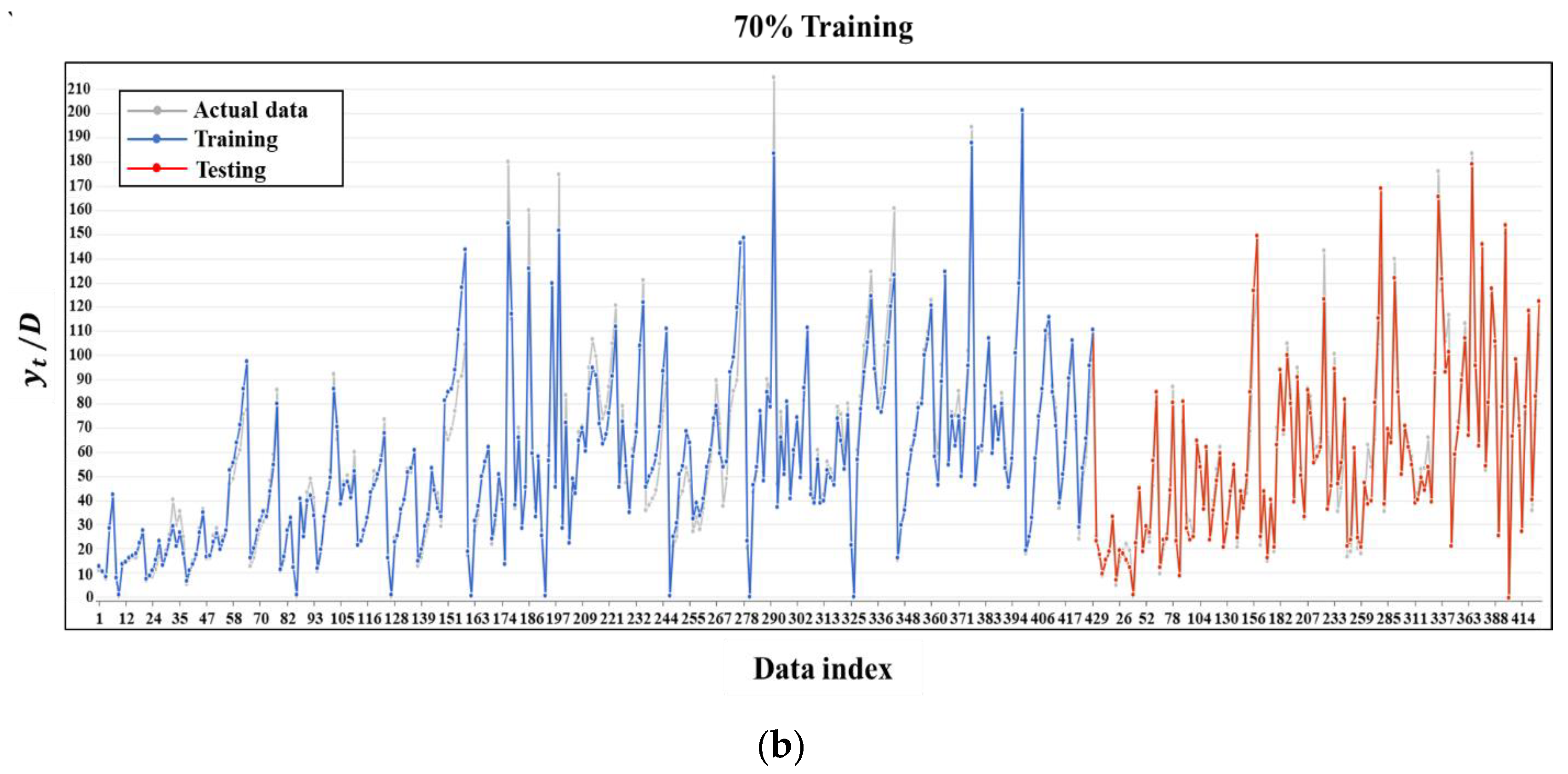
3.1. Statistical Assessment of Model Performance
3.2. Comparing GMDH Results with Previous Models
3.3. Uncertainty Analysis
4. Conclusions
- The GMDH model demonstrated excellent performance in predicting the dimensionless geometrical parameters ( and ) of inclined dense jets. The coefficient of determination () values indicated high accuracy, with values exceeding 0.94 for all parameters.
- Statistical indices such as the root mean squared error (RMSE) and mean absolute error (MAE) confirmed the high accuracy of the GMDH model. The low values of these indices, along with the high values, validate the reliability of the model in predicting geometrical characteristics.
- A comparative analysis with analytical and numerical models from previous studies showed that the GMDH model outperformed the other models in terms of accuracy and precision. The standard error of the estimate (SEE) results indicated that the GMDH model provided the most accurate predictions compared to the other models tested.
- The GMDH model’s predictive capability was demonstrated across a range of angles and geometrical parameters. It showed consistent and accurate predictions even for higher inclination angles, where other models exhibited limitations.
- The uncertainty analysis further validated the accuracy of the GMDH model, particularly in predicting the dimensionless parameter , which showed the lowest mean prediction error, the smallest uncertainty bandwidth, and a narrow confidence band for the 95% prediction error interval.
- Considering the comprehensive evaluation, including the statistical indices, the comparison with previous models, and the uncertainty analysis, the GMDH model emerged as a highly reliable and accurate method for the prediction of the geometrical parameters of inclined dense jets.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Petersen, L.K.; Heck, N.; Reguero, G.B.; Potts, D.; Hovagimian, A.; Paytan, A. Biological and Physical Effects of Brine Discharge from the Carlsbad Desalination Plant and Implications for Future Desalination Plant Constructions. Water 2019, 11, 208. [Google Scholar] [CrossRef]
- Bombar, G.; Dölgen, D.; Alpaslan, M.N. Environmental impacts and impact mitigation plans for desalination facilities. Desalination Water Treat. 2016, 57, 11528–11539. [Google Scholar] [CrossRef]
- Nemlioglu, S.; Roberts, P.J.W. Experiments on dense jets using three-dimensional laser-induced fluorescence (3DLIF). In Proceedings of the 4th International Conference on Marine Waste Water Disposal and Marine Environment, Antalya, Türkiye, 6–10 November 2006. [Google Scholar]
- Cipollina, A.; Brucato, A.; Grisafi, F.; Nicosia, S. Bench-Scale Investigation of Inclined Dense Jets. J. Hydraul. Eng. 2005, 131, 1017–1022. [Google Scholar] [CrossRef]
- Kikkert, G.A. Buoyant Jets with Two and Three-Dimensional Trajectories. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2006. Available online: https://ir.canterbury.ac.nz/items/30cdc6c9-3174-479c-9470-30a248cb11c4 (accessed on 2 September 2018).
- Zeitoun, M.A.; McIlhenny, W.F. Conceptual Designs of Outfall Systems for Desalination Plants. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 18–20 April 1971. OTC-1370-MS. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J.W. Dense Jet Discharges in Shallow Water. J. Hydraul. Eng. 2016, 142, 04015033. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C. Discussion of “Inclined Negatively Buoyant Discharges” by G.A. Kikkert, M.J. Davidson, and R.I. Nokes. J. Hydraul. Eng. 2008, 134, 1782–1784. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J.W. Effect of Nozzle Orientation on Dense Jets in Stagnant Environments. J. Hydraul. Eng. 2015, 141, 06015009. [Google Scholar] [CrossRef]
- Bashitialshaaer, R.; Larson, M.; Persson, K.M. An Experimental Investigation on Inclined Negatively Buoyant Jets. Water 2012, 4, 720–738. [Google Scholar] [CrossRef]
- Lindberg, W.R. Experiments on Negatively Buoyant Jets, with and without Cross-Flow. In Recent Research Advances in the Fluid Mechanics of Turbulent Jets and Plumes; Springer: Dordrecht, The Netherlands, 1994; pp. 131–145. [Google Scholar]
- Roberts Philip, J.W.; Toms, G. Inclined Dense Jets in Flowing Current. J. Hydraul. Eng. 1987, 113, 323–340. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C.; Papanicolaou, P.N. Inclined negatively buoyant jets 1: Geometrical characteristics. J. Hydraul. Res. 2011, 49, 3–12. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C.; Papanicolaou, P.N. Inclined negatively buoyant jets 2: Concentration measurements. J. Hydraul. Res. 2011, 49, 13–22. [Google Scholar] [CrossRef]
- Crowe, A. Inclined Negatively Buoyant Jets and Boundary Interaction. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2013. Available online: http://hdl.handle.net/10092/7895 (accessed on 2 July 2017).
- Bloomfield, L.J.; Kerr, R.C. Inclined turbulent fountains. J. Fluid Mech. 2002, 451, 283–294. [Google Scholar] [CrossRef]
- Shao, D.; Law, A.W.-K. Mixing and boundary interactions of 30° and 45° inclined dense jets. Environ. Fluid Mech. 2010, 10, 521–553. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Tsatsara, E.I. Mixing Characteristics of Inclined Turbulent Dense Jets. Environ. Process. 2019, 6, 525–541. [Google Scholar] [CrossRef]
- Roberts, P.J.W.; Ferrier, A.; Daviero, G. Mixing in Inclined Dense Jets. J. Hydraul. Eng. 1997, 123, 693–699. [Google Scholar] [CrossRef]
- Jiang, B.; Law, A.W.-K.; Lee, J.H.-W. Mixing of 30° and 45° Inclined Dense Jets in Shallow Coastal Waters. J. Hydraul. Eng. 2014, 140, 241–253. [Google Scholar] [CrossRef]
- Chung Kei Chris, L. Mixing of Inclined Dense Jets. Master’s Thesis, The University of Hong Kong, Pokfulam, Hong Kong, 2009. Available online: http://hdl.handle.net/10722/65319 (accessed on 2 September 2017).
- Lai, C.C.K.; Lee, J.H.W. Mixing of inclined dense jets in stationary ambient. J. Hydro Environ. Res. 2012, 6, 9–28. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J.W. Multiport Diffusers for Dense Discharges. J. Hydraul. Eng. 2014, 140, 04014032. [Google Scholar] [CrossRef]
- Oliver, C. Near Field Mixing of Negatively Buoyant Jets. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2012. Available online: http://hdl.handle.net/10092/6300 (accessed on 9 November 2017).
- Papakonstantis, I.G.; Tsatsara, E.I. Trajectory Characteristics of Inclined Turbulent Dense Jets. Environ. Process. 2018, 5, 539–554. [Google Scholar] [CrossRef]
- Papanicolaou, P.N.; Kokkalis, T.J. Vertical buoyancy preserving and non-preserving fountains, in a homogeneous calm ambient. Int. J. Heat Mass Transf. 2008, 51, 4109–4120. [Google Scholar] [CrossRef]
- Lee, J.H.W.; Chu, V.H. Turbulent Jets and Plumes: A Lagrangian Approach; Springer: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Jirka, G.H. Integral Model for Turbulent Buoyant Jets in Unbounded Stratified Flows. Part I: Single Round Jet. Environ. Fluid Mech. 2004, 4, 1–56. [Google Scholar] [CrossRef]
- Kikkert, G.A.; Davidson, M.J.; Nokes, R.I. Inclined Negatively Buoyant Discharges. J. Hydraul. Eng. 2007, 133, 545–554. [Google Scholar] [CrossRef]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. Predicting the near-field mixing of desalination discharges in a stationary environment. Desalination 2013, 309, 148–155. [Google Scholar] [CrossRef]
- Zaji, A.H.; Bonakdari, H. Robustness lake water level prediction using the search heuristic-based artificial intelligence methods. ISH J. Hydraul. Eng. 2019, 25, 316–324. [Google Scholar] [CrossRef]
- Alitaleshi, F.; Daghbandan, A. Using a multi-objective optimal design of GMDH type neural networks to evaluate the quality of treated water in a water treatment plant. Desalination Water Treat. 2019, 139, 123–132. [Google Scholar] [CrossRef]
- Naeini, S.A.; Moayed, R.Z.; Kordnaeij, A.; Mola-Abasi, H. Elasticity modulus of clayey deposits estimation using group method of data handling type neural network. Measurement 2018, 121, 335–343. [Google Scholar] [CrossRef]
- Parsaie, A.; Haghiabi, A.H. Improving Modelling of Discharge Coefficient of Triangular Labyrinth Lateral Weirs Using SVM, GMDH and MARS Techniques. Irrig. Drain. 2017, 66, 636–654. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Shaghaghi, S.; Khoshbin, F. Developing an expert group method of data handling system for predicting the geometry of a stable channel with a gravel bed. Earth Surf. Process. Landf. 2017, 42, 1460–1471. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Zahiri, A. Neuro-Fuzzy GMDH-Based Evolutionary Algorithms to Predict Flow Discharge in Straight Compound Channels. J. Hydrol. Eng. 2015, 20, 04015035. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Barani, G.-A.; Hessami-Kermani, M.-R. Evaluation of GMDH networks for prediction of local scour depth at bridge abutments in coarse sediments with thinly armored beds. Ocean Eng. 2015, 104, 387–396. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H.; Zaji, A.H.; Azimi, H.; Khoshbin, F. GMDH-type neural network approach for modeling the discharge coefficient of rectangular sharp-crested side weirs. Eng. Sci. Technol. Int. J. 2015, 18, 746–757. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Barani, G.A.; Hessami-Kermani, M.R. Group method of data handling to predict scour depth around vertical piles under regular waves. Sci. Iran. 2013, 20, 406–413. [Google Scholar] [CrossRef]
- Madandoust, R.; Bungey, J.H.; Ghavidel, R. Prediction of the concrete compressive strength by means of core testing using GMDH-type neural network and ANFIS models. Comput. Mater. Sci. 2012, 51, 261–272. [Google Scholar] [CrossRef]
- Alfaifi, H.; Abdolmajid, M.; Bonakdari, H. Experimental Investigation and Model Development of Geometric Characteristics of Negatively Buoyant Jets Inclined at 15° and 52° using GMDH Method. J. Coast. Res. 2020, 36, 636–653. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. Polynomial Theory of Complex Systems. IEEE Trans. Syst. Man Cybern. 1971, 1, 364–378. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H. Performance Evaluation of Adaptive Neural Fuzzy Inference System for Sediment Transport in Sewers. Water Resour. Manag. 2014, 28, 4765–4779. [Google Scholar] [CrossRef]
- GMDH Shell DS; GMDH Inc.: New York, NY, USA, 2019; Available online: https://gmdhsoftware.com/signup-ds/ (accessed on 18 August 2019).
- Roberts, P.J.; Abessi, O. Optimization of Desalination Diffusers Using Three-Dimensional Laser-Induced Fluorescence; Report Prepared for United States Bureau of Reclamation School of Civil and Environmental Engineering Georgia Institute of Technology; Report number: DWPR Report No. 167; Atlanta, GA, USA. 2014, p. 30332. Available online: https://www.researchgate.net/publication/283568475_Optimization_of_desalination_diffusers_using_three-dimensional_laser-induced_fluorescence (accessed on 2 December 2023).
- Jirka, G.H. Improved Discharge Configurations for Brine Effluents from Desalination Plants. J. Hydraul. Eng. 2008, 134, 116–120. [Google Scholar] [CrossRef]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. Removing the boundary influence on negatively buoyant jets. Environ. Fluid Mech. 2013, 13, 625–648. [Google Scholar] [CrossRef]
- Bonakdari, H.; Mohammadian, A. Evolutionary prediction of an inclined dense jet in shallow water. Desalination Water Treat. 2019, 155, 32–47. [Google Scholar] [CrossRef]
- Shaghaghi, S.; Bonakdari, H.; Gholami, A.; Ebtehaj, I.; Zeinolabedini, M. Comparative analysis of GMDH neural network based on genetic algorithm and particle swarm optimization in stable channel design. Appl. Math. Comput. 2017, 313, 271–286. [Google Scholar] [CrossRef]

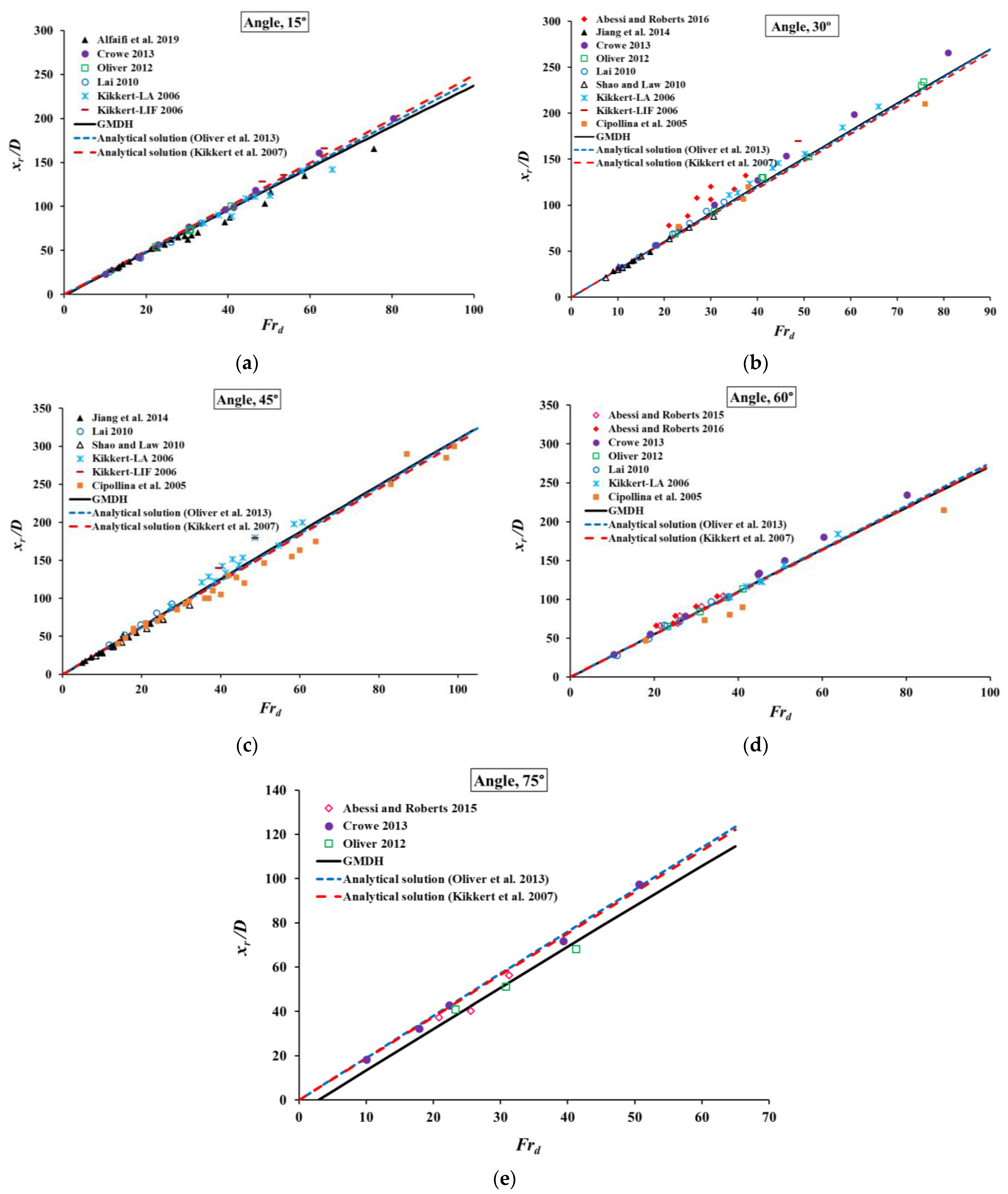
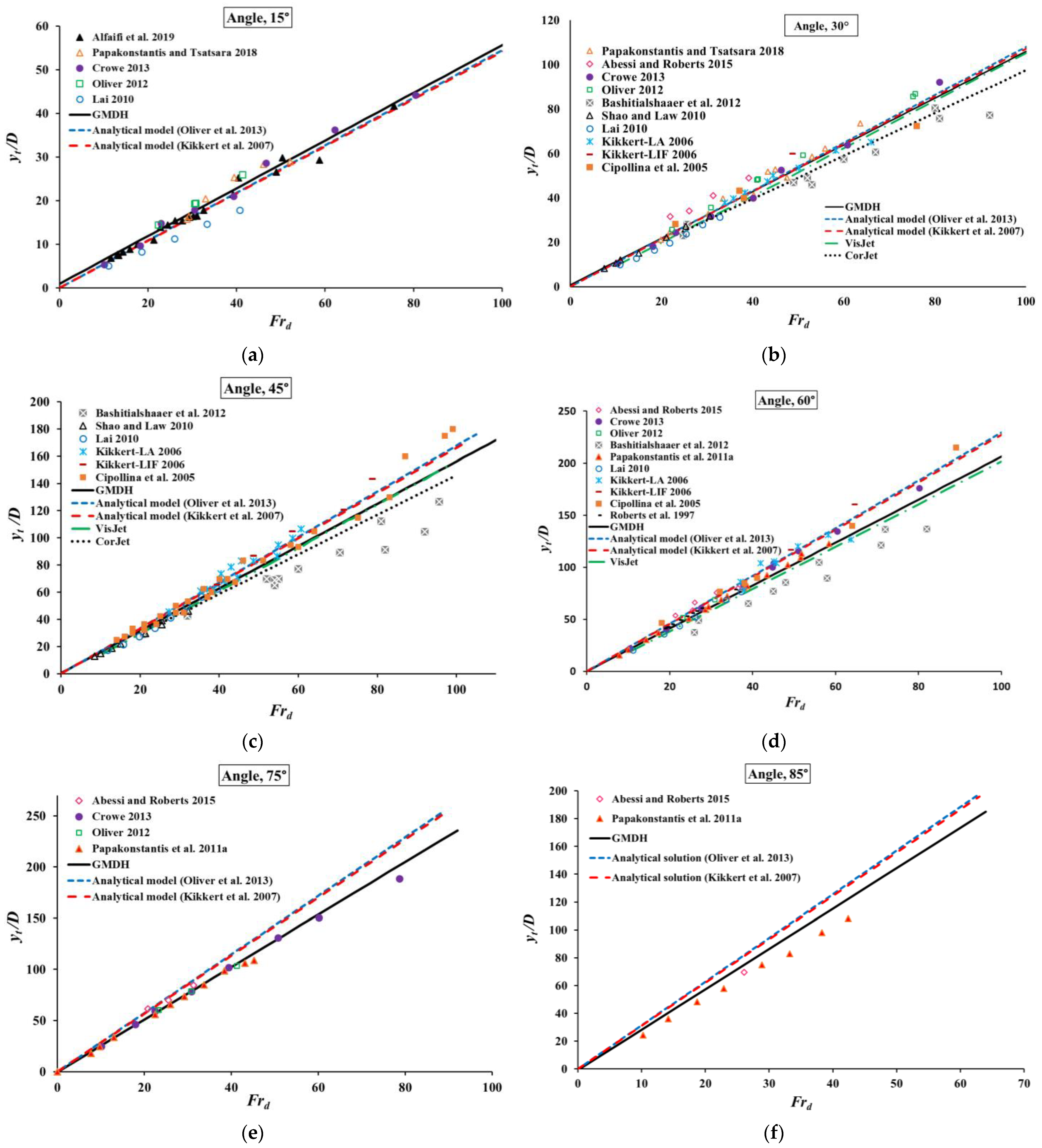
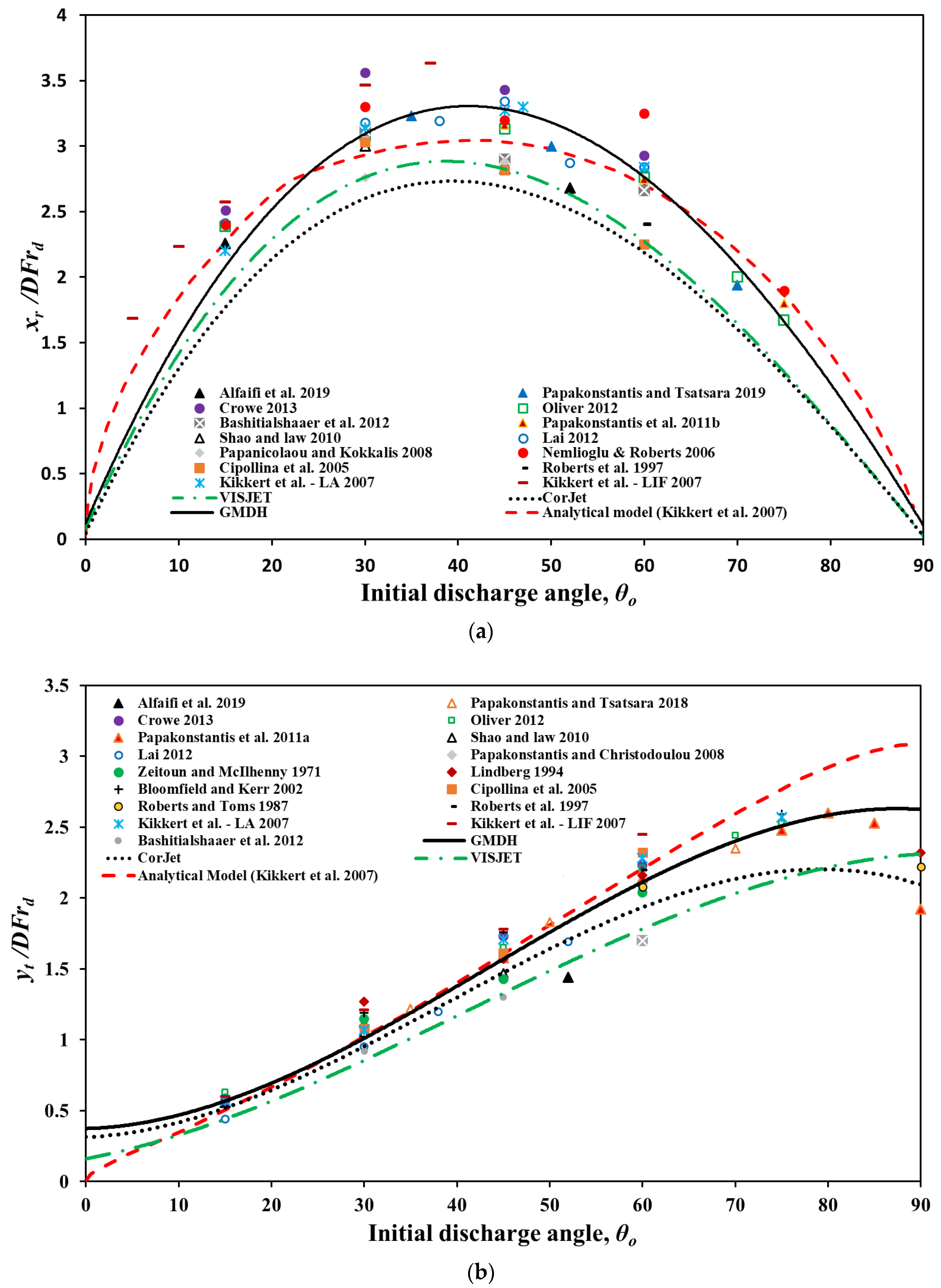
| No. | Investigators | Angles |
|---|---|---|
| 1 | Roberts et al. [19] | 60° |
| 2 | Cipollina et al. [4] | 30°, 45°, and 60° |
| 3 | Kikkert [5] | 15°, 30°, 45°, and 60° |
| 4 | Lai [21] | 15°, 30°, 38°, 45°, 52°, and 60° |
| 5 | Shao and Law [17] | 30° and 45° |
| 6 | Papakonstantis et al. [13] | 45°, 60°, 75°, 80°, and 85° |
| 7 | Oliver [24] | 15°, 30°, 45°, 60°, 70°, and 75° |
| 8 | Bashitialshaaer et al. [10] | 30°, 45°, and 60° |
| 9 | Abessi and Roberts [23] | 60° |
| 10 | Roberts and Abessi [45] | 15° |
| 11 | Jiang et al. [20] | 30° and 45° |
| 12 | Abessi and Roberts [9] | 15°, 20°, 30°, 40°, 45°, 50°, 55°, 60°, 65°, 70°, 75°, 80°, and 85° |
| 13 | Abessi and Roberts [7] | 30°, 45°, and 60° |
| 14 | Crowe [15] | 15°, 30°, 45°, 60°, 65°, 70°, and 75° |
| 15 | Papakonstantis and Tsatsara [25] | 15°, 30°, 35°, 50°, and 70° |
| 16 | Papakonstantis and Tsatsara [18] | 35°, 50°, and 70° |
| 17 | Alfaifi et al. [41] | 15° and 52° |
| Geometrical | GMDH Proposed Equations | |
|---|---|---|
| (13) | ||
| | (14) | |
| (15) | ||
| (16) |
| Geometrical Parameter | R2 | MAE | RMSE | R2 | MAE | RMSE |
|---|---|---|---|---|---|---|
| Training | Testing | |||||
| 0.948 | 5.911 | 8.239 | 0.936 | 6.809 | 9.192 | |
| 0.971 | 6.052 | 8.556 | 0.951 | 6.499 | 10.143 | |
| 0.962 | 4.009 | 5.711 | 0.947 | 4.458 | 6.861 | |
| 0.945 | 5.471 | 8.298 | 0.956 | 5.236 | 7.804 | |
| Geometrical Parameter | Angle | GMDH Model | CORJET | VISJET | Kikkert et al. [29] | Oliver et al. [30] |
|---|---|---|---|---|---|---|
| 15° | 6.39 | - | - | 7.94 | 6.86 | |
| 30° | 7.26 | - | - | 12.40 | 12.58 | |
| 45° | 10.82 | - | - | 11.72 | 10.77 | |
| 60° | 9.42 | - | - | 12.29 | 9.51 | |
| 75° | 4.35 | - | - | 20.80 | 4.99 | |
| 15° | 3.35 | - | - | 3.72 | 3.66 | |
| 30° | 3.82 | 7.86 | 7.57 | 7.40 | 7.57 | |
| 45° | 11.13 | 12.16 | 11.31 | 15.71 | 12.44 | |
| 60° | 9.81 | 12.17 | 10.96 | 18.72 | 12.31 | |
| 75° | 3.93 | - | - | 12.00 | 12.95 | |
| 85° | 9.06 | - | - | 15.53 | 16.39 |
| Predicted Geometrical Characteristic | Sample Size | MPE | WUB | 95% PEI | |
|---|---|---|---|---|---|
| 309 | +0.29 | 8.58 | ±0.96 | −0.66 to +1.25 | |
| 305 | −0.11 | 9.29 | ±1.04 | −1.15 to +0.93 | |
| 341 | −0.10 | 6.11 | ±0.65 | −0.75 to +0.55 | |
| 420 | −0.03 | 8.25 | ±0.79 | −0.82 to +0.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfaifi, H.; Bonakdari, H. Prediction of Geometrical Characteristics of an Inclined Negatively Buoyant Jet Using Group Method of Data Handling (GMDH) Neural Network. Fluids 2024, 9, 198. https://doi.org/10.3390/fluids9090198
Alfaifi H, Bonakdari H. Prediction of Geometrical Characteristics of an Inclined Negatively Buoyant Jet Using Group Method of Data Handling (GMDH) Neural Network. Fluids. 2024; 9(9):198. https://doi.org/10.3390/fluids9090198
Chicago/Turabian StyleAlfaifi, Hassan, and Hossein Bonakdari. 2024. "Prediction of Geometrical Characteristics of an Inclined Negatively Buoyant Jet Using Group Method of Data Handling (GMDH) Neural Network" Fluids 9, no. 9: 198. https://doi.org/10.3390/fluids9090198
APA StyleAlfaifi, H., & Bonakdari, H. (2024). Prediction of Geometrical Characteristics of an Inclined Negatively Buoyant Jet Using Group Method of Data Handling (GMDH) Neural Network. Fluids, 9(9), 198. https://doi.org/10.3390/fluids9090198








