Abstract
A model of quasilinear differential equations is derived in the context of Rational Extended Thermodynamics to investigate some non-equilibrium phenomena in nanofluids. Following the classical Buongiorno approach, the model assumes nanofluids to be suspensions of two phases: nanoparticles and the base fluid. The field variables are the classical ones and, in addition, the stress tensors and the heat fluxes of both constituents. Balance laws for all field variables are assumed. The obtained system is not closed; therefore, universal physical principles, such as Galilean Invariance and the Entropy Principles, are invoked to close the set of field equations. The obtained model is also written in terms of the whole nanofluid and compared with the classical Buongiorno model. This allowed also the identifications of some parameters in terms of experimental data. The obtained set of field equations has the advantage to recover the Buongiorno model when the phenomena are near equilibrium. At the same time it consists of a hyperbolic set of field equations. Hyperbolicity guarantees finite speeds of propagation and more suitable descriptions of transient regimes. The present model can be used in order to investigate waves, shocks and other phenomena that can be easily described in hyperbolic systems. Furthermore, as a first application and in order to show the potential of the model, stationary 1D solutions are determined and some thermal properties of nanofluids are studied. The solution exhibits, already in the simplest case herein considered, a more accurate evaluation of some fields like the stress tensor components.
1. Introduction
Nanofluids are engineering colloids, composed of nanoparticles and a base fluid. Material used as nanoparticles are oxides, such as alumina, titania and copper oxide, metals, such as copper and gold and also carbon nanotubes and diamond nanoparticles. The base fluid is water or organic fluid, such as ethanol and ethylene glycol. Nanoparticles size is very similar to those of the base fluid, so nanofluids are usually considered as a suspension of nanoparticles into the fluid with little gravitational settling.
The study of heat and mass transfer of nanofluids between two parallel plates in motion has been an interesting topic due to its wide spectrum of scientific and engineering applications such as hydrodynamical machines, micro-sized cooling systems, lubrication system, polymer processing, chemical processing equipment and preparation and dispersion of fog [1].
Boungiorno in [2] introduced a model inside the Classical Thermodynamic Theory that consists of four balance equations for two components and that is able to describe convective transport in nanofluids. The model considers nanofluids like mixtures of a base fluid and nanoparticles. In this paper a non-equilibrium model for nanofluids inside Rational Extended Thermodynamic Theory (RET) [3,4,5] is developed starting from the classical Buongiorno’s assumptions [2]. The main reason for the present investigation is that RET has shown very interesting results for mixtures [6] and moreover RET is more appropriate [3,4,5] than Classical Thermodynamics to the description of some non-equilibrium phenomena such as acceleration waves [7], shock waves [8,9], micro and nano-flows, second sound and light scattering [5,10,11].
Rational Extended Thermodynamics considers the dissipative fluxes as additional field variables and introduces for these new fields appropriate balance equations. For monoatomic gasses this kind of equations are obtained directly from the Boltzmann equation [12] while, for other materials, coherent balance equations must be assumed. In order to close the system, universal physical principles are adopted: Galilean invariance and Entropy Principles. The obtained set of field equations is symmetric hyperbolic. Hyperbolicity guarantees finite speeds of propagation, while symmetric hyperbolic systems imply the well-posedness of Cauchy problems (i.e., existence, uniqueness and continuous dependence on the data). Hyperbolic models overcome the paradox of infinite propagation speed of disturbances, and they are better suited to describe transient regimes.
RET was firstly formulated by Müller and Ruggeri [3] to investigate the behavior of monatomic gases, and then it was developed to study a wider range of gases: polyatomic gases, moderately dense gases, and gas mixtures [4,5]. For the description of non-rarefied gases, Ruggeri and Sugyama elaborated a model that consists of two hierarchies of moments: one for mass and the other for energy. Models with more than two hierarchies of moments have recently emerged [13].
In the last years, different studies on Extended Thermodynamics have been carried out on heat transfer in gas mixtures, see [5] and the references therein. The ET theory was also generalized to dense and rarefied polyatomic gases, both in the classical [14] and in the relativistic framework [15], where results are useful in cosmology to describe some aspects of the post-recombination era. A relativistic version of the kinetic theory for polyatomic gas is defined in [16], and relations between the fifteen-moments model for polyatomic gases and the fourteen-moments model for monatomic gases are revealed [17].
ET is also applied to the investigation of different materials like metal electrons [18], quantum systems [19], and graphene [20]. Unlike the ET theory, which was recently conceived to study the mixture of gases, it has largely developed in biological phenomena. In [21,22], an Extended Thermodynamic model for blood flow is defined in order to study the behavior of red blood cells in narrow vessels showing accordance between the analytical solutions of the model and experimental data. Furthermore, RET has been also applied to hyperbolic reaction–diffusion system biological models. See [23,24], where different patterns are studied, and [25], where a chronic disease is investigated, providing wave solutions that occur at finite velocity.
Remarkable studies have been carried out on heat transfer in different symmetries [26] and gas bubbles [27].
In this paper, it is shown how it is possible to obtain a hyperbolic model for nanofluids that generalizes the classical Buongiorno model [2]. It is shown that also in the simplest stationary heat transfer problem, the obtained solution is more accurate than the corresponding classical case, when some non-equilibrium phenomena occur.
The paper is organized as follows: In Section 2, the mathematical model of Buongiorno [2] is introduced. In Section 3, a model of quasilinear balance laws is defined in the context of Rational Extended Thermodynamics for the description of nanofluids, regarded as a suspension of nanoparticles in a fluid. Section 4, Section 5 and Section 6 are dedicated to the universal physical principles, which are invoked in Rational Extended Thermodynamics, in order to determine the constitutive variables. Section 7 is devoted to a different but equivalent form for the whole nanofluids field equations. In Section 8, production terms of balance equations are obtained through Maxwellian iterations at the first order and then by comparison with Navier–Stokes and Fourier laws and with experimental data of viscosity and thermal conductivity [2]. In Section 9, analytical solutions in the stationary 1D case are determined for the temperature of nanofluids, and the thermal properties of nanoparticles are discussed. Conclusions and future research perspectives are elaborated in Section 10.
2. Classical Buongiorno’s Theory
Buongiorno in [2] described nanofluids using the following set of balance equations:
The first equation represents the conservation law of mass for the whole nanofluid with the hypothesis of incompressibility; is the nanofluid velocity. The second equation is the conservation law of mass for nanoparticles. In this model, the density of nanofluid is assumed to be the average between the densities of nanoparticles and base fluid , i.e.,
with being the volumetric fraction. The vector represents the diffusion flux for the nanoparticles, which is given by
It is the sum of two contributions: Brownian diffusion and the thermophoresis phenomenon, which is equivalent to the Soret effect for gases or liquid mixtures. In [2], an exhaustive description of all effects is presented, and the coefficients and are explicitly evaluated in terms of the fields.
The third Equation (1)3 represents the balance law of momentum, with p as the total pressure and as the stress tensor for the whole nanofluid. The fourth equation is the conservation law of energy, with c being the specific heat of nanofluids
T is the temperature, is the heat flux, and denotes the specific particles’ enthalpy. The total stress tensor is expressed according to the Navier–Stokes law as
while the total heat flux is the sum of two contributions. The first is due to the Fourier law, and the second is related to the mass diffusion:
The coefficients and k represent, respectively, the viscosity and the heat conductivity of the whole nanofluid. In the applications in this paper, we consider a nanofluid to be composed of alumina and water. We use the following expressions for viscosity and thermal conductivity as reported in [2,28]:
with and being the viscosity and heat conductivity of water.
To have a more in-depth view of the thermophysical properties of nanofluids, restricted not only to the aluminum–water but also to the copper–water pair, one can refer to the appendix of [2] or in [28].
3. Rational Extended Thermodynamics
In order to investigate the thermophysical behavior of a nanofluid, a quasilinear model for its two components, the base fluid and nanoparticles, is developed. The present model contains 13 partial differential equations for the mass, momentum, stress tensor, and heat flux of each constituent. In fact, following the guidelines of Rational Extended Thermodynamics [3,4,5], the state of each component is not only given by the density, velocity, and temperature but also by the stress tensor and heat flux, which are regarded as additional field variables. Then, it is necessary to associate balance equations to these new quantities instead of assuming the classical Navier–Stokes and Fourier constitutive laws.
The set of the balance equations for the model is
where indicates the generic component of nanofluids; refers to nanoparticles, while corresponds to the base fluid.
In detail, Equation (9)1 represents the conservation law of mass for both components. Equation (9)2 is the conservation law for momentum, where is the corresponding flux, is the production term that takes into account the interaction forces between the two components, and the external force acting on the different constituents. In (9)3, we study the evolution of the moment that must be determined in terms of the field variables. We assume that the trace of this equation represents the balance law of energy for each constituent. The traceless part of (9)3 must furnish the balance equation for the stress tensor. are the production terms associated to . Round brackets in the indexes indicate symmetric part. The last Equation (9)4 must express the balance equation for heat flux when the density , the flux , and the production are expressed in terms of the field variables.
Following Buongiorno’s paper [2], also here, only a single equation for the total energy is considered. So in the following, we will take into account only the sum in of the traces and not separate balance equations. In this way, system (9) becomes a set of 25 equations for the 25 field variables: the two densities , the two velocities , the total temperature T, the two traceless parts of the stress tensors (square brackets in the indexes denote the traceless part of a symmetric tensor) and the two heat fluxes .
We need now to close the system by determining the unknown functions. Rational Extended Thermodynamics establishes that constitutive functions must be local and instantaneous, so they must depend, at each time and at each point, on field variables at the same time and at the same point and not on their gradients. So it must hold that:
for all unknown quantities, indicated with , in (9). We determine these functions by invoking some universal physical principles, such as Galilean invariance and the Entropy Principles.
4. Galilean Invariance
Galilean invariance imposes that the balance laws (9) must hold in every inertial frame, so they must be invariant under Galilean transformation. This principle yields the decomposition of the densities, fluxes and productions into convective and non-convective parts (see for details [3] page 35 and [29]):
where , , and are the velocity-independent parts of the corresponding fields. They are called internal parts. Some of these quantities are related to more common thermodynamic variables:
where is the stress tensor, is the heat flux, and is the total internal energy for the constituent. We observe, in fact, that (11)1 is the decomposition of the flux into stress tensor and the velocity-dependent part, while the trace of (11)4 gives the decomposition of the moment into twice internal energy and twice kinetic energy.
The insertion of (11) into (9) provides the explicit form of the balance equations, in which only the derivatives of velocities are present and not the velocities themselves, according to the requirement of Galilean invariance. Therefore, after some simple calculations, system (9) becomes
where is the material derivative appropriate to each component.
Because of the definition of a single temperature for nanofluids, we consider, as already said, a unique equation for the total energy that is given by the sum of the balance laws of energy for each component:
while we continue to deal with two different equations for the traceless parts of the stress tensor:
We underline that the system is closed if the constitutive variables are determined as follows:
In the next section, we will show that Rational Extended Thermodynamics is able to limit the generality of these relations by the exploitation of the Entropy Principle.
5. Entropy Principle
The Entropy Principle states that there exists a concave function h, the entropy density, that satisfies the balance law
for all solutions of the field Equation (13). Here, is the entropy flux, and is the entropy production.
The requirement of validity of the Entropy Principle means that the field Equation (13) provides some constraints for the fields that satisfy the entropy inequality. Rational Extended Thermodynamics [3] assumes the field equations to be constraints for the Entropy Principle, and it takes into account these constraints by the introduction of Lagrange multipliers [30] or main fields [31]: for the conservation law of mass, for the balance law of momentum, for the balance law of energy (in this case, we adopt a single Lagrange multiplier for the entire system because we consider a unique energy), for the balance law of stress tensor, and for the balance law of heat flux. So the entropy inequality can be recast as follows:
that must be valid for all and .
The presence of Lagrange multipliers adds new unknown quantities, but it helps in the determination of constitutive variables.
We are interested in studying thermodynamic processes not far from equilibrium, in which non-equilibrium fluxes and vanish. With this condition, constitutive variables can be expressed around the thermodynamic equilibrium as linear functions of the non-equilibrium fluxes:
The unknown functions , , , and depend on the densities and the temperature. In order to be coherent with all orders in (18), the entropic quantities and the Lagrange multipliers must be expanded until terms of the second order. So the entropy density and the entropy flux are given by
and the Lagrange multipliers become
The entropy inequality is solved by the substitution of (19)–(21) and setting the coefficients of all derivatives in the field variables equal to zero. A formidable set of both algebraic and differential equations for all functions is determined in (19)–(21). For simplicity, we write here only the equations that will be useful to determine the functions in (19)–(21):
- For the coefficients related to the entropy density:
- For the coefficients related to the entropy flux:
- For the coefficients related to Lagrange multipliers:
By combining and solving all these relations, we are able to determine the coefficients in (19)–(21) by which we have represented the entropy density and flux, the Lagrange multipliers, and in particular the constitutive variables, whose knowledge is essential to close the system.
It should be noted that, by vanishing the derivatives, what remains of entropic inequality is the residual inequality
that entails linear relations between the production terms and and the Lagrange multipliers and . The sign of the residual inequality must be verified once the unknown functions are determined, and it provides the validity of solutions that are physically acceptable.
6. Evaluation of the Coefficients near Equilibrium
First of all, the equilibrium terms associated to the entropy density are determined: By (22)1,2, the following relation is recovered,
that can be compared with the Gibbs equation of equilibrium thermodynamics:
This comparison yields the determination of the coefficients
where is the chemical potential or Gibbs free energy. So the expression of the equilibrium coefficient of the entropy density is
From these results, and together with relations (23)–(27), we obtain, after some long but simple computations, the final expressions of the constitutive relations:
- The constitutive variables
- The entropy density and entropy flux
- The Lagrange multipliers
In conclusion, from (13) a system of 25 balance laws for the 25 unknown fields , and is determined. It is closed except for the production terms. The system consists of the two conservations laws of mass (13)1, the two balance laws for the momentum (13)2, the conservation law for the total energy (14), the two balance equations for the traceless parts of the two stress tensors (15) and the two balance equations for the heat fluxes (13)4. The left-hand side of these equations is completely explicit in terms of the field variables through relations (33).
For the production terms, linear productions are considered. In particular, inside the BGK assumption [32], we assume that the productions are proportional to the corresponding densities minus their equilibrium values. With this assumption and by substituting the constitutive relations (33) into the field equation corresponding to the phase (13)1,2,4, (14), and (15), we obtain
In the last equations, is the diffusion flux, and , and are the relaxation times that will be evaluated with the Maxwellian iterations in Section 8. First, in order to compare this model with the classical theory, we have to introduce the field equations for the whole nanofluid, an alternative form that will be useful in Section 8.
7. Field Equations for the Whole Nanofluid
In the previous sections, we studied separately the field equations for the two different constituents of the nanofluid. The interaction between these two constituents was taken into account in the production terms. We proceed now to obtain the balance equations for the whole nanofluid from the balance equation for both constituents:
First of all, we define densities and fluxes for the whole nanofluid as the sum of the corresponding terms related to the two phases in the following form:
and for the production terms
We observe that the baricentric velocity coincides with the velocity of the nanofluid considered a single fluid. Furthermore, the whole production must vanish since it refers to the production terms of the conservation law for the total momentum, which must be a conservation law. The same holds for the trace of the third equation for the conservation law of the whole energy.
Then, the sum of (9) with , yields the thirteen-moments model:
which is the equivalent set of (9), but it corresponds to the whole nanofluid.
Using the constitutive relations for the two constituents (11), (33), (37), and (38), it is possible to recover the explicit form of the field equations. First of all, Equation (39) can be written in terms of the diffusion velocity and the diffusion flux , defined as
Indeed, by the use of these quantities and by the substitution of relations (11) into (37) and (38), it is possible to obtain the decomposition of the quantities F, M and P in terms of the convective and non-convective parts:
Clearly, these relations coincide with the consequence of the Galilean principle applied to the whole nanofluid. Furthermore, the whole internal moments , m and p depend on the internal moment of the two components by relations
In terms of these variables, it is possible to write Equation (39) in the explicit form
that is equivalent to Equation (13) with the difference that this set corresponds to the whole nanofluid. These equations are expressed in terms of the fields by use of (33) and (42).
It is then possible to note that Equation (43)1 coincides with the conservation law of the whole mass of the nanofluid, Equation (43)2 is the conservation law of the total momentum, and Equation (43)3 is the conservation law for the total energy, which coincides with the sum (14). The two remaining Equations (43)4,5 are the balance equations for the total stress tensor and the total heat flux.
In conclusion, it is equivalent to deal with the 25 fields equations appropriate to both constituents (36) with , or to take into account the equations corresponding to one constituent (let us say (36) ) and the equations for the whole nanofluid.
As it will be shown in the next section, this second form, introduced in this chapter, is more indicative of the comparison with the classical Buongiono model.
8. Comparison with the Classical Model
In this section, we compare the obtained field equations with the classical Buongiorno model.
Assuming that the whole fluid is incompressible and setting the constant in the conservation law of mass (43)1, this last equation coincides with the first classical Equation (1)1. Instead, inserting with the constant in the conservation law of mass for the first constituent (36)1 and taking into account the definitions (40), the balance law (1)2 is obtained.
The conservation laws for the momentum and energy for the whole nanofluid (43)2,3 coincide with Equation (1)3,4, when the same symbols are used.
The difference between the two theories lies in the remaining equations. In fact, as already said, classical thermodynamics assumes Fick (3), Navier–Stokes (5), and Fourier (6) laws in order to express the diffusion flux, the stress tensor, and the heat flux in terms of the fields. In this section, we will show that these three laws can be obtained from the balance laws for the momentum, the stress tensor, and the heat flux relative to the two constituents using the so-called Maxwellian iterations (MI). With this procedure, it will be possible to evaluate the relaxation times from the parameters that were evaluated by Buongiorno.
We proceed with the first MI, that is, we assume that the non-equilibrium quantities on the left-hand side of the Equation (36)2,4,5 must vanish. This assumption is verified since we assume that the relaxation times are small; therefore, on the left-hand side of the corresponding equations, the non-equilibrium variables can be neglected in comparison with the equilibrium quantities. So, in the first approximation, we recover from (36)2,4,5
These relations coincide with the Fick, Navier–Stokes, and Fourier laws for each constituent with appropriate diffusion coefficients, viscosities and heat conductivities. As already said, these relations are usually used in Classical Thermodynamics in order to express the diffusion flux, the stress tensor, and the heat flux in terms of the gradient of the density, velocity, and temperature. We can compare in details these relations with the classical Buongiorno model. Comparing (44)1 with (3) and taking into account that in Buongiorno , we have
The value of the diffusion coefficients , which is due to the Brownian diffusion, is given by the Einstein–Stokes’ equation [2]
where is the Boltzmann’s constant, is the viscosity of the fluid, and the nanoparticle diameter. The second coefficient that takes into account the thermophoretic or thermodiffusion effect is expressed by [2]
where [33] is a proportional factor, and k and are the thermal conductivities of the fluid and of the nanoparticles, respectively.
From the expression of the Navier–Stokes laws (44)2, it is possible to evaluate the relaxations times in terms of the two viscosities, that is,
Instead, comparing the Fourier laws (44)3, it is possible to evaluate the two relaxation times in terms of the two thermal conductivities:
Once the stress tensors and the heat fluxes of both constituents are identified, it is possible to recover the whole stress tensor and the whole heat flux from (42)1,2, respectively.
and these relations recover exactly the assumptions (5) and (6) in Buongiorno’s theory. In this way, the whole viscosity and the heat conductivity is the sum , so by (7) and (8), it is possible to evaluate the particles viscosity and heat conductivity in terms of the viscosity and heat conductivity of the fluid and for the particular case of alumina and water. Other kind of nanofluids can be evaluated in the same way.
9. Stationary 1D Solution
We propose as an application of the herein obtained model the stationary heat transfer problem along the one-dimensional direction: . For the sake of simplicity, we set and . We linearize the field equations around the constant state and , expressing every unknown function as the sum of a constant equilibrium value and a linear perturbation in the non-equilibrium variables that vanishes at equilibrium. Therefore, assuming that all fields in (36) depend only on the x-coordinate and neglecting all terms of the second order, we obtain
In terms of the dimensionless variables
where is the length of the 1D domain, , and with the expressions of the dimensionless relaxation times
the model can be recast in the following form:
This set of field equations can be easily analytically integrated. So, if we suppose that the initial values of the pressure for the two phase are identical, we compute the following solutions for the temperature field of the whole suspension and for each phase heat flux, stress tensor and pressure,
where the constants A and B are given by
while - are the integration constants that are determined by imposing boundary conditions. We suppose that temperature assumes the following boundary values at : and . Furthermore, since we deal with a linearized set of field equations, we assume a skew-symmetric profile for the temperature field, so must be verified. In this way, the solution for the temperature field is completely explicit, and it is shown in Figure 1. We observe that the temperature fields assume the expected behavior that is the sum of the classical linear behavior plus boundary layers due to the contribution of the hyperbolic sine in (55)1.
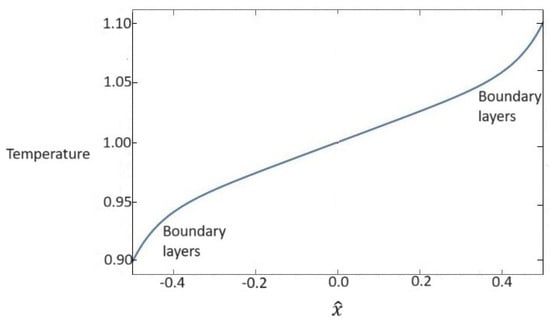
Figure 1.
Dependence of dimensionless values of temperature for the whole nanofluid on the x one-dimensional direction. Temperature presents a linear behavior plus boundary layers.
The corresponding heat fluxes are represented in Figure 2. We observe that the heat flux relative to the base fluid is negative, in accordance with the temperature behavior in Figure 1, while the heat flux for the nanoparticles has the opposite sign.
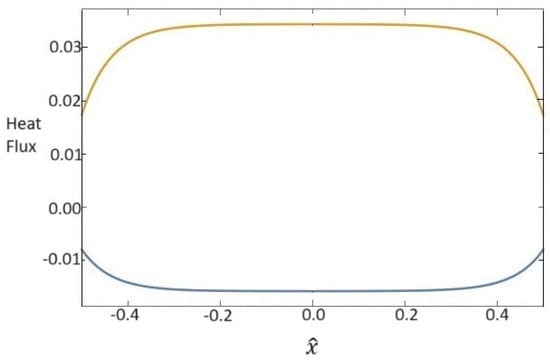
Figure 2.
Dependence of dimensionless heat fluxes for base fluid (blue line) and for nanoparticles (orange line) on the x one-dimensional direction.
In Figure 3, the components of the deviatoric parts of the stress tensor and the pressures both relative to the base fluid and nanoparticles are represented. It is deduced from (54)1 that the total sum of the stress tensor and pressure for each component is constant.
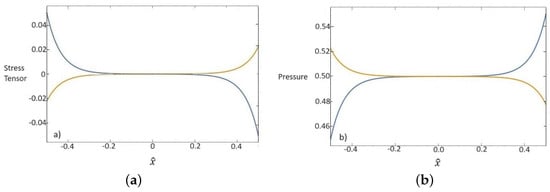
Figure 3.
Dependence of dimensionless values of stress tensor (a) and pressure (b) for base fluid (blue line) and nanoparticles (orange line) on the x one-dimensional direction.
10. Conclusions and Final Remarks
In conclusion, we make the following remarks:
- A quasilinear model for nanofluilds, considered a suspension of nanoparticles in a fluid, is introduced in the context of Rational Extended Thermodynamics. It consists of 13 partial differential equations for the mass, momentum, stress tensor, and heat flux appropriate to both components. Constitutive variables are determined through universal physical principles, and production terms are computed through Maxwellian iterations.
- The model is linearized and solved in the stationary and one-dimensional space in order to investigate some heat properties of nanofluids. Assuming nanofluid to be a suspension of water and alumina, it is shown that the behavior of the temperature field has a linear increase in the domain with boundary layers, which are more realistic than the only linear result, but they cannot be obtained inside the classical theory. Furthermore, the solution of the heat flux is depicted for both components, showing the behavior of the base fluid and the nanoparticles. An interesting result is the obtained solutions for the stress tensor components that do not identically vanish although the nanofluid is at rest, so a more accurate evaluation of the stress tensor in the whole nanofluid and in its constituents is carried out than the classical NS results. In fact, Extended Thermodynamics is able to recover this kind of solution as in the case of mixtures (see [6] and the references therein).
- In this study, all the unknown fields are determined and represented for each component of the nanofluid in order to provide a complete description of the heat problem. Furthermore, the set of field equations of the entire nanofluid is determined. The model presented here has the disadvantage that it contains many more equations than in classical thermodynamics and therefore, the determination of the solution is more complicated. On the contrary, the present model provides more accurate results. The integration of the model in the non-linear case is not at all simple and requires a thorough numerical integration, which we hope to carry out in future work. Also, the stationary solutions in the 1D domain in the presence of a flow could be an interesting study, with the comparison of the results with the corresponding solutions in the classical case.
- Moreover, the time-dependent behavior of the present model should be interesting. For hyperbolic models, as in this case, they have a wide range of applications. It could be interesting to study the acceleration and shock waves together with the shock structure and its evolution with time. Finally, we aim to study in future papers some different technical applications that deal also with nanofluids in the presence of a magnetic field. This study will be very interesting for technical applications, and the solution to the heat flux could be very interesting.
Author Contributions
Conceptualization, E.B. and A.P.; Formal analysis, E.B. and A.P.; Investigation, A.P.; Writing—review and editing, E.B. and A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
This research was funded by Istituto Nazionale di Alta Matematica Francesco Severi GNFM and by Mur-PRIN project entitled “Modelling complex biOlogical systeMs for biofuEl productioN and sTorAge: mathematics meets green industry (MOMENTA)” Project number PRIN202248TY47003.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| fluid or p for nanoparticles | |
| nanofluid velocity | |
| volumetric fraction | |
| diffusion flux | |
| density of nanofluid | |
| pressure | |
| stress tensor | |
| c | specific heat of nanofluid |
| T | temperature of nanofluid |
| heat flux | |
| enthalpy | |
| viscosity of nanofluid | |
| k | heat conductivity of nanofluid |
Abbreviations
| RET | Rational Extended Thermodynamics |
| ET | Extended Thermodynamics |
| BGK | Bhatnagar–Gross–Krook |
| MI | Maxwellian Iteration |
| NS | Navier–Stokes equations |
References
- Amani, M.; Amani, P.; Bahiraei, M.; Ghalambaz, M.; Ahmadi, G.; Wang, L.P.; Wongwises, S.; Mahian, O. Latest developments in nanofluid flow and heat transfer between parallel surfaces: A critical review. Adv. Colloid Interface Sci. 2021, 294, 102450. [Google Scholar] [CrossRef] [PubMed]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transfer. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Müller, I.; Ruggeri, T. Rational Extended Thermodynamics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Ruggeri, T.; Sugiyama, M. Rational Extended Thermodynamics beyond the Monatomic Gas; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ruggeri, T.; Sugiyama, M. Classical and Relativistic Rational Extended Thermodynamics of Gases; Springer: New York, NY, USA, 2021. [Google Scholar]
- Barbera, E.; Brini, F. Frame dependence of stationary heat transfer in an inert mixture of ideal gases. Acta Mech. 2014, 225, 3285–3307. [Google Scholar] [CrossRef]
- Ruggeri, T.; Sugiyama, M. Waves in Hyperbolic Systems. In Classical and Relativistic Rational Extended Thermodynamics of Gases; Springer: Cham, Switzerland, 2020; pp. 67–106. [Google Scholar]
- Weiss, W. Continuous shock structure in extended thermodynamics. Phys. Rev. E Part A 1995, 52, 5760. [Google Scholar] [CrossRef]
- Ruggeri, T.; Taniguchi, S. Shock waves in hyperbolic systems of nonequilibrium thermodynamics. In Applied Wave Mathematics II: Selected Topics in Solids, Fluids, and Mathematical Methods and Complexity; Springer: Cham, Switzerland, 2019; pp. 167–186. [Google Scholar]
- Weiss, W.; Müller, I. Light scattering and extended thermodynamics. Contin. Mech. Thermodyn. 1995, 7, 123–177. [Google Scholar] [CrossRef]
- Marques, W., Jr.; Kremer, G.M. Light scattering in binary mixtures of monatomic gases from an extended kinetic description. Contin. Mech. Thermodyn. 2002, 14, 45–53. [Google Scholar] [CrossRef]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Arima, T.; Carrisi, M.C.; Pennisi, S.; Ruggeri, T. Relativistic rational extended thermodynamics of polyatomic gases with a new hierarchy of moments. Entropy 2021, 24, 43. [Google Scholar] [CrossRef]
- Arima, T.; Carrisi, M.C.; Pennisi, S.; Ruggeri, T. Which moments are appropriate to describe gases with internal structure in Rational Extended Thermodynamics? Int. J. Non-Linear Mech. 2021, 137, 103820. [Google Scholar] [CrossRef]
- Pennisi, S.; Ruggeri, T. Relativistic extended thermodynamics of rarefied polyatomic gases. Ann. Phys. 2017, 377, 414–445. [Google Scholar] [CrossRef]
- Arima, T.; Carrisi, M.C.; Pennisi, S.; Ruggeri, T. Relativistic Kinetic Theory of Polyatomic Gases: Classical Limit of a New Hierarchy of Moments and Qualitative Analysis. Partial. Differ. Equations Appl. 2022, 3, 1–21. [Google Scholar] [CrossRef]
- Arima, T.; Carrisi, M.C. Monatomic gas as a singular limit of relativistic theory of 15 moments with non-linear contribution of microscopic energy of molecular internal mode. Ann. Phys. 2024, 460, 169576. [Google Scholar] [CrossRef]
- Barbera, E.; Brini, F. New extended thermodynamics balance equations for an electron gas confined in a metallic body. Ric. Mat. 2021, 70, 181–194. [Google Scholar] [CrossRef]
- Trovato, M. Quantum maximum entropy principle and quantum statistics in extended thermodynamics. Acta Appl. Math. 2014, 132, 605–619. [Google Scholar] [CrossRef]
- Trovato, M.; Falsaperla, P.; Reggiani, L. Maximum-entropy principle for ac and dc dynamic high-field transport in monolayer graphene. J. Appl. Phys. 2019, 125, 174901. [Google Scholar] [CrossRef]
- Barbera, E.; Pollino, A. An extended thermodynamics model for blood flow. Mathematics 2022, 10, 2977. [Google Scholar] [CrossRef]
- Barbera, E.; Pollino, A. A three-phase model for blood flow. Ric. Mat. 2023. [Google Scholar] [CrossRef]
- Consolo, G.; Curró, C.; Grifó, G.; Valenti, G. Oscillatory periodic pattern dynamics in hyperbolic reaction-advection-diffusion models. Phys. Rev. E 2022, 105, 034206. [Google Scholar] [CrossRef] [PubMed]
- Grifó, G.; Consolo, G.; Curró, C.; Valenti, G. Rhombic and hexagonal pattern formation in 2D hyperbolic reaction–transport systems in the context of dryland ecology. Phys. D Nonlinear Phenom. 2023, 449, 133745. [Google Scholar] [CrossRef]
- Barbera, E.; Pollino, A. A hyperbolic reaction–diffusion model of chronic wasting disease. Ric. Mat. 2023. [Google Scholar] [CrossRef]
- Barbera, E.; Brini, F. Stationary heat transfer in helicoidal flows of a rarefied gas. EPL 2017, 120, 34001. [Google Scholar] [CrossRef]
- Brini, F.; Seccia, L. Acceleration waves and oscillating gas bubbles modelled by rational extended thermodynamics. Proc. R. Soc. A 2022, 478, 20220246. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y. Hydrodynamic and Heat Transfer Study of Dispersed Fluids with Submicron Metallic Oxide Particles. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Ruggeri, T. Galilean invariance and Entropy Principle for systems of balance laws. The structure of Extended Thermodynamics. Contin. Mech. Thermodyn. 1989, 1, 3–20. [Google Scholar] [CrossRef]
- Liu, I.S. Method of Lagrange multipliers for exploitation of the entropy principle. Arch. Ration. Mech. Anal. 1972, 46, 131–148. [Google Scholar] [CrossRef]
- Ruggeri, T.; Strumia, A. Main field and convex covariant density for quasi-linear hyperbolic systems. Relativistic fluid dynamics. Ann. Inst. Henri Poincaré 1981, 34, 65–84. [Google Scholar]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511. [Google Scholar] [CrossRef]
- McNab, G.S.; Meisen, A. Thermophoresis in Liquids. Colloid Interface Sci. 1973, 44, 339. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).