N-Symmetric Interaction of N Hetons, II: Analysis of the Case of Arbitrary N
Abstract
1. Introduction
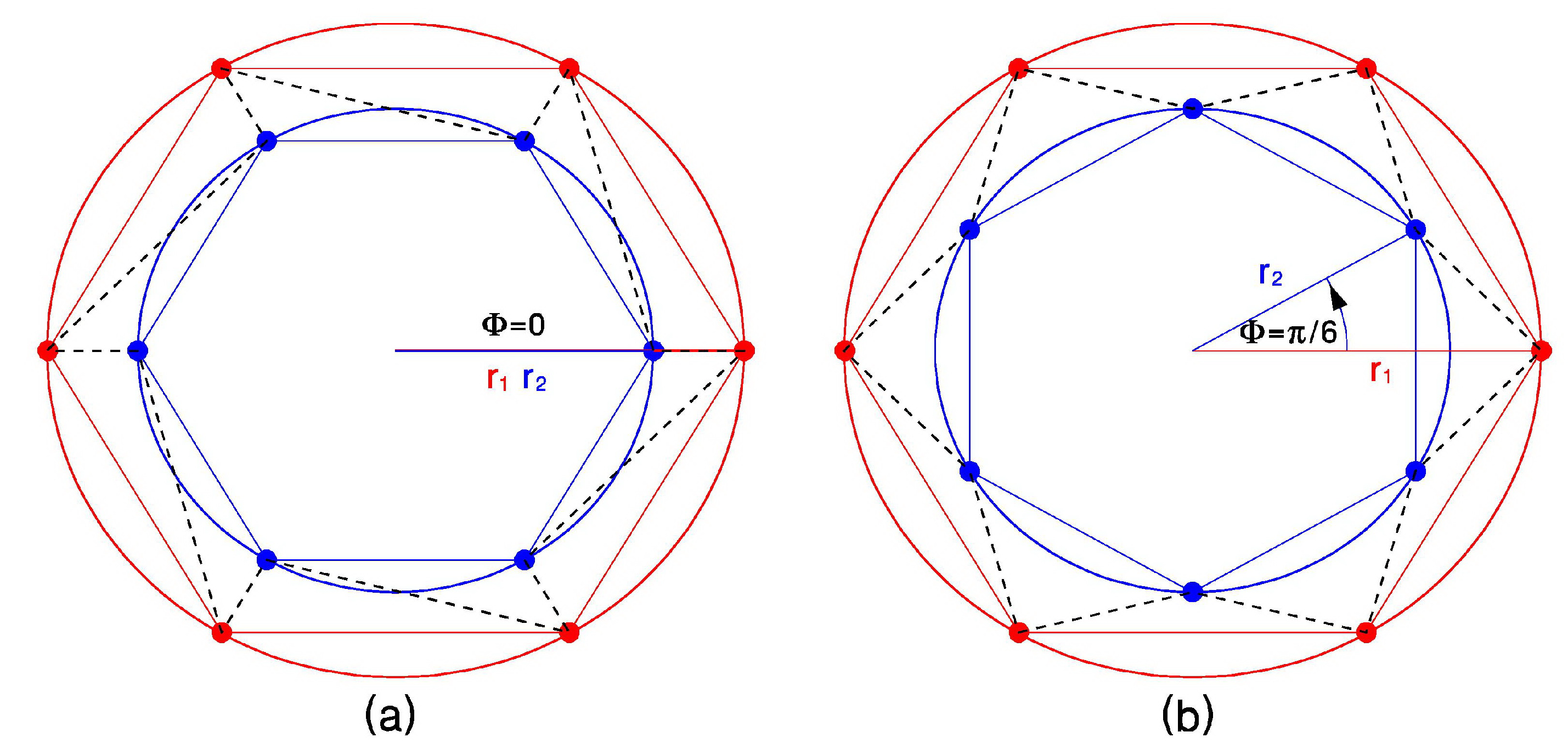
2. Mathematical Model and Problem Formulation
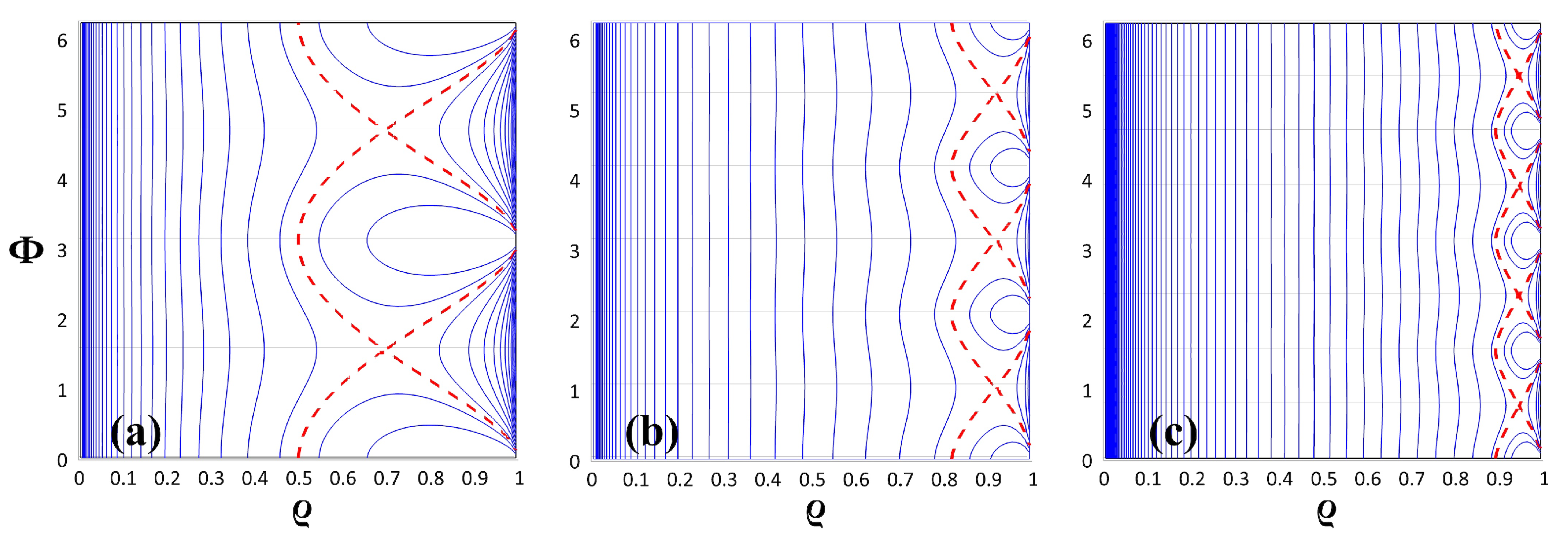
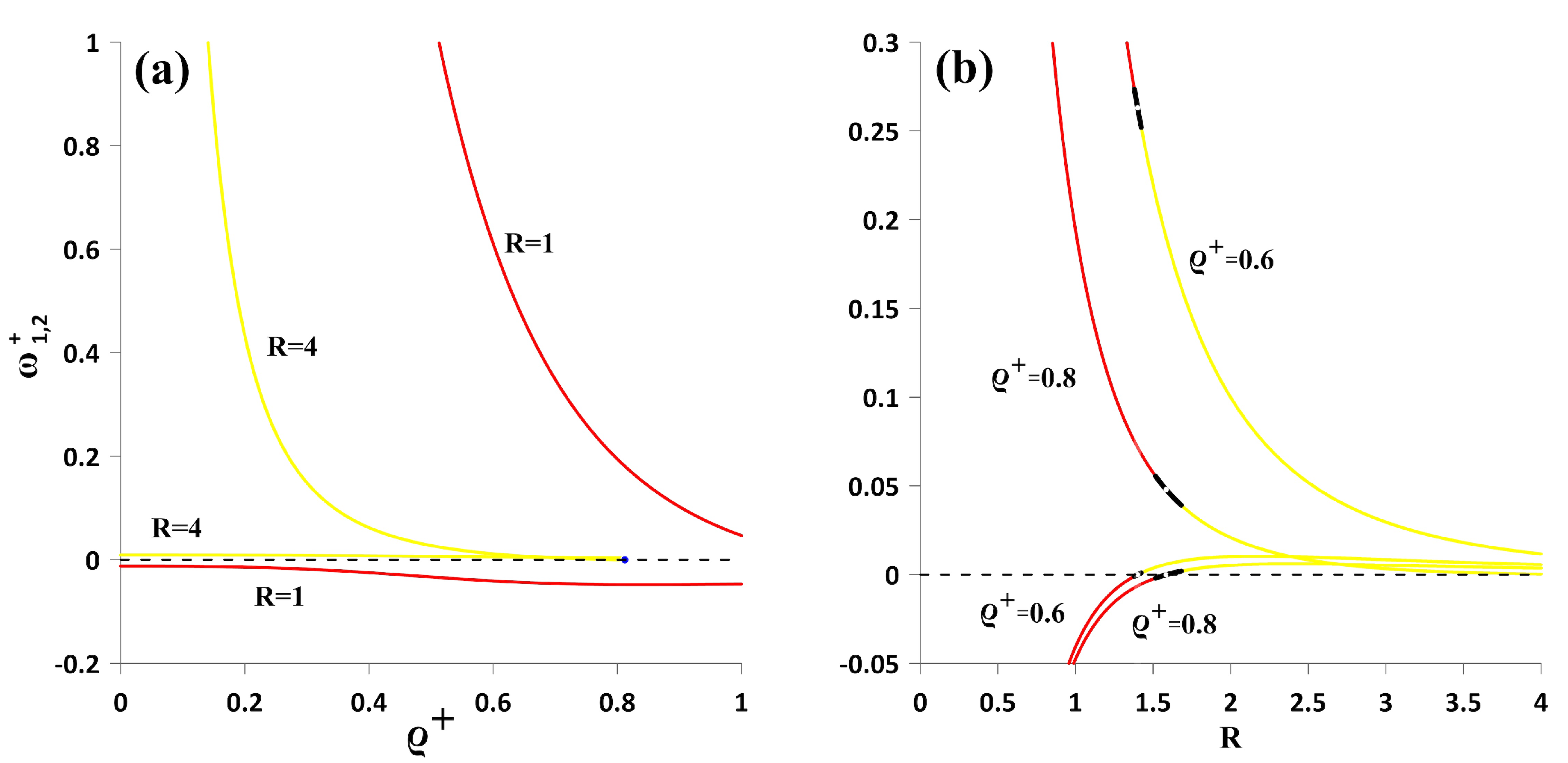
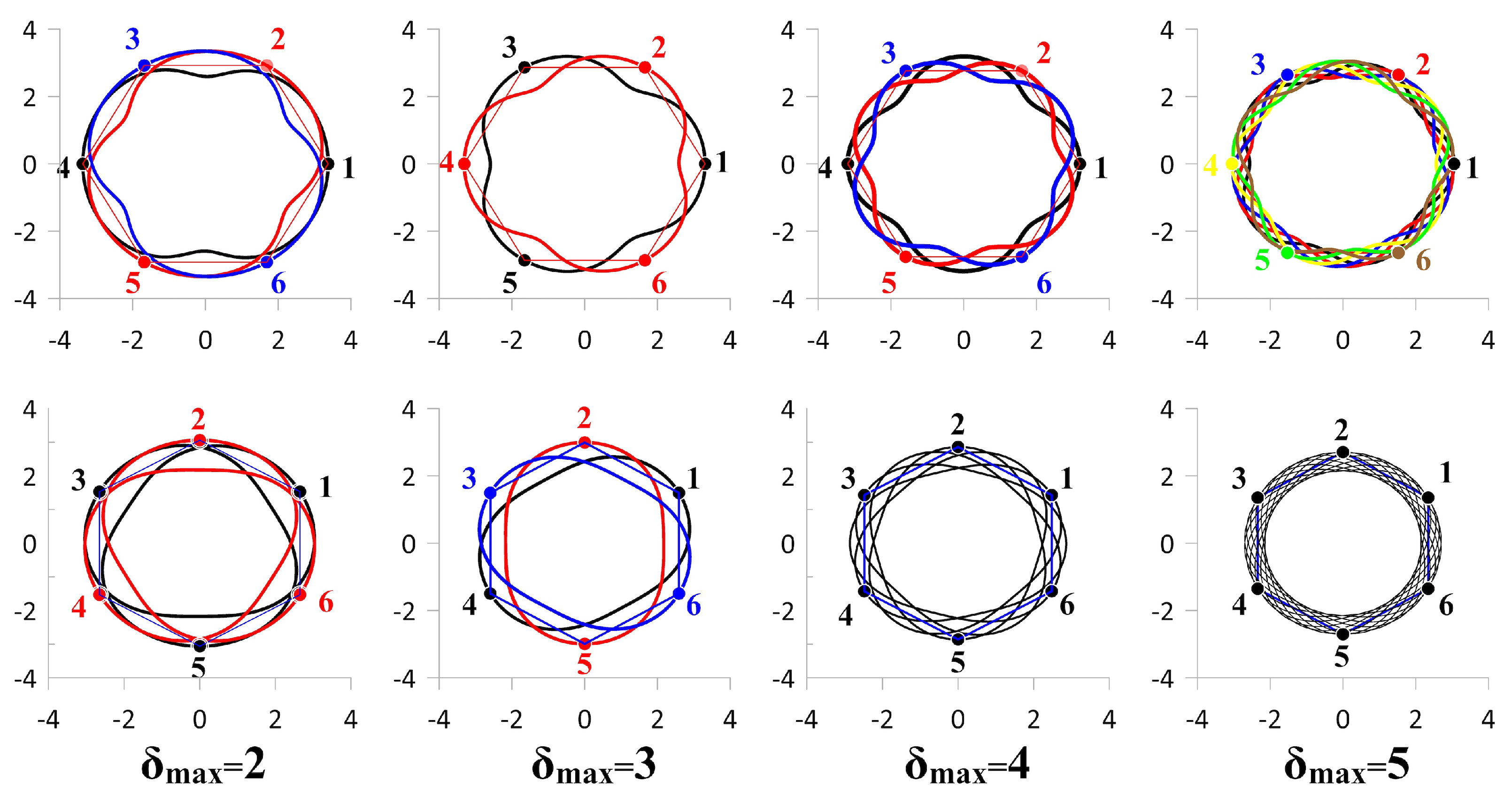
3. Analysis of Possible Motion Regimes
- (A)
- Unbounded motion within the interval , when ;
- (B)
- Localised (bounded and periodic) motion within the interval , when ;
- (C)
- Unbounded motion within the interval , when .
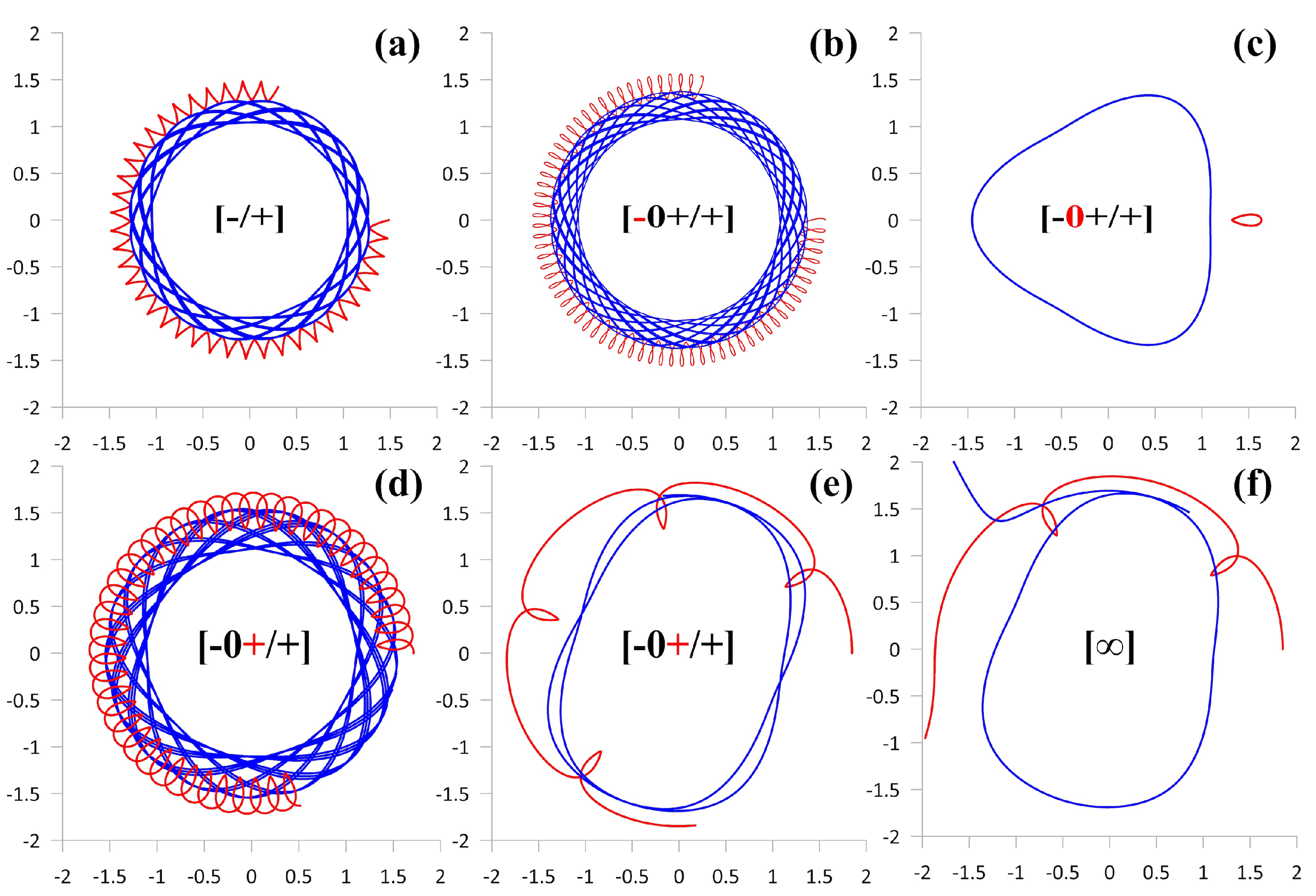
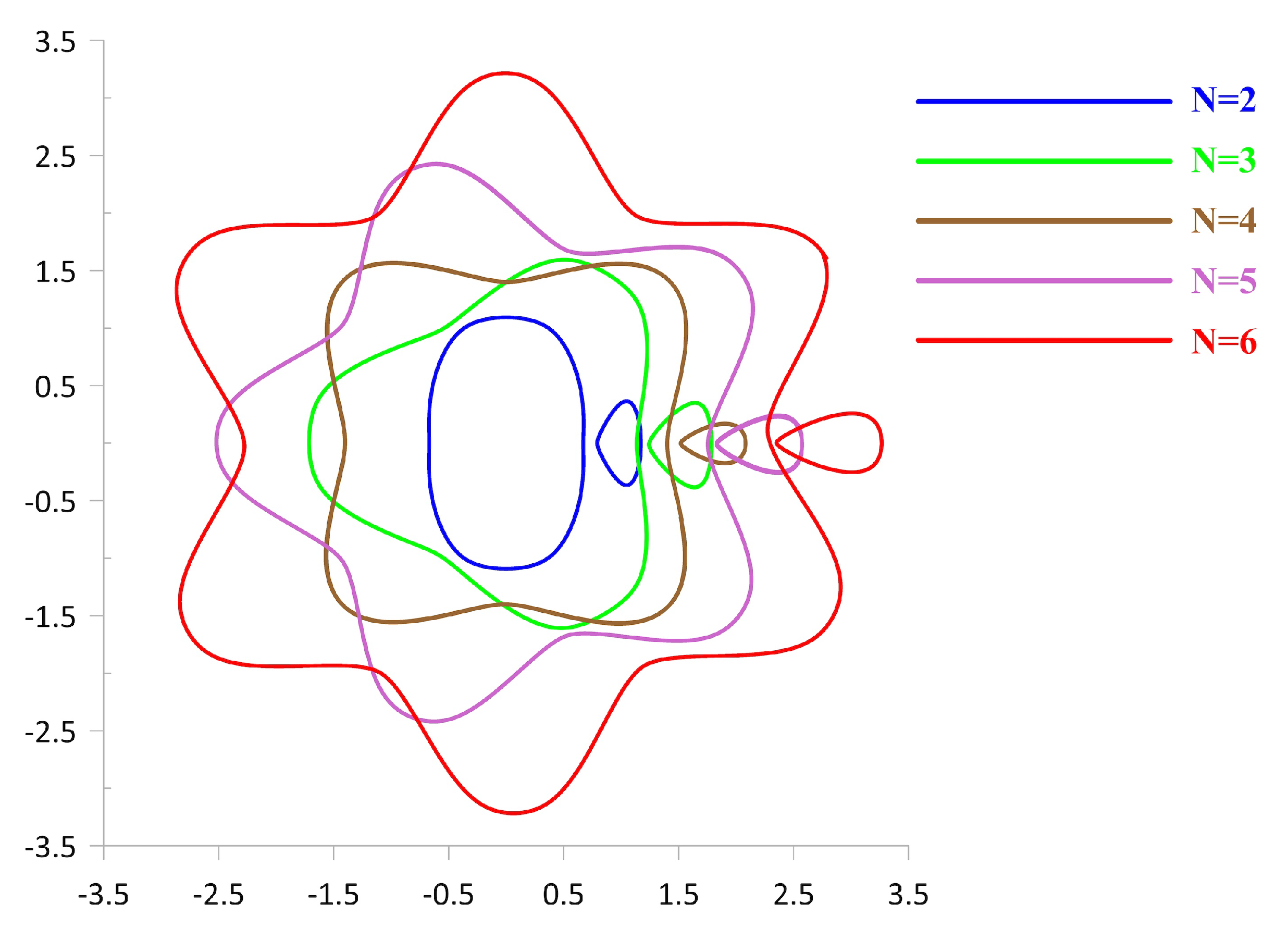
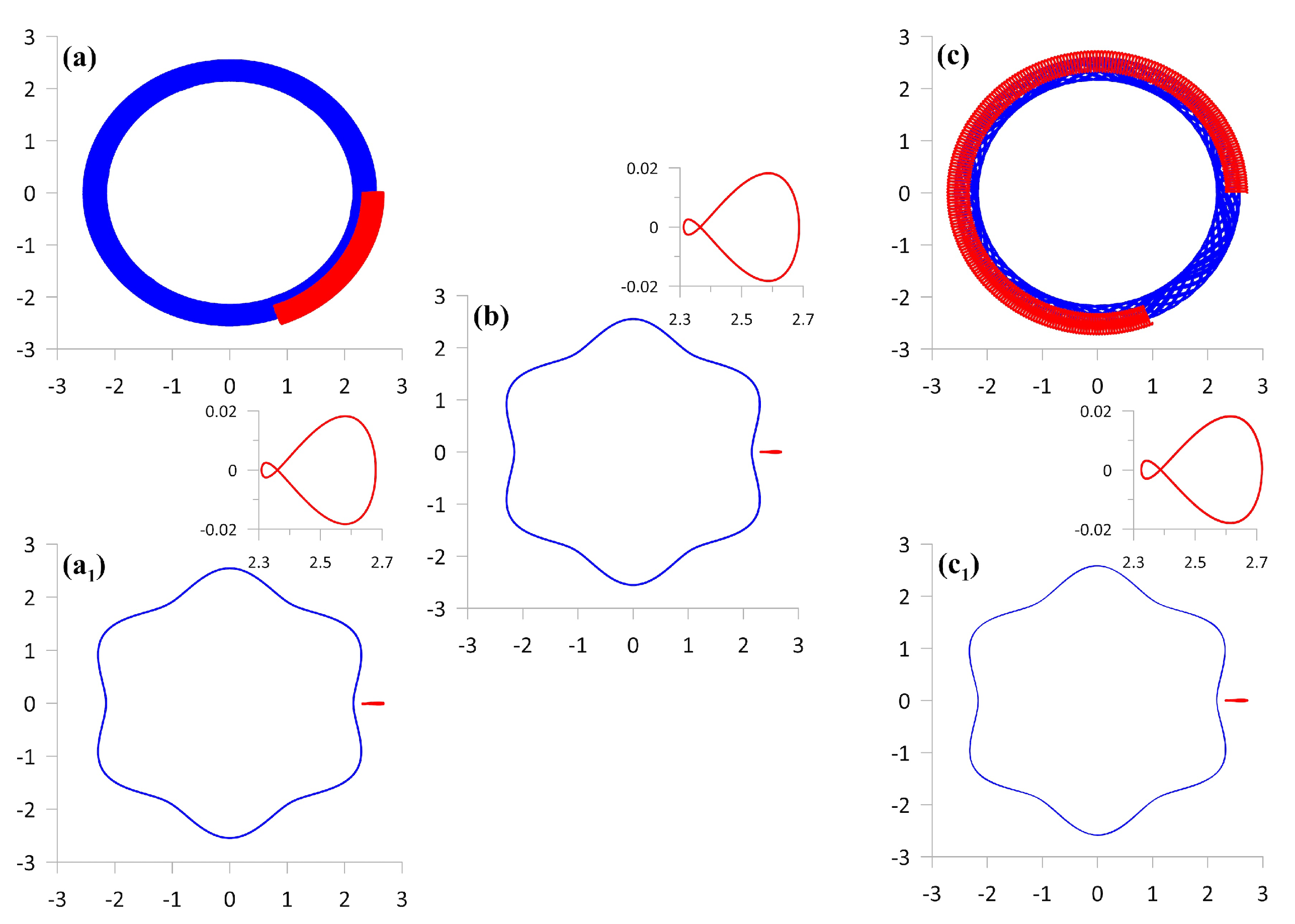
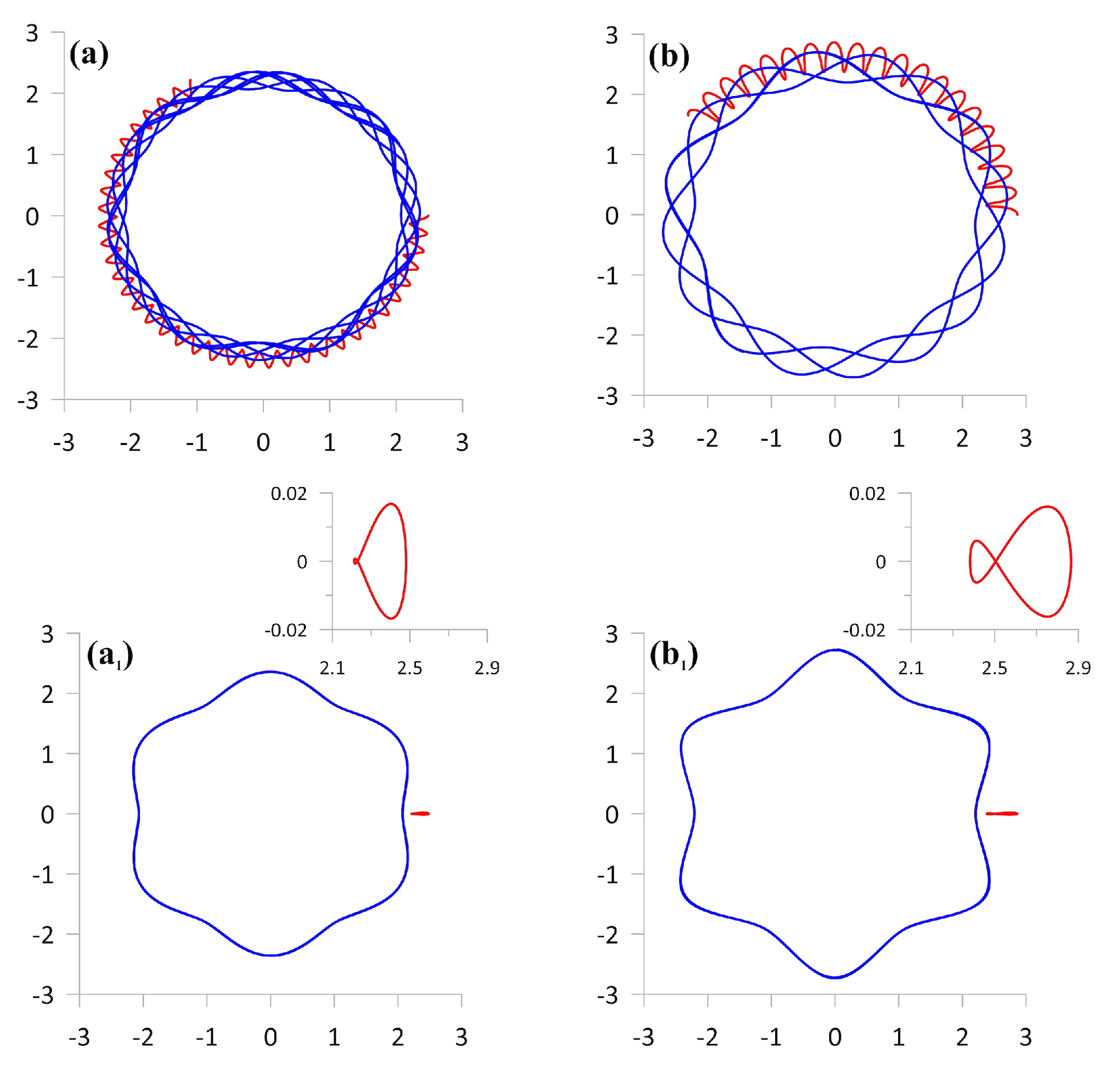
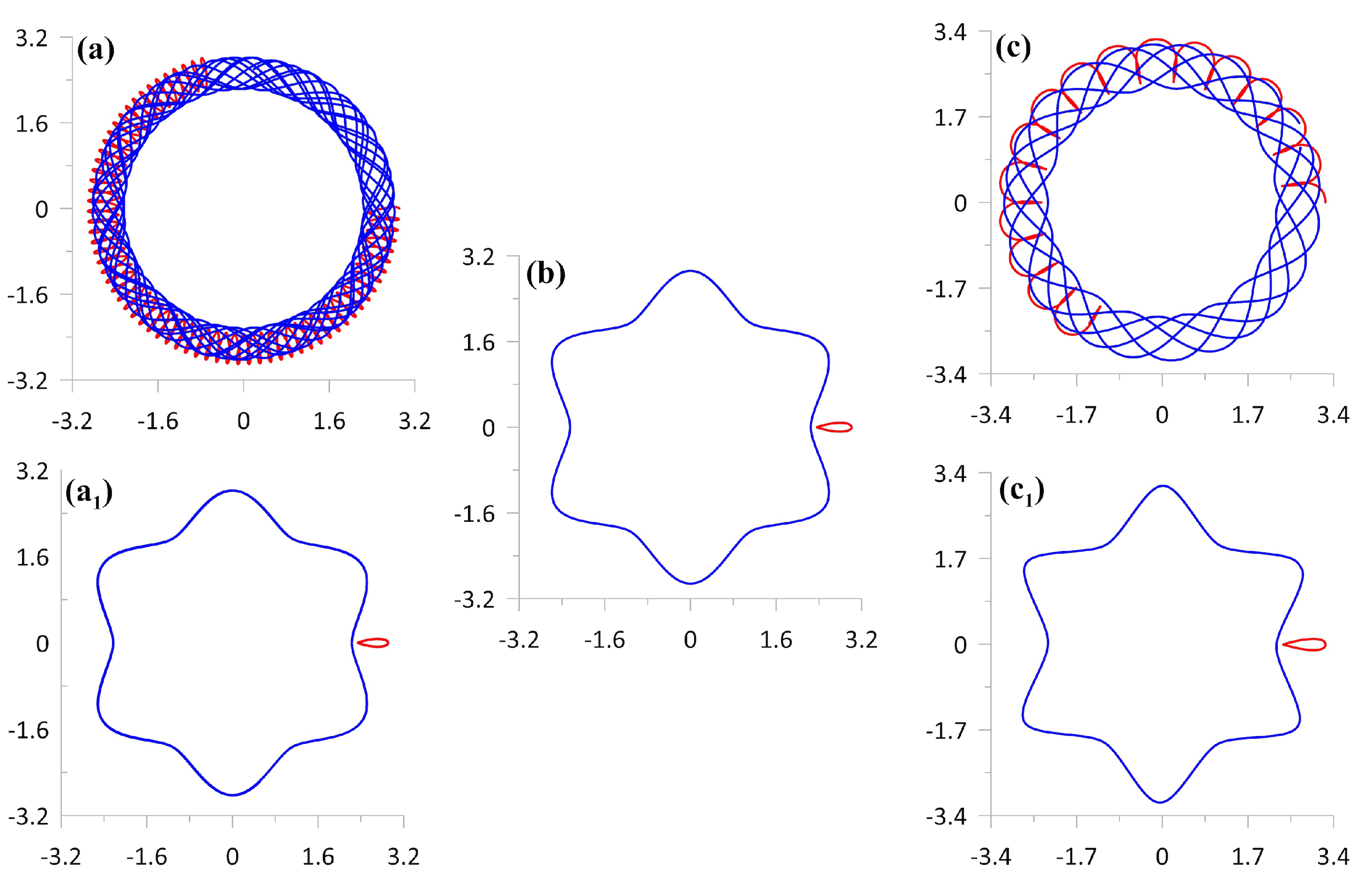
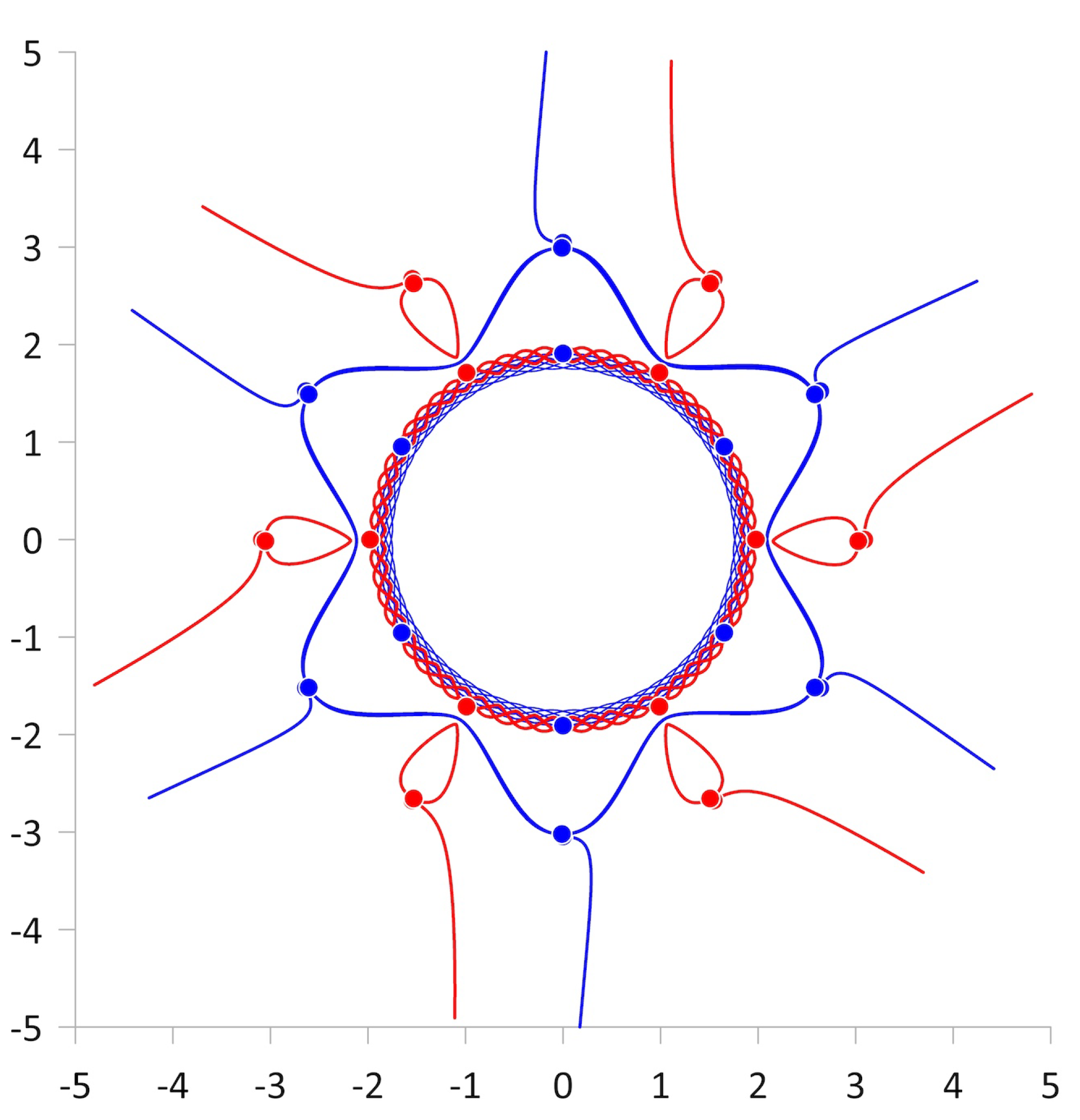
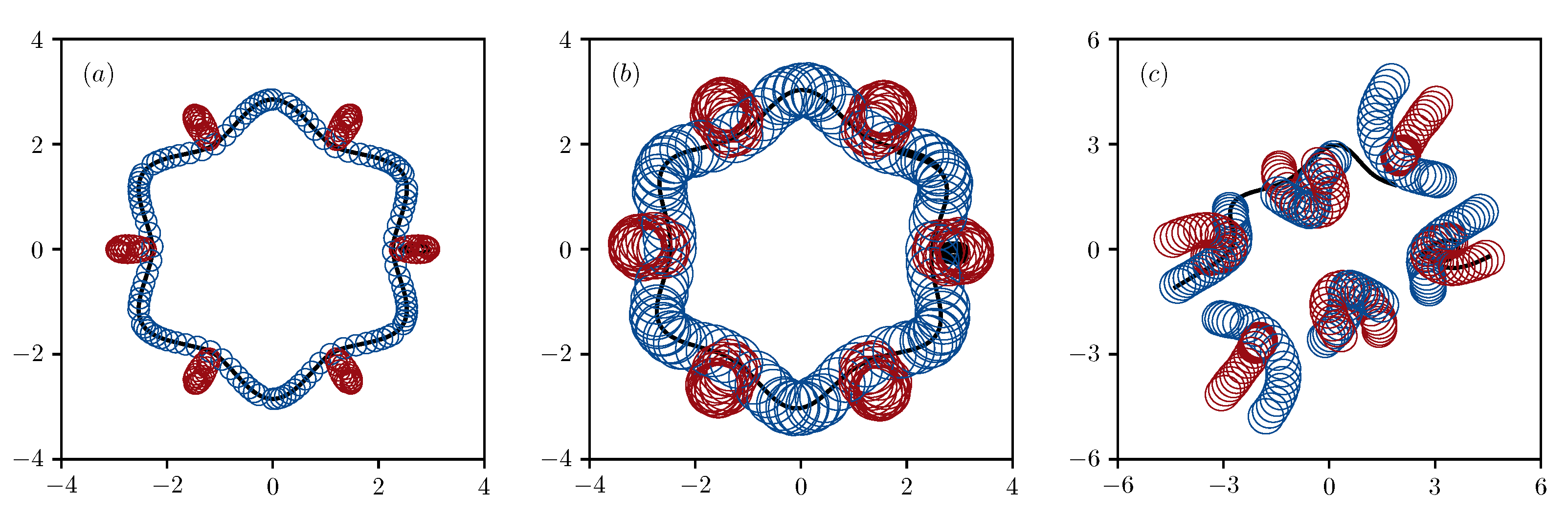
3.1. Examples of Trajectories: Absolute and Relative Choreographies
3.2. Direction of Rotation of the External Vortices
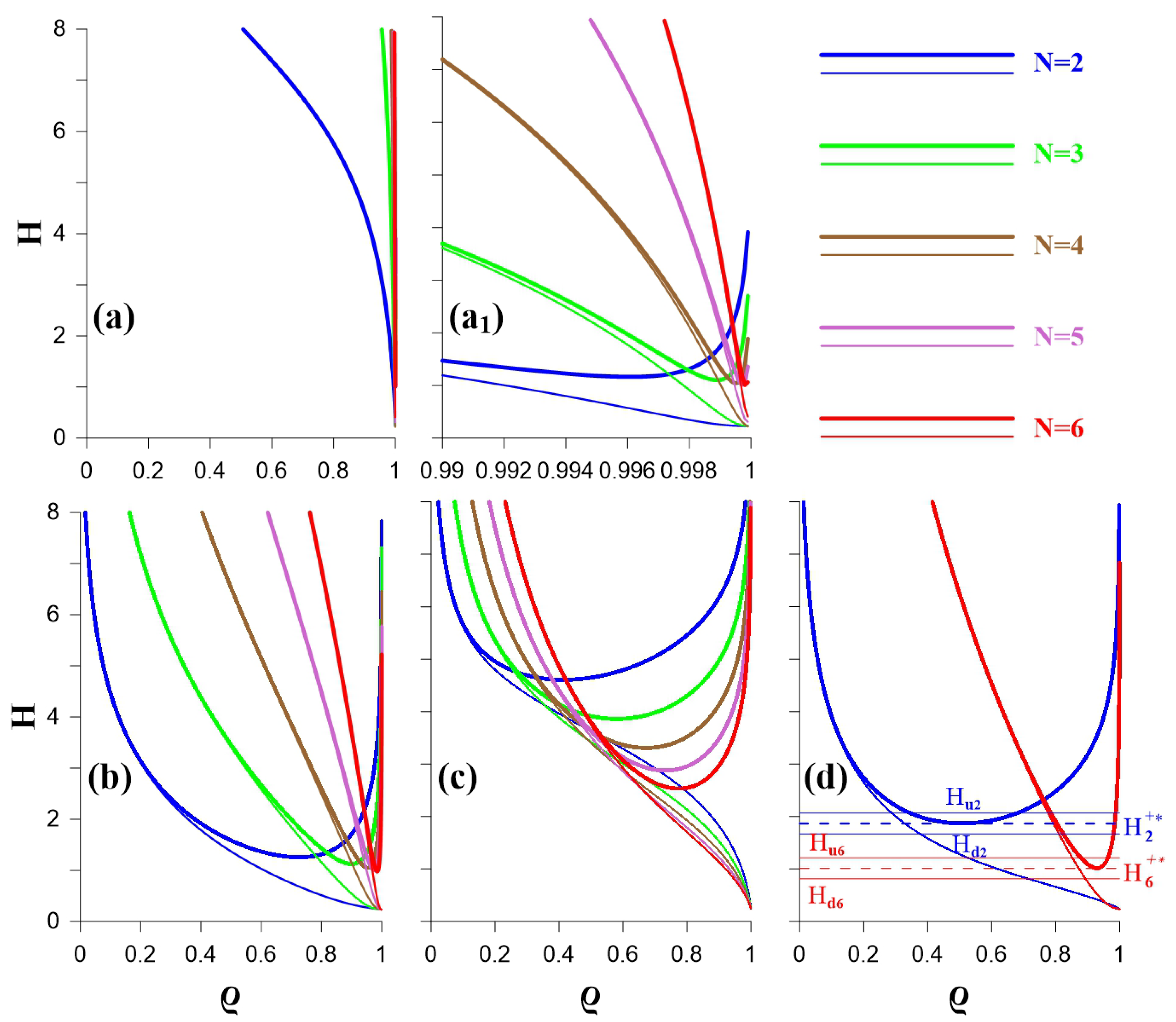
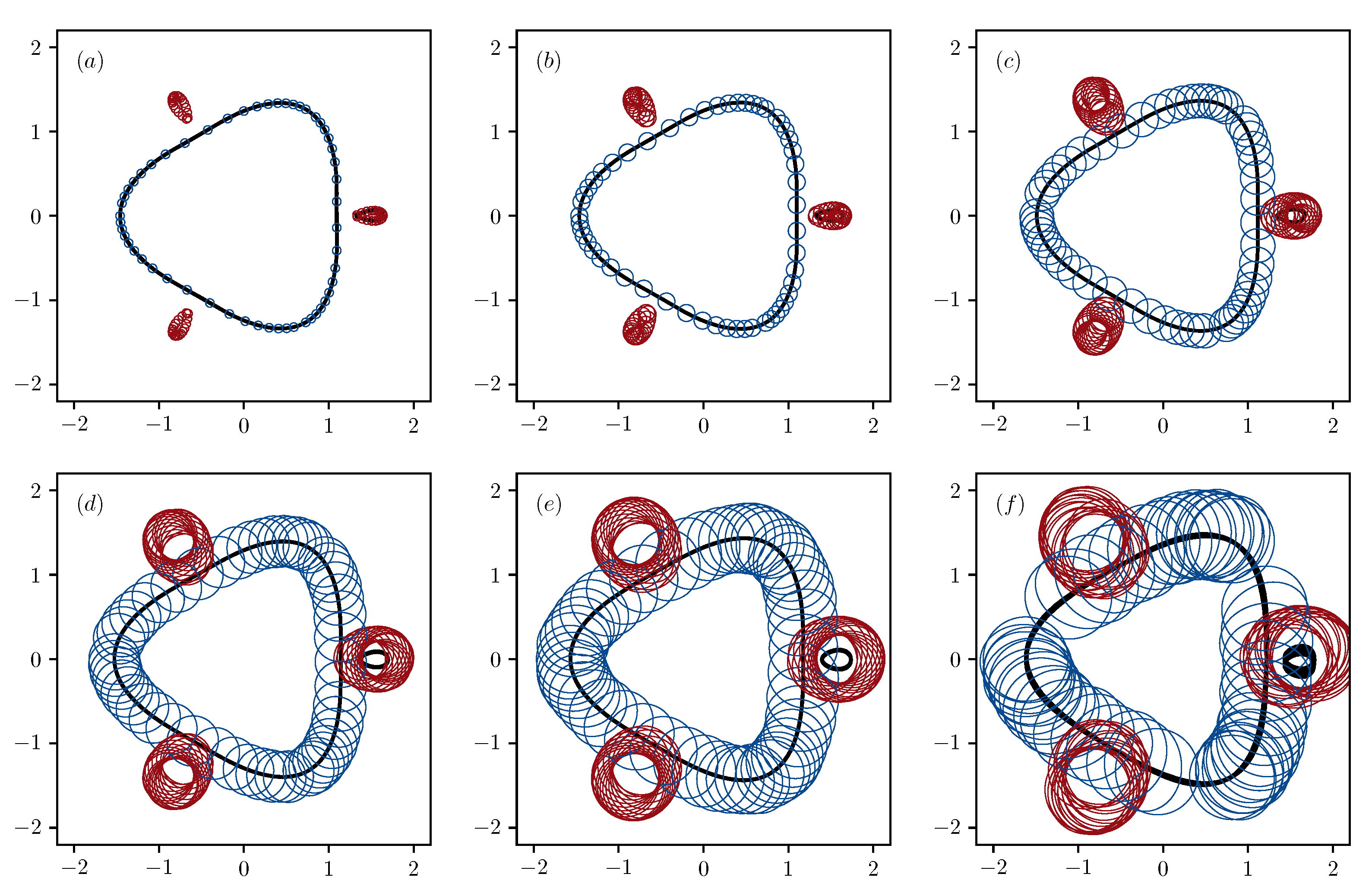
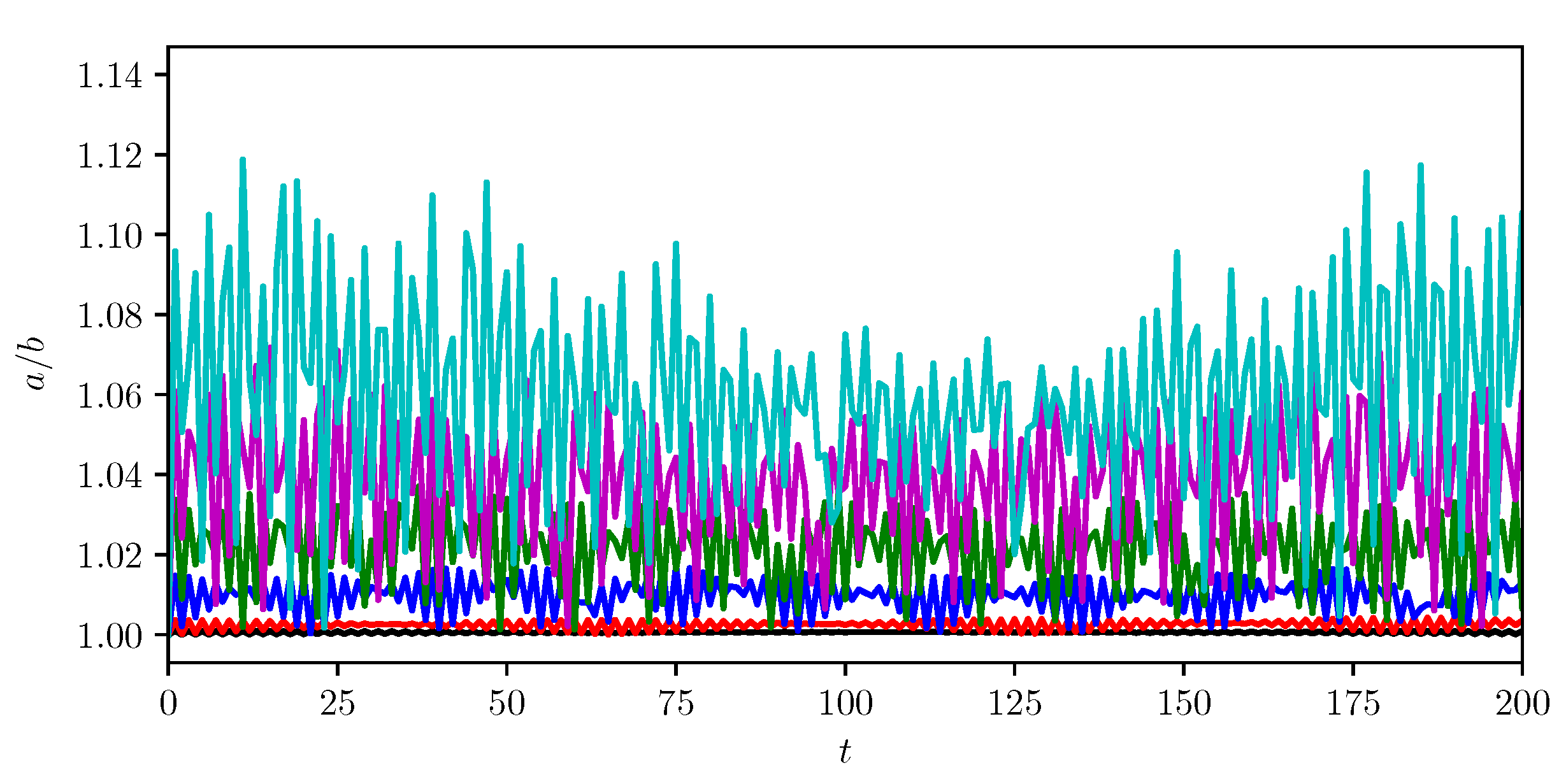
4. Finite-Core Hetons
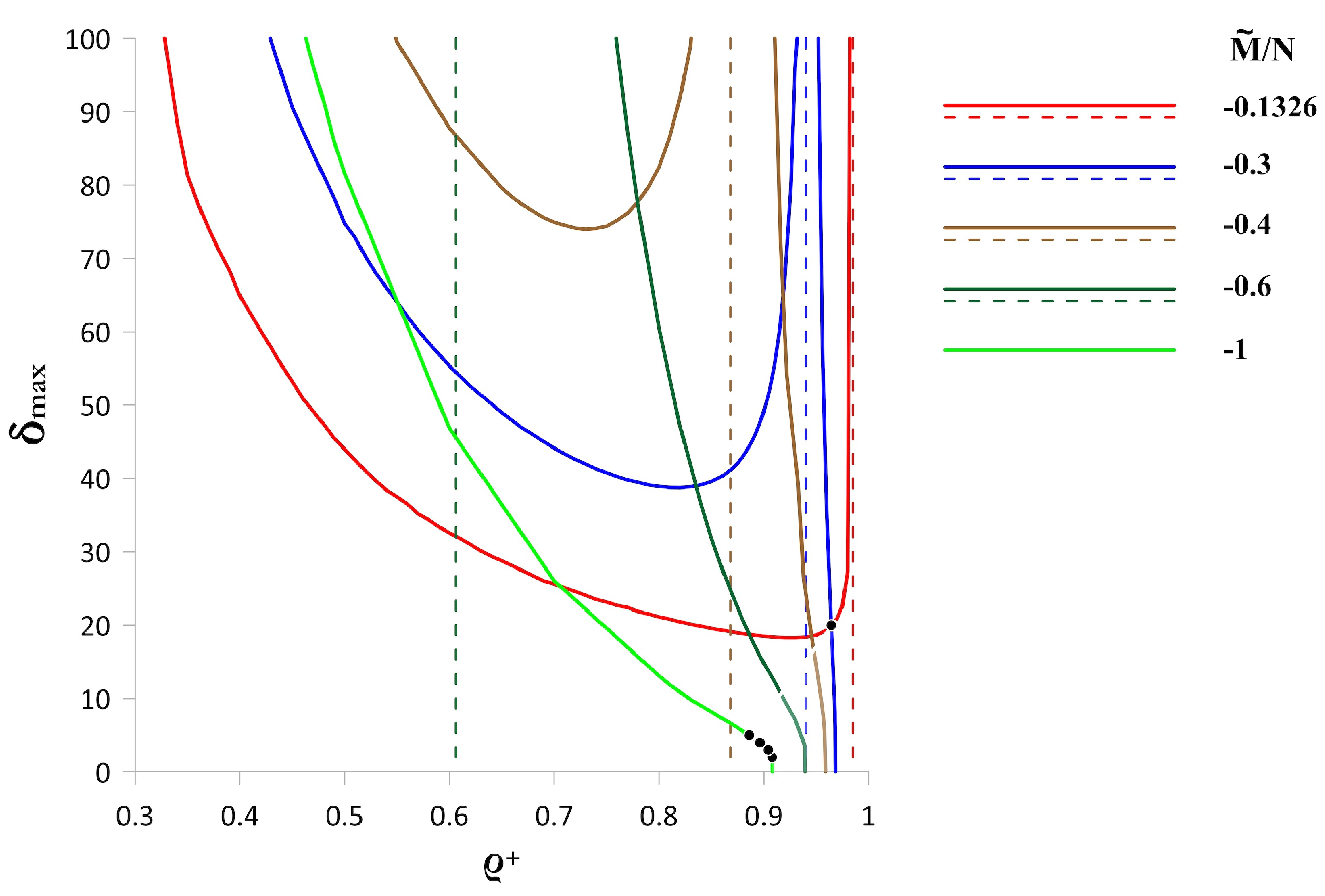
5. Discussion and Concluding Remarks
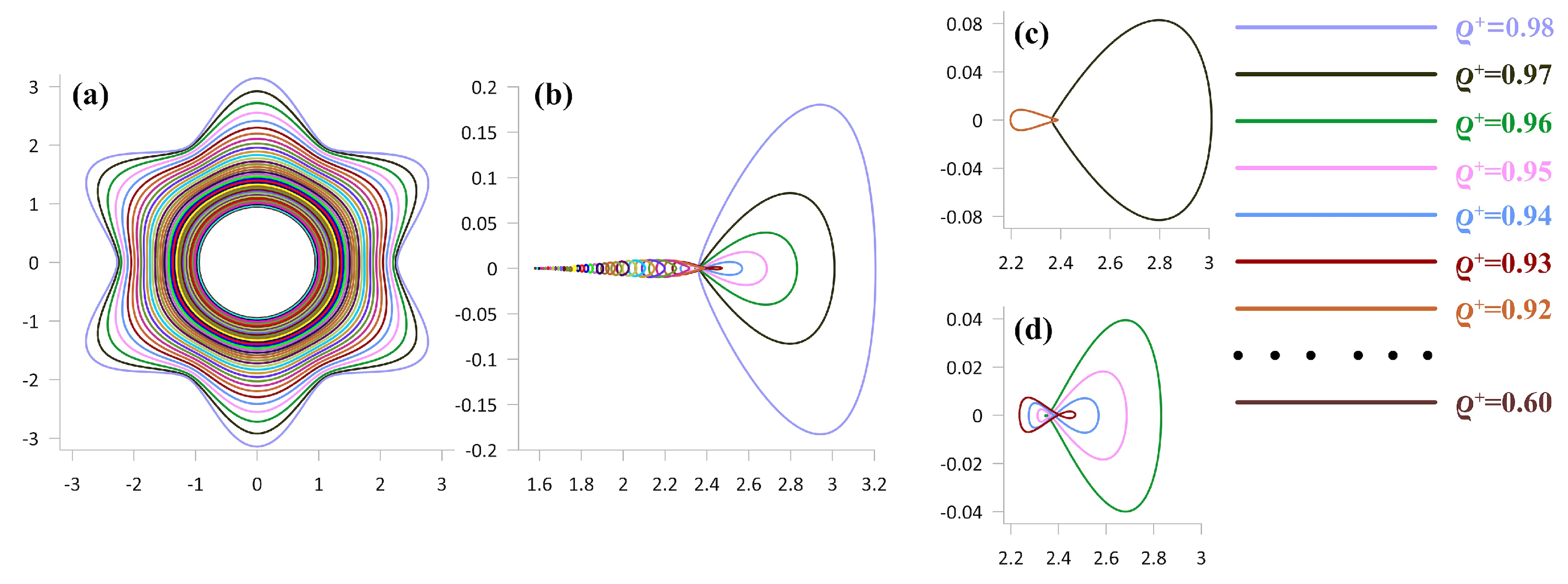
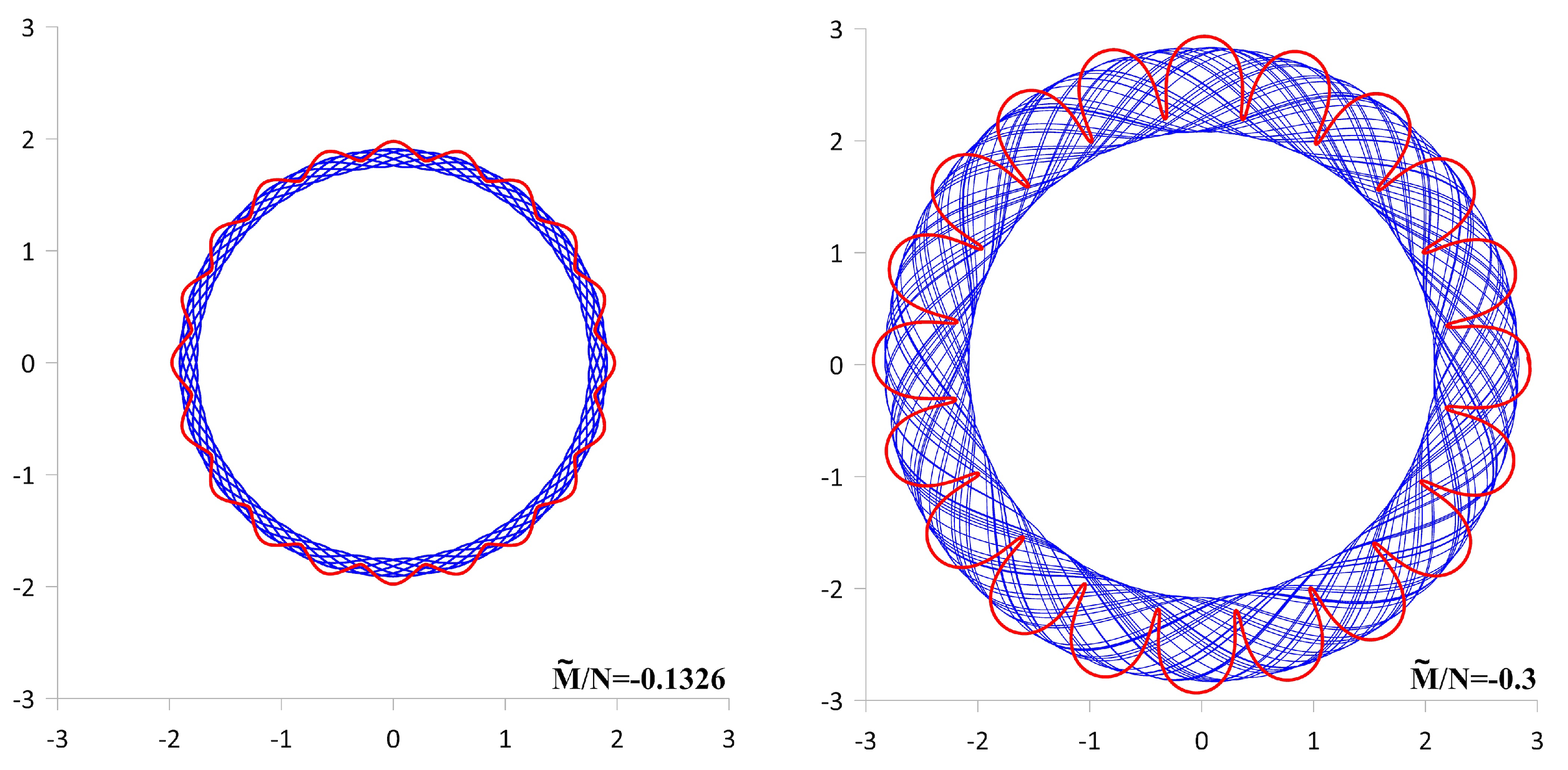
- = 0.9655: A regular mixing of warm water in both layers occurs inside an annular region, somewhat wider than the area occupied by the trajectories. The total transfer of warm fluid occurs in the cyclonic direction (type [+/+]).
- = 0.8954: All the vortices of the lower layer move move along a single trajectory in the cyclonic direction, and all the vortices of the upper layer move in the anticyclonic direction along another peripheral closed curves (type [0/+]). Both sets of vortices carry with them columns of fluid that are warmer than their surroundings.
- = 0.8960: the twelve vortices form six two-layer pairs with tilted axes, which scatter radially while preserving the N-fold symmetry of the system, and carrying warm water (motion type [∞]).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Some Useful Formulas and Results
Appendix B. Extreme Properties of the Hamiltonian
References
- Hogg, N.G.; Stommel, H.M. The heton, an elementary interaction between discrete baroclinic geostrophic vortices, and its implications concerning eddy heat-flow. Proc. R. Soc. Lond. Math. Phys. Sci. 1985, 397, 1–20. [Google Scholar]
- Hogg, N.G.; Stommel, H.M. Hetonic explosions: The breakup and spread of warm pools as explained by baroclinic point vortices. J. Atmos. Sci. 1985, 42, 1465–1476. [Google Scholar] [CrossRef]
- Gryanik, V.M. Dynamics of singular geostrophic vortices in a two-level model of atmosphere (ocean). Izvestiya Atmos. Ocean. Phys. 1983, 19, 171–179. [Google Scholar]
- Chao, S.-Y.; Shaw, P.-T. Eddy maintenance and attrition in a vertically sheared current under Arctic ice. J. Phys. Oceanogr. 1998, 28, 2427–2443. [Google Scholar] [CrossRef]
- Chao, S.-Y.; Shaw, P.-T. Close interactions between two pairs of heton-like vortices under sea ice. J. Geophys. Res. 1999, 104, 23591–23605. [Google Scholar] [CrossRef]
- Chao, S.-Y.; Shaw, P.-T. Fission of heton-like vortices under sea ice. J. Oceanogr. 1999, 55, 65–78. [Google Scholar] [CrossRef]
- Chao, S.-Y.; Shaw, P.-T. Slope-enhanced fission of salty hetons under sea ice. J. Phys. Oceanogr. 2000, 30, 2866–2882. [Google Scholar] [CrossRef]
- Chao, S.-Y.; Shaw, P.-T. Heton shedding from submarine-canyon plumes in an Arctic boundary current system: Sensitivity to the undercurrent. J. Phys. Oceanogr. 2003, 33, 2032–2044. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Chen, R.; Ayotte, B.A. Development of a point plume in the presence of background rotation. Phys. Fluids 1998, 10, 2369–2383. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Smith IV, D.C. Vortex structure in geophysical convection. Eur. J. Mech. B/Fluids 2001, 20, 437–470. [Google Scholar] [CrossRef]
- Gryanik, V.M.; Sokolovskiy, M.A.; Verron, J. Dynamics of heton-like vortices. Regul. Chaotic Dyn. 2006, 11, 417–438. [Google Scholar] [CrossRef]
- Klinger, B.A.; Marshall, J. Regimes and scaling laws for rotating deep convection in the ocean. Dyn. Atmos. Oceans 1995, 21, 221–256. [Google Scholar] [CrossRef]
- Legg, S.; Jones, H.; Visbeck, M. A heton perspective of baroclinic eddy transfer in localized open ocean convection. J. Phys. Oceanogr. 1996, 26, 2251–2266. [Google Scholar] [CrossRef]
- Legg, S.; Marshall, J. A heton model of the spreading phase of open-ocean deep convection. J. Phys. Oceanogr. 1993, 23, 1040–1056. [Google Scholar] [CrossRef]
- Legg, S.; Marshall, J. The influence of the ambient flow on the spreading of convected water masses. J. Marine Res. 1998, 56, 107–139. [Google Scholar] [CrossRef]
- Legg, S.; McWilliams, J.; Gao, J. Localization of deep ocean convection by a mesoscale eddy. J. Phys. Oceanogr. 1998, 28, 944–970. [Google Scholar] [CrossRef]
- Morel, Y.; McWilliams, J. Effect of isopycnal and diapycnal mixing on the stability of oceanic currents. J. Phys. Oceanogr. 2001, 31, 2280–2296. [Google Scholar] [CrossRef]
- Oliver, K.I.C.; Eldevik, T.; Stevens, D.P.; Watson, A.J. A Greenland Sea perspective on the dynamics of postconvective eddies. J. Phys. Oceanogr. 2008, 38, 2755–2771. [Google Scholar] [CrossRef]
- Serra, N.; Sadux, S.; Ambar, I. Observations and laboratory modeling of meddy generation of cape St. Vincent. J. Phys. Oceanogr. 2002, 32, 3–25. [Google Scholar] [CrossRef]
- Shaw, P.-T.; Chao, S.-Y. Effects of a baroclinic current on a sinking dense water plume from a submarine canyon and heton shedding. Deep Sea Res. Part I 2003, 50, 357–370. [Google Scholar] [CrossRef]
- Messori, G. The Sparadic Nature of Meridional Heat Transport in the Atmosphere. Ph.D. Thesis, Imperial College London, London, UK, 2013; p. 217. [Google Scholar]
- Mokhov, I.I.; Gryanik, V.M.; Doronina, T.N.; Lagun, D.E.; Mokhov, O.I.; Naumov, E.P.; Petukhov, V.K.; Tevs, M.V.; Khairullin, R.R. Vortex Activity in the Atmosphere: Tendencies of Changes; Institute of Atmospheric Physics of RAS: Moscow, Russia, 1993; 97p. [Google Scholar]
- Mokhov, I.I.; Doronina, T.N.; Gryanik, V.M.; Khairullin, R.R.; Korovkina, L.V.; Lagun, V.E.; Mokhov, O.I.; Naumov, E.P.; Petukhov, V.K.; Senatorsky, A.O.; et al. Extratropical cyclones and anticyclones: Tendencies of change. In The Life of Extratropical Cyclones; Gronas, S., Shapiro, M.A., Eds.; Geophysical Institute, University of Bergen: Bergen, Norway, 1994; Volume 2, pp. 56–60. [Google Scholar]
- Pedlosky, J. The instability of continuous heton clouds. J. Atmos. Sci. 1985, 42, 1477–1486. [Google Scholar] [CrossRef][Green Version]
- Griffiths, R.W.; Hopfinger, E.J. Experiments with baroclinic vortex pairs in a rotating fluid. J. Fluid Mech. 1986, 173, 501–518. [Google Scholar] [CrossRef]
- Griffiths, R.W.; Hopfinger, E.J. Coalescing of geostrophic vortices. J. Fluid Mech. 1987, 178, 73–97. [Google Scholar] [CrossRef]
- Helfrich, K.R.; Battisti, T.M. Experiments on baroclinic vortex shedding from hydrothermal plumes. J. Geophys. Res. 1991, 96, 12511–12518. [Google Scholar] [CrossRef]
- Thivolle-Cazat, E.; Sommeria, J.; Galmiche, M. Baroclinic instability of two-layer vortices in laboratory experiments. J. Fluid Mech. 2005, 544, 69–97. [Google Scholar] [CrossRef]
- Danilov, S.; Gryanik, V.; Olbers, D. Equilibration and Lateral Spreading of a Strip-Shaped Convection Region; Report 86; Alfred-Wegener-Institut für Polar- und Meeresforschung: Bremerhaven, Germany, 1998; p. 66. [Google Scholar]
- Danilov, S.; Gryanik, V.; Olbers, D. Equilibration and lateral spreading of a strip-shaped convection region. J. Phys. Oceanogr. 2001, 31, 1075–1087. [Google Scholar] [CrossRef]
- Doronina, T.; Gryanik, V.; Olbers, D.; Warncke, T. A 3D Heton Mechanism of Lateral Spreading in Lacalized Convection in a Rotating Stratified Fluid; Report 87; Alfred-Wegener-Institut für Polar- und Meeresforschung: Bremerhaven, Germany, 1998; 84p. [Google Scholar]
- Gryanik, V.M.; Doronina, T.N.; Olbers, D.; Warncke, T.H. The theory of three-dimensional hetons and vortex-dominated spreading in localized turbulent convection in a fast rotating stratified fluid. J. Fluid Mech. 2000, 423, 71–125. [Google Scholar] [CrossRef]
- Gryanik, V.M.; Borth, H.; Olbers, D. The Theory of Quasigeostrophic von Kármán Vortex Streets in Two-Layer Fluids on Beta-Plane and Intermittent Turbulent Jets; Alfred-Wegener-Institut für Polar- und Meeresforschung: Bremerhaven, Germany, 2001; Volume 106, 59p. [Google Scholar]
- Gryanik, V.M.; Borth, H.; Olbers, D. The theory of quasigeostrophic von Kármán vortex streets in two-layer fluids on beta-plane. J. Fluid Mech. 2004, 505, 23–57. [Google Scholar] [CrossRef]
- Gryanik, V.M.; Doronina, T.N. Advective transport of a conservative solute by baroclinic singular quasigeostrophic vortices in the atmosphere (ocean). Izvestiya Atmos. Ocean. Phys. 1990, 26, 1011–1026. [Google Scholar]
- Lim, C.C.; Majda, A.J. Point vortex dynamics for coupled surface/interior QG and propagating heton clasters in models for ocean convection. Geophys. Astrophys. Fluid Dyn. 2001, 94, 177–220. [Google Scholar] [CrossRef]
- Marshall, J.S. Chaotic oscillations and breakup of quasigeostrophic vortices in the N-layer approximation. Phys. Fluids 1995, 7, 983–992. [Google Scholar] [CrossRef]
- Jamaloodeen, M.I.; Newton, P.K. Two-layer quasigeostrophic potential vorticity model. J. Math. Phys. 2007, 48, 48. [Google Scholar] [CrossRef]
- Reznik, G.; Kizner, Z. Two-layer quasi-geostrophic singular vortices embedded in a regular flow: 1. Invariants of motion and stability of vortex pairs. J. Fluid Mech. 2007, 584, 185–202. [Google Scholar] [CrossRef]
- Reznik, G.; Kizner, Z. Two-layer quasi-geostrophic singular vortices embedded in a regular flow: 2. Steady and unsteady drift of individual vortices on a beta plane. J. Fluid Mech. 2007, 584, 203–223. [Google Scholar] [CrossRef]
- Shteinbuch-Fridman, B.; Makarov, V.; Kizner, Z. Transitions and oscillatory regimes in two-layer geostrophic hetons and tripoles. J. Fluid Mech. 2017, 810, 535–553. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Verron, J. Finite-core hetons: Stability and interactions. J. Fluid Mech. 2000, 423, 127–154. [Google Scholar] [CrossRef]
- Young, W.R. Some interactions between small numbers of baroclinic, geostrophic vortices. Geophys. Astrophys. Fluid Dyn. 1985, 33, 35–61. [Google Scholar] [CrossRef]
- Kozlov, V.F.; Makarov, V.G.; Sokolovskiy, M.A. Numerical model of the baroclinic instability of axially symmetric eddies in two-layer ocean. Izvestiya Atmos. Ocean. Phys. 1986, 22, 674–678. [Google Scholar]
- Helfrich, K.R.; Send, U. Finite-amplitude evolution of two-layer geostrophic vortices. J. Fluid Mech. 1988, 197, 331–348. [Google Scholar] [CrossRef]
- Polvani, L.M.; Zabusky, N.J.; Flierl, G.R. Applications of contour dynamics to two-layer quasi-geostrophic flows. Fluid Dyn. Res. 1988, 3, 422–424. [Google Scholar] [CrossRef]
- Polvani, L.M. Two-layer geostrophic vortex dynamics. 2. Alignment and two-layer V-states. J. Fluid Mech. 1991, 225, 241–270. [Google Scholar] [CrossRef]
- Reinaud, J.N. On the stability of continuously stratified quasi-geostrophic hetons. Fluid Dyn. Res. 2015, 47, 035510. [Google Scholar] [CrossRef]
- Kizner, Z. Stability and transitions of hetonic quartets and baroclinic modons. Phys. Fluids 2006, 18, 056601. [Google Scholar] [CrossRef]
- Makarov, V.G.; Sokolovskiy, M.A.; Kizner, Z. Doubly symmetric finite-core heton equilibria. J. Fluid Mech. 2012, 708, 397–417. [Google Scholar] [CrossRef][Green Version]
- Reinaud, J.; Carton, X. The stability and the nonlinear evolution of quasi-geostrophic hetons. J. Fluid Mech. 2009, 636, 109–135. [Google Scholar] [CrossRef]
- Reinaud, J.N.; Carton, X. Head on collisions between two quasi-geostrophic hetons in a continuously stratified fluid. J. Fluid Mech. 2015, 779, 144–180. [Google Scholar] [CrossRef]
- Reinaud, J.N.; Carton, X.; Dritschel, D.G. Interaction between a quasi-geostrophic buoyancy filament and a heton. Fluids 2017, 2, 37. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Sokolovskiy, M.A. Interaction of two-layer vortex pair with a submerged cylindrical obstacle in a two-layer rotating fluid. Phys. Fluids 2016, 28, 056602. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Carton, X. Baroclinic multipole formation from heton interaction. Fluid Dyn. Res. 2010, 42, 045501. [Google Scholar] [CrossRef][Green Version]
- Sokolovskiy, M.A.; Koshel, K.V.; Verron, J. Three-vortex quasi-geostrophic dynamics in a two-layer fluid. Part I. Analysis of relative and absolute motions. J. Fluid Mech. 2013, 717, 232–254. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Verron, J. Dynamics of Vortex Structures in a Stratified Rotating Fluid; Atmospheric and Oceanographic Sciences Library; Springer: Cham, Switzerland, 2014; Volume 47, p. 382. [Google Scholar]
- Sokolovskiy, M.; Verron, J.; Carton, X.; Gryanik, V. On instability of elliptical hetons. Theor. Comput. Fluid Dyn. 2010, 24, 117–123. [Google Scholar] [CrossRef][Green Version]
- Valcke, S.; Verron, J. On interactions between two finite-core hetons. Phys. Fluids 1993, A5, 2058–2060. [Google Scholar] [CrossRef]
- Verron, J.; Valcke, S. Scale-dependent merging of baroclinic vortices. J. Fluid Mech. 1994, 264, 81–106. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Koshel, K.V.; Dritschel, D.G.; Reinaud, J.N. N-symmetric interaction of N hetons. I: Analysis of the case N = 2. Phys. Fluids 2020, 32, 096601. [Google Scholar] [CrossRef]
- Koshel, K.V.; Reinaud, J.N.; Riccardi, G.; Ryzhov, E.A. Entrapping of a vortex pair interacting with a fixed point vortex revisited. I. Point vortices. Phys. Fluids 2018, 30, 096603. [Google Scholar] [CrossRef]
- Reinaud, J.N.; Koshel, K.V.; Ryzhov, E.A. Entrapping of a vortex pair interacting with a fixed point vortex revisited. II. Finite size vortices and the effect of deformation. Phys. Fluids 2018, 30, 096604. [Google Scholar] [CrossRef]
- Simó, C. New families of solutions to the N-body problems. In European Congress of Mathematics: Barcelona, July 10–14, 2000, Volume I; Casacuberta, C., Miró-Roig, R.M., Verdera, J., Xambó-Descamps, S., Eds.; Progress in Mathematics; Birkhäuser Basel: Basel, Switzerland, 2001; Volume 201, pp. 101–115. [Google Scholar]
- Borisov, A.V.; Mamaev, I.S.; Kilin, A.A. Absolute and relative choreographies in the problem of point vortices moving on a plane. Regul. Chaotic Dyn. 2004, 9, 101–111. [Google Scholar] [CrossRef]
- Borisov, A.V.; Kilin, A.A.; Mamaev, I.S. The dynamics of vortex rings: Leapfrogging, choreographies and the stability problem. Regul. Chaotic Dyn. 2013, 18, 33–62. [Google Scholar] [CrossRef]
- Bartsch, T. Periodic solutions of singular first-order Hamiltonian systems of N-vortex type. Arch. Math. 2016, 107, 413–422. [Google Scholar] [CrossRef]
- Calleja, R.C.; Doedel, E.J.; García-Azpeitia, C. Choreographies in the n-vortex problem. Regul. Chaotic Dyn. 2018, 23, 595–612. [Google Scholar] [CrossRef]
- Dai, Q.; Gebhard, B.; Bartsch, T. Periodic solutions of N-vortex type Hamiltonian systems near the domain boundary. SIAM J. Appl. Math. 2018, 78, 977–995. [Google Scholar] [CrossRef]
- Dritschel, D.G. Contour surgery: A topological reconnection scheme for extended integrations using contour dynamics. J. Comput. Phys. 1988, 79, 240–266. [Google Scholar] [CrossRef]
- NIST Digital Library of Mathematical Functions. Available online: https://dlmf.nist.gov/.





| 0.05 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 0.8897 | 0.8904 | 0.8935 | 0.8978 | 0.9025 | 0.9078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koshel, K.V.; Sokolovskiy, M.A.; Dritschel, D.G.; Reinaud, J.N. N-Symmetric Interaction of N Hetons, II: Analysis of the Case of Arbitrary N. Fluids 2024, 9, 122. https://doi.org/10.3390/fluids9060122
Koshel KV, Sokolovskiy MA, Dritschel DG, Reinaud JN. N-Symmetric Interaction of N Hetons, II: Analysis of the Case of Arbitrary N. Fluids. 2024; 9(6):122. https://doi.org/10.3390/fluids9060122
Chicago/Turabian StyleKoshel, Konstantin V., Mikhail A. Sokolovskiy, David G. Dritschel, and Jean N. Reinaud. 2024. "N-Symmetric Interaction of N Hetons, II: Analysis of the Case of Arbitrary N" Fluids 9, no. 6: 122. https://doi.org/10.3390/fluids9060122
APA StyleKoshel, K. V., Sokolovskiy, M. A., Dritschel, D. G., & Reinaud, J. N. (2024). N-Symmetric Interaction of N Hetons, II: Analysis of the Case of Arbitrary N. Fluids, 9(6), 122. https://doi.org/10.3390/fluids9060122







