Circular Fluid Heating—Transient Entropy Generation
Abstract
1. Introduction
2. Methodology
2.1. Analytical Approach
- −
- hydraulic irreversibilities were not considered in the analysis presented in this paper;
- −
- heat exchange with the environment was minimized and neglected in the analytical modeling;
- −
- the effects of sudden fluid (air) deflection, local fluid mixing, and frictional forces on heat exchange were also not considered in this work;
- −
- it was assumed that the inlet temperature of the air in the housing remained constant;
- −
- the physical properties of the air and housing materials were based on average temperature values.
2.2. Experimental Approach
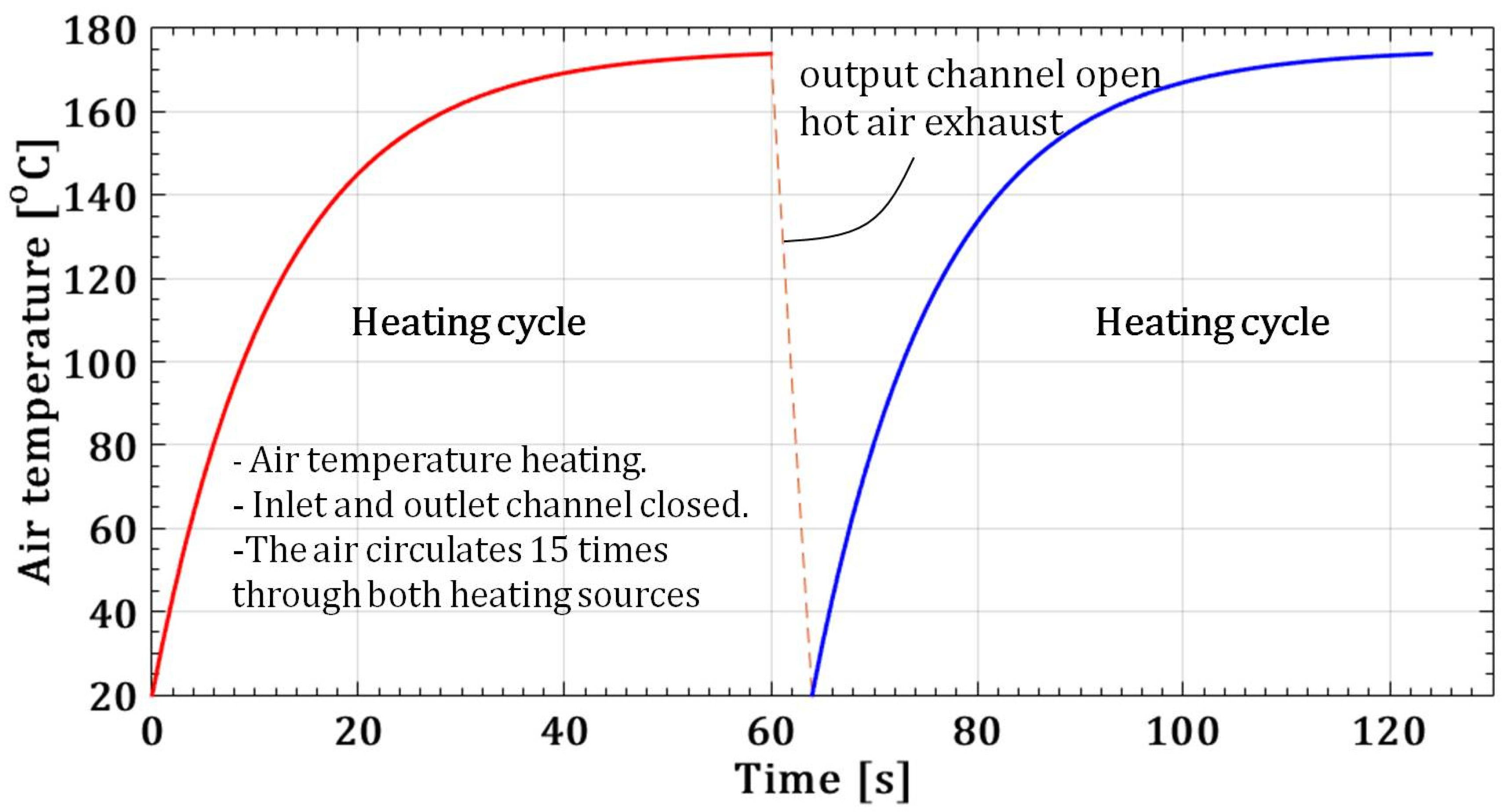
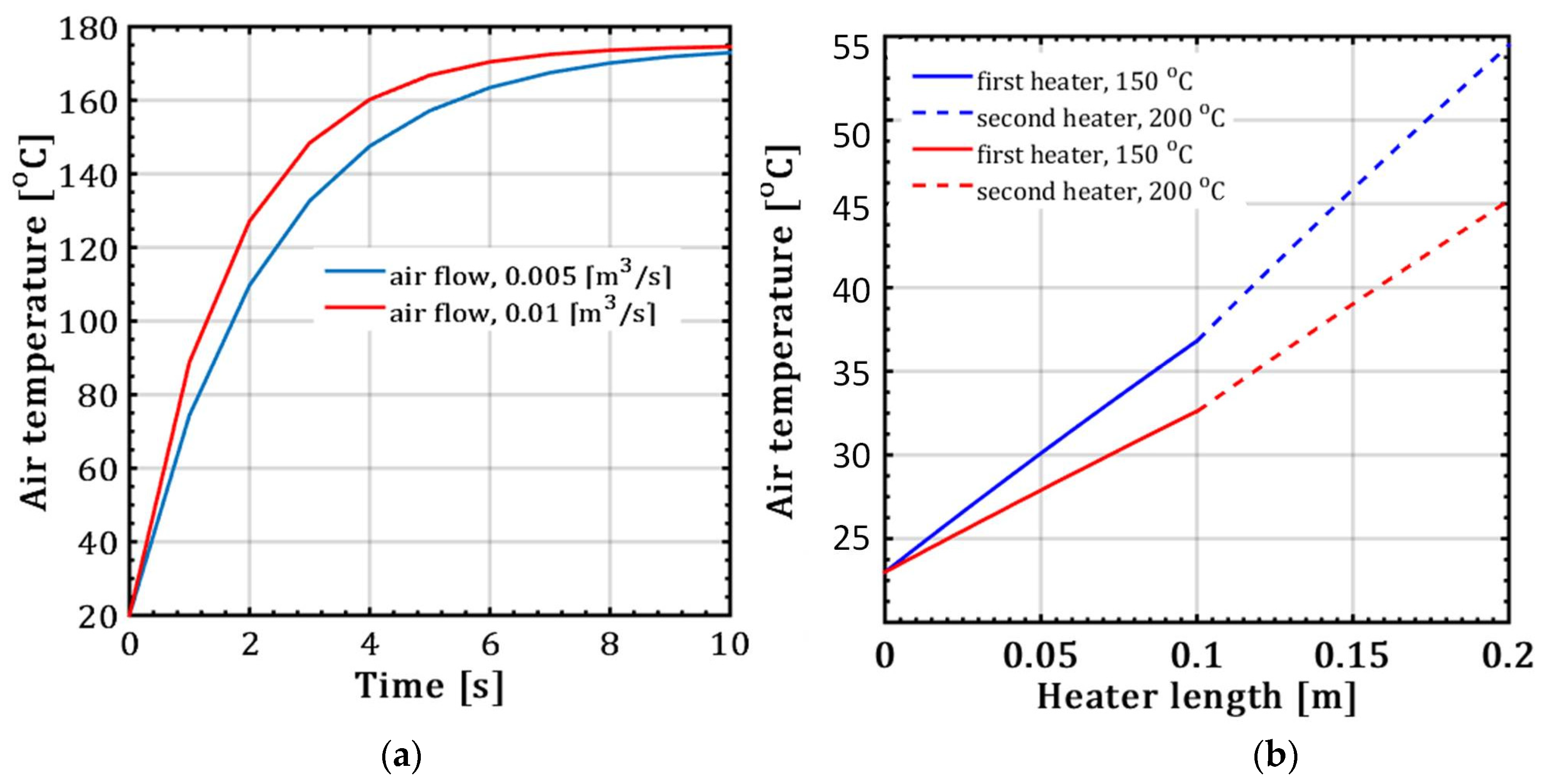
3. Results and Discussion
4. Conclusions
- From an analytical point of view, a mathematical model of the total thermal entropy is established as a function of the geometric and process parameters of the heating system. The analytical model is based on the constant temperatures of the PTC heaters, but it also allows for the consideration of transient temperatures of the heating sources.
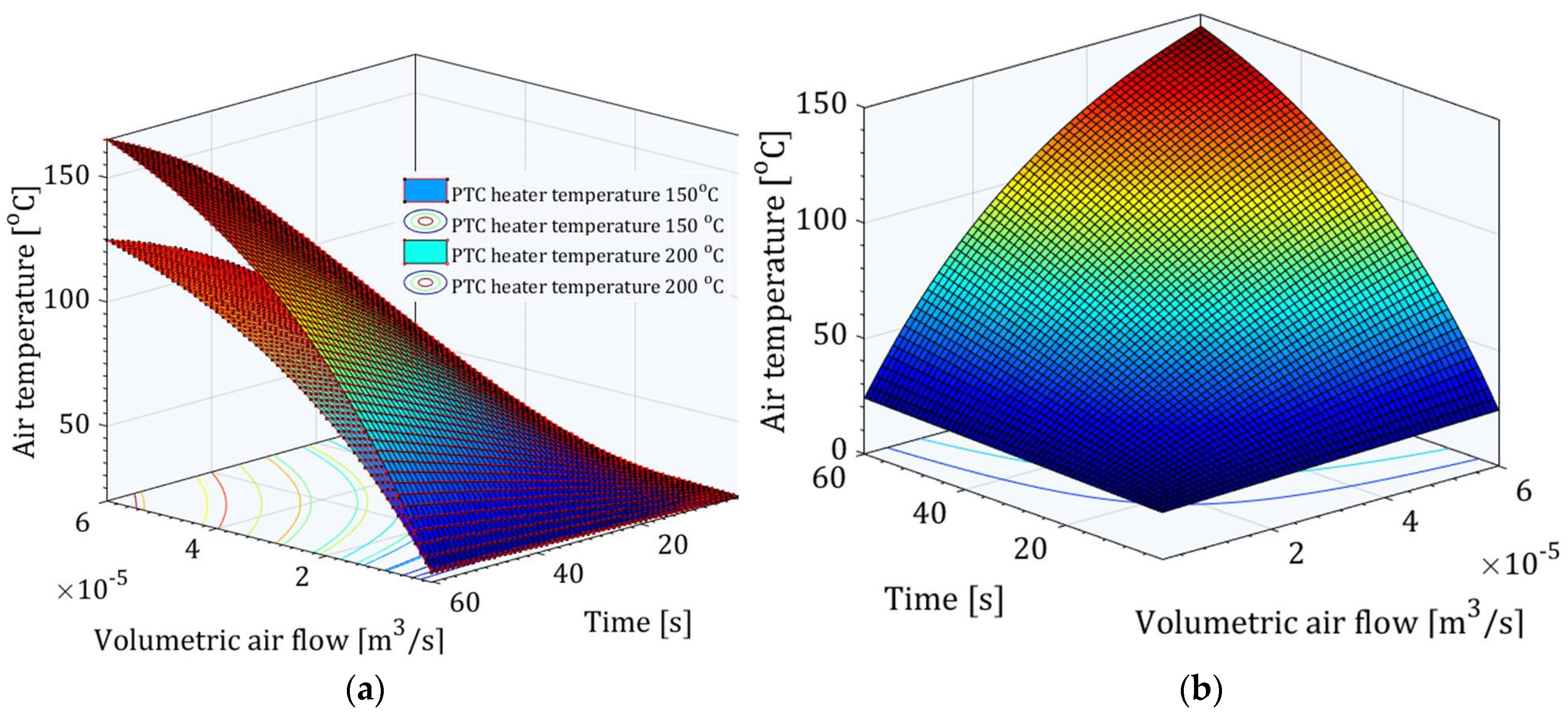
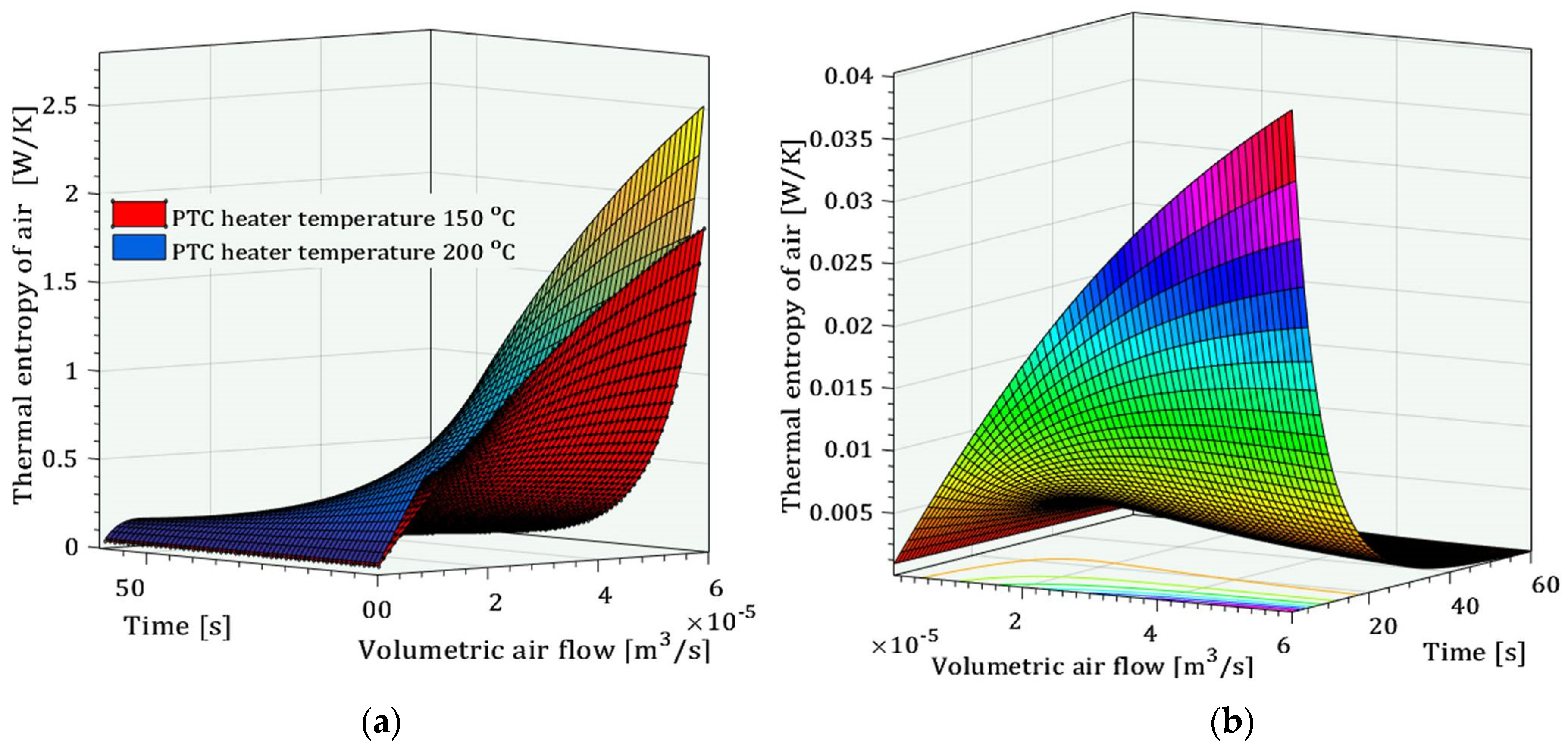
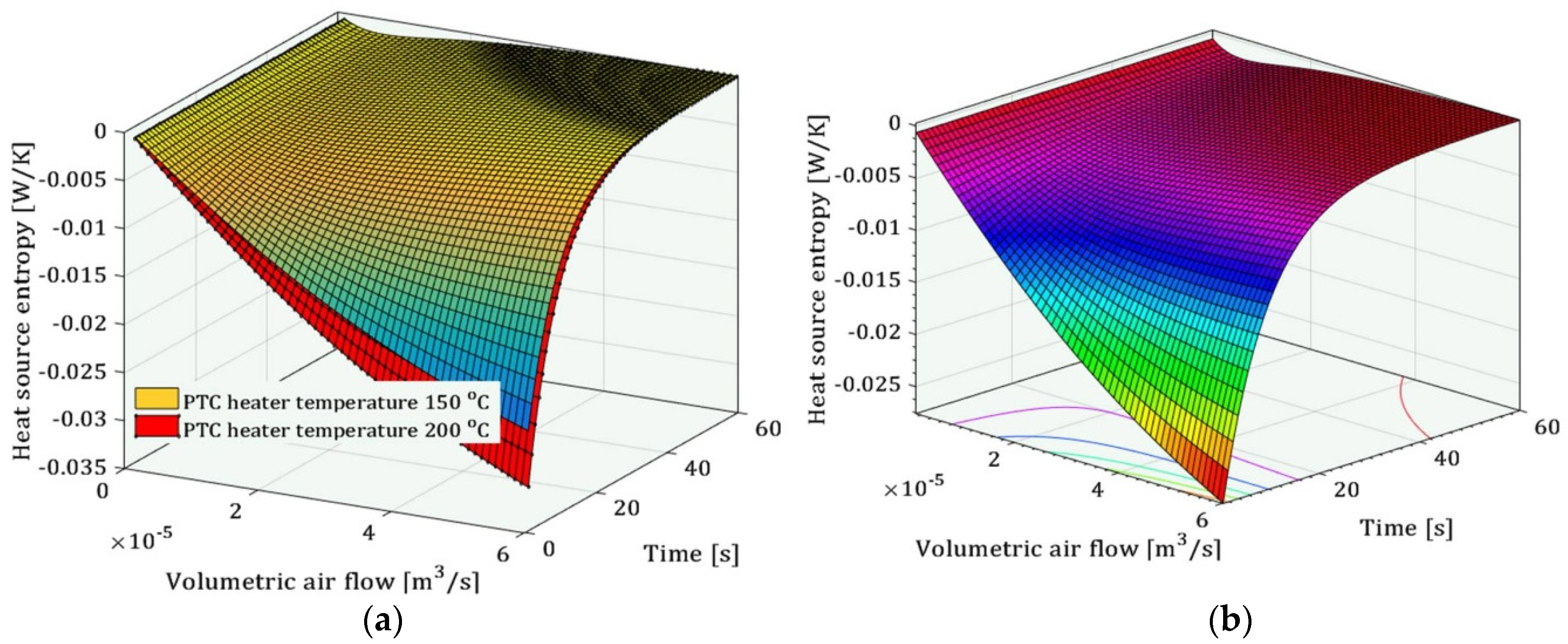
- The established analytical model indicates the influence of the volumetric air flow and the temperature of the PTC heater on the transient temperature and thermal entropy of the air, as well as the thermal entropy of the PTC heater. The transient, thermally generated air entropy increases rapidly with the increase in the heating time and volumetric air flow inside the channel during circular heating. Additionally, a higher temperature in the heating source results in an increase in thermal entropy.
- From an experimental point of view, the temperatures of the PTC heaters are transient and the expressions for their rate of change over time can be incorporated into the established analytical model. The experimental results indicate a minimal amount of transient thermal entropy, which directly implies the optimal geometrical and process parameters of the circular heating system.
- By keeping the geometrical parameters constant in this analysis, the minimum transient thermal entropy determines the optimal time for air release from the casing.
- The minimum transient thermal entropy of the circular heating of air is the basis for the automation of the process of circular heating for any fluid. Furthermore, by removing the constraints imposed in this work, the optimization can be used for geometrical and process parameters.
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ta.A | air temperature in section A, K |
| Ta.B | air temperature in section B, K |
| Tfo.1 | fin base temperature in section A, K |
| Tfo.2 | fin base temperature in section B, K |
| Va | volumetric flow rate, m3s−1 |
| Afo | cross-sectional area of fin, m2 |
| Af | fin surface, m2 |
| h | fin height, m |
| L | heater length, m |
| Sgen.a | transient thermal entropy of air, WK−1 |
| Sgen.hs | heat source entropy, WK−1 |
| ca | specific heat capacity, Jkg−1K−1 |
| Dh | hydraulic diameter of channel, m |
| ReDh | channel Reynolds number, - |
| wa.o | air velocity in front of channel, ms−1 |
| wch | air velocity within channel, ms−1 |
| P | fin perimeter, m |
| Greek symbols | |
| δ | fin distance, m |
| δf | fin thickness, m |
| α | convective heat transfer coefficient, Wm−2K−1 |
| λ | conductive heat transfer coefficient, Wm−1K−1 |
| τ | time, s |
| υa | kinematic viscosity, m2s−1 |
| ρa | air density, kgm−3 |
| ηf | fin efficiency, - |
References
- Ma, L.; Zhao, X.; Sun, H.; Wu, Q.; Liu, W. Experimental Study of Single Phase Flow in a Closed-Loop Cooling System with Integrated Mini-Channel Heat Sink. Entropy 2016, 18, 128. [Google Scholar] [CrossRef]
- Archana, V.; Vaidya, A.M.; Vijayan, P.K. Flow Transients in Supercritical CO2 Natural Circulation Loop. Procedia Eng. 2015, 127, 1189–1196. [Google Scholar] [CrossRef]
- Thippeswamy, L.R.; Kumar Yadav, A. Heat transfer enhancement using CO2 in a natural circulation loop. Sci. Rep. 2020, 10, 1507. [Google Scholar] [CrossRef] [PubMed]
- Bade, M.H.; Bandyopadhyay, S. Targeting Minimum Heat Transfer Fluid Flow for Multiple Heat Demands. Comput. Aided Chem. Eng. 2012, 31, 675–679. [Google Scholar]
- Sharma, M.; Vijayan, P.K.; Pilkhwal, D.S.; Asako, Y. Asako Steady state and stability characteristics of natural circulation loops operating with carbon dioxide at supercritical pressures for open and closed loop boundary conditions. Nucl. Eng. Des. 2013, 265, 737–754. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, T.; Feng, B.; Yuan, Y.; Li, F.; Feng, G.; Jiang, Z. Thermal and fluid processes in a closed-loop geothermal system using CO2 as a working fluid. Renew. Energy 2020, 154, 351–367. [Google Scholar] [CrossRef]
- Rittidech, S.; Sangiamsuk, S. Internal flow patterns on heat transfer performance of a closed-loop oscillating heat pipe with check valves. Exp. Heat Transf. 2012, 25, 48–57. [Google Scholar] [CrossRef]
- Dehshali, M.E.; Nazari, M.A.; Shafii, M.B. Thermal performance of rotating closed-loop pulsating heat pipes:Experimental investigation and semi-empirical correlation. Int. J. Therm. Sci. 2018, 123, 14–26. [Google Scholar] [CrossRef]
- Ando, M.; Okamoto, A.; Nagai, H. Start-up and heat transfer characteristics of oscillating heat pipe with different check valve layouts. Appl. Therm. Eng. 2021, 196, 117286. [Google Scholar] [CrossRef]
- Song, E.-H.; Lee, K.-B.; Rhi, S.-H.; Kim, K. Thermal and Flow Characteristics in a Concentric Annular Heat Pipe Heat Sink. Energies 2020, 13, 5282. [Google Scholar] [CrossRef]
- Jilte, R.; Ahmadi, M.H.; Kumar, R.; Kalamkar, V.; Mosavi, A. Cooling Performance of a Novel Circulatory Flow Concentric Multi-Channel Heat Sink with Nanofluids. Nanomaterials 2020, 10, 647. [Google Scholar] [CrossRef] [PubMed]
- Mustafa, J.; Alqaed, S.; Siddiqui, M.A. Thermally Driven Flow of Water in Partially Heated Tall Vertical Concentric Annulus. Entropy 2020, 22, 1189. [Google Scholar] [CrossRef] [PubMed]
- Wiriyasart, S.; Naphon, P. Thermal to electrical closed-loop thermoelectric generator with compact heat sink modules. Int. J. Heat Mass Transf. 2021, 164, 120562. [Google Scholar] [CrossRef]
- Siddique, A.R.M.; Muresan, H.; Majid, S.H.; Mahmud, S. An adjustable closed-loop liquid-based thermoelectric electronic cooling system for variable load thermal management. Therm. Sci. Eng. Prog. 2019, 10, 245–252. [Google Scholar] [CrossRef]
- Chang, S.W.; Gao, J.Y.; Shin, H.L. Thermal performances of turbulent tubular flows enhanced by ribbed and grooved wire coils. Int. J. Heat Mass Transf. 2015, 90, 1109–1124. [Google Scholar] [CrossRef]
- Chyu, M.C. Thermal analysis of the electrically heated cylindrical test section for heat transfer experiments. Exp. Therm. Fluid Sci. 1988, 1, 19–27. [Google Scholar] [CrossRef]
- Hsiao, S.Y.; Wei, P.S.; Wang, Z.O. Three-dimensional temperature field in a line-heater embedded by a spiral electric resistor. Appl. Therm. Eng. 2006, 26, 916–926. [Google Scholar] [CrossRef]
- Wang, M.C.; Chen, Y.P.; Wu, J.F.; Dong, C. Heat transfer enhancement of folded helical baffle electric heaters with one-plus-two U-tube units. Appl. Therm. Eng. 2016, 102, 586–595. [Google Scholar] [CrossRef]
- Alic, F. The non-dimensional analysis of nanofluid irreversibility within novel adaptive process electric heaters. Appl. Therm. Eng. 2019, 152, 13–23. [Google Scholar] [CrossRef]
- Samal, B.; Barik, A.K.; Awad, M.M. Thermo-fluid and entropy generation analysis of newly designed loops for constructal cooling of a square plate. Appl. Therm. Eng. 2019, 156, 250–262. [Google Scholar] [CrossRef]
- Miguel, A.F. A study of entropy generation in tree-shaped flow structures. Int. J. Heat Mass Transf. 2016, 92, 349–359. [Google Scholar] [CrossRef]
- Liu, M.; Li, S.; Wu, Z.; Zhang, K.; Wang, S.; Liang, X. Entropy generation analysis for grooved structure plate flow. Eur. J. Mech.—B/Fluids 2019, 77, 87–97. [Google Scholar] [CrossRef]
- Wei, S.; Chen, L.; Sun, F. Constructal Entransy Dissipation Minimization of Round Tube Heat Exchanger Cross-Section. Int. J. Therm. Sci. 2011, 50, 1285–1292. [Google Scholar] [CrossRef]
- Alic, F. Entransy Dissipation Analysis and New Irreversibility Dimension Ratio of Nanofluid Flow. Energies 2020, 13, 114. [Google Scholar] [CrossRef]
- Wu, J.; Liang, X. Application of Entransy Dissipation Extremum Principle in Radiative Heat Transfer Optimization. Sci. China Ser. 2008, 51, 1306–1314. [Google Scholar] [CrossRef]
- Teertstra, P.; Yovanovich, M.M.; Culham, J.R. Analytical forced convection modeling of plate fin heat sinks. J. Electron. Manuf. 2000, 10, 253–261. [Google Scholar] [CrossRef]
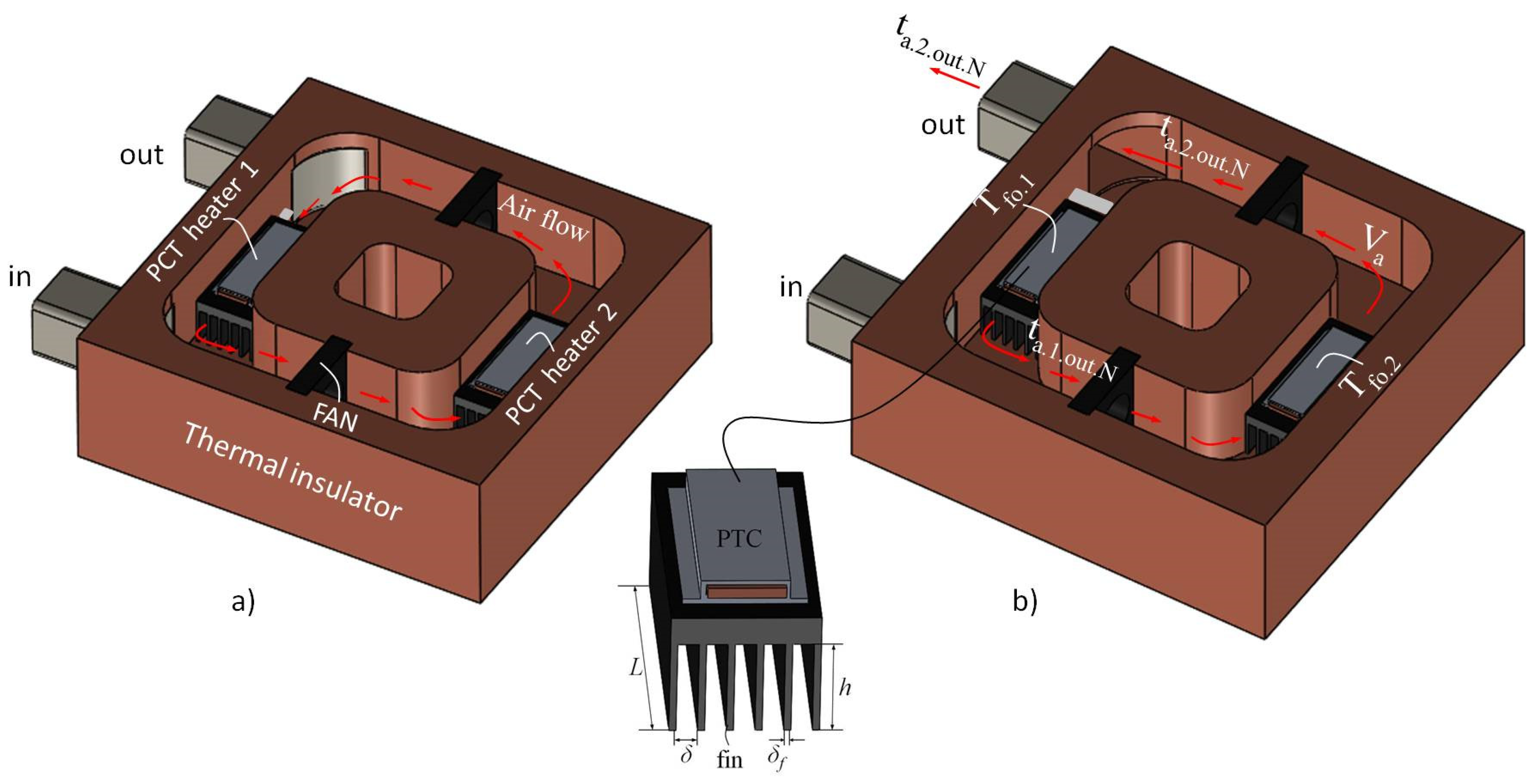



| L [m] | δf [m] | δ [m] | nf [-] | h [m] | ta.o [°C] | tf.o.1 [°C] | tf.o.2 [°C] | Heater Type | Fluid |
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.002 | 0.006 | 6 | 0.025 | 20 | 150 | 200 | PTC 230V ac, 75 × 35 × 8.5 mm | Air |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alic, F. Circular Fluid Heating—Transient Entropy Generation. Fluids 2024, 9, 119. https://doi.org/10.3390/fluids9050119
Alic F. Circular Fluid Heating—Transient Entropy Generation. Fluids. 2024; 9(5):119. https://doi.org/10.3390/fluids9050119
Chicago/Turabian StyleAlic, Fikret. 2024. "Circular Fluid Heating—Transient Entropy Generation" Fluids 9, no. 5: 119. https://doi.org/10.3390/fluids9050119
APA StyleAlic, F. (2024). Circular Fluid Heating—Transient Entropy Generation. Fluids, 9(5), 119. https://doi.org/10.3390/fluids9050119







