A Variational Surface-Evolution Approach to Optimal Transport over Transitioning Compact Supports with Domain Constraints
Abstract
1. Introduction
Novelties and Contributions Presented in This Work
2. Spatiotemporal Hypersurface
2.1. Assumptions
2.1.1. Compact Support
2.1.2. Balanced Density
2.1.3. Smoothness
2.1.4. Piece-Wise Smooth Boundary
2.1.5. Smooth Extension
2.2. Local Geometry
2.2.1. Parameterization
2.2.2. Unit Normal
2.2.3. Metric Tensor
2.2.4. Area Element
2.2.5. Normal Variations
3. Spatiotemporal Formulation of Optimal Mass Transport
3.1. Spatiotemporal Advection Field
3.2. Solenoidal Vector Field
3.3. Extended Velocity
3.3.1. Local Kinetic Energy
3.3.2. Extended Velocity
3.3.3. Generalized Momentum
3.4. Variational Formulation
3.4.1. Action Integral
3.4.2. First Variation
3.4.3. Optimality Condition for
3.4.4. Partial Gradient with Respect to (Fixed Support)
3.4.5. Shape Optimality Condition for
3.4.6. Conjectures on the Existence of Optimal Transport with Intermediate Support Constraints
4. Shape Optimization Strategy with Added Density Prior
4.1. Density Prior
4.2. Optimality Conditions and Partial Gradients
4.3. Optimization in (Fixed Support)
4.3.1. Computing an Initial Solenoidal Field
4.3.2. Iterated Gradient Descent for the Solenoidal Field
4.4. Total Shape Gradient
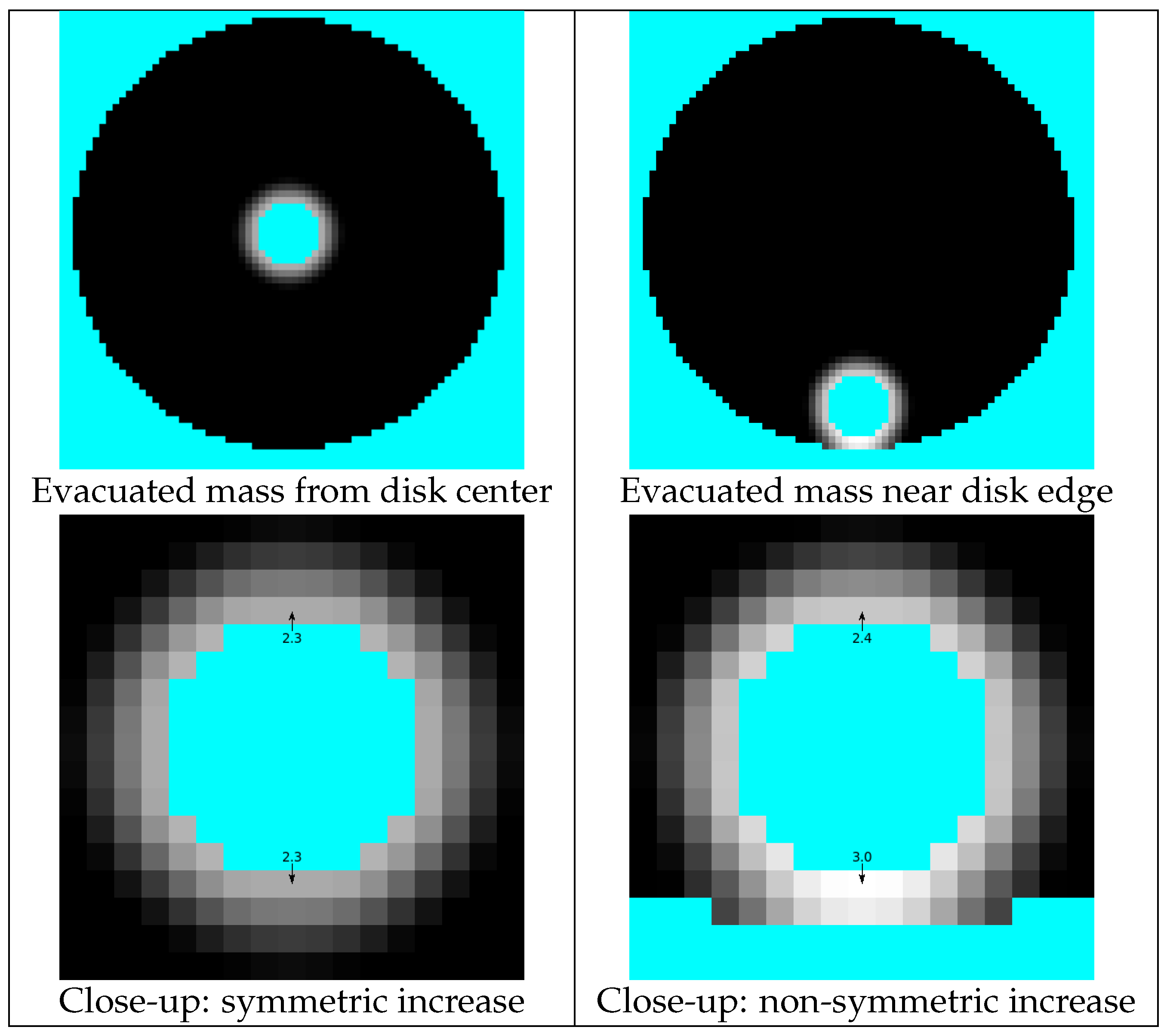
5. Results
5.1. Interpolation between Two Different Non-Convex Supports
5.2. Optimal Transport with Support Constraints
5.2.1. Known Densities with Intermediate Support Constraints
5.2.2. Unknown Final Density but with Known Support
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detailed First Variation and Gradient Calculation
Appendix B. Coupled Boundary and Flux Perturbations
References
- Monge, G. Mémoire sur la Théorie des Déblais et des Remblais; Histoire de l’Académie Royale des Sciences de Paris; Imprimerie Royale: Paris, France, 1781. [Google Scholar]
- Kantorovich, L.V. On a problem of monge. CR (Dokl.) Acad. Sci. URSS (NS) 1948, 3, 225–226. [Google Scholar] [CrossRef]
- Gangbo, W.; McCann, R. The geometry of optimal transportation. Acta Math. 1996, 177, 113–161. [Google Scholar] [CrossRef]
- Villani, C. Topics in Optimal Transportation; American Mathematical Soc.: Ann Arbor, MI, USA, 2003. [Google Scholar]
- Villani, C. Optimal Transport: Old and New; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 338. [Google Scholar]
- Evans, L.C.; Gangbo, W. Differential equations methods for the Monge-Kantorovich mass transfer problem. In Memoirs of the American Mathematical Society; American Mathematical Soc.: Ann Arbor, MI, USA, 1999; Volume 137, no. 653. [Google Scholar]
- Rachev, S.T.; Rüschendorf, L. Mass Transportation Problems: Volume I: Theory; Probability and Its Applications; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Carlen, E.A.; Maas, J. An analog of the 2-Wasserstein metric in non-commutative probability under which the Fermionic Fokker–Planck equation is gradient flow for the entropy. Commun. Math. Phys. 2014, 331, 887–926. [Google Scholar] [CrossRef]
- Haker, S.; Zhu, L.; Tannenbaum, A.; Angenent, S. Optimal mass transport for registration and warping. Int. J. Comput. Vis. 2004, 60, 225–240. [Google Scholar] [CrossRef]
- Mittnenzweig, M.; Mielke, A. An entropic gradient structure for lindblad equations and generic for quantum systems coupled to macroscopic models. arXiv 2016, arXiv:1609.05765. [Google Scholar]
- Rachev, S.T.; Rüschendorf, L. Mass Transportation Problems: Volumes I and II; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Mathews, J.C.; Nadeem, S.; Pouryahya, M.; Belkhatir, Z.; Deasy, J.O.; Levine, A.J.; Tannenbaum, A.R. Functional network analysis reveals an immune tolerance mechanism in cancer. Proc. Natl. Acad. Sci. USA 2020, 117, 16339–16345. [Google Scholar] [CrossRef] [PubMed]
- Benamou, J.-D.; Brenier, Y. A computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem. Numer. Math. 2000, 84, 375–393. [Google Scholar] [CrossRef]
- Otto, F. The geometry of dissipative evolution equations: The porous medium equation. Commun. Partial. Differ. Equ. 2001, 26, 101–174. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, Y.; Haker, S.; Tannenbaum, A. An image morphing technique based on optimal mass preserving mapping. IEEE Trans. Image Process. 2007, 16, 1481–1495. [Google Scholar] [CrossRef] [PubMed]
- Haker, S.; Tannenbaum, A.; Kikinis, R. Mass preserving mappings and image registration. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2001: 4th International Conference Utrecht, The Netherlands, 14–17 October 2001; Proceedings 4; Springer: Berlin/Heidelberg, Germany, 2001; pp. 120–127. [Google Scholar]
- Chen, Y.; Georgiou, T.; Pavon, M. On the Relation Between Optimal Transport and Schrödinger Bridges: A Stochastic Control Viewpoint. J. Optim. Theory Appl. 2016, 169, 671–691. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R. Level Set Methods and Dynamic Implicit Surfaces; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Sethian, J. Level Set Methods Fast Marching Methods; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Sapiro, G. Geometric Partial Equations and Image Analysis; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Susskind, L.; Friedman, A. Special Relativity and Classical Field Theory: The Theoretical Minimum; Hachette Book Group: New York, NY, USA, 2017. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yezzi, A. A Variational Surface-Evolution Approach to Optimal Transport over Transitioning Compact Supports with Domain Constraints. Fluids 2024, 9, 118. https://doi.org/10.3390/fluids9050118
Yezzi A. A Variational Surface-Evolution Approach to Optimal Transport over Transitioning Compact Supports with Domain Constraints. Fluids. 2024; 9(5):118. https://doi.org/10.3390/fluids9050118
Chicago/Turabian StyleYezzi, Anthony. 2024. "A Variational Surface-Evolution Approach to Optimal Transport over Transitioning Compact Supports with Domain Constraints" Fluids 9, no. 5: 118. https://doi.org/10.3390/fluids9050118
APA StyleYezzi, A. (2024). A Variational Surface-Evolution Approach to Optimal Transport over Transitioning Compact Supports with Domain Constraints. Fluids, 9(5), 118. https://doi.org/10.3390/fluids9050118






