Characterization Data for the Establishment of Scale-Up and Process Transfer Strategies between Stainless Steel and Single-Use Bioreactors
Abstract
1. Introduction
2. Materials and Methods
2.1. Reactor Setup and Operation Parameters
2.2. Experimental Procedure to Measure the Global Mixing Time
2.3. Experimental Procedure to Measure the Volumetric Mass Transfer Coefficient
2.4. Modeling of Mass Transfer Performance
3. Results
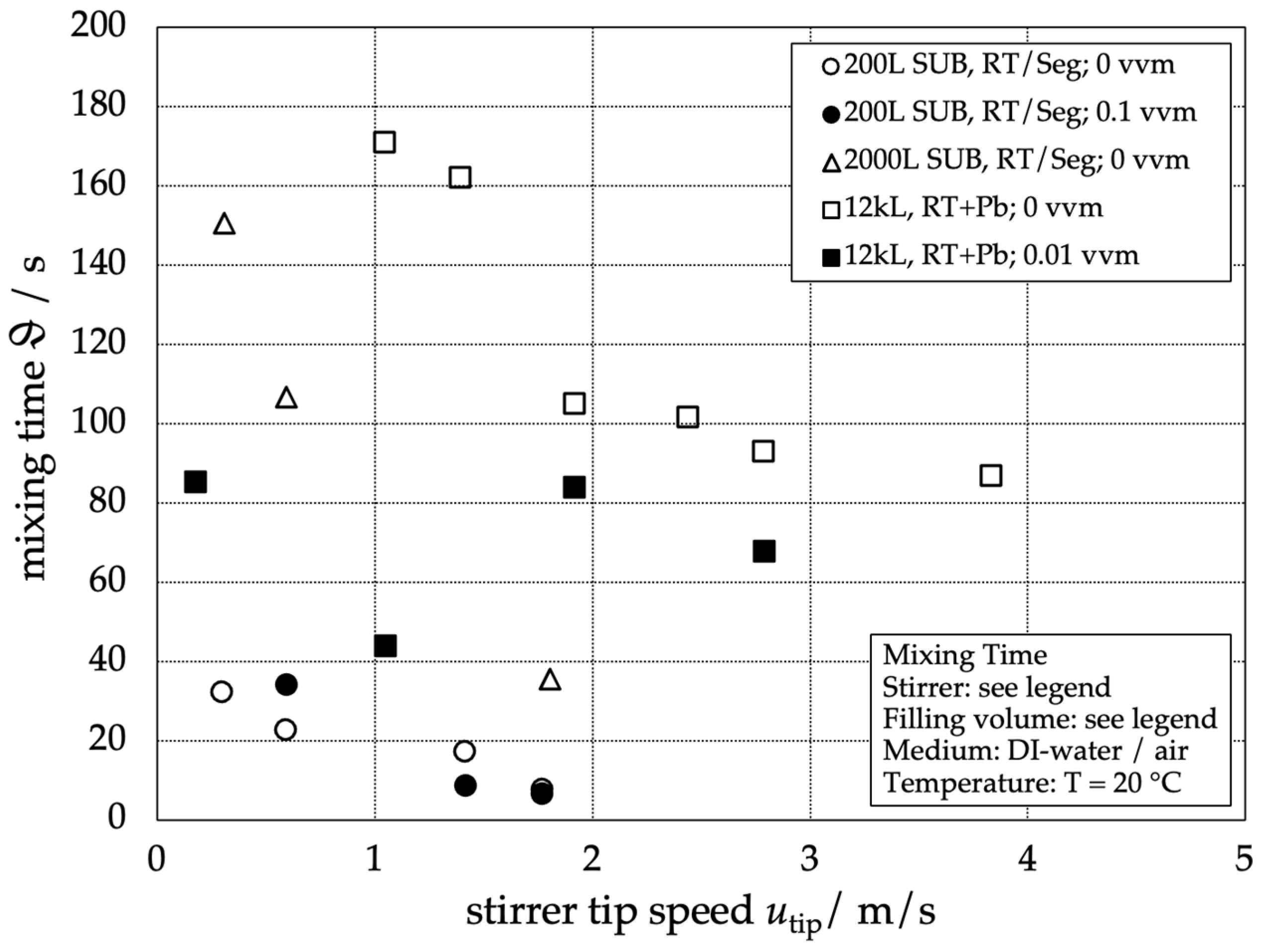
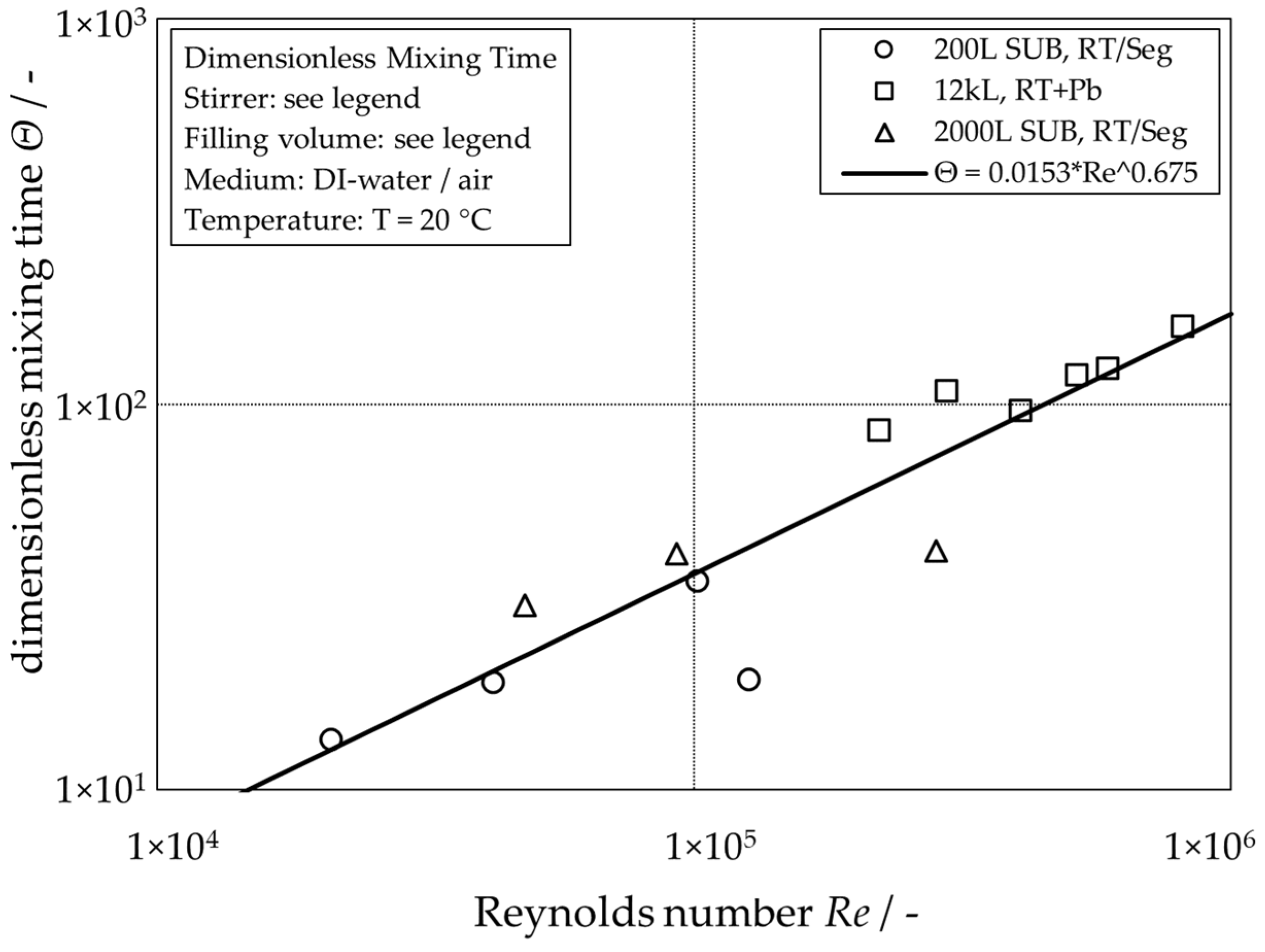
3.1. Mixing Time
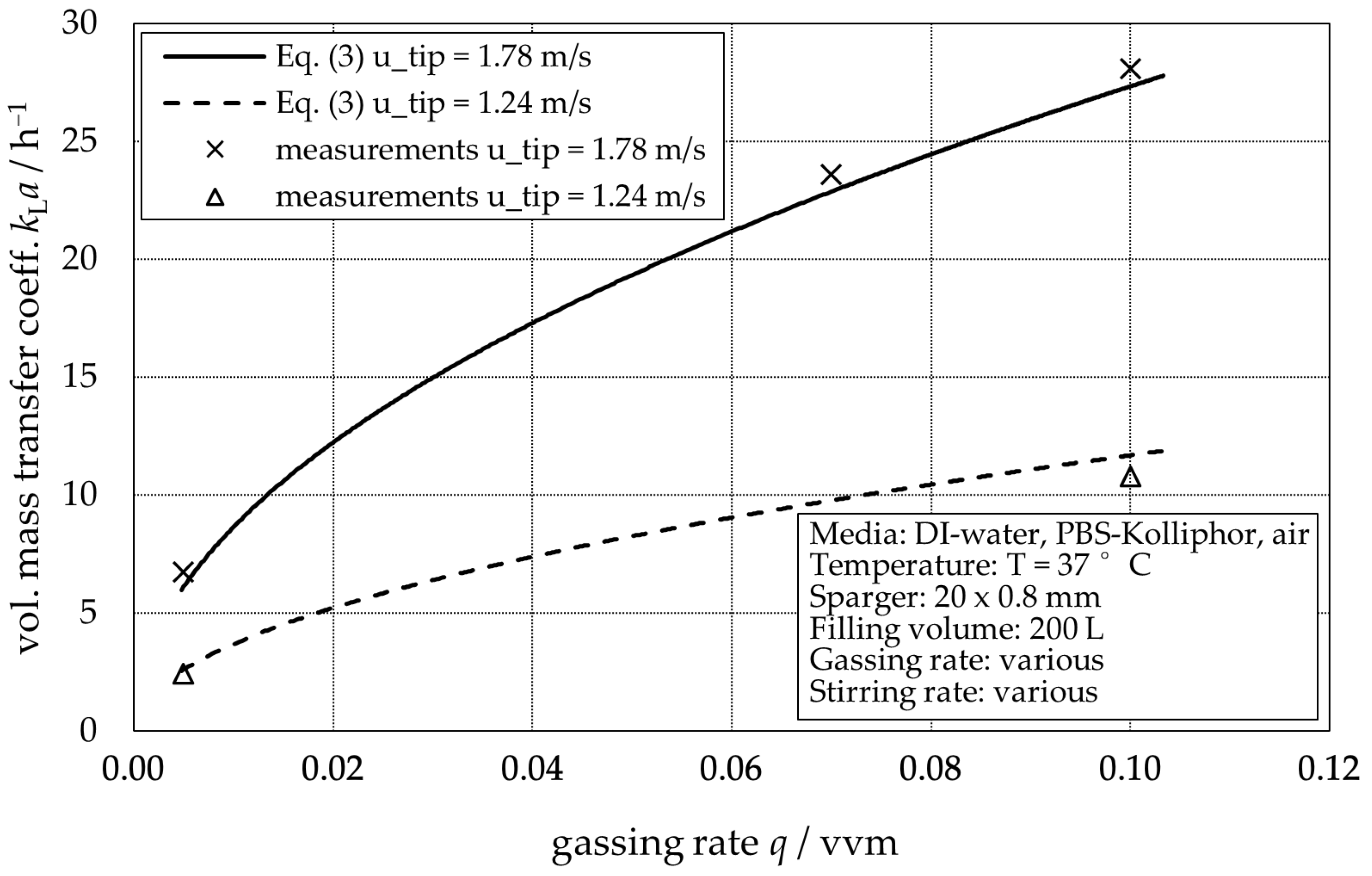
3.2. Mass Transfer Performance and Modelling
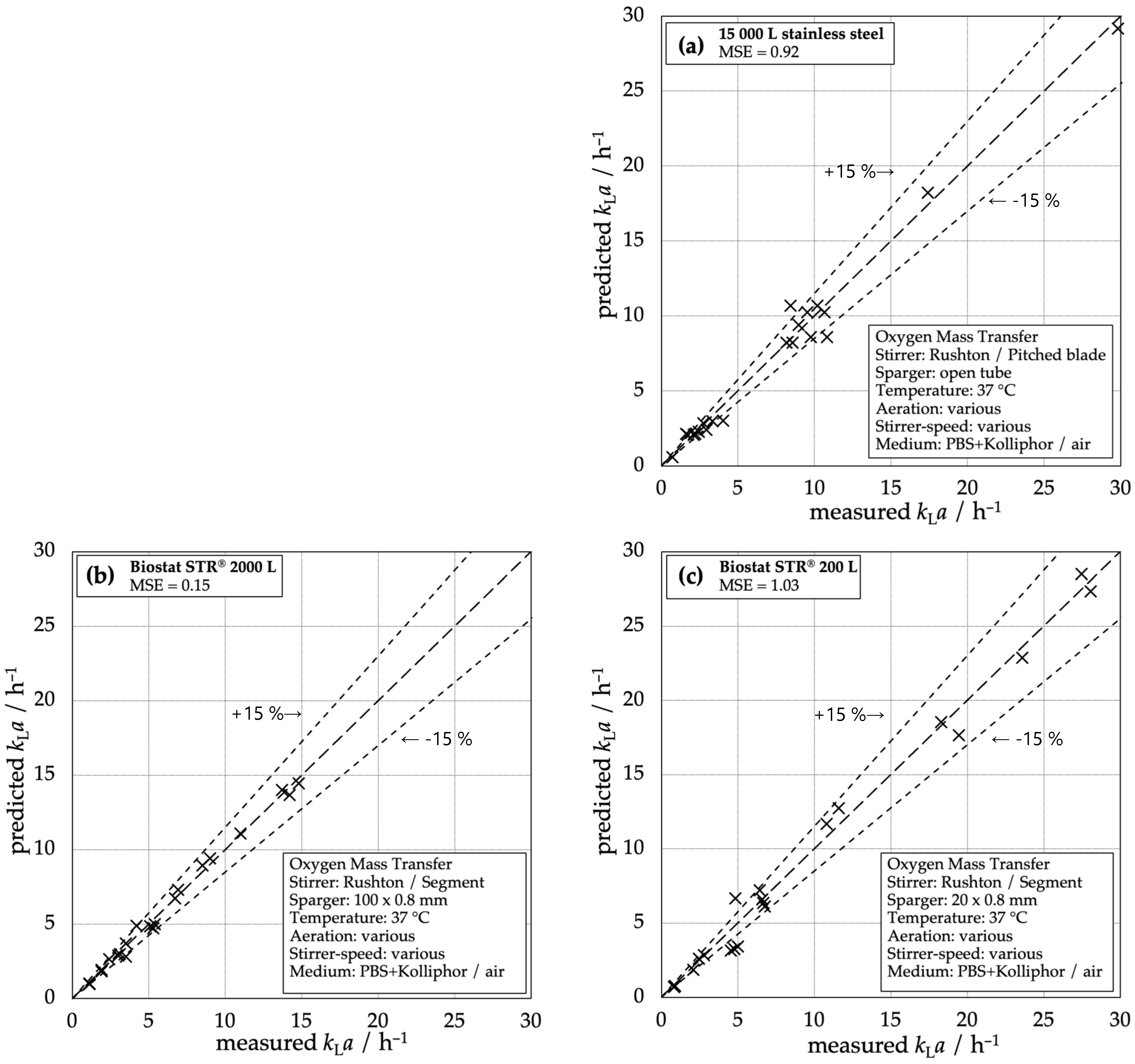
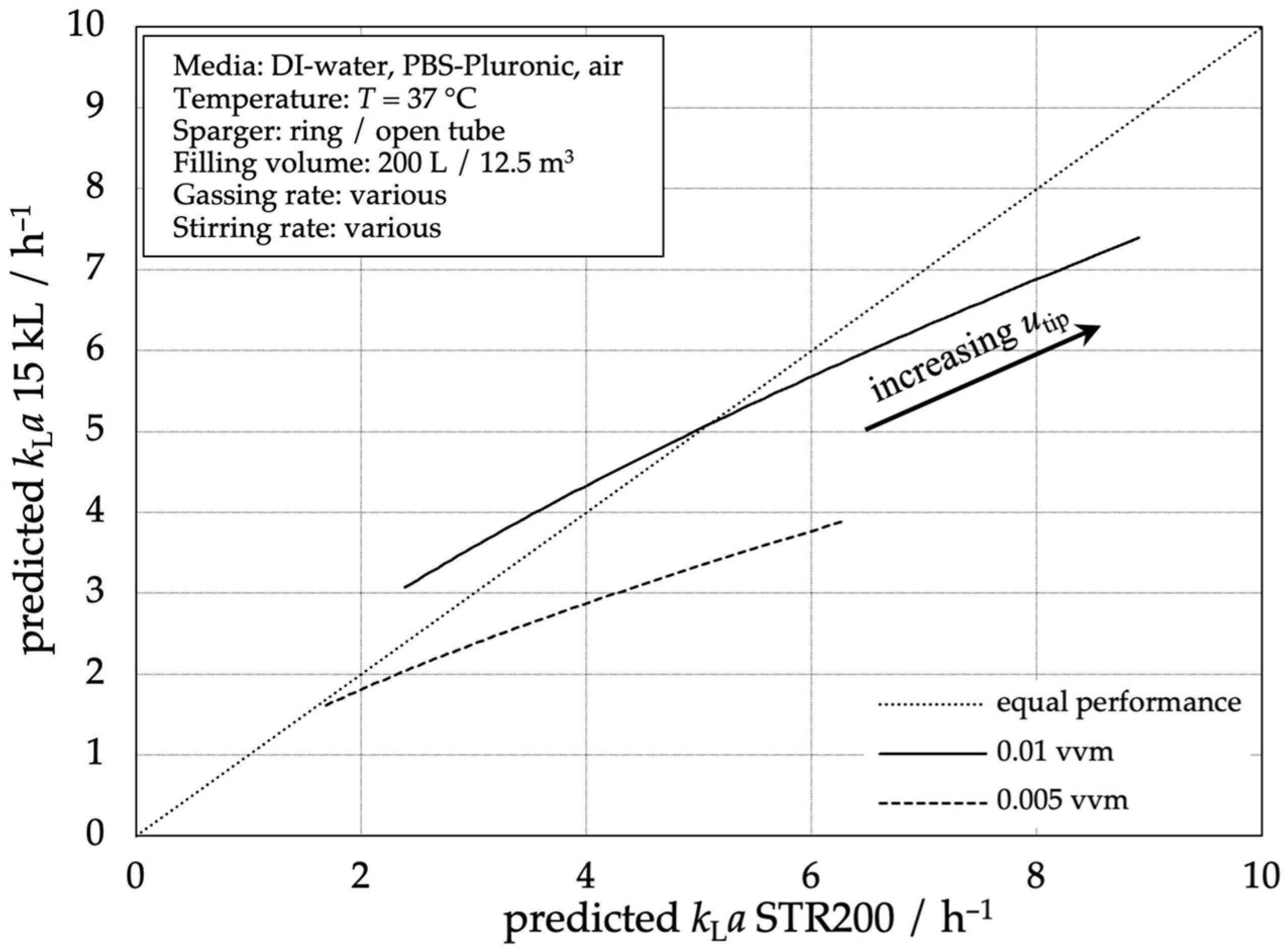
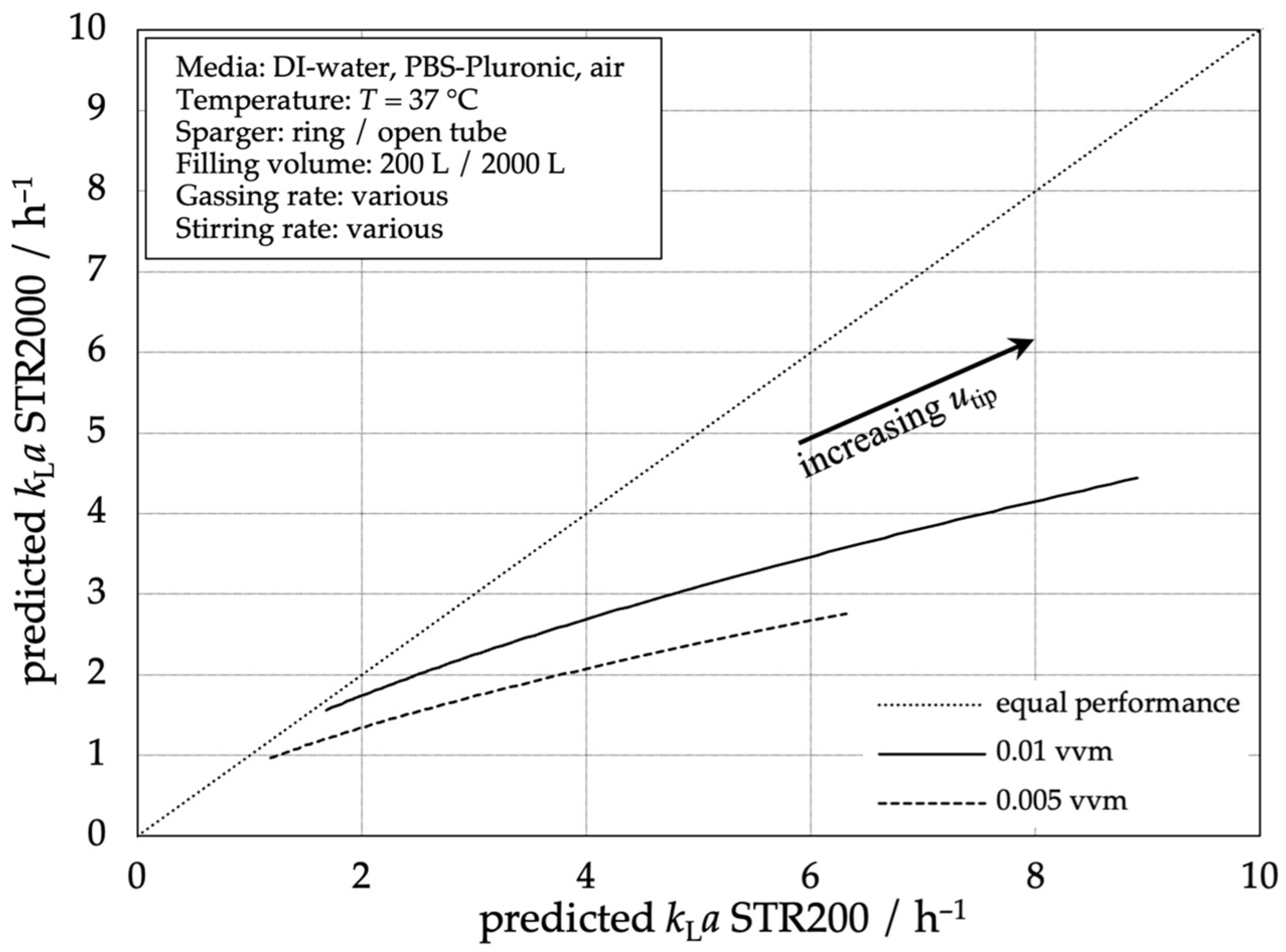
3.3. Comparison of the Correlations for Different Scales and Reactors
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DECHEMA | Gesellschaft für Chemische Technik und Biotechnologie e. V. | |
| Eq | equation | |
| FDA | Food and Drug Administration | |
| MSE | mean squared error | |
| OTR | oxygen transfer rate | |
| Pb | pitched blade impeller | |
| PBS | phosphate-buffered saline | |
| RT | Rushton Turbine | |
| Seg | segment impeller | |
| STR | stirred-tank reactor | |
| SUB | single-use bioreactor | |
| TUHH | Hamburg University of Technology | |
| Nomenclature | ||
| Characteristic Numbers | ||
| Re | stirrer Reynolds number | |
| Greek Symbols | ||
| empirical parameter | - | |
| empirical parameter | - | |
| empirical parameter | - | |
| mixing time | s | |
| dimensionless mixing time | - | |
| density | kg m−3 | |
| dynamic viscosity | Pa s | |
| Roman Symbols | ||
| a | specific area | m−1 |
| c | concentration | - |
| C | empirical parameter | - |
| c* | saturation concentration | - |
| d | diameter | m |
| k | mass transfer coefficient | m s−1 |
| n | stirring frequency | s−1 |
| OTR | oxygen transfer rate | s−1 |
| P | power | W |
| t | time | s |
| T | temperature | °C |
| u | stirrer velocity | m s−1 |
| V | volume | m3 |
| v | gas velocity | m s−1 |
| vvm | volumetric gassing rate | s−1 |
| Subscripts | ||
| e | electrode | |
| L | liquid | |
| mod. | modified | |
| O2 | oxygen | |
| R | impeller | |
| S | superficial | |
| tip | stirrer tip | |
References
- Löffelholz, C.; Kaiser, S.C.; Kraume, M.; Eibl, R.; Eibl, D. Dynamic Single-Use Bioreactors Used in Modern Liter- and M3- Scale Biotechnological Processes: Engineering Characteristics and Scaling Up. In Disposable Bioreactors II; Eibl, D., Eibl, R., Eds.; Advances in Biochemical Engineering/Biotechnology; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–44. ISBN 978-3-642-45158-4. [Google Scholar]
- Fitschen, J.; Hofmann, S.; Kursula, L.; Haase, I.; Wucherpfennig, T.; Schlüter, M. Advances in Characterization of Industrial Bioreactors for Cell Culture Process. In Biopharmaceutical Manufacturing: Progress, Trends and Challenges; Pörtner, R., Ed.; Cell Engineering; Springer International Publishing: Cham, Switzerland, 2023; pp. 67–111. ISBN 978-3-031-45669-5. [Google Scholar]
- Garcia-Ochoa, F.; Gomez, E. Bioreactor Scale-up and Oxygen Transfer Rate in Microbial Processes: An Overview. Biotechnol. Adv. 2009, 27, 153–176. [Google Scholar] [CrossRef] [PubMed]
- Recommendations for Process Engineering Characterisation of Single-Use Bioreactors and Mixing Systems by Using Experimental Methods; 2nd completely revised edition; DECHEMA Gesellschaft für Chemische Technik und Biotechnologie e.V: Frankfurt am Main, Germany, 2020; ISBN 978-3-89746-227-4.
- Garcia-Ochoa, F.; Gomez, E.; Santos, V.E.; Merchuk, J.C. Oxygen Uptake Rate in Microbial Processes: An Overview. Biochem. Eng. J. 2010, 49, 289–307. [Google Scholar] [CrossRef]
- Zlokarnik, M. Rührtechnik; Springer: Berlin/Heidelberg, Germany, 1999; ISBN 978-3-642-63675-2. [Google Scholar]
- De Wilde, D.; Dreher, T.; Christian, Z.; Husemann, U.; Greller, G.; Adams, T.; Fenge, C. Superior Scalability of Single-Use Bioreactors. Innov. Cell Cult. 2014, 14, 14–19. [Google Scholar]
- Rosseburg, A.; Fitschen, J.; Wutz, J.; Wucherpfennig, T.; Schlüter, M. Hydrodynamic Inhomogeneities in Large Scale Stirred Tanks—Influence on Mixing Time. Chem. Eng. Sci. 2018, 188, 208–220. [Google Scholar] [CrossRef]
- Rosseburg, A. Influence of Heterogeneous Bubbly Flows on Mixing and Mass Transfer Performance in Stirred Tanks for Mammalian Cell Cultivation: A Study in Transparent 3 L and 12 000 L Reactors; Cuvillier: Göttingen, Germany, 2019; ISBN 978-3-7369-6108-1. [Google Scholar]
- Hiby, J.W. Definition and measurement of quality of mixing in liquid. Chem.-Ing.-Tech. 1979, 51, 7. [Google Scholar]
- Fitschen, J.; Hofmann, S.; Wutz, J.; Kameke, A.v.; Hoffmann, M.; Wucherpfennig, T.; Schlüter, M. Novel Evaluation Method to Determine the Local Mixing Time Distribution in Stirred Tank Reactors. Chem. Eng. Sci. X 2021, 10, 100098. [Google Scholar] [CrossRef]
- Kraume, M. Mischen und Rühren. In Transportvorgänge in der Verfahrenstechnik: Grundlagen und Apparative Umsetzungen; Kraume, M., Ed.; VDI-Buch; Springer: Berlin/Heidelberg, Germany, 2004; pp. 527–569. ISBN 978-3-642-18936-4. [Google Scholar]
- Van’t Riet, K. Review of Measuring Methods and Results in Nonviscous Gas-Liquid Mass Transfer in Stirred Vessels. Ind. Eng. Chem. Proc. Des. Dev. 1979, 18, 357–364. [Google Scholar] [CrossRef]
- Merchuk, J.C.; Yona, S.; Siegel, M.H.; Zvi, A.B. On the First-Order Approximation to the Response of Dissolved Oxygen Electrodes for Dynamic KLa Estimation. Biotechnol. Bioeng. 1990, 35, 1161–1163. [Google Scholar] [CrossRef] [PubMed]
- Gourich, B.; Vial, C.; El Azher, N.; Belhaj Soulami, M.; Ziyad, M. Influence of Hydrodynamics and Probe Response on Oxygen Mass Transfer Measurements in a High Aspect Ratio Bubble Column Reactor: Effect of the Coalescence Behaviour of the Liquid Phase. Biochem. Eng. J. 2008, 39, 1–14. [Google Scholar] [CrossRef]
- Sieblist, C.; Jenzsch, M.; Pohlscheidt, M. Influence of Pluronic F68 on Oxygen Mass Transfer. Biotechnol. Prog. 2013, 29, 1278–1288. [Google Scholar] [CrossRef] [PubMed]


| System | Stainless Steel | Biostat STR® 2000 L | Biostat STR® 200 L |
|---|---|---|---|
| Working Volume | 8000 L–12,500 L | 1400 L–2000 L | 160 L–200 L |
| Vessel Diameter | 2.000 m | 1.295 m | 0.595 m |
| Impeller Type (bottom, top) | Rushton, Pitched-Blade | Rushton, Segment | Rushton, Segment |
| Impeller Diameter | 0.665 m | 0.492 m | 0.225 m |
| Angle Top Impeller | 45° | 30° | 30° |
| Stirrer Speed Range | 30 rpm–80 rpm | 35 rpm–70 rpm | 62 rpm–150 rpm |
| Aeration Range | 20 Lpm–250 Lpm | 10 Lpm–100 Lpm | 1 Lpm–20 Lpm |
| Sparger Type | Open Tube | Ring (0.8 mm × 200) | Ring (0.8 mm × 20) |
| Baffles | 4 × 200 mm | no baffles | no baffles |
| Stainless Steel Stirred Tank | Biostat STR® 2000 L | Biostat STR® 200 L | |
|---|---|---|---|
| utip | |||
| vvm | |||
| V |
| Coefficient | Stainless Steel Stirred Tank | Biostat STR® 2000 L | Biostat STR® 200 L |
|---|---|---|---|
| C | 25.84 | 29.40 | 25.58 |
| α | 1.64 | 1.53 | 2.45 |
| β | 0.92 | 0.69 | 0.50 |
| γ | 0.81 | 0.55 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernemann, V.; Fitschen, J.; Leupold, M.; Scheibenbogen, K.-H.; Maly, M.; Hoffmann, M.; Wucherpfennig, T.; Schlüter, M. Characterization Data for the Establishment of Scale-Up and Process Transfer Strategies between Stainless Steel and Single-Use Bioreactors. Fluids 2024, 9, 115. https://doi.org/10.3390/fluids9050115
Bernemann V, Fitschen J, Leupold M, Scheibenbogen K-H, Maly M, Hoffmann M, Wucherpfennig T, Schlüter M. Characterization Data for the Establishment of Scale-Up and Process Transfer Strategies between Stainless Steel and Single-Use Bioreactors. Fluids. 2024; 9(5):115. https://doi.org/10.3390/fluids9050115
Chicago/Turabian StyleBernemann, Vincent, Jürgen Fitschen, Marco Leupold, Karl-Heinz Scheibenbogen, Marc Maly, Marko Hoffmann, Thomas Wucherpfennig, and Michael Schlüter. 2024. "Characterization Data for the Establishment of Scale-Up and Process Transfer Strategies between Stainless Steel and Single-Use Bioreactors" Fluids 9, no. 5: 115. https://doi.org/10.3390/fluids9050115
APA StyleBernemann, V., Fitschen, J., Leupold, M., Scheibenbogen, K.-H., Maly, M., Hoffmann, M., Wucherpfennig, T., & Schlüter, M. (2024). Characterization Data for the Establishment of Scale-Up and Process Transfer Strategies between Stainless Steel and Single-Use Bioreactors. Fluids, 9(5), 115. https://doi.org/10.3390/fluids9050115









