A Compressible Formulation of the One-Fluid Model for Two-Phase Flows
Abstract
1. Introduction
2. Governing Equations
3. Numerical Scheme
- The initial step involves the inertial term computation of Equations (2) and (6). As the l.h.s. of the mentioned equations has the same mathematical structure , with , , a general approach is used to compute temporary variables (denoted ) in the operator splitting framework [12]. As the density is also a required variable, Equation (1) is also used in the numerical scheme in order to provide an approximation of the density.In practice, , , is first initialised before the time integration using a third-order accurate strong stability preserving Runge–Kutta (SSP-RK3) time integrator [18]:where and are the velocities correctly extrapolated to maintain scheme accuracy [19]. To ensure that remains bounded during advection, high-order schemes such as CUI, WENO, or even CUBISTA are used (see [19] and the references herein for more details).At the end of this step, discrete consistency between the temporary density, ; momentum, ; and energy, variables is ensured. Furthermore, as Equation (1) is a pure advection equation, directly provides a predicted density: .
- With the knowledge of , the termophysical properties of the one-fluid model are updated. For , , , , and r, by using an arithmetic mixing law,where denotes the property corresponding to phase i. Note that the density is not updated as its value is already known from step 1.
- The geometrical properties, normal properties , and curvature , of the interface are evaluated. Here, a smoothed color function is computed from a diffusion step applied on and the definitioncan be used in the CSF expression of where is the surface tension and is the interface localisation.
- From the EoS of an ideal gas, the temperature T can be expressed as a function of the solved variables and e,and can be injected into the mass conservation (Equation (5)) that couples solved quantities , p, and e. However, the velocity norm prevents an implicit coupling due to the non-linearity. The total derivative will then be made explicit in the following for non isothermal flows.
- Using the new density and the temporary momentum from step 1, the physical and interface properties from steps 3 and 4, and the temperature definition from step 5, the mass conservation, augmented by the compressibility and dilatation effects, and the momentum equations read, with a first-order time discretization,where only the velocity and pressure fields are implicity coupled and constitute the unknown vector of the underlying linear system. This latter is solved with a BiCGStab(2) solver [21], where an efficient block triangular preconditioner, improving the convergence of the iterative solver as explained in [10,11], is used.A last discussion concerns the linearization of the term into . This choice relies essentially on the available stencils from the incompressible version of the used solver [11]. Another approach, where , with being the pressure or the temperature field, is one again approximated with the application of step 1 to a conservative evolution equation for , is also considered.
- Finally, we update the total energy using the intermediate total energy computed in step 1 and all other variables now known at time :The total energy at the end of the time iteration is deduced from .
4. Results
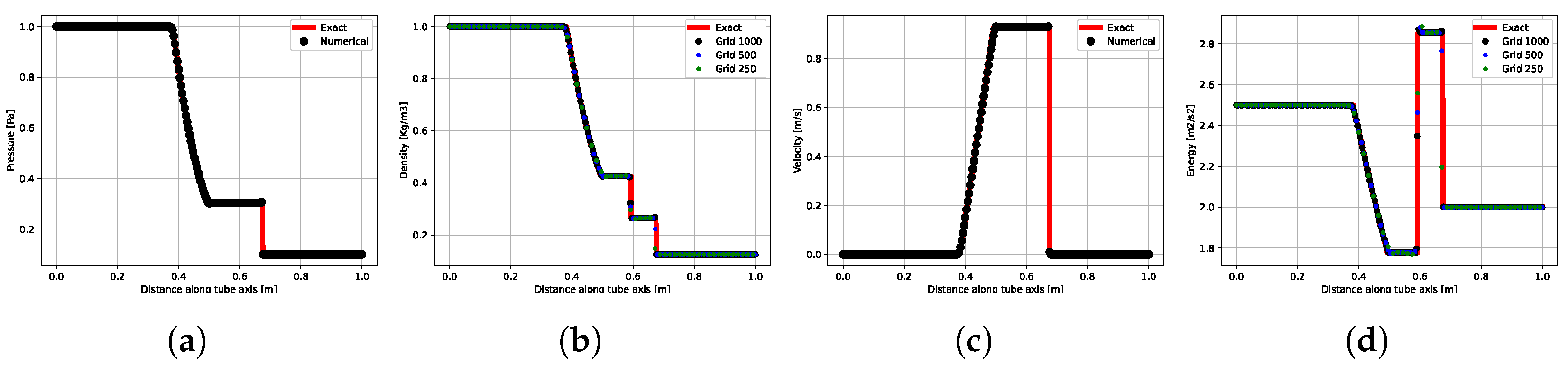
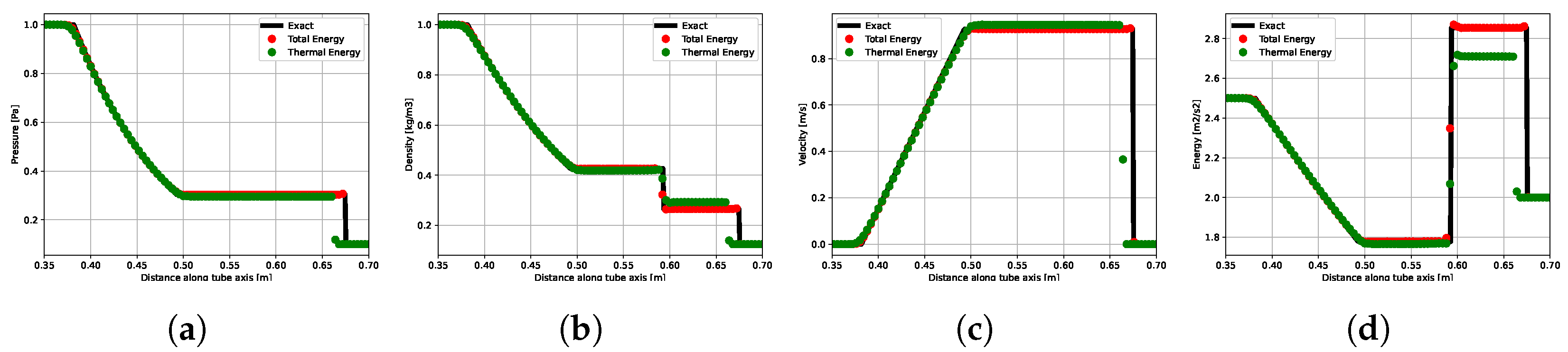
4.1. Sod’s Shock Tube Problem
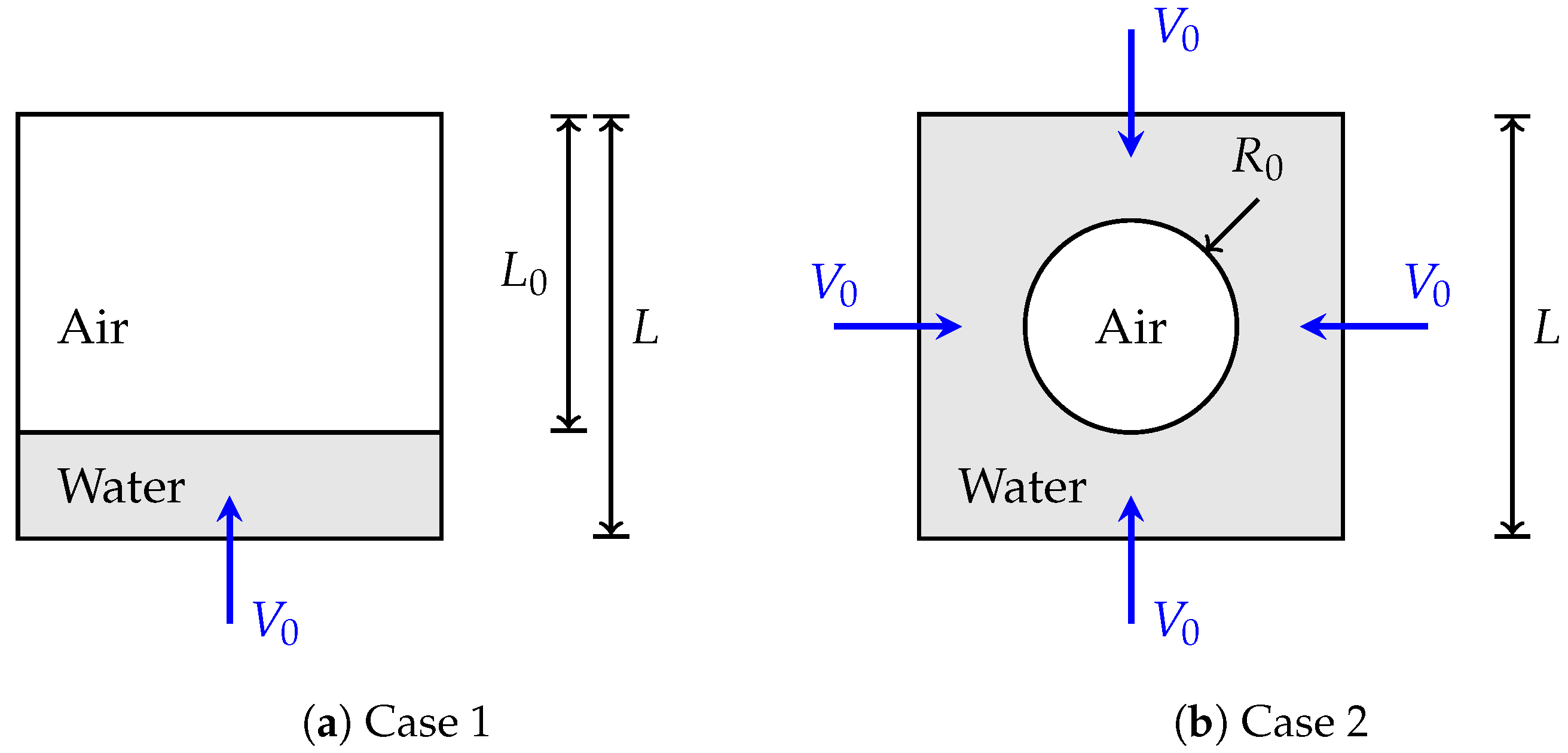
4.2. Isothermal Case for a Viscous Flow without Capillary Effects
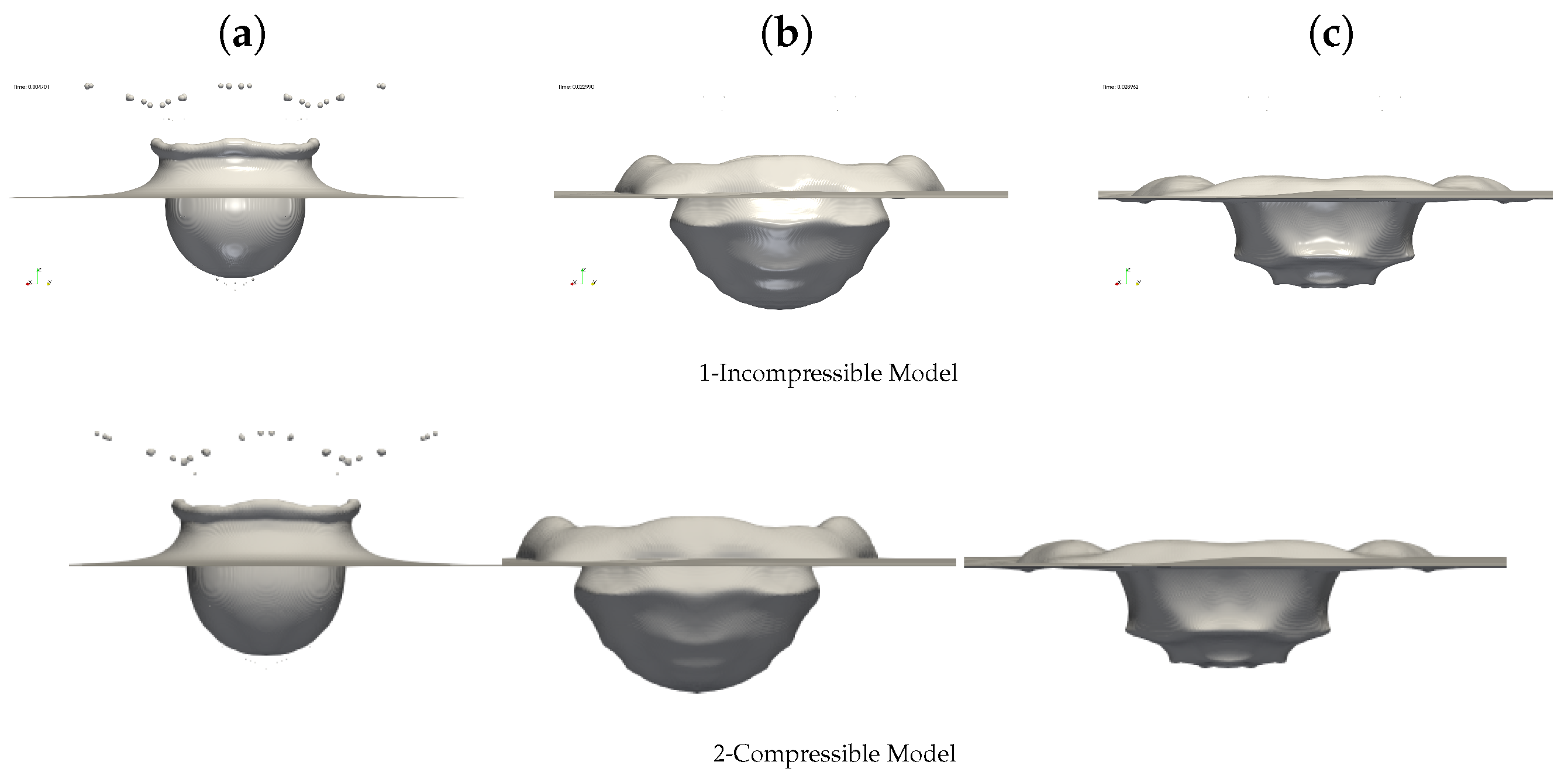
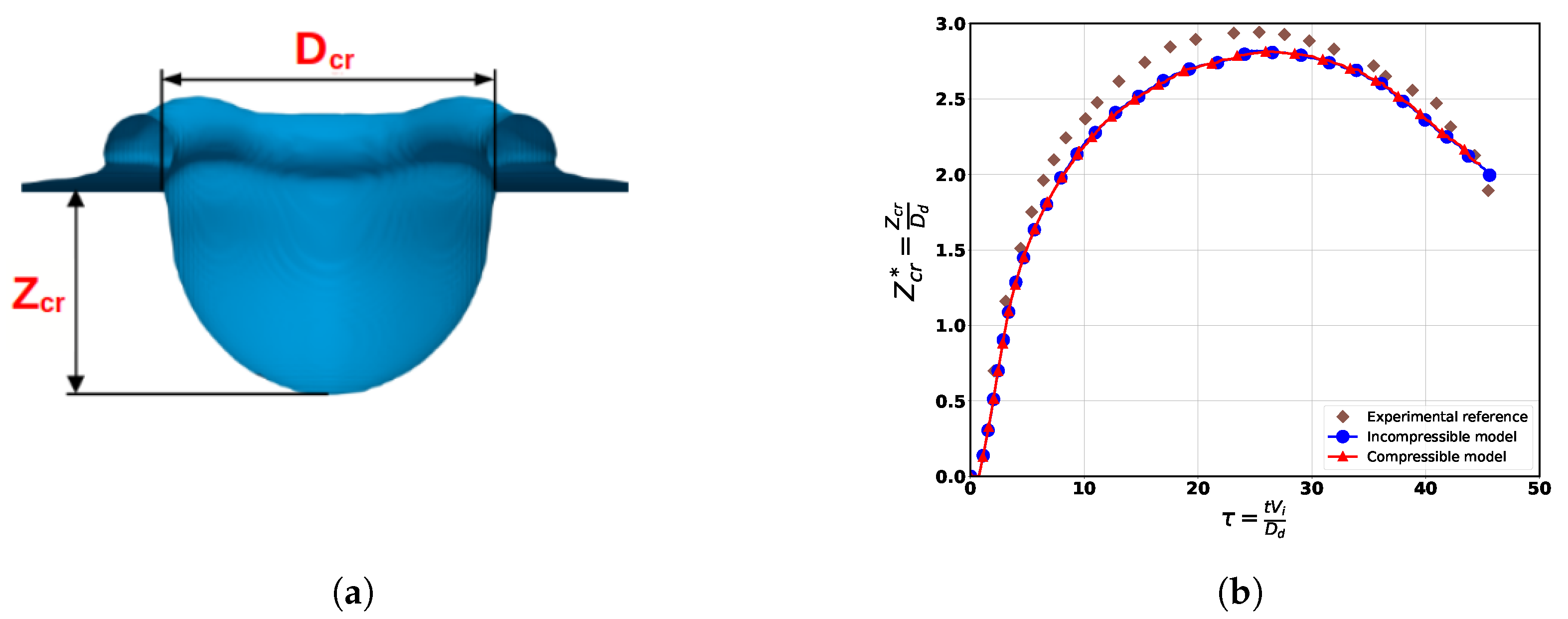
4.3. Isothermal Case for a Viscous Flow with Capillary Effects: Drop Impact on Viscous Liquid Film
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yoon, S.Y.; Yabe, T. The unified simulation for incompressible and compressible flow by the predictor-corrector scheme based on the CIP method. Comput. Phys. Commun. 1999, 119, 149–158. [Google Scholar] [CrossRef]
- Kwatra, N.; Su, J.; Grétarsson, J.T.; Fedkiw, R. A method for avoiding the acoustic time step restriction in compressible flow. J. Comput. Phys. 2009, 228, 4146–4161. [Google Scholar] [CrossRef]
- Caltagirone, J.P.; Vincent, S.; Caruyer, C. A multiphase compressible model for the simulation of multiphase flows. Comput. Fluids 2011, 50, 24–34. [Google Scholar] [CrossRef]
- Shyue, K.M.; Xiao, F. An Eulerian interface sharpening algorithm for compressible two-phase flow: The algebraic THINC approach. J. Comput. Phys. 2014, 268, 326–354. [Google Scholar] [CrossRef]
- Nourgaliev, R.; Luo, H.; Weston, B.; Anderson, A.; Schofield, S.; Dunn, T.; Delplanque, J.P. Fully-implicit orthogonal reconstructed Discontinuous Galerkin method for fluid dynamics with phase change. J. Comput. Phys. 2016, 305, 964–996. [Google Scholar] [CrossRef]
- Urbano, A.; Bibal, M.; Tanguy, S. A semi implicit compressible solver for two-phase flows of real fluids. J. Comput. Phys. 2022, 456, 111034. [Google Scholar] [CrossRef]
- Fuster, D.; Popinet, S. An all-Mach method for the simulation of bubble dynamics problems in the presence of surface tension. J. Comput. Phys. 2018, 374, 752–768. [Google Scholar] [CrossRef]
- Saade, Y.; Lohse, D.; Fuster, D. A multigrid solver for the coupled pressure-temperature equations in an all-Mach solver with VoF. J. Comput. Phys. 2023, 476, 111865. [Google Scholar] [CrossRef]
- El Ouafa, M.; Vincent, S.; Le Chenadec, V. Navier-stokes solvers for incompressible single- and two-phase flows. Commun. Comput. Phys. 2021, 29, 1213–1245. [Google Scholar] [CrossRef]
- El Ouafa, M.; Vincent, S.; Le Chenadec, V. Monolithic solvers for incompressible two-phase flows at large density and viscosity ratios. Fluids 2021, 6, 23. [Google Scholar] [CrossRef]
- El Ouafa, S.; Vincent, S.; Le Chenadec, V.; Trouette, B. Fully-coupled parallel solver for the simulation of two-phase incompressible flows. Comput. Fluids 2023, 265, 105995. [Google Scholar] [CrossRef]
- El Ouafa, M. Développement d’un Solveur Tout-Couplé Parallèle 3D Pour la Simulation des Écoulements Diphasiques Incompressibles à Forts Rapports de Viscosités et de Masses Volumiques. Ph.D. Thesis, Université Gustave Eiffel, Champs-sur-Marne, France, 2022. [Google Scholar]
- Abgrall, R.; Saurel, R. Discrete equations for physical and numerical compressible multiphase mixtures. J. Comput. Phys. 2003, 186, 361–396. [Google Scholar] [CrossRef]
- Saurel, R.; Abgrall, R. A Multiphase Godunov Method for Compressible Multifluid and Multiphase Flows. J. Comput. Phys. 1999, 150, 425–467. [Google Scholar] [CrossRef]
- Drui, F.; Larat, A.; Le Chenadec, V.; Kokh, S.; Massot, M. A hierarchy of two-fluid models with specific numerical methods for the simulation of bubbly flows/acoustic interactions. In Proceedings of the APS Division of Fluid Dynamics Meeting Abstracts, APS Meeting Abstracts, San Francisco, CA, USA, 23–25 November 2014; p. R33.003. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Le Métayer, O.; Saurel, R. The Noble-Abel stiffened-gas equation of state. Phys. Fluids 2016, 28, 046102. [Google Scholar] [CrossRef]
- Gottlieb, S.; Shu, C.W.; Tadmor, E. Strong Stability-Preserving High-Order Time Discretization Methods. SIAM Rev. 2001, 43, 89–112. [Google Scholar] [CrossRef]
- Nangia, N.; Griffith, B.E.; Patankar, N.A.; Bhalla, A.P.S. A robust incompressible Navier-Stokes solver for high density ratio multiphase flows. J. Comput. Phys. 2019, 390, 548–594. [Google Scholar] [CrossRef]
- Weymouth, G.D.; Yue, D.K.P. Conservative volume-of-fluid method for free-surface simulations on cartesian-grids. J. Comput. Phys. 2010, 229, 2853–2865. [Google Scholar] [CrossRef]
- Dongarra, J.J.; Duff, I.S.; Sorensen, D.C.; Van der Vorst, H.A. Numerical Linear Algebra for High Performance Computers; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998. [Google Scholar]
- Sod, G.A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 1978, 27, 1–31. [Google Scholar] [CrossRef]
- Bisighini, A.; Cossali, G.E.; Tropea, C.; Roisman, I.V. Crater evolution after the impact of a drop onto a semi-infinite liquid target. Phys. Rev. E 2010, 82, 036319. [Google Scholar] [CrossRef]
- Zheng, W.; Zhu, B.; Kim, B.; Fedkiw, R. A new incompressibility discretization for a hybrid particle MAC grid representation with surface tension. J. Comput. Phys. 2015, 280, 96–142. [Google Scholar] [CrossRef]
- Lentine, M.; Cong, M.; Patkar, S.; Fedkiw, R. Simulating Free Surface Flow with Very Large Time Steps. In Proceedings of the Eurographics/ACM SIGGRAPH Symposium on Computer Animation, Lausanne, Switzerland, 29–31 July 2012; Lee, J., Kry, P., Eds.; The Eurographics Association: Eindhoven, The Netherlands, 2012. [Google Scholar] [CrossRef]


| Air | Water | |
|---|---|---|
| Density (kg) | 1000 | |
| Viscosity (Pas) | ||
| Compressibility () | ||
| Specific gas constant r (JK/kg) | 287 | − |
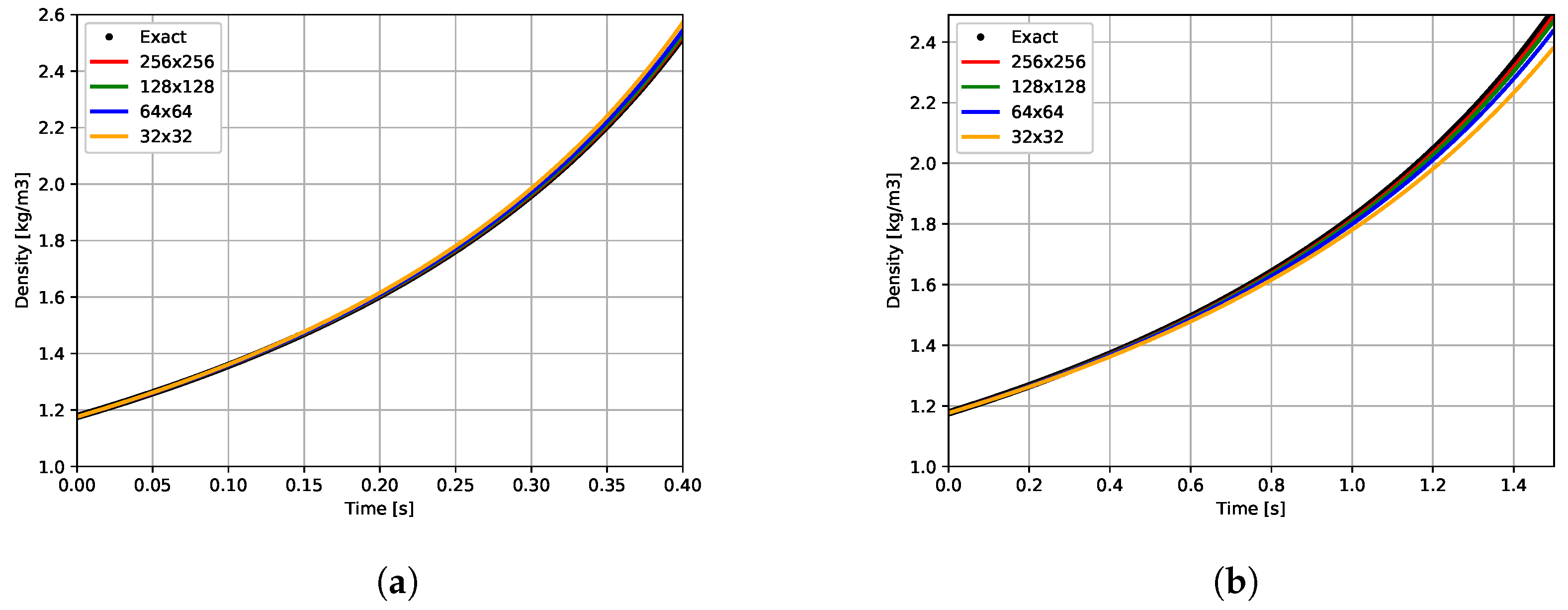
| Case 1 | ||||||
| Mesh | Error | order | p | Error | order | |
| 2.571 | 2.172 × 10−2 | 2.217 × 105 | 2.114 × 10−2 | |||
| 2.544 | 1.093 × 10−2 | 0.98 | 2.194 × 105 | 1.034 × 10−2 | 1.03 | |
| 2.531 | 5.580 × 10−3 | 0.97 | 2.182 × 105 | 4.980 × 10−3 | 1.05 | |
| 2.524 | 2.840 × 10−3 | 0.97 | 2.176 × 105 | 2.240 × 10−3 | 1.15 | |
| Extrapolation | 2.517 | 3.730 × 10−4 | 0.97 | 2.170 × 105 | 1.200 × 10−3 | 0.97 |
| Case 2 | ||||||
| Mesh | Error | order | p | Error | order | |
| 2.383 | 4.784 × 10−2 | 2.123 × 105 | 1.652 × 10−2 | |||
| 2.441 | 2.482 × 10−2 | 0.94 | 2.149 × 105 | 4.310 × 10−3 | 0.93 | |
| 2.474 | 1.137 × 10−2 | 1.12 | 2.182 × 105 | 4.980 × 10−3 | 1.00 | |
| 2.490 | 5.210 × 10−3 | 1.12 | 2.188 × 105 | 2.030 × 10−3 | 1.08 | |
| Extrapolation | 2.503 | 1.630 × 10−5 | 1.12 | 2.189 × 105 | 1.640 × 10−3 | 1.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Ouafa, S.; Vincent, S.; Le Chenadec, V.; Trouette, B.; Fereka, S.; Chadil, A. A Compressible Formulation of the One-Fluid Model for Two-Phase Flows. Fluids 2024, 9, 90. https://doi.org/10.3390/fluids9040090
El Ouafa S, Vincent S, Le Chenadec V, Trouette B, Fereka S, Chadil A. A Compressible Formulation of the One-Fluid Model for Two-Phase Flows. Fluids. 2024; 9(4):90. https://doi.org/10.3390/fluids9040090
Chicago/Turabian StyleEl Ouafa, Simon, Stephane Vincent, Vincent Le Chenadec, Benoît Trouette, Syphax Fereka, and Amine Chadil. 2024. "A Compressible Formulation of the One-Fluid Model for Two-Phase Flows" Fluids 9, no. 4: 90. https://doi.org/10.3390/fluids9040090
APA StyleEl Ouafa, S., Vincent, S., Le Chenadec, V., Trouette, B., Fereka, S., & Chadil, A. (2024). A Compressible Formulation of the One-Fluid Model for Two-Phase Flows. Fluids, 9(4), 90. https://doi.org/10.3390/fluids9040090







