Computational Fluid Dynamics Prediction of External Thermal Loads on Film-Cooled Gas Turbine Vanes: A Validation of Reynolds-Averaged Navier–Stokes Transition Models and Scale-Resolving Simulations for the VKI LS-94 Test Case
Abstract
1. Introduction
- Bypass Transition: This occurs when the laminar BL is disrupted by significant external disturbances, such as high levels of freestream turbulence, abruptly accelerating the transition. For example, in turbomachinery blading, attached boundary layers are exposed to relevant freestream turbulence levels, and the transition is likely to be triggered by Klebanoff streaks.
- Oblique Transition: This is a 3D phenomenon typically initiated by the leading edge or surface imperfections. These disturbances then grow moving downstream and form oblique wave patterns, eventually breaking down into turbulent flow.
- Separated-Flow Transition: An adverse pressure gradient leads to the separation of the laminar BL from the surface, generating a free shear layer. Its instability causes the transition and the reattachment in the form of a turbulent BL. This transition type is relevant for turbine blades with high-lift characteristics, operating at high angles of attack, or in off-design conditions.
- Shock-Induced Transition: This is particularly relevant in high-speed gas turbines, where the transition is triggered by shock waves interacting with the boundary layer. The shock wave causes a sudden increase in boundary layer thickness and eventually the transition.
2. Test Case
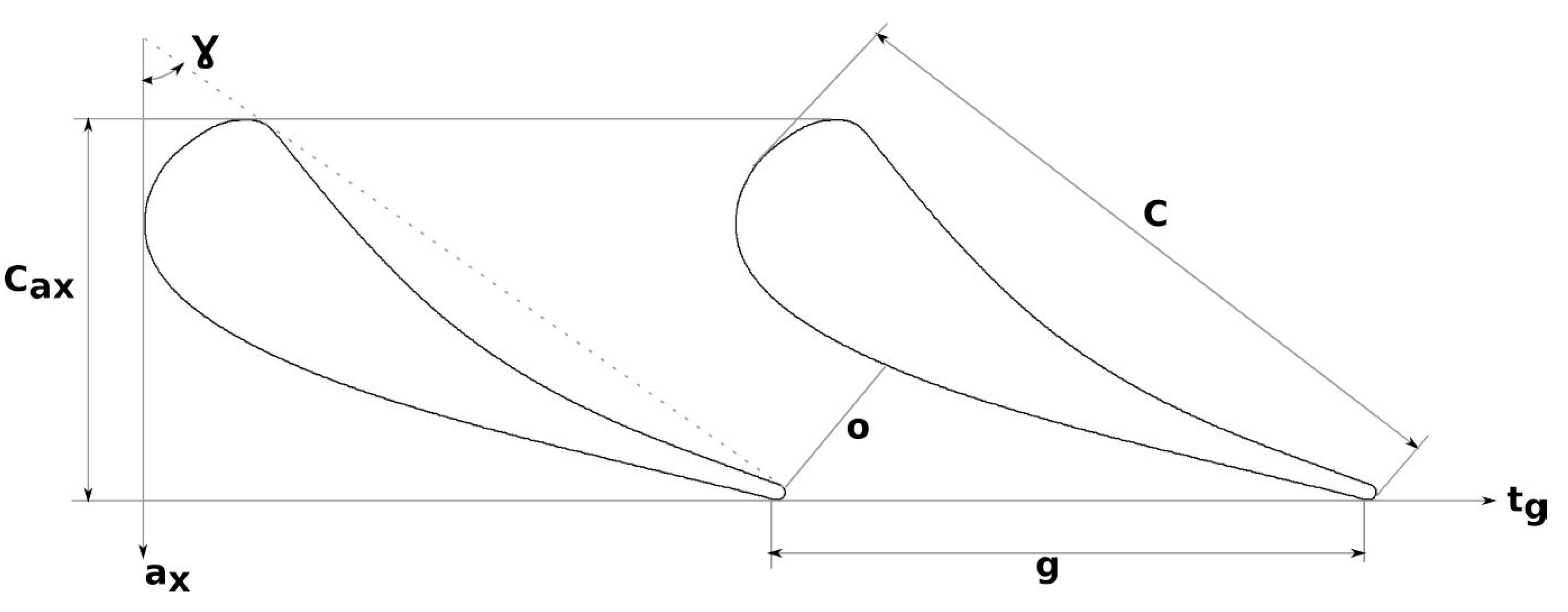
2.1. Vane Profile and Cascade Parameters
2.2. Cooling System Configuration
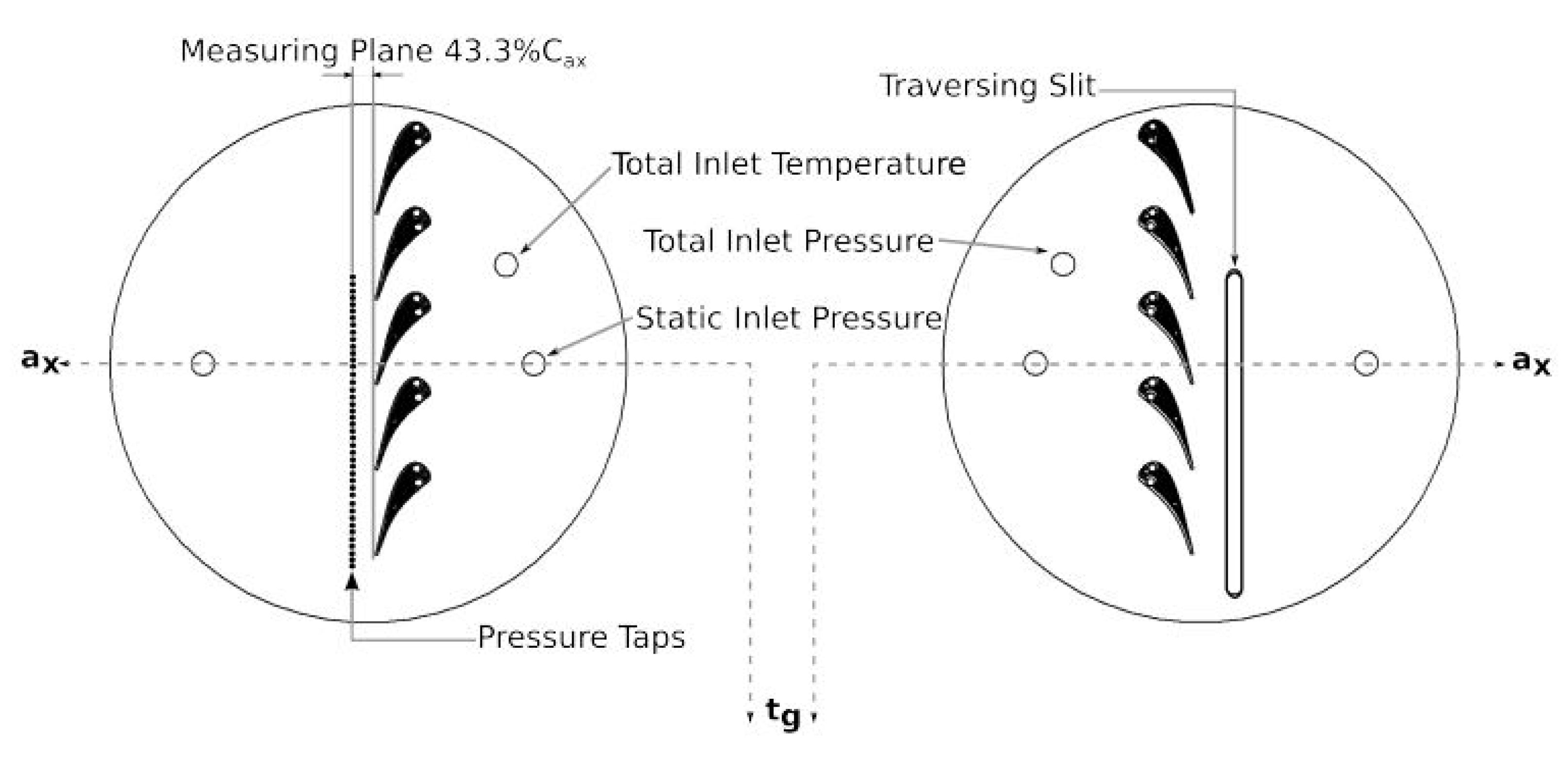
2.3. Experimental Configuration
3. Computational Methodology
3.1. Computational Domain
3.2. Numerical Setup and Boundary Conditions
3.3. Transition Modeling
3.3.1. Transition Model
3.3.2. Transition Model (Transition SST Model)
3.3.3. Transition Model (Intermittency Model)
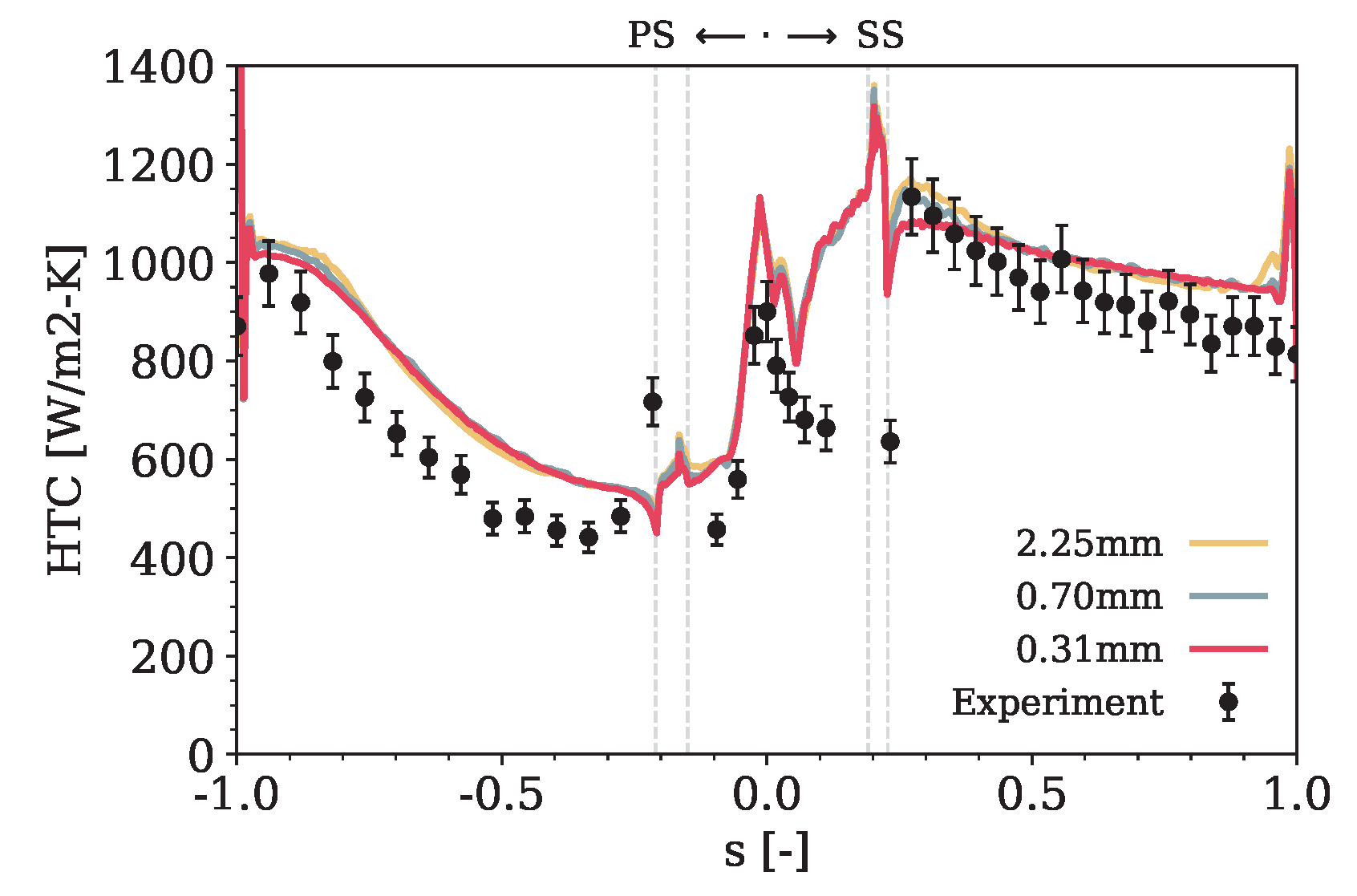
3.4. Mesh Sensitivity
3.5. Scale-Resolving Modeling
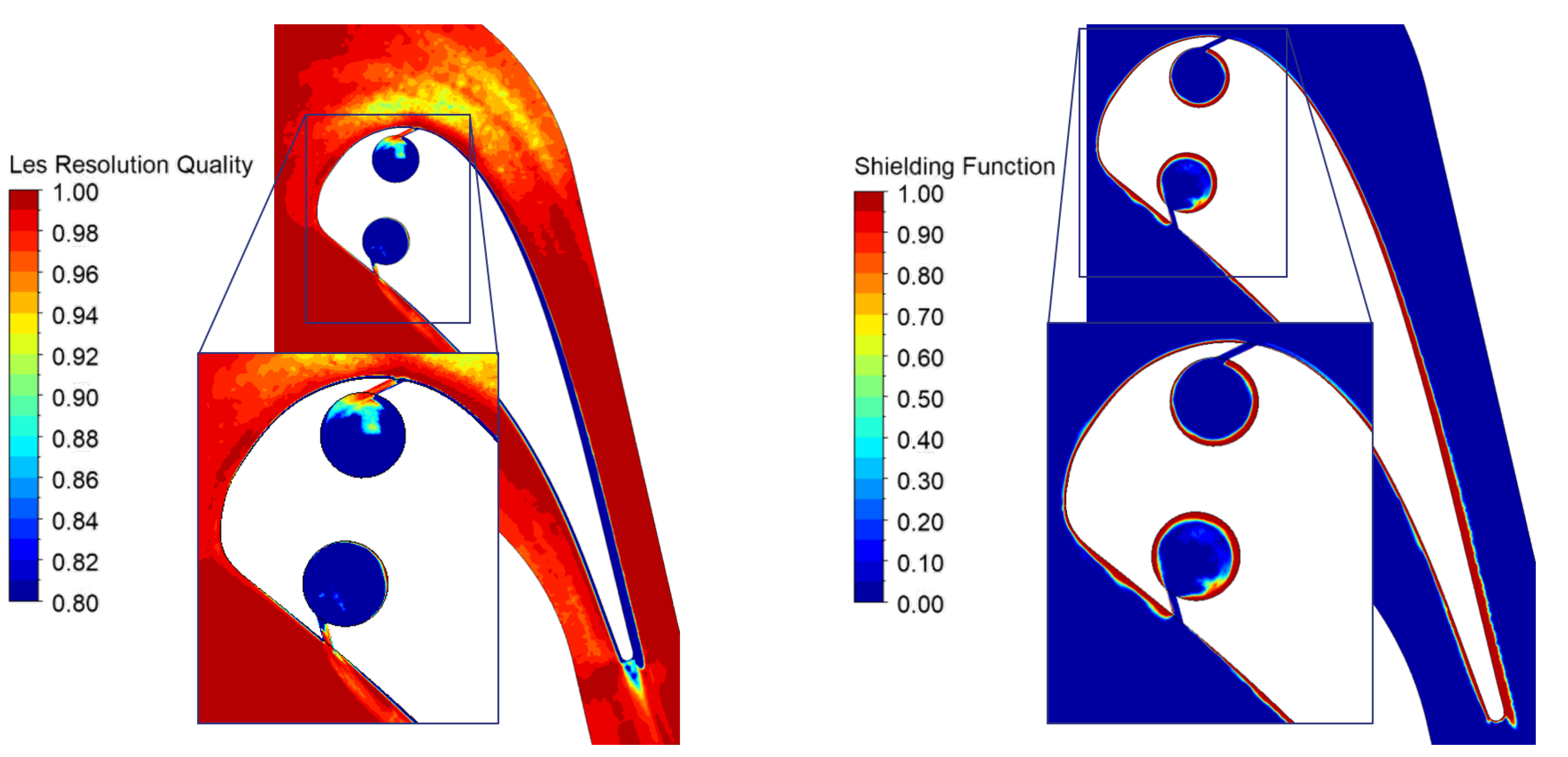
3.6. SBES Quality
4. Results
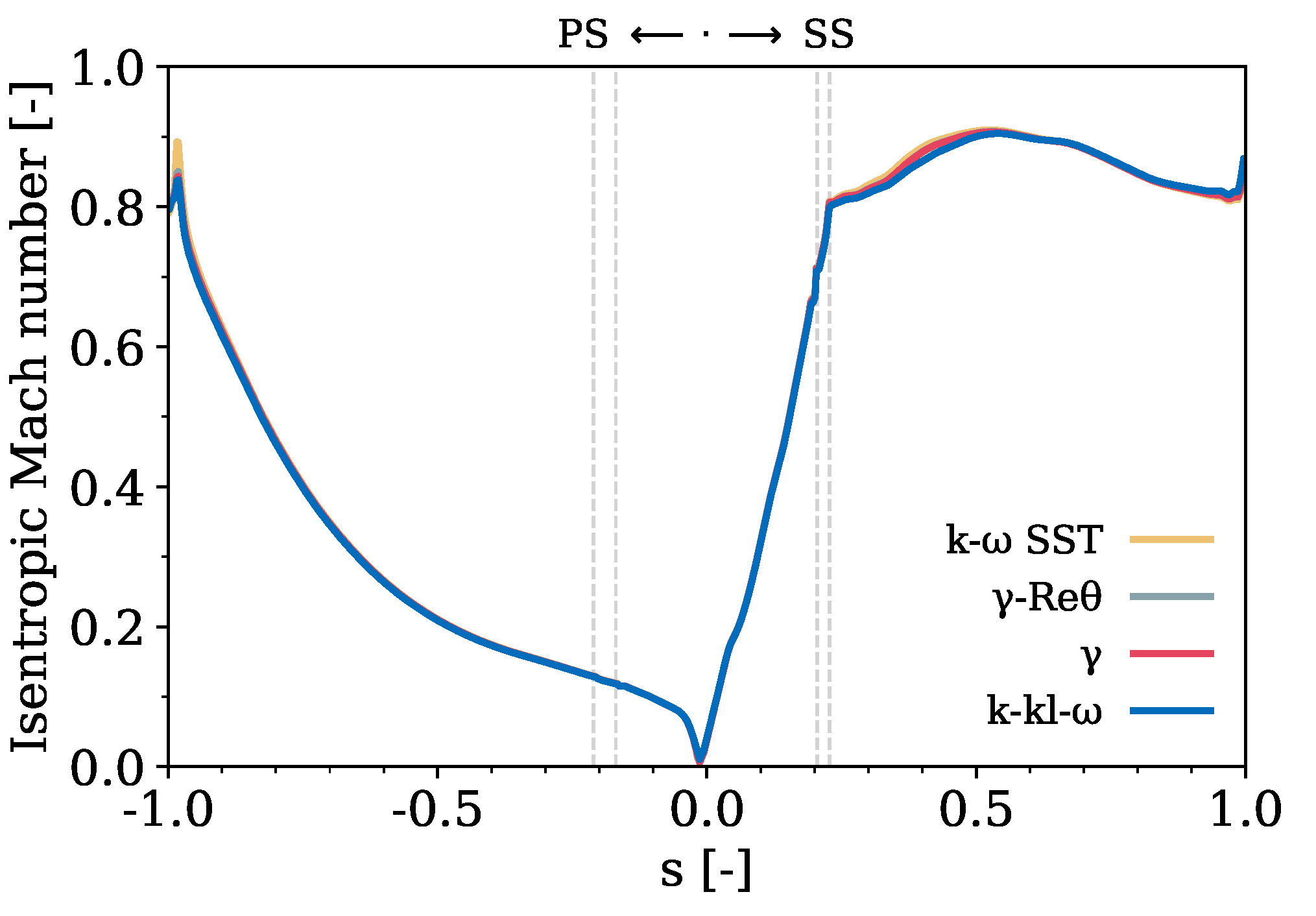
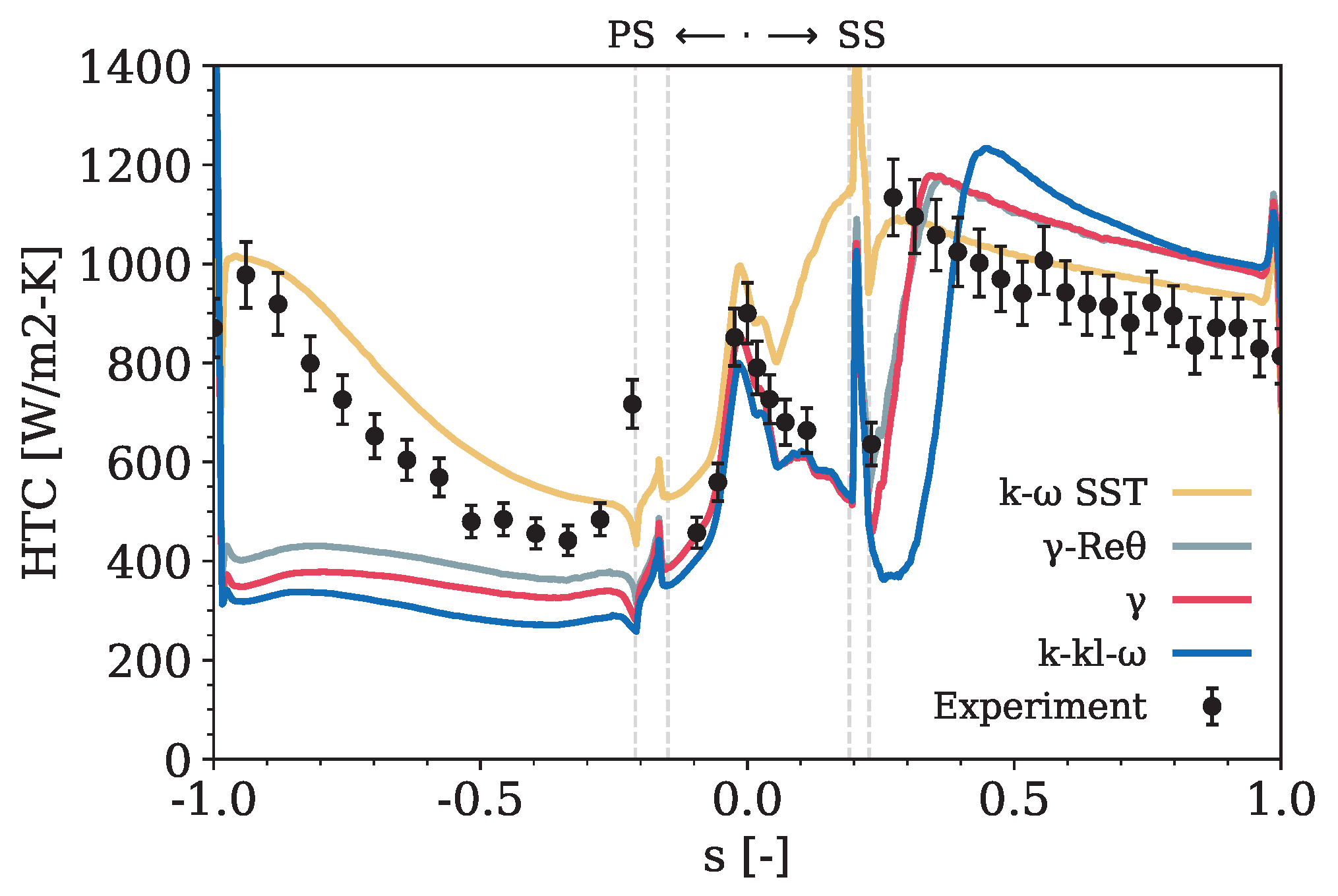
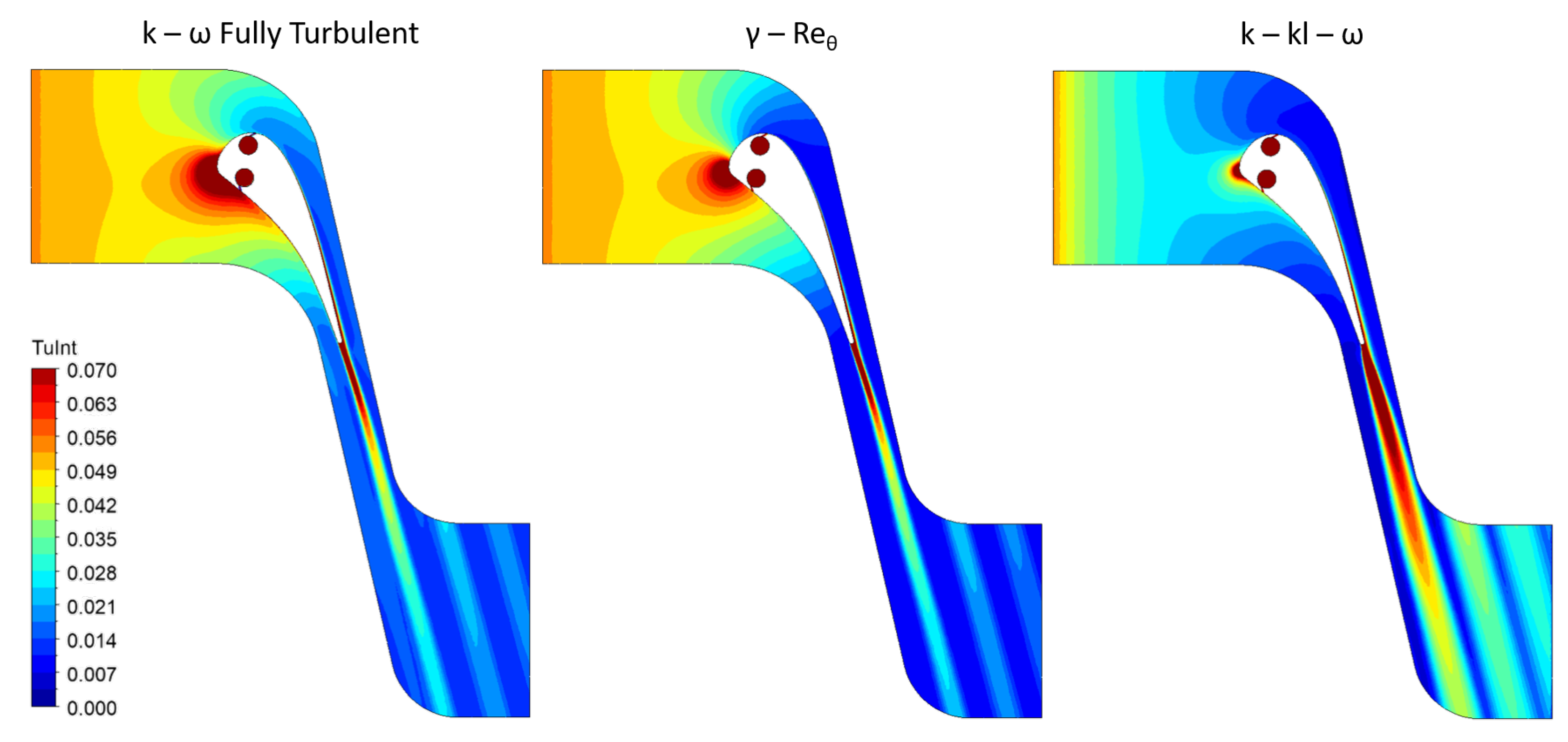
4.1. Assessment of Transition Models
4.1.1. Uncooled
4.1.2. PS Injection
4.1.3. SS Injection
4.2. Assessment of RANS vs. SBES
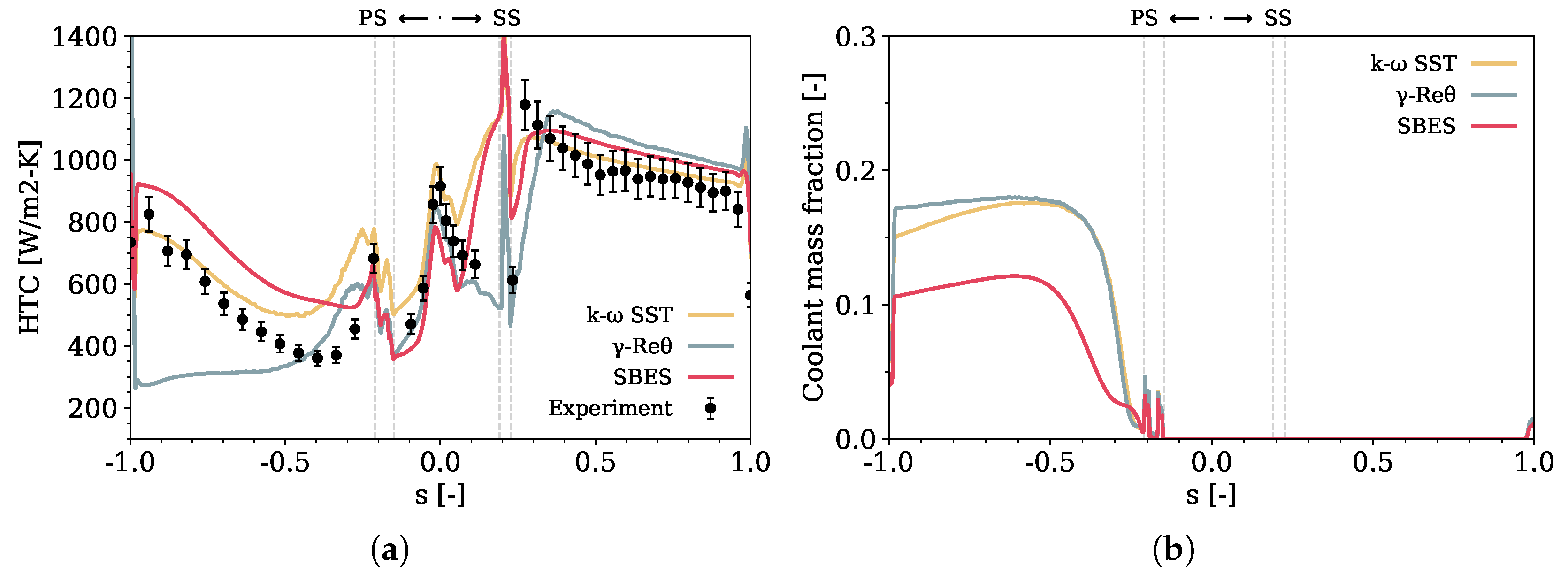
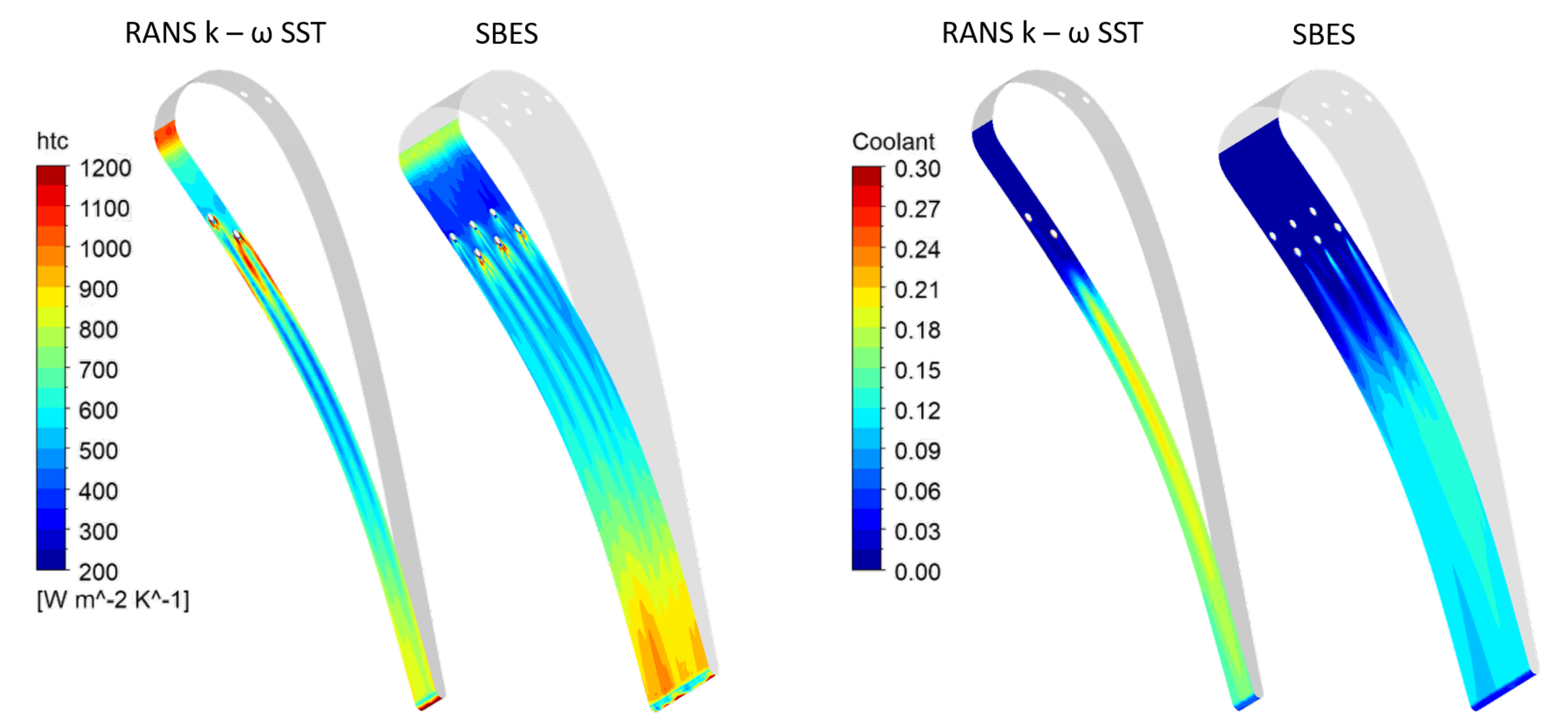
4.2.1. PS Injection
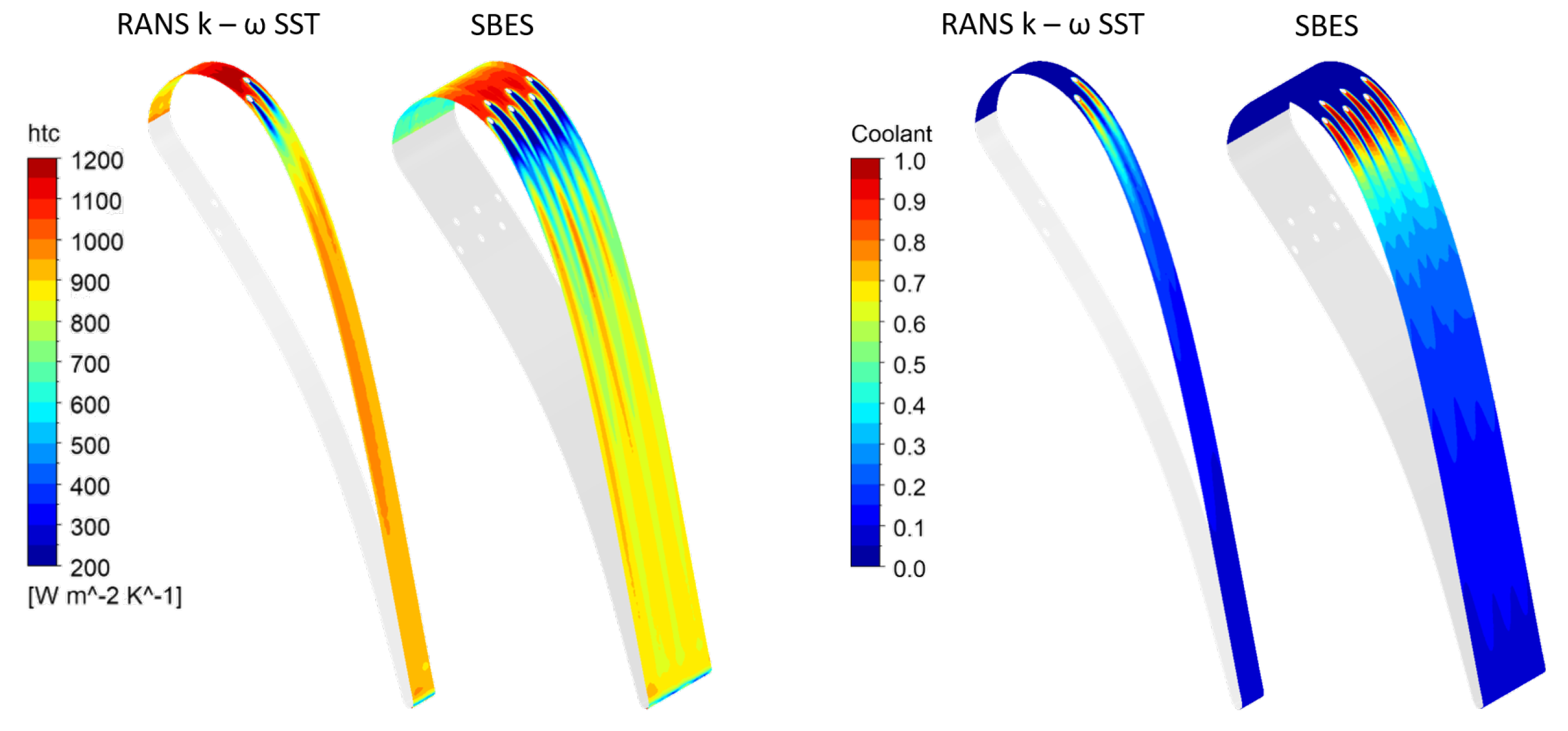
4.2.2. SS Injection
5. Conclusions
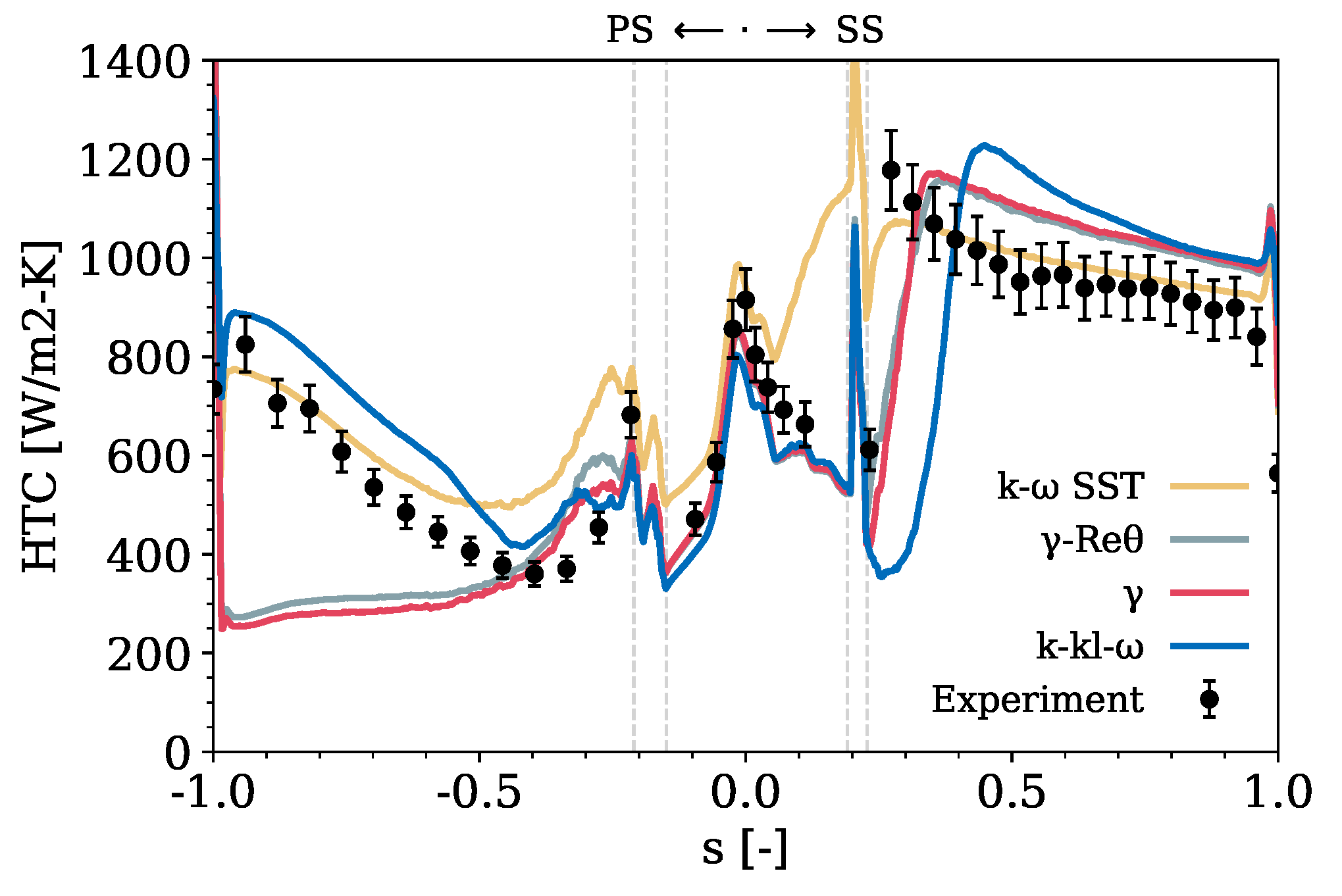
- The SST model tends to overestimate the heat transfer coefficient along the entire blade profile. However, employing a model that tends to overestimate the heat transfer coefficient can be advantageous for ensuring that the design incorporates sufficient cooling and structural robustness to handle higher thermal loads than might occur in operation.
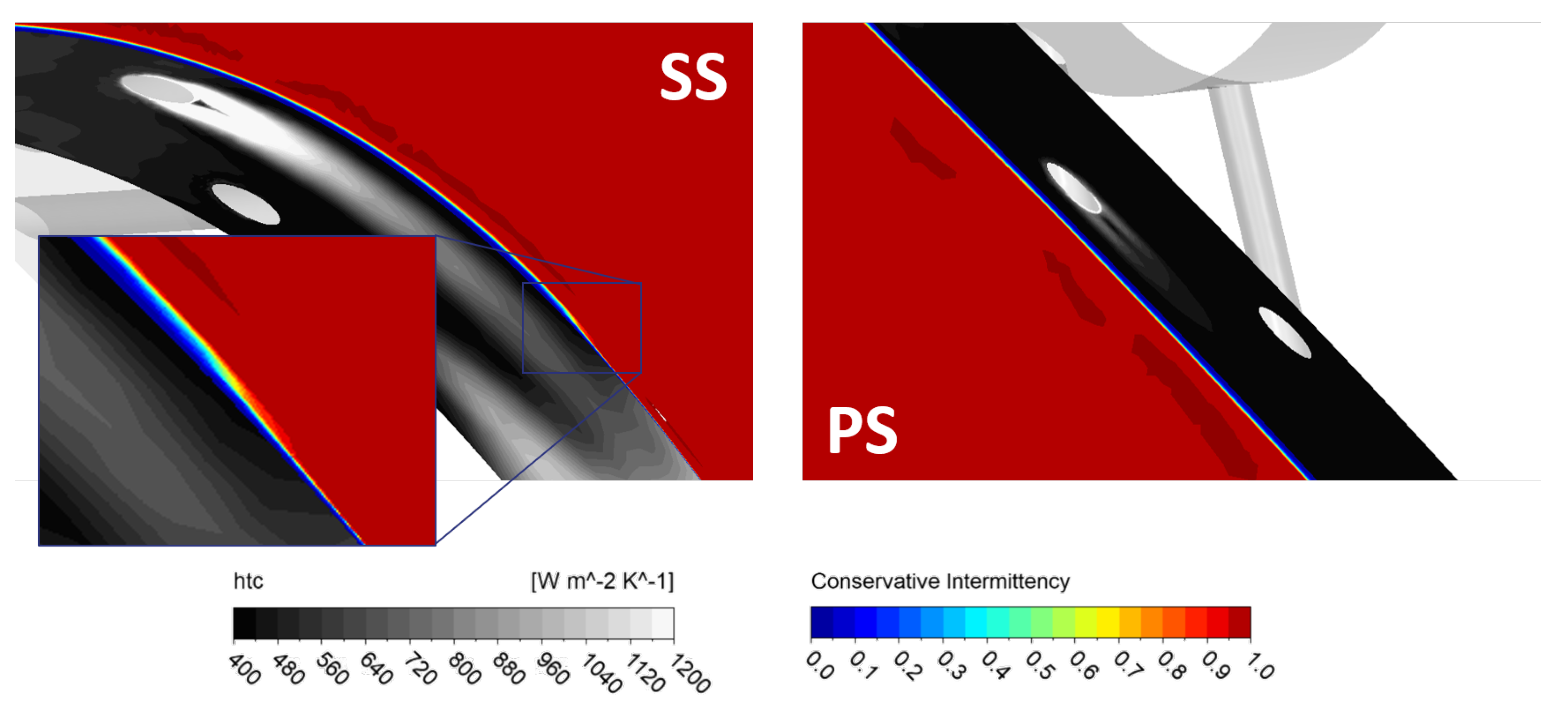
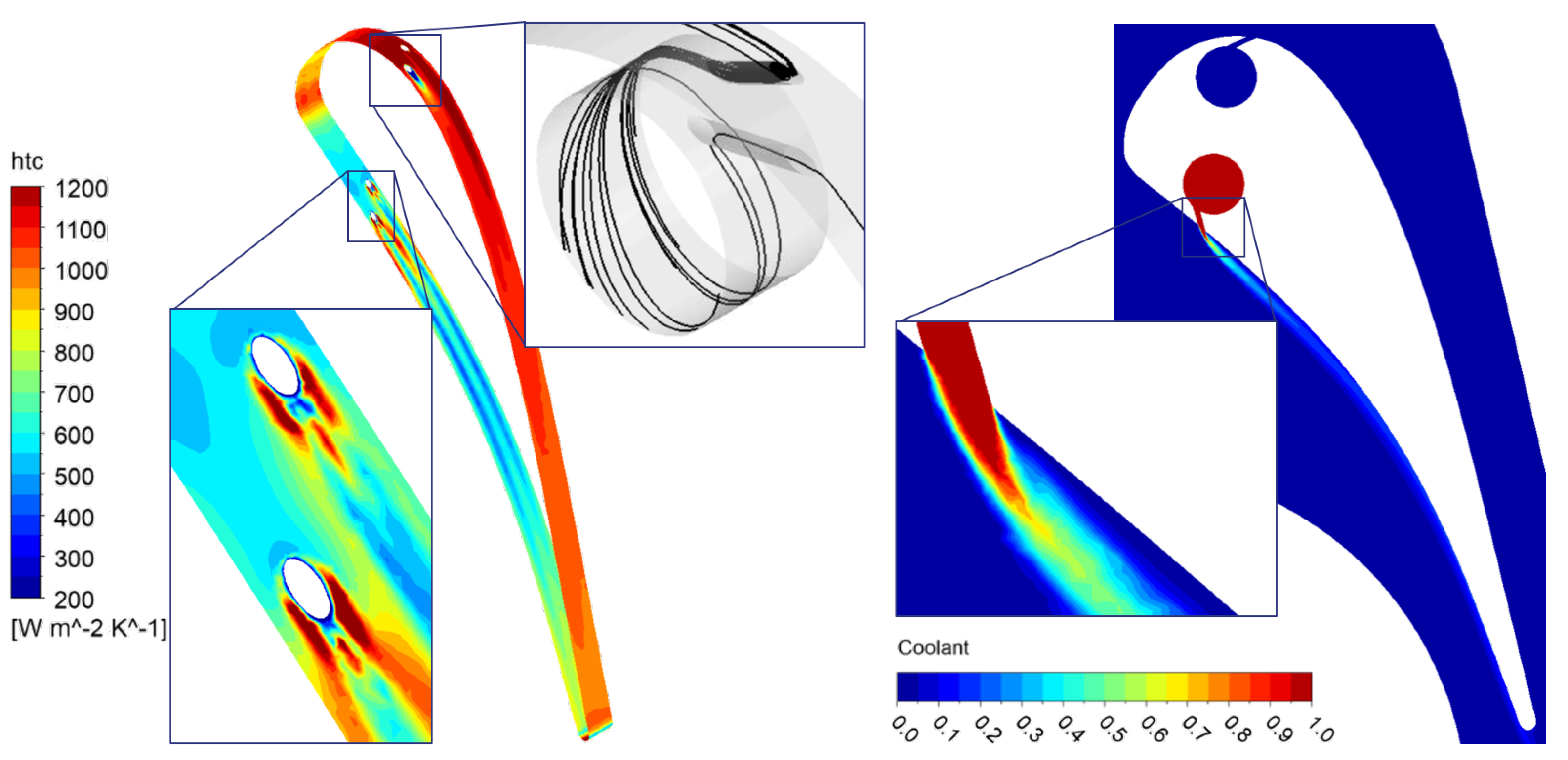
- Caution must be exercised regarding the mixed performance of the transition models in different vane areas. While accurately capturing the behavior at the leading edge, their performance is less consistent elsewhere: the and models significantly underestimate the heat transfer coefficient on the PS and overestimate it on the SS independently of the film-cooling injection, suggesting an excessive turbulence production downstream of the transition point. Further, the SS shows a transition from laminar to turbulent flow. In contrast, the PS exhibits a persistent laminar flow, leading to lower heat transfer coefficient prediction. This is not completely unexpected, as the cooling holes act as a ‘trip’ in the experiments but not for the transition models, and none of these models are calibrated under ‘tripped’ conditions. The model delays the transition on the SS but is the only transition model capable of reproducing this effect on the PS.
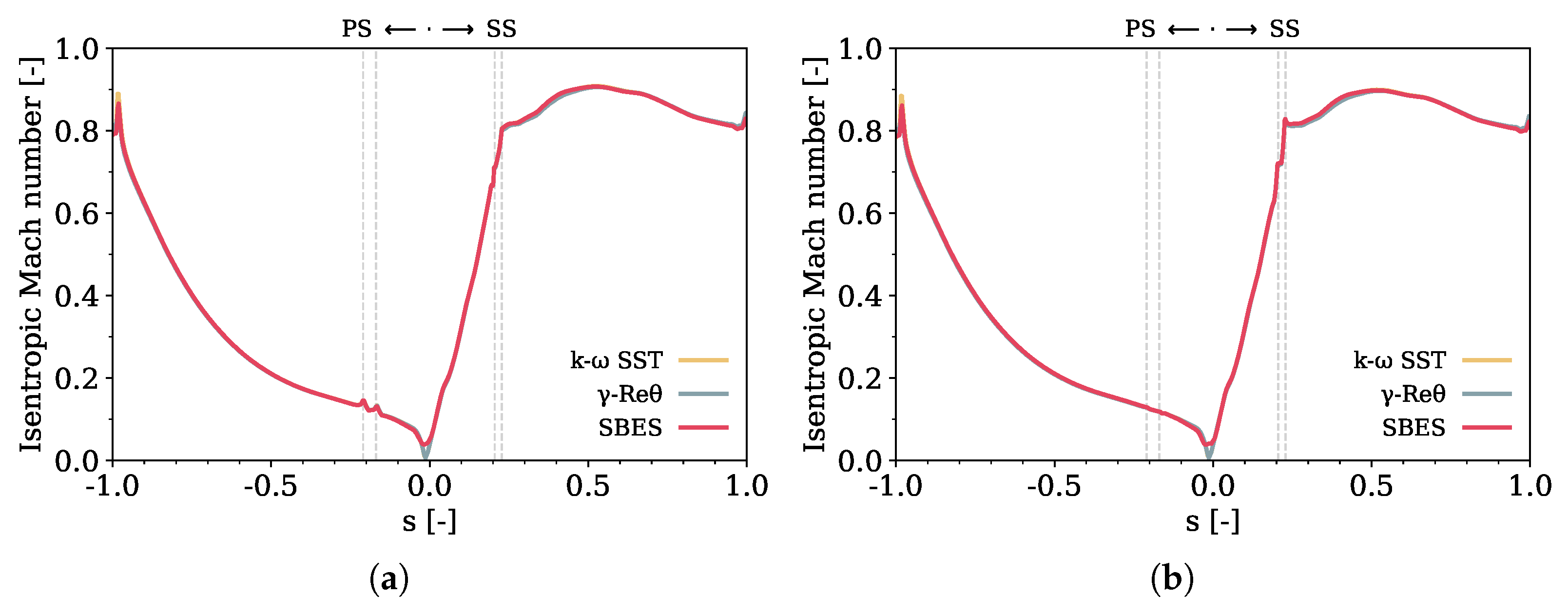
- Careful considerations are necessary concerning the use of the SBES approach in this test case. The SBES results do not show a general improvement in predicting the thermal behavior of the vane, even though an LES treatment of the mainstream would be expected to improve the prediction of mixing-related phenomena, such as film-cooling injection and its impact on the thermal loads. Despite this, it is worth considering that the shielding function might limit the benefits by enforcing a RANS solution in the boundary layer. In addition, this specific test case is highly dependent on turbulence, which for SBES, is generated at the inlet differently compared to RANS.
- Based on considerations of the predictive accuracy over the mesh and computational cost requirements, this study notes that for this highly boundary condition-dependent test case, a low-order analysis, such as the one with the SST RANS approach, can be preferred over a high-order one since it produces results similar to SBES and is more conservative than what can be achieved with transition models, which is valuable in the design phase.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Menzies, K. Delivering better power: The role of simulation in reducing the environmental impact of aircraft engines. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130316. [Google Scholar] [CrossRef] [PubMed]
- Han, J.C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Walters, D.K.; Cokljat, D. A Three-Equation Eddy-Viscosity Model for Reynolds-Averaged Navier–Stokes Simulations of Transitional Flows. J. Fluids Eng. 2008, 130, 121401. [Google Scholar] [CrossRef]
- Langtry, R.; Menter, F. Transition Modeling for General CFD Applications in Aeronautics. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Langtry, R.B. A Correlation-Based Transition Model Using Local Variables for Unstructured Parallelized CFD Codes. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2006. [Google Scholar] [CrossRef]
- Menter, F.R.; Smirnov, P.E.; Liu, T.; Avancha, R. A one-equation local correlation-based transition model. Flow Turbul. Combust. 2015, 95, 583–619. [Google Scholar] [CrossRef]
- Esfahanian, V.; Shahbazi, A.; Ahmadi, G. Conjugate Heat Transfer Simulation of Internally Cooled Gas Turbine Vane. In Proceedings of the CFD Society of Canada Conference, Montréal, QC, Canada, 28–29 April 2011. [Google Scholar]
- Papa, F.; Madanan, U.; Goldstein, R.J. Modeling and Measurements of Heat/Mass Transfer in a Linear Turbine Cascade. J. Turbomach. 2017, 139, 091002. [Google Scholar] [CrossRef]
- Bacci, T.; Gamannossi, A.; Mazzei, L.; Picchi, A.; Winchler, L.; Carcasci, C.; Andreini, A.; Abba, L.; Vagnoli, S. Experimental and CFD analyses of a highly-loaded gas turbine blade. Energy Procedia 2017, 126, 770–777. [Google Scholar] [CrossRef]
- Dick, E.; Kubacki, S. Transition Models for Turbomachinery Boundary Layer Flows: A Review. Int. J. Turbomach. Propuls. Power 2017, 2, 4. [Google Scholar] [CrossRef]
- Babajee, J. Detailed Numerical Characterization of the Separation-Induced Transition, including Bursting, in a Low-Pressure Turbine Environment. Ph.D. Thesis, Ecole Centrale de Lyon, Écully, France. Institut von Karman de Dynamique des Fluides, Rhode-Saint-Genèse, Belgium, 2013. [Google Scholar]
- Jonsson, I.; Deshpande, S.; Chernoray, V.; Thulin, O.; Larsson, J. Experimental and Numerical Study of Laminar-Turbulent Transition on a Low-Pressure Turbine Outlet Guide Vane. J. Turbomach. 2021, 143, 101011. [Google Scholar] [CrossRef]
- Bassi, F.; Fontaneto, F.; Franchina, N.; Ghidoni, A.; Savini, M. Turbine vane film cooling: Heat transfer evaluation using high-order discontinuous Galerkin RANS computations. Int. J. Heat Fluid Flow 2016, 61, 610–625. [Google Scholar] [CrossRef]
- Liu, Y.; Li, P.; Jiang, K. Comparative assessment of transitional turbulence models for airfoil aerodynamics in the low Reynolds number range. J. Wind. Eng. Ind. Aerodyn. 2021, 217, 104726. [Google Scholar] [CrossRef]
- Aftab, S.M.A.; Mohd Rafie, A.S.; Razak, N.A.; Ahmad, K.A. Turbulence Model Selection for Low Reynolds Number Flows. PLoS ONE 2016, 11, e0153755. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Arnone, A.; Bertini, F. A CFD Study of Low Reynolds Number Flow in High Lift Cascades. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air: Turbomachinery, Parts A, B, and C, Glasgow, UK, 14–18 June 2010; Volume 7. [Google Scholar] [CrossRef]
- Pacciani, R.; Rubechini, F.; Arnone, A.; Lutum, E. Calculation of Steady and Periodic Unsteady Blade Surface Heat Transfer in Separated Transitional Flow. J. Turbomach. 2012, 134, 061037. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, P.; Huang, H.; Han, W. Conjugate Heat Transfer Analysis of a High Pressure Air-Cooled Gas Turbine Vane. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air: Heat Transfer, Parts A and B, Glasgow, UK, 14–18 June 2010; Volume 4, pp. 501–508. [Google Scholar] [CrossRef]
- Zhang, H.; Zou, Z.; Li, Y.; Ye, J.; Song, S. Conjugate heat transfer investigations of turbine vane based on transition models. Chin. J. Aeronaut. 2013, 26, 890–897. [Google Scholar] [CrossRef]
- Lin, G.; Kusterer, K.; Ayed, A.H.; Bohn, D.; Sugimoto, T. Conjugate Heat Transfer Analysis of Convection-cooled Turbine Vanes Using γ-Reθ Transition Model. Int. J. Gas Turbine Propuls. Power Syst. 2014, 6, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Enico, D. External Heat Transfer Coefficient Predictions on a Transonic Turbine Nozzle Guide Vane Using Computational Fluid Dynamics. Master’s Thesis, Linköping University, Applied Thermodynamics and Fluid Mechanics, Linköping, Sweden, 2021. [Google Scholar]
- Daugulis, E. Numerical Study of Gas Turbine Nozzle Guide Vane External Heat Transfer and Showerhead Film Cooling Effectiveness by Means of Hybrid RANS-LES CFD Modelling. Master’s Thesis, Delft University of Technology, Delft, The Netherland, 2022. [Google Scholar]
- Giel, P.W.; Boyle, R.J.; Bunker, R.S. Measurements and Predictions of Heat Transfer on Rotor Blades in a Transonic Turbine Cascade. J. Turbomach. 2004, 126, 110–121. [Google Scholar] [CrossRef]
- Johnsson, R.; Asiegbu, L. CFD Based External Heat Transfer Coefficient Predictions on a Transonic Film-Cooled Gas Turbine Guide Vane: A Computational Fluid Dynamics Study on the Von Karman Institute LS94 Test Case. Master’s Thesis, Linköping University, Applied Thermodynamics and Fluid Mechanics, Linköping, Sweden, 2022. [Google Scholar]
- Arts, T.; De Rouvroit, M.L.; Rutherford, A. Aero-Thermal Investigation of a Highly Loaded Transonic Linear Turbine Guide Vane Cascade; von Karman Institute for Fluid Dynamics: Rhode Saint Genèse, Belgium, 1990. [Google Scholar]
- Gehrer, A.; Jericha, H. External Heat Transfer Predictions in a Highly Loaded Transonic Linear Turbine Guide Vane Cascade Using an Upwind Biased Navier–Stokes Solver. J. Turbomach. 1999, 121, 525–531. [Google Scholar] [CrossRef]
- Martelli, F.; Adami, P.; Belardini, E. Heat Transfer Modelling in GAS Turbine Stage; University of Florence: Florence, Italy, 2003. [Google Scholar]
- Gourdain, N.; Duchaine, F.; Gicquel, L.Y.M.; Collado, E. Advanced Numerical Simulation Dedicated to the Prediction of Heat Transfer in a Highly Loaded Turbine Guide Vane. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air: Turbomachinery, Parts A, B, and C, Glasgow, UK, 14–18 June 2010; Volume 7, pp. 807–820. [Google Scholar] [CrossRef][Green Version]
- Fontaneto, F. Aero-Thermal Performance of a Film-Cooled High Pressure Turbine Blade/Vane: A Test Case for Numerical Codes Validation. Ph.D. Thesis, University of Bergamo, Bergamo, Italy, 2014. [Google Scholar]
- Fontaneto, F.; Lavagnoli, S.; Arts, T. The LS-94 film cooled high pressure turbine vane: An extension to the LS-89 test case. Turbo Expo Power Land Sea Air 2024, Under review. [Google Scholar]
- Consigny, H.; Richards, B.E. Short Duration Measurements of Heat-Transfer Rate to a Gas Turbine Rotor Blade. J. Eng. Power 1982, 104, 542–550. [Google Scholar] [CrossRef]
- Camci, C.; Arts, T. Experimental Heat Transfer Investigation Around the Film-Cooled Leading Edge of a High-Pressure Gas Turbine Rotor Blade. J. Eng. Gas Turbines Power 1985, 107, 1016–1021. [Google Scholar] [CrossRef]
- Schultz, D.L.; Jones, T.V. Heat-transfer measurements in short-duration hypersonic facilities. Document, AD0758590 Agard, 1973.
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- ANSYS, Inc. Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Langtry, R.B.; Menter, F.R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2012, 47, 2894–2906. [Google Scholar] [CrossRef]
- Slotnick, J.P.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D.J. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; NASA/CR–2014-218178 Technical Report; NASA: Washington, DC, USA, 2014. [Google Scholar]
- Spalart, P.R. Comments on the Feasibility of LES for Wings and on the Hybrid RANS/LES Approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997; pp. 137–147. [Google Scholar]
- Menter, F. Stress-Blended Eddy Simulation (SBES)—A New Paradigm in Hybrid RANS-LES Modeling. In Proceedings of the Progress in Hybrid RANS-LES Modelling, Strasbourg, France, 26–28 September 2016; Hoarau, Y., Peng, S.H., Schwamborn, D., Revell, A., Eds.; pp. 27–37. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. Synthetic Turbulence Generators for RANS-LES Interfaces in Zonal Simulations of Aerodynamic and Aeroacoustic Problems. Flow Turbul. Combust 1905, 93, 63–92. [Google Scholar] [CrossRef]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Andreini, A.; Caciolli, G.; Da Soghe, R.; Facchini, B.; Mazzei, L. Numerical Investigation on the Heat Transfer Enhancement due to Coolant Extraction on the Cold Side of Film Cooling Holes. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Volume 5B: Heat Transfer, Düsseldorf, Germany, 16–20 June 2014. V05BT14A004. [Google Scholar] [CrossRef]





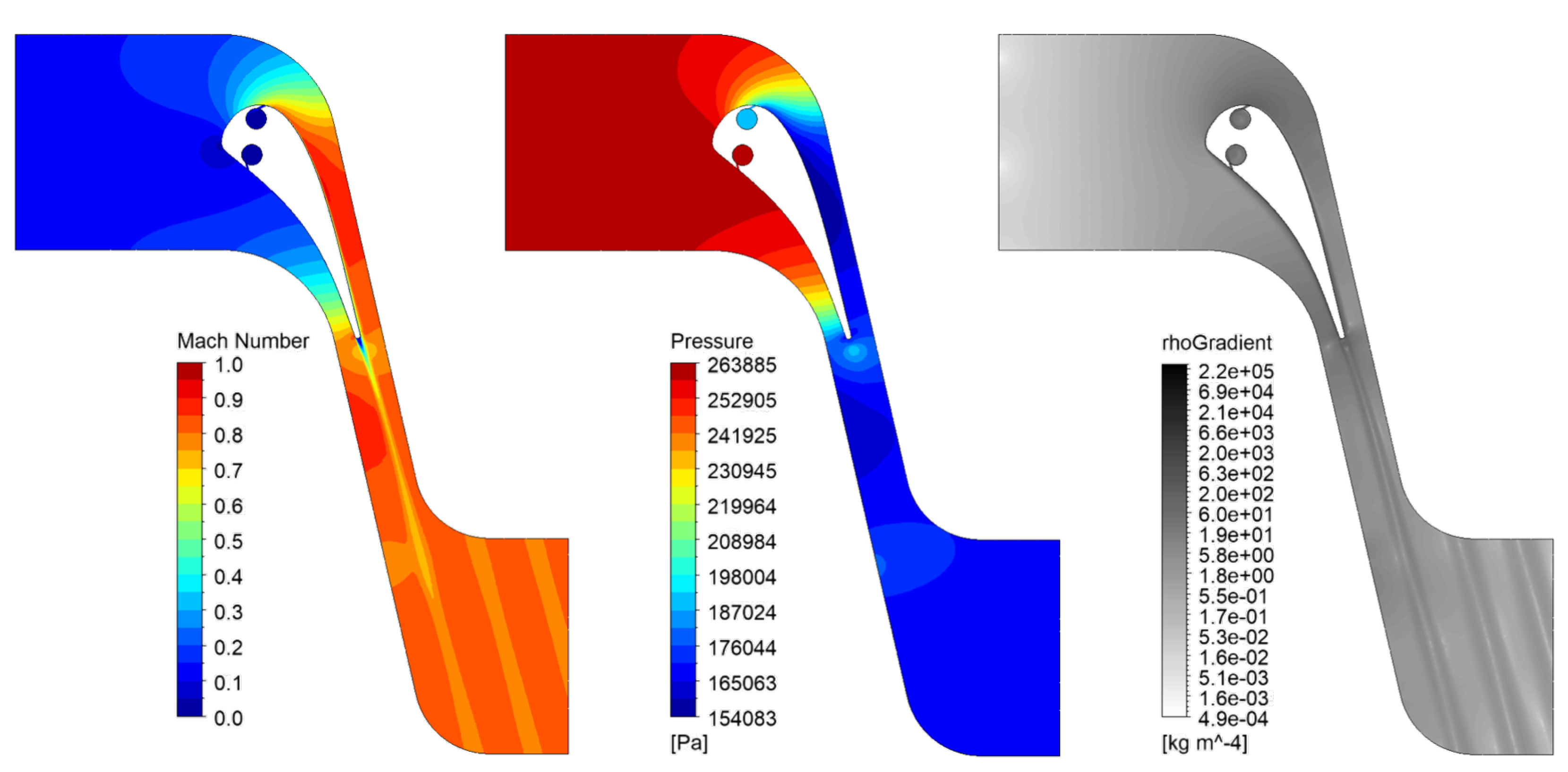





| Parameter | Symbol | Value |
|---|---|---|
| Chord [mm] | C | 67.65 |
| Axial chord [mm] | 36.985 | |
| Stagger angle [] | 55 | |
| Throat [mm] | o | 14.93 |
| Pitch [mm] | g | 57.5 |
| Vane height [mm] | h | 100 |
| Trailing-edge radius [mm] | 4.13 |
| Parameter | Suction Side | Pressure Side | ||
|---|---|---|---|---|
| Diameter [mm] | 0.5 | 0.5 | ||
| Pitch [mm] | 1.5 | 1.5 | ||
| Coordinates [mm] | Row 1 | Row 2 | Row 1 | Row 2 |
| X = 2.52 | X = 4.05 | X = 13.96 | X = 16.59 | |
| Y = 15.70 | Y = 19.95 | Y = 2.19 | Y = 2.90 | |
| Angles [] | Row 1 | Row 2 | Row 1 | Row 2 |
| 35 | 35 | 35 | // to Row 1 | |
| Number of holes | Row 1 | Row 2 | Row 1 | Row 2 |
| 33 | 32 | 33 | 32 | |
| Section | Quantities | |
|---|---|---|
| Inlet | 148.7 | Turbulence (HW) |
| upstream of | ||
| leading edge | ||
| Outlet | 43.3 | Total pressure wakes (PP) |
| downstream of | ||
| trailing edge | ||
| Coolant | ||
| / | ||
| Test Case | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [K] | [K] | [Pa] | [Pa] | [Pa] | [g/s] | [-] | [-] | [K] | [-] | [mm] | |
| Uncooled | 414.3 | - | 262,674 | 168,501 | - | - | 0.853 | 1,627,122 | 290.7 | 5.3% | 7.5 |
| SS injection | 419.8 | 295.0 | 260,952 | 168,844 | 216,567 | 2.553 | 0.815 | 1,556,992 | 291.6 | 5.3% | 7.5 |
| PS injection | 423.5 | 271.6 | 262,995 | 168,891 | 285,062 | 3.651 | 0.822 | 1,558,704 | 292.5 | 5.3% | 7.5 |
| Parameter | Non-Cooled | SS Injection | PS Injection |
|---|---|---|---|
| Global sizing [mm] | 1 | 1 | 1 |
| Surface sizing [mm] | 0.20 | 0.20 | |
| 0.31 | 0.31 | 0.31 | |
| 0.70 | |||
| 2.25 | |||
| Prismatic layers | 10 | 10 | |
| 20 | 20 | ||
| 30 | 30 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandrin, S.; Mazzei, L.; Da Soghe, R.; Fontaneto, F. Computational Fluid Dynamics Prediction of External Thermal Loads on Film-Cooled Gas Turbine Vanes: A Validation of Reynolds-Averaged Navier–Stokes Transition Models and Scale-Resolving Simulations for the VKI LS-94 Test Case. Fluids 2024, 9, 91. https://doi.org/10.3390/fluids9040091
Sandrin S, Mazzei L, Da Soghe R, Fontaneto F. Computational Fluid Dynamics Prediction of External Thermal Loads on Film-Cooled Gas Turbine Vanes: A Validation of Reynolds-Averaged Navier–Stokes Transition Models and Scale-Resolving Simulations for the VKI LS-94 Test Case. Fluids. 2024; 9(4):91. https://doi.org/10.3390/fluids9040091
Chicago/Turabian StyleSandrin, Simone, Lorenzo Mazzei, Riccardo Da Soghe, and Fabrizio Fontaneto. 2024. "Computational Fluid Dynamics Prediction of External Thermal Loads on Film-Cooled Gas Turbine Vanes: A Validation of Reynolds-Averaged Navier–Stokes Transition Models and Scale-Resolving Simulations for the VKI LS-94 Test Case" Fluids 9, no. 4: 91. https://doi.org/10.3390/fluids9040091
APA StyleSandrin, S., Mazzei, L., Da Soghe, R., & Fontaneto, F. (2024). Computational Fluid Dynamics Prediction of External Thermal Loads on Film-Cooled Gas Turbine Vanes: A Validation of Reynolds-Averaged Navier–Stokes Transition Models and Scale-Resolving Simulations for the VKI LS-94 Test Case. Fluids, 9(4), 91. https://doi.org/10.3390/fluids9040091







