Prediction of Critical Heat Flux during Downflow in Fully Heated Vertical Channels
Abstract
1. Introduction
2. Previous Work
2.1. Experimental Work
2.2. Prediction Methods
3. Data Analysis
4. Discussion
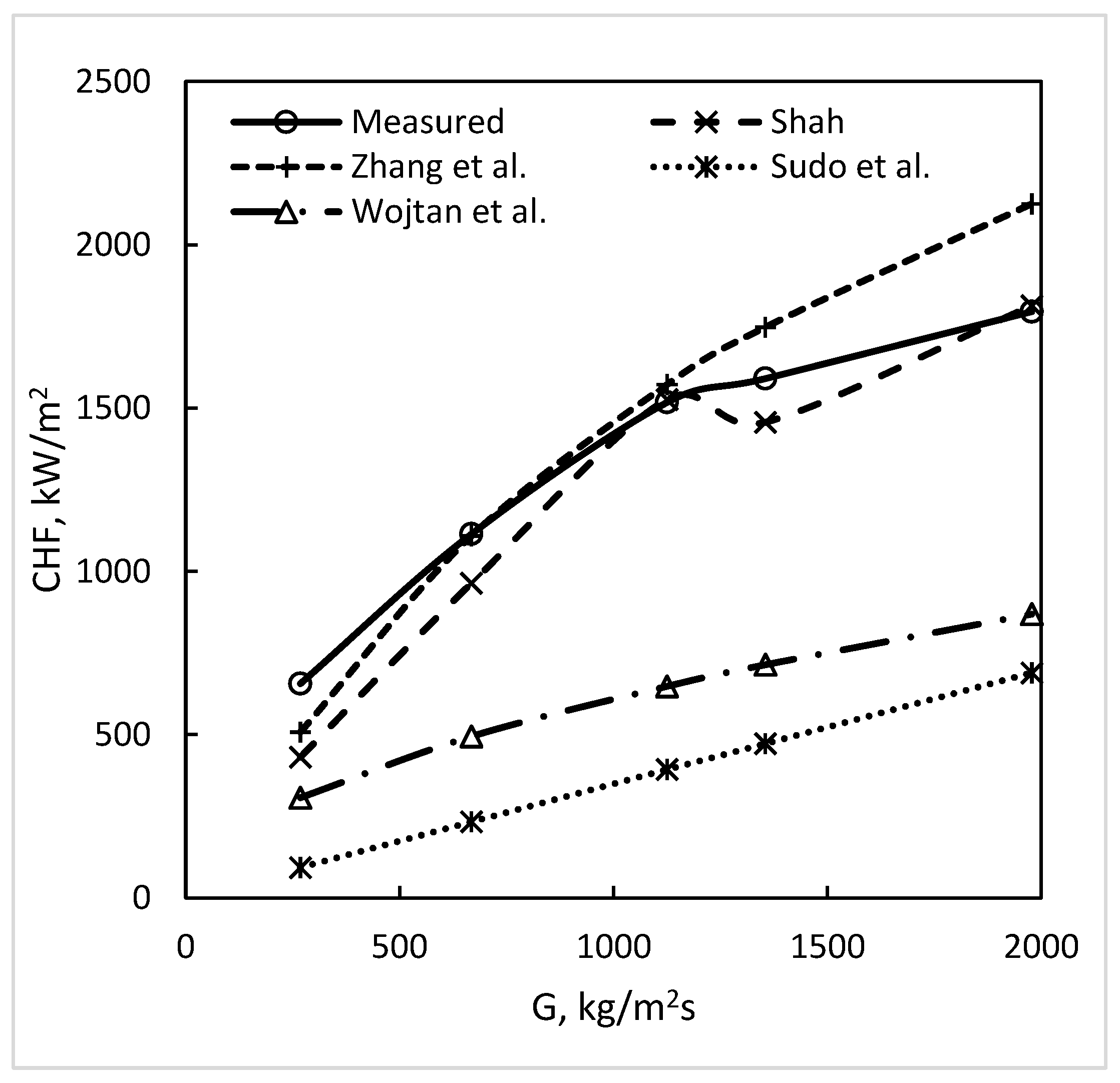
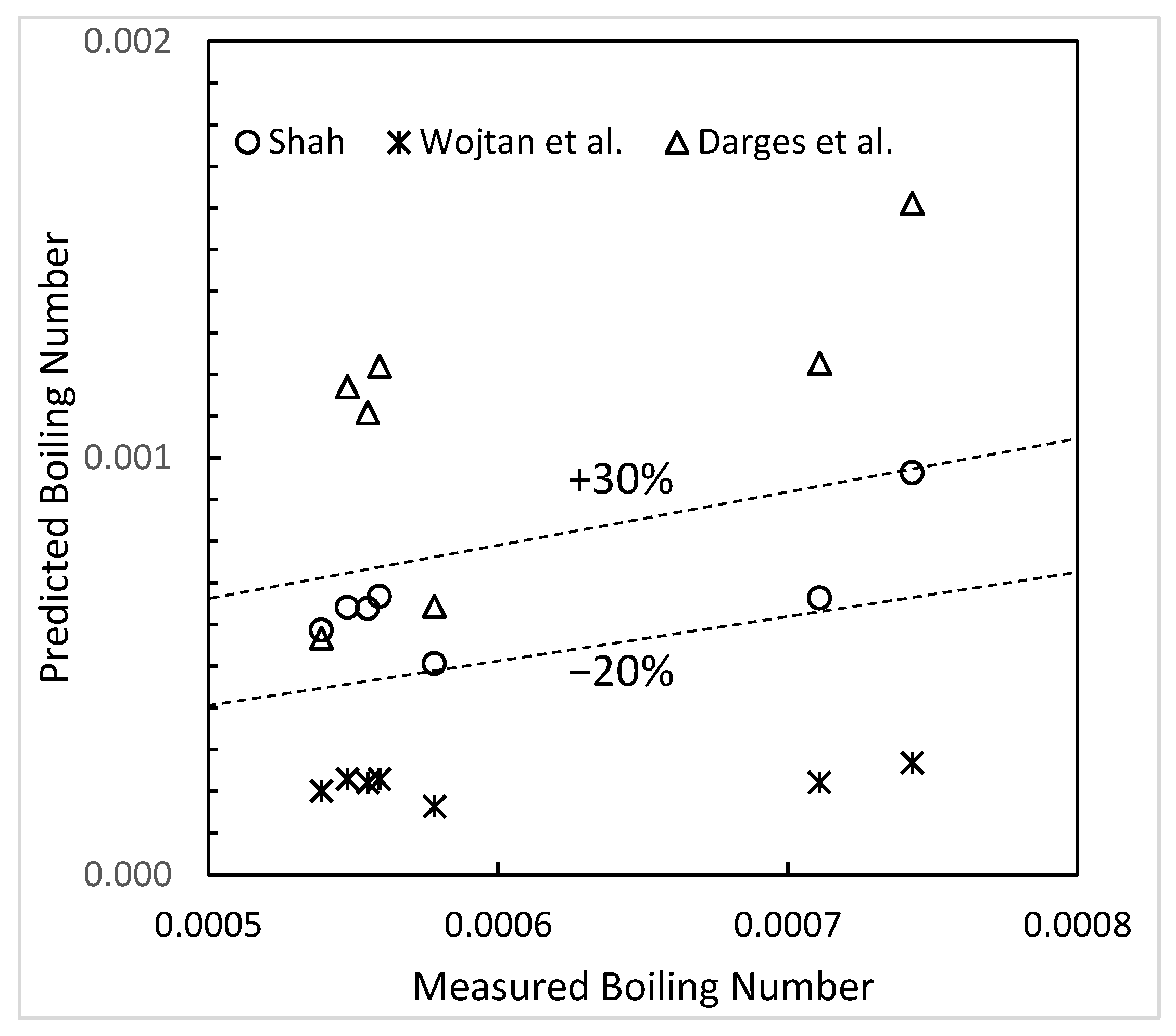
4.1. Accuracy of Correlations
4.2. Comparison of Upflow and Downflow Data
4.3. Effect of Channel Shape
4.4. Recommendations for Design
5. Conclusions
- Literature on CHF during downflow in vertical channels was studied. Some researchers reported up to 30% lower CHF in downflow compared to upflow at low flow rates. Many authors reported no effect of flow direction or even higher CHF during downflow.
- Data were analyzed for CHF during downflow in fully heated channels from 11 sources. These included several diverse fluids (water, nitrogen, refrigerants) in round and rectangular channels, reduced pressure from 0.0045 to 0.625, mass flux from 15 to 21,761 kg/m2s, inlet quality from −1.3 to 0, and exit quality from −0.2 to 1.09. These were compared to four correlations for upflow CHF and three applicable to downflow.
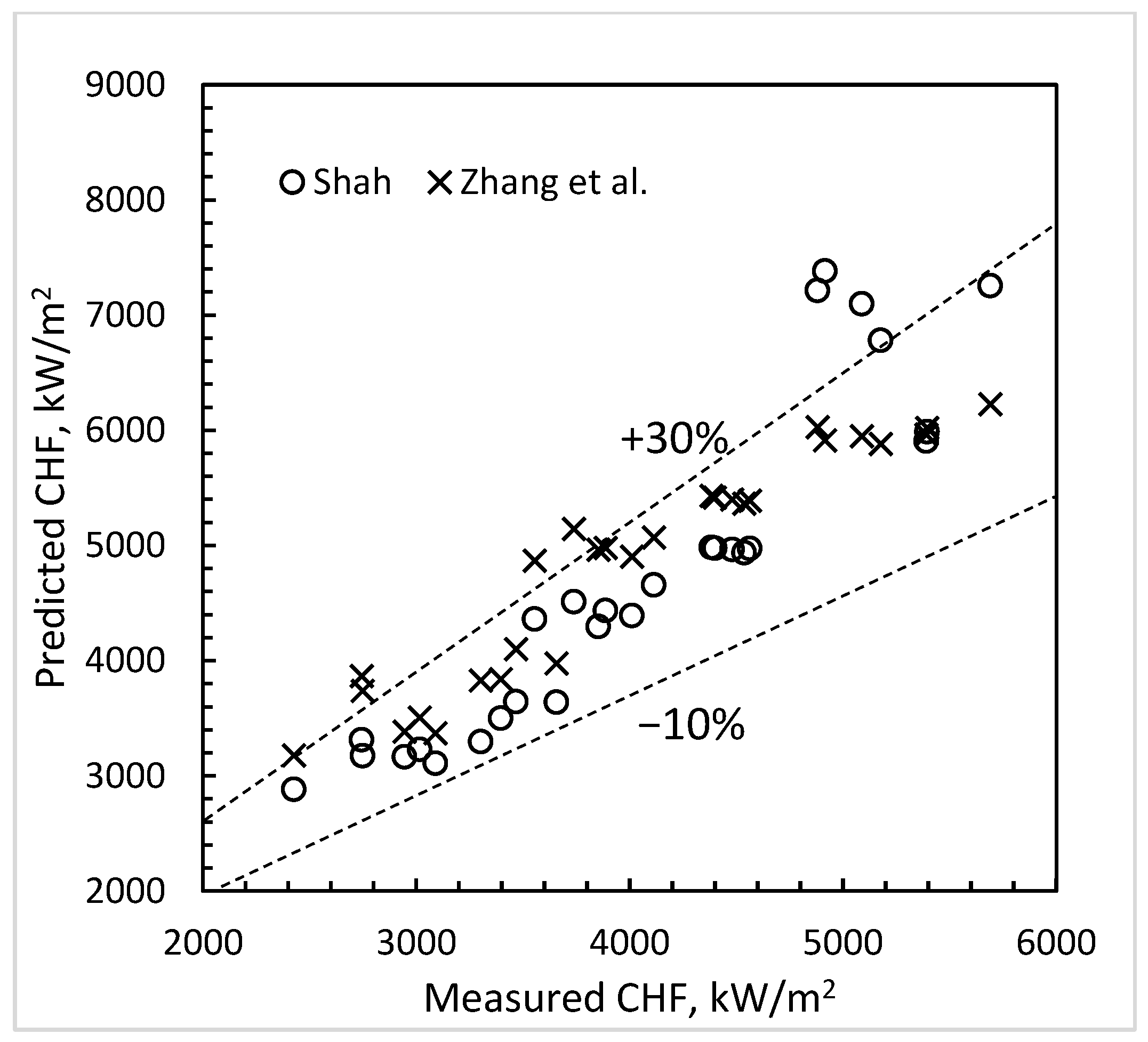
- The correlations for CHF in downflow had large deviations with most data. The upflow correlations of Shah and Katto–Ohno gave good agreement with downflow data, their MAD being 21.9% and 18.9%, respectively for the 304 data points.
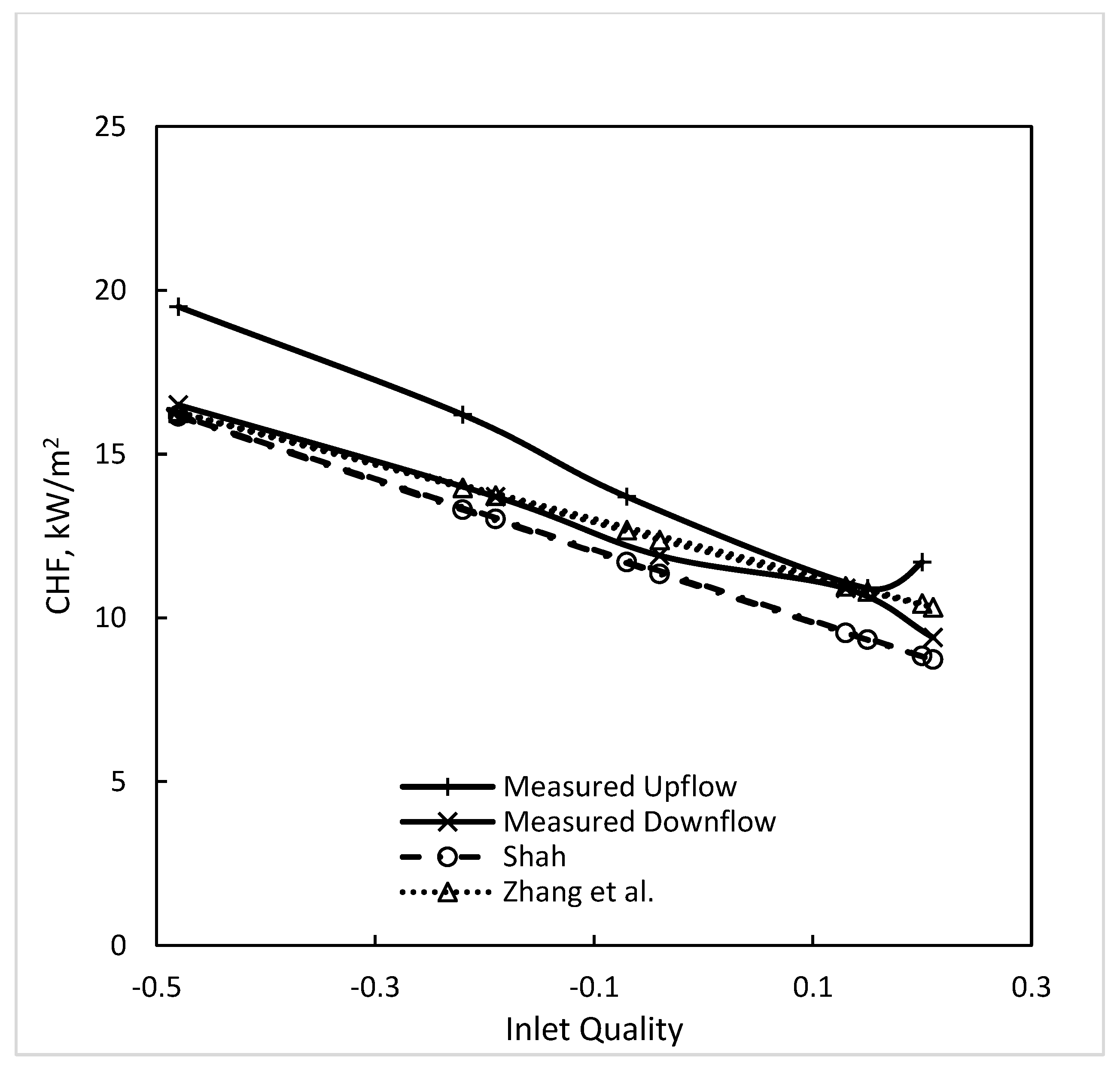
- A comparison of data from studies in which CHF during both upflow and downflow was measured showed that most of them do not show any effect of orientation. Some show differences up to ±15%, with some having higher CHF in upflow and others having higher CHF in downflow. Such deviations are well within the accuracy of most correlations.
- The correlations of Shah and Katto–Ohno are recommended for calculating CHF during downflow, subject to the minimum calculated with a flooding correlation.
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AF | Flow area, m2 |
| AH | Heated area, m2 |
| Bdθ | Bond number defined by Equation (12), dimensionless |
| Bo | Boiling number at CHF, =qc/(G iLG), dimensionless |
| CpL | Specific heat of liquid at constant pressure, kJ/kg K |
| CHF | Critical heat flux |
| D | Diameter of channel, m |
| DHP | Equivalent diameter based on heated perimeter, =(4 × flow area)/(heated perimeter), m |
| DHYD | Hydraulic equivalent diameter, =(4 × flow area)/(wetted perimeter), m |
| Frθ | Froude number defined by Equation (11), dimensionless |
| g | Acceleration due to gravity, m/s2 |
| G | Mass flux, kg/m2s |
| G* | Dimensionless mass flux defined by Equation (5), dimensionless |
| iLG | Latent heat of vaporization, kJ/kg |
| H | Height of channel, m |
| K | Constant in Kutateladze formula for pool boiling CHF, dimensionless |
| kL | Thermal conductivity of liquid, W/(mK) |
| L, LC | Heated length of channel from the entrance to the location of CHF, m |
| MAD | Mean absolute deviation, dimensionless |
| N | Number of data points, dimensionless |
| p | Pressure, Pa |
| pc | Critical pressure, Pa |
| pr | Reduced pressure = p/pc, dimensionless |
| q* | Dimensionless CHF defined by Equation (4), dimensionless |
| qc | Critical heat flux, kW/m2 |
| T | Temperature, K |
| ΔTSC | =(TSAT − TL), K |
| W | Width of channel, m |
| WeD | Weber number defined by Equation (10), dimensionless |
| x | Thermodynamic vapor quality, dimensionless |
| xc | Critical quality, i.e., quality at CHF, dimensionless |
| xin | Quality at inlet to heated section, dimensionless |
| Y | Parameter for correlating CHF in Shah correlation, dimensionless |
| Greek Symbols | |
| λ | Characteristic length defined by Equation (6), dimensionless |
| ρ | Density, kg/m3 |
| μ | Dynamic viscosity, Pa·s |
| σ | Surface tension, N/m |
| θ | Inclination of flow direction from horizontal, degree (0° is horizontal, 90° is vertical up) |
| Subscripts | |
| G | vapor |
| L | liquid |
| SAT | at saturated condition |
| SC | at subcooled condition |
| wall | of wall |
References
- Barnett, P.G. An Investigation into the Validity of Certain Hypotheses Implied by Various Burnout Correlations; Rep. AEEW-R-214; United Kingdom Atomic Energy Authority: Abingdon, UK, 1963. [Google Scholar]
- Chen, B. The upflow and downflow critical heat flux of water and freon in a vertical tube and its flow direction factor. At. Energy Sci. Technol. 1993, 27, 112–119. (In Chinese) [Google Scholar]
- Gambill, W.R.; Bundy, R.D. HFIR Heat-Transfer Studies of Turbulent Water Flow in Thin Rectangular Channels; ORNL-3079, TID-4500; Oak Ridge National Laboratory for the US Atomic Energy Commission: Oak Ridge, TN, USA, 1961. [Google Scholar]
- Papell, S.S.; Simoneau, R.J.; Brown, D.D. Buoyancy Effects on Critical Heat Flux of Forced Convective Boiling in Vertical Flow; NASA Technical Note D-3672; NASA: Washington, DC, USA, 1966. [Google Scholar]
- Papell, S.S. Combined Buoyancy and Flow Direction Effects on Saturated Boiling Critical-Heat Flux in Liquid Nitrogen; NASA TM X-68086; NASA: Washington, DC, USA, 1977. [Google Scholar]
- Kirby, G.J.; Stainforth, R.; Kinneir, J.H. A Visual Study of Forced Convection Boiling. Part 2. Flow Patterns and Burnout for a Round Test Section; AEEW-R 506, Quoted in Cumo et al., (1977); United Kingdom Atomic Energy Authority, Reactor Group: Winfrith, UK, 1967. [Google Scholar]
- Cumo, M.; Bertoni, R.; Cipriani, R.; Palazzi, G. Up-Flow and Down-Flow Burnout; Mechanical Engineering Pub for the Institution of Mechanical Engineers: London, UK, 1977. [Google Scholar]
- Lazarek, G.M.; Black, S.H. Evaporative heat transfer, pressure drop and critical heat flux in a small vertical tube with R-113. Int. J. Heat Mass Transf. 1982, 25, 945–960. [Google Scholar]
- Mishima, K.; Nishihara, H.; Michiyoshi, I. Boiling burnout and flow instabilities for water flowing in a round tube under atmospheric pressure. J. Heat Mass Transf. 1985, 28, 1115–1129. [Google Scholar]
- Remizov, O.; Sergeev, V.; Yurkov, Y. Experimental investigation of deterioration in heat-transfer with up-flow and down-flow of water in a tube. Therm. Eng. 1983, 30, 549–551. [Google Scholar]
- Deqiang, S.; Hong, J.; Junkai, F.E.N.G. An experimental study of upward and downward flow critical heat flux in a vertical round tube. In Proceedings of the 4th Miami International Symposium on Multi-Phase Transport Particulate Phenomena (Condensed Papers), Miami Beach, FL, USA, 15–17 December 1987. [Google Scholar]
- Chang, S.H.; Baek, W.P.; Bae, T.M. A study of critical heat flux for low flow of water in vertical round tubes under low pressure. Nucl. Eng. Des. 1991, 132, 225–237. [Google Scholar]
- Kays, W.M. Boiling. In Handbook of Heat Transfer; Rohsenow, W.M., Hartnett, J.P., Eds.; McGraw-Hill: New York, NY, USA, 1973; pp. 13-50–13-75. [Google Scholar]
- Ami, T.; Harada, T.; Umekawa, H.; Ozawa, M. Influence of tube diameter on critical heat flux in downward flow. Multiph. Sci. Technol. 2015, 27, 77–97. [Google Scholar] [CrossRef]
- Shah, M.M. Two-Phase Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Sudo, Y.; Miyata, K.; Ikawa, H. Experimental study of differences in dnb heat flux between upflow and downflow in vertical rectangular channel. J. Nucl. Sci. Technol. 1985, 22, 604–618. [Google Scholar] [CrossRef]
- Hirose, Y.; Sibamoto, Y.; Takashi Hibiki, T. Critical heat flux for downward flows in vertical round pipes. Prog. Nucl. Energy 2024, 168, 105027. [Google Scholar]
- Darges, S.J.; Devahdhanush, V.S.; Mudawar, I. Assessment and development of flow boiling critical heat flux correlations for partially heated rectangular channels in different gravitational environments. Int. J. Heat Mass Transf. 2022, 196, 123291. [Google Scholar]
- Shah, M.M. Improved general correlation for critical heat flux in uniformly heated vertical tubes. Int. J. Heat Fluid Flow 1987, 8, 326–335. [Google Scholar]
- Katto, Y.; Ohno, H. An improved version of the generalized correlation of critical heat flux for the forced convection boiling in uniformly heated vertical tubes. Int. J. Heat Mass Transf. 1984, 27, 1641–1648. [Google Scholar]
- Shah, M.M. Applicability of general correlations for CHF in conventional tubes to mini/macro channels. Heat Transf. Eng. 2017, 38, 1–10. [Google Scholar]
- Wojtan, L.; Revellin, R.; Thome, J.R. Investigation of saturated critical heat flux in a single uniformly heated microchannel. Exp. Therm. Fluid Sci. 2006, 30, 765–774. [Google Scholar]
- Sripada, R.; Mendu, S.S.; Tentu, D.; Varanasi, S.S.; Veeredhi, V.R. Development of correlation for critical heat flux for vertically downward two-phase flows in round tubes. Exp. Heat Transf. 2021, 34, 393–410. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Reference Fluid Thermodynamic and Transport Properties, REFPROP Version 9.1; NIST: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Dougherty, T.; Fighetti, C.; Reddy, G.; Yang, B.W. Critical heat flux for vertical upflow and downflow in uniform tubes at low pressures. In Proceedings of the Third International Symposium on Multi-Phase Flow and Heat Transfer, Xi’an, China, September 1994. [Google Scholar]
- Ruan, S.W.; Bartsch, G.; Yang, S.M. Characteristics of the critical heat flux for downward flow in a vertical tube at low flow rate and low pressure conditions. Exp. Therm. Fluid Sci. 1993, 7, 296–306. [Google Scholar] [CrossRef]
- DeBartoli, R.A.; Green, S.J.; LeTourneau, B.W.; Troy, M.; Weiss, A. Forced Convection Heat Transfer Burnout Studies for Water in Rectangular Channels and Round Tubes at Pressures above 500 Psia; WAPD-188, TID-4500; US Department of Commerce: Washington, DC, USA, 1958. [Google Scholar]
- Collier, J.G.; Thome, J.R. Convective Boiling & Condensation, 3rd ed.; Oxford University Press: Oxford, UK, 1994. [Google Scholar]






| Source | Channel Shape | D (DHYD), mm | Lc/D | Fluid | pr | G Kg/m2s | Y*x10−4 | xin | xc | N | Deviations of Correlations, %. MAD (Upper Row)/AD (Lower Row) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Katto–Ohno | Zhang et al. | Wojtan et al. | Darges et al. | Sudo et al. | Hirose et al. | Shah | |||||||||||
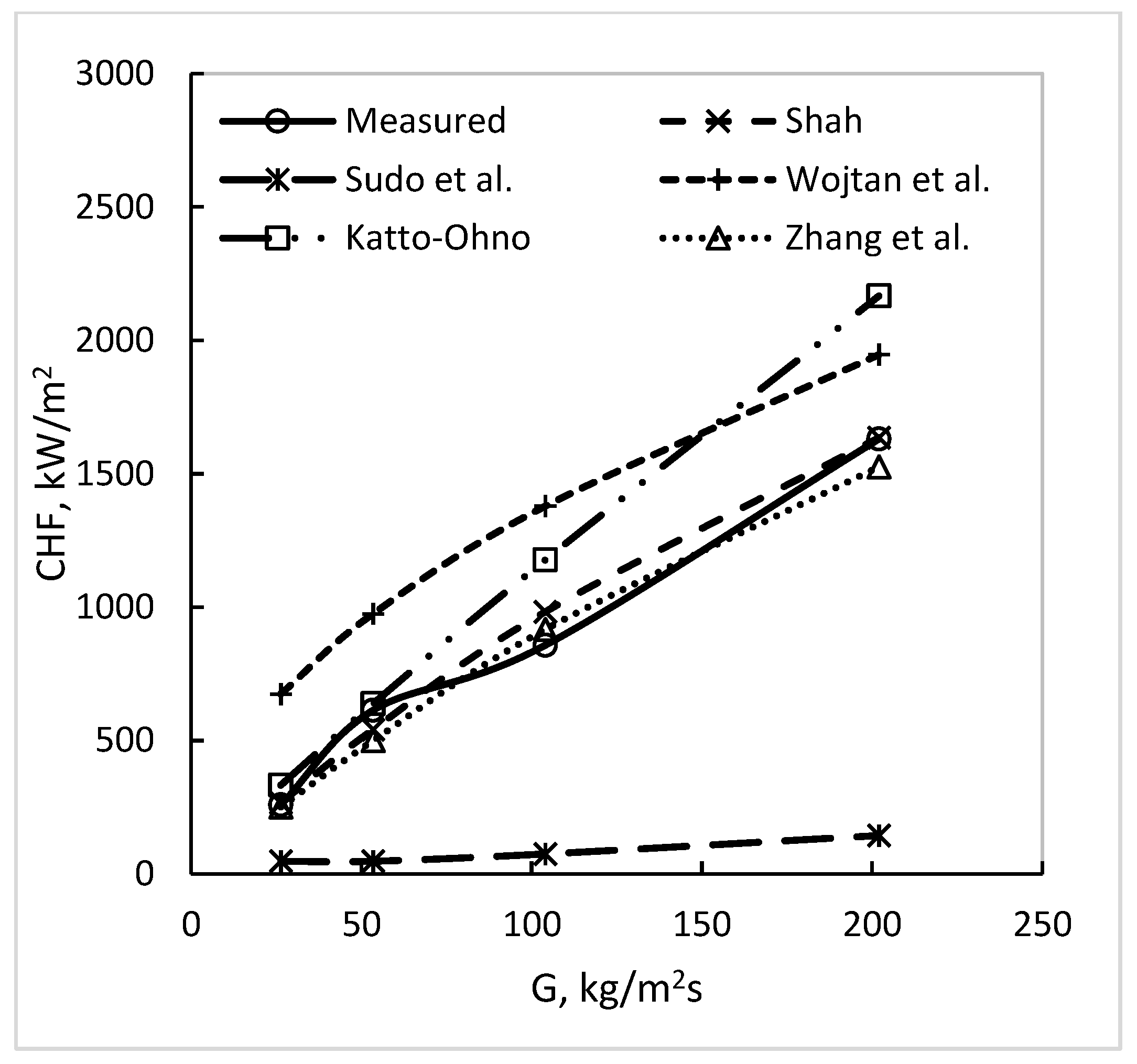
| Dougherty et al., (1994) [25] | Round | 15.9 | 153 | water | 0.0209 | 1706 8010 | 320 3200 | −0.28 −0.15 | 0.00 0.26 | 28 | 17.3 17.3 | 21.1 21.1 | 37.3 −37.3 | 0.7 8.6 | 9.8 −5.5 | 36.7 −36.7 | 15.8 15.8 |
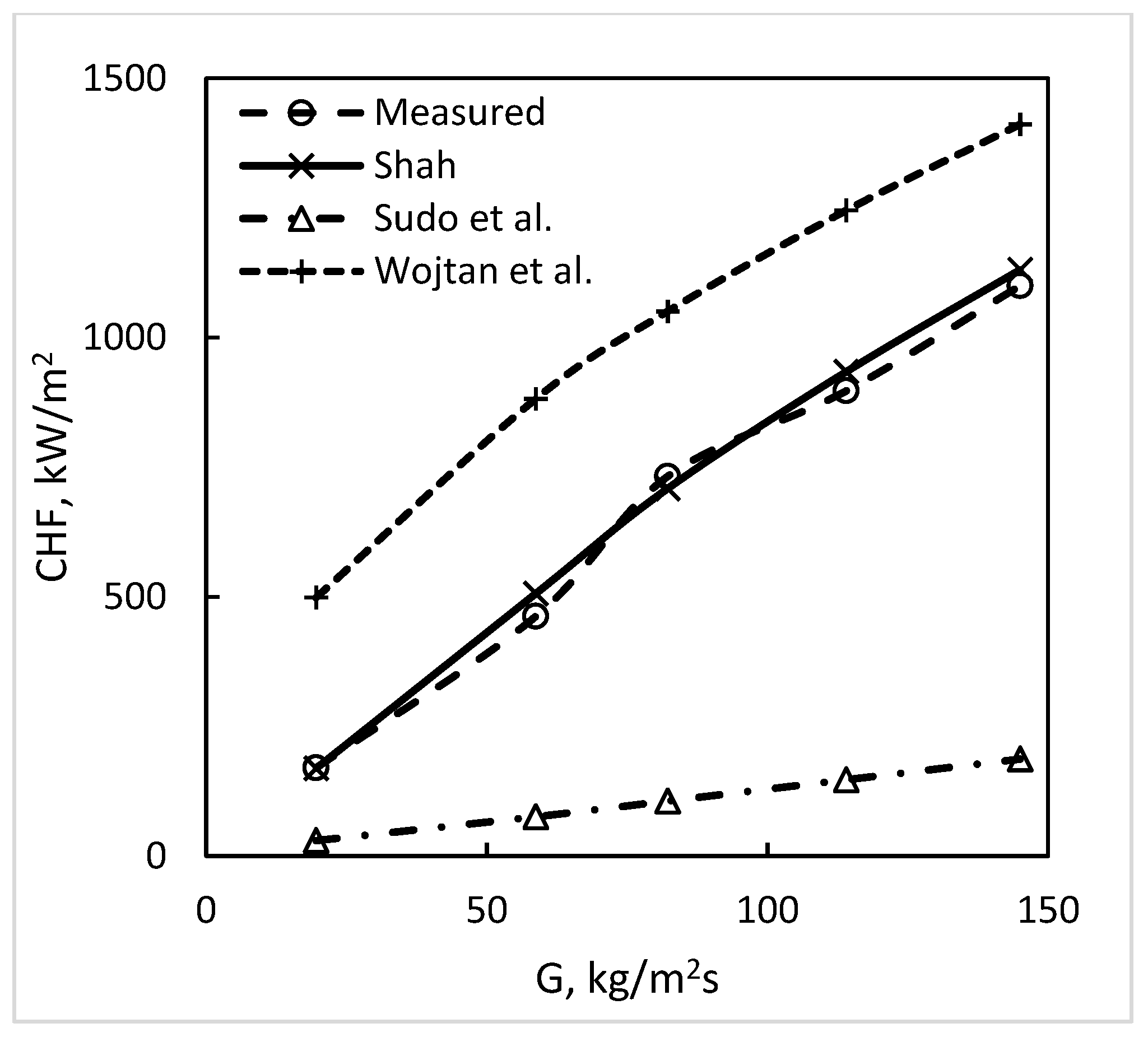
| Mishima et al., (1985) [9] | Round | 6.0 | 57.3 | water | 0.0045 | 20 239 | 0.067 6.0 | −0.13 −0.04 | 0.55 0.84 | 13 | 20.7 20.7 | 8.6 −5.1 | 64.0 64.0 | 26.7 16.9 | 56.9 −56.9 | 26.8 −18.1 | 6.1 0.2 |
| Lazarek & Black (1982) [8] | Round | 3.1 | 81.9 | R-113 | 0.0383 | 235 498 | 9.1 35 | −0.22 −0.02 | 0.72 0.89 | 9 | 4.3 −0.5 | 12.3 −12.3 | 19.1 −19.1 | 88.7 88.7 | 51.5 −51.5 | 34.0 −34.0 | 26.1 −26.1 |
| Chang et al., (1991) [12] | Round | 9.0 | 76 | water | 0.0045 | 15 25 | 0.05 0.14 | −0.15 | 0.77 | 3 | 18.8 18.8 | 13.0 −13.0 | 141.4 141.4 | 329.8 −329.8 | 19.0 −19.0 | 27.3 27.3 | 7.6 −7.6 |
| 114 | 0.08 3.8 | −0.15 −0.06 | 0.72 0.83 | 17 | 36.7 36.7 | 7.0 −1.2 | 64.2 64.2 | 105.2 105.2 | 19.8 −6.6 | 20.9 −14.7 | 8.8 8.2 | ||||||
| Ruan et al., (1993) [26] | Round | 9.0 | 44.3 | water | 0.0045 0.0317 | 26 203 | 0.12 5.7 | −0.07 −0.01 | −0.05 1.08 | 20 | 11.9 4.1 | 19.6 −18.9 | 44.2 43.0 | 24.9 5.2 | 65.5 −65.5 | 22.6 −12.1 | 17.0 −15.0 |
| DeBortoli et al., (1957) [27] | Rect. 25.4 W, 2.46 H | (4.49) | 153 | water | 0.6251 | 205 978 | 4.2 250 | −0.20 −0.04 | 0.10 0.97 | 9 | 10.0 −6.4 | 18.3 5.5 | 50.0 −50.0 | 390.7 390.7 | 13.8 −0.2 | 24.0 −24.0 | 14.3 11.0 |
| 68.1 | 313 457 | 9 18 | −0.13 | 0.15 | 2 | 18.6 18.6 | 20.8 −20.8 | 69.3 −69.3 | 251.9 251.9 | 73.8 −73.8 | 57.0 −57.0 | 19.8 −19.9 | |||||
| Rect, 1.27 W, 2.4 H | (2.42) | 126 | 457 768 | 12 31 | −1.31 −1.22 | 0.21 0.34 | 4 | 12.6 12.6 | 15.1 −15.1 | 72.7 −72.7 | 379.8 379.8 | 62.3 −62.3 | 65.2 −65.2 | 18.8 −18.8 | |||
| Gambill & Bundy (1961) [3] | Rect. 2.5 W × 2.5 H | (2.5) | 186 | water | 0.0500 0.1719 | 7465 21,761 | 1100 7700 | −0.59 −0.33 | −0.10 −0.06 | 7 | 18.1 9.7 | 16.8 4.7 | 63.6 −63.6 | 76.7 76.7 | 37.7 −37.7 | 65.5 −65.5 | 15.6 10.1 |
| Pappel et al., (1966) [4] | Round | 12.5 | 24.4 | Nitrogen | 0.2032 0.4859 | 119 434 | 9.5 81 | −0.51 −0.19 | −0.11 0.01 | 5 | 47.7 45.9 | 26.2 18.2 | 35.1 27.3 | 298.9 298.9 | 47.5 −47.5 | 122.9 122.9 | 69.6 69.6 |
| 0.1016 0.4046 | 484 2557 | 100 2400 | −0.51 −0.08 | −0.36 −0.01 | 52 | 18.1 18.1 | 24.8 12.7 | 66.8 65.8 | 145.0 145.0 | 32.5 −20.3 | 173.6 173.6 | 26.5 26.5 | |||||
| Pappel (1972) [5] | Round | 12.5 | 24.4 | Nitrogen | 0.1060 0.3004 | 168 455 | 16 98 | 0.00 | 0.14 0.33 | 12 | 19.1 17.8 | 20.3 20.3 | 78.4 78.4 | 192.4 192.4 | 33.6 −33.6 | 174.0 174.0 | 73.0 73.0 |
| 488 2544 | 100 1900 | 0.00 | 0.04 0.12 | 40 | 12.2 11.3 | 60.9 60.9 | 179.7 179.7 | 221.9 221.9 | 28.4 13.3 | 334.9 334.9 | 24.0 12.0 | ||||||
| Cumo et al., (1977) [7] | Round | 7.8 | 282 | R-12 | 0.2587 0.4231 | 130 1000 | 3.6 160 | −0.44 0.28 | 0.37 1.1 | 74 | 20.4 13.8 | 32.1 29.4 | 31.4 −29.9 | 877.8 877.8 | 64.9 −18.8 | 33.4 27.4 | 14.9 4.8 |
| Remizov et al., (1983) [10] | Round | 10.0 | 234 511 | Water | 0.6209 | 350 500 | 18 34 | −0.11 −0.06 | 0.76 0.88 | 6 | 23.5 23.5 | 39.9 39.9 | 37.9 −37.9 | 1181.4 1181.4 | 89.0 −89.0 | 16.8 16.8 | 25.9 25.9 |
| 700 | 61 | −0.03 −0.02 | 0.43 0.46 | 3 | 55.1 55.1 | 93.1 93.1 | 26.7 −26.7 | 1139.9 1139.9 | 94.0 −94.0 | 40.1 40.1 | 70.9 70.9 | ||||||
| All sources | Round, rectangular | 2.4 15.9 | 44 186 | Water, R-12, R-113, N2 | 0.0045 0.6251 | 15 21,761 | 0.05 7700 | −1.31 0.00 | −0.10 1.1 | 304 | 18.9 15.7 | 28.8 20.0 | 66.4 32.4 | 350.2 341.8 | 266.6 199.4 | 103.9 80.3 | 21.9 13.7 |
| Source | Channel Type | DHYD | Fluid | Shah | Katto and Ohno | Zhang et al. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Downflow | Upflow | Downflow | Upflow | Downflow | Upflow | |||||
| Pappel et al., (1966) [4] | Round tube | 12.8 | Nitrogen | 30.3 30.3 | 17.0 12.4 | 20.7 20.5 | 13.2 5.6 | 25.0 13.2 | 21.2 −2.8 | |
| Pappel (1972) [5] | Round tube | 12.8 | Nitrogen | 35.3 35.3 | 14.3 3.9 | 13.8 12.1 | 13.2 −9.4 | 51.5 51.5 | 26.9 21.9 | |
| Dougherty et al., (1994) [25] | Round tube | 15.9 | Water | 15.8 15.8 | 14.5 12.7 | 17.3 17.3 | 14.4 13.7 | 21.1 21.1 | 21.4 21.4 | |
| Mishima et al., (1985) [9] | Round tube | 6.0 | Water | 6.1 0.2 | 13.0 0.6 | 20.7 20.7 | 24.1 22.2 | 8.6 −5.1 | 15.0 −4.7 | |
| Lazarek & Black (1982) [8] | Round tube | 3.1 | R-113 | 26.1 −26.1 | 26.9 −26.9 | 4.3 −0.5 | 4.4 −1.9 | 12.3 −12.3 | 12.8 −12.8 | |
| Chang et al., (1991) [12] | Round tube | 6.0 | Water | 8.8 8.2 | 10.6 8.9 | 36.7 36.7 | 37.9 37.9 | 7.0 −1.2 | 7.9 1.7 | |
| Remizov et al., (1983) [10] | Round tube | 10.0 | Water | 40.9 40.9 | 42.2 42.2 | 34.1 34.1 | 35.7 35.7 | 57.6 57.6 | 59.5 59.5 | |
| DeBortoli et al., (1957) [27] | Rectangular channel | 4.49 | Water | 15.3 −12.7 | 19.9 * −19.9 | 11.6 −8.6 | 9.0 * 9.0 | 18.7 0.71 | 17.5 * −17.5 | |
| 2.42 | Water | 18.8 −18.8 | 12.5 ** 0.2 | 12.6 12.6 | 19.8 ** 19.8 | 15.1 −15.1 | 2.8 ** −1.8 | |||
| Cumo et al., (1977) [7] | Round tube | 7.8 | R-12 | 14.9 4.8 | 18.4 −7.6 | 20.4 13.8 | 17.7 −0.4 | 32.1 29.4 | 26.7 12.3 | |
| All sources | 22.2 15.7 | 17.2 14.1 | 19.3 16.6 | 18.7 17.7 | 29.4 22.7 | 22.6 9.3 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, M.M. Prediction of Critical Heat Flux during Downflow in Fully Heated Vertical Channels. Fluids 2024, 9, 79. https://doi.org/10.3390/fluids9030079
Shah MM. Prediction of Critical Heat Flux during Downflow in Fully Heated Vertical Channels. Fluids. 2024; 9(3):79. https://doi.org/10.3390/fluids9030079
Chicago/Turabian StyleShah, Mirza M. 2024. "Prediction of Critical Heat Flux during Downflow in Fully Heated Vertical Channels" Fluids 9, no. 3: 79. https://doi.org/10.3390/fluids9030079
APA StyleShah, M. M. (2024). Prediction of Critical Heat Flux during Downflow in Fully Heated Vertical Channels. Fluids, 9(3), 79. https://doi.org/10.3390/fluids9030079






