1. Introduction
Spray drying of emulsions is a widely used technique for the production of oleaginous powders. An oil-in-water emulsion is first atomized into fine droplets, which are then dried into particles with encapsulated oil droplets by subsequent contact with a hot air stream [
1,
2,
3]. In the food, pharmaceutical, and chemical industries, pressure-swirl nozzles are commonly used for the atomization step, as they are generally more efficient and provide better atomization results in comparison to solid-cone nozzles [
4,
5]. During atomization, the liquid is strongly accelerated through a narrow gap and subjected to high shear and elongational stresses. The stresses acting on the liquid can cause deformation and breakup of the dispersed oil droplets, leading to a change in the set oil droplet size. The size of the oil droplets in the resulting powder is directly related to physical and sensorial properties of the powder, as well as the release of bioactive compounds in the reconstituted product [
6]. Understanding the influence of atomization conditions on the oil droplet breakup is necessary in order to enable a targeted, understanding-based product design. It has been shown in previous studies [
7,
8,
9,
10,
11,
12] that the oil droplet size is influenced by the atomization step, depending on the kind of atomizer and the energy input. For pressure-swirl nozzles, atomization pressure and viscosity ratio between oil and emulsion have been identified as other relevant parameters for oil droplet breakup. Limited impact was found for the initial oil droplet size [
7], while no significant impact was found for the emulsion viscosity [
8]. When atomizing emulsions with high oil concentrations, the droplet size is not only determined by breakup, but also coalescence [
13]. In this study, the effect of coalescence was excluded by working at very low disperse phase fractions. However, especially for pressure swirl atomization, information about the influence of the geometric nozzle design on the oil droplet breakup is scarce. Therefore, the present study investigates the impact of the variation of geometric features of pressure swirl nozzles on oil droplet breakup for different atomization pressures.
In hollow-cone atomizers, liquid is fed into a swirl chamber and an air core is created due to high tangential velocities imparted on the liquid. As the rotating liquid approaches the atomizer exit, a thin liquid lamella is formed in the outlet orifice. Upon exiting the nozzle, the lamella expands outwards, forming a hollow cone and becoming thinner until the conical sheet breaks up into fine spray droplets [
5]. While various types of hollow-cone pressure-swirl nozzles have been developed, they are commonly differentiated in the way the liquid is set in a swirling motion [
14,
15]. This includes pressure-swirl nozzles with an axial inlet and helical slots (
Figure 1a), as well as nozzles with tangential inlet holes and a swirl chamber (
Figure 1b).
The current understanding of oil droplet breakup mechanisms during atomization is based on theories developed for emulsification processes. To achieve oil droplet breakup, the external deformation stresses imparted on the droplets by the surrounding liquid must exceed the droplet capillary pressure [
16,
17]. These deformation stresses consist mainly of shear and elongational stresses acting on the droplet’s surface. In pressure-swirl nozzles, high shear stresses are expected in areas with small cross-sections, namely, the inlet ports and the outlet orifices. Furthermore, elongational stresses can be expected in areas where the droplet is quickly accelerated, e.g., when the liquid is pushed through a small opening such as a nozzle orifice or inlet ports, and therefore extended in the direction of flow [
18].
Oil droplet breakup in laminar flow can be described by the capillary number
Ca, which can be calculated for breakup due to either shear or elongational stress. According to the literature [
19,
20], elongational stresses are expected to be much lower in comparison to shear stresses in the liquid film in the outlet orifice. Due to the small thickness of the liquid film in this area, stresses are generally anticipated to be highest in the nozzle orifice, making them crucial for oil droplet breakup. Additionally, it is well established that changes in inlet port area can affect flow characteristics such as volume flow rate, which in turn could influence stresses and thus oil droplet breakup in the outlet orifice.
Renze et al. [
21] showed that predominantly shear stresses determine the flow inside the nozzle orifice. Therefore, this study focuses on the capillary number for breakup in laminar shear flow.
Ca is defined according to Equation (1), with the shear rate
in s
−1, the shear viscosity of the continuous phase
measured in Pa·s, the droplet radius
x in m, and the interfacial tension σ measured in N/m at the oil-water-interface as influencing parameters (Equation (1)). The viscosity of the continuous phase is used here in place of the emulsion viscosity, as very low disperse phase fractions were worked with.
Oil droplet breakup occurs when a critical capillary number
Cacr is exceeded for a sufficiently long time period [
13,
17]. The value of
Cacr highly depends on the type of flow that is acting on the droplet, as well as the emulsion’s viscosity ratio
. Grace [
17] defined
as the ratio of the viscosity of the dispersed phase
to the viscosity of the continuous phase
. Assuming a simple shear flow at quasi-steady state,
Cacr has a minimum of around 0.5 for a viscosity ratio in the range of 0.1 <
< 1 [
17,
22]. For higher values of
, the critical capillary number increases, and it is generally assumed that at
> 4, drops rotate and do not break up anymore.
The maximum shear stresses in the liquid film in the outlet orifice can be estimated according to a model proposed by Taboada et al. [
7]. The model was used to estimate capillary numbers for different atomization conditions and to compare them with the critical capillary numbers
Cacr for shear. The results showed increasing oil droplet breakup with increasing shear rates in the liquid lamella at the outlet orifice, and it was concluded that laminar shear stresses in the liquid lamella at the outlet orifice dominate the oil droplet breakup. Furthermore, the model was used in Taboada et al. [
8] to estimate capillary numbers for different emulsion viscosities and viscosity ratios. The authors used Equation (2) to fit their experimental data, proving it to be effective in describing oil droplet sizes after atomization.
Many authors state that different nozzle design types and geometrical properties influence nozzle flow characteristics [
5,
23,
24]. Understanding the flow characteristics is essential, as they determine the liquid velocity and the liquid film thickness [
25]. These parameters are known to influence the spray droplet size during pressure-swirl atomization. Furthermore, the flow characteristics can be expected to correlate with stresses that may lead to breakup of the oil droplets. As the current mechanistic understanding of the flow characteristics in pressure-flow nozzles is limited, key flow parameters such as liquid velocity and liquid film thickness need to be determined experimentally to estimate the stresses acting on the oil droplets. This can be done by determining the volume flow rate
QL measured in L·min
−1 and the dimensionless discharge coefficient
Cd. The discharge coefficient is described by Equation (3), with
do being the nozzle outlet orifice diameter in m,
the emulsion density in kg·m
−3, and Δ
p the atomization pressure in Pa.
The discharge coefficient represents the ratio of the actual volume flow rate to the theoretical value [
5], and is commonly used to characterize throughput characteristics in pressure-swirl nozzles [
15,
26]. From the discharge coefficient, the liquid film thickness can be derived using geometrical considerations. When the atomization is performed at low pressures, and a stable air core is not yet formed, the discharge coefficient increases with increasing atomization pressure [
27]. As soon as an air core is formed, a part of the outlet orifice is blocked by the air core, and the discharge coefficient is expected to decrease [
28]. In general, pressure-swirl atomizers are operated below
Cd < 0.6 [
15].
Another method to analyse atomization performance and droplet breakup is the energy density model [
29], which was originally developed in the emulsification literature to compare emulsification results from different machine types or dispersion geometries [
16]. The model correlates the resulting oil droplet diameter with the specific energy that is applied to the volume
EV in which stresses are high enough for droplet disruption. As typically broad droplet size distributions result from droplet breakup in industrial emulsification machines, a characteristic value is used in the equation to describe the correlation between resulting droplet size and energy density applied. Very often the Sauter mean diameter SMD is used, simplistically as the mean value of the distribution. However, from the point of view of droplet size reduction theory, the maximum surviving diameter should be calculated. A suitable characteristic value would therefore rather be the
x90,3 value of the resulting distribution; see Equation (4):
with
C being a constant depending on the viscosity of the dispersed phase, while the exponent b relates to the breakup mechanism. This exponent
b strongly depends on the stresses dominating droplet breakup. Stähle et al. [
29] showed in their work that the energy density is equal to the liquid pressure difference Δ
p in pressure swirl nozzles (Equation (5)):
Information about the exponent b of Equation (4) can be used to gain knowledge about the flow characteristics inside the nozzle: For
b = 1 a laminar flow can be assumed, while values around
b = 0.24 − 0.4 indicate a turbulence-dominated flow [
16]. It must be noted that this model only applies when all stresses resulting from the pressure drop in the atomizer are high enough and act long enough for droplet deformation and breakup to occur [
16,
30]. This may be assumed for pressure-swirl atomizers, as Stähle et al. [
29] showed in their work. To predict the resulting droplet diameter, Equation (4) (i.e., the
b/
C—values) can only be taken if the break-up determining flows do not change significantly [
16], i.e., when geometrically similar atomizers are compared. However, the
b values give interesting information on the flow conditions inside the atomizer, and thus help in interpreting oil droplet breakup differences when changing atomizer geometry or scaling them up.
The aim of this study is the investigation of the impact of nozzle geometry on oil droplet breakup during pressure swirl atomization and the transfer of the principles found at pilot-scale to industrial-scale. For this, three main hypotheses were formulated:
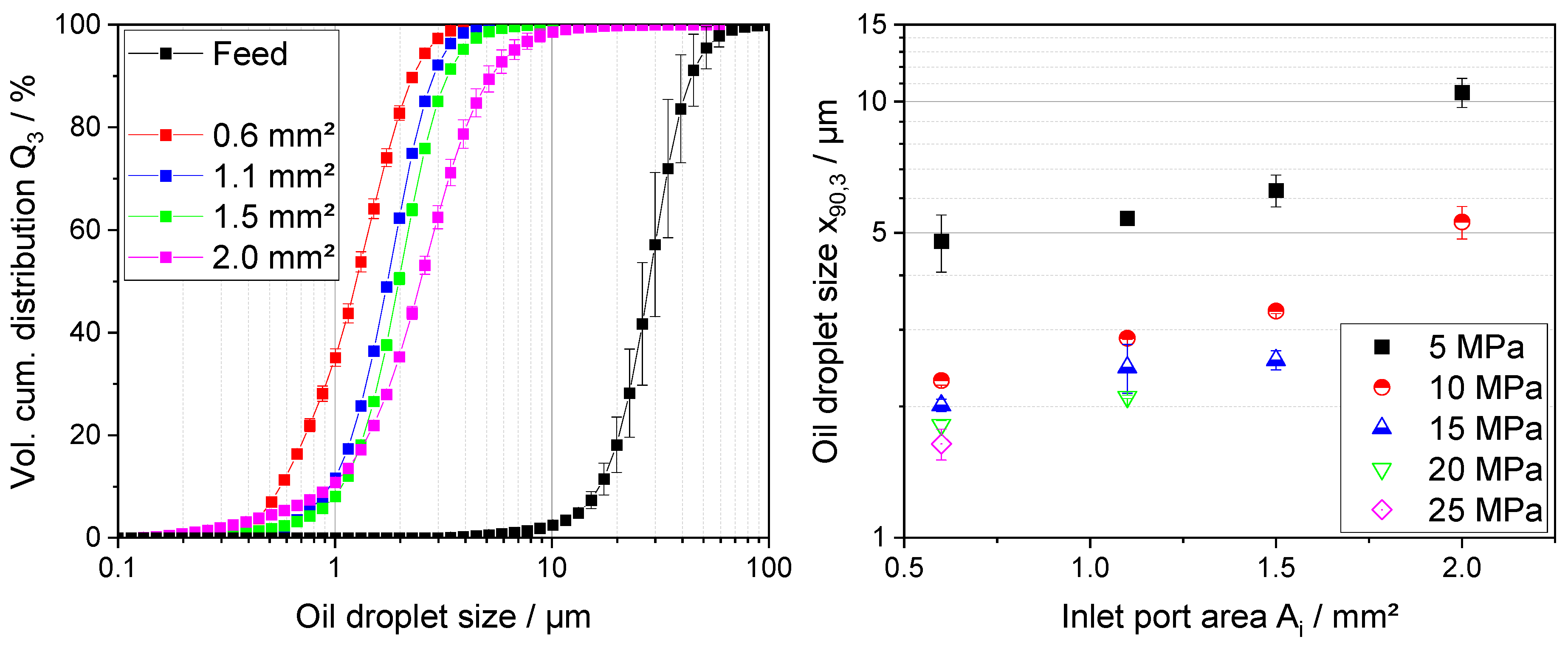
Oil droplet breakup decreases with smaller inlet port area at a constant pressure. This hypothesis is based on the assumption that a decrease in inlet port area leads to a decrease in volume flow rate, and consequently to smaller shear stresses in the nozzle outlet, as the liquid velocity decreases.
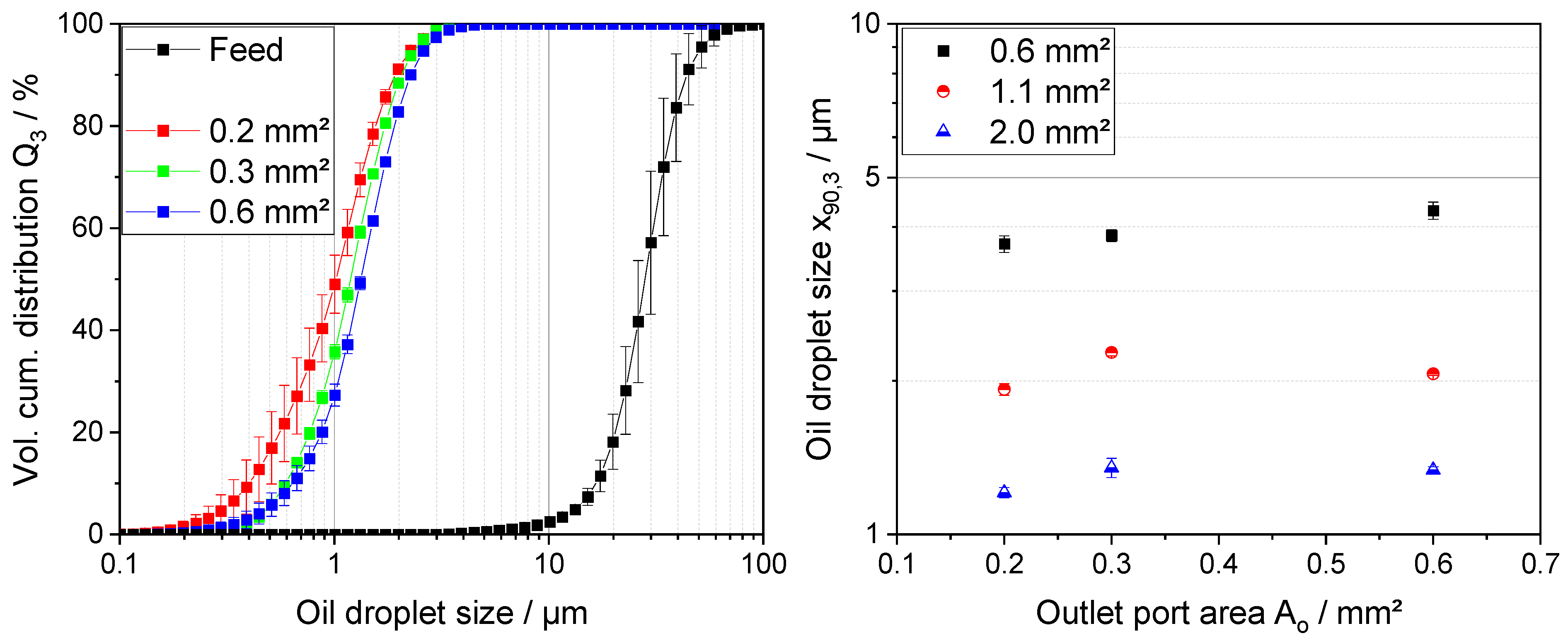
Oil droplet breakup increases with smaller outlet orifice area. This hypothesis assumes that a smaller outlet orifice leads to increasing shear rates due to higher liquid velocities, as the cross-sectional flow area decreases.
Based on the expectation that oil droplet size after atomization is solely dependent on the acting shear rates, it can be hypothesized that the proposed model should also hold up for changes in geometry, as long as geometrical similarity of the nozzles can be assumed and the residence time in the nozzle orifice is sufficient to reach equilibrium conditions.
To investigate these hypotheses, two different nozzles with axial and tangential inlets were used in pilot-scale applications. Additionally, the impact of different inlet port and outlet orifice areas was investigated. To describe the results, two different models were compared to provide insight for an appropriate and practical atomization process design for industrial application. The model developed by Taboada et al. [
7] was used to calculate shear rates in the nozzle outlet. For comparison, the energy density model was used for its benefit of ease of use and the knowledge it provides about flow characteristics. As the aim of this study is to improve process design for large-scale applications, further trials at industrial-scale were conducted for selected nozzles to investigate the applicability of the findings at higher volume flow rates in scaled-up nozzles. The model proved successful in describing and predicting oil droplet breakup for changes of atomization pressure and emulsion viscosity at pilot- and industrial-scale. While the model was not readily able to predict the impact of changes in nozzle geometry and dimensions on oil droplet breakup based on the estimated shear rates, the scalability of the findings at pilot-scale were successfully proven.
4. Discussion
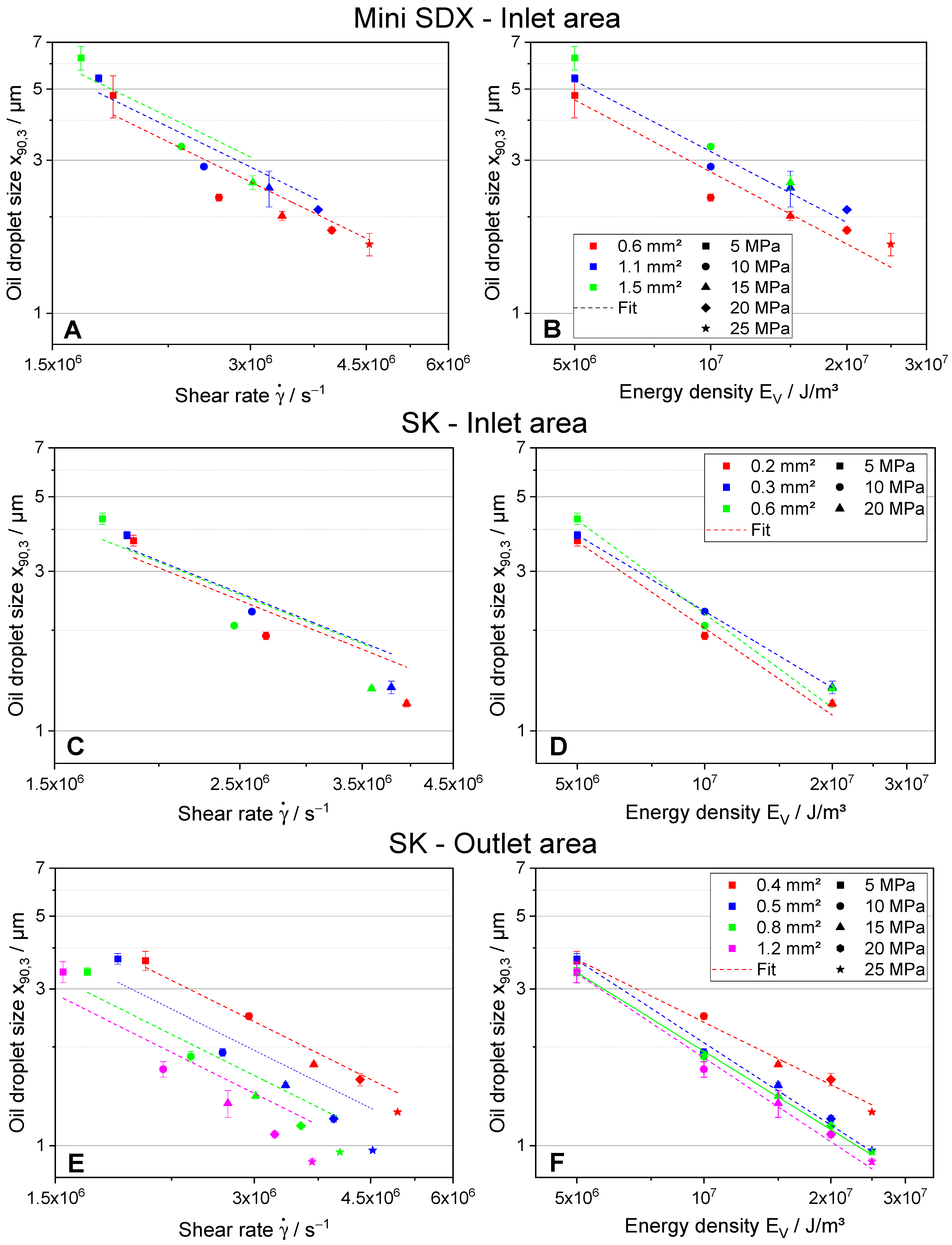
Before going into detailed discussion of the hypotheses, the overall impact of atomization pressure Δ
p on the ODS is discussed. As the ODS exhibits a narrow and monomodal distribution for all investigated nozzle components, the impact of nozzle geometry and atomization pressure will be discussed further using the characteristic value x
90,3 of the droplet size distributions. Considering the individual nozzle configurations, the
x90,3 values decrease with increasing Δ
p and therefore increasing
EV, as more energy is available for droplet breakup when atomizing at higher pressures. The coefficients of determination R
2 for all investigated nozzle configurations showed values from R
2 = 0.83 − 0.97 using the model of Taboada et al. [
7]. Similar values for R
2 were reported in the literature [
8] using the same model system containing MCT-oil. This confirms that the model describes the impact of changes in the atomization pressure on the ODS in a reasonable manner for all nozzle configurations.
Hypothesis 1. Influence of Changes of Inlet Area Ai on Oil Droplet Breakup.
Decreasing the inlet port area resulted in a reduction of film thickness
t and mean liquid velocity
for both the Mini SDX and SK (
Table 3). Based on these results, no unambiguous expectation on shear rates in the outlet orifice can be extracted, as
t and
counteract each other. The results for the Mini SDX showed a decrease in
x90,3 values with decreasing
Ai (
Figure 6A). This result implies an increase in shear rates, which is confirmed by the values for the shear rates estimated using the model of Taboada et al. [
7]. As a smaller
Ai leads to larger shear rates and increased oil droplet breakup at a constant pressure, the expected trend from Hypothesis 1 is not observed for the Mini SDX. Nonetheless, the observed trend for the estimated shear rates fit to the data of the ODS. This is generally not the case for the SK. While an increase in estimated shear rates for smaller
Ai is observed for the SK as well (
Figure 6C), the ODS does not correlate with the increased shear rates as expected. No clear trend for the ODS depending on the shear rates at constant atomization pressure can be observed. Given the fundamental differences in construction between the Mini SDX and SK, it is assumed that different flow characteristics in the nozzles are responsible for this observation.
To further describe and evaluate the experimental data, the energy density model was employed to assess possible alterations in flow characteristics when atomizing with different nozzle configurations (
Figure 6B,D,F). The results for
b,
C, and R
2 (
Table 4) already demonstrate the weakness and the strength of this model. The empirical determination of the values
b and
C compromises theoretical prediction potential, but enhances the model’s ability to fit the experimental data with a higher coefficient of determination R
2. This reflects the higher degree of freedom of the energy density model with its two variables (Equation (4)) compared to the model of Taboada et al. [
7]. For the Mini SDX, the values for
b decrease from the smallest inlet port to the largest at almost constant values for
C, potentially indicating a transition in flow characteristics from laminar flow to a more transitional flow (
Table 4). This is corroborated by the estimated values for the Reynolds number Re, which also suggest a flow in the transitional regime. A shift in flow characteristics might contribute to the deviation of the Mini SDX results to the anticipated outcome according to Hypothesis 1. In contrast, the energy density model only provides limited additional insights for different
Ai of the SK. Only minor differences in
b are observed between the different inlet ports at near constant
C, in addition to the impact on Re being lower.
Hypothesis 2. Influence of Changes of Outlet Area Ao on Oil Droplet Breakup.
To investigate if the model by Taboada et al. [
7] is specifically limited for SK inlet port variations or for the SK as a whole, atomization experiment using different outlet orifices were conducted. Looking at the results (
Figure 6E), the estimated shear rates increase for both decreasing
Ao at constant Δ
p, as well as for increasing Δ
p at constant
Ao. Based on Hypothesis 2, the ODS would be anticipated to decrease with increasing shear rates. Contrary to this expectation, the ODS increases with increasing estimated shear rates for changes in
Ao at constant Δ
p. The model’s simplicity may hinder a reliable estimation of the main stresses responsible for oil droplet breakup. Critical effects such as viscous losses may be misrepresented, leading to shear rate trends not matching the experimental results. Additionally, the flow characteristics and stress profiles throughout the whole nozzle could play a more significant role for droplet breakup than previously anticipated, and should be considered for prediction of oil droplet breakup. The assumption that other zones besides the nozzle orifice influence oil droplet breakup contradicts common reports from the literature [
19,
20]. It is generally assumed that stresses in the outlet orifice are sufficiently high to override the impact of the rest of the nozzle. This assumption is also challenged by Ballesteros and Gaukel [
34]. The authors investigated the local shear and elongation stress as well as stress histories in comparable geometries of the Mini SDX and SK by means of computational fluid dynamics simulation. The results showed that not only in the outlet region of a nozzle high shear rates can be expected, but also in the inlet area. As the oil droplets are larger when they pass the inlet area, a first breakup may happen at this point. In addition, the authors gave a detailed analysis of the stresses and found out that especially in the inlet region, elongational stresses can dominate the breakup. They proposed that oil droplet breakup may happen as a two-step process. A first droplet breakup happens in the inlet ports mainly due to elongational stresses, while another droplet breakup may occur due to shear stresses in the nozzle outlet orifice. This more complex breakup mechanism obviously cannot be properly captured by the simplified model from Taboada et al. [
7].
The energy density model shows only minor differences in the exponent b for changes in Ao of the SK at near constant values of C. This indicates similar breakup mechanisms in the outlet orifice, further supporting the assumption that it is an oversimplification to solely investigate the shear rates in the outlet orifice to describe and try to predict oil droplet breakup in pressure-swirl nozzles.
Hypothesis 3. Scale-up to Industrial Applications.
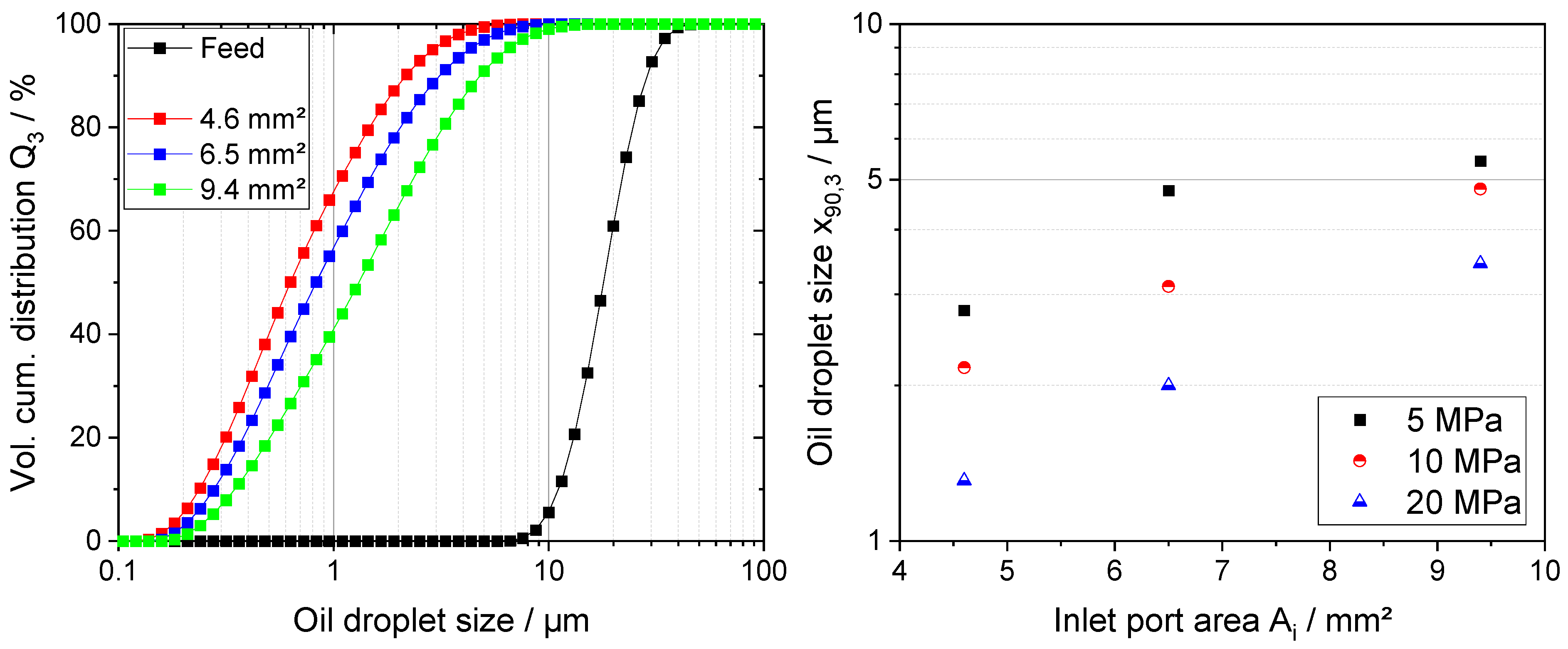
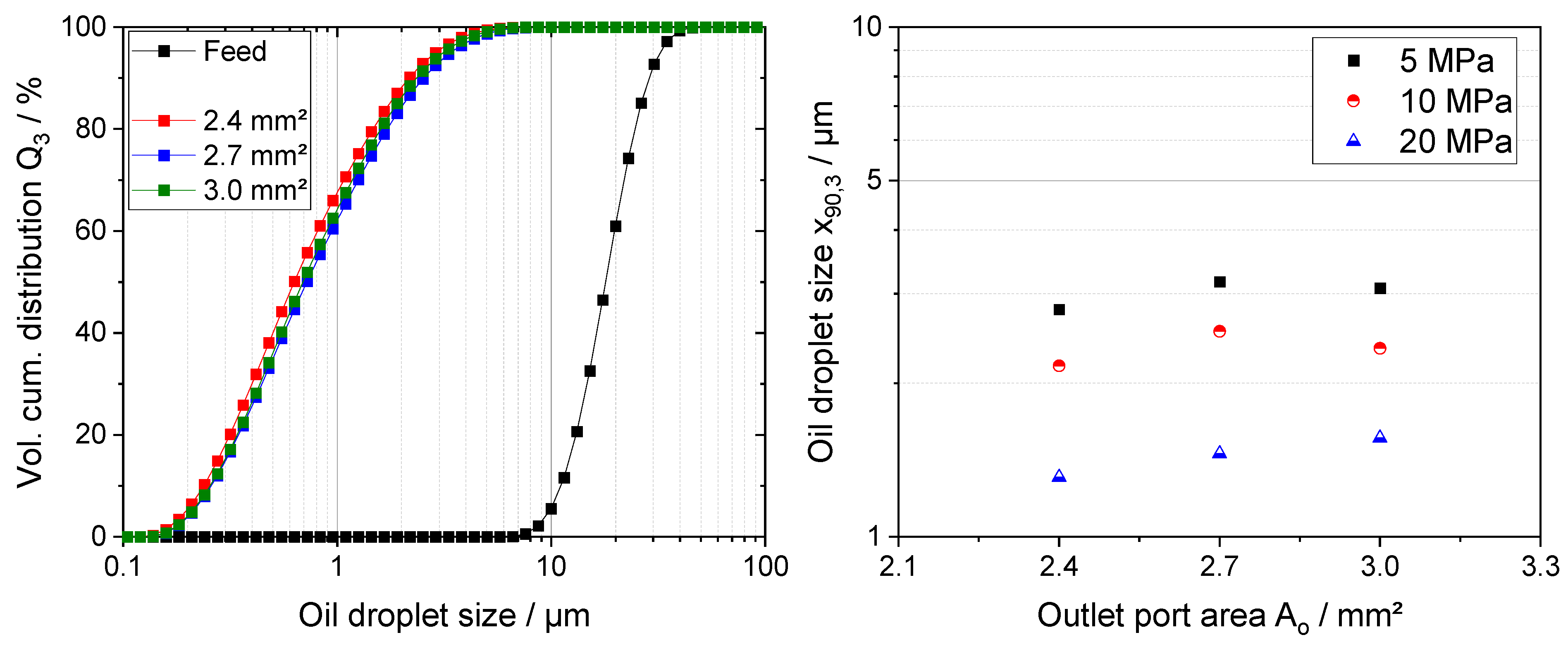
For scale-up to industrial conditions, the SDX V was chosen for its geometrical similarities to the Mini SDX. The results for the impact of changes in the SDX V on x90,3 align with anticipation based on pilot-scale findings using the Mini SDX. The x90,3 values decrease with higher shear rates. This indicates that the fundamental principles remain valid even for nozzles accommodating larger volume flow rates.
The pilot-scale results demonstrate that the applicability of the model of Taboada et al. [
7] is highly dependent on the nozzle that is used. While it failed to accurately capture the impact of different nozzle configurations for the SK, it yielded reasonable results for the Mini SDX for both changes in Δ
p as well as
Ai. To assess if the model applies to SDX-type nozzles at industrial volume flow rates as well, the experimental data of the SDX V was fitted according to the shear-rate-based model proposed by Taboada et al. (Equation (2)). The obtained values of R
2 showed generally similar results to the reported R
2 for model systems containing MCT oil of [
8]. This confirms that the model describes the impact of changes in the atomization pressure on the ODS in a reasonable manner for all nozzle configurations.
Given the assumption of a simple shear flow in quasi-steady state, and that the composition and thus viscosity, as well as interfacial tension, were the same for all experiments, the critical capillary number is constant at
Cacr,th = 0.7. Using the estimated shear rate and measured
x90,3 values, a value for
Cacr was calculated and compared to
Cacr,th. These values would ideally coincide, assuming that the model correctly calculates the shear rates. This is not the case for the Mini SDX, as all values of
Cacr were above the theoretical value of
Cacr,th = 0.7, indicating that the model overestimates the acting shear rates. It is essential to note that the calculated shear rates are maximum shear rates and are neglecting any potential viscous losses that occur at these high-pressure applications, possibly leading to the overestimation of the shear rates. For the SDX V nozzle, the calculated critical capillary numbers
Cacr of 0.36 to 0.60 are lower than the expected theoretical value of 0.7, suggesting that shear rates were underestimated by the model. It has to be noted that the calculation of the capillary number assumes a spherical droplet in equilibrium conditions. This is likely not the case, as it was shown by Ballesteros and Gaukel [
34] that oil droplets are already partially broken up in the inlet port of the nozzle. Another notable observation is in cases where larger oil droplets were observed despite larger estimated shear rates, both at pilot- and industrial-scale (
Figure 6A). A possible explanation could be an insufficient residence time of the oil droplets in the high-stress zone of the nozzle orifice. Based on the results of Ballesteros and Gaukel [
34], this is likely not the case, as the residence time in the nozzle orifice is expected to be much higher than the critical breakup time of oil droplets.
To investigate the potential of extrapolating the results from pilot-scale to industrial-scale, the ODSs obtained at specific shear rates are compared for the Mini SDX and SDX V nozzle. One would assume the shear rates to be in a similar range for both nozzles, given the similar magnitude of ODS after atomization. However, the shear rates are estimated to be about four times smaller in the SDX V compared to the Mini SDX. This shows, again, that the values for the estimated shear rates cannot be extrapolated to predict ODS when using a different nozzle or different nozzle components, falsifying Hypothesis 3. As the model fails to accurately predict shear rates, the correlation between shear rates and ODS needs to be investigated for each geometry individually.
The energy density model was employed to assess possible changes in flow characteristics when atomizing with different nozzle configurations of the SDX V. Furthermore, the results show excellent coefficients of determination R
2 for the fitted data, with values of up to 0.99. Similar to the Mini SDX, a major decrease in
b for decreasing
Ai can be observed for the SDX V. In case of the SDX V, the results show a change from droplet breakup in a relatively laminar flow
b = 0.83 to a value of 0.31, which is commonly associated with droplet breakup in a more turbulent regime. These results alone do not allow the conclusion that droplet breakup occurs in a turbulent flow regime, a notion that is reinforced when taking the greatly varying results for the constant
C into account. As the results using the energy density model are inconclusive, the calculated Reynolds numbers (
Table 6) are considered as well. The results show a shift in the Reynolds numbers also indicating a change in flow characteristics. The impact of a change in
Ao on the key parameters
b and Re is comparatively much smaller.
The energy density model was used to investigate flow characteristics within the nozzles, giving insight into oil droplet breakup mechanisms. Theoretically, it can also be used for extrapolating known relations from a small-scale nozzle to a larger nozzle, offering an alternative parameter for scale-up. However, certain prerequisites have to be met. Firstly, sufficiently high stresses need to act for a sufficient time for breakup to occur. This was shown by Ballesteros and Gaukel [
34] to be the case for pilot-scale nozzles. Secondly, the flow conditions responsible for oil droplet breakup have to be similar. The energy density model shows dramatically different values for the slope
C and the exponent
b when comparing the Mini SDX and SDX V, highlighting the differences in flow characteristics between the pilot- and industrial-scale nozzles. This demonstrates why no reliable prediction of oil droplet breakup can be obtained using the theoretical models.
5. Conclusions
This study focused on the impact of nozzle geometry of pressure-swirl nozzles on oil droplet breakup during atomization of emulsions. Objects of the investigations were at pilot-scale an SK nozzle with an axial inlet and a Mini SDX nozzle with a tangential inlet. A model [
7] was employed to estimate the shear stresses inside different nozzles in an idealized and simplified manner, and draw conclusions on oil droplet breakup and oil droplet size after atomization. To gain further insight regarding oil droplet breakup mechanisms and flow conditions in the different nozzles, the energy density model following Karbstein [
16] and Stähle et al. [
29] was used. To explore the applicability of the findings at industrial-scale, the SDX V nozzle was selected. It was hypothesized that final ODS after atomization depends on the shear rate in the nozzle outlet under the condition that equilibrium conditions can be achieved. Therefore, this study examined different inlet ports, outlet orifices, and atomization pressures, focusing on throughput characteristics, estimated shear rates, and ODS after atomization.
The discharge coefficient generally decreased with higher atomization pressures, smaller inlet areas Ai, and larger outlet areas Ao. Notably, changes in the inlet port area significantly influenced final ODS for the Mini SDX, as the ODS decreases with smaller inlet port areas and higher shear rates in contrast to the anticipation of Hypothesis 1. In contrast to Hypothesis 2, a decrease of the outlet orifice area of the SK leads to an increase in ODS, even though the estimated shear rates increased. These findings suggest that the flow characteristics in high-stress zones besides the nozzle outlet orifice, such as the inlet ports, may play a crucial role in oil droplet breakup. Applying these principles to larger volume flow rates using the industrial-scale SDX V nozzle generally reflected the principles found in pilot-scale.
In general, the simplified model of Taboada et al. [
7] showed acceptable agreement with ODS results for describing the impact of the atomization pressure. The model also showed acceptable agreement for the results obtained with the SDX V, obtaining fits with a similar coefficient of determination compared to pilot-scale. However, the model was not able to properly predict the impact of changes in the nozzle geometry on oil droplet breakup in pressure-swirl nozzles, ultimately falsifying Hypothesis 3. It is assumed that the limitations of the model are two-fold. On one hand, the results by the energy density model indicate changing flow characteristics. On the other hand, the relationship between shear rate and ODS needs to be established for each nozzle individually. The energy density model generally proved to be more effective in describing oil droplet sizes depending on atomization pressure, as it has a higher degree of freedom with its two variables.
To validate the observed phenomena and gain further insight into the flow characteristics in the atomizer, local stress histories during atomization should be deduced over the whole nozzle geometry for different nozzle configurations. This could give further insight into the dominating stresses leading to oil droplet breakup, namely, shear or elongation stresses. The knowledge gained could be used to improve predictions of oil droplet breakup.
This study provides valuable insights into the influence of nozzle geometry and dimensions on oil droplet breakup during atomization of emulsions. Exploring different nozzle geometries and investigating the scale-up potential of the observed phenomena, these findings open avenues for further research, utilizing further CFD simulations to unravel flow characteristics in the nozzle, as well as the impact of changes in nozzle geometry on the stress history of an oil droplet.