Effect of Droplet Viscosity Ratio and Surfactant Adsorption on the Coalescence of Droplets with Interfacial Viscosity

Abstract

Surface rheology becomes important for droplets with adsorbed proteins, solid particulates, lipids, or polymers, and understanding how surface rheology alters basic droplet processes like coalescence provides insight into the processing of dispersions in industrial and biological systems. In this work, we model the approach of two equal-size deformable droplets under an axisymmetric, biaxial extensional flow in the Stokes flow limit. We explore how the viscosity contrast between the drop and suspending fluid alters the film drainage behaviour when interfacial viscosity is present. For a clean droplet at a fixed capillary number, the drainage time is observed to be independent of the viscosity ratio ($\lambda$) for $\lambda \le \mathcal{O}\left(1\right)$, while the drainage increases linearly with the viscosity ratio for $\lambda \ge \mathcal{O}\left(1\right)$. Surface viscosity increases the drainage time by causing the thin film between the droplets to flatten and widen, and shifts the viscosity ratio at which the aforementioned scaling behaviour changes to larger values. The drainage time is increased more significantly at lower viscosity ratio values than higher values. In the second half of the paper, we examine how surface viscosity alters film drainage when the surfactant can be soluble. We examine the kinetically controlled adsorption/desorption limit. We find that surfactant solubility abolishes surface tension gradients and increases the prominence of surface viscosity effects, the effects of which are quantified for Boussinesq numbers $Bq\sim \mathcal{O}\left(0.1\right)$.

1. Introduction

For droplet interfaces embedded with lipids, fatty acids, proteins, solid particles, or polymers, the lateral in-plane interactions between the adsorbed surfactant molecules can yield a rheologically complex response to surface deformations. Interfacial rheology is defined as the relationship between the extra interfacial stresses arising from the mechanical behaviour of the complex membrane and the resultant surface deformation. For many years, the focus of experimental studies has been on measuring shear and dilatational surface viscous and elastic properties of fluid-fluid complex interfaces using different experimental techniques such as interfacial shear rheometer, micro-buttons, Langmuir/radial troughs, oscillating droplet, and double wall rings [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. In addition to surfactant transport and solubility effects, interfacial rheology can play an essential role in the dynamics of droplet suspensions common in various industrial and scientific applications, e.g., droplet deformation, breakup, and coalescence.

When two droplets come close together to coalesce or adhere, a thin liquid film forms between the two droplets. Figure 1 shows the zoomed-in image of the thin film formed between the two droplets. The drainage of this film alters the critical conditions under which coalescence occurs. The film drainage process can be characterized into three steps: (a) approach of two droplets under external forcing, (b) formation of a thin film, and (c) eventual film rupture when the critical film thickness is reached. Factors that govern the drainage of the thin liquid film are: viscosity contrast between the inner and outer fluid, solubility of surfactant in the inner and outer fluid phase, Marangoni effects arising from surface tension gradients, surfactant dilution, and surface rheology effects. Earlier work on coalescence derived theoretical models that provided scaling relationships for film drainage time and critical conditions for film rupture for a flattened/dimpled film in the limiting situations of immobile, partially mobile, and fully mobile surfaces [17,18,19,20,21,22,23,24]. The focus of some studies has been on modelling the coalescence process between two droplets with a clean interface and the effect of surfactant transport (Marangoni effects from surface convection) using experiments and numerical simulations for insoluble surfactants [20,25,26].

It is well known that coalescence between two droplets is favoured by weak collisions. However, in the case of droplets with an elastic interface (for instance, capsule) or a surface yield stress (for instance, Pickering emulsions), surface rheology inverts this trend, and the doublet formation is shown to be favoured by fast, violent collisions [28]. On the other hand, for droplets with only viscous membranes, our recent work has shown that coalescence is favoured by gentle, slow collisions between the two droplets [27]. This work also found that surface viscosity delays the film drainage like Marangoni effects, but does so in completely different manner, creating a wider and flatter film (thus reducing the pressure gradients for drainage), whereas Marangoni effects create a dimpled film (due to backflow from surface tension gradients). Although coalescence has been studied for many years, there are still many underexplored areas regarding the role of surface rheology. For example, it is unknown how surface rheology affects film drainage for different values of viscosity ratio and when surfactant adsorption/desorption is present.

Certain fatty alcohols, fatty acids, and lipids in a liquid-disordered phase exhibit a viscous-like response when subjected to shear and dilatational deformations (for example, DPPC, POPC, eggSM, Eicosanol and Hexadecanol) [1,3,29,30,31,32,33,34,35,36,37,38]. These surfactants can be used in experimental setups where findings from this work can be tested in future experimental studies examining the coalescence of droplets with surface viscosity. When the surface rheology is predominantly viscous, the Boussinesq-Scriven law is a common constitutive equation that provides a linear relationship between the interfacial stress arising from viscous dissipation (i.e., surface viscosities) and the surface rate of deformation. In this study, we will extend our earlier work [27] to understand the impact of droplet viscosity ratio on the coalescence of two equal-sized droplets when surface viscosity is present. We model the viscous droplet interface using the Boussinesq-Scriven equation [39,40]. In the second half of the paper, we incorporate the effect of surfactant solubility in the limit of kinetically controlled adsorption.

2. Method of Analysis

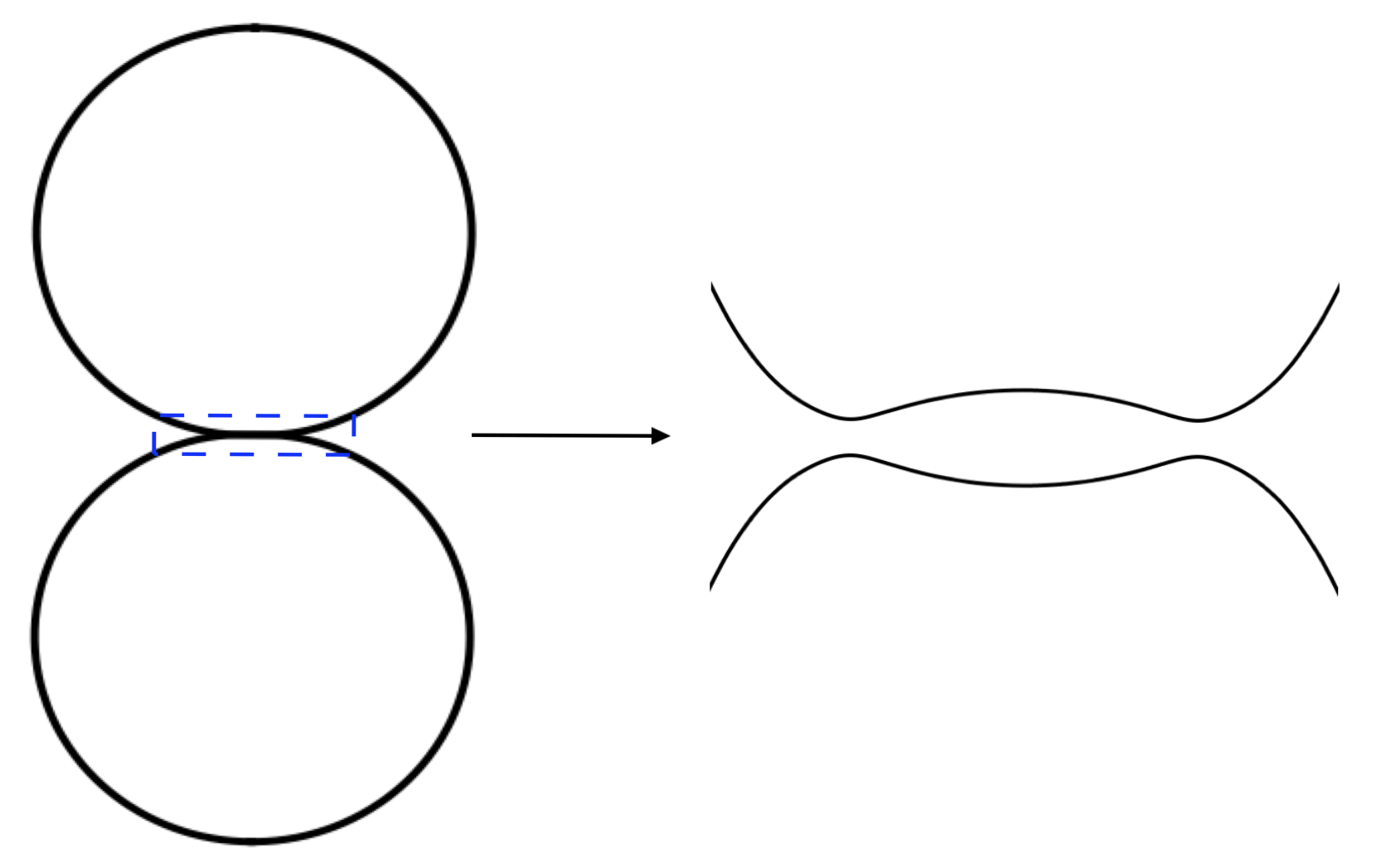
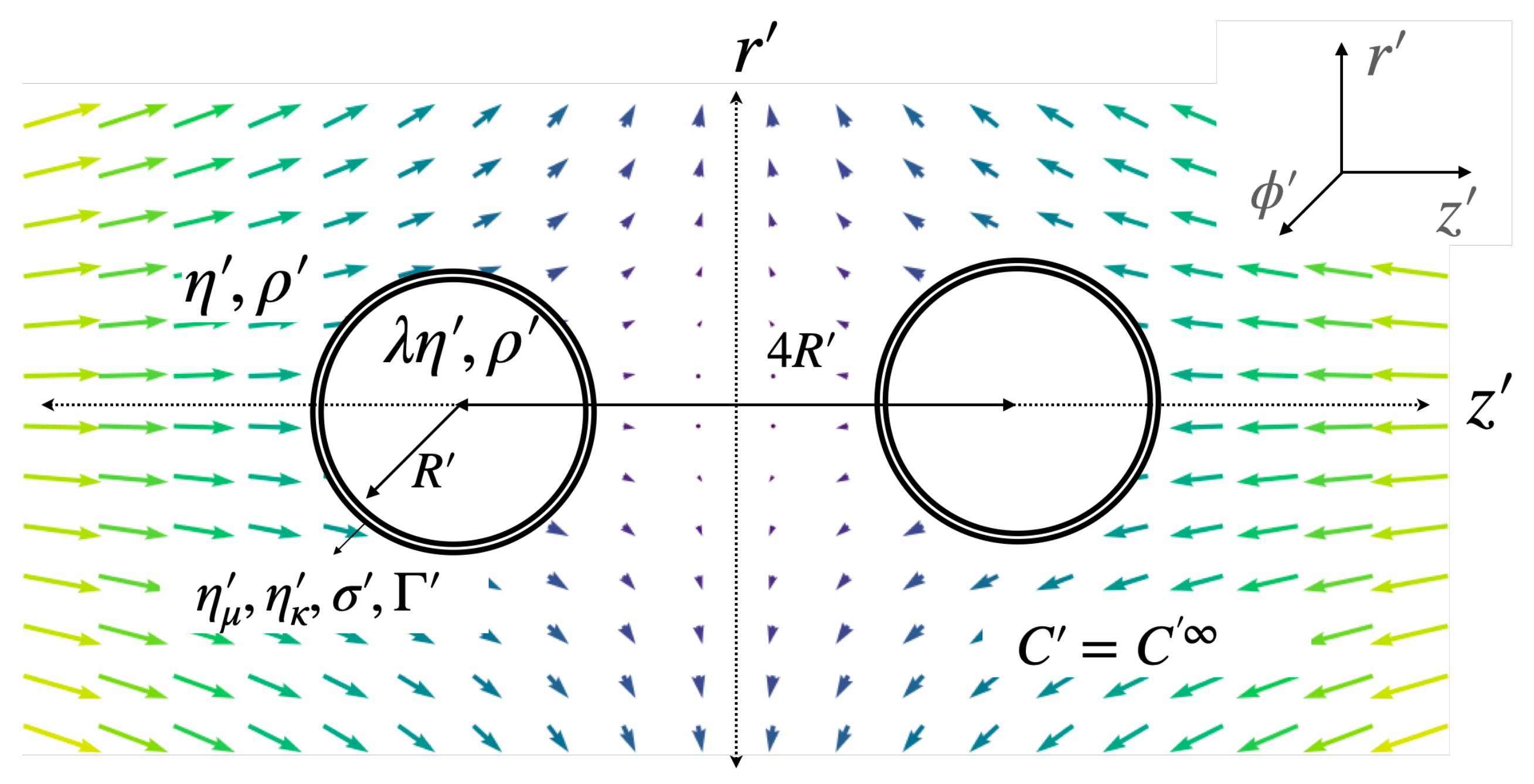
2.1. Problem Overview

Using boundary element simulations, we numerically model head-on collision between two droplets. Figure 2 shows the schematic of the problem setup. Two equal-sized deformable droplets (initially spherical with radius $R^{\prime }$) are placed at a separation of $4R^{\prime }$ (measured from the center of one droplet to another) in a biaxial extensional flow field. The disperse phase has viscosity $\lambda {\eta }^{\prime }$ and density ${\rho }^{\prime }$, and the continuous phase has viscosity ${\eta }^{\prime }$ and density ${\rho }^{\prime }$. The viscous surfactant monolayer at the droplet interface has surface shear viscosity ${\eta }_{\mu }^{\prime }$, surface dilatational viscosity ${\eta }_{\kappa }^{\prime }$, local surface tension ${\sigma }^{\prime }$, and local surfactant concentration ${\mathrm{\Gamma }}^{\prime }$. To incorporate the effect of adsorption-desorption controlled surfactant, we approximate the surfactant concentration in the bulk as uniform $C^{\prime }={C^{\prime }}^{\infty }$. Since the system is symmetric about the $z^{\prime }$-axis, we formulate the flow equations and boundary conditions in an axisymmetric domain, i.e., polar cylindrical coordinates $(z^{\prime },r^{\prime },{\varphi }^{\prime })$ [25,41]. The external biaxial extensional flow field ${\mathit{u}}_{\infty }^{\prime }$ is represented as:

$${\mathit{u}}_{\infty }^{\prime }=\frac{G^{\prime }}{2}·\left[\begin{array}{c}-2z^{\prime }\\ r^{\prime }cos{\varphi }^{\prime }\\ r^{\prime }sin{\varphi }^{\prime }\end{array}\right],$$

(1)

where $G^{\prime }$ is the strain rate of the external flow. Under this flow field, the droplet system is compressed along the $z^{\prime }$ axis and extended isotropically along the other two axes.

2.2. Non-Dimensionalization

We non-dimensionalize all lengths by radius $R^{\prime }$, viscosities by ${\eta }^{\prime }$, times by ${G^{\prime }}^{-1}$, velocities by $G^{\prime }{R}^{\prime }$, bulk stresses by ${\eta }^{\prime }{G}^{\prime }$, surface stresses by $R^{\prime }{\eta }^{\prime }{G}^{\prime }$, surface tension and interface concentrations by their equilibrium values ${\sigma }_{eq}^{\prime }$ and ${\mathrm{\Gamma }}_{eq}^{\prime }$, and bulk surfactant concentration by ${C^{\prime }}^{\infty }$. We note that throughout the manuscript, the dimensional and dimensionless quantities are represented using primed and un-primed variables, respectively.

2.3. Governing Equations

We present the governing equations in this section in dimensionless form. The colliding droplets are highly viscous such that the flow inside and outside the droplet is governed by Stokes equations.

$$\begin{array}{c}\hfill \lambda {\mathbf{\nabla }}^2{\mathit{u}}^d=\mathbf{\nabla }{p}^d,\mathbf{\nabla }·{\mathit{u}}^d=0,\end{array}$$

(2a)

$$\begin{array}{c}\hfill {\mathbf{\nabla }}^2{\mathit{u}}^c=\mathbf{\nabla }{p}^c,\mathbf{\nabla }·{\mathit{u}}^c=0.\end{array}$$

(2b)

In the above equations, ${\mathit{u}}^d$ and ${\mathit{u}}^c$ are the velocity vectors in the drop and suspending phases, respectively. Quantity $\lambda$ is the droplet viscosity ratio.

The boundary conditions at the interface are:

• Continuity of velocity

  $${\mathit{u}}^{\mathit{d}}={\mathit{u}}^{\mathit{c}}={\mathit{u}}_{\mathit{s}},$$

  (3)

  where, ${\mathit{u}}_{\mathit{s}}$ is the velocity of the droplet interface.
• Force balance

  $$({\mathit{\tau }}^c-{\mathit{\tau }}^d)·\mathit{n}={\mathit{f}}_{\mathit{v}}+\frac{1}{Ca}\left(\sigma \mathit{n}\mathbf{\nabla }·\mathit{n}-{\mathbf{\nabla }}_{\mathit{s}}\sigma \right)-\frac{A}{Ca{h}^3}\mathit{n}.$$

  (4)

In Equation (4), ${\mathit{\tau }}^c-{\mathit{\tau }}^d$ is the traction jump across the interface, $\mathit{n}$ is the outward pointing normal vector, ${\mathit{f}}_{\mathit{v}}$ is the interfacial traction from surface rheology given by Boussinesq-Scriven constitutive equation [39,40], $Ca=\frac{G^{\prime }{\eta }^{\prime }{R}^{\prime }}{{\sigma }_{eq}^{\prime }}$ is the capillary number, $\sigma$ is the normalized surface tension, ${\mathbf{\nabla }}_{\mathit{s}}=(\mathit{I}-\mathit{nn})·\mathbf{\nabla }$ is the surface gradient, $A=\frac{A_h}{6\pi {R^{\prime }}^2{\sigma }_{eq}^{\prime }}$ is the dimensionless Hamaker constant, and h is the local film thickness.

In our previous work on droplet coalescence, we have shown that the film drainage behaviour is not altered by the relative ratio of dilatational to shear viscosity ${\lambda }_{ds}=\frac{{\eta }_{\kappa }^{\prime }}{{\eta }_{\mu }^{\prime }}$ but rather depends on their sum $Bq=\frac{{\eta }_{\mu }^{\prime }+{\eta }_{\kappa }^{\prime }}{R^{\prime }{\eta }^{\prime }}$ [27]. In this study, we assume equal surface shear and dilatational viscosity ${\eta }_{\mu }^{\prime }={\eta }_{\kappa }^{\prime }$. The Boussinesq number $Bq$ is defined as $Bq=\frac{{\eta }_{\mu }^{\prime }+{\eta }_{\kappa }^{\prime }}{R^{\prime }{\eta }^{\prime }}$. For droplet with equal surface shear and dilatational viscosity, the expression for interfacial viscous traction using Boussinesq-Scriven constitutive relationship is [39,40]

$${\mathit{f}}_{\mathit{v}}=-{\mathbf{\nabla }}_{\mathit{s}}·\frac{Bq}{2}[\mathit{P}·({\mathbf{\nabla }}_{\mathit{s}}{\mathit{u}}_{\mathit{s}}+{{\mathbf{\nabla }}_{\mathit{s}}{\mathit{u}}_{\mathit{s}}}^T)·\mathit{P}],$$

(5)

where, $\mathit{P}=\mathit{I}-\mathit{nn}$ is the projection operator on the surface.

We present the effect of adsorption-desorption controlled surfactant on coalescence dynamics in Section 5. The surface concentration satisfies a convection diffusion equation [42,43]:

$$\frac{\partial \mathrm{\Gamma }}{\partial t}+{\mathbf{\nabla }}_{\mathit{s}}·\left(\mathrm{\Gamma }{\mathit{u}}_{\mathit{t}}\right)+\mathrm{\Gamma }({\mathbf{\nabla }}_s·\mathit{n})({\mathit{u}}_{\mathit{s}}·\mathit{n})=\frac{1}{P{e}_s}{\mathbf{\nabla }}_s^2\mathrm{\Gamma }+j_{kin}$$

(6)

where, ${\mathit{u}}_{\mathit{t}}={\mathit{u}}_{\mathit{s}}-\mathit{n}({\mathit{u}}_{\mathit{s}}·\mathit{n})$ is the tangential component of the interfacial velocity, ${\displaystyle P{e}_s=\frac{G^{\prime }{R^{\prime }}^2}{D_s^{\prime }}}$ is the surface Peclet number, and $D_s^{\prime }$ is the interface diffusivity of the surfactant. The term $j_{kin}$ represents the surfactant exchange to/from the bulk fluid. In case of insoluble surfactant, $j_{kin}=0$. In case of soluble surfactant, surfactant exchange is often a two-step process. Surfactants diffuse from the bulk liquid to the surface, followed by adsorption/desorption kinetics. For micrometer-sized droplets in emulsions, the adsorption process is found to be kinetically limited (i.e., diffusion time ≪ adsorption time) [44,45,46]. In these situations, one approximates the concentration in the bulk as uniform $C=1$. The expression for $j_{kin}$ in dimensional form becomes

$$j_{kin}^{\prime }=k_a^{\prime }{C^{\prime }}^{\infty }({\mathrm{\Gamma }}_{\infty }^{\prime }-{\mathrm{\Gamma }}^{\prime })-k_d^{\prime }{\mathrm{\Gamma }}^{\prime },$$

(7)

where, $k_a^{\prime }$ and $k_d^{\prime }$ are adsorption/desorption constants [47,48]. Equation (7) in dimensionless form can be represented as below:

$$j_{kin}=Bi(1+K)(1-\mathrm{\Gamma }).$$

(8)

In the above equation, $Bi=\frac{k_d^{\prime }}{G^{\prime }}$ is the Biot number which describes the timescale of surface convection to the timescale of desorption. The quantity $K=\frac{k_a^{\prime }{C}_{\infty }^{\prime }}{k_d^{\prime }}$ is the equilibrium partition coefficient between the bulk phase and the interface.

The surface tension $\sigma$ is related to the surfactant’s surface concentration $\mathrm{\Gamma }$ through Langmuir equation of state. The equation of state in simplified form is shown below:

$$\sigma =1+Eln\left(\frac{{\mathrm{\Gamma }}_{\infty }-\mathrm{\Gamma }}{{\mathrm{\Gamma }}_{\infty }-1}\right),$$

(9)

In Equation (9), $E=\frac{R_G^{\prime }{T}^{\prime }{\mathrm{\Gamma }}_{\infty }^{\prime }}{{\sigma }_{eq}^{\prime }}$ is the surface elasticity number. $R_G^{\prime }$ is the ideal gas constant, $T^{\prime }$ is the absolute temperature, ${\mathrm{\Gamma }}_{\infty }^{\prime }$ is the maximum packing density for a given surfactant system, and ${\mathrm{\Gamma }}_{\infty }=\frac{{\mathrm{\Gamma }}_{\infty }^{\prime }}{{\mathrm{\Gamma }}_{eq}^{\prime }}$. A detailed derivation of Equation (9) can be found in [27].

2.4. Dimensionless Parameters

Since the coalescence is promoted by gentle collisions, we look at capillary number values in the range $\mathcal{O}\left({10}^{-4}\right)\le Ca\le \mathcal{O}\left({10}^{-2}\right)$. We assume a micro-meter sized droplet with radius $R^{\prime }=27$ μm. We choose this value to benchmark our simulations against previous literature [25] that did not consider surface viscous effects. Based on experimentally relevant values of shear rate $G’\sim O\left(1\right)$${\mathrm{s}}^{-1}$ and surfactant diffusivity $D_s^{\prime }\sim \mathcal{O}({10}^{-14}-{10}^{-8})$ m²/s [49,50], the surface Peclet number can take a wide range of values $P{e}_s\sim O\left({10}^{-2}\right)-O\left({10}^4\right)$. We choose $P{e}_s=5$ in our simulations, consistent with the value chosen in the paper [25]. In surfactant literature, the value of surface elasticity is found to be $E\ll 1$ [18,48,51,52]. For our simulations, we choose two values: $E=0$ corresponding to the case when Marangoni effects are negligible, and $E=0.2$ which is closer to the upper bound found in the literature. The initial surfactant coverage is equal to be the equilibrium coverage, which we choose to be ${\mathrm{\Gamma }}_{\infty }^{-1}={\displaystyle \frac{{\mathrm{\Gamma }}_{eq}^{\prime }}{{\mathrm{\Gamma }}_{\infty }^{\prime }}}=\frac{1}{2}$. We set the value of dimensionless Hamaker constant $A=4.99\ast {10}^{-11}$.

In this paper, we add surface viscosity and surfactant solubility to the above effects. The value of Boussinesq number $Bq$ is based on the experimentally measured values of surface viscosity $({10}^{-6}-{10}^{-2})$ N·s/m reported in literature [1,3,29,31,53,54,55,56]. For soluble surfactant, we assume large value of Biot number $Bi=100$. At equilibrium, the equilibrium partition coefficient K satisfies the following equation: $\frac{{\mathrm{\Gamma }}_{eq}^{\prime }}{{\mathrm{\Gamma }}_{\infty }^{\prime }}=\frac{K}{K+1}$ and for simulations the value is set to $K=1$ for ${\mathrm{\Gamma }}_{\infty }=2$.

The dimensionless parameters employed in this study are summarized in

Table 1. Dimensionless parameters.

$\lambda$	Viscosity ratio	${\displaystyle \frac{\mathrm{Inner}\mathrm{fluid}\mathrm{viscosity}}{\mathrm{Outer}\mathrm{fluid}\mathrm{viscosity}}}$	$0.005\le \lambda \le 5$
$Ca$	Capillary number	${\displaystyle Ca=\frac{G^{\prime }{\eta }^{\prime }{R}^{\prime }}{{\sigma }_{eq}^{\prime }}}$	${10}^{-4}\le Ca\le {10}^{-2}$
$Bq$	Boussinesq parameter	${\displaystyle Bq={\displaystyle \frac{{\eta }_{\kappa }^{\prime }+{\eta }_{\mu }^{\prime }}{R^{\prime }{\eta }^{\prime }}}}$	$0\le Bq\le 0.5$
$P{e}_s$	Surface Peclet number	${\displaystyle P{e}_s=\frac{G^{\prime }{R^{\prime }}^2}{D_s}}$	$P{e}_s=5$
E	Surface elasticity number	${\displaystyle E=\frac{R_G^{\prime }{T}^{\prime }{\mathrm{\Gamma }}_{\infty }^{\prime }}{{\sigma }_{eq}^{\prime }}}$	${\displaystyle E=\{0,0.2\}}$
${\mathrm{\Gamma }}_{\infty }$	Initial surfactant coverage	${\displaystyle {\mathrm{\Gamma }}_{\infty }={\displaystyle \frac{{\mathrm{\Gamma }}_{\infty }^{\prime }}{{\mathrm{\Gamma }}_{eq}^{\prime }}}}$	${\mathrm{\Gamma }}_{\infty }=2$
$Bi$	Biot number	${\displaystyle Bi=\frac{k_d^{\prime }}{G^{\prime }}}$	$Bi=100$
K	Equilibrium partition coefficient	${\displaystyle K=\frac{k_a^{\prime }{C}_{\infty }^{\prime }}{k_d^{\prime }}}$	$K=1$

.

2.5. Numerical Implementation

Using the axisymmetric boundary integral equation, the velocity at interfacial location ${\mathit{x}}_{\mathbf{0}}$ can be computed using the expression [41,57]:

$$\begin{array}{c}{\mathit{u}}_{\mathit{s}}\left({\mathit{x}}_{\mathbf{0}}\right)={\mathit{u}}_{\infty }\left({\mathit{x}}_{\mathbf{0}}\right)-\frac{1}{8\pi }{\int }_{C_1+C_2}\mathit{M}(\mathit{x},{\mathit{x}}_{\mathbf{0}})·(({\mathit{\tau }}^c-{\mathit{\tau }}^d)·\mathit{n})dl\left(\mathit{x}\right)\hfill \\ \hfill +\frac{1}{4\pi }\frac{1-\lambda }{1+\lambda }{\int }_{C_1+C_2}^{PV}\mathit{q}(\mathit{x},{\mathit{x}}_{\mathbf{0}})·{\mathit{u}}_{\mathit{s}}\left(\mathit{x}\right)dl\left(\mathit{x}\right).\end{array}$$

(10)

In the above equation, $\mathit{M}$ is the axisymmetric free space Green’s function [41,57], $\mathit{q}$ is the double layer potential [41,57], and $dl$ is the differential arc length along the droplet interface. The integral is carried out along the contour of both droplets $(C_1+C_2)$. We discretize the droplet interface into N nodes connected by $N+1$ elements. We use cubic spline interpolation to represent interfacial location, velocity, and local surfactant concentration. The detailed numerical implementation to solve the boundary integral equation, compute surfactant concentration, and discretize the droplet’s surface can be found in [27]. We assume the droplet shapes are initially spherical with $N=100$ on each droplet’s interface. At $t=0$, the surfactant is assumed to be uniformaly distributed on the droplet interface. Below is the numerical scheme to obtain the evolution of droplet shapes with time:

• The velocity vector ${\mathit{u}}_{\mathit{s}}$ on the droplet’s interface at time t for a given droplet shape and surfactant concentration is evaluated using the boundary integral Equation (10).
• After velocity vector is computed at time t, we use explicit Euler’s method to obtain the updated droplet mesh points at time $t+\Delta t$.
• Re-meshing is performed based on the procedure described in [27] as the mesh points become too close or too separated.
• Using velocity from time t and position vector from time $t+\Delta t$, we solve the surfactant convection-diffusion Equation (6) to obtain the updated surfactant concentration using implicit Euler’s method at time $t+\Delta t$.

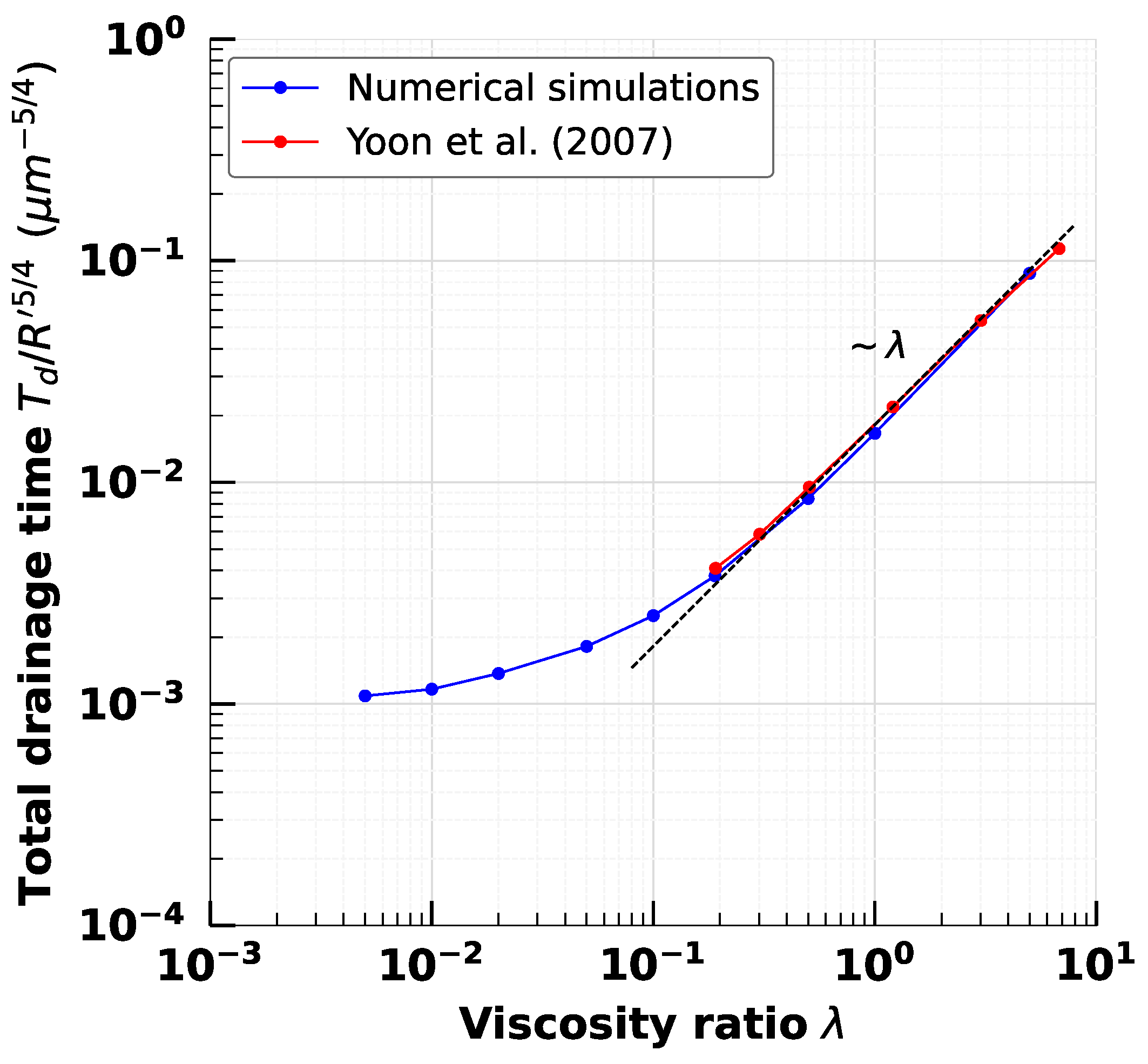
3. Validation: Clean Droplet Coalescence

In this section, we validate the accuracy of our numerical simulations against previous literature [25]. Figure 3a,b shows the evolution of film shape versus time for a clean droplet system (i.e., no surfactant—$Bq=0$, $E=0$) with viscosity ratio $\lambda =0.19$ at $Ca=0.0008$ and $Ca=0.015$, respectively. We observe that our numerical results (shown by black curves) compare well against the results from the previous computational study investigating the effect of viscosity ratio on film drainage [25] (shown by yellow dashed curves). At the larger value of capillary number $Ca=0.015$, the dimpling effects are more pronounced, and it takes a longer time for the film to drain. The total drainage time $T_d$ is measured from the instance when the center-to-center distance between the droplets is $2R^{\prime }$ to the point where the thin film approaches rupture (when $h={10}^{-4}$). The total drainage time is $T_d=0.042$ at $Ca=0.0008$ and $T_d=1.224$ at $Ca=0.015$. The coalescence between two droplets is facilitated by slow collisions, and the total time for the film to drain increases upon increasing the capillary number.

In Figure 4a,b, we show the effect of viscosity ratio on the film profiles of clean droplets (i.e., $E=0$, $Bq=0$) at $Ca=0.004$. At a low value of viscosity ratio $\lambda =0.01$ (Figure 4a), the droplet remains almost spherical up to the point of rupture. However, at a larger value of viscosity ratio $\lambda =1.0$ (Figure 4b), dimpling effects are observed and it also takes longer for the film to drain. The total drainage time $T_d=0.072$ at $\lambda =0.01$ and $T_d=1.034$ at $\lambda =1.0$.

Figure 5 shows how the total drainage time scaled by droplet radius ($R^{\prime }=27$ μm) changes with viscosity ratio $\lambda$ for a clean droplet system ($Bq=0$) at $Ca=0.004$. The blue dots represent our numerical results and the red dots represent result from [25]. At larger viscosity ratio values, a linear dependence of drainage time with viscosity ratio is observed $T_d\sim \lambda$ from both numerical simulation and scaling theory discussed in [25]. The scaling argument presented by [25] approximates the thin film as a flat disk. This assumption is valid at larger values of viscosity ratio where the film forms a dimpled shape, but is not valid for smaller values of viscosity ratio where the film shape is more akin to a spherical cap.

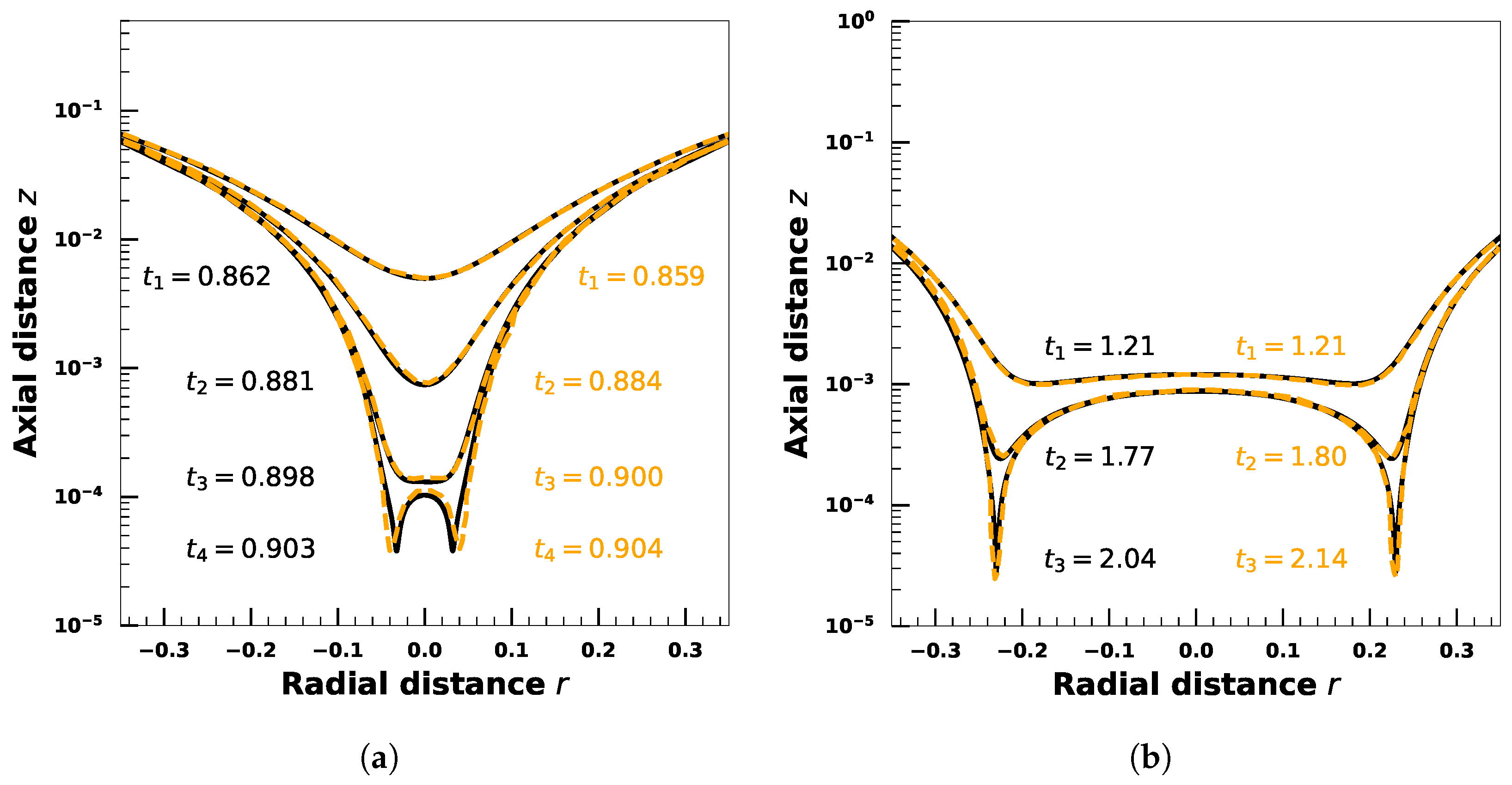
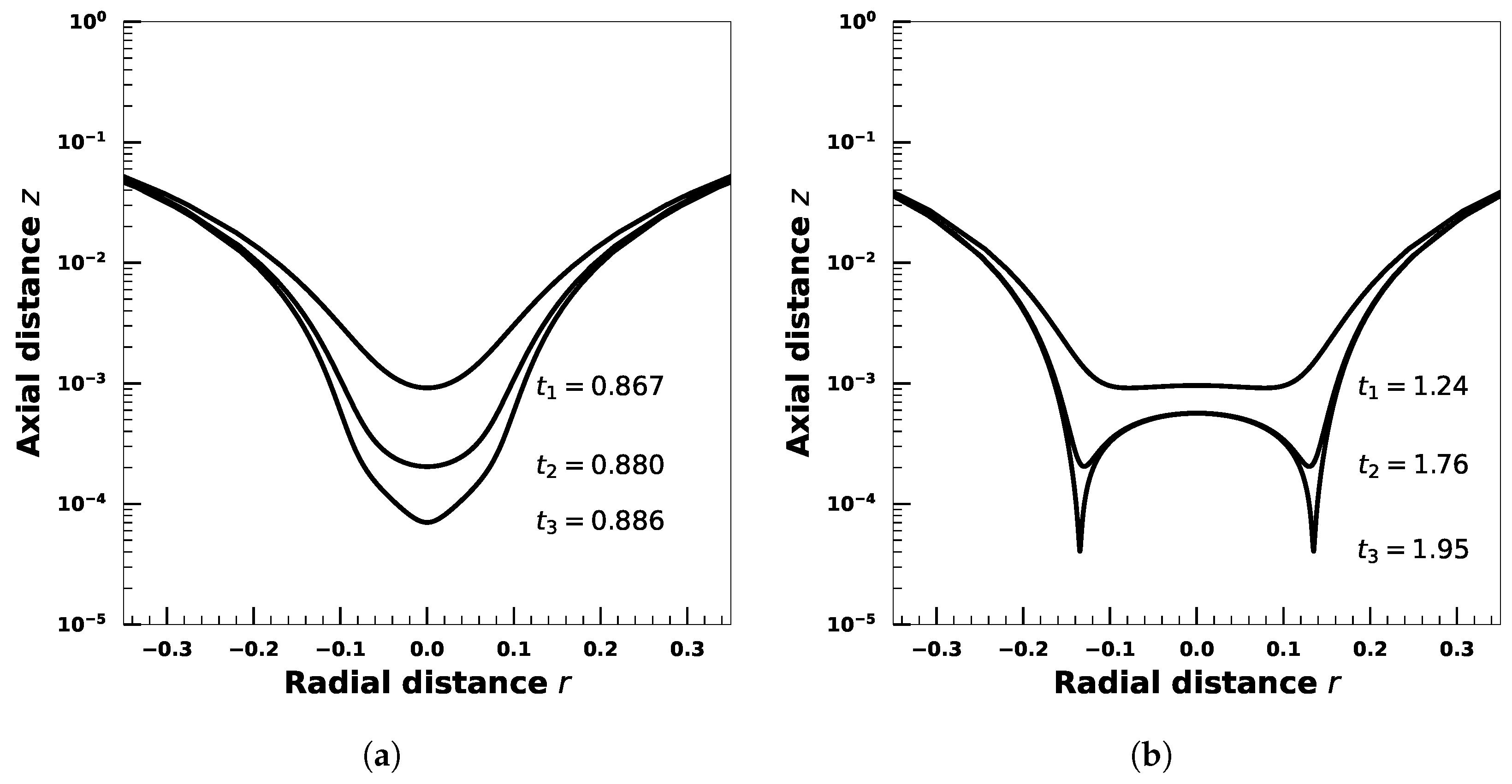
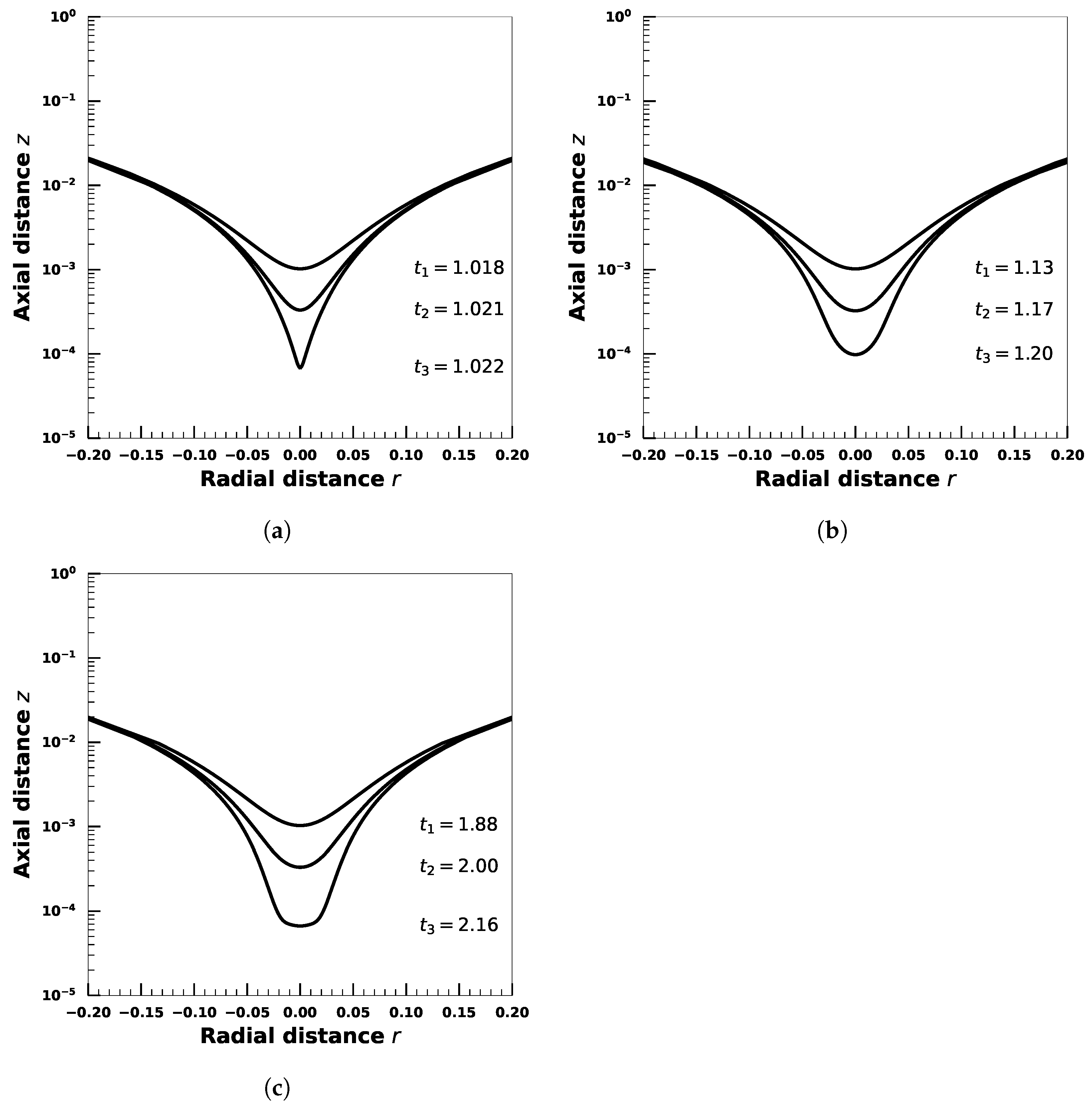
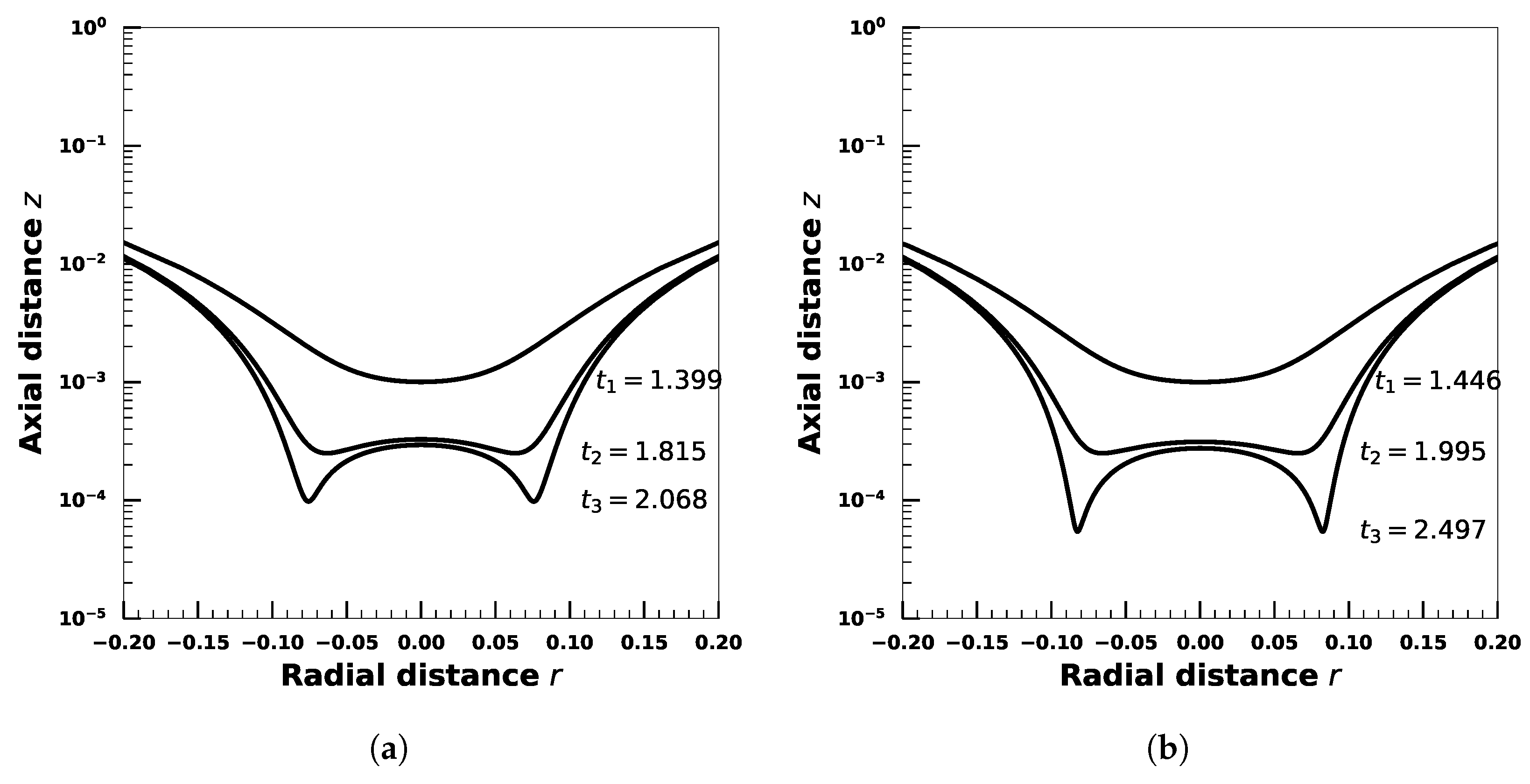
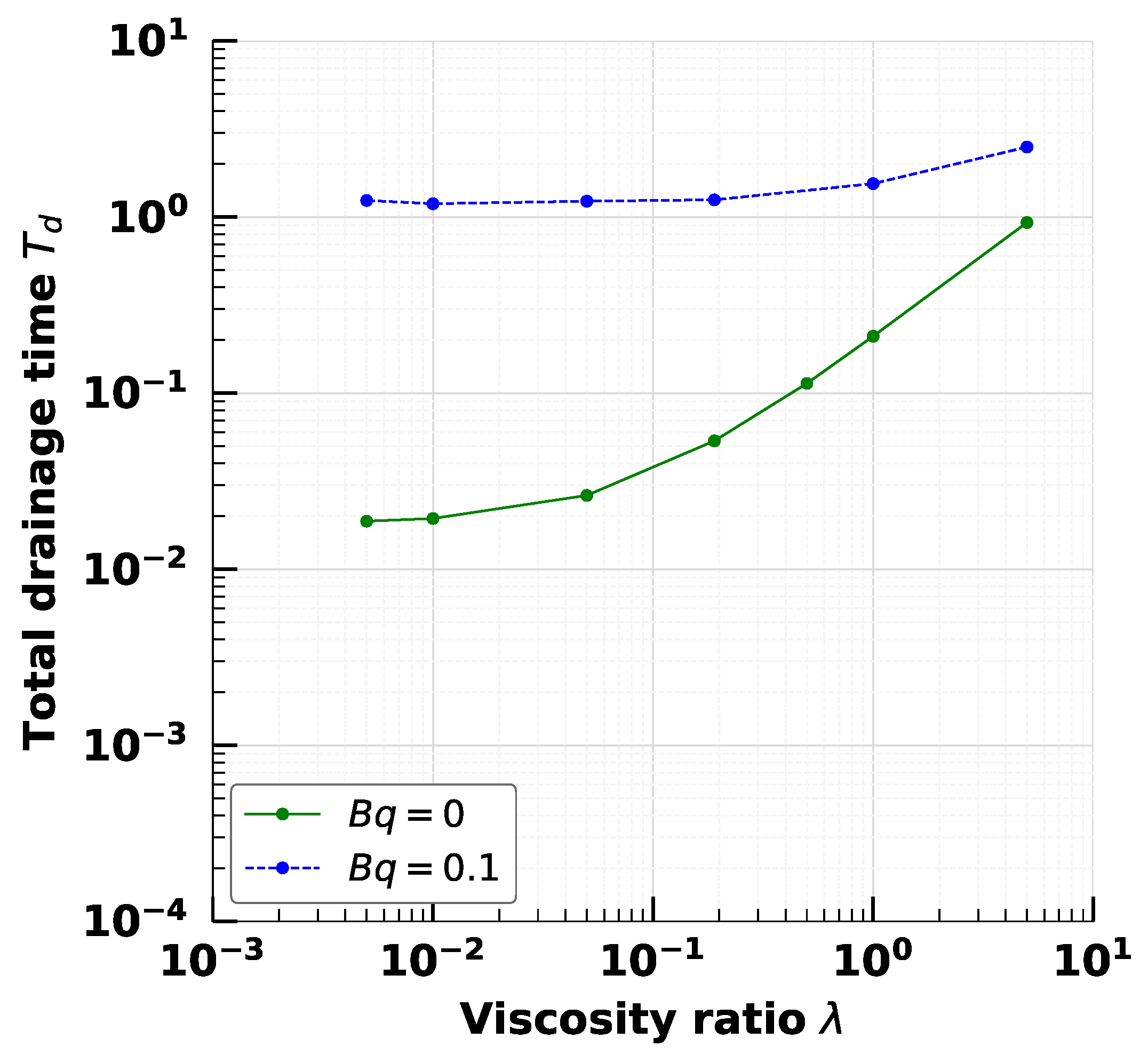
4. Effect of Droplet Viscosity Ratio on Droplets with Interfacial Viscosity

In this section, we explore the effect of the droplet viscosity ratio $\lambda$ on the coalescence behaviour of a droplet system when surface viscosity is present. We neglect surface tension inhomogeneities and assume the surfactant is homogeneously distributed over the interface ($E=0$). This situation corresponds to the case when surface viscous effects are much more significant than Marangoni effects, which holds for droplets in nano/micro-emulsions. When the Marangoni effects are significant, the drainage behaviour becomes independent of the droplet viscosity ratio [26].

Figure 6 shows the evolution of film shape versus time at a very low viscosity ratio $\lambda =0.005$ and very low capillary number $Ca=0.0002$. Three cases are shown: (a) clean droplet $Bq=0$ (Figure 6a), (b) droplet with $Bq=0.1$ (Figure 6b), and (c) droplet with $Bq=0.5$ (Figure 6c). At a low capillary number and low viscosity ratio, dimpling effects are not observed, and the droplet remains almost spherical until the film ruptures. As $Bq$ increases, the interfacial viscosity widens and flattens the film, and slows down the film drainage. Upon increasing $Bq$ from 0 to 0.1, drainage time increases by a factor of 13.82.

In Figure 7, we look at the evolution of film shape versus time at a very high viscosity ratio $\lambda =5.0$ and the same capillary number $Ca=0.0002$. Two cases are shown: (a) clean droplet $Bq=0$ (Figure 7a), and (b) droplet with surface viscosity $Bq=0.1$ (Figure 7b). We see that increasing $Bq$ from 0 to 0.1 increases the drainage time by $33\%$ and like before, dimpling effects are not observed. In Figure 8, we plot the total drainage time as a function of viscosity ratio $\lambda$ at capillary number $Ca=0.0002$ for a clean droplet ($Bq=0$, shown by green points) and droplet with surface viscosity at $Bq=0.1$ (shown by blue points) and $Bq=0.2$ (shown by red points). We observe that interfacial viscosity increases the drainage time and appears to delay the transition at which the scaling changes from $T_d\sim {\lambda }^0$ to $T_d\sim {\lambda }^1$. The effect of interfacial viscosity on drainage time is more prominent at lower values of viscosity ratio than larger values of viscosity ratio.

Next, we discuss the impact of viscosity ratio on droplet coalescence at a higher value of capillary number $Ca=0.001$. Figure 9 shows the drainage profiles for a clean droplet ($Bq=0$) and droplet with surface viscosity ($Bq=0.1$) at a low viscosity ratio $\lambda =0.005$. The clean droplet is almost spherical as it drains, whereas, at $Bq=0.1$, surface viscosity significantly flattens the film and increases the drainage time by a factor of 16.9. In Figure 10, we plot the evolution of the drainage profile with time at a higher value of viscosity ratio $\lambda =5.0$ and at the same capillary number $Ca=0.001$. We see that at the large value of viscosity ratio, the film develops a dimpled shape for both the clean droplet (Figure 10a) and the droplet with surface viscosity (Figure 10b). Upon increasing $Bq$ from 0 to 0.1, the increase in drainage time is $44\%$. Upon comparing Figure 6 and Figure 7 with Figure 9 and Figure 10, we see that upon increasing $Bq$ at the same viscosity ratio, a higher fractional increase in drainage time is observed at $Ca=0.001$ compared to $Ca=0.0002$.

In Figure 11, we plot total drainage time as a function of viscosity ratio $\lambda$ at capillary number $Ca=0.001$ for a clean droplet ($Bq=0$, shown by green points) and droplet with surface viscosity at $Bq=0.1$ (shown by blue points). At high capillary number $Ca=0.001$ also, we observe the same qualitative trends as in Figure 8, i.e., surface viscosity delays drainage with a larger effect at low values of viscosity ratio. The surface viscosity also appears to delay the transition from $T_d\sim {\lambda }^0$ scaling to $T_d\sim {\lambda }^1$.

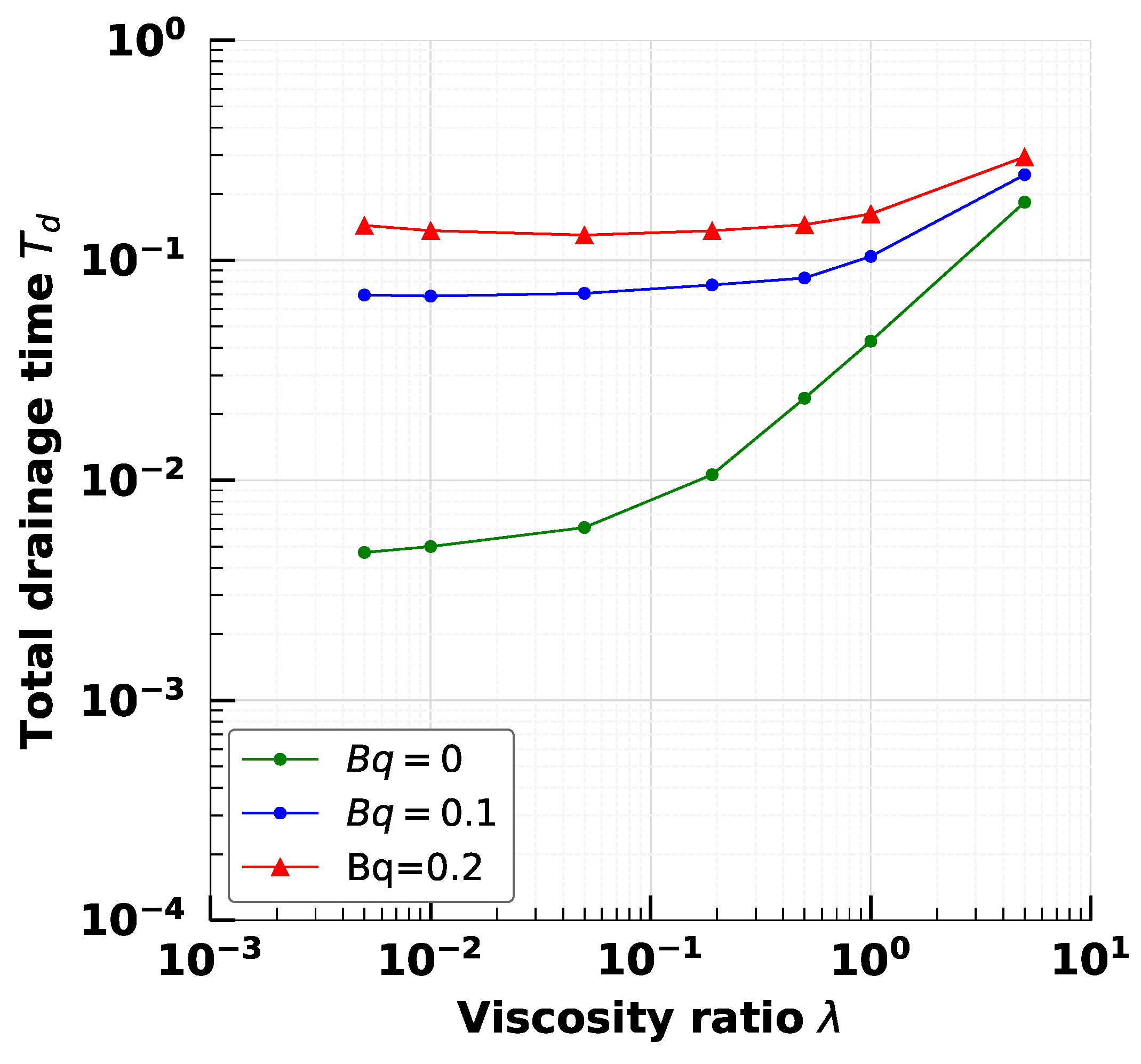
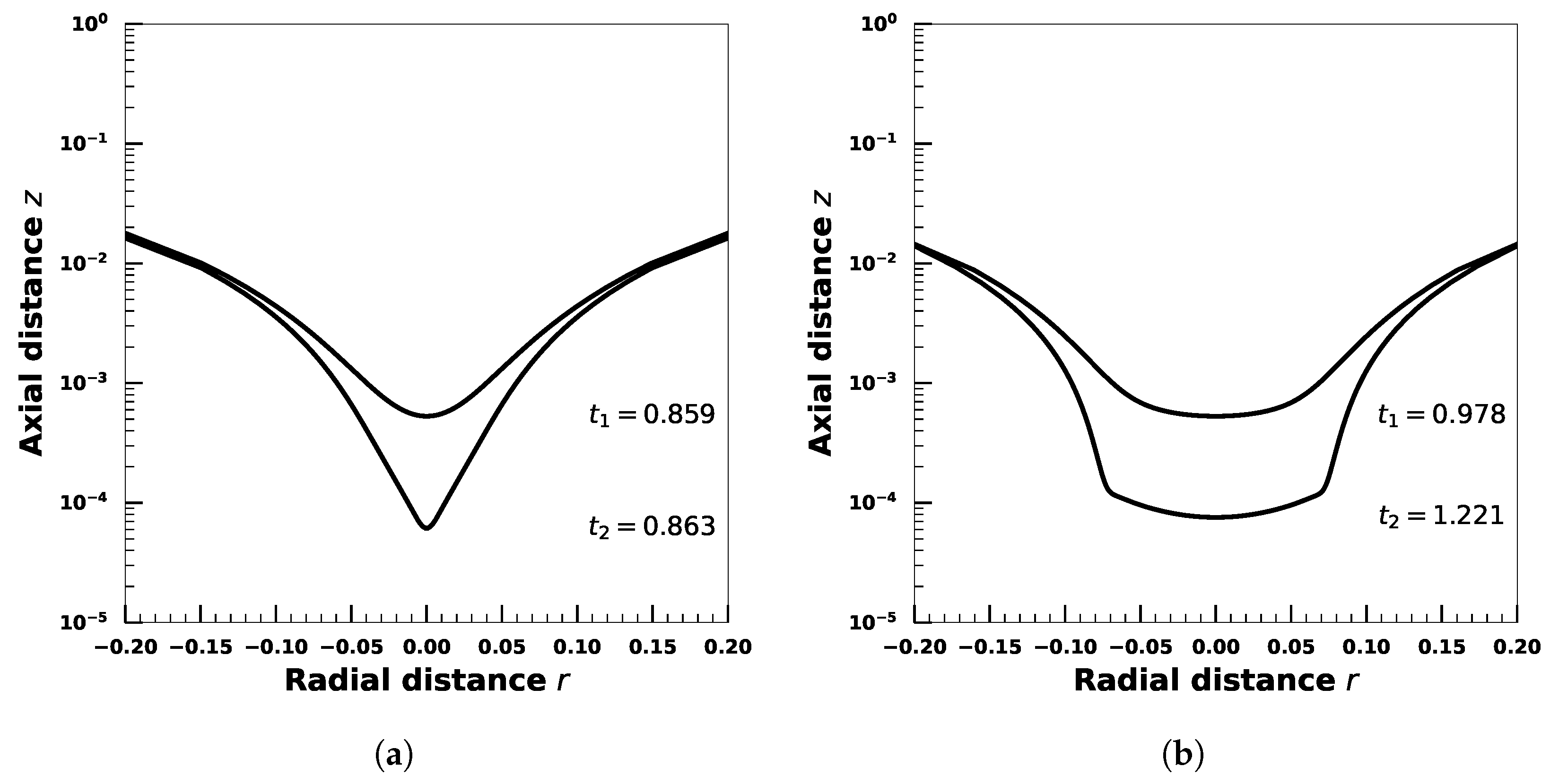
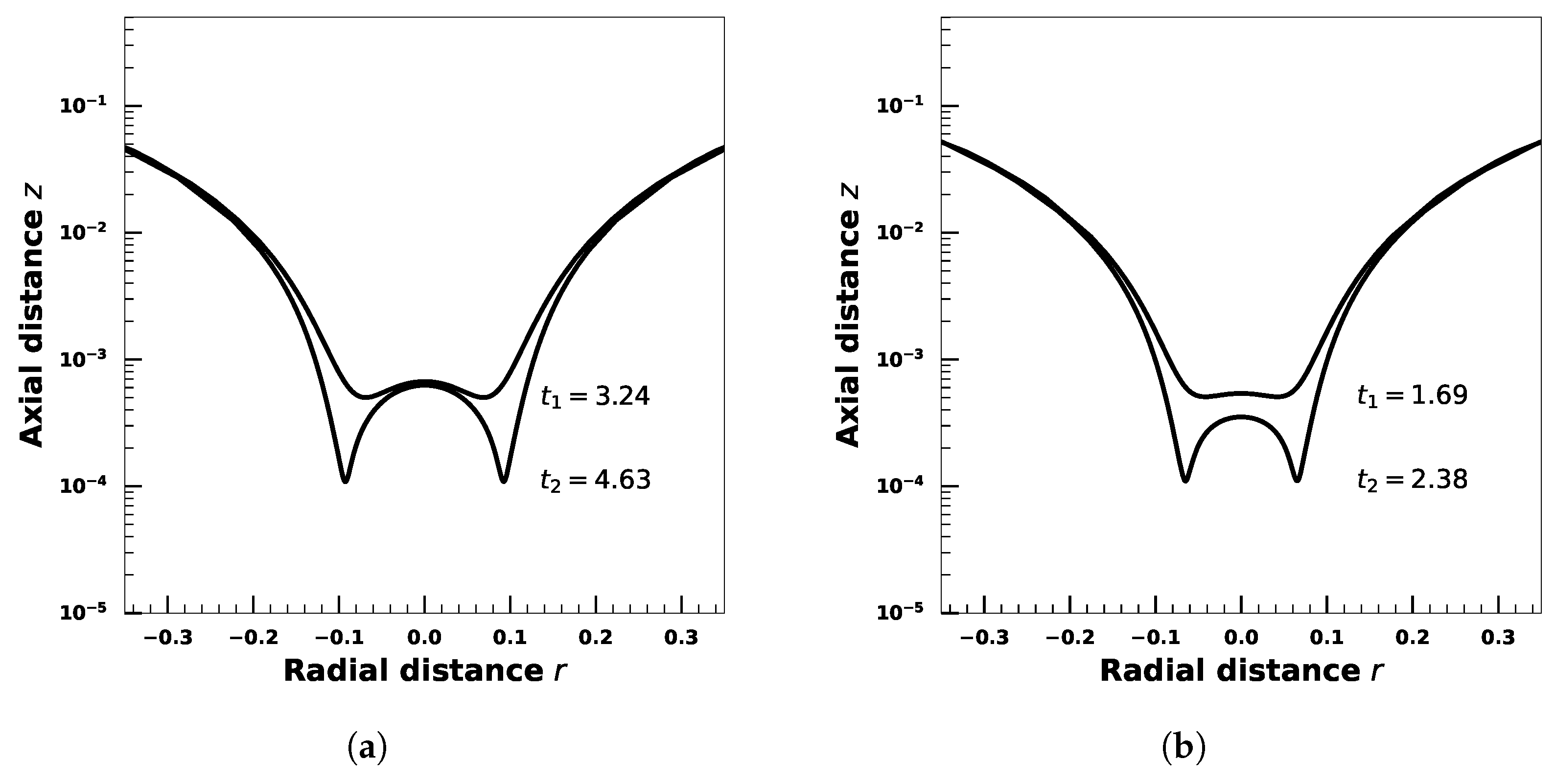
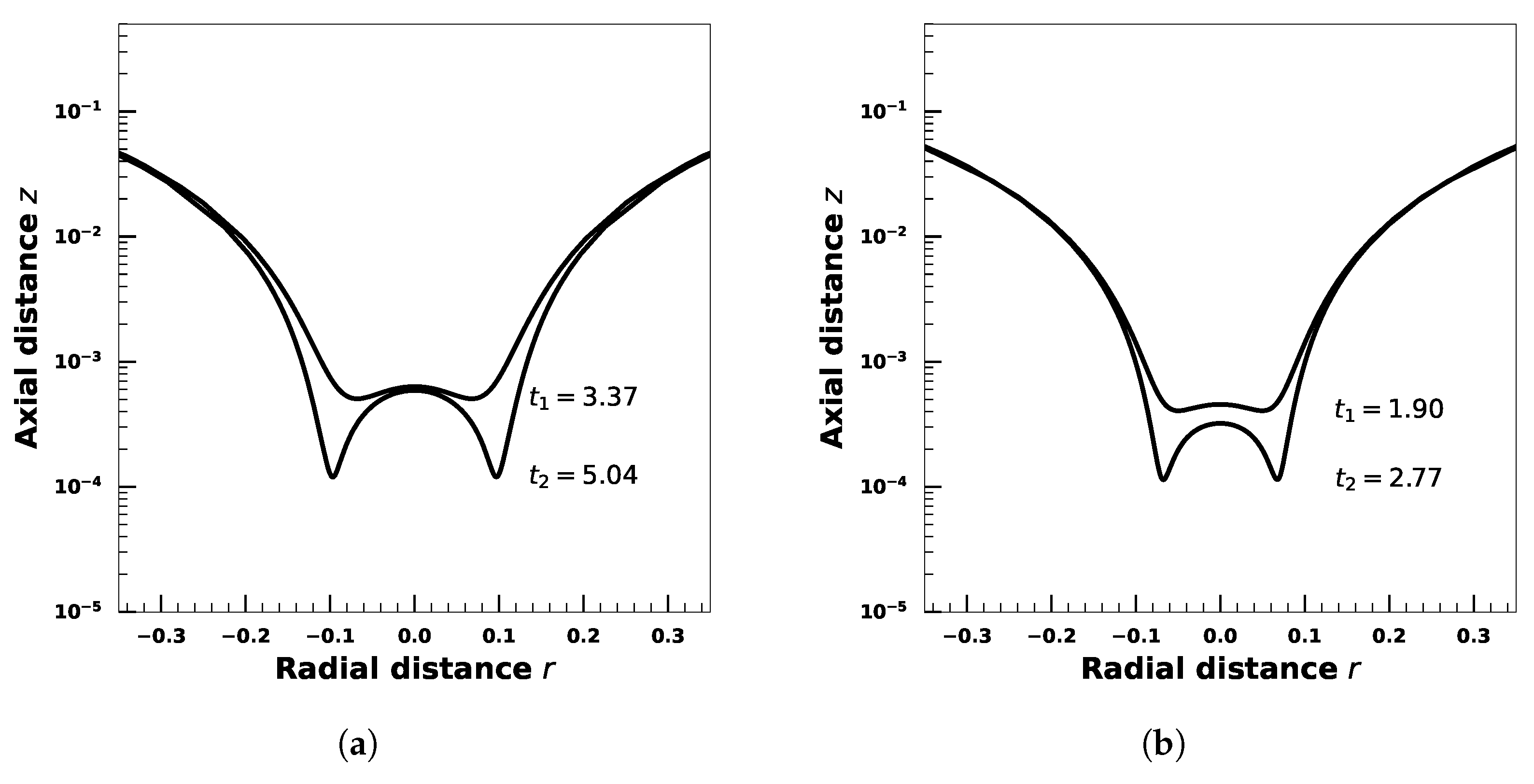
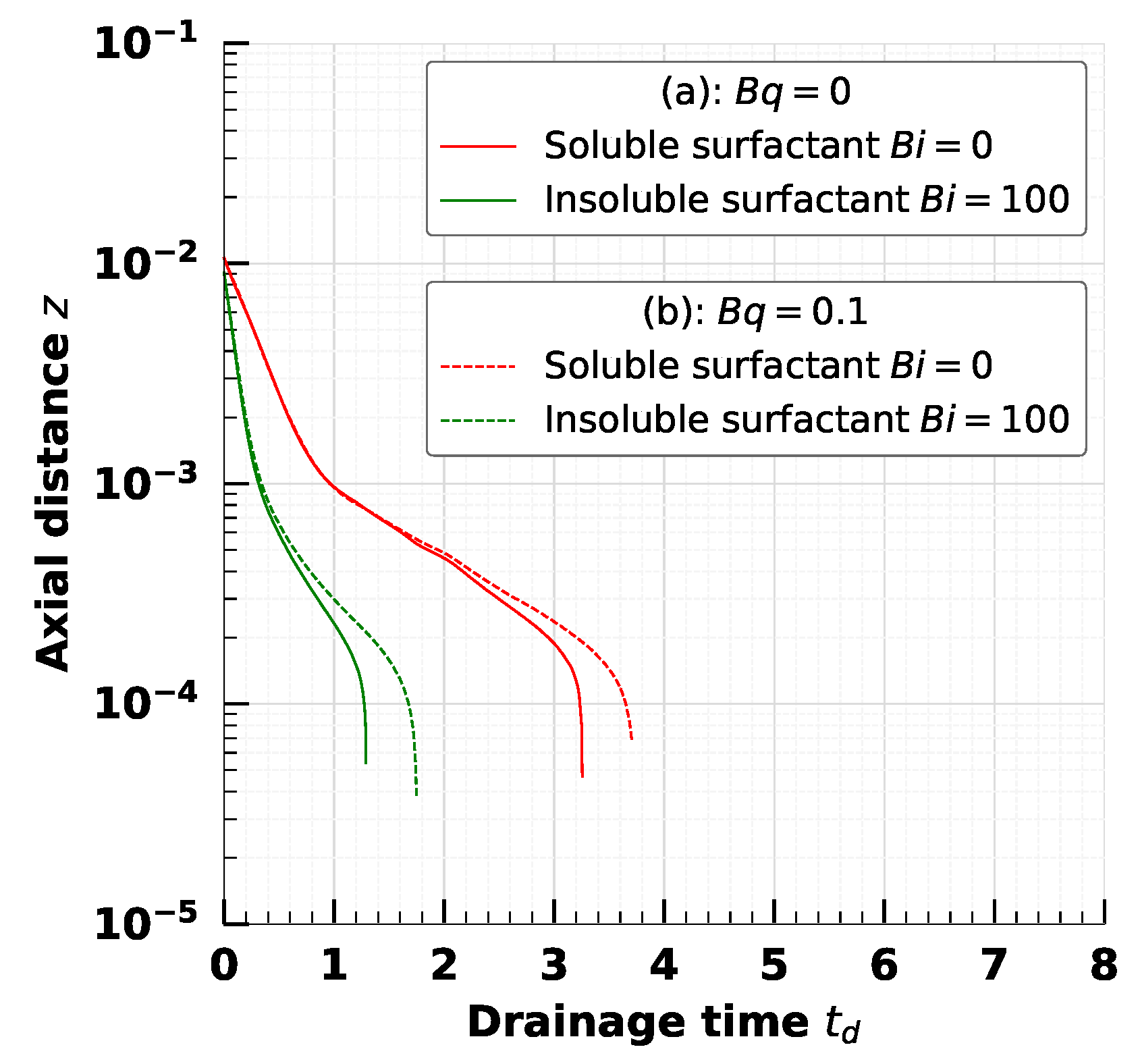
5. Effect of Adsorption-Desorption Controlled Surfactant When Interfacial Viscosity Is Present

In this section, we explore the role of surfactant solubility in the limit of kinetically controlled adsorption/desorption on droplet dynamics.

In Figure 12, we show the evolution of drainage profiles with time for droplets when Marangoni flows are present (i.e., surface tension gradients). We will first consider the situation when no surface viscosity is present ($Bq=0$). Two cases are shown: (a) droplet with Biot number $Bi=0$ (Figure 12a), and (b) droplet with $Bi=100$ (Figure 12b). The dimensionless parameters are: $\lambda =1$, $Ca=0.001$, $Bq=0$, $P{e}_s=5$, and $E=0.2$. We observe that total drainage time $T_d=3.25$ at $Bi=0$ and $T_d=1.29$ at $Bi=100$. At very low values of Biot number $Bi\ll 1$, the surfactant is essentially insoluble. Previous literature examining the effect of insoluble surfactant on droplet dynamics has shown that Marangoni stresses enhance the dimpling of the film and increase the total drainage time compared to a clean droplet at the same value of capillary number [26,27]. For the droplet system with soluble surfactant (Figure 12b), the surfactant adsorption/desorption effects minimize the surface tension gradients and Marangoni flows. As a result, we observe that at $Bi=100$, the film drains faster compared to a droplet system with insoluble surfactant ($Bi=0$). The reduction in total drainage time observed is roughly $60\%$. In Figure 13, we show the evolution of drainage profiles with time for a droplet system with Marangoni effects at a slightly lower value of capillary number $Ca=0.0005$ for two cases: (a) droplet with insoluble surfactant $Bi=0$, and (b) droplet with soluble surfactant $Bi=100$. The dimensionless parameters are: $\lambda =1$, $Bq=0$, $P{e}_s=5$, and $E=0.2$. We observe the total drainage time $T_d=2.24$ at $Bi=0$ and $T_d=1.05$ at $Bi=100$. Here, the reduction in total drainage time observed upon increasing $Bi$ from 0 to 100 is roughly $53\%$ at $Ca=0.0005$. Upon comparing Figure 12 and Figure 13, we can say that dimpling effects are more pronounced for the droplet system at a higher value of capillary number, and therefore, it also takes a longer time for film to drain. Another observation that can be made is that increasing $Bi$ from 0 to 100 leads to a more significant decrease in total drainage time at $Ca=0.001$ compared to the droplet at $Ca=0.0005$.

In Figure 14, we look at the role of surfactant solubility for a droplet when surface viscosity is present ($Bq=0.1$). Two cases are shown: (a) droplet with Biot number $Bi=0$ (Figure 14a), and (b) droplet with $Bi=100$ (Figure 14b). The dimensionless parameters are: $\lambda =1$, $Ca=0.001$, $Bq=0.1$, $P{e}_s=5$, and $E=0.2$. Upon comparing Figure 12a and Figure 14a in the insoluble limit $Bi=0$, surface viscosity increases the total drainage time by roughly $13\%$ compared to the droplet without surface viscosity. However, for the droplet with soluble surfactant (Figure 12b and Figure 14b), surface viscosity increases the total drainage time by roughly $35\%$ compared to the droplet without surface viscosity. Figure 15 shows the evolution of film thickness with drainage time $t_d$ for (a) a droplet without surface viscosity ($Bq=0$) at $Bi=0$ and $Bi=100$, and (b) a droplet with surface viscosity ($Bq=0.1$) at $Bi=0$ and $Bi=100$. The dimensionless parameters are: $\lambda =1$, $Ca=0.001$, $P{e}_s=5$, and $E=0.2$. The drainage time $t_d$ is measured from the start of the drainage process when the center-to-center distance between the two droplets is $2R^{\prime }$. We note that the adsorption/desorption effects minimize the surface tension gradients and also accentuate interfacial rheological effects.

In previous literature, it has been reported that in the case of insoluble surfactant limit, above the critical interfacial coverage of surfactant, the film drainage behaviour is independent of droplet viscosity ratio $\lambda$ at a given capillary number [26]. In Figure 16, for a droplet with soluble surfactant $Bi=100$, we show the evolution of film shape with time at viscosity ratio $\lambda =0.05$ and $\lambda =1.0$. The dimensionless parameters are: $Ca=0.001$, $P{e}_s=5$, $E=0.2$, and $Bq=0$. We observe that results for the two cases ($\lambda =0.05$ and $\lambda =1$) overlap, i.e., the coalescence behaviour is found to be independent of the droplet viscosity ratio even for soluble surfactants.

6. Conclusions

In this work, we studied the impact of droplet viscosity ratio $\lambda$ on the head-on collision of two droplets when interfacial viscosity is present on the drop interface. We modelled the interfacial stresses arising from the surface viscosity using the Boussinesq–Scriven constitutive relationship [39,40].

In the case of a clean droplet, previous literature has shown that total drainage time scales linearly with $\lambda$ at large values of viscosity ratio [25]. At moderate and high viscosity ratio $\lambda \ge \mathcal{O}\left(1\right)$, the droplet develops a dimpled shape at large capillary numbers $Ca\sim \mathcal{O}\left({10}^{-3}\right)$. However, at very low viscosity ratio $\lambda \ll 1$, the thin film remains spherical as it drains even at large capillary numbers $Ca\sim \mathcal{O}\left({10}^{-3}\right)$. At very low capillary numbers $Ca\sim \mathcal{O}\left({10}^{-4}\right)$, droplet shapes remain almost spherical up to the point of rupture, regardless of viscosity ratio, i.e., no dimpling effects are observed.

When surfactants are present on the droplet, the drainage behaviour changes. If surface viscous effects are present and Marangoni effects are negligible (e.g., micro or nanoemulsions), we observe that surface viscosity increases the total drainage time and flattens/widens the film compared to a clean droplet, at a given viscosity ratio and capillary number. In the case of a clean droplet, at larger viscosity ratio values, a linear dependence of drainage time with viscosity ratio is observed $T_d\sim \lambda$. We observe that the surface viscosity appears to delay the transition from $T_d\sim {\lambda }^0$ scaling to $T_d\sim {\lambda }^1$ compared to a clean droplet at the same value of capillary number. At a given capillary number, surface viscosity effects are more pronounced for the droplet at lower values of viscosity ratio than higher values, sometimes increasing the drainage time by an order of magnitude. A similar impact of viscosity ratio is also observed in other droplet processes (droplet breakup, deformation, and sedimentation) [58,59,60].

In the second half of the paper, we examine the impact of surfactant solubility in the limit of kinetically controlled adsorption/desorption. We find that, for a droplet with soluble surfactant, adsorption/desorption effects reduce the surface tension gradients and Marangoni flows compared to the droplet with insoluble surfactant. Since the Marangoni effects are weaker with soluble surfactant, surface rheological effects play a more prominent effect on droplet dynamics as the Biot number increases. At $Ca=0.001$, upon increasing $Bq$ from 0 to 0.1, for droplet with insoluble surfactant ($Bi=0$), surface viscosity increases the drainage time by $13\%$ whereas for droplets with soluble surfactant ($Bi=100$), surface viscosity increases the drainage time by $35\%$.