The Influence of Two-Dimensional Temperature Modulation on Floating Droplet Dynamics
Abstract
:1. Introduction
2. Formulation of the Problem
3. Manipulation by a Stationary Droplet
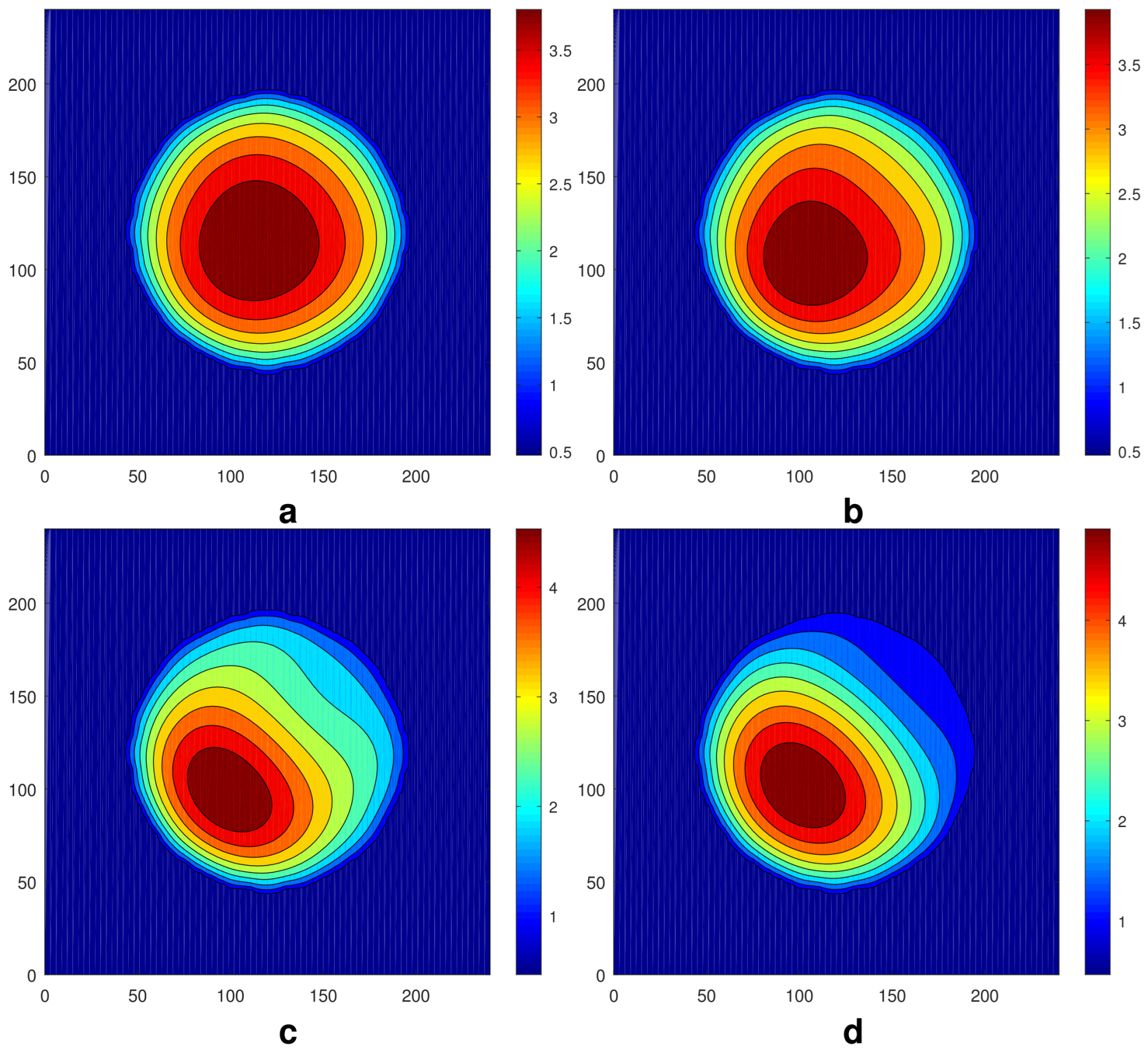
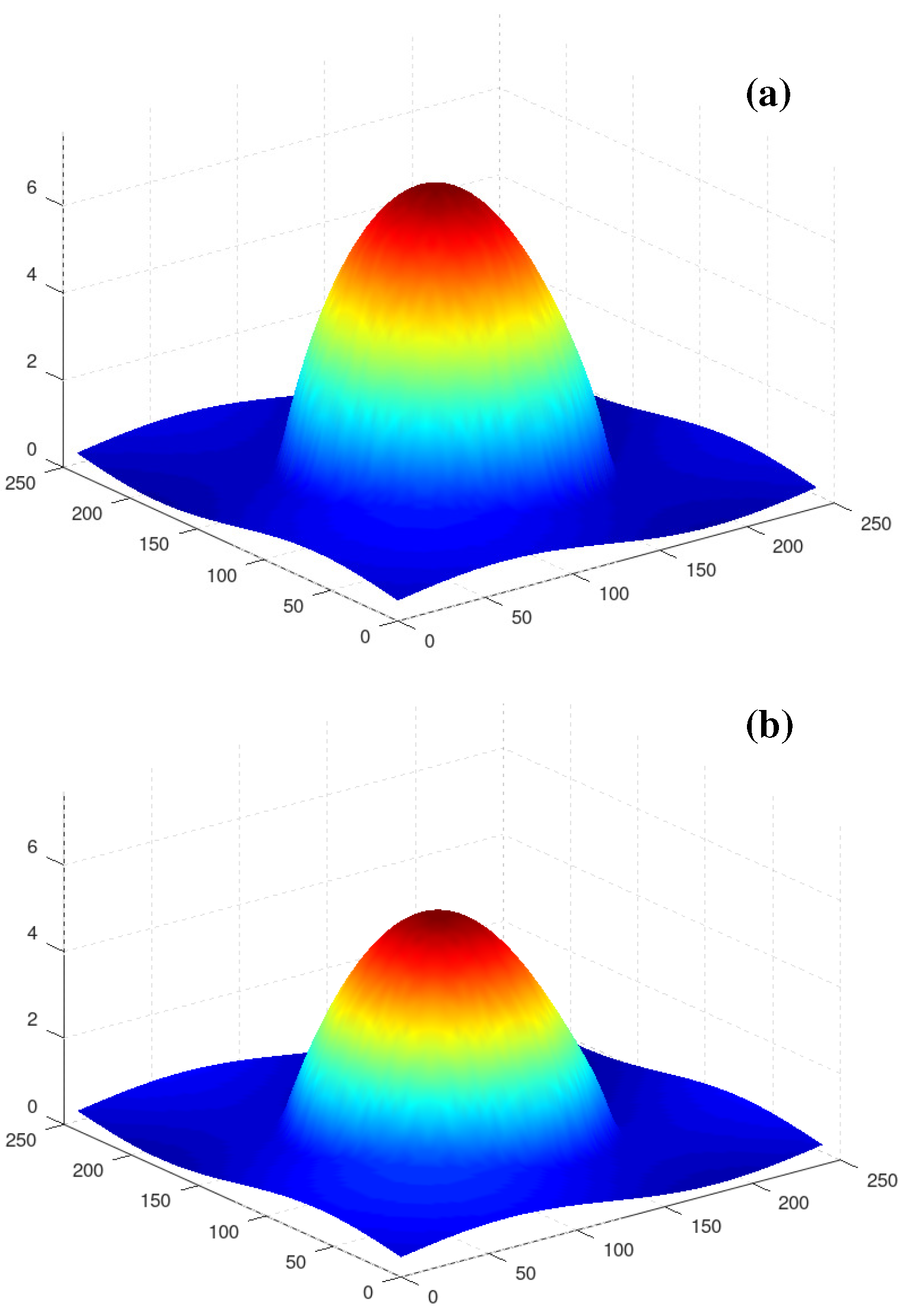
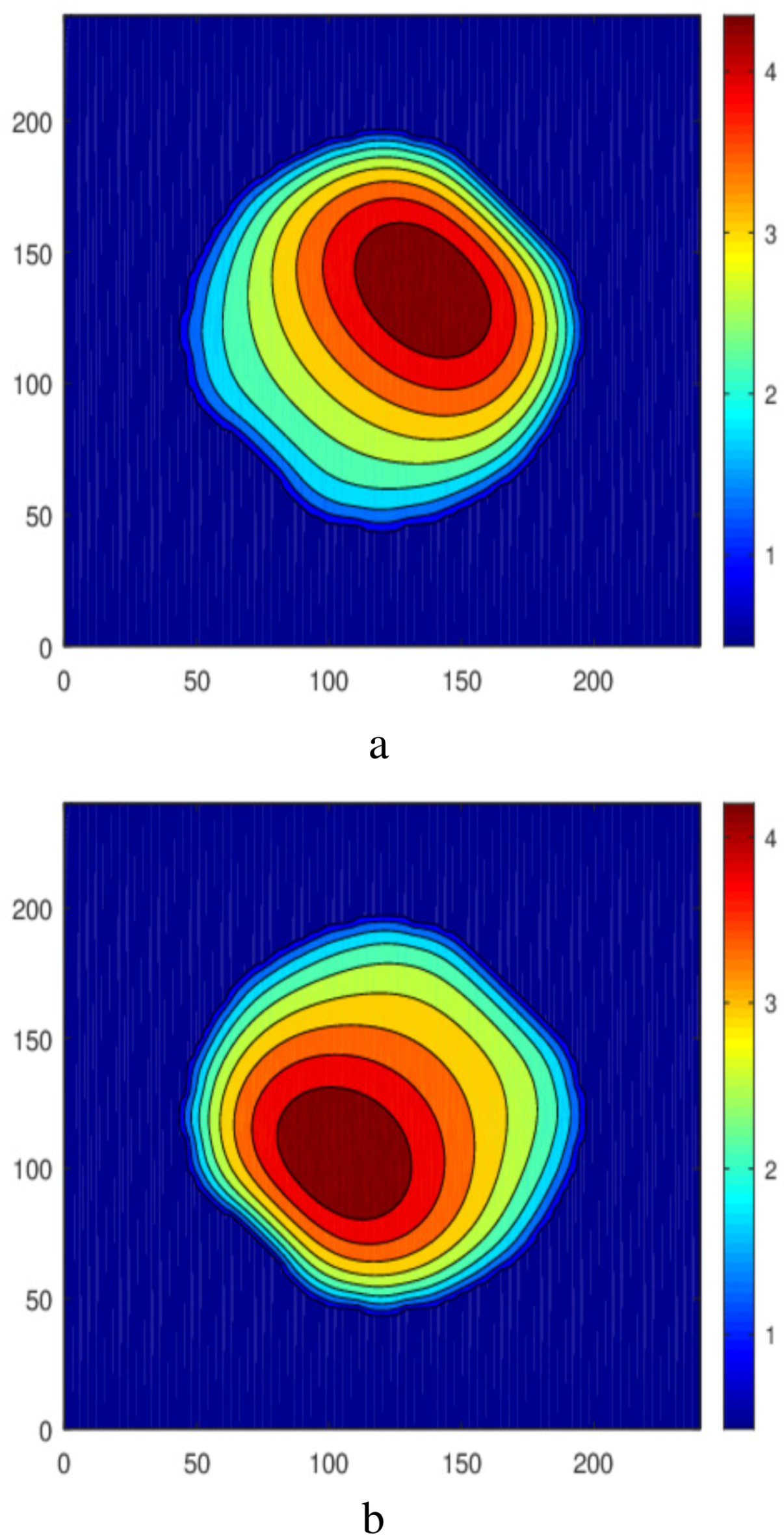
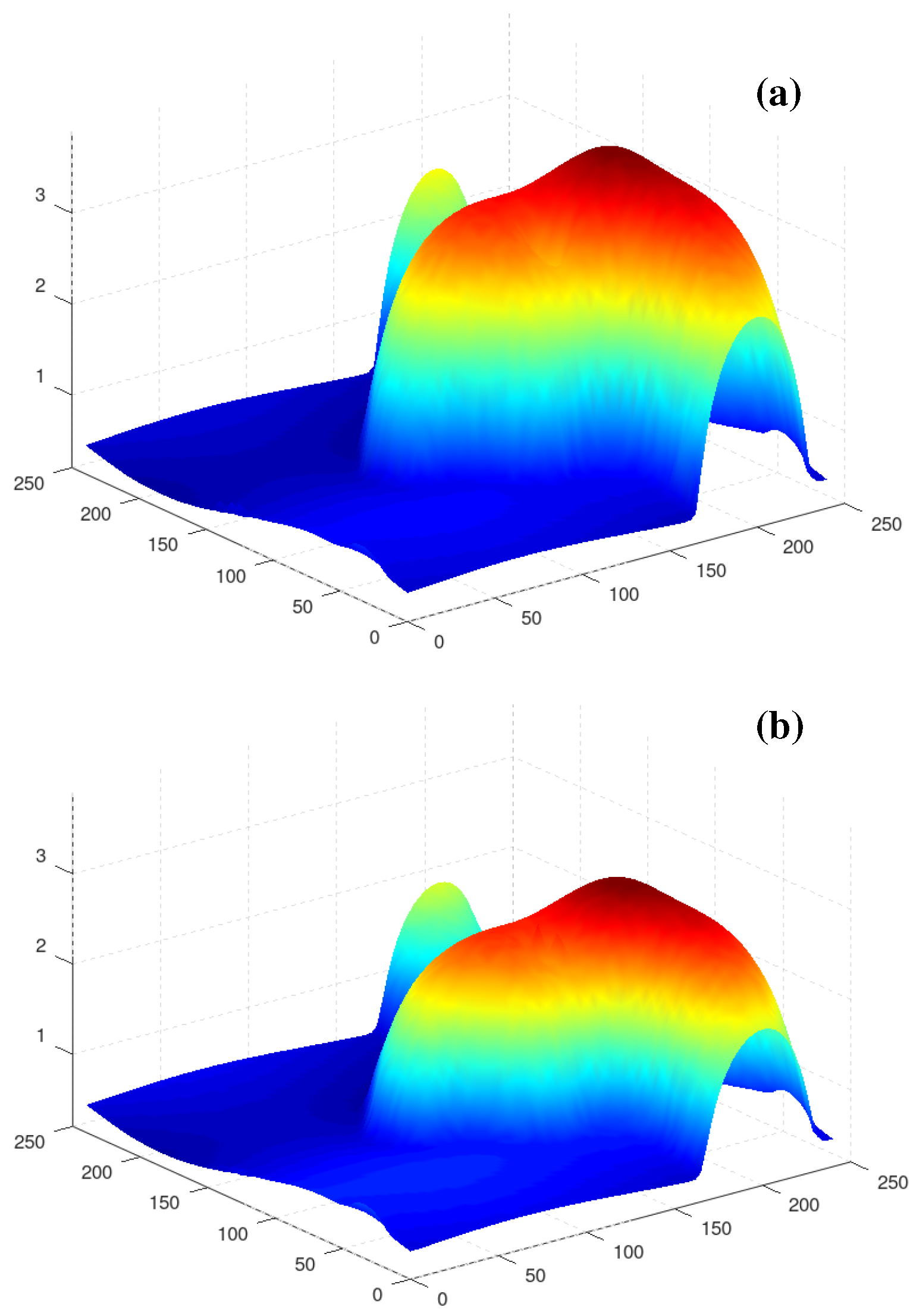
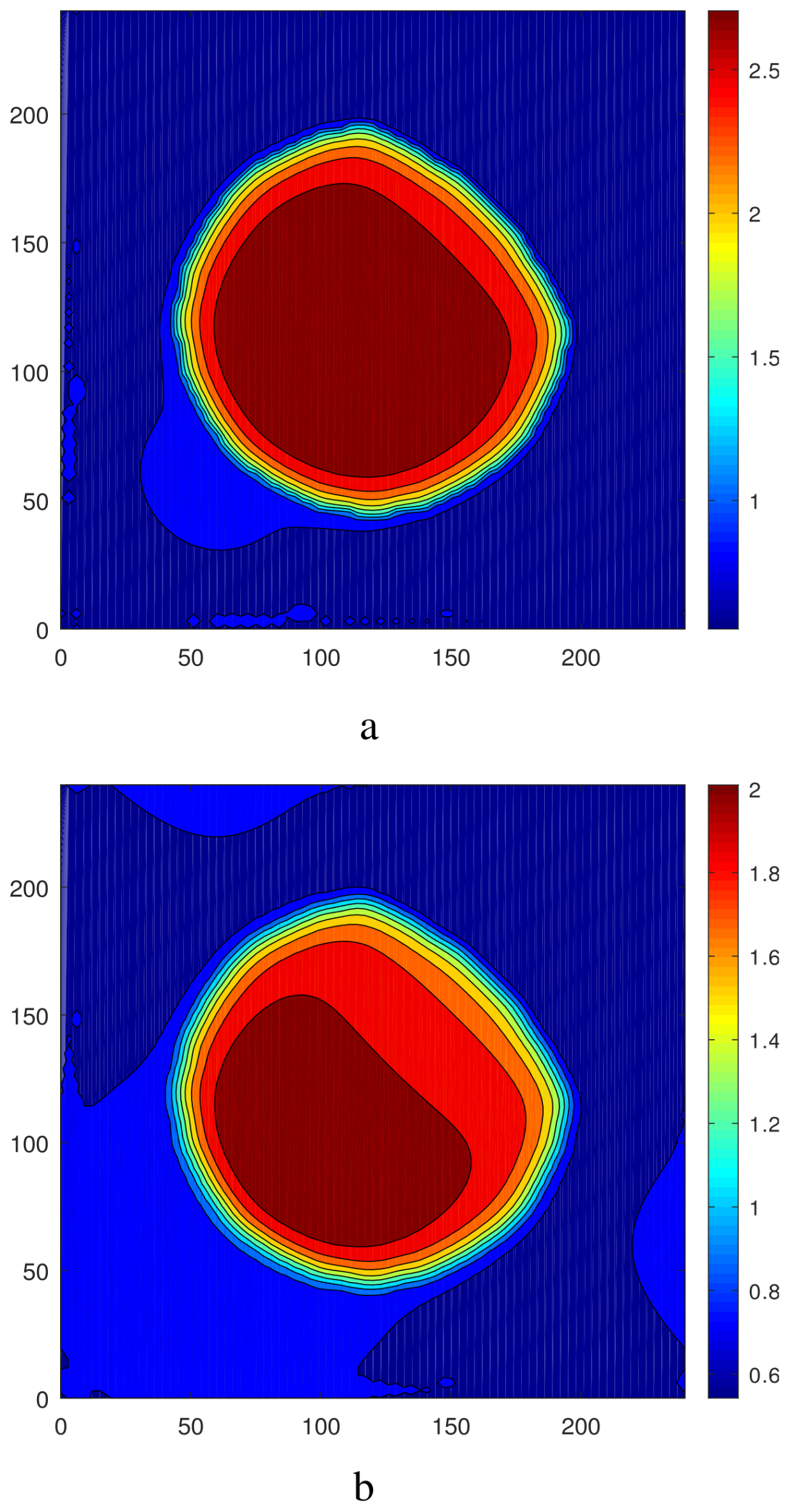
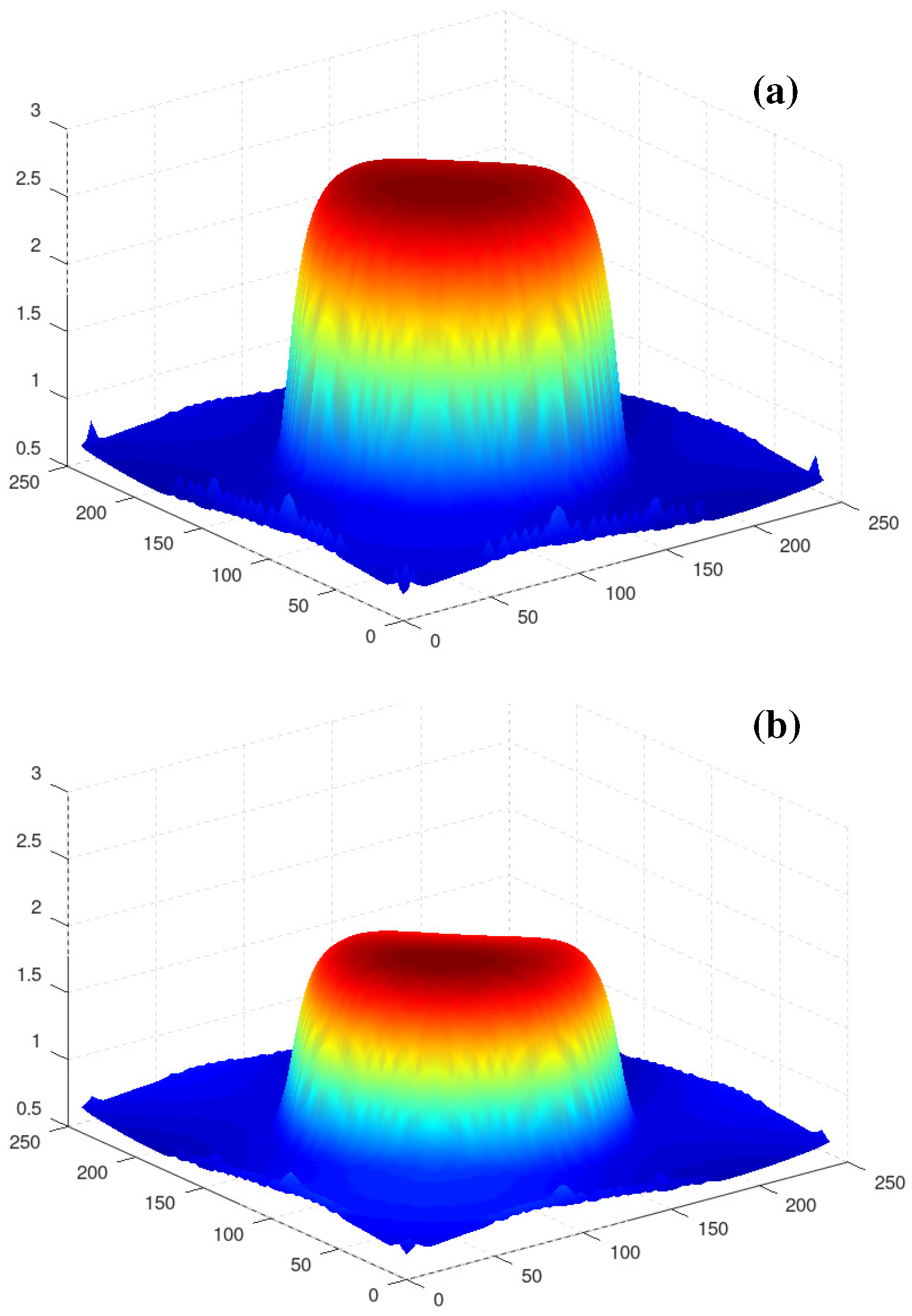
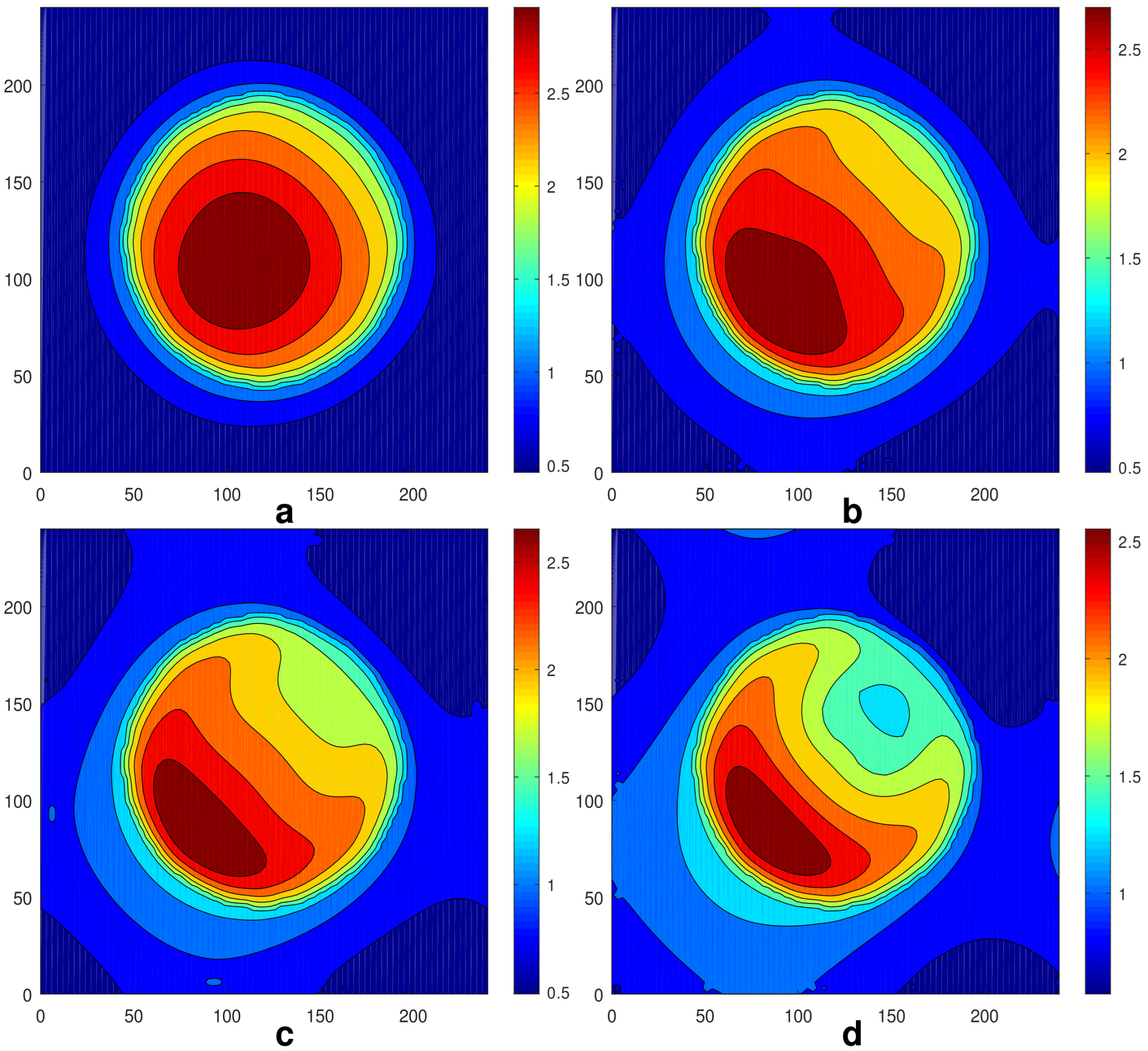
3.1. The Case of Axisymmetric Initial Conditions
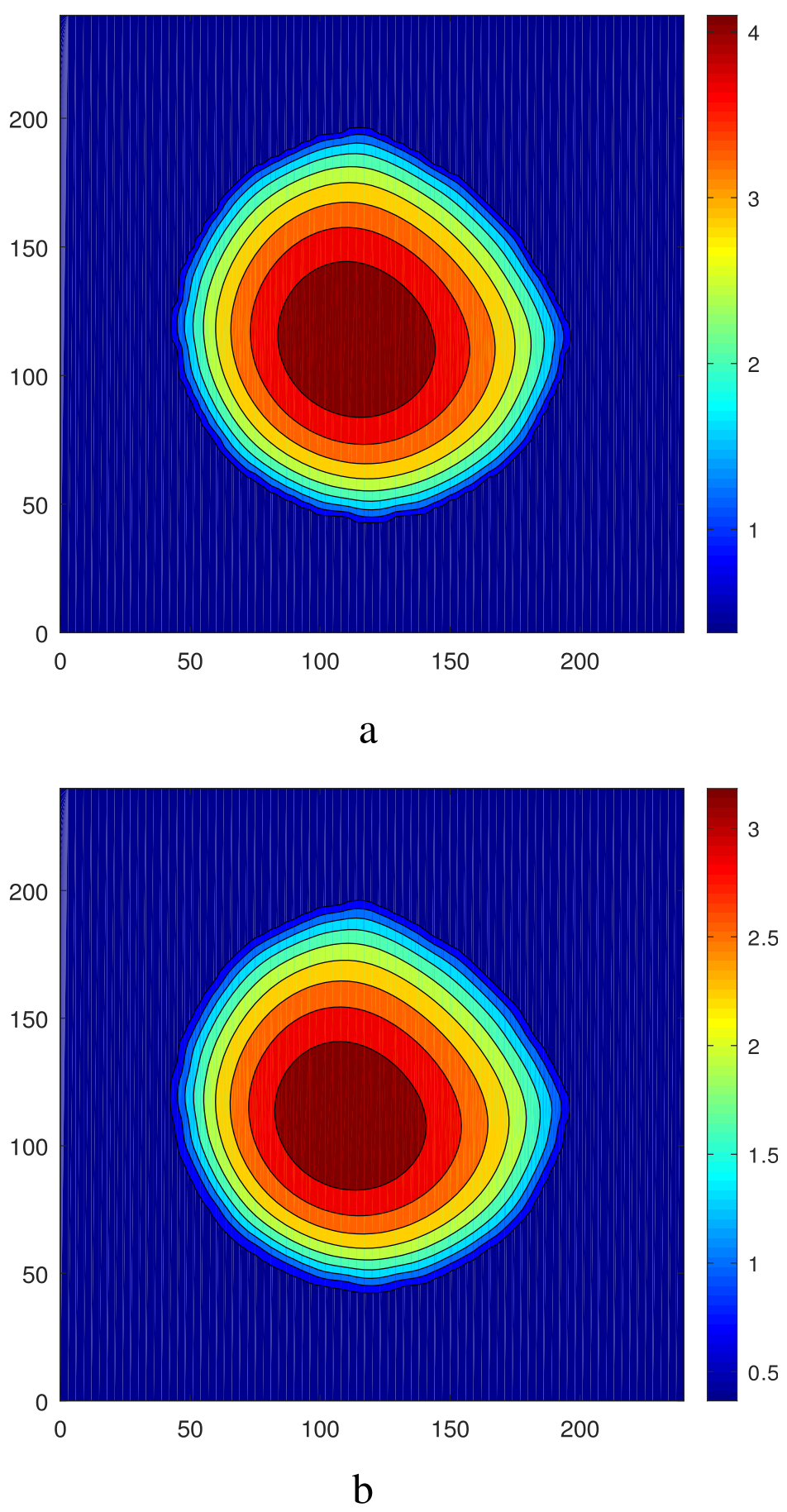
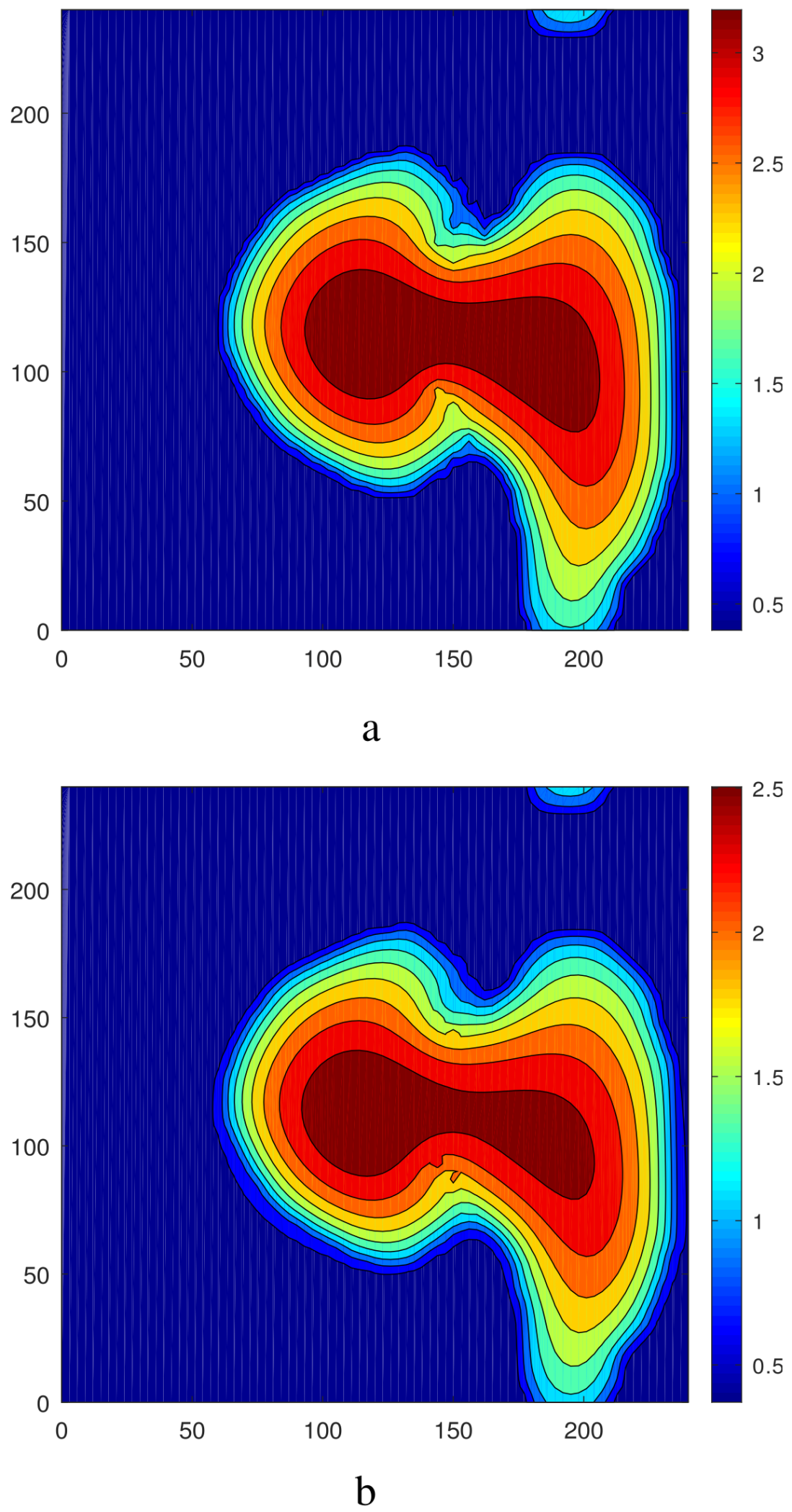
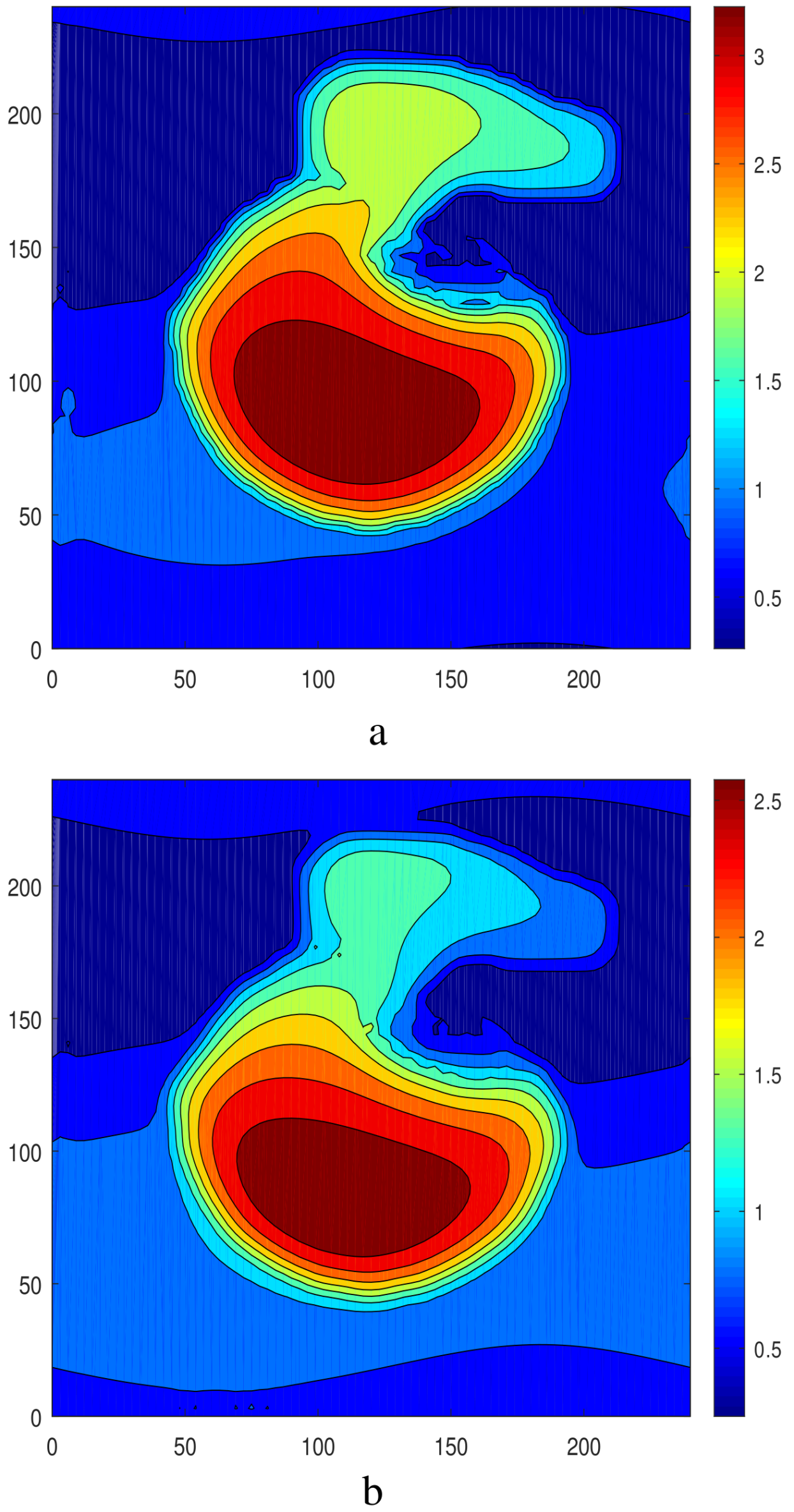
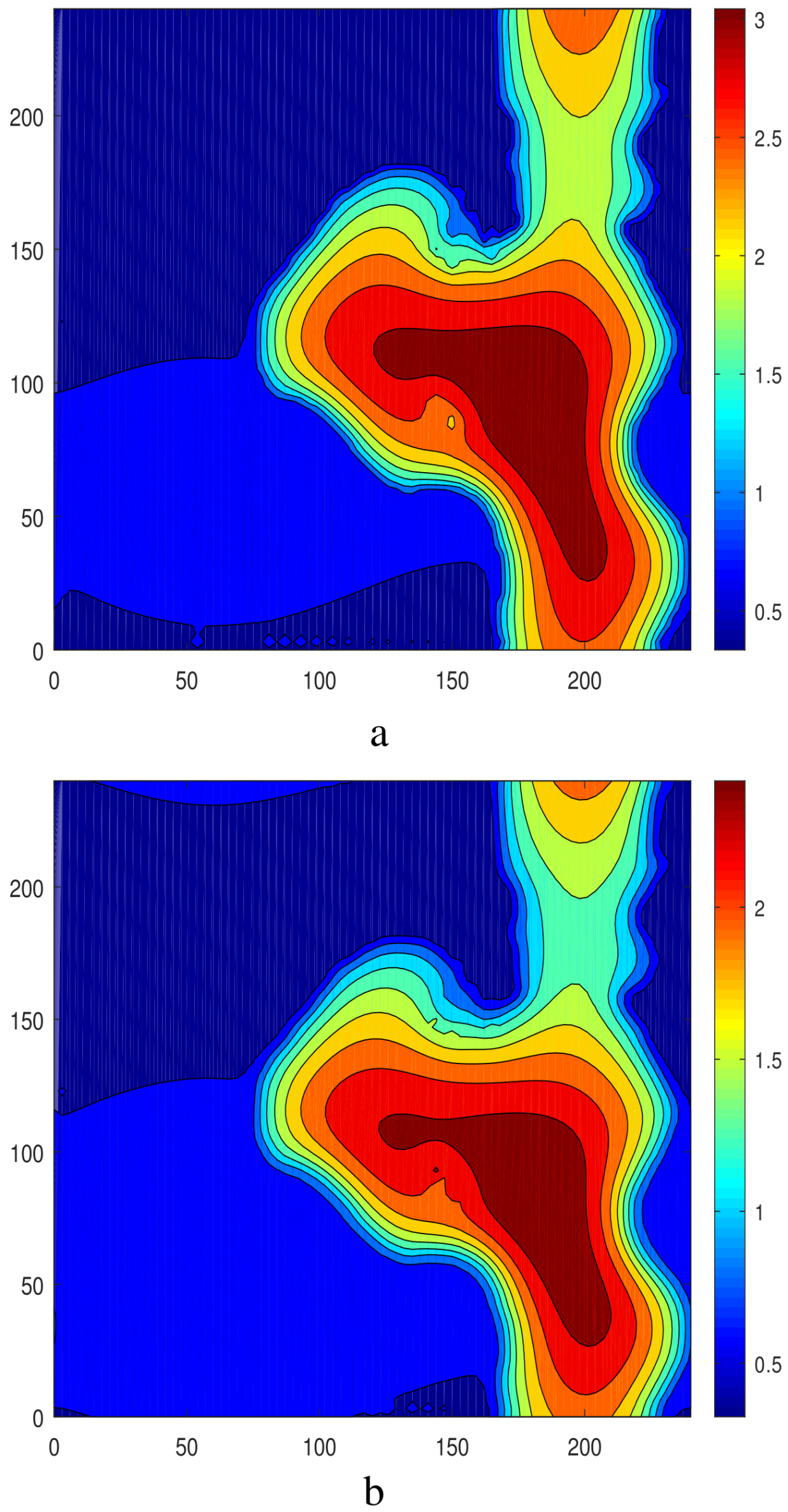
3.2. The Case of Nonaxisymmetric Initial Conditions
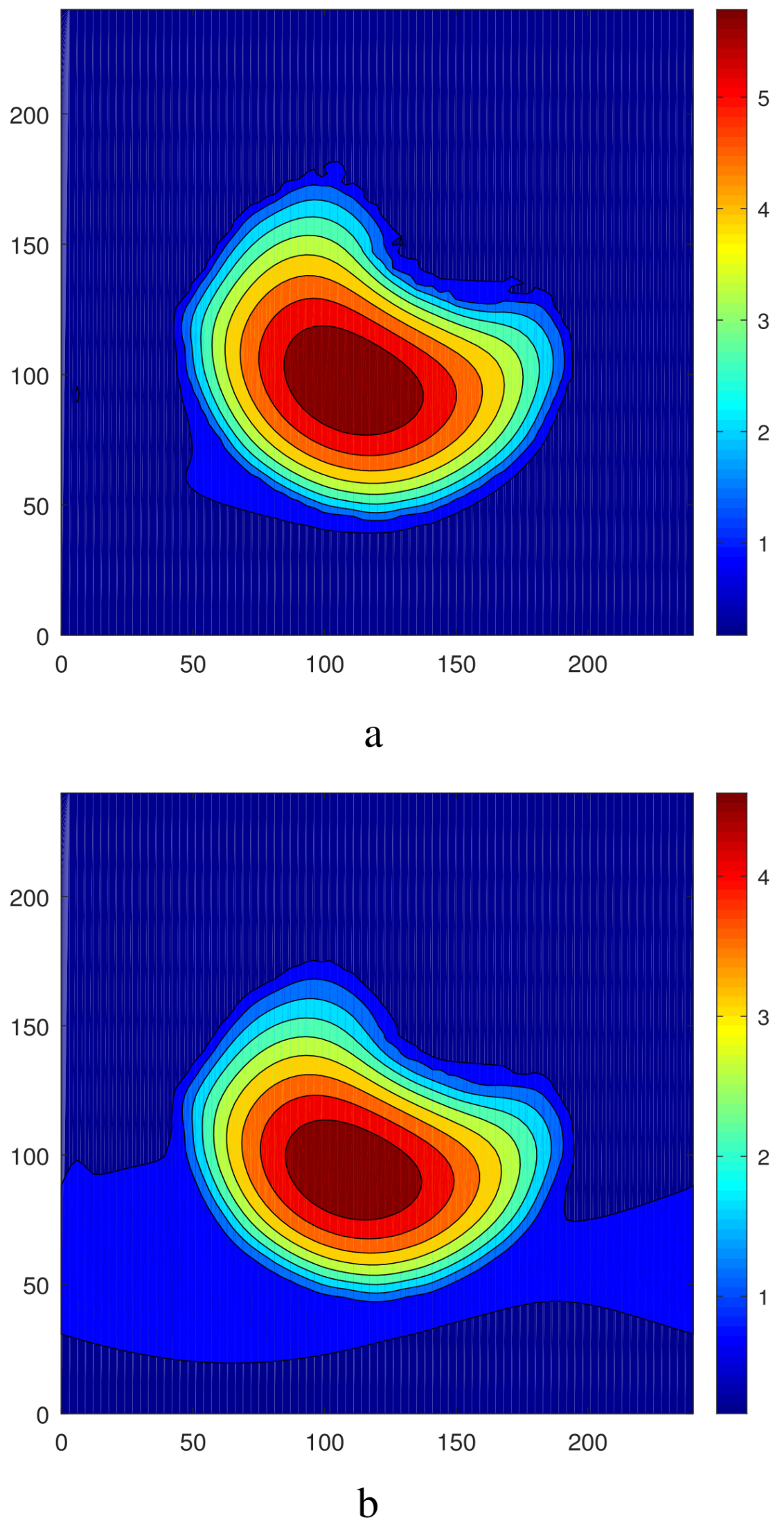
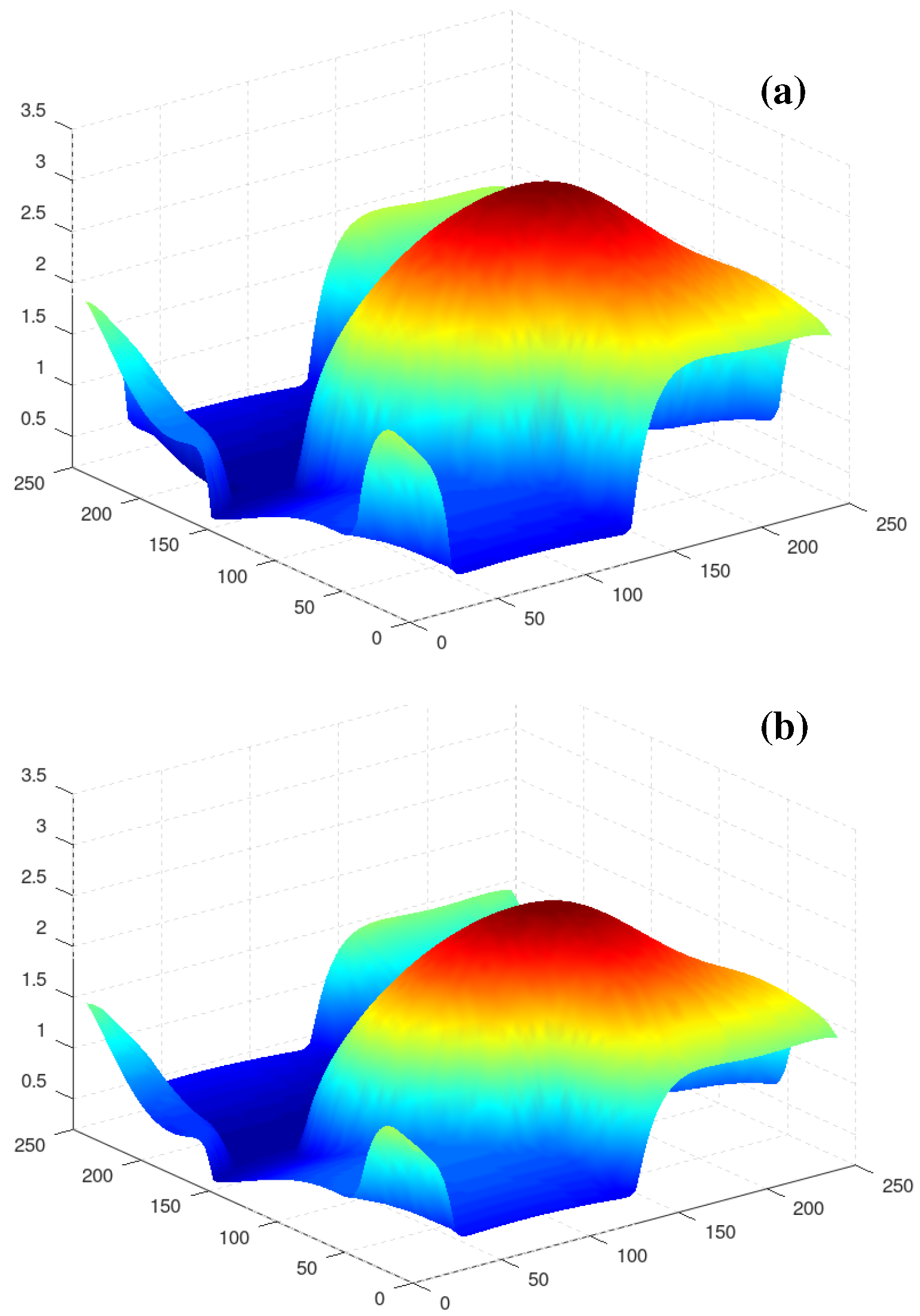
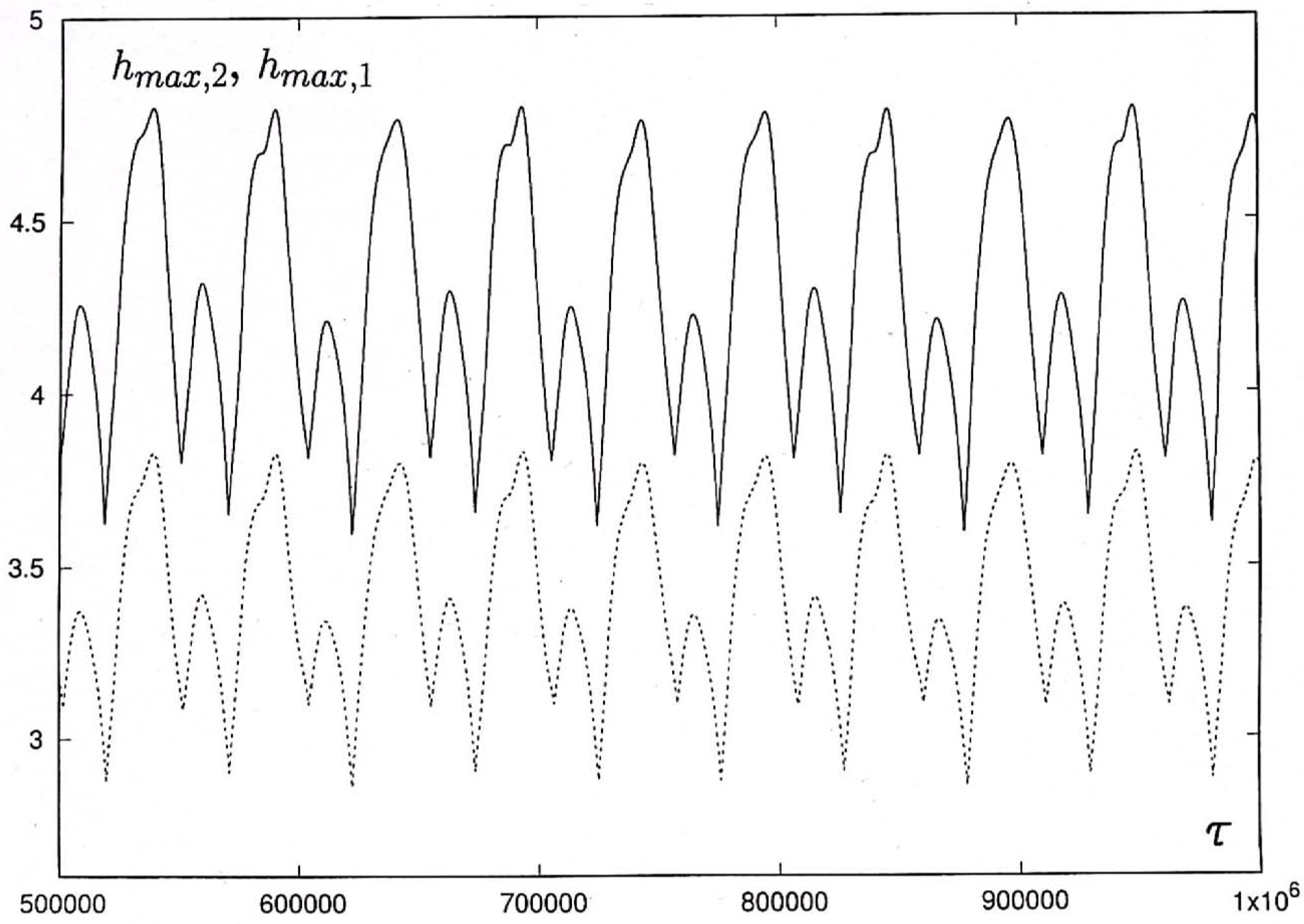
4. Droplet Oscillations
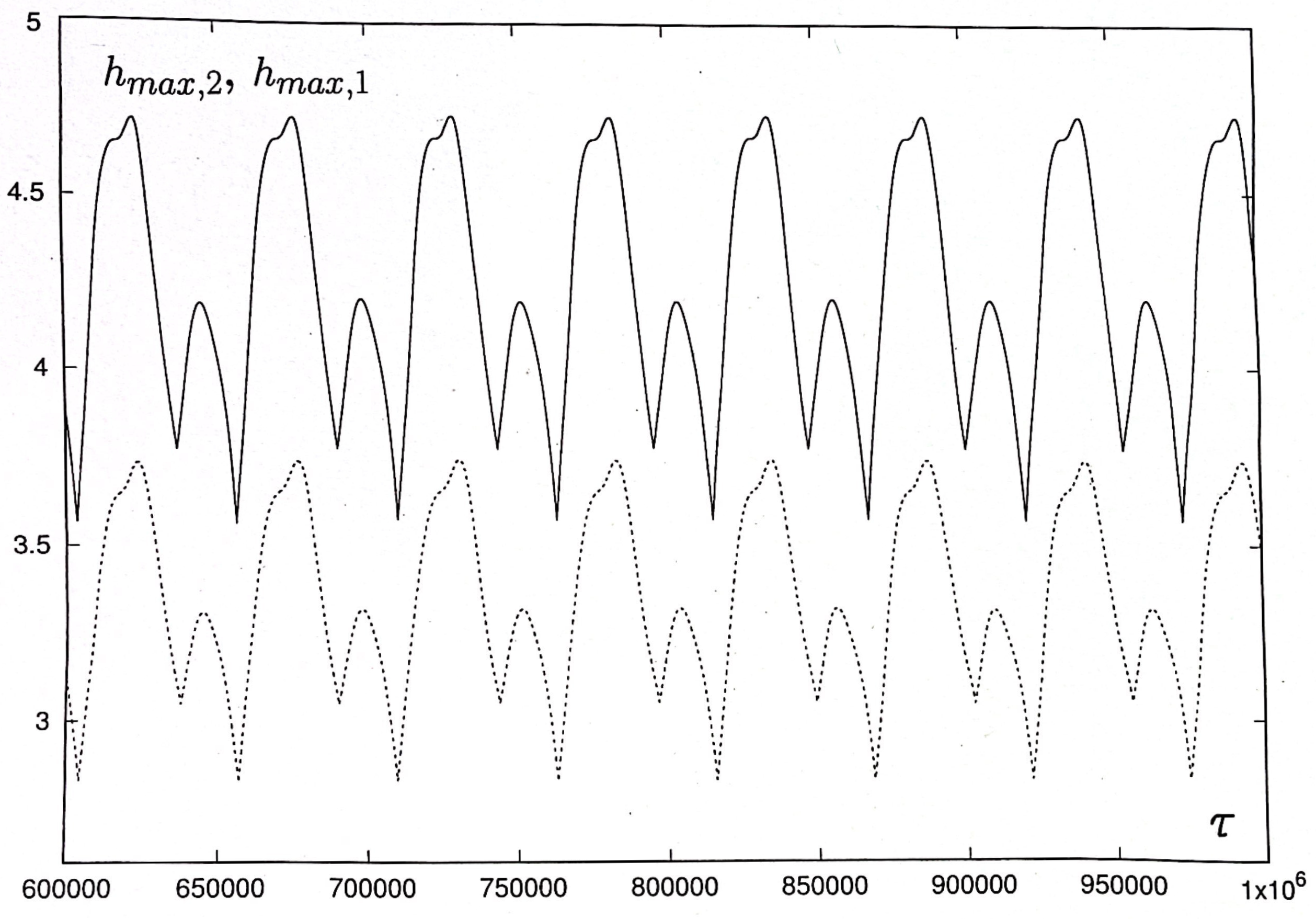
4.1. Suppression of Oscillations
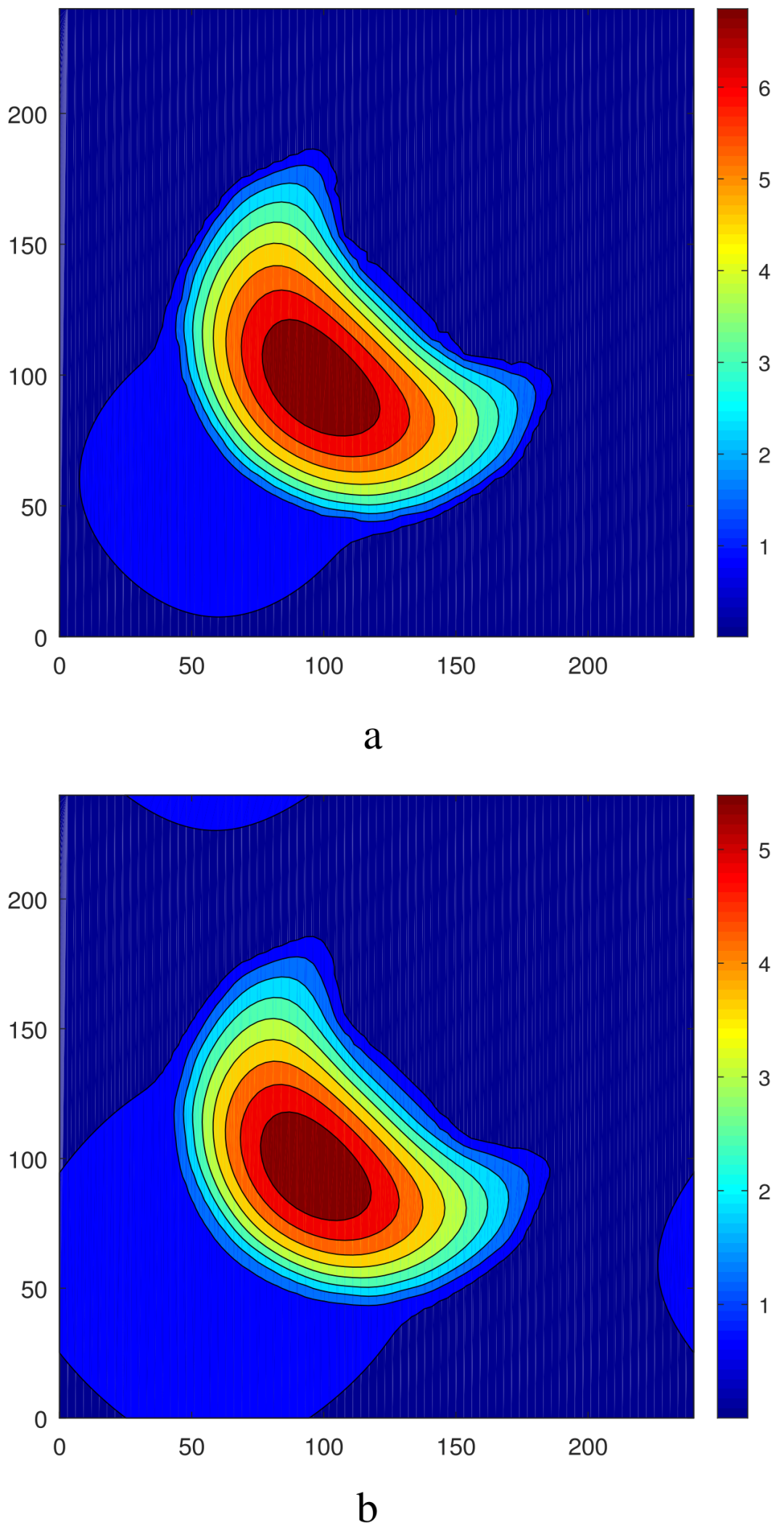
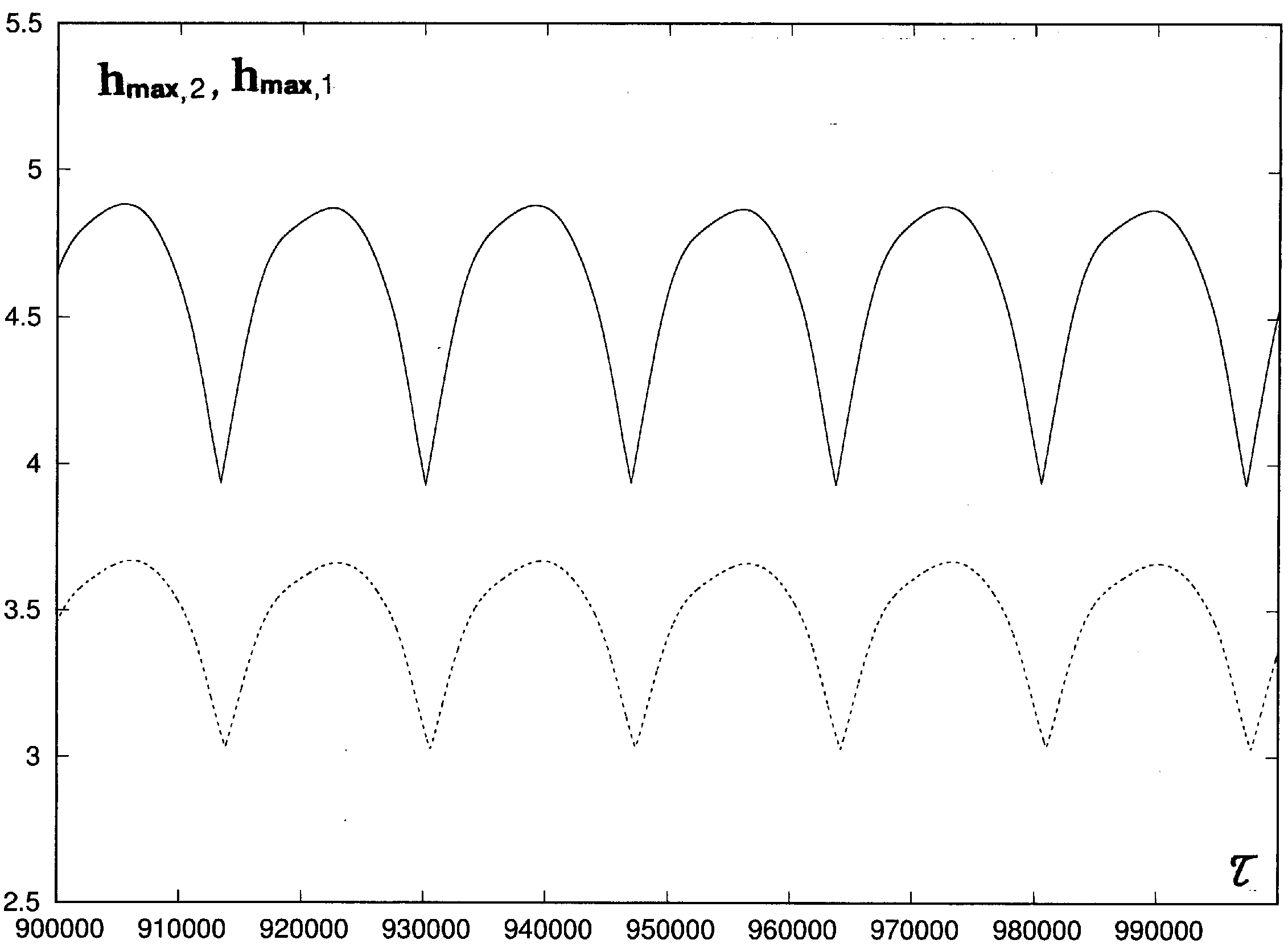
4.2. Excitation of Oscillations
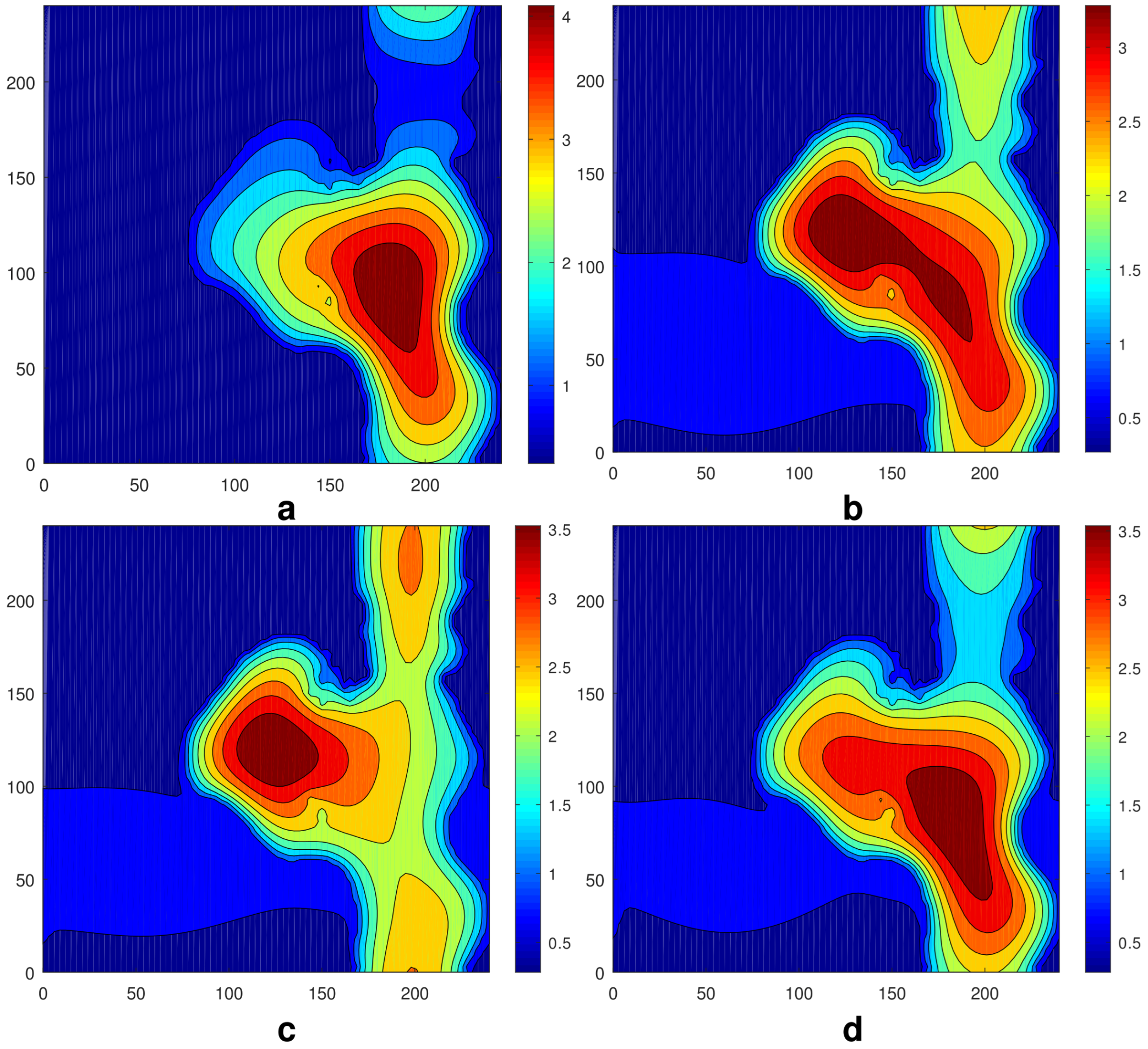
5. The Influence of Gravity on the Droplet Dynamics
6. The Influence of the Biot Number on the Shape of the Droplet
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- de Gennes, P.G. Wetting: Statics and dynamics. Rev. Mod. Phys. 1985, 57, 827. [Google Scholar] [CrossRef]
- de Gennes, P.G.; Brochard-Wyart, F.; Quérxex, D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Labanieh, L.; Nguyen, T.N.; Zhao, W.A.; Kang, D.K. Floating droplet array: An ultrahigh-throughput device for droplet trapping, real time analysis and recovery. Micromachines 2015, 60, 1469–1482. [Google Scholar] [CrossRef] [PubMed]
- Yamini, Y.; Rezazadeh, M.; Seidi, S. Liquid-phase microextraction—The different principles and configurations. TRAC—Trends Anal. Chem. 2019, 112, 264–272. [Google Scholar] [CrossRef]
- Ju, G.; Yang, X.; Li, L.; Cheng, M.; Shi, F. Removal of oil spills through a self-propelled smart device. Chem. Asian J. 2019, 14, 2435–2439. [Google Scholar] [CrossRef] [PubMed]
- Rybalko, S.; Magome, N.; Yoshikawa, K. Forward and backward laser-guided motion of an oil droplet. Phys. Rev. E 2004, 70, 046301. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Moon, J.K.; Lee, K.; Kim, K.; Pak, H.K. Breathing, crawling, budding, and splitting of a liquid droplet under laser heating. Soft Matter 2014, 10, 2679–2684. [Google Scholar] [CrossRef] [PubMed]
- Buffone, C. Formation, stability and hydrothermal waves in evaporating liquid lenses. Soft Matter 2019, 15, 1970–1978. [Google Scholar] [CrossRef]
- Nepomnyashchy, A.; Simanovskii, I. Droplets on the liquid substrate: Thermocapillary oscillatory instability. Phys. Rev. Fluids 2021, 6, 034001. [Google Scholar] [CrossRef]
- Nepomnyashchy, A.A.; Simanovskii, I.B. Marangoni instability in ultrathin two-layer films. Phys. Fluids 2007, 19, 122103. [Google Scholar] [CrossRef]
- Greco, E.F.; Grigoriev, R.O. Thermocapillary migration of interfacial droplets. Phys. Fluids 2009, 21, 042105. [Google Scholar] [CrossRef]
- Yakshi-Tafti, E.; Cho, H.J.; Kumar, R. Droplet actuation on a liquid layer due to thermocapillary motion: Shape effect. Appl. Phys. Lett. 2010, 96, 264101. [Google Scholar] [CrossRef]
- Keiser, L.; Bense, H.; Colinet, P.; Bico, J.; Reyssat, E. Marangoni bursting: Evaporation induced emulsification of binary mixtures on a liquid layer. Phys. Rev. Lett. 2017, 118, 074504. [Google Scholar] [CrossRef]
- Neumann, F. Vorlesungen über die Theorie der Capllarität; Teubner: Leipzig, Germany, 1894. [Google Scholar]
- Kriegsmann, J.J.; Miksis, M.J. Steady motion of a drop along a liquid interface. SIAM J. Appl. Math. 2003, 64, 18. [Google Scholar] [CrossRef]
- Craster, R.V.; Matar, O.K. On the dynamics of liquid lenses. J. Colloid Interface Sci. 2006, 303, 503–516. [Google Scholar] [CrossRef] [PubMed]
- Pototsky, A.; Bestehorn, M.; Merkt, D.; Thiele, U. Morphology changes in the evolution of liquid two-layer films. J. Chem. Phys. 2005, 122, 224711. [Google Scholar] [CrossRef] [PubMed]
- Nepomnyashchy, A.A.; Simanovskii, I.B. Effect of gravity on the dynamics of non-isothermic ultra-thin two-layer films. J. Fluid Mech. 2010, 661, 1–31. [Google Scholar] [CrossRef]
- Nepomnyashchy, A.; Simanovskii, I. Nonlinear Marangoni waves in a two-layer film in the presence of gravity. Phys. Fluids 2012, 24, 032101. [Google Scholar] [CrossRef]
- Oron, A.; Davis, S.H.; Bankoff, S.G. Long-scale evolution of thin liquid films. Rev. Mod. Phys. 1997, 69, 931. [Google Scholar] [CrossRef]
- Pototsky, A.; Oron, A.; Bestehorn, M. Vibration-induced flotation of a heavy liquid drop on a lighter liquid film. Phys. Fluids 2019, 31, 087101. [Google Scholar] [CrossRef]
- Sternling, C.V.; Scriven, L.E. On cellular convection driven by surface tension gradients: Effects of mean surface tension and surface viscosity. J. Fluid Mech. 1964, 19, 321–340. [Google Scholar]
- Géoris, P.; Hennenberg, M.; Lebon, G.; Legros, J.C. Investigation of thermocapillary convection in a three-liquid-layer systems. J. Fluid Mech. 1999, 389, 209–228. [Google Scholar] [CrossRef]
- Princen, H.M. Shape of Interfaces, Drops, and Bubbles. In Surface and Colloid Science; Matijevic, E., Ed.; Wiley: New York, NY, USA, 1969; Volume 2, p. 1. [Google Scholar]
- Nepomnyashchy, A.; Simanovskii, I. Marangoni instabilities of droplets on the liquid substrate under the action of a spatial temperature modulation. J. Fluid Mech. 2022, 936, A26. [Google Scholar] [CrossRef]
- Nepomnyashchy, A.; Simanovskii, I.; Legros, J.C. Interfacial Convection in Multilayer Systems, 2nd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Nepomnyashchy, A.; Simanovskii, I. The influence of two-dimensional temperature modulation on nonlinear Marangoni waves in two-layer films. J. Fluid Mech. 2018, 846, 944–965. [Google Scholar] [CrossRef]


















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nepomnyashchy, A.; Simanovskii, I. The Influence of Two-Dimensional Temperature Modulation on Floating Droplet Dynamics. Fluids 2024, 9, 6. https://doi.org/10.3390/fluids9010006
Nepomnyashchy A, Simanovskii I. The Influence of Two-Dimensional Temperature Modulation on Floating Droplet Dynamics. Fluids. 2024; 9(1):6. https://doi.org/10.3390/fluids9010006
Chicago/Turabian StyleNepomnyashchy, Alexander, and Ilya Simanovskii. 2024. "The Influence of Two-Dimensional Temperature Modulation on Floating Droplet Dynamics" Fluids 9, no. 1: 6. https://doi.org/10.3390/fluids9010006
APA StyleNepomnyashchy, A., & Simanovskii, I. (2024). The Influence of Two-Dimensional Temperature Modulation on Floating Droplet Dynamics. Fluids, 9(1), 6. https://doi.org/10.3390/fluids9010006





