From Navier to Stokes: Commemorating the Bicentenary of Navier’s Equation on the Lay of Fluid Motion
Abstract
1. Introduction
2. The Problem of the Motion of Fluids
3. Structure of the Matter: Continuum or Atomic?
4. Navier’s Equation
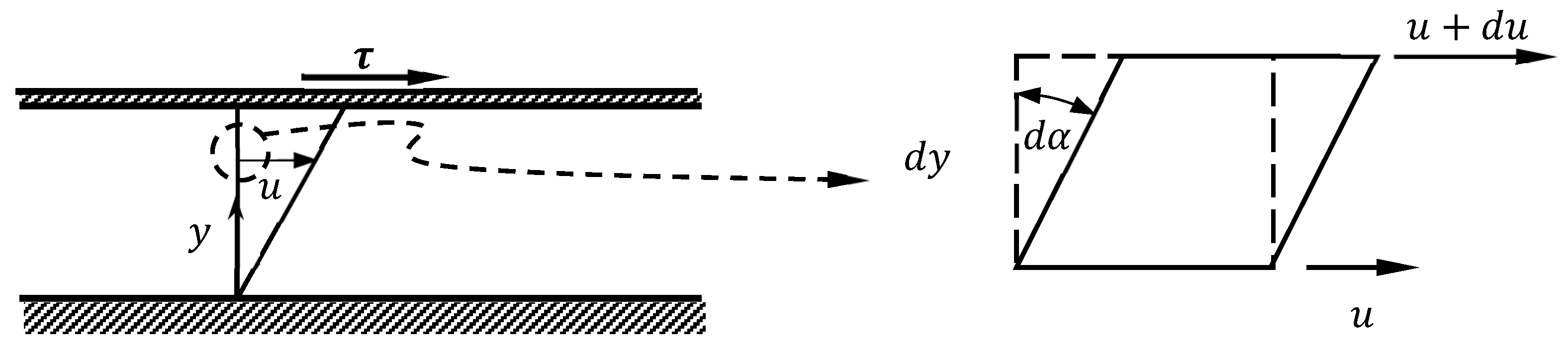
5. Viscosity
6. The Other Equations of Fluid Motion
6.1. Augustin-Louis Cauchy (1789–1857)
6.2. Siméon-Denis Poisson (1781–1840)
6.3. Adhémar Jean Claude Barré de Saint-Venant (1797–1886)
6.4. George Gabriel Stokes (1819–1903)
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McKeon, R.M. Navier, Claude-Louis-Marie-Henri. In Dictionary of Scientific Biography; Gillispie, C.C., Ed.; Charles Scribner’s Sons: New York, NY, USA, 1981; Volume 10, pp. 2–5. [Google Scholar]
- Darrigol, O. Between Hydrodynamics and Elasticity Theory: The First Five Births of the Navier-Stokes Equation. Arch. Hist. Exact Sci. 2002, 56, 95–150. [Google Scholar] [CrossRef]
- Castelli, B. Della Misura dell’Acque Correnti; Per Francesco Caualli: Roma, Italy, 1639. [Google Scholar]
- Newton, I. Philosophiæ Naturalis Principia Mathematica; Printer S. Pepys, Printing of the Royal Society: London, UK, 1687. [Google Scholar]
- Spencer, J.B.; Brush, S.G.; Osler, M.J. “Scientific Revolution”. Encyclopedia Britannica. Available online: https://www.britannica.com/science/Scientific-Revolution (accessed on 18 September 2022).
- Busard, H.L.L. François Viète. In Dictionary of Scientific Biography; Gillispie, C.C., Ed.; Charles Scribner’s Sons: New York, NY, USA, 1981; Volume 14, pp. 18–25. [Google Scholar]
- Mahoney, M.S. Descartes: Mathematics and Physics. In Dictionary of Scientific Biography; Gillispie, C.C., Ed.; Charles Scribner’s Sons: New York, NY, USA, 1981; Volume 10, pp. 55–61. [Google Scholar]
- Rouse, H.; Ince, S. History of Hydraulics; Dover Publications, Inc.: New York, NY, USA, 1963. [Google Scholar]
- Bernoulli, D. Hydrodynamica, Sive de Viribus et Motibus Fluidorum Commentarii; Printer: Johan Heinrich Deckeri: Basilea, Switzerland, 1738. [Google Scholar]
- D’Alembert, J.L.R. Traité de L’équilibre et du Mouvement des Fluides; Imprimerie de Jean-Baptiste Coignard: Paris, France, 1744. [Google Scholar]
- D’Alembert, J.L.R. Paradoxe proposé aux Géometres sur la Resistance des Fluides. In Opuscules Mathématiques; Tome V; Première Partie, Imprimerie de Chardon: Paris, France, 1768; pp. 132–138. [Google Scholar]
- Euler, L. Découverte d’un nouveau principe de mécanique. In Mémoires de l’Académie Royale des Sciences et des Belles-Lettres de Berlin; Tome VI; Chez Haude et Spenee: Berlin, Germany, 1752; pp. 185–217. [Google Scholar]
- Euler, L. Principes généraux de l’état de l’équilibre des fluids. In Mémoires de l’Académie Royale des Sciences et des Belles-Lettres de Berlin; Tome XI; Chez Haude et Spenee: Berlin, Germany, 1757; pp. 217–273. [Google Scholar]
- Euler, L. Principes généraux du mouvement des fluids. In Mémoires de l’Académie Royale des Sciences et des Belles-Lettres de Berlin; Tome XI; Chez Haude et Spenee: Berlin, Germany, 1757; pp. 274–315. [Google Scholar]
- Euler, L. Continuation des Recherches sur la théorie du mouvement des fluids. In Mémoires de l’Académie Royale des Sciences et des Belles-Lettres de Berlin; Tome XI; Chez Haude et Spenee: Berlin, Germany, 1757; pp. 316–361. [Google Scholar]
- Lagrange, J.-L. Mémoire sur la théorie du mouvement des fluids. In Nouveaux Mémoires de l’Académie Royale des Sciences et des Belles-Lettres de Berlin; 1781. Also, In Oeuvres de Lagrange, Tome IV; Imprimeur Gauthier-Villars: Paris, France; pp. 695–748.
- Poisson, S.D. Mémoire sur l’équilibre et le mouvement des corps élastiques. In Mémoires de l’Académie des Sciences de l’Institut de France; Tome VIII; Read in the Meeting of l’Académie de Paris on 14 April 1828; Bachelier, Imprimeur-Libraire: Paris, France, 1829; pp. 357–570. [Google Scholar]
- Boussinesq, J. Leçons Synthétiques de Mécanique Générale Servant d’Introduction au Cours de Mécanique Physique; Gauthier-Villars et Fils, Imprimeurs-Libraires: Paris, France, 1889. [Google Scholar]
- Lucrecio. Naturaleza de las Cosas, Prose version in Spanish of “De rerum natura”, translated by Manuel Rodríguez-Navas; Printed by Agustín Avrial; Imprenta de la Compañía de Impresores y Libreros: Madrid, Spain, 1892. [Google Scholar]
- Whyte, L.L. Essay on Atomism: From Democritus to 1960; Wesleyan University Press: Middletown, CT, USA, 1961. [Google Scholar]
- Newton, I. Sir Isaac Newton’s Mathematical Principles of Natural Philosophy and His System of the World; Translated into English by Andrew Motte in 1729. The translations revised, and supplied with an historical and explanatory appendix, by Florian Cajori. Volume One: The Motion of Bodies. Eighth Printing; University of California Press: Berkeley, CA, USA, 1974. [Google Scholar]
- Boscovich, R.J. De Vitribus Vivis Dissertatio; Impresor Komarek: Roma, Italy, 1745. [Google Scholar]
- Boscovich, R.J. Philosophiæ Naturalis Theoria; Prostat Viennæ Austriæ, in Officina Libraria Kaliwodiana: Viena, Austria, 1758. [Google Scholar]
- Laplace, P.S. Exposition du Système du Monde; Imprimerie du Cercle-Social: Paris, France, 1796; 2 volumes. [Google Scholar]
- Laplace, P.S. Exposition du Système du Monde, 2nd ed.; Imprimerie de Crapelet: Paris, France, 1798. [Google Scholar]
- Laplace, P.S. Exposition du Système du Monde, 3rd ed.; Chez Courcier: Paris, France, 1808. [Google Scholar]
- Laplace, P.S. Sur l’Action Capillaire. In Supplément au Dixième Livre du Traité de Mécanique Céleste; Tome Quatrième; Chez Courcier: Paris, France, 1805; pp. 1–50. [Google Scholar]
- Navier, C.L. Sur les Lois des mouvemens des fluides, en ayant egard à l’adhesion des molecules. Ann. Chim. Phys. 1821, 19, 244–260, Errata in p. 448. [Google Scholar]
- Navier, C.L. Sur les Lois du Mouvement des Fluides. Mémoires L’Académie des Sci. L’institut Fr. 1823, 6, 389–416, Read in the Académie Royale des Sciences on 18 March 1822. [Google Scholar]
- Girard, M. Mémoire sur le mouvement des fluides dans les tubes capillaires, et l’influence de la température sur ce movement. In Mémoires des Sciences Mathématiques et Physiques de l’Institut de France; Années 1813, 1814, 1815; Chez Firmin Didot: Paris, France, 1818; pp. 249–380, Read in l’Académie, on 30 April 30 and 6 Mai 1816. [Google Scholar]
- White, F.M. Mecánica de Fluidos; Fifth edition in Spanish; Mc Graw Hill: Madrid, Spain, 2004. [Google Scholar]
- Massey, B. Mechanics of Fluids, 8th ed.; Taylor & Francis: New York, NY, USA, 2006. [Google Scholar]
- Munson, B.R.; Young, D.F.; Okiishi, T.H.; Huebsch, W.W. Fundamentals of Fluid Mechanics, 6th ed.; John Wiley & Sons, Inc.: Jefferson City, MO, USA, 2009. [Google Scholar]
- Granger, R.A. Fluid Mechanics; Dover Publications, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Streeter, V.L.; Wylie, E.B.; Bedford, K.W. Mecánica de Fluidos; Ninth edition in Spanish Edición; Mc Graw Hill: Santafé de Bogotá, Colombia, 1999. [Google Scholar]
- Shames, I.H. Mecánica de Fluidos; Third edition in Spanish; Mc Graw Hill: Santafé de Bogotá, Colombia, 2001. [Google Scholar]
- de las Casas, C. Vocabvlario de las Dos Lengvas Toscana y Castellana; Printed in Casa de Alonso: Sevilla, Spain, 1576. [Google Scholar]
- Real Academia Española. Diccionario de la Lengua Castellana; Tomo Sexto que contiene las letras S, T, U, V, X, Y, Z; Imprenta de la Real Academia Española: Madrid, España, 1739. [Google Scholar]
- Wiedemann, G. Ueber die Bewegung der Flüssigkeiten im Kreise der geschlossenen galvanischen Säule und ihre Beziehungen zur Elektrolys. Ann. Phys. Chem. 1856, 175, 177–233. [Google Scholar] [CrossRef]
- Cauchy, A. Recherches sur l’équilibre et le mouvement intérieur des corps solides ou fluides, élastiques on non élastiques. Bull. des Sci. par la Société Philomatique de Paris 1823, 9–13, Imprimerie de Plassan: Paris, France. [Google Scholar]
- Poisson, S.D. Mémoire sur les équations générales de l’équilibre et du mouvement des corps solides élastiques et des fluids. J. L’École Polytech. 1831, Tome XIII, 1–174, Read in the meeting of l’Académie des Sciences de Paris on 12 October 1829. [Google Scholar]
- Saint-Venant, A. Note à joindre au Mémoire sur la dynamique des fluides. Compte Rendu Séances L’académie Sci. 1843, 17, 1240–1244, Presented on 14 April 1834. [Google Scholar]
- Stokes, G.G. On the Theories of the Internal Friction of Fluids in Motion, and of the Equilibrium and Motion of Elastic Solids. Trans. Camb. Philos. Soc. 1845, 8, 287–317. [Google Scholar]
- Hager, W.H.; Hutter, K.; Castro-Orgaz, O. Correspondence between de Saint-Venant and Boussinesq 5: Viscosity and hydraulic resistance. Comptes Rendus. Mécanique 2021, 349, 145–166. [Google Scholar] [CrossRef]
- Reynolds, O. On the Theory of Lubrication and its Application to Mr. Beauchamp Tower’s Experiments, including an Experimental Determination of the Viscosity of Olive Oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Saint-Venant, A. Théorie du mouvenment non permanenl des eaux, avec application aux crues des rivières et à l’introduction des marées dans leur lit. Compte Rendu Séances L’académie Sci. 1871, 63, 147–154, (deduction of equations) and; pp. 237–249 (application). [Google Scholar]
- MacTutor. Adhémar Jean Claude Barré de Saint-Venant. MacTutor History of Mathematics. Available online: https://mathshistory.st-andrews.ac.uk/Biographies/Saint-Venant/ (accessed on 3 October 2023).
- Saint-Venant, A. L’Institut. J. Général Sociétés Trav. Sci. Fr. L’Etranger. 1834, 49, 126. [Google Scholar]
- Saint-Venant, A. Mémoire sur le Calcul des efféts des machines à vapeur; contenant des équations générales de l’écoulement permanent ou périodique des fluides, en tenant compte de leurs dilatations et de leurs changements de température et sans supposer qu’ils se meuvent par tranches parallèles, ni par filets indépendants. Compte Rendu Séances L’Académie Sci. 1838, 6, 45–47. [Google Scholar]
- Boussinesq, J. Essai sur la Théorie des Eaux Courantes. Mémoires Présentés par Divers. Savants a L’Académie des Sci. 1877, 23, 1–680. [Google Scholar]
- Saint-Venant, A. Formules et Tables Nouvelles pour la Solution des Problems Relatifs aux eaux Courantes; Imprimé par E. Thunot et Cie: Paris, France, 1851; Also, in Annales des Mines; Quatrième Série 1851, 20, 183–357. [Google Scholar]
- Saint-Venant, A. Note sur la détermination expérimentale des forces retardatrices du movement des liquids. Comptes Rendus Hebd. Séances L’Académie Sci. 1846, 22, 306–309. [Google Scholar]
- Stokes, G.G. Mathematical and Physical Papers by George Gabriel Stokes; The University Press: Cambridge, UK, 1880; Volume 1. [Google Scholar]
- Stokes, G.G. On the Steady Motion of Incompressible Fluids. Trans. Camb. Philos. Soc. 1842, 7, 439–453. [Google Scholar]
- Stokes, G.G. Report on Recent Researches in Hydrodynamics. In Proceedings of the Sixteenth Meeting of the British Association for the Advancement of Science, Southampton, UK, 10–15 September 1846; Richard and John E. Taylor, Printers. Oxford University Press: London, UK, 1847; pp. 1–20. [Google Scholar]
- Stokes, G.G. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Trans. Camb. Philos. Soc. 1850, 9, 8–106. [Google Scholar]
- Rothstein, J.P. Slip on Superhydrophobic Surfaces. Annu. Rev. Fluid Mech. 2010, 42, 89–109. [Google Scholar] [CrossRef]
- Helmholtz, H.; von Piotrowski, G. Über Reibung tropfbarer Flüssigkeiten. Sitzungsberichte Kais. Akad. Wiss. 1860, 40, 607–658. [Google Scholar]
- Vinogradova, O.I. Slippage of water over hydrophobic surfaces. Int. J. Miner. Process. 1999, 56, 31–60. [Google Scholar] [CrossRef]
- Ronceray, M.P. Recherches sur l’écoulement dans les tubes capillaires. Ann. Chim. Phys. 1911, 22, 107–125. [Google Scholar]
- Schnell, E. Slippage of water over nonwettable surfaces. J. Appl. Phys. 1956, 27, 1149–1152. [Google Scholar] [CrossRef]
- Churaev, N.V.; Sobolev, V.D.; Somov, A.N. Slippage of liquids over lyophobic solid surfaces. J. Colloid Interface Sci. 1984, 97, 574–581. [Google Scholar] [CrossRef]
- Lauga, E.; Brenner, M.P.; Stone, H.A. Microfluidics: The non-slip boundary condition. In Springer Handbook of Experimental Fluid Mechanics; Tropea, C., Yarin, A.L., Foss, J.F., Eds.; Springer: Berlin, Germany, 2007; pp. 1210–1240. [Google Scholar]
- Cheng, J.-T.; Giordano, N. Fluid flow through nanometer-scale channels. Phys. Rev. E 2002, 65, 031206-1–031206-5. [Google Scholar] [CrossRef]








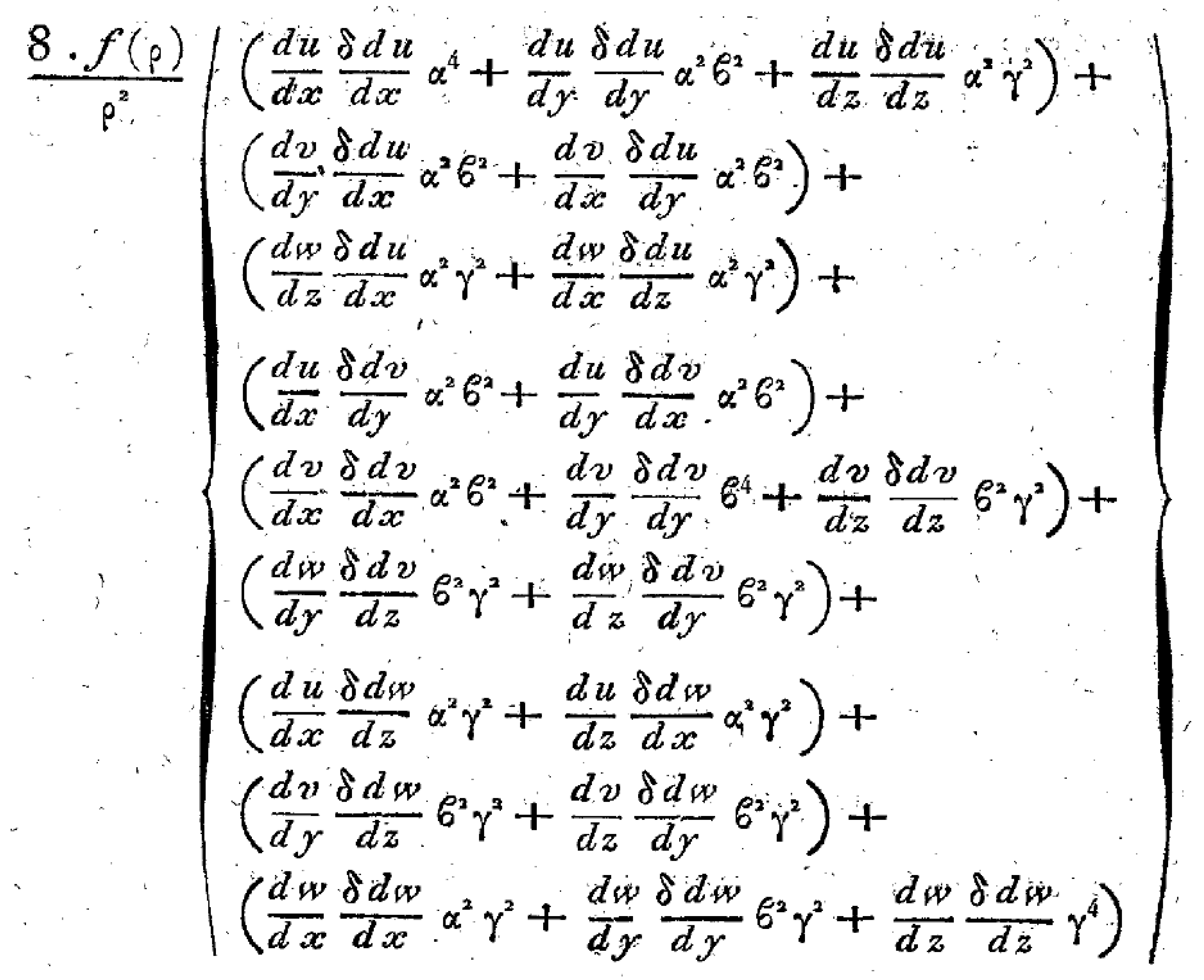
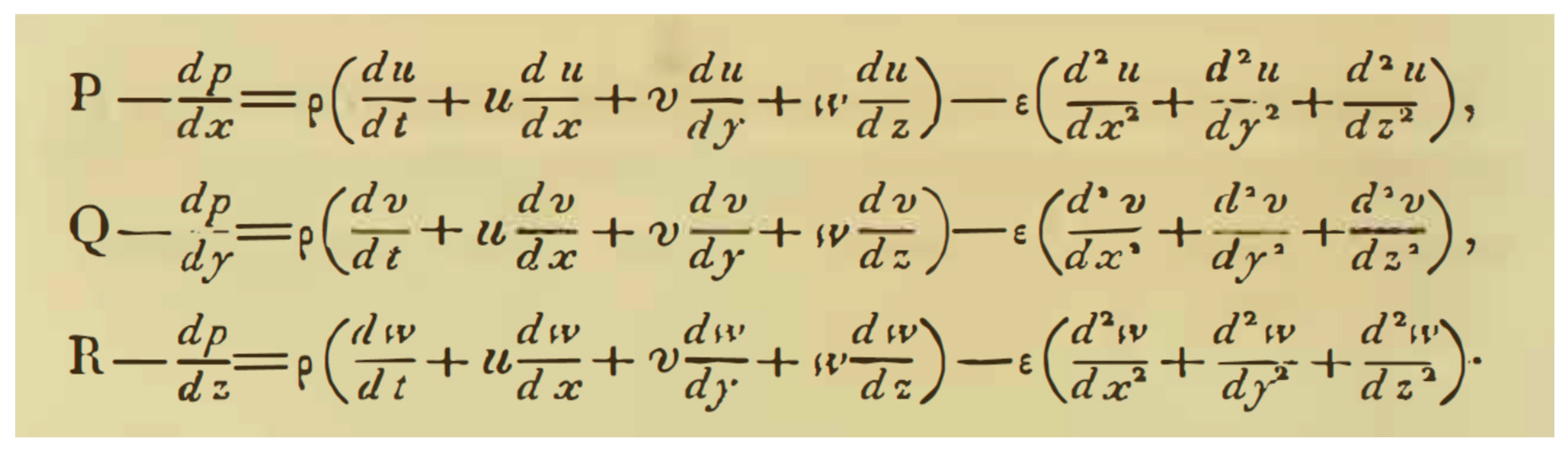






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamburrino, A. From Navier to Stokes: Commemorating the Bicentenary of Navier’s Equation on the Lay of Fluid Motion. Fluids 2024, 9, 15. https://doi.org/10.3390/fluids9010015
Tamburrino A. From Navier to Stokes: Commemorating the Bicentenary of Navier’s Equation on the Lay of Fluid Motion. Fluids. 2024; 9(1):15. https://doi.org/10.3390/fluids9010015
Chicago/Turabian StyleTamburrino, Aldo. 2024. "From Navier to Stokes: Commemorating the Bicentenary of Navier’s Equation on the Lay of Fluid Motion" Fluids 9, no. 1: 15. https://doi.org/10.3390/fluids9010015
APA StyleTamburrino, A. (2024). From Navier to Stokes: Commemorating the Bicentenary of Navier’s Equation on the Lay of Fluid Motion. Fluids, 9(1), 15. https://doi.org/10.3390/fluids9010015







