Bulk Cavitation in Model Gasoline Injectors and Their Correlation with the Instantaneous Liquid Flow Field
Abstract
1. Introduction
2. Experimental Methods and Analysis
2.1. Injector Models, Experimental Setup, and Measurement Conditions
2.2. Proper Orthogonal Decomposition (POD)
3. Results
3.1. Visualization of ‘Bulk’ Cavitation
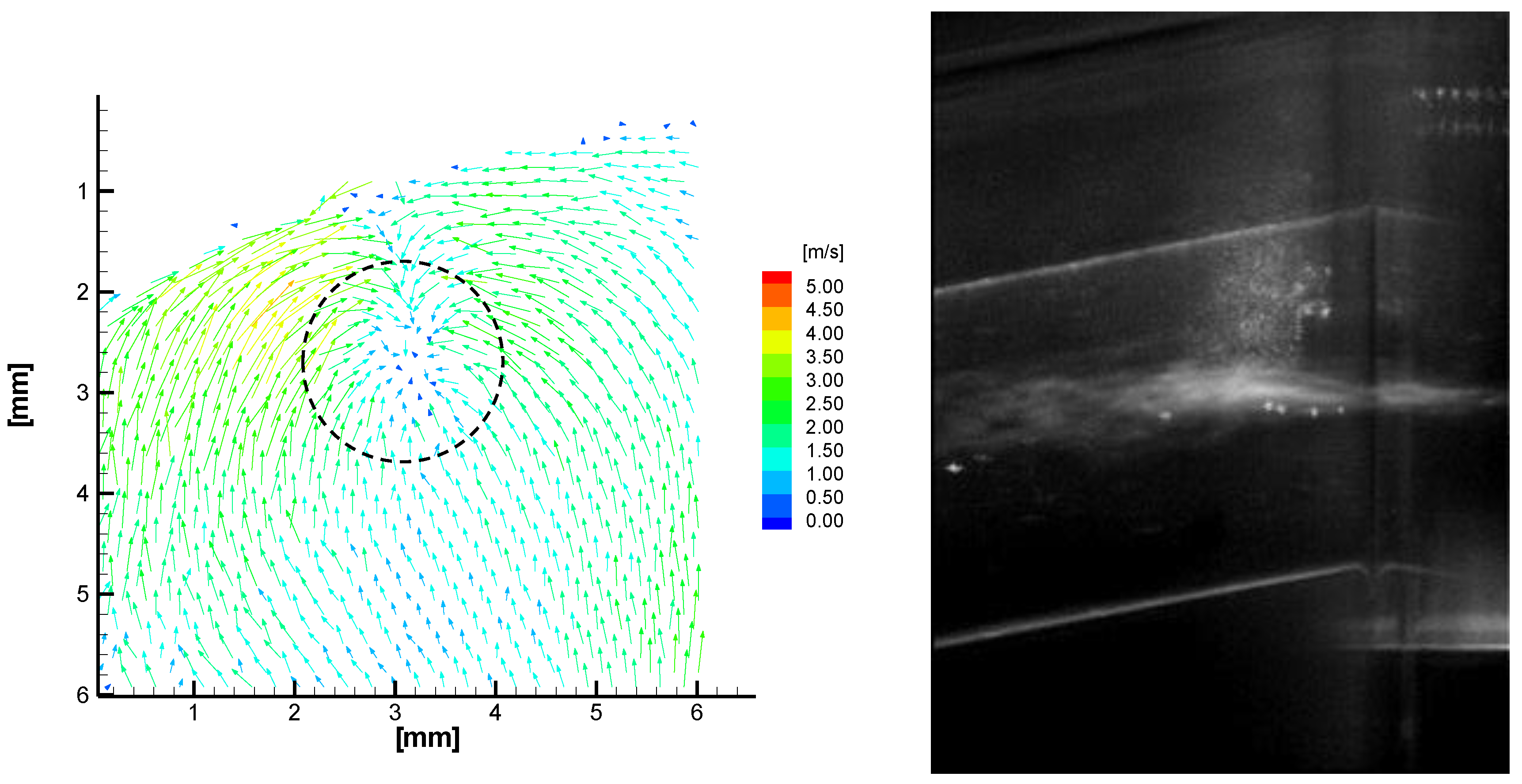
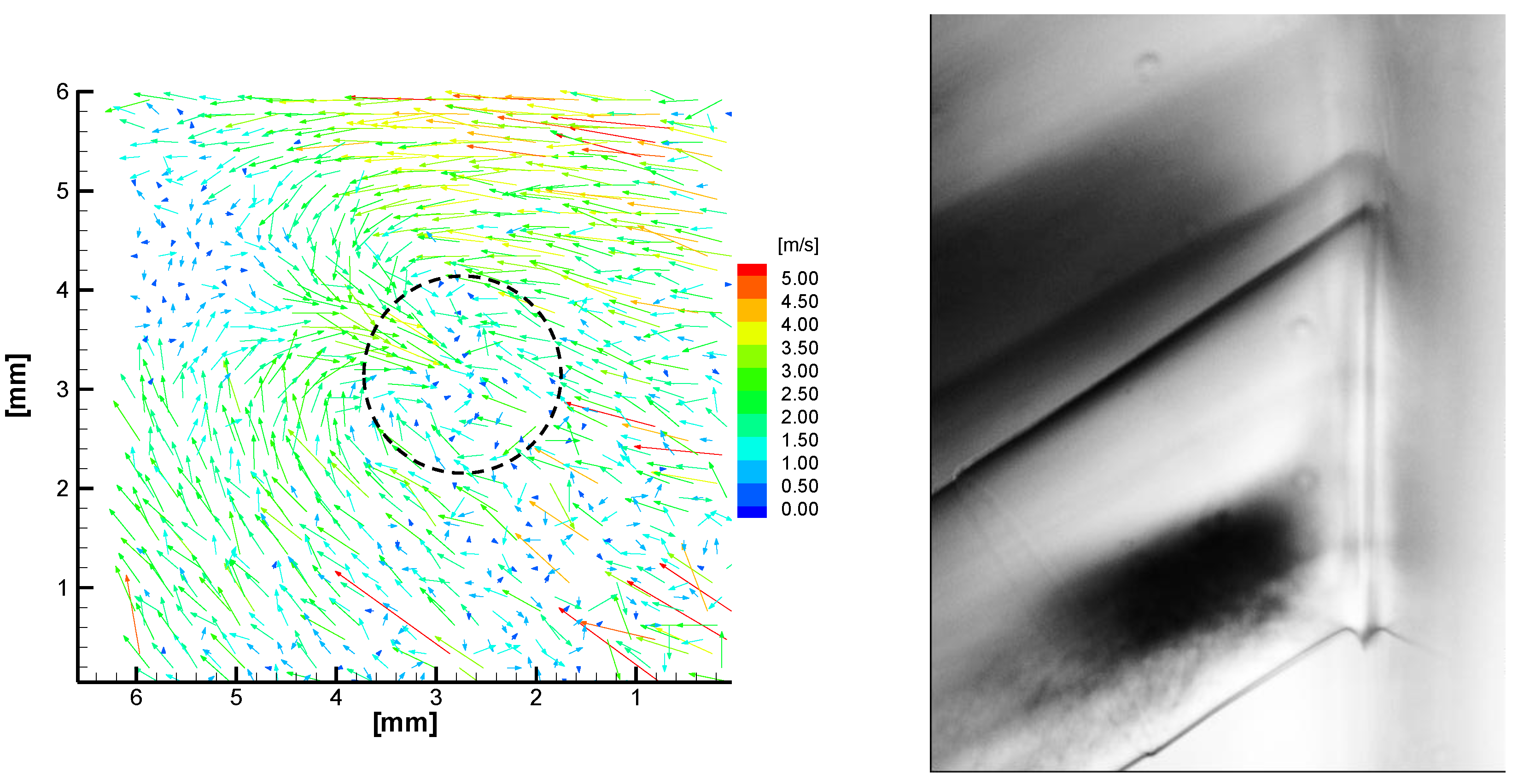
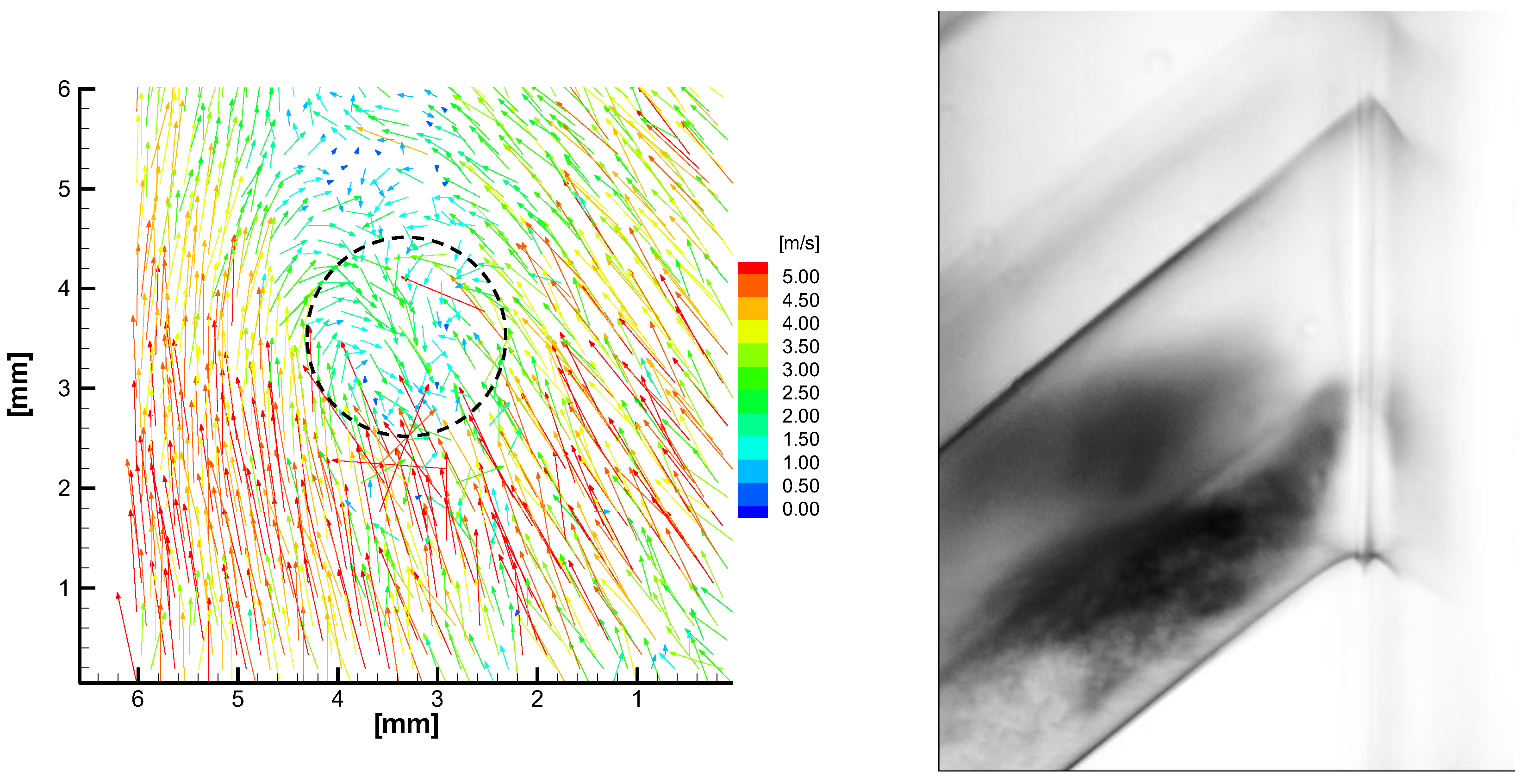
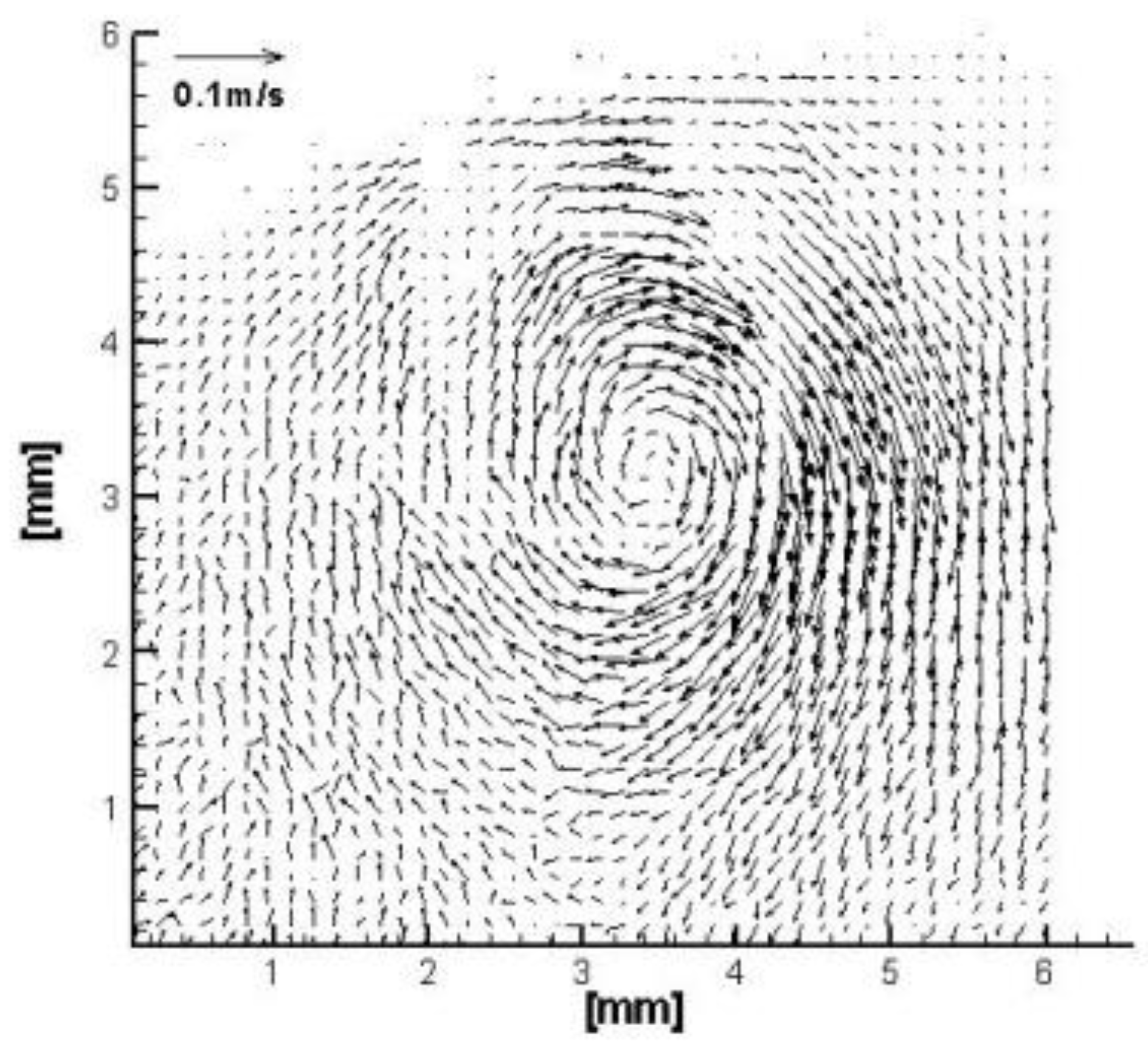
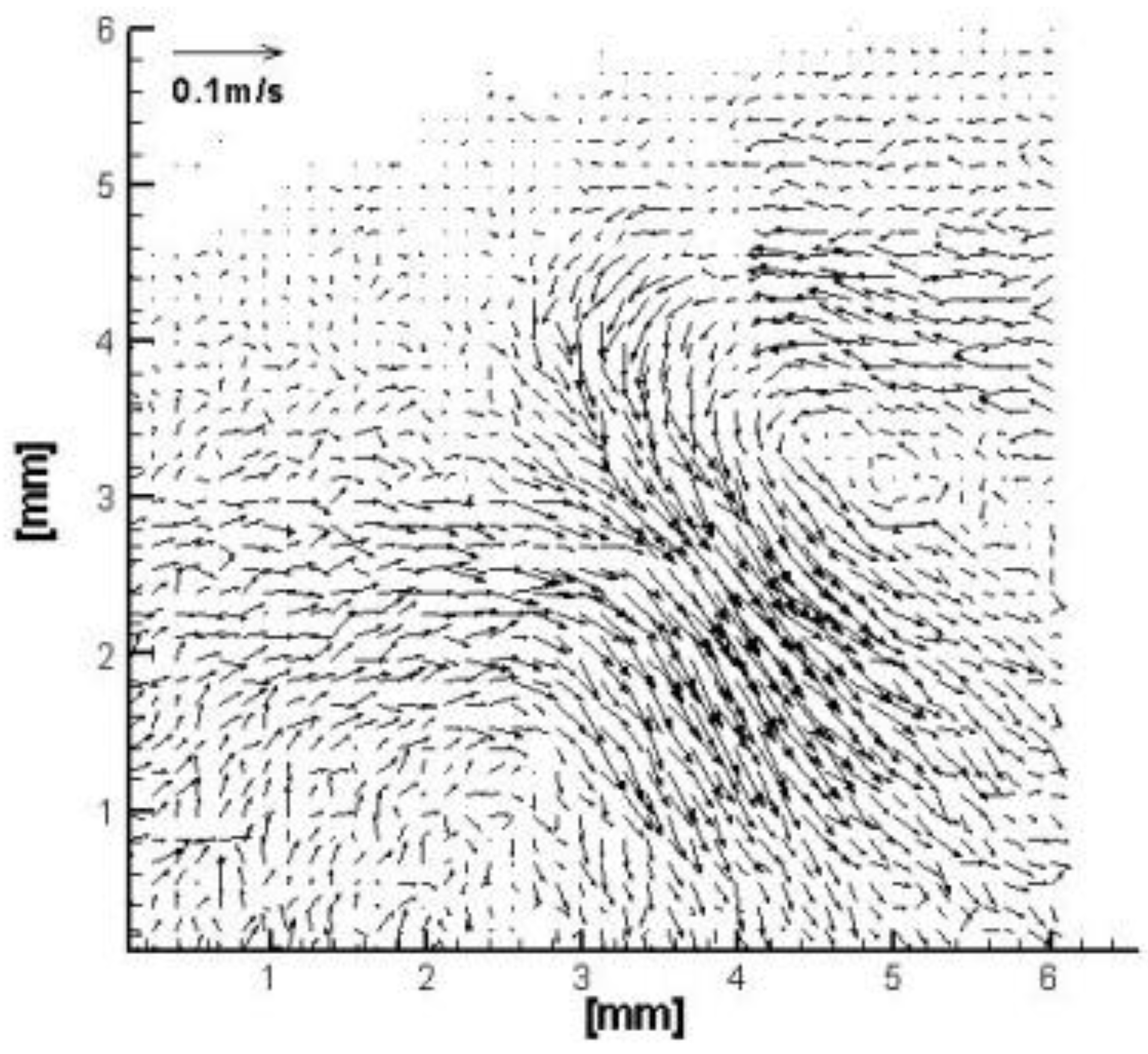
3.2. Mean Flow Field and Cavitation Visualization
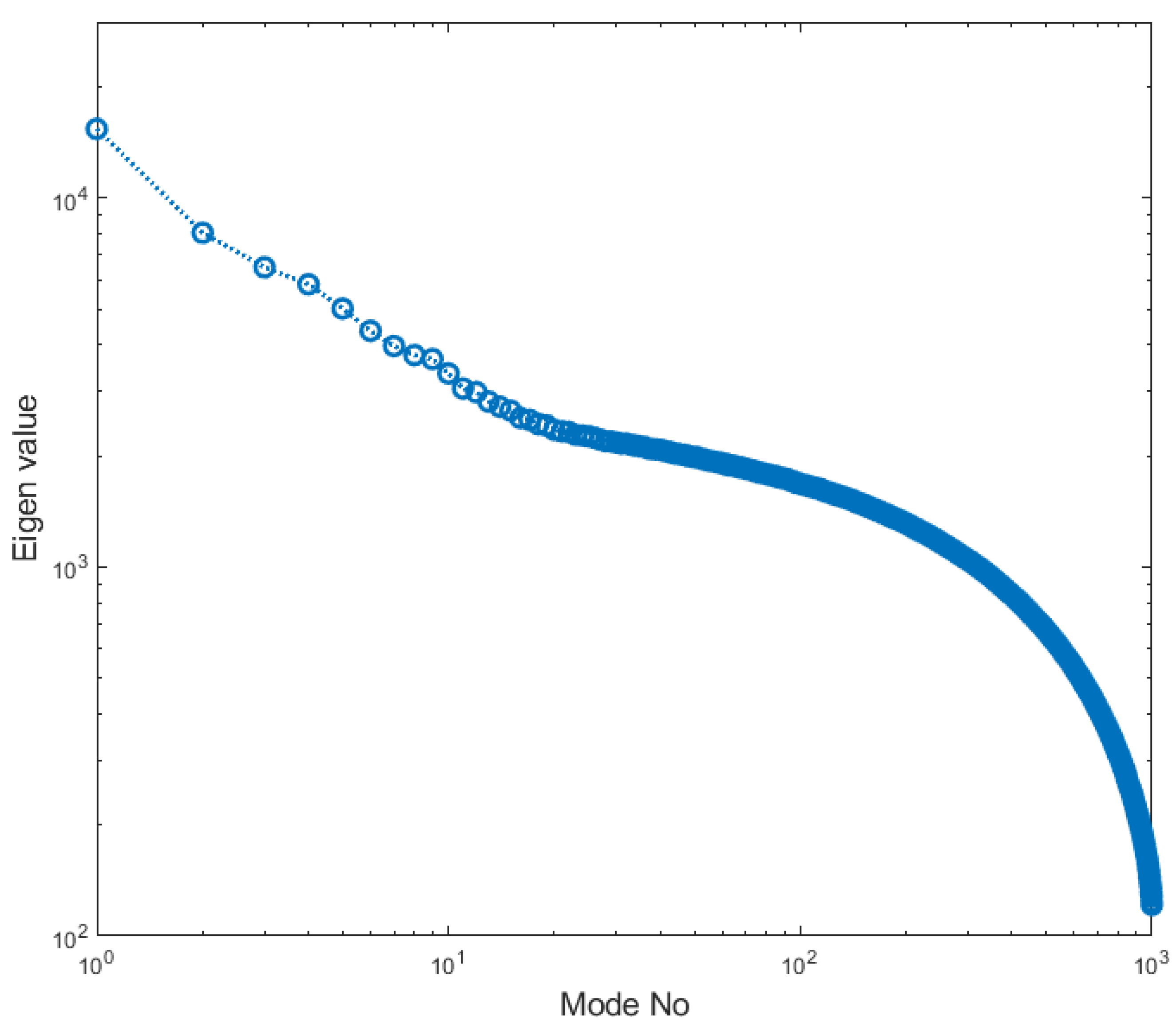
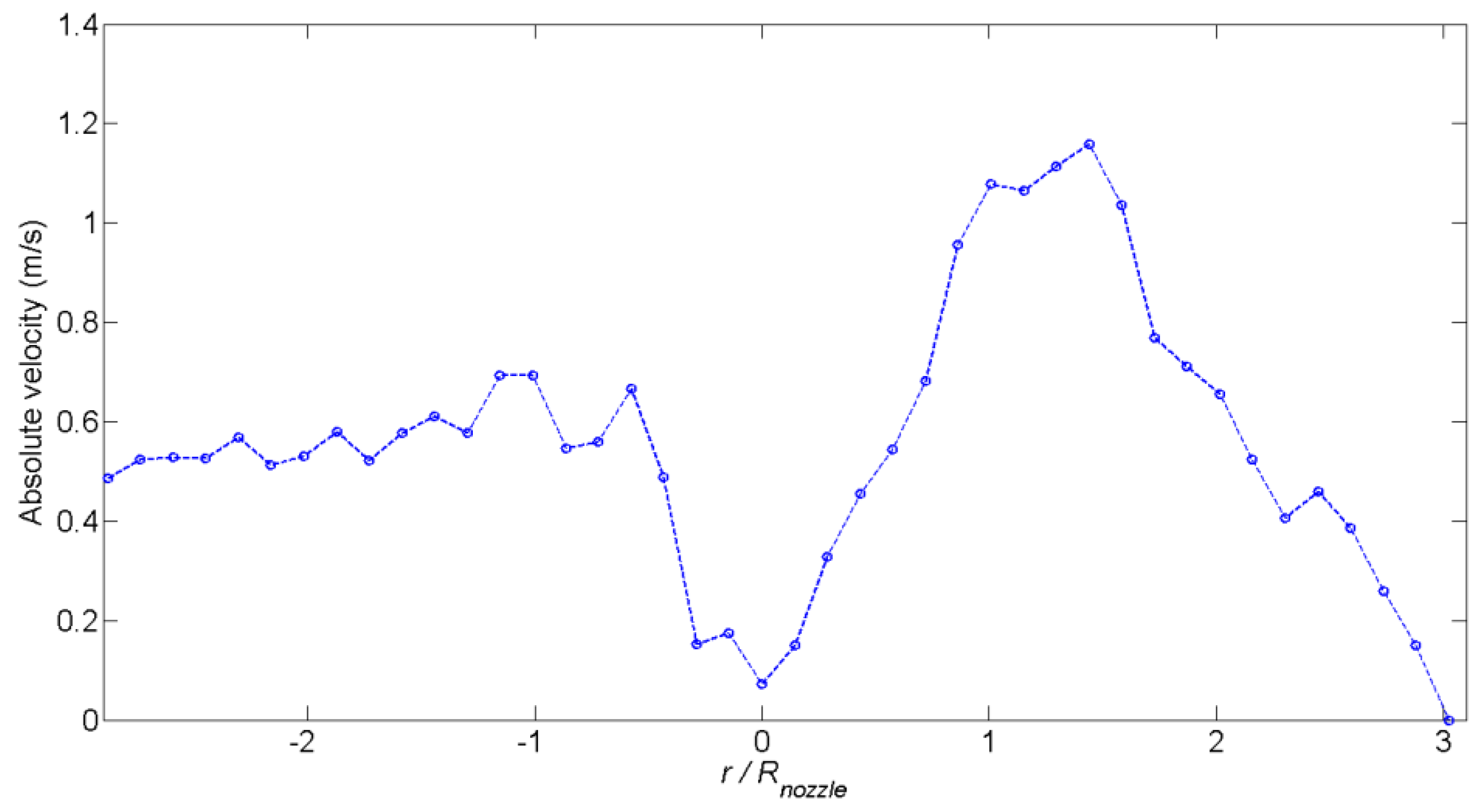
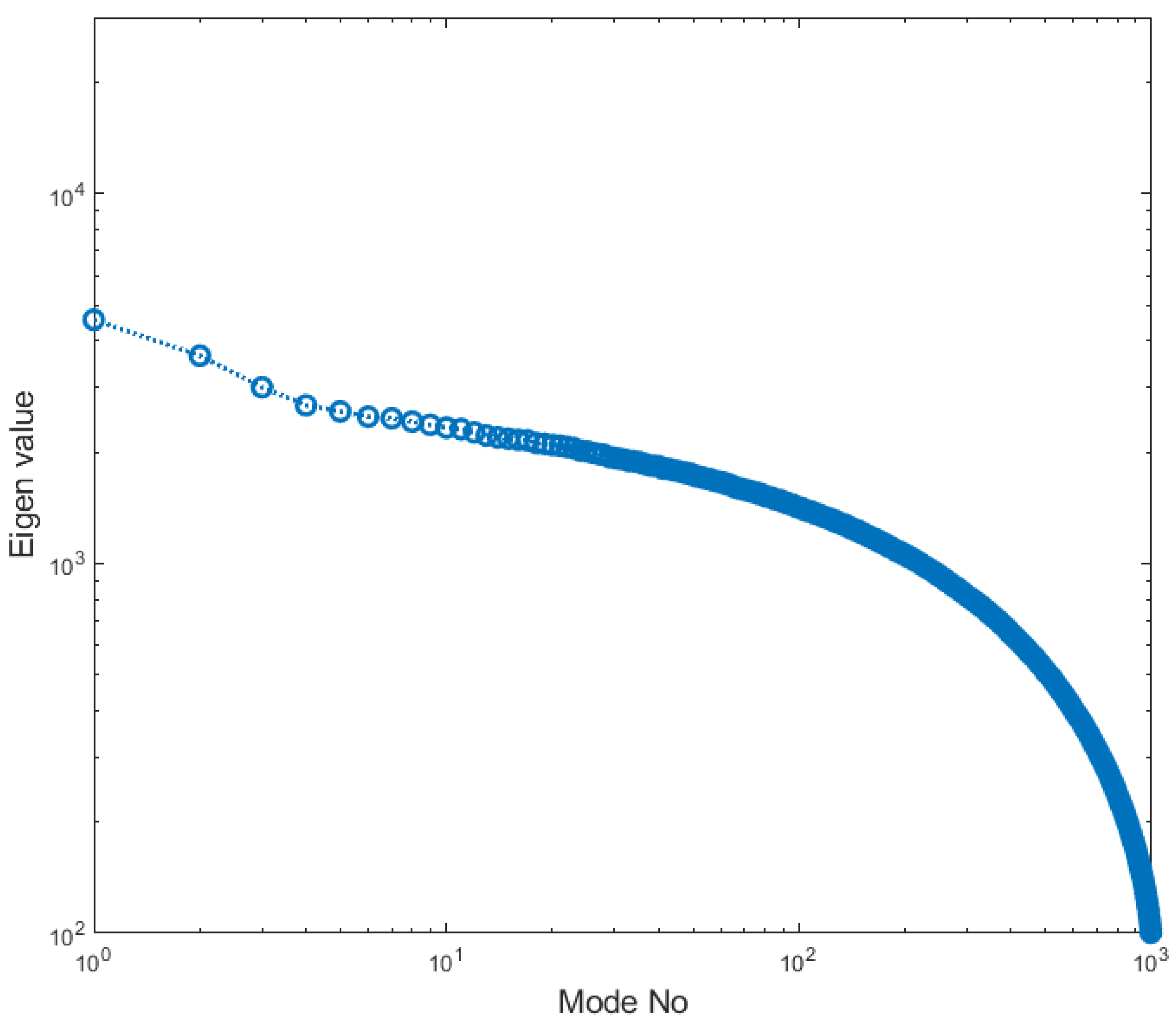
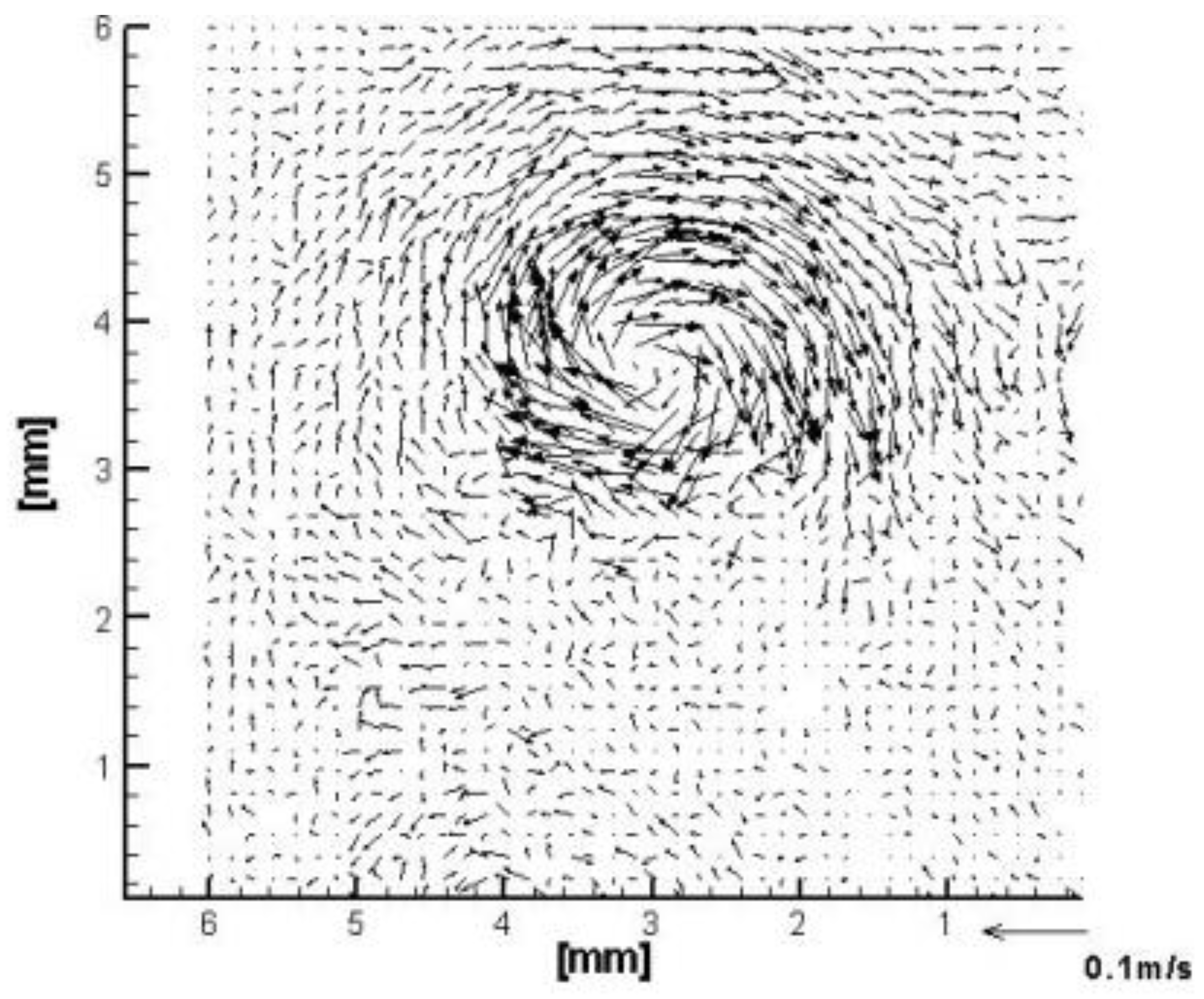
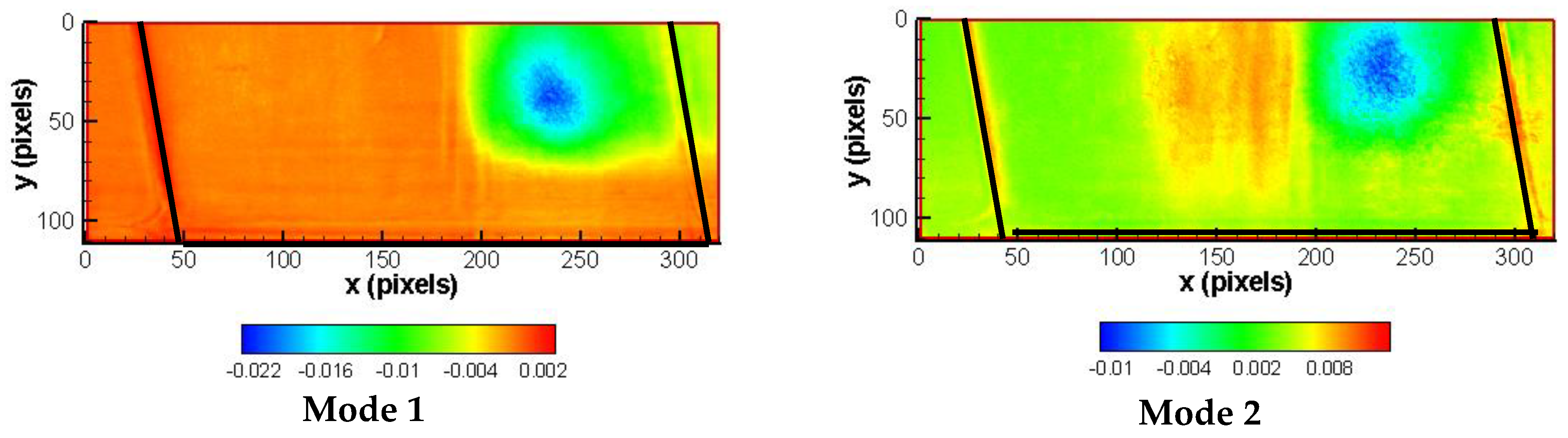
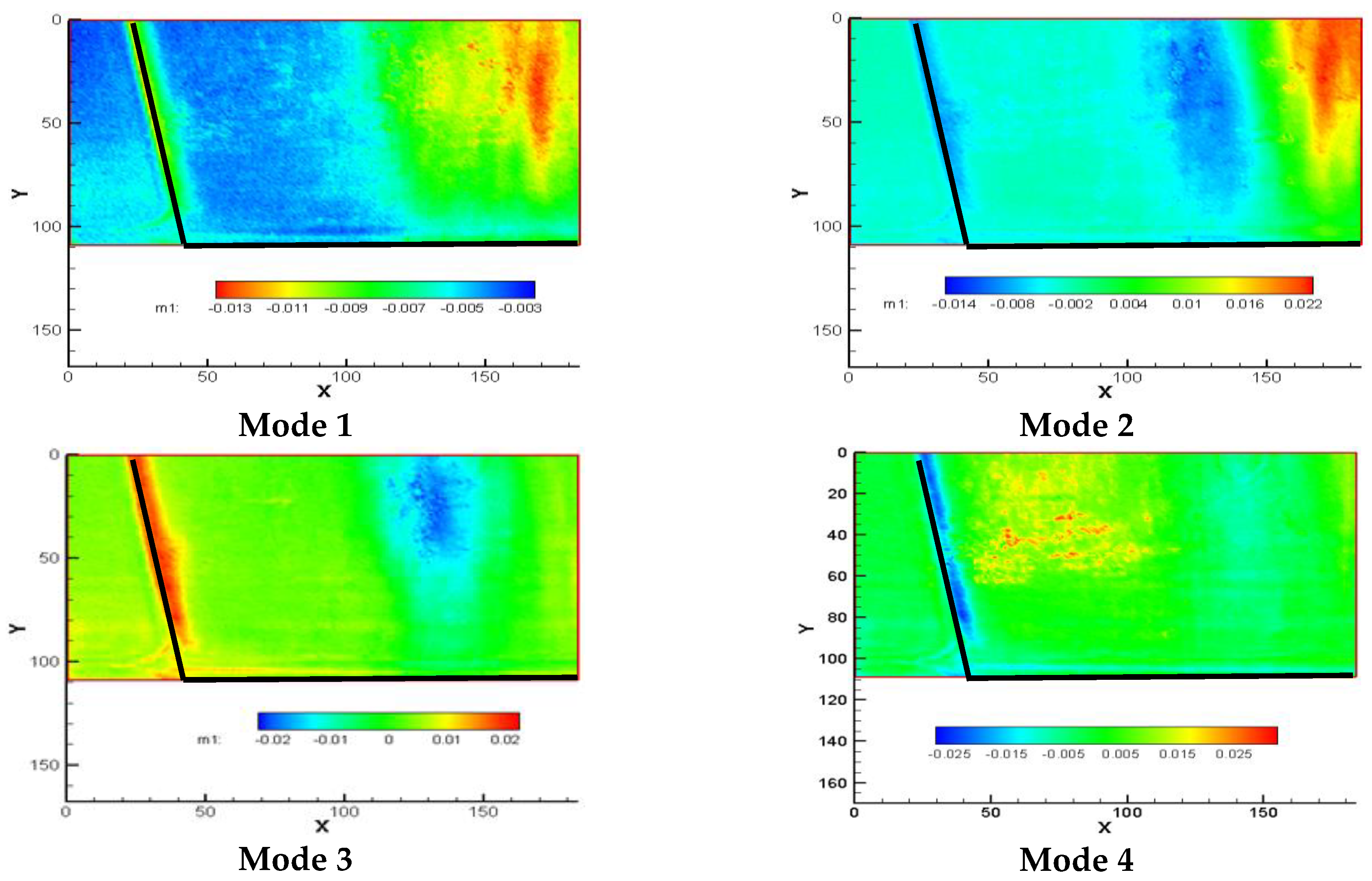
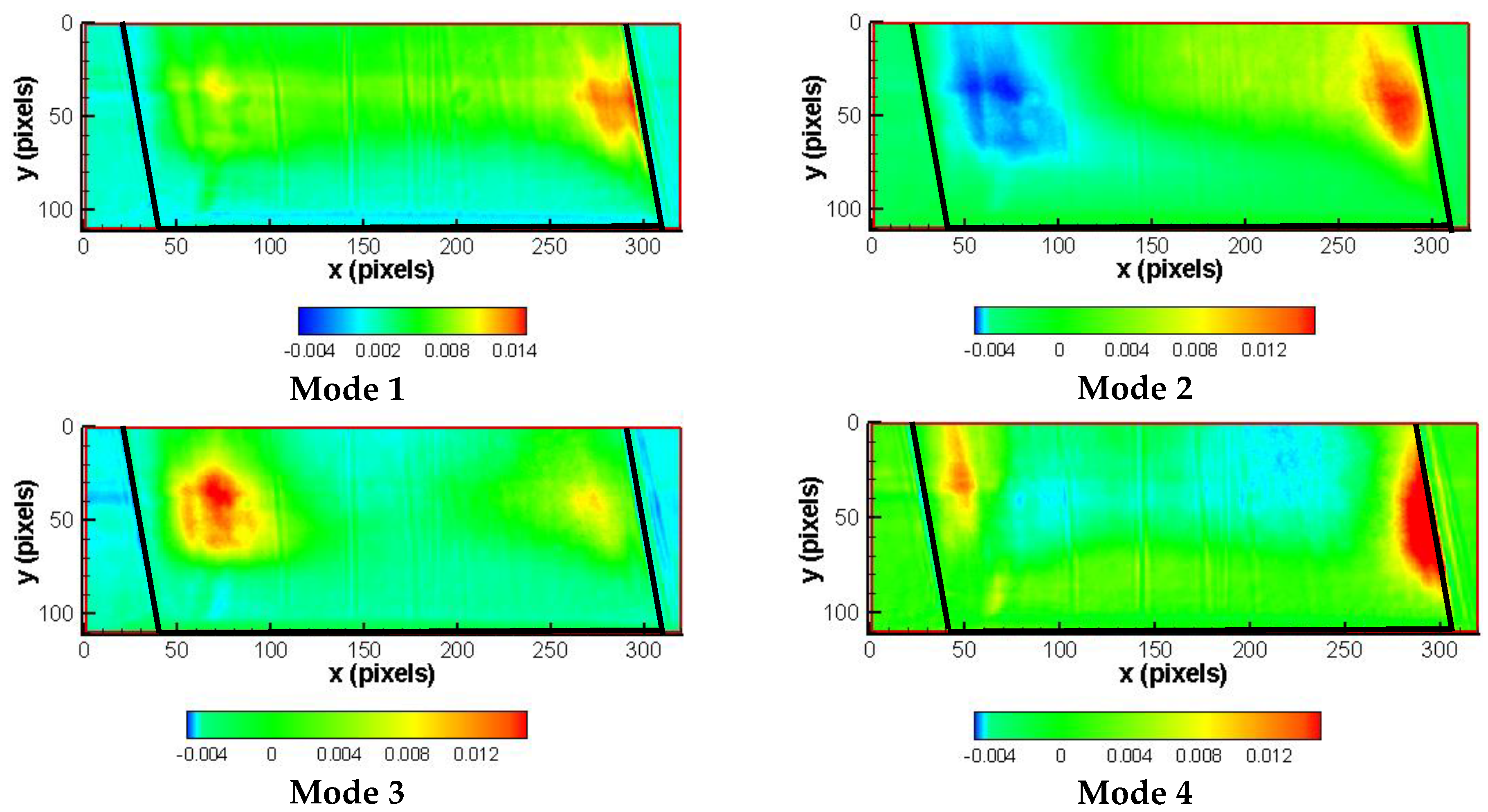
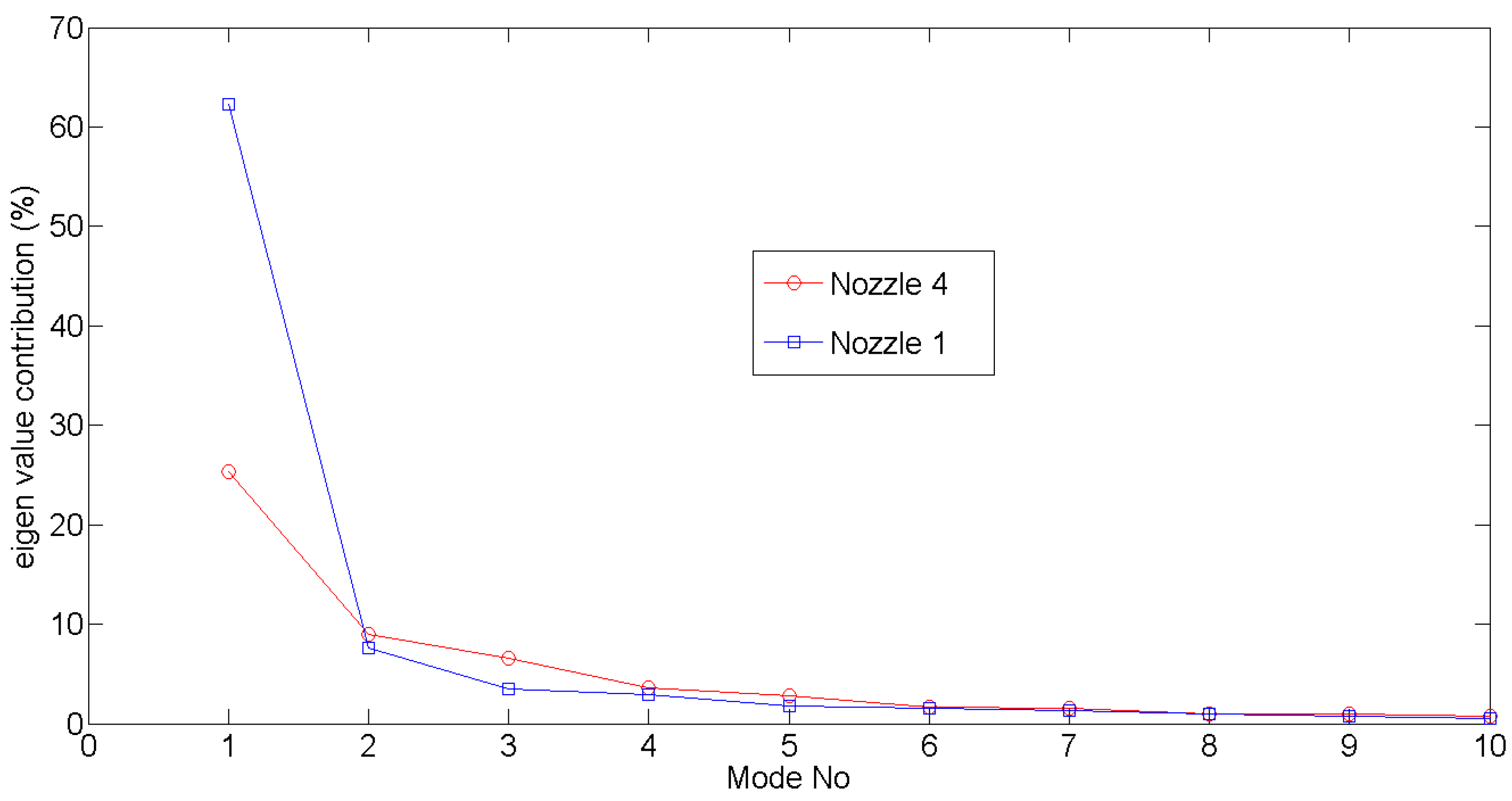
3.3. Proper Orthogonal Decomposition (POD) of Liquid Velocity Field in Cavitating Flow Conditions
3.4. POD of Shadowgraphic Cavitation Images of Type B Injector Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Payri, F.; Bermudez, V.; Payri, R.; Salvador, F.J. The influence of cavitation on the internal flow and the spray characteristics in diesel injection nozzles. Fuel 2004, 83, 419. [Google Scholar] [CrossRef]
- Ulrich, H.; Lehnert, B.; Guénot, D.; Svendsen, K.; Lundh, O.; Wensing, M.; Berrocal, E.; Zigan, L. Effects of liquid properties on atomization and spray characteristics studied by planar two-photon fluorescence. Phys. Fluids 2022, 34, 083305. [Google Scholar] [CrossRef]
- Oda, T.; Hiratsuka, M.; Goda, Y.; Kanaike, S.; Ohsawa, K. Experimental and Numerical Investigation about Internal Cavitating Flow and Primary Atomization of a Large-Scaled VCO Diesel Injector with Eccentric Needle; ILASS-Europe: Brno, Czech Republic, 2010. [Google Scholar]
- Watanabe, H.; Nishikori, M.; Hayashi, T.; Suzuki, M.; Kakehashi, N.; Ikemoto, M. Visualization analysis of relationship between vortex flow and cavitation behaviour in diesel nozzle. Int. J. Engine Res. 2015, 16, 5. [Google Scholar] [CrossRef]
- Zhong, W.; He, Z.; Wang, Q.; Shao, Z.; Tao, X. Experimental study of flow regime characteristics in diesel multi-hole nozzles with different structures and enlarged scales. Int. Commun. Heat Mass Transf. 2014, 59, 1. [Google Scholar] [CrossRef]
- McGinn, P.; Tretola, G.; Vogiatzaki, K. Unified modeling of cavitating sprays using a three-component volume of fluid method accounting for phase change and phase miscibility. Phys. Fluids 2022, 34, 082108. [Google Scholar] [CrossRef]
- Kim, J.H.; Nishida, K.; Yoshizaki, T.; Hiroyasu, H.H. Characterization of Flows in the Sac Chamber and the Discharge Hole of a D.I. Diesel Injection Nozzle by Using a Transparent Model Nozzle. SAE Tech. Pap. 1997, 972942, 11–23. [Google Scholar]
- Arcoumanis, C.; Flora, H.; Gavaises, M.; Badami, M.M. Cavitation in Real–Size Multi–Hole Diesel Injector Nozzles; SAE International: Diego County, CA, USA, 2000; Volume 109, pp. 1485–1500. [Google Scholar]
- Arcoumanis, C.; Flora, H.; Gavaises, M.; Kampanis, N.; Horrocks, R. Investigation of Cavitation in a Vertical Multi-Hole Injector; SAE International: Diego County, CA, USA, 1999; Volume 108, pp. 661–678. [Google Scholar]
- Gilles-Birth, I.; Bernhardt, S.; Spicher, U.; Rechs, M. A Study of the In-Nozzle Flow Characteristics of Valve Covered Orifice Nozzles for Gasoline Direct Injection. SAE Tech. Pap. 2005, 1, 3684. [Google Scholar]
- Nouri, J.M.; Mitroglou, N.; Yan, Y.; Arcoumanis, C. Internal Flow and Cavitation in a Multi-hole Injector for Gasoline Direct-Injection Engines. SAE Tech. Pap. 2007, 1, 1405. [Google Scholar]
- Kolokotronis, D.; Hardalupas, Y.; Taylor, A.M.K.P.; Aleiferis, P.G.; Arioka, A.; Saito, M. Experimental Investigation of Cavitation in Gasoline Injectors. SAE Tech. Pap. 2010, 1, 1500. [Google Scholar]
- Reid, B.A.; Hargrave, G.K.; Garner, C.P.; Wigley, G. An investigation of string cavitation in a true-scale fuel injector flow geometry at high pressure. Phys. Fluids 2010, 22, 031703. [Google Scholar] [CrossRef]
- Mitroglou, N.; McLorn, M.; Gavaises, M.; Soteriou, C.; Winterbourne, M. Instantaneous and ensemble average cavitation structures in Diesel micro-channel flow orifices. Fuel 2014, 116, 736. [Google Scholar] [CrossRef]
- Reid, B.A.; Gavaises, M.; Mitroglou, N.; Hargrave, G.K.; Garner, C.P.; Long, E.J.; McDavid, R.M. On the formation of string cavitation inside fuel injectors. Exp. Fluids 2014, 55, 1662. [Google Scholar] [CrossRef]
- Giannadakis, E.; Gavaises, M.; Arcoumanis, C. Modelling of cavitation in diesel injector nozzles. J. Fluid Mech. 2008, 616, 153. [Google Scholar] [CrossRef]
- Gavaises, A.M.; Arcoumanis, C.C. Vortex flow and cavitation in diesel injector nozzles. J. Fluid Mech. 2008, 610, 195. [Google Scholar]
- Gavaises, M.; Andriotis, A.; Papoulias, D.; Mitroglou, N.; Theodorakakos, A. Characterization of string cavitation in large-scale Diesel nozzles with tapered holes. Phys. Fluids 2009, 21, 52. [Google Scholar] [CrossRef]
- Salvador, F.J.; Romero, J.V.; Rosello, M.D.; Martinez-Lopez, J. Validation of a code for modelling cavitation phenomena in Diesel injector nozzles. Math. Comput. Model. 2010, 52, 1123. [Google Scholar] [CrossRef]
- Chang, N.A.; Yakushiji, R.; Dowling, D.R.; Ceccio, S.L. Cavitation visualization of vorticity bridging during the merger of co-rotating line vortices. Phys. Fluids 2007, 19, 058106. [Google Scholar] [CrossRef]
- Choi, J.; Ceccio, S.L. Dynamics and noise emission of vortex cavitation bubbles. J. Fluid Mech. 2007, 575, 1. [Google Scholar] [CrossRef]
- Walther, J.; Schaller, J.K.; Wirth, R.; Tropea, C. Characterization of Cavitating Flow Fields in Transparent Diesel Injection Nozzles Using Fluorescent Particle Image Velocimetry (FPIV). In Proceedings of the ILASS 2000, Darmstadt, Germany, 11–13 September 2000. [Google Scholar]
- Roth, M.H.; Gavaises, M.; Arcoumanis, C. Cavitation Initiation, Its Development and Link with Flow Turbulence in Diesel Injector Nozzles; SAE International: Diego County, CA, USA, 1999; Volume 111, pp. 561–580. [Google Scholar]
- Allen, J.; Hargrave, G.; Khoo, Y. In-Nozzle and Spray Diagnostic Techniques for Real-Sized Pressure Swirl and Plain Orifice Gasoline Direct Injectors. SAE Tech. Pap. 2003, 1, 3151. [Google Scholar]
- Aleiferis, P.G.; Hardalupas, Y.; Kolokotronis, D.; Taylor, A.M.K.P.; Arioka, A.; Saito, M. Experimental Investigation of the Internal Flow Field of a Model Gasoline Injector Using Micro-Particle Image Velocimetry. SAE Trans. J. Fuels Lubr. 2006, 115, 597. [Google Scholar]
- Aleiferis, P.G.; Hardalupas, Y.; Kolokotronis, D.; Taylor, A.M.K.P.; Kimura, T. Investigation of the Internal Flow Field of a Diesel Model Injector Using Particle Image Velocimetry and CFD. SAE Tech. Pap. 2007, 1, 1897. [Google Scholar]
- Mauger, C.; Méès, L.; Michard, M.; Azouzi, A.; Valette, S. Shadowgraph, Schlieren and interferometry in a 2D cavitating channel flow. Exp. Fluids 2012, 53, 1895. [Google Scholar] [CrossRef]
- Mauger, C.; Méès, L.; Michard, M.; Lance, M. Velocity measurements based on shadowgraph-like image correlations in a cavitating micro-channel flow. Int. J. Multiph. Flow 2014, 58, 301. [Google Scholar] [CrossRef]
- Mauger, C. Cavitation in a Diesel Injector Model Micro-Channel: Visualization Methods and Influence of Surface Condition. Ph.D. Thesis, École Centrale Lyon, Lyon, France, 2012. [Google Scholar]
- Charalambides, G. Charge Stratified HCCI Engine. Ph.D. Thesis, Department of Mechanical Engineering, Imperial College London, London, UK, 2006. [Google Scholar]
- Franc, J.P.; Michel, J.M. Fundamentals of Cavitation; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; ISBN 1-4020-2232-8. [Google Scholar]
- Loeve, M.M. Probability Theory; van Nostrand: Princeton, NJ, USA, 1955. [Google Scholar]
- Golub, G.; Loan, C.V. Matrix Computations; North Oxford Academic: Oxford, UK, 1983. [Google Scholar]
- Kumar, A.; Sahu, S. Liquid jet disintegration memory effect on downstream spray fluctuations in a coaxial twin-fluid injector. Phys. Fluids 2020, 32, 073302. [Google Scholar] [CrossRef]
- Charalampous, G.; Hadjiyiannis, C.; Hardalupas, Y. Proper orthogonal decomposition of primary breakup and spray in co-axial airblast atomizers. Phys. Fluids 2019, 31, 043304. [Google Scholar] [CrossRef]
- Charalampous, G.; Hardalupas, Y. Application of Proper Orthogonal Decomposition to the morphological analysis of confined co-axial jets of immiscible liquids with comparable densities. Phys. Fluids 2014, 26, 113301. [Google Scholar] [CrossRef]
- Kumar, A.; Sahu, S. Large scale instabilities in coaxial air-water jets with annular air swirl. Phys. Fluids 2019, 31, 124103. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. In Proceedings of the International Colloqium on the Fine Scale Structure of the Atmosphere and its Influence on Radio Wave Propagation, Nauka, Moscow, 1967. [Google Scholar]
- Kolokotronis, D. Experimental Investigation of the Internal Flow Field of Model Fuel Injectors. Ph.D. Thesis, Department of Mechanical Engineering, Imperial College London, London, UK, 2007. [Google Scholar]
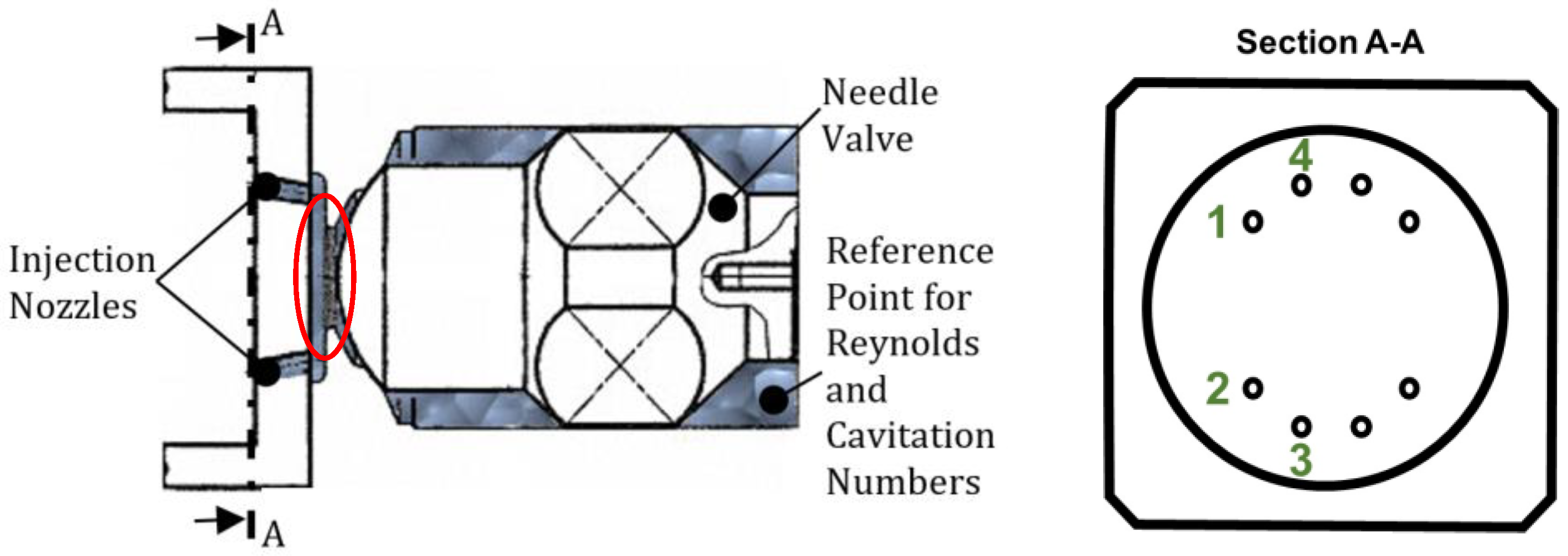
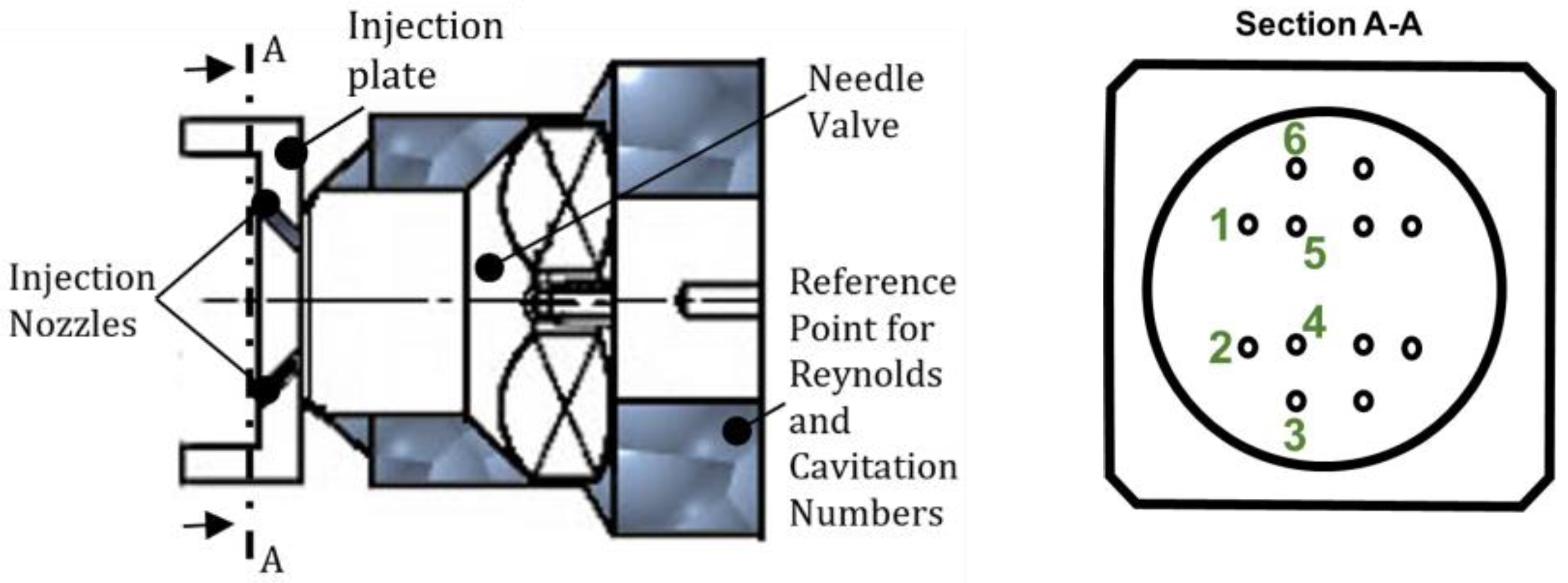


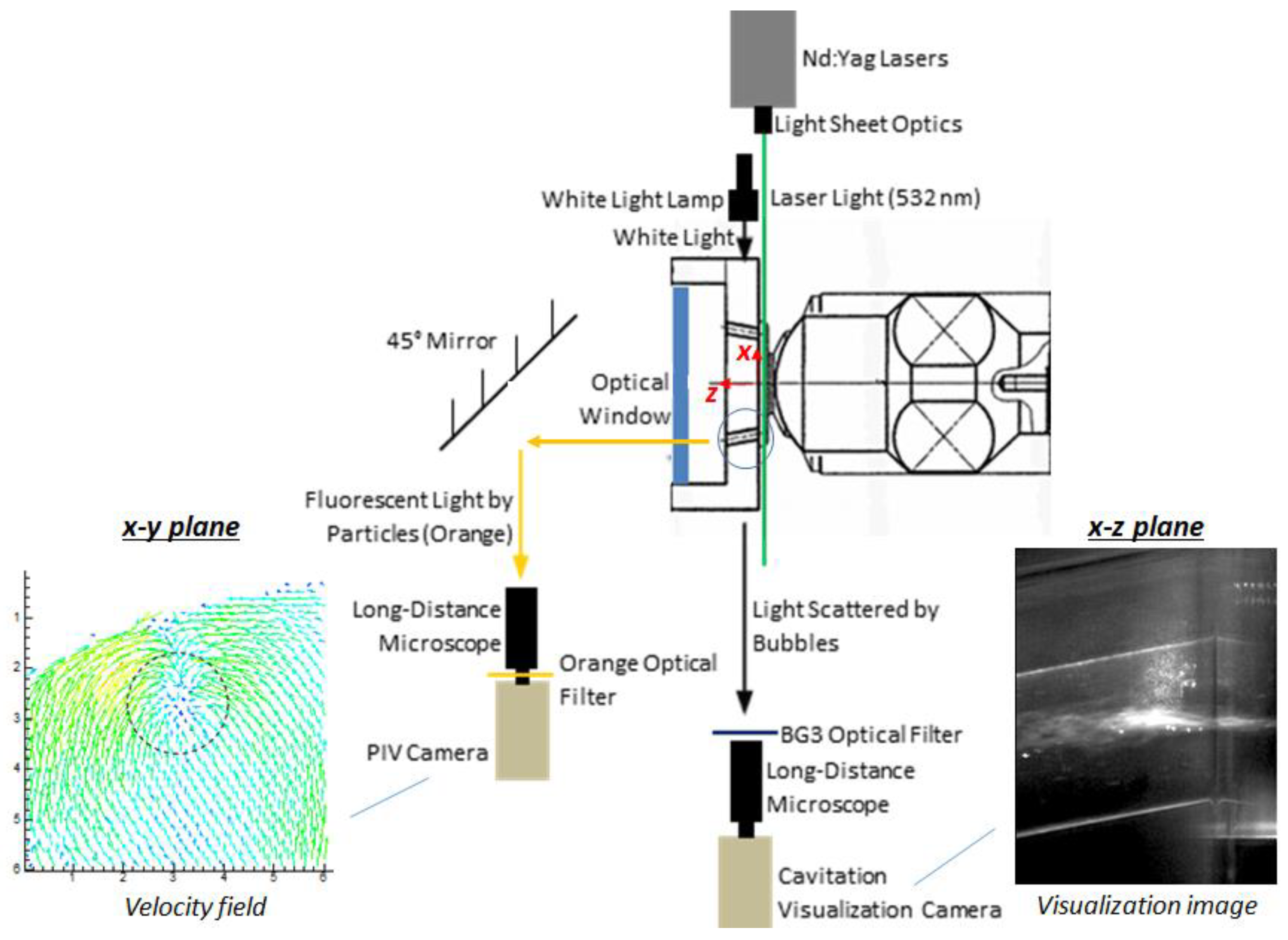







| Type A | Type B | Type C | |
|---|---|---|---|
| Reynolds Number | 10,700 | 11,550 | 9200 |
| Cavitation Number | 2700 | 2300 | 6400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolokotronis, D.; Sahu, S.; Hardalupas, Y.; Taylor, A.M.K.P.; Arioka, A. Bulk Cavitation in Model Gasoline Injectors and Their Correlation with the Instantaneous Liquid Flow Field. Fluids 2023, 8, 214. https://doi.org/10.3390/fluids8070214
Kolokotronis D, Sahu S, Hardalupas Y, Taylor AMKP, Arioka A. Bulk Cavitation in Model Gasoline Injectors and Their Correlation with the Instantaneous Liquid Flow Field. Fluids. 2023; 8(7):214. https://doi.org/10.3390/fluids8070214
Chicago/Turabian StyleKolokotronis, Dimitrios, Srikrishna Sahu, Yannis Hardalupas, Alex M. K. P. Taylor, and Akira Arioka. 2023. "Bulk Cavitation in Model Gasoline Injectors and Their Correlation with the Instantaneous Liquid Flow Field" Fluids 8, no. 7: 214. https://doi.org/10.3390/fluids8070214
APA StyleKolokotronis, D., Sahu, S., Hardalupas, Y., Taylor, A. M. K. P., & Arioka, A. (2023). Bulk Cavitation in Model Gasoline Injectors and Their Correlation with the Instantaneous Liquid Flow Field. Fluids, 8(7), 214. https://doi.org/10.3390/fluids8070214







