Abstract
The oscillation of the liquid interface in axisymmetric Hele-Shaw cells (conical and flat) is experimentally studied. The cuvettes, which are thin conical layers of constant thickness and flat radial Hele-Shaw cells, are filled with two immiscible liquids of similar densities and a large contrast in viscosity. The axis of symmetry of the cell is oriented vertically; the interface without oscillations is axially symmetric. An oscillating pressure drop is set at the cell boundaries, due to which the interface performs radial oscillations in the form of an oscillating “tongue” of a low-viscosity liquid, periodically penetrating into a more viscous liquid. An increase in the oscillation amplitude leads to the development of a system of azimuthally periodic structures (fingers) at the interface. The fingers grow when the viscous liquid is forced out of the layer and reach their maximum in the phase of maximum displacement of the interface. In the reverse course, the structures decrease in size and, at a certain phase of oscillations, take the form of small pits directed toward the low-viscosity fluid. In a conical cell, a bifurcation of period doubling with an increase in amplitude is found; in a flat cell, it is absent. A slow azimuthal drift of finger structures is found. It is shown that the drift is associated with the inhomogeneity of the amplitude of fluid oscillations in different radial directions. The fingers move from the region of a larger to the region of a lower amplitude of the interface oscillations.
1. Introduction
The dynamics of immiscible two-phase fluids in thin slotted channels and porous media is an important topic in the natural and engineering fields. Porous media are common in nature and technological processes and are relevant to many areas of activity: mining of liquid and gaseous minerals (Paşa and Titaud [1]), seepage flows and water treatment (Herzig et al. [2]), and carbon dioxide capture (De Paoli et al. [3]). The main application of the research results is for the process of exploration and production of hydrocarbons.
Due to the complexity of describing the theory and conducting experiments to study the motion of a fluid in a real porous medium, a method for modeling a porous medium using Hele-Shaw cells of various geometries is widely used. The closest model is a flat radial layer. The fluid motion in such a model obeys Darcy’s law, as in a porous medium. In the case when the dynamics of the interface between immiscible liquids is considered, it is characterized by a nonlinear mode of development of instability. One of the most spectacular modes of instability is called the Saffman–Taylor instability. This type of instability (Saffman and Taylor [4]) was discovered when a liquid was injected into a shallow rectangular channel filled with another immiscible, more viscous liquid. It is noted that the formation of fingers depends on the ratio of the height of the channel to its width. And also, the viscous forces normal to the displacement front are a destabilizing factor. The instability mechanism consists of the formation of finger structures on a morphologically unstable interface of a low-viscosity liquid when a more viscous one is displaced.
In the case of slow motion of liquids in porous media and in flat channels, the force of viscous interaction is decisive. In addition, the flow of fluids (interfaces) can be characterized using relative viscosity and capillary number, depending on the velocity of the displacing fluid and interfacial surface tension (Lenormand et al. [5]). Li et al. [6] theoretically and experimentally considered the dynamics of the interface between liquids during the formation of the Saffman–Taylor instability. A theoretical model is proposed that predicts the shape and number of developing viscous finger-like structures. A model has been developed that includes the parameters of the interfacial boundary of fluids (viscosity, interfacial tension) and the layer thickness, which describes the flow rate of the displacing fluid and pressure. Reinelt [7] theoretically calculates the width and length of finger structures depending on the capillary number. The theory is in qualitative agreement with the experimental data. With respect to the capillary number, a theoretical model was constructed for the distance between adjacent fingers of instability to the layer thickness by Fernandez et al. [8]. Accounting for the wettability of layer boundaries (Anjos et al. [9]) and the interfacial tension (Rocha and Miranda [10]) in the study of the morphological instability of the interface between liquids in thin layers determines the observed supercritical dynamics.
When moving a fluid on a large scale or at high flow rates, the inertia forces must be taken into account. For high-speed flows in porous media, a nonlinear relationship is observed between the fluid velocity and the pressure gradient. Consideration of the inertia force manifests itself most strongly with a change in the viscosity of liquids at high Reynolds numbers (Rabbani et al. [11]). It is found that the growth rate of the finger instability and the fractal number decrease with increasing inertial effects. It has been theoretically shown by Dias and Miranda [12] and Dias and Miranda [13] that both in rectangular and radial geometries, inertial effects have a stabilizing effect on interfacial perturbations in the supercritical region and determine the type of morphological instability.
Singh et al. [14] provide a brief but concise review of articles on the Saffman–Taylor instability in a radial Hele-Shaw cell and describe the governing parameters. An important area of research is the development of methods for controlling and suppressing viscous fingering. It turns out that the process of pattern formation is strongly influenced by the shape of the cell. In particular, many works are devoted to the consideration of the displacement of a viscous fluid in a Hele-Shaw cell with non-parallel boundaries. For example, the authors (Zhao et al. [15]) focus on the features of fingertip splitting depending on the sign of the gap gradient: pumping the liquid in the direction of expansion leads to the growth of the fingers and their subsequent splitting. Conversely, when the cell is narrowed, the structures become more stable. Later this result was confirmed theoretically (Dias and Miranda [16]). In Reference [17], it was found that in the tapered geometry, the onset of the interfacial instability is determined by the ratio of the depth gradient to the capillary number. This means that the presence of a taper makes it possible to control the Saffman–Taylor instability in both rectangular and radial Hele-Shaw cells. The effect of the capillary number on the viscous fingering in radially tapered Hele-Shaw cells was studied in Reference [18]. In the cylindrical cell case (Miranda [19]), it was found that the rate of linear growth and competition between the fingers are suppressed by increasing the radius of curvature, which determines the structure of the fingers.
In a lot of experimental and theoretical works, the effect of oscillations was studied against the background of a constant displacement of liquids. In the case when the displacement fluid flow rate varies (Arun et al. [20]), both suppression of supercritical structures (stabilization) and generation of structures with different wavenumbers (destabilization) depending on the specified frequency are observed. At the same time, the oscillatory dynamics of the interface between immiscible liquids in the absence of the average displacement flow remains poorly studied.
Reference [21] describes the first discovered instability that occurs when the interface of liquids with a high contrast of viscosities oscillates in a flat radial layer. A significant difference from previous studies is the zero average fluid flow, that is, the absence of constant fluid displacement. When the boundary oscillates, it is found that instability arises in a threshold manner in the form of azimuth-periodic fingers of a low-viscosity fluid. The fingers manifest themselves only in part of the oscillation period (in the displacement phase in the direction of a more viscous liquid). It is shown that the threshold for the onset of finger instability is determined by the amplitude of the interface oscillations. Further studies for various frequencies and thicknesses of the working layer (Karpunin and Kozlov [22]) showed that the instability threshold is determined by two dimensionless parameters. The first is the range of oscillations of the interface (the length of the “tongue” of a low-viscosity liquid penetrating into a high-viscosity one) with respect to the thickness of the working layer of the liquid. The second is the capillary number, calculated through the flow rate of the oscillating movement of the “tongue” and the dynamic viscosity of a more viscous liquid. In the geometry of a rectangular Hele-Shaw cell (Kozlov and Vlasova [23]), it was found that oscillations of the interface lead to two effects. As the vibration amplitude increases, the interface takes the form of a dynamically balanced “hill” against the background of vibrations with zero average flow rate. Simultaneously with the emerging deformation, finger instability develops, similar to that observed in the radial Hele-Shaw cell (Kozlov et al. [21]). In contrast to the radial layer, there is also a mode of period-doubling of finger structures. Probably, the differences are due to the interaction of the oscillating liquids with the side walls.
This study is devoted to the study of the oscillatory dynamics of the interface between liquids with a large contrast of viscosities and close density in a gravity field in the absence of the side walls. Such an implementation is possible in a coaxial conical layer. Vibration frequencies, working layer thicknesses, and working fluids are equivalent to those described in Reference [21] and Reference [22]. The main difference between the problem under consideration and the radial formulation is the study of the threshold for the occurrence of the detected Saffman–Taylor instability and supercritical dynamics in conical geometry. One of the tasks is to study the influence of the shape (conical or flat) of an axisymmetric Hele-Shaw cell on the oscillatory dynamics of the interface of immiscible liquids with a large contrast of viscosity and close density.
2. Experimental Setup and Methods
The cell is an axisymmetric gap of constant thickness h formed by two conical boundaries (Figure 1a).
The gap is formed between a truncated cone labeled 1 with base diameters of 30.0 and 140.0 mm and a Plexiglas parallelepiped labeled 2 with a conical hole.
A metal rod labeled 3 with a diameter of 6.0 mm is pressed along the symmetry axis of the truncated cone. The rod and cone 1 are fixed in the parallelepiped 2 with a lock nut, ensuring the formation of an axisymmetric gap between the conical surfaces. The rod and the lock nut are threaded, which lets you change smoothly the gap thickness h. The apertures of the cones are identical and are 90°. The leak tightness of the layer and the position of cone 1 relative to block 2 are provided by an aluminum cap labeled 4 in the form of a ring with rubber rings. There is a hole with a diameter of 120 mm in the aluminum cap through which the fluid dynamics is monitored. We also manufactured the expansion compartment labeled 5 in the form of a ring 21 mm wide and 20 mm high and the compartment labeled 6 with a volume of 19.8 cm3 to reduce the hydrodynamic resistance of the fluid and provide pressure homogeneity near the top and bottom boundaries of the cell. Since the conical layer is located inside the parallelepiped, optical distortions during photo and video recording of the interface are negligible.

Figure 1.
Scheme of the experimental setup: (a) scheme of the experimental cell in the axial section; (b) image of the interface section in phases of the maximum expansion and the maximum contraction.
The fluid flow rate oscillates according to the law (Figure 1a). The push–pull hydraulic pump, which is a cylindrical cavity divided into two parts by a flexible rubber membrane, is connected to the nozzles labeled 7 and 8 of the cell to ensure the oscillatory motion of fluid in the cell. An electrodynamic vibrator transmits oscillations to the membrane and, hence, to the fluid in the cell. The oscillation frequency varies in the range of Hz. Oscillations of the pump membrane are transmitted to the fluid in the hydraulic circuit that is equipped with two separating membranes. This allows the liquids in the cell to be separated from the liquid in the pump. A detailed description of the pump design can be found in Reference [21]. In the experiments, the cell is vertical so that the gravitational force acts along the axis of symmetry. The gap width h is equal to 1.9 mm in all experiments, while the cell length L (the distance from the cone apex to the expansion compartment 5) is equal to 99 mm.
We use water or an aqueous solution of sodium iodide and silicone PMS-1000 as immiscible fluids. The physical properties of all fluids are given in Table 1. The oil density is the same in all experiments, while the density and kinematic viscosity of a heavy fluid (aqueous solution of sodium iodide) vary. Yet, the relative density of fluids is close to unity. The kinematic viscosity of the oil is several orders of magnitude higher than the viscosity of water and aqueous solutions of NaI.

Table 1.
Physical parameters of liquids.
Due to gravity, the water or aqueous solution of NaI is located at the bottom of the cell. Improving the clarity of the interface is achieved by adding food coloring (an aqueous solution of sodium iodide) to the water. The initial position of the interface is set when filling the cell with fluid. First, we fill the cell with an aqueous solution through nozzle 8. Then, we pour the oil slowly. When viewed from above, the interface appears as a circle. The position of the interface is characterized by the distance l calculated by the formula , where r is the radial distance (Figure 1a).
We focus on the study of the oscillatory dynamics of the interface between two immiscible fluids. According to recent studies by Kozlov et al. [21] and Kozlov and Vlasova [23], the oscillating interface is unstable to the growth of low-viscosity fingers. In the present work, the position of the interphase boundary is also determined. The finger instability observed in the conical cell is compared with that previously studied in the radial cell in Reference [21].
The radial distance r is used to characterize patterns when photographing from the top view (Figure 1b). In the supercritical region, the considered area of the interface in azimuth turns out to be significant. Thus, in directions different in azimuth, the structure and type of instability can differ from each other. As will be shown below, this is associated with a non-uniform oscillation amplitude. For this reason, we use a local approach when analyzing interfacial pattern formation. When determining the peak-to-peak displacement of the interface , the extreme positions of the interface are measured along the cone generatrix. Here, is the distance from the symmetry axis to the maximum position of the interface; is the distance from the symmetry axis to the minimum position of the interface; and is the peak-to-peak displacement of the interface measured along the cone generatrix. Then, the height of the viscous fingers is calculated by the formula , where is the distance from the axis of symmetry to the base of the finger.
3. Experimental Results
3.1. Oscillatory Finger Instability
The initial shape of the interface is a circle in radial and conical Hele-Shaw cells. The interface performs radial oscillations relative to its initial position in the subcritical region. According to the observations, the interface maintains a concentric shape in the phases of the maximum displacement (Figure 2a and Figure 3a). An increase in the oscillation amplitude leads to the quasi-stationary irregular ripple formation, which oscillates with a period equal to the period of the liquid oscillation (Figure 2b and Figure 3c). The behavior of the interface in the course of oscillations in a conical and flat radial cell is similar. When reaching the critical amplitude, the instability develops in the form of azimuthally distributed low-viscosity fingers: the low-viscosity fluid penetrates the high-viscosity one when the interface moves towards the latter (Figure 2c and Figure 3d). When the interface moves towards the low-viscosity fluid, the fingers almost disappear. The instability is local: the viscous fingering develops at the part of the interface due to the asymmetry of the initial position of the interface. With a further increase in the oscillation amplitude, fingers cover the entire interface.

Figure 2.
Photographs of the interface in the radial Hele-Shaw cell at , Hz, and mm: (a) below the threshold of the oscillatory finger instability; (b) near the instability threshold; (c,d) above the instability threshold as the amplitude of oscillation increases. Images (b–d) are obtained by overlaying photographs taken in the phases of the minimum (dark blue) and maximum (light blue) length of the interface.
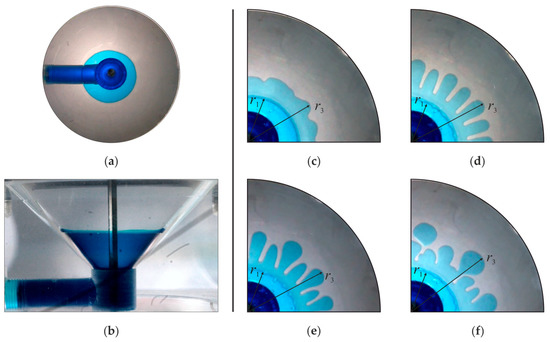
Figure 3.
Photographs of the interface in the conical Hele-Shaw cell at and Hz: (a) below the threshold of the oscillatory finger instability, view from above; (b) below the threshold of the oscillatory finger instability, side view; (c) near the instability threshold; (d–f) above the instability threshold as the amplitude of oscillation increases. Images (c–f) are obtained by overlaying photographs taken in the phases of the minimum () and maximum () length of the interface.
This instability was previously discovered in experiments with a radial Hele-Shaw cell in Reference [21] and was characterized as an oscillatory Saffman–Taylor instability. Fingers of a low-viscosity liquid develop in the process of displacement of a more viscous one and reach a maximum in the phase of maximum expansion of the interfacial boundary. A specific feature of the instability is the change in the position of the fingers through the period of oscillation. When the interface length is minimum, regular pits are observed at the interface. They appear due to the difference between the velocities of fingers and troughs while the interface moves towards the low-viscosity fluid. Fingertips move quickly and bend the interface in the phase of maximum contraction due to density-related inertia. This, in turn, leads to a change in the position of the fingers–pits through a period of oscillation.
Thus, the violation of the axial symmetry of the oscillating interface occurs in two stages. The first one is an irregular symmetry breaking which is probably associated with the roughness of the cell walls caused by unwanted pollution. These perturbations lead to the periodic development of irregular patterns with the frequency of interface oscillations. Such irregular patterns, sometimes in the form of fingers, develop at a fraction of a period (in the phase of displacement of a viscous fluid) and completely die out in the same period. They belong to the quasi-stationary instability and could be observed at relatively small amplitudes of interface oscillations. The second stage (viscous fingering) is the fingering pattern formation, which has a specific feature: when the interface length is minimum, regular pits occur there where low-viscosity fingers collapse. The development of alternating fingers and pits is considered the threshold for oscillatory finger instability. The latter leads to the fact that the position of the fingers changes through the period. The development of precisely such structures is further taken as the threshold of “oscillatory finger instability”. This instability is consistent with the Floquet theory when the memory of finger structures does not fade away during a period and is preserved in the form of a regular relief at the interface in the phase of maximum displacement of the latter towards a low-viscosity liquid.
According to the observations, the dynamics of an oscillating interface between fluids of slightly different densities at the instability threshold in conical and flat radial Hele-Shaw cells are similar. Moreover, the critical relative amplitudes of the interface oscillations in experiments with identical fluids at the same oscillation frequencies agree well with each other in the conical and flat radial cells.
A further increase in the oscillation amplitude is not followed by a change in the structure of instability in a radial Hele-Shaw cell (Figure 2d). An increase in the oscillation amplitude leads to an increase in the length of low-viscosity fingers. Finally, fingertips break up into drops. When the interface contracts, these drops penetrate the low-viscosity fluid. An increase in the amplitude of oscillations results in a transition to a new regime of interface oscillations in the conical cell. We observe patterns with a doubled period in the phase of the maximum expansion of the interface (Figure 3e). The azimuthal period-doubling mode is characterized by the azimuthal alternation of long and short fingers of a low-viscosity liquid, with the preservation of the alternation “finger—pit” through the oscillation period. Such patterns for the traditional arrangement of fluids in circular axisymmetric Hele-Shaw cells are observed for the first time. A further increase in the oscillation amplitude leads to the droplet formation and subsequent return to the bulk of the low-viscosity fluid (Figure 3f) by analogy with what happens in a radial cell (Figure 2d).
3.2. Period Doubling
The angular distance between pits in the phase of maximum compression of the interface and the distance from the cell axis are characteristic lengths of the finger patterns (see Figure 1b). This is because the tips formed after the disappearance of the fingers then become sources of perturbations when the low-viscosity fluid penetrates the high-viscosity one. The interface length changes over the oscillation cycle, so we choose the azimuthal wavenumber in the phase of the maximum compression as the characteristic size.
Here we consider the dynamics of the finger patterns in the supercritical domain. The wavenumber almost does not change with an increase in the oscillation amplitude along a fixed radial direction. Herewith, disturbances with different wavelengths simultaneously exist at the interface. This explains the significant difference in measuring the wavenumber for given values of (Figure 4). When increasing , the second mode with half wavenumber mm−1 appears along with the fundamental mode (red symbols in Figure 4). Photographs of the interface in the supercritical domain are shown in Figure 3. One can find that all fingers are coupled. This indicates a spatial period-doubling of the pattern, which is typical for the system under consideration. A similar effect was observed in a rectangular Hele-Shaw cell under oscillations of the fluid–fluid interface (Kozlov and Vlasova [23]). On the contrary, the period-doubling for the traditional arrangement of fluids was not observed in a radial Hele-Shaw cell (Karpunin and Kozlov [22]).
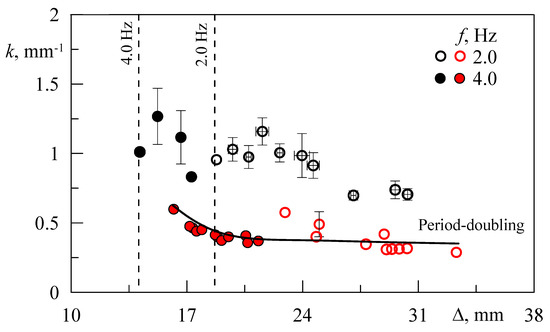
Figure 4.
The wavenumber versus the peak-to-peak displacement of the interface at . Vertical dashed lines indicate the threshold values of for and Hz. The black (red) symbols illustrate the wavenumber of regular (period-doubling) fingers.
Period-doubling is observed at different oscillation frequencies for all fluid pairs. According to the observations, the period-doubling patterns coexist with regular fingers of the same length. This is due to the local character of the instability: the velocity and the peak-to-peak displacement of the interface change along the azimuth axis due to the different distances of the interface from the symmetry axis of the cell.
The threshold value of the interface peak-to-peak displacement decreases with an increase in the oscillation frequency in a radial cell (Karpunin and Kozlov [22]). This is also valid for the conical cell: the dashed lines in Figure 4 indicate the threshold values of the interface oscillation amplitude at different frequencies. At the same time, the supercritical structures with an equal certain type of spatial distribution of fingers are characterized by close wave numbers regardless of the specified vibration frequency.
It should be noted that the finger patterns become asymmetric when the period-doubling occurs: One of the adjacent fingers grows much faster and has a greater length in the phase of maximum displacement than the other one (Figure 3). Neighboring fingers differ in both radial and azimuthal sizes. The longer finger has a thin neck and a rather massive head resembling a mushroom, while its neighbor narrows when the interface expands. In the phase of maximum contraction, pits appear where longer fingers were previously located. When increasing , the fingers collapse, and fingertips break up into drops (Figure 3f). While the interface is contracting, the droplets are drawn into the low-viscosity fluid. The temporal dynamics of the finger during an oscillation cycle are shown in Figure 5. It is clear that functions and are not sine-shaped, which can be explained by the change in the shape of the interface. The growth rate of the fingers is slower than the retraction one, and the fingers reach their maximum length at (compare dashed lines that mark value , in Figure 5a,b). Apparently, this effect is explained by the unequal shape of the finger’s cross-section in the phases of expansion and contraction. This is beyond the scope of this work and is a subject for further research. The length and the radial velocity of the adjacent fingers differ when the period-doubling occurs (Figure 5b,d). On close observation, one can find that a small finger is drawn into an adjacent large finger while the interface expands. This may be due to the excessive capillary pressure inside the little finger due to the large curvature of the fingertip. Presumably, it is the capillary effects that lead to the uneven growth of neighboring fingers (period-doubling phenomenon) upon reaching the critical size along the length.

Figure 5.
The temporal dynamics of the fingers in the conical Hele-Shaw cell at , , and Hz: (a) regular finger before the period-doubling bifurcation; (b) two adjacent fingers after the bifurcation (red circles and black dots). Graphs (c,d) show the dependence of the fingertip radial velocity on time (symbols correspond to those shown in (a,b)).
3.3. Azimuthal Drift of Fingers
In addition to the mentioned alternation of viscous fingers and pits, the effect of slow azimuthal drift was revealed. According to the observations, different fingers can move in opposite directions (Figure 6). To study the azimuthal drift, photographs of the interface were taken in the phase of maximum expansion with a time interval of . Thus, the effect of alternating fingers and pits was excluded from consideration.
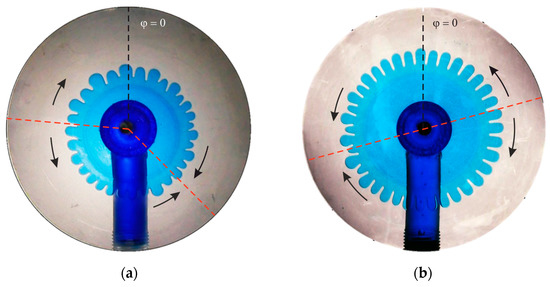
Figure 6.
The photographs of the interface at the start of the measurements of the azimuthal drift at (a) and Hz; (b) and Hz. The black dashed line corresponds to the azimuth reference direction. The red dashed lines indicate azimuthal directions where drift is absent. Black arrows show the drift direction.
Figure 7 and Figure 8 illustrate (a) the azimuthal coordinate of the fingers vs. time, (b) the interface shape at the start of the measurements, and (c) the peak-to-peak displacement of the fingertips. Figure 6 shows the interface at the start of the measurements.
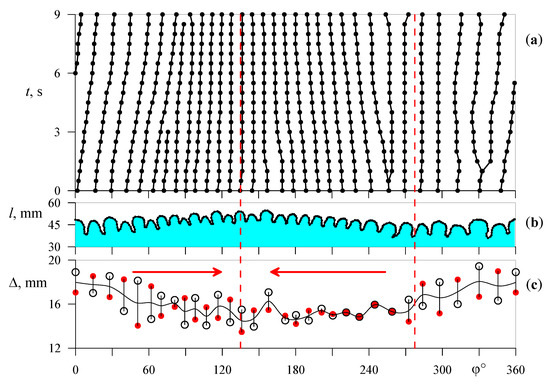
Figure 7.
(a) The temporal dynamics of the interface, (b) the interface shape at the start of the measurements (see Figure 6a), and (c) the peak-to-peak displacement of the fingertips at and Hz. Red and black symbols correspond to the peak-to-peak displacement of the fingertips at time interval (period-doubling phenomenon). The red dashed lines indicate azimuthal directions where drift is absent. Red arrows show the drift direction.
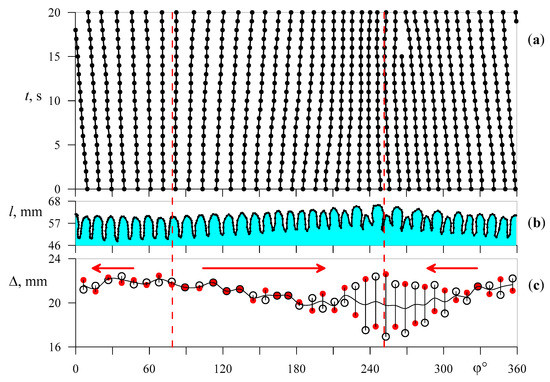
Figure 8.
(a) The temporal dynamics of the interface, (b) the interface shape at the start of the measurements (see Figure 6b), and (c) the peak-to-peak displacement of the fingertips at and Hz. Red and black symbols correspond to the peak-to-peak displacement of the fingertips at time interval . The red dashed lines indicate azimuthal directions where drift is absent. Red arrows show the drift direction.
The azimuthal drift was studied sometime after the end of the rearrangement of the fingers associated with the initial development of instability. One can find that fingers move along the azimuthal direction at different rates. The azimuth position of some fingers does not change with time. New fingers continuously emerge in selected regions of the interface while, in other regions, there is a merger of the drifting fingers. Most often, there is only one region of emergence and only one region of merger. The positions of the emergence and merger regions vary in different experiments. In addition, the azimuth drift was very slow or non-existent in some experiments. A comparison of the time diagrams in Figure 7c and Figure 8c shows that the fingers drift from the region of the greatest amplitude of the interface oscillations to the region of the smallest one. The drift velocity , as well as the drift direction, vary along the azimuthal coordinate, while the maximum velocity depends on the oscillation frequency. For example, the maximum drift velocity is at a frequency of Hz (Figure 7), while at Hz (Figure 8) at a relative density of . Notice that the effect of the interfacial drift is observed for all pairs of fluids if the oscillation amplitude changes along the azimuthal direction. On the contrary, the effect is zero when the interface oscillations are uniform.
The drift of low-viscosity fingers needs further systematic study. However, it can be assumed that it is caused by the averaged flows of a low-viscosity liquid against the background of its oscillations. This may be due to the generation of steady streaming [24,25]. In this case, the averaged vorticity generated in the Stokes boundary layers that are inhomogeneous in oscillation amplitude excites the average fluid motion outside the Stokes layers, directed from the region of high amplitudes of the oscillatory velocity component. The latter is consistent with the results of experimental observations.
For the period-doubling mode, the peak-to-peak displacement (for example, the solid line in the range in Figure 8b,c) is calculated as the arithmetic average between the small and large finger displacement in other words, on the average of peak-to-peak displacement after . This is determined by the change in the location of the large and small fingers in each pair after .
4. Discussion
For the analysis of the azimuthal drift, we determine the interface shape in the phase of the maximum displacement (Figure 9). Here, the circles indicate the height of the fingertips shown in Figure 7b. The interface is non-axisymmetric: the coordinate of the minimum height corresponds to the maximum of peak-to-peak displacement (Figure 7c) and to the region of the emergence of viscous fingers, while the coordinate of the minimum of peak-to-peak displacement shows the region of the merger. A comparison of the peak-to-peak displacement (Figure 7c) with the interface displacement (Figure 9a) shows that the position of the interface in the conical cell determines the oscillation amplitude. The farther the interface is from the cell axis, the smaller the amplitude of the interface oscillations. Obviously, this follows from a linear increase in the circumference with an increase in the radial size of the interface. In turn, an increase in the amplitude of the interface oscillations causes an increase in the angular size of the fingers (Figure 9b,c). As will be shown below, this is typical for oscillatory finger instability. Therefore, the peak-to-peak displacement of the interface is the governing parameter of the problem which determines (a) the threshold for the instability, (b) the wavelength of the fingering instability, and (c) the azimuthal drift of fingers.
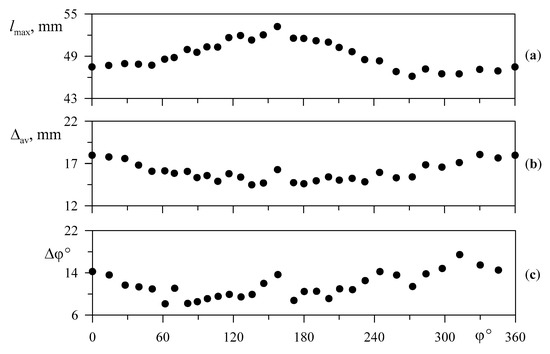
Figure 9.
The azimuthal distribution of (a) the maximum displacement of the interface; (b) the average peak-to-peak displacement of the interface oscillations; (c) the azimuthal wavelength of the fingering instability. The symbols correspond to those shown in Figure 7.
Let us introduce the dimensionless parameter , where is the relative displacement of the interface oscillations at the threshold for the fingering instability. The parameter allows comparison of the wavenumbers of the fingering instability observed in radial (Karpunin and Kozlov [22]) and conical Hele-Shaw cells (Figure 10).
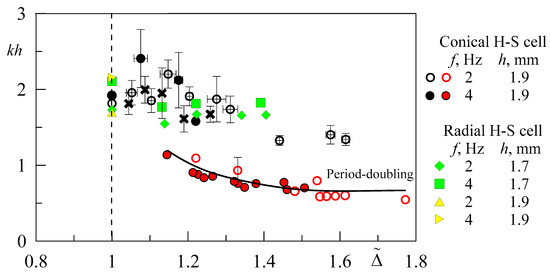
Figure 10.
The dependence of the dimensionless wavenumber on the parameter at . The crosses indicate wavenumbers from the data shown in Figure 7b.
In the above graph, the value corresponds to the threshold for the fingering instability. It should be noted that for the traditional arrangement of fluids, only regular (without period-doubling) fingers appear in radial Hele-Shaw cells (Kozlov et al. [21], Karpunin and Kozlov [22]). The threshold value for a conical cell and a flat radial layer for equal vibration frequencies have close values. So for a conical cell at Hz, the value is . For a flat radial layer, at the same frequency, at mm and at mm (Karpunin and Kozlov [22]).
One can find that dimensionless wavenumbers for conical (red and black symbols) and radial (green and yellow symbols) cells agree well with each other. It can be concluded that the origin of the finger-type instability in the conical and radial Hele-Shaw cells is of the same type, and the threshold is determined by the relative amplitude of the interface oscillations. A specific feature of the fingering instability in the conical cell is the period-doubling mode, which manifests itself in the overcritical region. Recently, period-doubling was also revealed in experiments with a rectangular Hele-Shaw cell in Reference [23]. The absence of this phenomenon in the radial cell indicates that the doubling of the period in the conical cell is associated with constrained conditions for finger growth; in the radial cell, neighboring fingers grow without intensive interference with each other.
At the threshold of development of finger instability, structures with one wavenumber develop, which agrees with the results of linear analysis (in the case of a quasi-stationary approach to stability). It can be assumed that the observed doubling of the spatial period is a purely supercritical nonlinear phenomenon typical for various hydrodynamic systems.
Figure 10 also shows the results of the wavenumber measurements versus the amplitude of coexisting fingers (taken from one data sample) at and Hz (see Figure 7b), when the oscillation amplitude and the wavenumber of the finger patterns vary along the interface. These data agree well with all other experimental data samples, which proves the validity of the local method for determining the instability threshold and the evolution of fingers with an increase in .
5. Conclusions
The stability of an oscillating interface between two fluids with high viscosity contrast in an axisymmetric conical Hele-Shaw cell is experimentally studied. The instability in the form of low-viscosity fingers develops when the critical amplitude of oscillation is reached. The entire experimental results are compared with the data obtained in the plane radial Hele-Shaw cell. In both cases, the densities of the high-viscous and low-viscosity fluids are close to each other, and therefore gravity does not have a significant effect. It is found that the threshold for instability is determined by the relative amplitude of the interface oscillations. The data obtained in cells of different shapes agree well with each other. A noticeable difference is observed for the supercritical region: period doubling is observed at in the conical cell. The adjacent fingers are asymmetric: one of the fingers grows much faster than the other, and therefore, the fingers significantly differ in length in the phase of maximum displacement of the viscous fluid. It is concluded that this effect is caused by capillary force, which manifests itself more in constrained conditions, that is absent in a flat Hele-Shaw cell where a low-viscosity fluid is surrounded by a high-viscosity one.
It is revealed that the dimensionless wavenumber of the instability decreases with an increase in the amplitude of interface oscillations. The data obtained in cells of different shapes are consistent with each other.
According to the observations, the low-viscosity fingers drift in the azimuthal direction. New fingers emerge in the selected region of the interface, while in the other region, there is a merger of the drifting fingers. It is shown that the drift is due to the azimuthal inhomogeneity of the amplitude of interface oscillations: fingers drift from the region of the greatest amplitude of the interface oscillations to the region of the smallest one.
Author Contributions
Conceptualization, V.K., S.S. and I.K.; methodology, V.K., S.S. and I.K.; formal analysis, V.K., S.S. and I.K.; investigation, S.S. and I.K.; data curation, V.K., S.S. and I.K.; writing—original draft preparation, V.K., S.S. and I.K.; writing—review and editing, V.K., S.S. and I.K.; visualization, S.S. and I.K.; supervision, V.K.; project administration, V.K. All authors have read and agreed to the published version of the manuscript.
Funding
The Government of the Perm region and the Russian Foundation for Basic Research financially supported this research (grant № 20-41-596011).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Paşa, G.; Titaud, O. A class of viscosity profiles for oil displacement in porous media or Hele-Shaw cell. Transp. Porous Media 2005, 58, 269–286. [Google Scholar] [CrossRef]
- Herzig, J.P.; Leclerc, D.M.; Goff, P.L. Flow of suspensions through porous media—Application to deep filtration. Ind. Eng. Chem. 1970, 62, 8–35. [Google Scholar] [CrossRef]
- De Paoli, M.; Zonta, F.; Soldati, A. Influence of anisotropic permeability on convection in porous media: Implications for geological CO2 sequestration. Phys. Fluids 2016, 28, 056601. [Google Scholar] [CrossRef]
- Saffman, P.G.; Taylor, G.I. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 1958, 245, 312–329. [Google Scholar]
- Lenormand, R.; Touboul, E.; Zarcone, C. Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech. 1988, 189, 165–187. [Google Scholar] [CrossRef]
- Li, S.; Lowengrub, J.S.; Fontana, J.; Palffy-Muhoray, P. Control of viscous fingering patterns in a radial Hele-Shaw cell. Phys. Rev. Lett. 2009, 102, 174501. [Google Scholar] [CrossRef]
- Reinelt, D.A. The effect of thin film variations and transverse curvature on the shape of fingers in a Hele–Shaw cell. Phys. Fluids 1987, 30, 2617–2623. [Google Scholar] [CrossRef]
- Fernandez, J.; Kurowski, P.; Limat, L.; Petitjeans, P. Wavelength selection of fingering instability inside Hele–Shaw cells. Phys. Fluids 2001, 13, 3120–3125. [Google Scholar] [CrossRef]
- Anjos, P.H.; Zhao, M.; Lowengrub, J.; Bao, W.; Li, S. Controlling fingering instabilities in Hele-Shaw flows in the presence of wetting film effects. Phys. Rev. E 2021, 103, 063105. [Google Scholar] [CrossRef]
- Rocha, F.M.; Miranda, J.A. Manipulation of the Saffman-Taylor instability: A curvature-dependent surface tension approach. Phys. Rev. E 2013, 87, 013017. [Google Scholar] [CrossRef]
- Rabbani, S.; Abderrahmane, H.; Sassi, M. Inertial effects on dynamics of immiscible viscous fingering in homogenous porous media. Fluids 2019, 4, 79. [Google Scholar] [CrossRef]
- Dias, E.O.; Miranda, J.A. Influence of inertia on viscous fingering patterns: Rectangular and radial flows. Phys. Rev. E 2011, 83, 066312. [Google Scholar] [CrossRef]
- Anjos, P.H.A.; Dias, E.O.; Miranda, J.A. Radial fingering under arbitrary viscosity and density ratios. Phys. Rev. Fluids 2017, 2, 084004. [Google Scholar] [CrossRef]
- Singh, A.; Singh, Y.; Pandey, K.M. Viscous fingering instabilities in radial Hele-Shaw cell: A review. Mater. Today Proc. 2020, 26, 760–762. [Google Scholar] [CrossRef]
- Zhao, H.; Casademunt, J.; Yeung, C.; Maher, J.V. Perturbing Hele-Shaw flow with a small gap gradient. Phys. Rev. A 1992, 45, 2455. [Google Scholar] [CrossRef] [PubMed]
- Dias, E.O.; Miranda, J.A. Finger tip behavior in small gap gradient Hele-Shaw flows. Phys. Rev. E 2010, 82, 056319. [Google Scholar] [CrossRef] [PubMed]
- Al-Housseiny, T.T.; Stone, H.A. Controlling viscous fingering in tapered Hele-Shaw cells. Phys. Rev. Fluids 2013, 25, 092102. [Google Scholar] [CrossRef]
- Anjos, P.H.A.; Dias, E.O.; Miranda, J.A. Fingering instability transition in radially tapered Hele-Shaw cells: Insights at the onset of nonlinear effects. Phys. Rev. Fluids 2018, 3, 124004. [Google Scholar] [CrossRef]
- Miranda, J.A. Analytical approach to viscous fingering in a cylindrical Hele-Shaw cell. Phys. Rev. E 2002, 65, 026303. [Google Scholar] [CrossRef]
- Arun, R.; Dawson, S.T.; Schmid, P.J.; Laskari, A.; McKeon, B.J. Control of instability by injection rate oscillations in a radial Hele-Shaw cell. Phys. Rev. Fluids 2020, 5, 123902. [Google Scholar] [CrossRef]
- Kozlov, V.G.; Karpunin, I.E.; Kozlov, N.V. Finger instability of oscillating liquid–liquid interface in radial Hele-Shaw cell. Phys. Fluids 2020, 32, 102102. [Google Scholar] [CrossRef]
- Karpunin, I.E.; Kozlov, V.G. Oscillatory Dynamics of the Liquid Interface in a Radial Hele-Shaw Cell. Appl. Mech. Eng. 2023, 3, 62–73. (In Russian) [Google Scholar] [CrossRef]
- Kozlov, V.; Vlasova, O. Oscillatory dynamics of immiscible liquids with high viscosity contrast in a rectangular Hele-Shaw channel. Phys. Fluids 2022, 34, 032121. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary-Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Gershuni, G.Z.; Lyubimov, D.V. Thermal Vibrational Convection; Wiley: Chichester, UK, 1998. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).