1. Introduction
With the introduction of small and medium UAVs into everyday commercial and non-commercial operations, the importance of accurate, reliable, and robust sensing systems has become more and more apparent. This is especially true in the case of AI-powered autonomous flight, where machine learning algorithms are employed to make critical decisions without human intervention. Various strategies for safe and effective autonomous flight control exist for navigation [
1,
2], which rely on a number of sensing and inertial systems. However, with the increase in the scale of such operations, it is important that flight is also optimised for efficiency.
The primary difference between conventional flight control strategies in both manned and unmanned fixed-wing flight, in contrast to the flight control seen in natural fliers such as birds and insects, is the sensing distribution and redundancy. Rather than the conventional reliance on single point-mass calculations, coupled with a finite number of reduced pressure readings from selected points over the aircraft body, it is seen that natural fliers will rely on a plethora of distributed sensors around the body, providing a real-time picture of flow phenomena that can be correlated to specific flight conditions. Investigations of biologically inspired sensors have shown a variety of natural fliers using wing receptors to detect temporal flow and pressure changes, in addition to variations in amplitude for signals of the same frequency for executive decision making in flight control and stabilisation [
3]. This is important when considering the high flexibility of such natural fliers in comparison to the relatively rigid airframes of current aircraft and their associated complex flight dynamics models [
4]. Even in high-speed flight, mechanoreceptors on fast fliers have the ability to scale with flow conditions to a high level of sensitivity [
5], which is critical during high-speed stoops where small changes to angle of attack (AoA) can have significant effects on lift generation and flight stability [
6].
Inspired from nature, wind-hair receptors were explored in [
7] to detect changes in the boundary layer velocity profiles, giving detailed information of the overall flow conditions. When those sensors are exposed to flow, they show a deflection response as a result of the length-integrated load distribution along the filamentous hairs. Their response was tested under the different shape factors of the velocity profile and for different boundary layer thicknesses, and the researchers concluded that such wind-hairs are sensitive to flow profile changes from favourable to adverse pressure gradients. Micro-pillar shear stress sensors are even able to directly sense the velocity gradient at the wall [
8] and, as such, can be used to detect local flow reversals [
9]. Their mechanical behavior is well defined under static and dynamic load conditions; therefore, the sensors can quantify the wall-shear stress in magnitude and direction. This, however, limits the size of those sensors in practical applications to the scale of the viscous boundary layer, which is typically in the sub-millimeter range. For practical application, larger “wind-hairs” could be a compromise between gain in sensitivity (stronger bending forces) and the loss of spatial resolution that occurs due to the wall-normal integration effect.
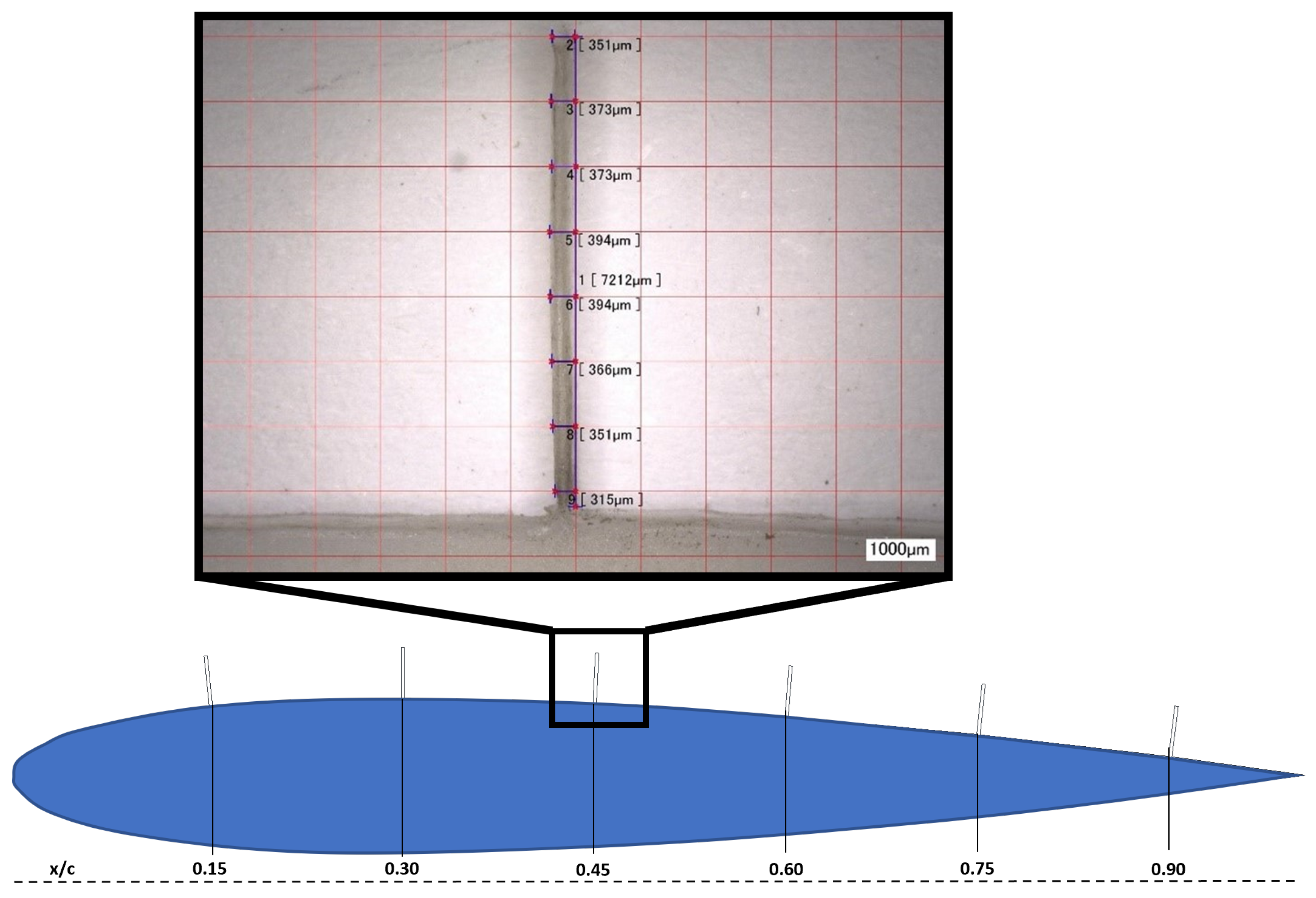
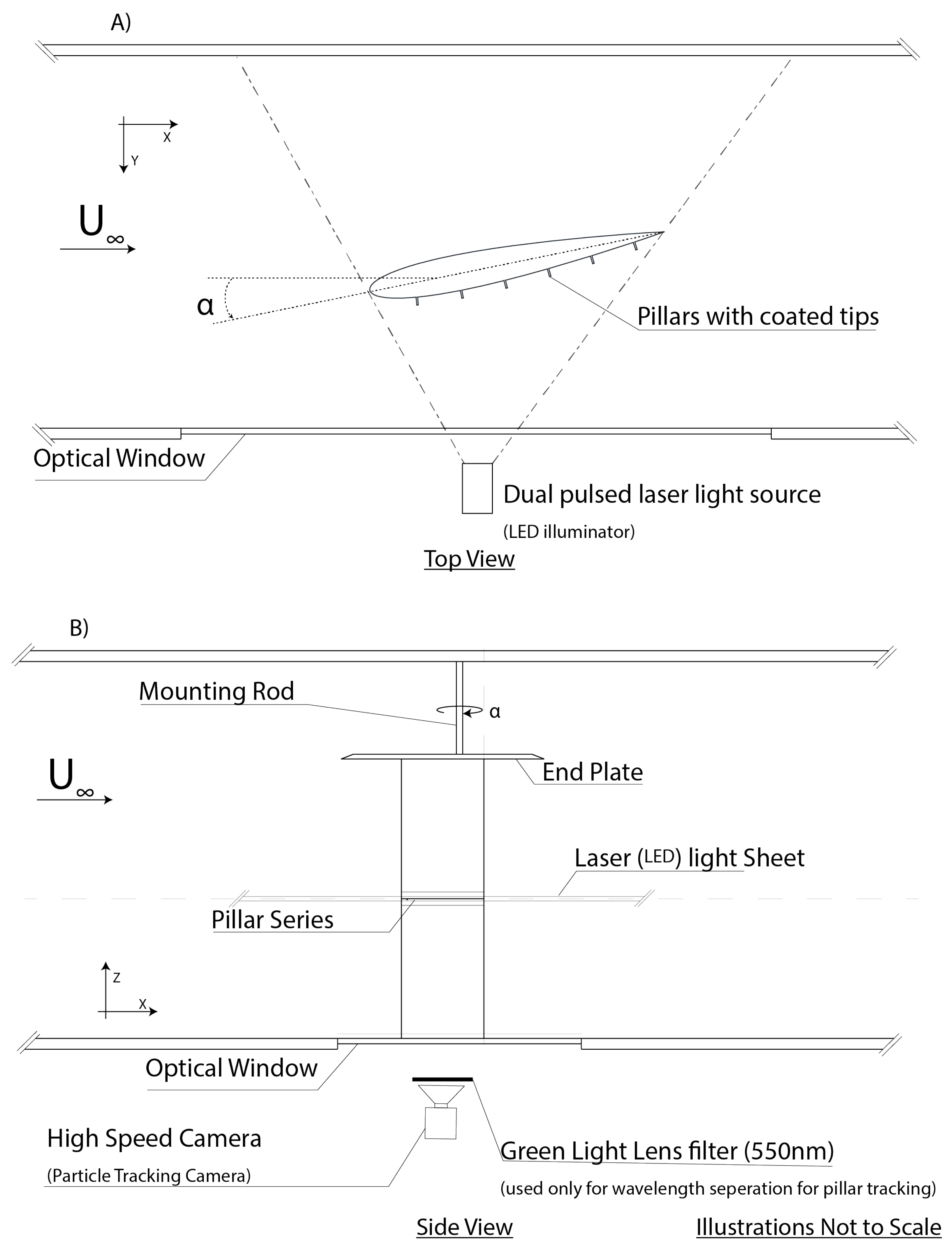
This paper will introduce work carried out on elastic bio-inspired wind-hairs in the form of flexible cantilever structures used for aerofoil flow sensing on an NACA0012 model. Moreover, the novel incorporation of remote optical tracking of such pillars is discussed using a combination of physical wavelength separation, on-board high-speed photography, and a cross-correlation algorithm to obtain a real-time output from such sensors while mitigating the requirement of a physical connection. It is not guaranteed that a physical connection between a sensor and computer on-board a compact UAV will always be available, especially with the emergence of materials of higher strength-to-weight ratios and with modern manufacturing techniques allowing the creation of more complex designs optimised for efficiency rather than internal space. Thus, such remote optical monitoring of sensors allows the capability to obtain flow measurements from areas that otherwise would remain unreachable with traditional point-pressure measurements to provide an AI flight controller with a more complete flow picture for decision making.
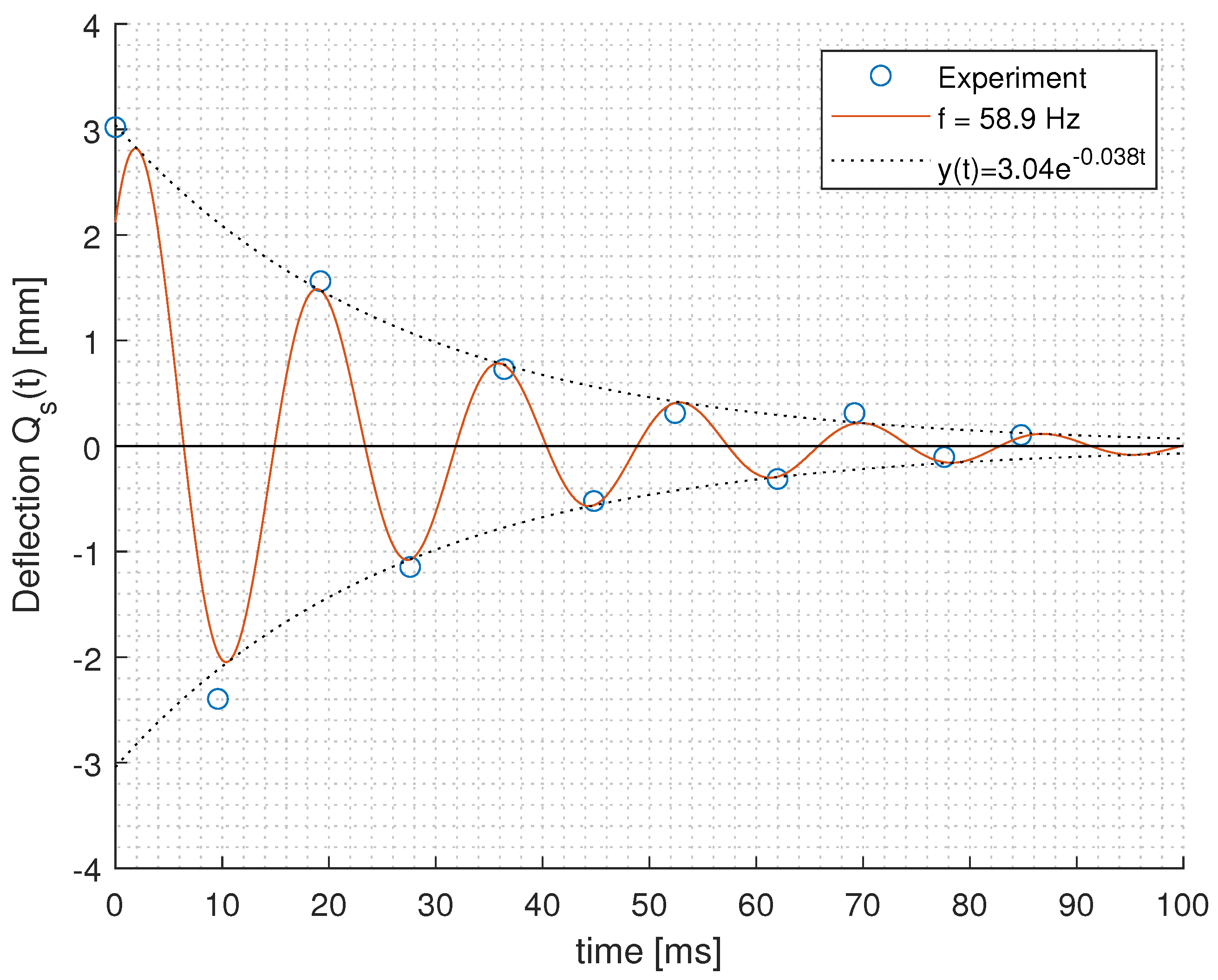
The design, fabrication, characterisation, and calibration of the sensor system is discussed, in addition to in situ calibration and FEA simulations that were carried out to characterise the sensor response in air. Furthermore, several use cases for such sensors are presented in a series of wind-tunnel experiments simulating the flight conditions and system response when placed in a single-row array over the suction side of an aerofoil. Mounting the sensors on an NACA0012 foil was chosen as a use case to explore the sensor’s response to varying conditions at low Reynolds numbers. The flow over an NACA0012 at such Reynolds numbers is well known from the literature [
10,
11,
12] and is within the range for conditions faced by most small- and medium-scale UAVs.
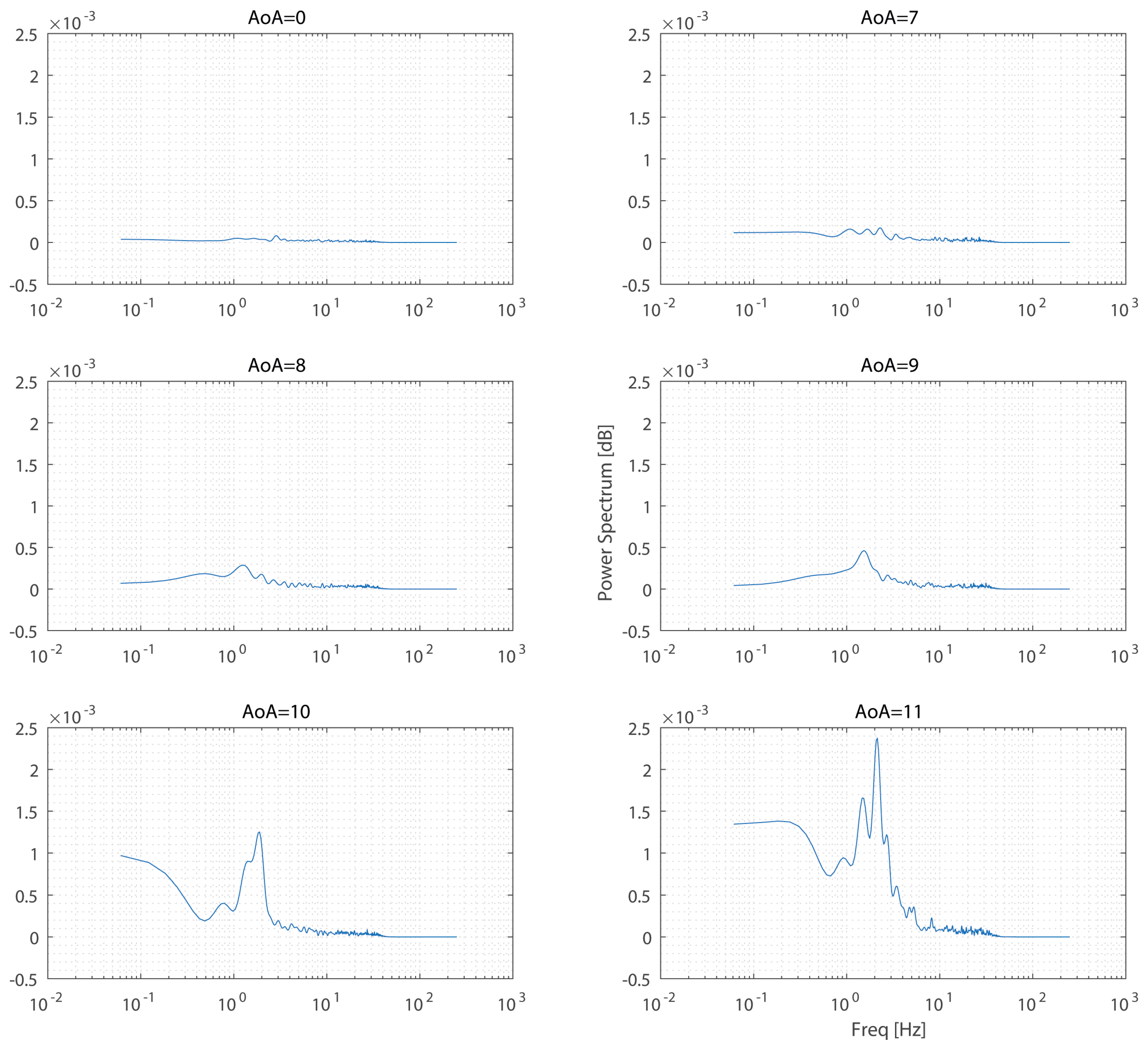
Firstly, sensitivity to the growth of the boundary layer over the suction side of the aerofoil and its relationship to changes in AoA are explored, and the time-averaged response to such conditions is obtained and compared. Furthermore, characteristic fluctuations of the velocity profile that correlate to flow phenomena unique to those AoAs that are incipient to flow separation are detected. Such correlations are known to exist from previous CFD simulations and TR-PIV measurements on an NACA0012 aerofoil undergoing stall [
13,
14,
15], where it was seen that the frequency of the low-frequency oscillations increased with AoA at the onset of stall.
4. Discussion
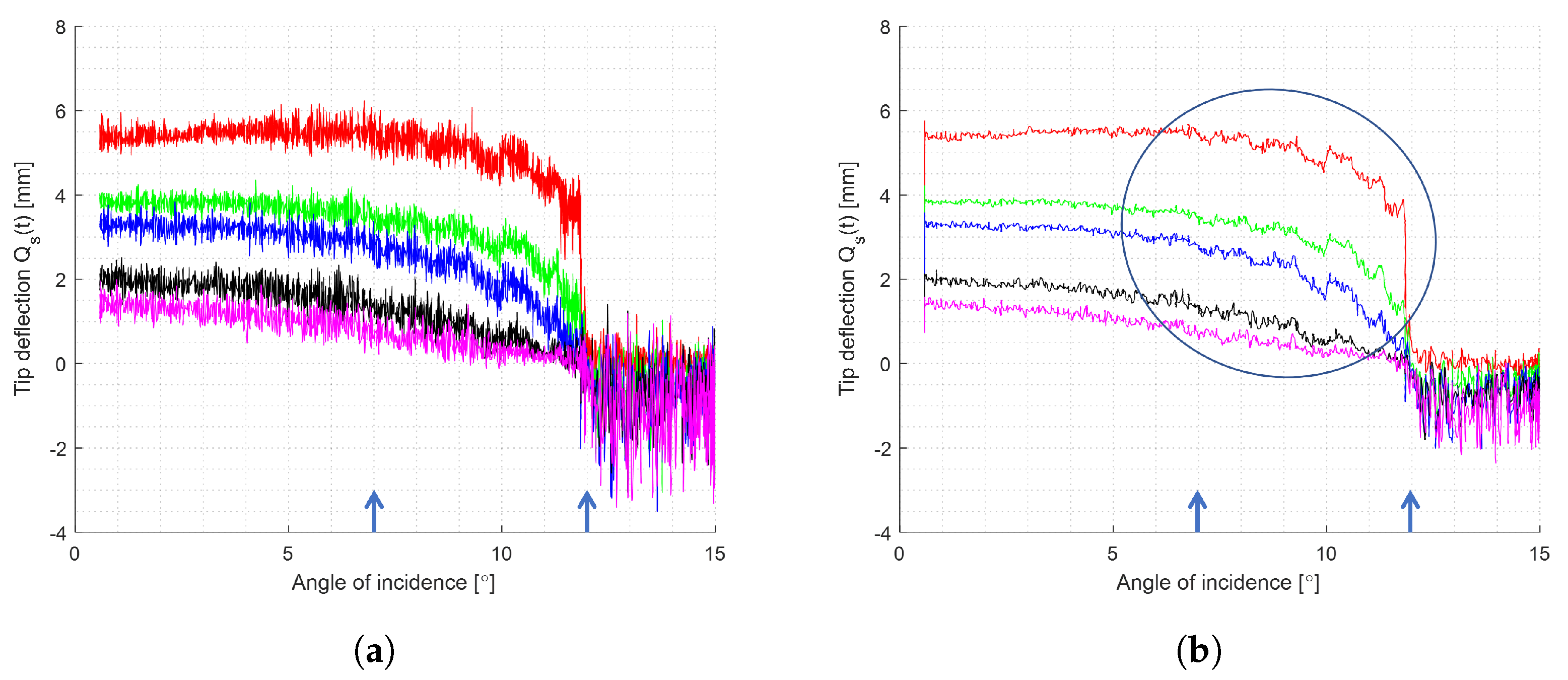
The experimental work presented in this paper has shown the potential for optically tracked flexible pillar sensors to act as “digital tufts”, providing real-time high temporal resolution data that correlate with local flow velocities, from which further data of the flow structures over the wing can be summarized. The use of these sensors for aerofoil sensing was tested, and particular markers were identified that characterized incipient stall conditions. These markers include negative deflections of the aft-most pillars, an increase in the RMS of the fluctuations from the aft-most pillars, and low-frequency oscillations in the fluctuating component of sensor deflection.
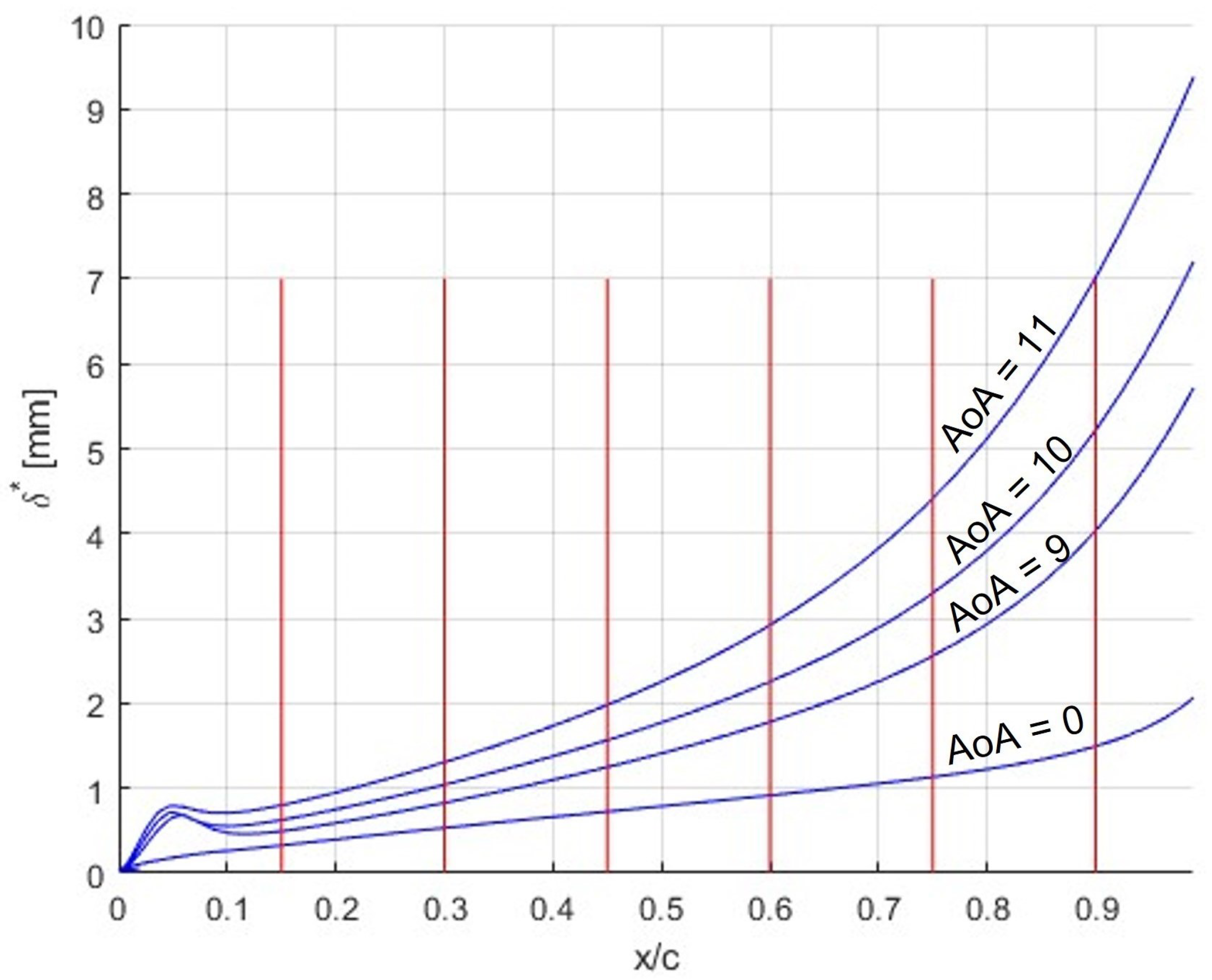
For static conditions of the aerofoil, the time-averaged deflections of all pillars across the chord of the wing show a unique combination that is indicative of the instantaneous AoA prior to stall. That is, by observation of the trend of mean deflection of the sensors in downstream direction, which is represented by the gradient of the mean pillar deflections, it can be seen as unique to each AoA. This result is due to the variation of the boundary layer with chord and AoA (
Figure 16) and the resulting integration effect on the pillar sensors. The sensitivity of such a type of sensor to the thickness and the shape factor of the boundary layer has been shown already in [
7] and is confirmed herein by the observed results for varying AoA.
This use case is intended as a proof of concept for this type sensors to investigate their capability of sensing aerofoil flow conditions and detecting incipient stall. It was seen that particular markers were present to characterise those conditions. Firstly, instances of negative deflection, that is, the deflection of the pillar sensors in the direction opposite to the free-stream flow and past the wind-off position, were seen on the aft-most pillars. These are indicative of growing local flow instabilities and reversed flow situations, which were seen to be present in the high pre-stall AoAs. Moreover, by monitoring the fluctuating component of sensor deflection, an increase in the RMS of the fluctuations from those aft-most pillars was also seen in those AoAs incipient to flow separation and stall. Both of these markers occur with a response time in the order of the sensor response time, which is less than 100 ms. Finally, spectral analysis of the fluctating components from the signal showed particular low-frequency oscillations occurring in the AoAs leading up to stall. Previous data in literature let us hypothesise that the low-frequency oscillations are linked to the quasi-periodic breathing of the laminar separation bubble formed over the suction side of the wing. The frequency and intensity of such a signature, as tracked by the flexible pillar sensors, can be correlated with the flight condition, specifically the AoA. Alternatively, other correlations can be tested for specific flight conditions in training or learned from application to be identified by training a specialised neural network. However the applications are not limited to aerofoil sensing, and further development would be required for direct application on commercial UAVs. Although the mean component is fairly robust and with a low response time, particularly when monitoring over an array where the redundancy of the received signals would allow for a reliable reading, the oscillations used to characterise incipient stall are of a relatively low frequency, occurring at Strouhal numbers on the order of 0.02. Thus, they would be marginally useful as a standalone system, but further work incorporating such sensors into a suite would allow such measurements to be used in conjunction with other measurements, such as a sharp increase in the detected angle of incidence, to more reliably characterise incipient stall.
Optical tracking was explored herein as a method to obtain the pillar deflection readings remotely without any physical connection to the sensor. This is meant to exploit the physical nature of the sensor deflections, which would not be present with other measurement types, such as pressure measurements. The applications of the optical tracking of flow measurements would be where physical connections are not possible or not optimal, and such lightweight optical equipment may offer an alternative to obtain measurements from areas that would otherwise either go unsensed or where it would mitigate the cost justification for obtaining measurements from such an area. Furthermore, where pressure sensing may not be applicable, such as in underwater flows, optically tracked pillars can act as an alternative to provide a flow picture for analysis.
There is a general limitation with such hair-type sensor arrays. First is the fact that those sensors are invasive to the flow, and second is the fact that their dynamics may interfere with the output of one another; thus, the pillars must be spaced apart appropriately to avoid interaction effects and to ensure that the reading from each pillar is representative of the surrounding flow conditions. The pillars in the use cases presented herein were spaced at 20 diameters apart to mitigate inter-pillar disturbances. A further improvement would be to offset every other pillar in the span-wise direction to further lessen these effects. That way, their readings can be considered collectively, as in (
Figure 8), or individually, as in (
Figure 11), to provide accurate flow condition information. It is, furthermore, suggested in future designs to size the pillars that are unaffected by boundary layer flow appropriately so that they are sufficiently distant from the reconfiguration limit of deflection while maintaining sensitivity along the remainder of the array. This can be achieved by varying the leading-edge-most pillar dimensions and structural properties from those further aft. Moreover, the sensors presented herein are intended as a proof of concept rather than a plug-and-play solution. Further work is required in terms of manufacturing technology and equipment to produce pillars with dimensions that can vary depending on the operating fluid. The pillars were designed to find a balance between facilitating optical tracking from standard optical systems mounted on-board and providing the least possible disturbance to the flow. This is a trade-off between reducing the dimensions of the pillars such that their invasive character is reduced and the resolution limit of the imaging system, where smaller structures lead to less visibility and lower optical resolution. The arrangement used herein, together with the rather moderate Re-number flows tested, represent a good practical compromise of the given system for the envisioned application of such sensors on small UAVs.
Pillar sensors can provide a multitude of velocity and velocity-derived data to be used for real-time diagnostics. Compared to wool tuft visualisations, the pillar sensors’ capability to encode the mean and fluctuating part of the local velocity provides more rich diagnostics of the current flow state. Spectral analyses of the signal in conjunction with pattern recognition algorithms were used here to identify specific quantities unique to the flight conditions. Introducing and training a specialised neural network to identify the local flow conditions, such as was carried out with similar nature-inspired sensors in [
19], is planned as a further development of this system. Furthermore, spatial near-wall flow field recovery techniques can be applied from the relative sparse sensor placement using deep learning. For timely decision making and response to signals in an aeronautical system in situ, the signals must be collected and processed “on the fly” with optical systems that can filter out irrelevant data using physical means such as wavelength separation, in addition to computational means, and then process that data within the required time period. Using on-line object tracking, it was possible to train the camera on the relevant pillar tips to instantaneously output a time-series of coordinates corresponding to the pillar tip deflections for a specified time period and sampling rate. These type of recordings with multiple levels of filtering and pre-processing are often affected by corrupt or sparse data. Emerging technologies in reconstructing such data structures such as sparse representation and compressive sensing can allow for the timely and efficient onboard processing of these data for subsequent flight or flow control decision making [
25].
Finally, span-wise data can be obtained by including an entire array of these pillar sensors spanning a wing. These can be used over the skin of a wing in a wind tunnel or fitted onto the system in operation. An example application for such an array would be to characterise localised stall over the span of a washed-out wing, where stall typically occurs near the wing-root, providing a real-time reading of remaining aerodynamic lift or aileron efficiency. Current work on the sensors is looking at local flow conditions at post-stall AoA as a way of characterising span-wise local stall phenomena simply from tip-deflection data of the pillars (
Figure 17). The response from the fore-most pillars in this paper were seen to be least affected by local flow instabilities and more reflective of the free-stream flow conditions. Thus, further work incorporating these pillars into 2D arrays will investigate the capability of obtaining a fuller picture of the free-stream flow by monitoring the response of those fore-most pillars to induced flow disturbances, such as wake-turbulence or gusts. Coherent signatures of flow events over several pillar sensor positions is a way to distinguish noise from relevant structures. Thus, these can be separated by eliminating those signals that occur with no chord-wise phase delays, and for further robustness, can be correlated with signals from an on-board accelerometer. This, coupled with the developed signal processing from the sensors, will allow the ability to provide diagnostic data for an aerodynamic system’s performance over a wide regime of flow conditions. This leads into the development of a system of biologically inspired sensors, which react in a predictable manner to changes in flow conditions within the flight regime of small- to medium-sized UAVs, which can be used in situ to promptly provide diagnostic data to a flight control system or can be used for diagnostics in experimental conditions.