Numerical Modelling of Water Flashing at Sub-Atmopsheric Pressure with a Multi-Regime Approach
Abstract
1. Introduction

1.1. Experiments at Sub-Atmospheric Pressure
1.2. Bibliographical Synthesis of the Flash Boiling Models
2. Models
2.1. The Neptune_cfd Code
2.2. Equations Solved
2.3. The Liquid/Bubble Model
2.3.1. Interfacial Momentum Transfer
2.3.2. Interfacial Enthalpy Transfer
2.4. The Generalised Large Interface Model (GLIM)
2.4.1. Interfacial Momentum Transfer
2.4.2. Interfacial Enthalpy Transfer
3. Saury’s Experiments
3.1. The Experimental Facility
3.2. Mesh, Initial Conditions and Boundary Conditions
4. Results and Discussion
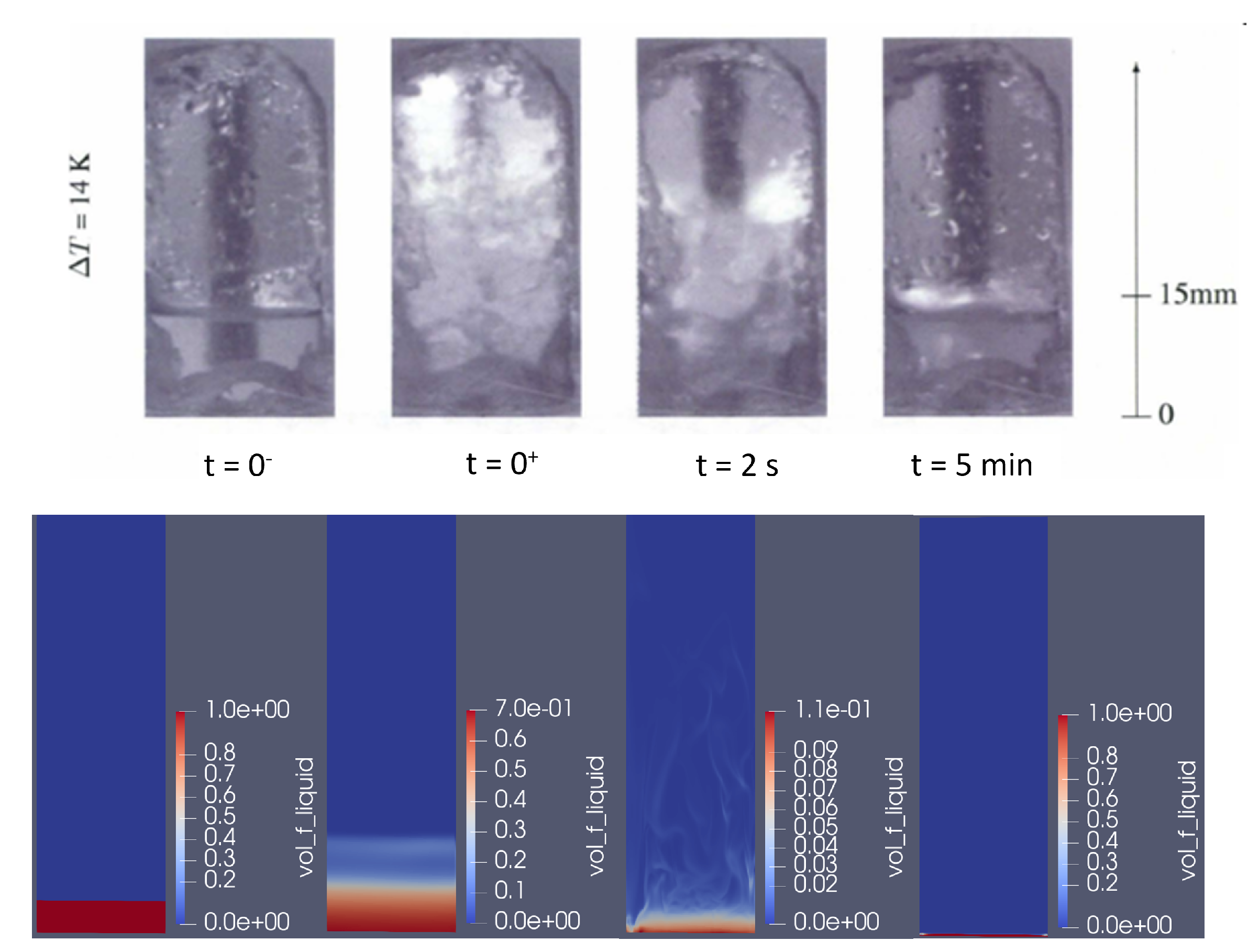
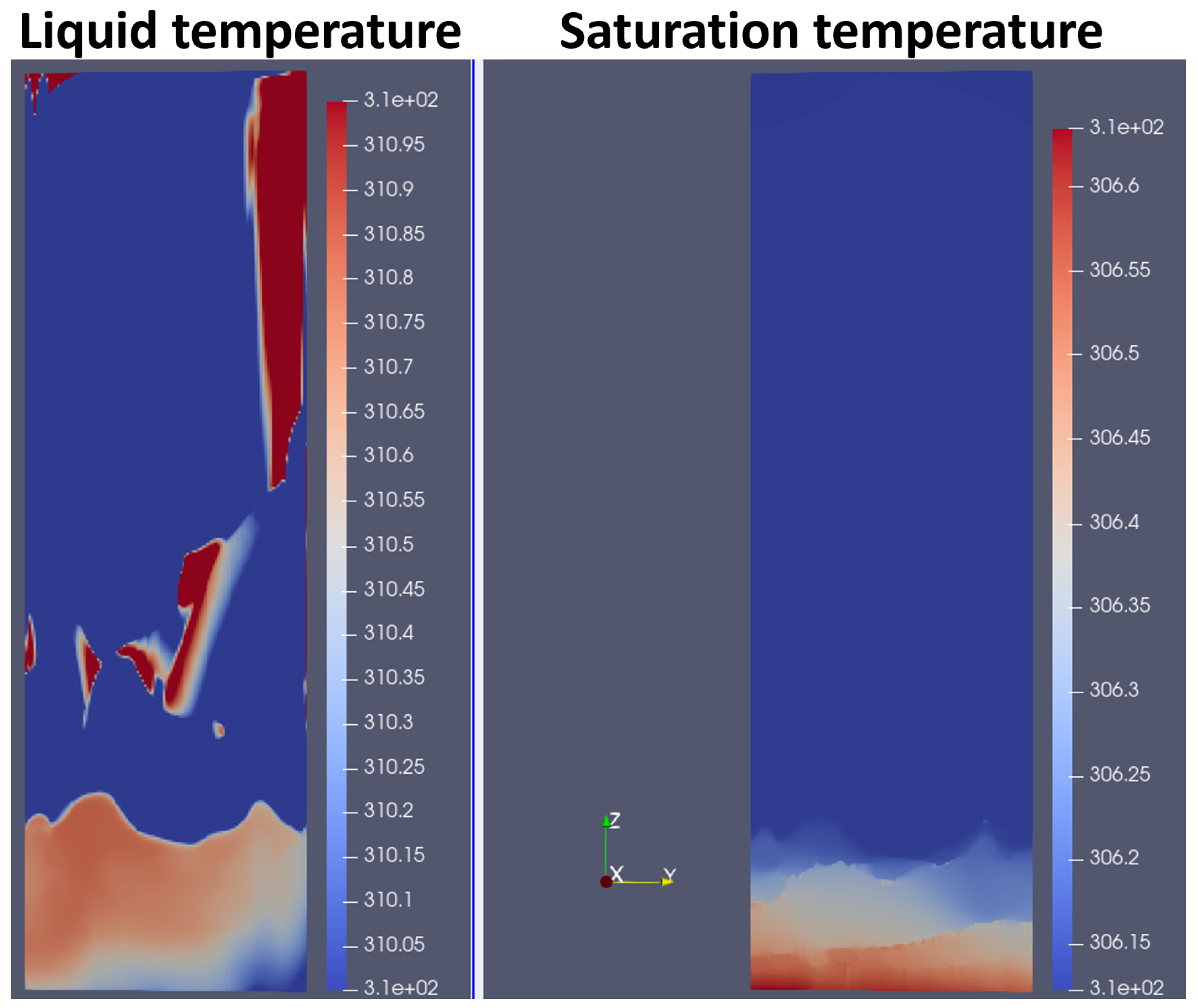
4.1. Qualitative Results
4.2. Quantitative Results
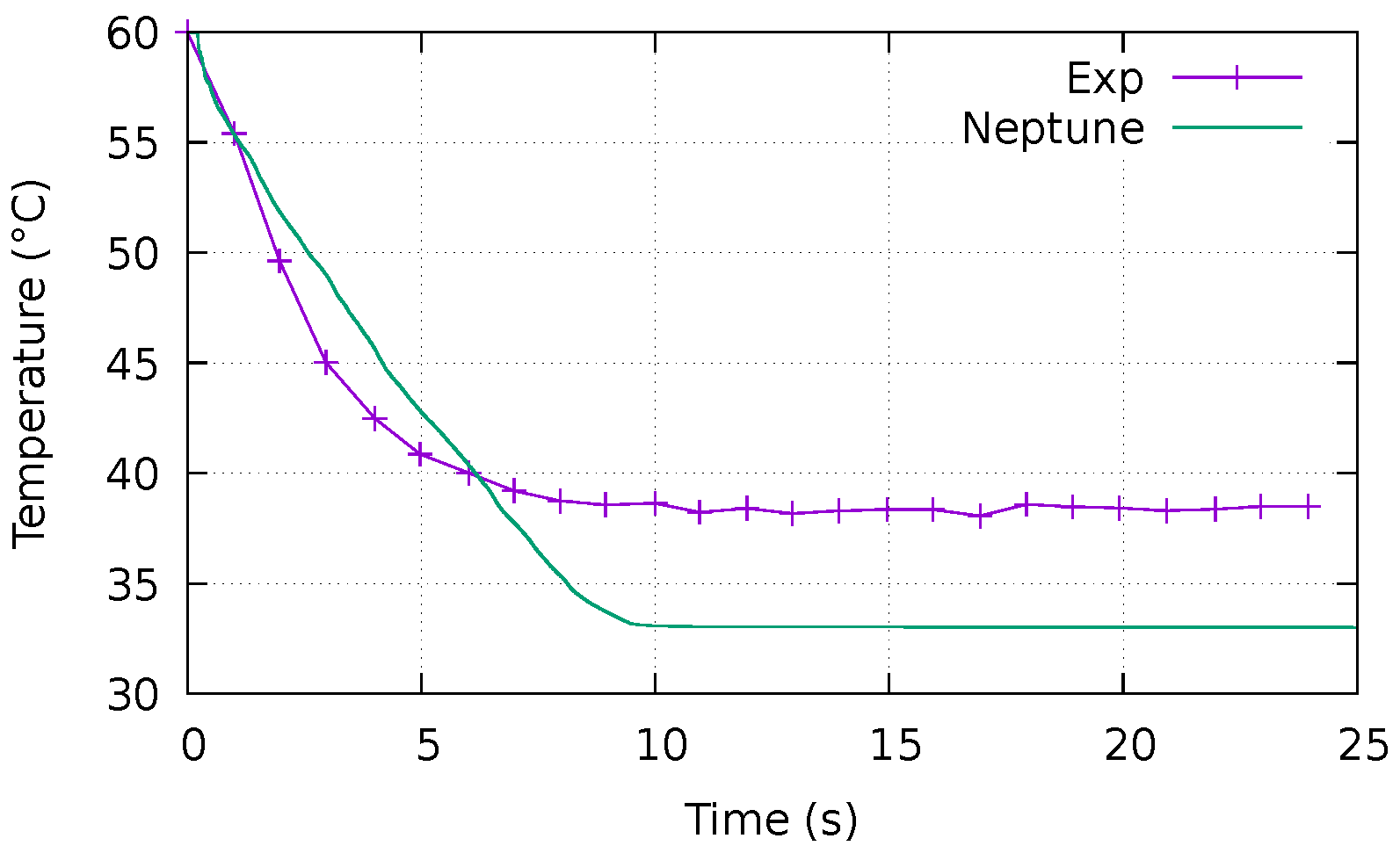
4.2.1. Evolution of the Temperature over Time
- 1.
- Experimental uncertainties on the temperature ( C according to Saury [1]);
- 2.
- Errors during the digitisation of the experimental results from the graphs given by Saury ( C, particularly visible in Figure 9a);
- 3.
- Computation of the asymptotic pressure with the ideal gas law (the error is difficult to quantify);
- 4.
- Finally, Saury [1] explained that some experimental errors might come from the measurement of the liquid height, and affect the results by a few percent.
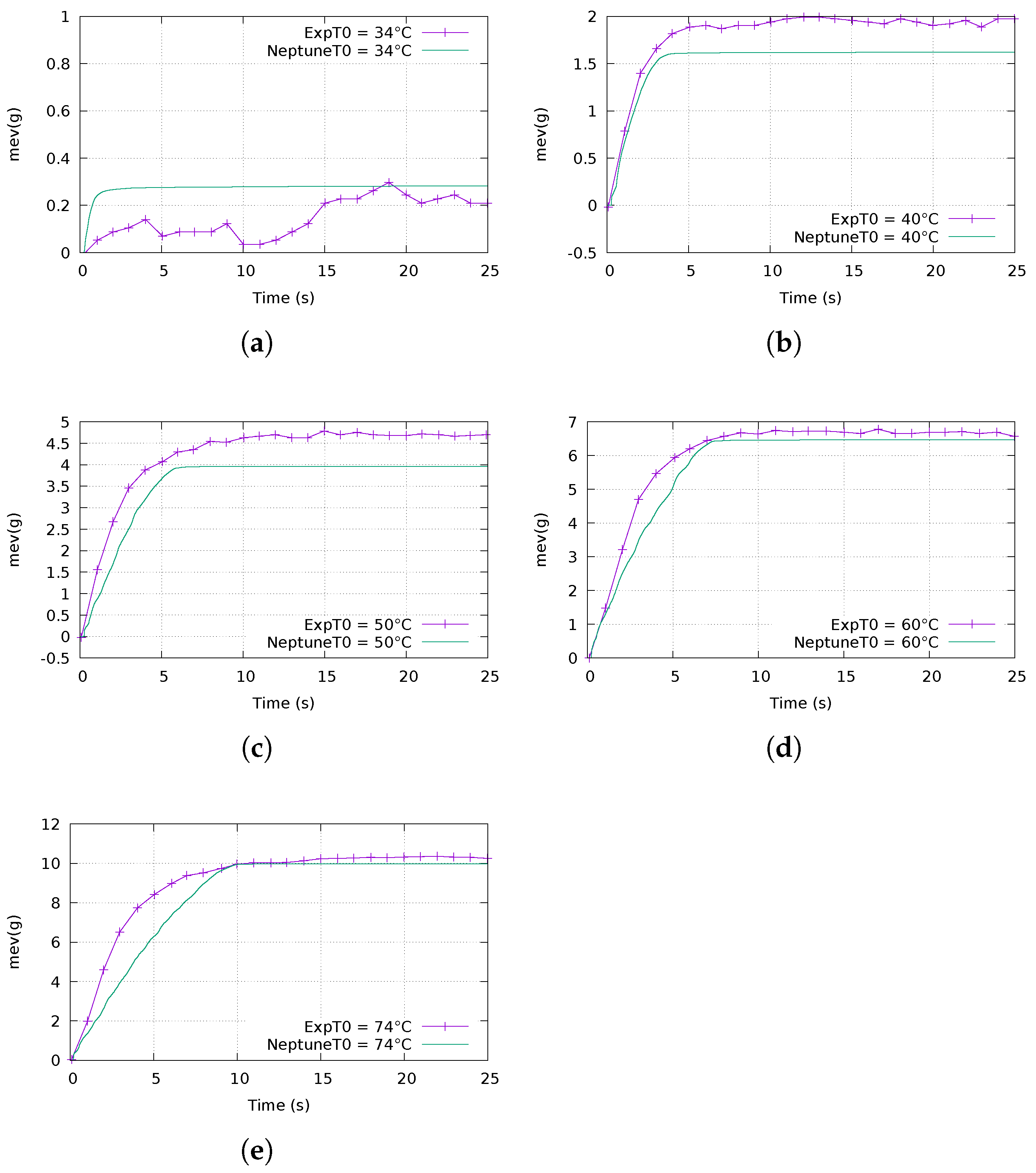
4.2.2. Evolution of the Evaporated Mass over Time
- 1.
- In one experiment, the initial pressure in the vacuum chamber is mbar and the initial temperature is C, which represents a 14 C superheat;
- 2.
- In the other experiment, the initial pressure is mbar and the initial temperature is C, which also represents a 14 C superheat.
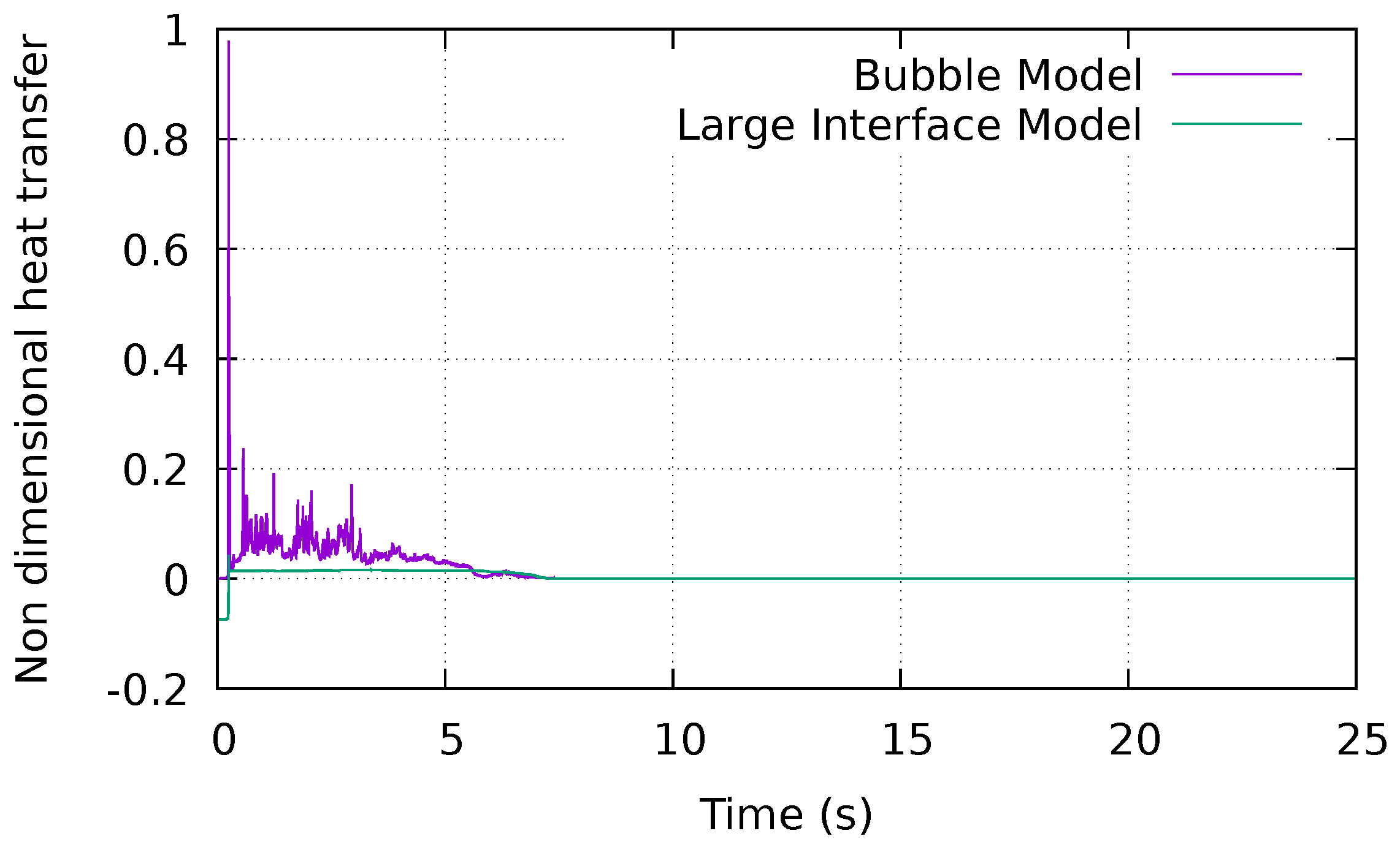
4.3. Boiling at the Interface during the Second Stage
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
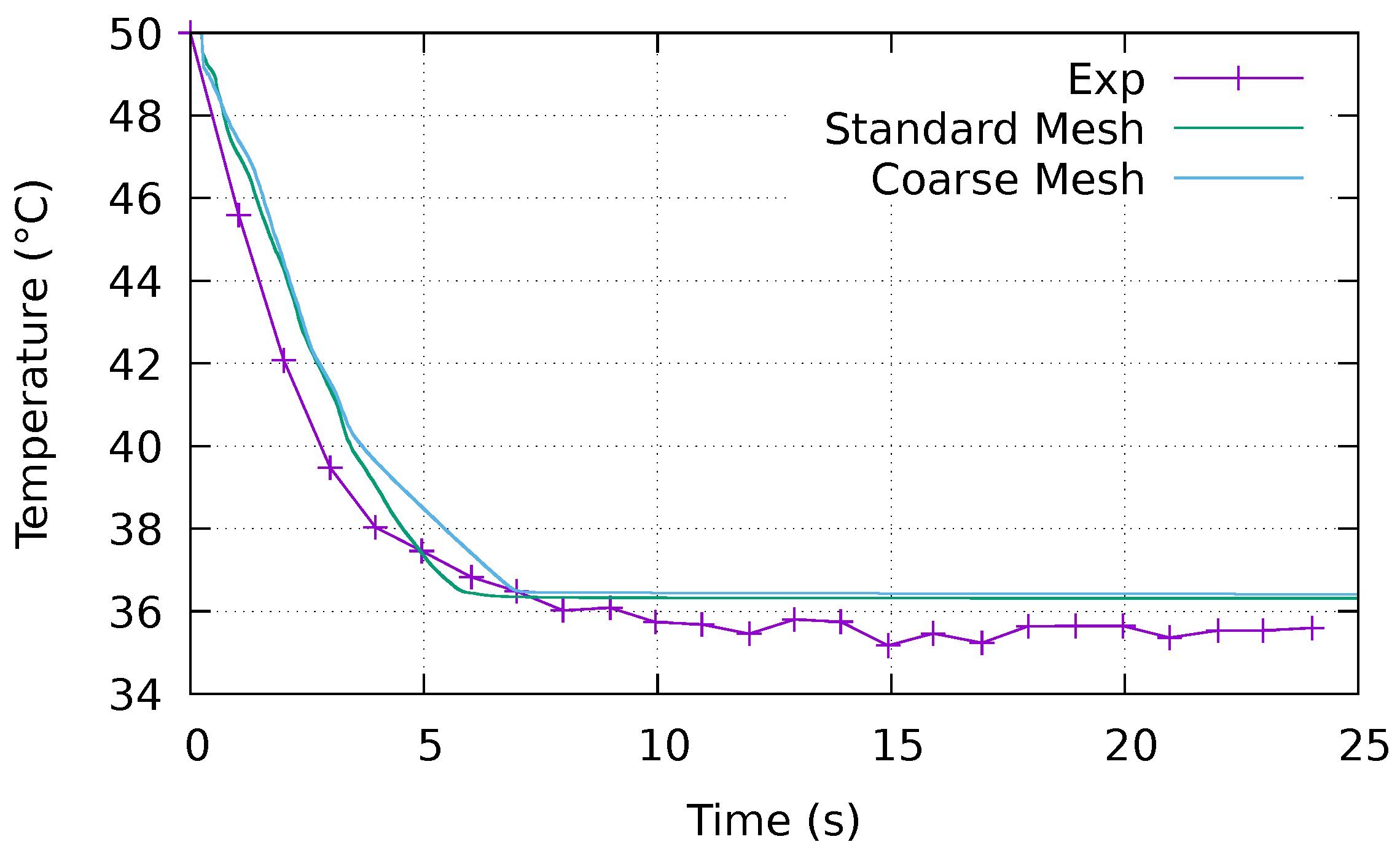
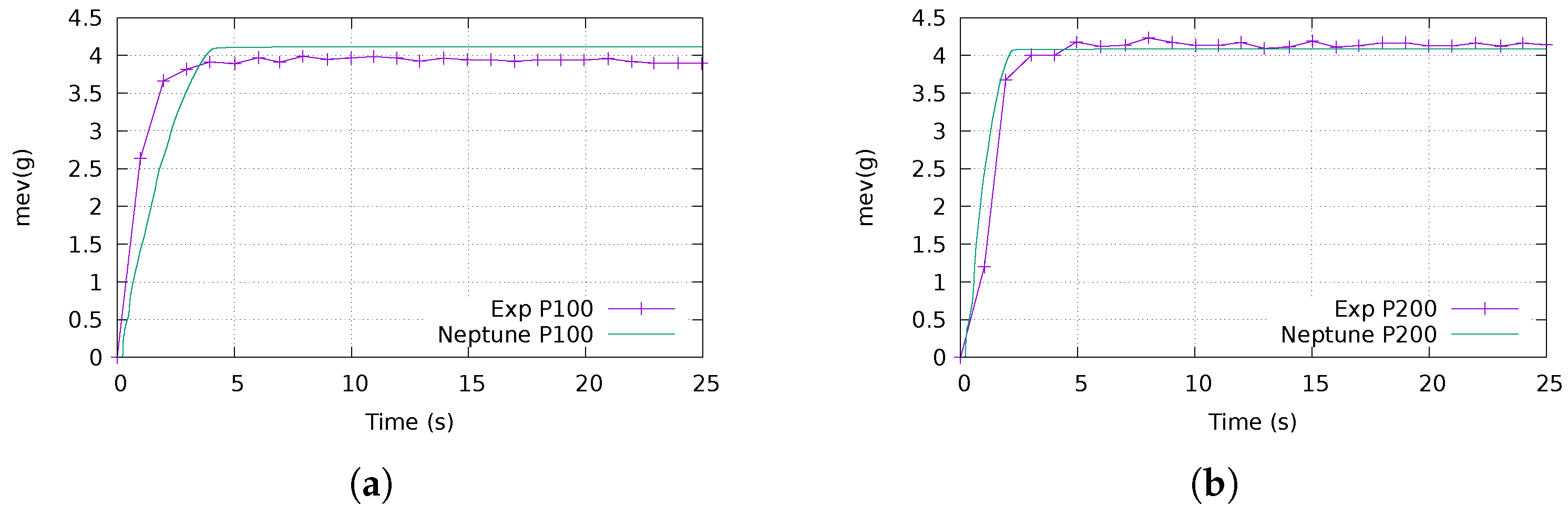
Appendix A. Mesh Sensitivity
References
- Saury, D. Etude Expérimentale de l’Évaporation d’un Film d’Eau. Ph.D. Thesis, Université de Valenciennes et du Hainaut-Cambrésis, Valenciennes, France, 2003. [Google Scholar]
- Lv, H.; Wang, Y.; Wu, L.; Hu, Y. Numerical simulation and optimization of the flash chamber for multi-stage flash seawater desalination. Desalination 2019, 465, 69–78. [Google Scholar] [CrossRef]
- Woods, A.; Bloom, F.; Orloff, D. Modeling of flash evaporation I: Formulation of the mathematical model. Math. Comput. Model. 2000, 32, 1153–1169. [Google Scholar] [CrossRef]
- Mimouni, S.; Boucker, M.; Laviéville, J.; Guelfi, A.; Bestion, D. Modelling and computation of cavitation and boiling bubbly flows with the NEPTUNE_CFD code. Nucl. Eng. Des. 2008, 238, 680–692. [Google Scholar] [CrossRef]
- Narayanan, C. Numerical simulation of flashing using a pressure-based compressible multiphase approach and a thermodynamic cavitation model. Int. J. Multiph. Flow 2021, 135, 103511. [Google Scholar] [CrossRef]
- Hurisse, O.; Quibel, L. Simulations of water-vapor two-phase flows with non-condensable gas using a Noble-Able-Chemkin stiffened gas equation of state. Comput. Fluids 2022, 239, 105399. [Google Scholar] [CrossRef]
- Miyatake, O.; Murakami, K.; Kawata, Y. Fundamental experiments with flash evaporation. Heat Transf.-Jpn. Res. 1973, 2, 89–100. [Google Scholar]
- Gopalakrishna, S.; Purushothaman, V.; Lior, N. An experimental study of flash evaporation from liquid pools. Desalination 1987, 65, 139–151. [Google Scholar] [CrossRef]
- Augusto, C.; Ribeiro, J.; Gaspar, A.; Costa, J. Low-pressure-vaporization of free water—Characterization of the boiling regimes. Int. J. Therm. Sci. 2014, 77, 19–26. [Google Scholar] [CrossRef]
- Wang, C.; Xu, R.; Chen, X.; Jiang, P.; Liu, B. Study on water flash evaporation under reduced pressure. Int. J. Heat Mass Transf. 2019, 131, 31–40. [Google Scholar] [CrossRef]
- Enoki, K.; Ono, M.; Okawa, T.; Kristiawan, B.; Wijayanta, A.T. Water flow boiling heat transfer in vertical minichannel. Exp. Therm. Fluid Sci. 2020, 117, 110147. [Google Scholar] [CrossRef]
- Ishii, M. Thermo-fluid dynamic, theory of two phase. In Collection de la Direction des Etudes et Recherches d’Electricité de France; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Delhaye, J.M.; Giot, M. Thermal-Hydraulics of Two-Phase Systems for Industrial Design and Nuclear Engineering; Hemisphere: New York, NY, USA, 1981. [Google Scholar]
- Guelfi, A. NEPTUNE—A new software platform for advanced nuclear thermal hydraulics. Nucl. Sci. Eng. 2007, 156, 281–324. [Google Scholar] [CrossRef]
- Mimouni, S. Modeling and computation of cavitation and boiling bubbly flows with the NEPTUNE_CFD code. Nucl. Sci. Eng. 2008, 156, 281–324. [Google Scholar]
- Speziale, C.G.; Sarkar, S.; Gatski, T.B. Modelling the pressure–strain correlation of turbulence: An invariant dynamical systems approach. J. Fluid Mech. 1991, 227, 245–272. [Google Scholar] [CrossRef]
- Ishii, M.; Zuber, N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Tomiyama, A.; Tamai, H.; Zun, I.; Hosokawa, S. Transverse migration of single bubbles in simple shear flows. Chem. Eng. Sci. 2002, 57, 1849–1858. [Google Scholar] [CrossRef]
- Zuber, N. On the dispersed two-phase flow in the laminar flow regime. Chem. Eng. Sci. 1964, 19, 897–917. [Google Scholar] [CrossRef]
- Berne. Analyse Critique des Modèles d’Autovaporisation Utilisés dans le Calcul des Écoulements Diphasiques en Conduites. Ph.D. Thesis, Ecole Centrale Paris, Gif-sur-Yvette, France, 1983. [Google Scholar]
- Mérigoux, N.; Lavieville, J.; Mimouni, S.; Guingo, M.; Baudry, C. A generalized large interface to dispersed bubbly flow approach to model two-phase flows in nuclear power plant. In Proceedings of the 6th Workshop on Computational Fluid Dynamics for Nuclear Reactor Safety (CFD4NRS-6), Cambridge, MA, USA, 13–15 September 2016. [Google Scholar]
- Mer, S.; Praud, O.; Neau, H.; Merigoux, N.; Magnaudet, J.; Roig, V. The emptying of a bottle as a test case for assessing interfacial momentum exchange models for Euler–Euler simulations of multi-scale gas-liquid flows. Int. J. Multiph. Flow 2018, 106, 109–124. [Google Scholar] [CrossRef]
- Davy, G.; Reyssat, E.; Vincent, S.; Mimouni, S. Euler–Euler simulations of condensing two-phase flows in mini-channel: Combination of a sub-grid approach and an interface capturing approach. Int. J. Multiph. Flow 2022, 149, 103964. [Google Scholar] [CrossRef]
- Honda, H.; Wijayanta, A.; Takata, N. Condensation of R407C in a horizontal microfin tube. Int. J. Refrig. 2005, 28, 203–211. [Google Scholar] [CrossRef]
- Griffith, P.; Wallis, G.B. Two-Phase Slug Flow. J. Heat Transf. 1961, 83, 307–318. [Google Scholar] [CrossRef]
- Taitel, Y.; Bornea, D.; Dukler, A.E. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes. AIChE J. 1980, 26, 345. [Google Scholar] [CrossRef]
- Murzyn, F.; Chanson, H. Free-Surface Fluctuations in Hydraulic Jumps: Experimental Observations. Exp. Therm. Fluid Sci. 2009, 33, 1055–1064. [Google Scholar] [CrossRef]
- Mimouni, S.; Foissac, A.; Lavieville, J. CFD modelling of wall steam condensation by a two-phase flow approach. Nucl. Eng. Des. 2011, 241, 4445–4455. [Google Scholar] [CrossRef]
- Loiseau, C.; Mimouni, S.; Studer, E. Numerical simulation of wall condensation and spray using the MISTRA experiments. Nucl. Eng. Des. 2023, 402, 112111. [Google Scholar] [CrossRef]
- Coste, P. A Large Interface Model for two-phase CFD. Nucl. Eng. Des. 2013, 255, 38–50. [Google Scholar] [CrossRef]
- Wen, C.; Yu, Y. Mechanics of Fluidization. Chem. Eng. Prog. 1966, 162, 100–111. [Google Scholar]
- Mimouni, S.; Lamy, J.S.; Lavieville, J.; Guieu, S.; Martin, M. Modelling of sprays in containment applications with A CMFD code. Nucl. Eng. Des. 2010, 240, 2260–2270. [Google Scholar] [CrossRef]
- Manon, E. Contribution à l’Analyse et à la Modélisation Locale des Écoulements Bouillants Sous-Saturés dans les Conditions des Réacteurs à Eau sous Pression. Ph.D. Thesis, Ecole Centrale Paris, Gif-sur-Yvette, France, 2000. [Google Scholar]
- Saury, D.; Harmand, S.; Siroux, M. Experimental study of flash evaporation of a water film. Int. J. Heat Mass Transf. 2002, 45, 3447–3457. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. 36-ParaView: An end-user tool for large-data visualization. Vis. Handb. 2005, 717, 50038-1. [Google Scholar]
- Bruhat, G. Cours de Physique Générale, 6th ed.; Masson: Issy-les-Moulineaux, France, 1968. [Google Scholar]
- Massart, F. Aide Mémoire du Thermicien; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]




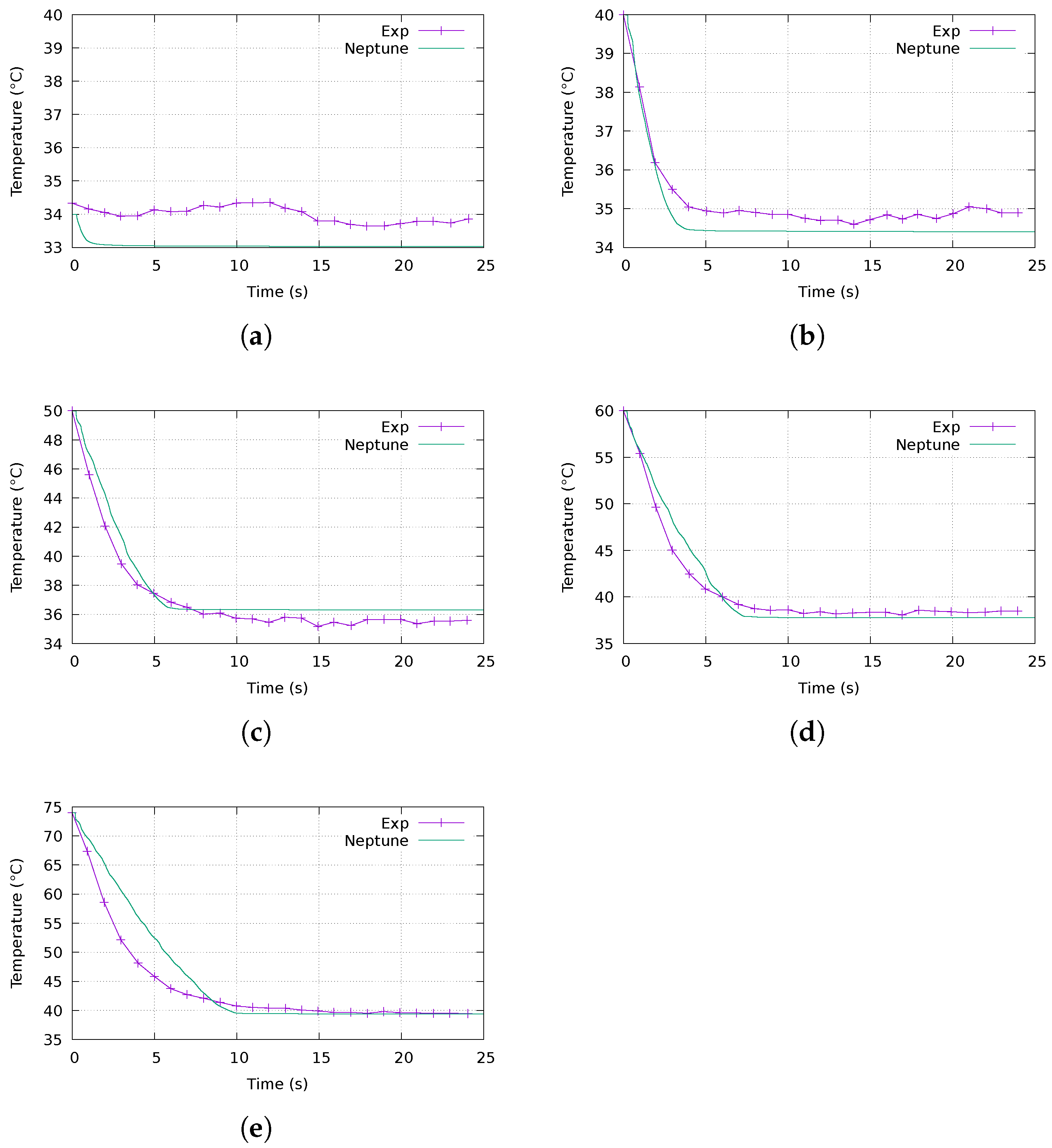

| (C) | (mol) | (mbar) | (C) | |
|---|---|---|---|---|
| 34 | 0.2 | 0.011 | 50 | 33.0 |
| 40 | 2 | 0.11 | 54 | 34.3 |
| 50 | 4.5 | 0.25 | 60 | 36.2 |
| 60 | 6.8 | 0.38 | 65 | 37.6 |
| 74 | 10.0 | 0.56 | 71 | 39.0 |
| (C) | (kg/m) | (kJ/kg) |
|---|---|---|
| 34 | 994.05 | 2433 |
| 40 | 992.26 | 2419 |
| 50 | 988.10 | 2390 |
| 60 | 983.22 | 2360 |
| 74 | 975.38 | 2320 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loiseau, C.; Mimouni, S.; Colmont, D.; Vincent, S. Numerical Modelling of Water Flashing at Sub-Atmopsheric Pressure with a Multi-Regime Approach. Fluids 2023, 8, 143. https://doi.org/10.3390/fluids8050143
Loiseau C, Mimouni S, Colmont D, Vincent S. Numerical Modelling of Water Flashing at Sub-Atmopsheric Pressure with a Multi-Regime Approach. Fluids. 2023; 8(5):143. https://doi.org/10.3390/fluids8050143
Chicago/Turabian StyleLoiseau, Clément, Stéphane Mimouni, Didier Colmont, and Stéphane Vincent. 2023. "Numerical Modelling of Water Flashing at Sub-Atmopsheric Pressure with a Multi-Regime Approach" Fluids 8, no. 5: 143. https://doi.org/10.3390/fluids8050143
APA StyleLoiseau, C., Mimouni, S., Colmont, D., & Vincent, S. (2023). Numerical Modelling of Water Flashing at Sub-Atmopsheric Pressure with a Multi-Regime Approach. Fluids, 8(5), 143. https://doi.org/10.3390/fluids8050143







