Abstract
Nowadays, wind energy is one of the most cost-effective and environmentally friendly energies in high demand due to shortages in fossil fuels and the necessity to reduce global carbon footprint. One of the main goals of wind turbine development is to increase the power output of the turbine either by increasing the turbine blade swept area or increasing the velocity of the wind. In this article, a proprietary augmentation system was introduced to increase the power output of vertical axis wind turbines (VAWT) by increasing the free stream velocity to more than two folds. The system comprises two identical airfoiled casings within which the turbine/turbines are seated. The results showed that the velocity slightly increases when decreasing the gap between the casing. It was also found that changing the angle of attack of the housing has more impact on the augmented airspeed. CFD technique was used to assess the velocity and flow of air around the system.
1. Introduction
Today, wind energy is considered the most cost-effective solution among other renewable energies leading to its installed capacity being increased day by day [1]. As of the end of 2014, there were around 300 small wind turbine manufacturers, of which 75% were mainly invested in the horizontal axis wind turbine (HAWT) while 20% were invested in vertical axis wind turbines (VAWT), and 5% in their combination [2]. The total global wind power capacity is now up to 837 GW, and the global wind energy market is expected to grow by 6.6% per year on average [3].
The kinetic energy from the wind is extracted by the wind turbine and, subsequently, converted into electrical power. Wind turbines have a limited power output. The ratio of the output power to the available wind power is defined as the power coefficient (Cp). For open flow, the maximum efficiency of a wind turbine is approximately 59%, as set by the Beltz limit [4]. HAWT is widely used in wind energy conversion technology as it has high power efficiency compared to VAWT [5]. However, VAWT can produce energy at various and diffuse velocity conditions [6]. VAWT is classified into two groups, the lift type and the drag type [7]. Drag type VAWT have concave cup-shaped blades like the Savonius turbines, which produce high torque but low rotational speed hence less electrical power than the lift type [8]. Darrieus turbines, on the other hand, have airfoil-shaped blades. When the wind flow interacts with the blades, the turbine starts rotating as aerodynamic lift forces are created; however, this type of turbine has the disadvantage of self-starting problems [9].
To improve the energy efficiency of VAWT, rotor modifications, and augmentation systems require more attention from researchers. Wong et al. [10] reviewed the performance improvement of VAWT research. Karmakar [11] reviewed and summarized various flow augmentation techniques used to increase the generated power by VAWT. Their review covered more than 36 different designs of the most relevant work of known augmentation methods, like deflectors, guide vanes, converging ducts, diffusers, and stators that are incorporated with VAWTs to create a venturi effect at the inlet. The current design can concentrate the airflow and reduce negative torque with the help of an airfoil-like stator where the turbine is seated. Unlike most of the available designs, it can enhance the power augmentation to eight folds by simply adding an airfoil-like stator around existing turbines. The stator can be made from simple materials, like sail fabric or metal sheet, and can be easily guided with mechanical or electronic means to optimize its performance.
2. Materials and Methods
Wind turbines generated power is dependent on wind speed. The performance of a wind turbine system improves with the increase of this speed. As mentioned earlier, the maximum efficiency of a wind turbine is around 59%. However, this efficiency can go beyond this limit with the help of augmentation devices in which wind flow is concentrated [12]. With the potential flow assumption for the air, the power output of the wind turbines can be expressed by the following equation,
where Cp is the power coefficient, ρ is the air density, A is the swept area of blades, and U∞ is the wind speed. The power coefficient, Cp, is defined as the ratio of the extracted power to the available power [1].
P = ½ Cp ρ A U∞3
Augmentation techniques have been utilized to significantly enhance the performance, in terms of power coefficient values and self-start ability, of wind turbines. Augmentation devices like deflectors, guide vanes, converging ducts, diffusers, and stators are incorporated with the VAWT to create a venturi effect at the inlet. This results in higher positive torque and improves the self-start ability of VAWT [11]. According to the direction of flow, augmentation devices are categorized into two groups, single directional inlet flow, and omnidirectional inlet flow. For omnidirectional flow, devices are fitted surrounding the wind turbine to capture the wind from all directions. For single-directional flow, augmented devices are primarily installed on the upwind side. There is also a need for yawing mechanisms to capture the wind from different directions [11].
In this study, a new augmentation stator was introduced to increase the output power of a vertical axis wind turbine, mainly of the drag type turbines, by using a convergent-divergent flow channel. This channel is created by utilizing two identical but opposing airfoils. The reduction in the area increases the speed of air and hence increases the output power of the turbine. Figure 1 shows a CAD drawing of the proposed system. A drag-type turbine, in this case, the Savonius rotor turbine, is used. One turbine or two counter-rotating turbines are fitted within the stators. The returning blades are isolated from the wind, and only the concave side of the turbine is impinged by the accelerated flow.
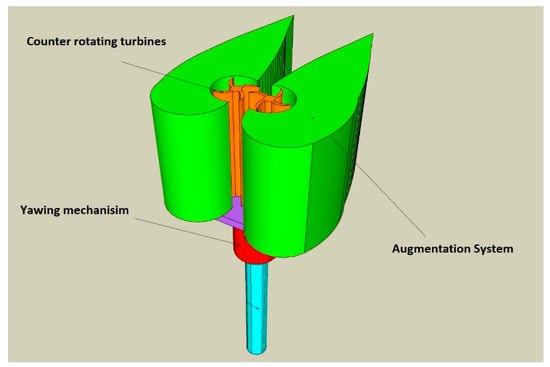
Figure 1.
CAD drawing of the proposed augmentation system.
2.1. Computational Model
Momentum models and Computational Fluid Dynamics (CFD) are the two basic methods used to study the aerodynamic performance of VAWT. The primary advantage of momentum models is that they resolve issues more quickly than the alternative method. Although computational fluid dynamics has been a useful design tool for researching wind turbine efficiency, the simulation of mesh formation in three-dimensional analyses takes a long time [13]. The flow of air within the augmentation system was simplified by assuming a two-dimensional model without turbines. The goal is to investigate the flow of air within such a system and investigate the impact of different turbines experimentally in future work. The two-dimensional flow domain is discretized into small cells to create a two-dimensional mesh prior to performing the numerical simulation. This mesh was created by ANSYS Fluent 19.0 (ANSYS, Canonsburg, PA, USA).
2.2. Governing Equations and Boundary Conditions
In this computational model, the two-dimensional fluid flow is simulated by solving the continuity equation and the time-averaged, turbulent, incompressible flow momentum equation. The continuity equation is described as follows:
The Reynolds-Average Navier Stokes equation (RANS) is written as:
The Reynolds stress term on the right side of Equation (3) is solved by the k-ω shear stress transport turbulence model (k-ω SST). Equations (4) and (5) are the two-equations to close the Reynolds-Average Navier Stokes equations:
where:
where, k is the turbulence kinetic energy, w is the turbulence frequency, y is the distance to the nearest wall, S is the invariant measure of the strain rate, ρ is the density, and Ui is the flow velocity. F1 and F2 are blending functions that are equal to zero away from the surface (k-e model) and switch over to one inside the boundary layer (k-w model). It should be noted that a production limiter is used in the SST model to prevent the build-up of turbulence in stagnation regions an essential part of the SST model.
Due to the sensitivity of the k-ω turbulence model to the free-stream value of turbulence applied at the inlet of the flow domain, the model is not accurate in these types of zones. On the other hand, the k-ε turbulence model is sensitive near the walls and needs a damping function to predict the more accurate values of model coefficients. However, (k-ω SST) model attempts to address the problems of the previously mentioned turbulence models. This is performed by applying two blending functions, F1 and F2. The first blending function F1 is given below:
F1 will have a different value (0 ≤ F1 ≤ 1) at every single cell of the mesh, depending on how far/or close this cell is from the boundaries (walls). Its value will be 1.0 at the wall where the k-ω turbulence model is applied and approaches 0.0 away from the walls where the k-ε model is activated. The value of F1 changes smoothly from the wall to the far field by using a hyperbolic tangent function with an argument that is dependent on the distance from the closest wall. In this way, there will be a smooth transition from the k-ω to the k-ε model, whereas the intermediate cells of the mesh will be using a blend of the two models. This represents the baseline stress transport model. However, with this blending function, the wall shear stress is over-predicted [14]. To overcome this issue, another blending function F2 is included in this model, which acts as a viscosity limiter.
In this case, if the product of F2 and S, the magnitude of shear strain, is large, the turbulent dynamic viscosity will be limited/reduced. This model will give a better description of flow with adverse pressure gradients, especially in the external aerodynamics, like flow around airfoils, and provide better separation prediction [14].
A two-dimensional numerical simulation was performed using ANSYS Fluent 19.0 to study the flow characteristics throughout the augmentation system. The shear stress transport (SST) k-ω turbulence model was implemented in this research to solve the Reynolds-averaged Navier–Stokes (RANS) equations since it provides a better prediction of the flow that has boundary layer separation or undergoes adverse pressure gradient. It is to stress that the SST model owes much of its success to the robust and accurate near-wall formulation of the 1988 Wilcox k-ω model. [14]. The model switches to k−ϵ behavior in the free-stream field to avoid the sensitivity of the k-ω model to the turbulence properties near the inlet free-stream. The flow domain is discretized using the second-order upwind method with the SIMPLE scheme for pressure–velocity coupling. The mesh structure is created using the ANSYS meshing tool. Near-wall zones have a denser mesh structure compared to the far fields to capture the near-wall turbulence. The two-dimensional airfoil used in the simulation is NACA 2424, which has a maximum thickness of 24% that is sufficient to encompass the wind turbine. The full scale of the airfoil chord, C, in this study is 5.0 m. Two free-stream air velocities were tested, 3.0 m/s and 5.0 m/s, to evaluate their effect on the target augmented airspeed. These speeds are equivalent to gentle breeze weather (8–12 mph) [15]. Three cases of the minimum gap between the two airfoils were tested by the CFD model. These gaps are 30 cm, 40 cm, and 50 cm, which represent 6%, 8%, and 10% of the airfoil chord, respectively. The flow domain starts 5.0 m ahead of the airfoil leading edge and ends 15.0 m behind the airfoil trailing edge.
The flow domain was discretized into a two-dimensional mesh of hexagonal elements to perform the CFD computational solution and analysis. Three meshes were created with different sizes, Table 1, to study the mesh size independence of the solution. The flow domain was reduced by 50% when considering the line of symmetry at the midline between the two airfoils. Mesh boarders start one chord length ahead of the airfoil and extend three chord lengths downstream behind the airfoil and two chord lengths below, Figure 2 and Figure 3. The distance between the airfoil and the line of symmetry will be half of the total gap between the two airfoils (i.e., convergence divergence throat).

Table 1.
Size of the 2D meshes used for mesh independency.
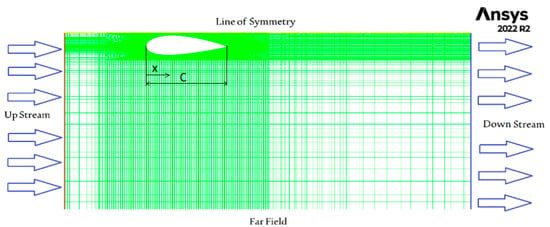
Figure 2.
Generated mesh for the CFD solution (268,107 cells).
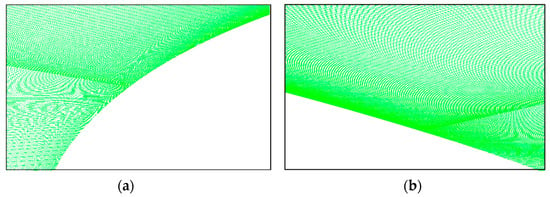
Figure 3.
Generated mesh for the CFD solution near the wall of the airfoil (268,107 cells) (a) near the upper leading-edge wall, (b) near the upper trailing edge wall.
Table 2 shows the boundary conditions that are applied to study the effect of changing the free stream air velocity, the angle of attack, α, and the gap between the two airfoils.

Table 2.
Boundary conditions of simulations.
Mesh independency is evaluated by calculating the discretization error based on a selected property. That property will be the velocity profile along the line of symmetry. The discretization error is estimated by a systematic refinement of the three meshes following the guidelines of Roache [16], considering two levels of refinements. The ratio between the number of cells in the finer mesh to that in the coarse mesh is called the refinement ratio, which is the same in the two levels of refinement, having a value of (1.45).
The discretization error in the first level of refinement, Ed, is described as:
whereas the refined mesh discretization error is given by the equation:
where U1 and U2 are the velocity based on the first mesh and the refined mesh, respectively. Rr is the refinement ratio (h2/h1), h1 is the number of cells in the first mesh, h2 is the number of cells in the refined mesh, p is the observed order of truncation rate decay, which is equal to . Discretization error estimation shows a very small difference between the results obtained by using the three meshes. Figure 4 depicts the discretization error estimation of the two levels of refinement following Roache guidelines [16]. The property tested in this figure is air velocity above the airfoil chord at the line of symmetry, Vc. It shows a very small difference between the results obtained by using the three meshes.
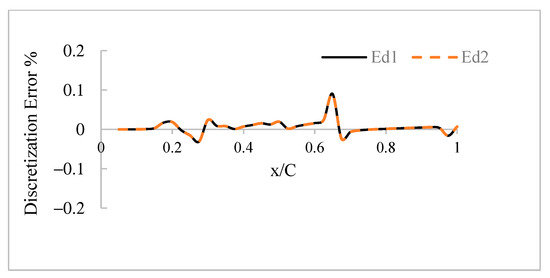
Figure 4.
Discretization error comparison between three meshes and two levels of refinement.
Figure 5 shows the normalized air velocity along the line of symmetry versus the airfoil chord (x/C) for the three meshes. Mesh#3 was used to perform the computational solution in this research because there was no significant difference in the time of convergence to the solution.
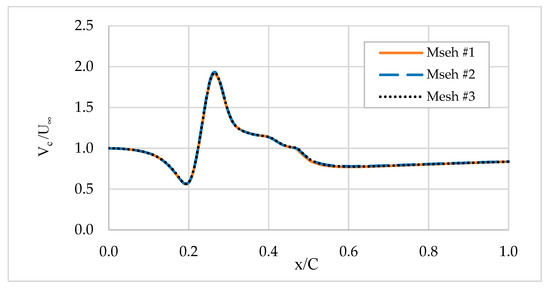
Figure 5.
Normalized air velocity profile (Vc/U∞) versus the normalized chord of the airfoil (x/C) based on the results from the three meshes at U∞ = 3.0 m/s and 0.0° angle of attack.
A set of two 3D-printed NACA 2424 airfoils with 200 mm chord length and 100 mm span (1:25 scale of the proposed system) was used to validate the CFD model results, Figure 6. Validation is defined as the process of determining the degree to which a model is an accurate representation of the real world from the perspective of the intended uses of the model [17]. The 3D- printed airfoils were covered with smooth glossy paper to minimize surface roughness. Based on the selected scale, a 20 mm gap, equivalent to a 50 cm full-scale gap, was chosen for this test. Velocities were tested at 4 locations on the centerline between the airfoils and 60 mm above the bottom surface of the airfoils using a 3 mm diameter pitot-static tube with a mainstream velocity of 10 m/s (Re ≈ 127,000). Velocities were directly measured with EXTECH® HD350 differential pressure manometer with an accuracy of ±(1%FS) @ 5.00 to 10.00 m/s. The main failing of using Pitot tubes is that their measurement inaccuracy is typically about ±5% [18]. The difference between the measured and the simulated velocity values are shown in Table 3. The difference between the experimental and simulated data was small and did not exceed 8%, which provides enough confidence in the developed CFD model.

Figure 6.
Three-dimensional printed augmentation system model inside a wind tunnel.

Table 3.
Experimental wind tunnel vs. CFD velocity data for the NACA 2424 augmentation system (chord = 200 mm, span = 100 mm, gap = 20 mm, α = 0°, U∞ = 10 m/s).
3. Results
Figure 7 shows the velocity contours around the 2D airfoils for different pitch angles and mainstream velocities. The velocity increases within the narrow region between the airfoils. The flow decelerates in the wake of the system, and this deceleration is higher with positive angles of attack. This can be explained by the fact that circulation takes place in the divergent part of the augmentation system. Separation is seen at x/C ≈ 0.45 in Figure 8. There is also a flow acceleration witnessed around the external parts of the airfoils as well. Figure 9 and Figure 10 show centerline velocities for different gaps with α = +5° for mainstream velocities of 3 and 5 m/s, respectively. Both figures show higher velocities with smaller gaps, but the increase in velocity is not substantial when compared with the change in velocity due to changes in pitch angle, as seen in Figure 11. This figure also indicates a change in the maximum velocity location with the change in the pitch angle. When the angle shifts from 5° inward to 5° outward, the maximum velocity location, x/C, shifts from 0.26 to 0.41, with x/C = 0.32 at 0° pitch angle. The figure also displays a rapid drop in the velocity, which means the flow recovers closer to the turbine stator and hence allowing other turbines to be installed not far behind it. This is due to the larger divergent region for this pitch angle with respect to the other cases. Flow separation can occur mainly when the flow slows down, and therefore the pressure increases in the streamwise flow [19]. The backflow within the flow separation region acts as an obstructing volume inside the diffuser leading to local acceleration of the flow. This has some effect on turbine performance [20]. More mass flow was observed by [21] to the wind turbine inside a “diffuser-like” shroud with a low-pressure region in the exit neighborhood of the diffuser by vortex formation. The velocity and pressure will recover shortly after the airfoil trailing edge. This needs to be further investigated, though with a larger flow domain, larger angles of attack, and higher wind speeds.
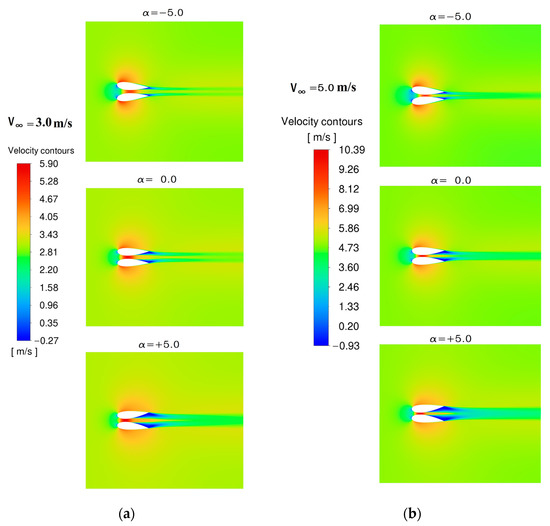
Figure 7.
Velocity contours for different pitch angles with 30 cm gap (a) U∞ = 3 m/s and (b) U∞ = 5 m/s).
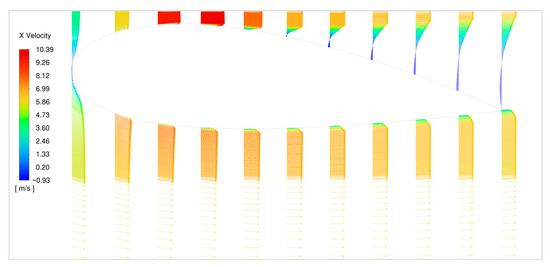
Figure 8.
Velocity vectors around the lower airfoil (+5° pitch angle, U∞ = 5 m/s, 30 cm gap).
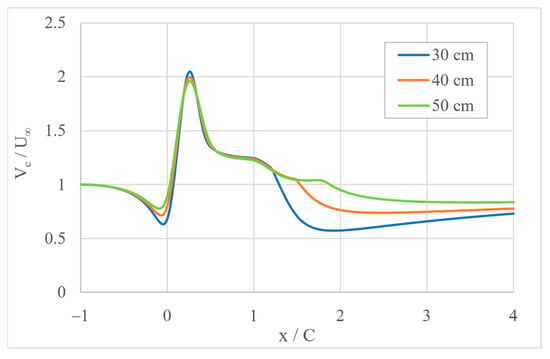
Figure 9.
Center line velocity change along the augmentation system with different gaps and (U∞ = 5 m/s, +5° pitch angle).
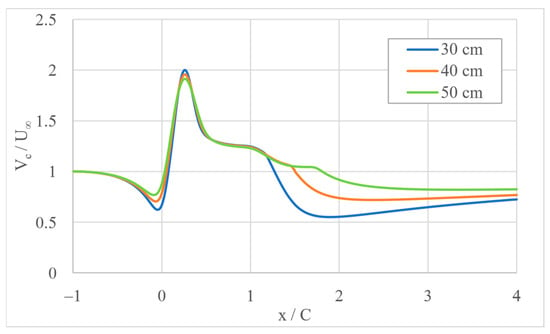
Figure 10.
Center line velocity change along the augmentation system with different gaps (U∞ = 3 m/s, +5° pitch angle).
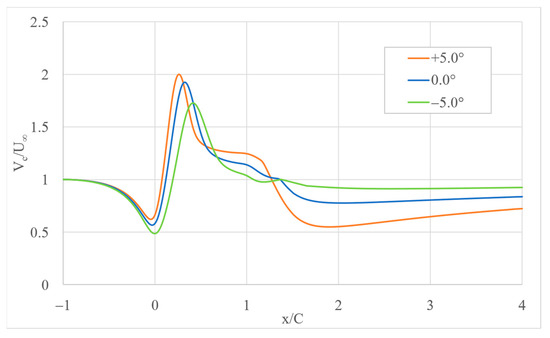
Figure 11.
Center line normalized velocity as a function of pitch angle (U∞ = 3 m/s, 30 cm gap).
For the same gap and pitch angle, the velocity profiles remain the same, with a slight change in the relative velocity values at the maximum velocity region and in the wake of the airfoil, Figure 12. A mainstream velocity of 10 m/s was also investigated. The higher the mainstream velocity, the higher the velocity ratio achieved. Figure 13 shows the maximum velocities achieved with different configurations. The figure evidently shows that the pitch angle changes have more impact on the maximum velocity in comparison to the impact of the gap. This allows designers to utilize larger turbines to be installed, thus allowing more power generation from the same augmentation system. However, the velocity profile in the wake of the airfoils changes considerably with the gap, as seen in Figure 12. This is important to investigate when installing another turbine in the wake of the first one.
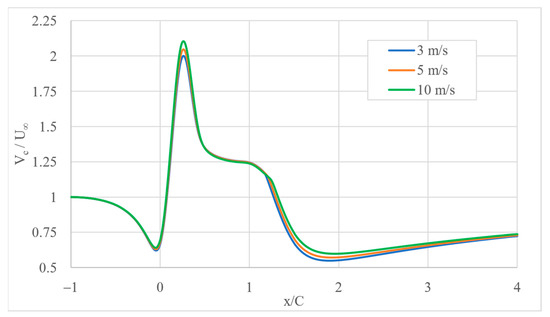
Figure 12.
Centre line velocity change along the augmentation system at different wind speeds (gap = 30 cm, +5° pitch angle).
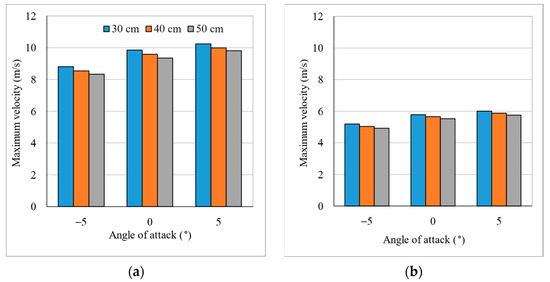
Figure 13.
Maximum velocities at different gaps and angles of attacks. (a) U∞ = 5 m/s (b) U∞ = 3 m/s.
The available power of the mainstream (function of velocity cubed), P∞, can be greatly increased simply by increasing the flow velocity. Equation (1) was used to calculate the available power with Cp = 1. Figure 14 shows the increase in the available power for a one-meter-long stator with a 0.3 m gap in the proposed system. The available power for a turbine can be increased to more than eight folds by simply enclosing it with this system. Regardless of the many constraints that might impede the performance of such a system, the power output will positively improve the energy harvest of existing vertical axis turbines.
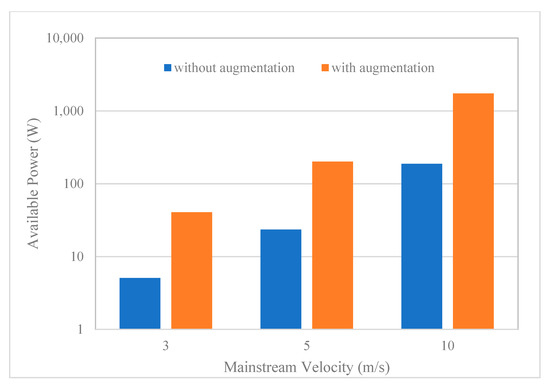
Figure 14.
Available wind power for a wind turbine with a projected area of (0.3 m × 1) with and without augmentation system (30 cm gap and +5° pitch angle).
It should be noted that experimental data were needed to verify this claim since many factors, such as turbine type, turbine stator interaction, and other factors, should be taken into consideration.
4. Conclusions
In this study, a new augmentation stator was introduced to increase the output power of a vertical axis wind turbine, mainly of the drag type turbines, by using a convergent-divergent flow channel. This channel is created by utilizing two identical but opposing airfoils. The reduction in the area increases the speed of air and hence increases the output power of the turbine. One turbine or two counter-rotating turbines are fitted within the stators. The returning blades are isolated from the wind, and only the concave side of the turbine is impinged by the accelerated flow. Velocity was found to increase within the narrow region between the airfoils. The flow also decelerates in the wake of the system, and this deceleration is higher with positive angles of attack. There is also flow acceleration witnessed around the external parts of the airfoils as well. Higher velocities with smaller gaps were observed, but the increase in velocity is not substantial when compared with the change in velocity due to changes in pitch angle. The change in the maximum velocity location changes with the pitch angle. The maximum velocity location shifts from 0.26 to 0.41 when the angle shifts from 5° inward to 5° outward. For the same gap and pitch angle, the velocity profiles remained were found to be the same, with a slight change in the relative velocity values at the maximum velocity region and in the wake of the airfoil. The results show that the available power can be amplified to more than eight folds, thus allowing higher power outputs with smaller turbines or with lower wind speeds. The current advancement in control engineering allows such systems to be easily controlled and reconfigured when air velocity magnitude or direction changes. CFD analysis is very challenging and time-consuming for such applications; therefore, an experimental setup to assess flow, such as Particle Image Velocimetry (PIV), for an actual turbine-augmentation system can be suggested. The study requires further investigation with different wind speeds, different convergent-divergent geometries, as well as different turbine types.
5. Patents
The proposed system embodiment has been filed as a provisional patent with the USPTO, application #63/352,470, on 25 June 2022, by Hayder Salem and Adel Mohammedredh.
Author Contributions
Conceptualization, H.S. and A.M.; methodology, H.S.; software, A.M.; validation, A.M. and A.A.; formal analysis, H.S.; writing—original draft preparation, H.S.; writing—review and editing, A.M. and A.A.; supervision, H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons, Ltd.: New York, NY, USA, 2001. [Google Scholar]
- Zilberman, M. Optimization of Small, Low Cost, Vertical Axis Wind Turbine for Private and Institutional Use. ACE Res. Propos. 2017, 9, 043302. [Google Scholar] [CrossRef]
- Global Wind Report 2022. Available online: https://gwec.net/global-wind-report-2022/ (accessed on 9 December 2022).
- Betz, A. Introduction to the Theory of Flow Machines; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Mohammed, A.; Ouakad, H.; Sahin, A.; Bahaidarah, H. Vertical axis wind turbine aerodynamics: Summary and review of momentum models. J Energy Resour. Technol. 2019, 141, 050801. [Google Scholar] [CrossRef]
- Muratoglu, A.; Yuce, M.I. Design of a River Hydrokinetic Turbine Using Optimization and CFD Simulations. J. Energy Eng. 2017, 143, 04017009. [Google Scholar] [CrossRef]
- Sagharichi, A.; Zamani, M.; Ghasemi, A. Effect of solidity on the performance of variable-pitch vertical axis wind turbine. Energy 2018, 161, 753–775. [Google Scholar] [CrossRef]
- Akwa, J.; Vielmo, H.; Petry, A. A review on the performance of Savonius wind turbines. Renew Sustain. Energy Rev. 2012, 16, 3054–3064. [Google Scholar] [CrossRef]
- Jin, X.; Zhao, G.; Gao, K.; Ju, W. Darrieus vertical axis wind turbine: Basic research methods. Renew Sustain. Energy Rev. 2015, 42, 212–225. [Google Scholar] [CrossRef]
- Wong, K.; Chong, W.; Sukiman, N.; Poh, S.; Shiah, Y.-C.; Wang, C.-T. Performance enhancements on vertical axis wind turbines using flow augmentation systems: A review. Renew Sustain. Energy Rev. 2017, 73, 904–921. [Google Scholar] [CrossRef]
- Karmakar, S.; Chattopadhyay, H. A review of augmentation methods to enhance the performance of vertical axis wind turbine. Sustain. Energy Technol. Assess. 2022, 53, 102469. [Google Scholar] [CrossRef]
- Jamieson, P. Innovation in Wind Turbine Design, 2nd ed.; Wiley: Hoboken, NJ, USA, 2018; Chapter 4; ISBN 978-1119137900. [Google Scholar]
- Wilson, R. Wind-turbine aerodynamic. J. Ind. Aerodyn. 1980, 5, 357–372. [Google Scholar] [CrossRef]
- Menter, F. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- National Weather Service. Available online: https://www.weather.gov/mfl/beaufort (accessed on 9 December 2022).
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. Trans. Am. Soc. Mech. Eng. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- American Institute of Aeronautics and Astronautics. Guide for the Verification and Validation of Computational Fluid Dynamics Simulations; AIAA: Reston, VA, USA, 1998; ISBN 978-1563472855. [Google Scholar]
- Morris, A.S.; Langari, R. Measurement and Instrumentation Theory and Application; Third Edition 2020 Copyright ©; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Hajaali, A.; Stoesser, T. Flow Separation Dynamics in Three-Dimensional Asymmetric Diffusers Flow. Turbul. Combust. 2022, 108, 973–999. [Google Scholar] [CrossRef]
- Hashem, I.; Mohamed, M.H. Aerodynamic performance enhancements of H-rotor Darrieus wind turbine. Energy 2018, 142, 531–545. [Google Scholar] [CrossRef]
- Ohya, Y.; Karasudani, T.; Sakurai, A.; Abe, K.; Inoue, M. Development of a shrouded wind turbine with a flanged diffuser. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 524–539. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).