Abstract
With regard to drying fresh grain prior to storage, the drying tower with a downward moving bed with hot air is often used, which always has high energy consumption during operation. To optimize the operation, according to the actual operating parameters of a corn drying tower with hot air, a heat balance model was established, and the heat transfer between the hot air and corn flow in a downward moving bed was analyzed. Since the downward moving time is short, the heat absorbed by corn significantly depends on the heat transfer coefficient, mainly the convective heat transfer, between the hot air and corn surface. To determine the convective heat transfer coefficient, a hot air drying experimental system for corn grains was established, and the effects of hot air temperature and wind speed on the central temperature and moisture content of corn grains were analyzed. Utilizing the heat balance model, the convective heat transfer coefficients between corn particles and hot air were calculated. The total convective heat transfer coefficients are in the range of 39.4–53.8 W/m2 · K. With an average value of 46.7 W/m2 · K, drying energy efficiencies in different drying zones in the drying tower were calculated, and the accuracy of the model was verified by the operation data. Due to the high inlet temperature of hot air, the maximum energy efficiency of the first zone is 60.15%, whereas when the temperature of hot air in the second drying tower is 140 °C, the energy efficiency is only 41.97%. Therefore, under the premise of ensuring the drying rate, the temperature of hot air of the second zone should be appropriately reduced to improve the whole drying energy efficiency.
1. Introduction
In agriculture, drying technology is mainly applied to grain drying, which has significant meaning in the view of social life and economical aspect. Due to the different climates when crops mature, the moisture content of crops varies greatly [1], which affects its storage. Therefore, developing a highly efficient and economical drying process becomes an urgent task to improve grain quality, as well as the value of comprehensive utilization and deep processing.
Generally, the downer drying technology is commonly used to dry grain, and the hot blast stove burns biomass in order to provide a hot blast source to avoid CO2 release, which can meet the requirements of the double carbon policy. During the operation, it is found that the drying system has an unstable operation, low efficiency, and high energy consumption, and thus, the structure and operation need to be optimized theoretically. The main process in this drying system is the convective heat transfer process between the hot air and downward moving grain particles, such as corn. The hot air flows by crossing the surface of corn, and the heat is transferred to the medium through the convective heat transfer to increase the temperature of corn. The moisture on the surface and inside of corn continuously evaporates and diffuses into the hot air, and finally reaches an equilibrium [2]. During the whole drying process, heat transfer and mass transfer in corn interact with each other. The beginning and middle stages of drying are commonly referred to as external condition control processes, wherein the heat and mass transfer efficiency depends on the external drying conditions, such as hot air temperature, flow rate, relative humidity, and pressure. At the same time, drying is also affected by the corn surface temperature and effective heat exchange area. Generally, to improve the drying efficiency, a higher hot air temperature is typically used to enhance the heat transfer. With the tight and smooth skin of corn, if the temperature is significantly high, the moisture under the skin of corn particles cannot be released in time, resulting in excessive internal pressure and deformation, which deteriorates the quality of corn [3,4]. Therefore, selecting the appropriate hot air temperature and wind speed, i.e., the appropriate convective heat transfer coefficient, is an effective way to improve the energy efficiency of the whole drying process.
Kong N et al. [5] studied the effects of drying process parameters, such as hot air temperature, initial moisture content of materials, and hot air speed, on the drying characteristic and stress of a single corn particle based on the three-dimensional solid model, and obtained the influence law of drying conditions in the drying process. Zheng F et al. [6] analyzed the changing rules of grain moisture-binding energy and state parameters of the grain drying system. Based on the energy analysis of the drying system, the authors established the safe storage and drying process of wet grain, and a high-efficient and energy-saving storage dryer was designed, which was confirmed from both theoretical and experimental aspects. Chi G [7] analyzed the heat and mass transfer characteristics of the corn drying process in the prototype drying tower, determined the key similarity criterion based on the three similarity standards, and calculated the heat required to remove moisture from corn in each drying section of the simulated experimental system.
It is clear to see that these studies generally have certain limitations: (1) The actual situation of single corn and multi-corn is quite different, and the experimental conclusions cannot be directly applied to industrial practice; (2) the field test of the drying system cannot accurately obtain the change in temperature and moisture content of corn at different heights due to the difficulty and the limitation of testing conditions; (3) the convective heat transfer between the corn and wind gas, including the heat transfer between the corn particles as well as the corn and hot air, is quite different from the one that only considers the convective heat transfer between the corn and hot air. Therefore, specific experimental and modeling work on the heating transfer behavior in the drying process is urgently needed.
In the present paper, with the basic principle of downward moving bed with hot air drying, according to the structure and operating parameters of the hot air drying system, the heat balance model of the corn drying process was established. Due to the limited residence time, the heat transfer mainly depends on the convective heat transfer coefficient, which was determined by specially designed corn drying test systems. In the experiment, the effects of hot air temperature and wind speed on the change in central temperature and moisture content of corn particles were measured online. With heat balance calculation, the changes in hot air temperature and moisture content of corn particles were calculated, and the corresponding range of convective heat transfer coefficient was fitted. By selecting an average convective heat transfer coefficient of 46.7 W/m2 · K, the energy efficiency of each drying zone of the downward moving bed drying tower with hot air was calculated and well-verified with the operation data. Finally, the optimal operation scheme was presented to improve the energy efficiency of the whole drying tower. This heat balance model of the downward moving bed drying tower with hot air can work as an efficient tool to optimize the design and operation of the grain drying process, which achieves sustainable development in the food industry.
2. Model Development
2.1. Basic Properties of Corn Particle
The moisture content of corn particles is as high as 22%, which is the initial moisture content of corn particles measured by weight loss with the drying method at 110 °C for 1.5 h. Corn (Liangyu 99) is a heat-sensitive material, wherein a significantly high drying temperature will cause the deformation of corn skin, and a significantly low temperature will make it difficult to dry the grain to the best quality (i.e., the best storage temperature for corn) in a short time. During counter-current drying, corn particles fall from a certain height, in which the hot air with high temperature and low humidity directly contacts and heats the corn particles with low temperature and high humidity. In the process of air diffusion, the temperature decreases, and the moisture content increases. The moisture content of hot air at the exhaust port has been nearly saturated. However, in the counter-current drying system, the temperature of the corn itself is close to the wind temperature in the late drying period. Therefore, it should be ensured that the temperature of the hot air is not significantly high in the drying process; otherwise, it will cause grain cracks and other quality damaging problems due to overheating [8]. The basic parameters of corn are listed in Table 1.

Table 1.
Basic parameters of corn particle.
2.2. Drying System
Figure 1 is the downward moving bed drying system in a granary. The drying chamber is divided into three zones from top to bottom. At the beginning of the drying process, the corn after impurity removal enters the wet grain barn through the wet grain elevator. In turn, under the action of gravity, the corn passes through the different stages of the drying tower. By adjusting the temperature and wind speed of hot air, the corn is dried to the target moisture, and then transported to storage after cooling. In this process, the airflow is introduced into the main drying tower by the hot air blower through the heat exchanger for grain drying [9]. The exhaust steam after drying the grain is recovered by the waste heat recovery room to improve the ambient temperature in the wet barn. The structure and operating parameters of the drying tower are shown in Figure 1 and Table 2.
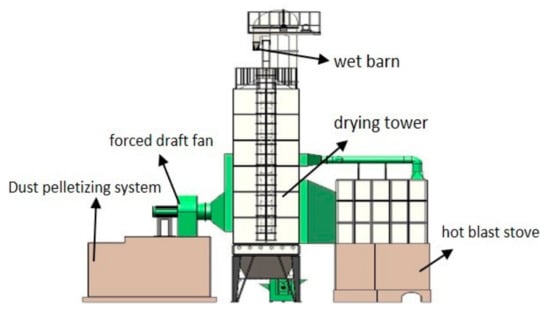
Figure 1.
Typical drying system of the downward moving bed.

Table 2.
Structure and operation parameters of the drying tower.
Extending the residence time of corn in the tower is an effective way to dry the corn to the target moisture. Therefore, it is necessary to establish a heat balance model to calculate the inlet and outlet temperature of hot air and the change in corn moisture content, and then to improve the energy efficiency of the drying tower by changing the operating parameters.
2.3. Heat Balance Calculation of Drying Tower
Transverse circulation area of hot air:
where L is the height of the drying section. Inlet enthalpy of hot air:
where Tgas is the inlet temperature of hot air. Apparent velocity:
where the thermal airflow rate in the equation is q = 71,000 Nm3/h. Corn contact time:
Gas-solid contact area:
Hot air outlet enthalpy:
where Tgas out is the outlet temperature of hot air. Hot air release:
Mean hot air temperature:
The average temperature difference between the corn and hot air:
where Tbed out is the export temperature of corn and the temperature of corn itself Tbed = −15 °C. Heat transfer:
where h is the convective heat transfer coefficient, W/m2 · K. The heat capacity of corn and moisture heat absorption:
where the specific heat capacity of corn is Cp = 2 kJ/kg · K, and the specific heat of moisture is Cp water = 4.18 kJ/kg · K. Heat absorption of ice melting into moisture:
where the processing capacity is G = 8.38 kg/s, corn moisture content is Yw-bed = 22%, and the heat of dissolution of ice is Ih = 335 kJ/kg. Moisture evaporation:
where the latent heat of vaporization of free moisture is rh = 2257 kJ/kg. Absolute humidity:
Relative humidity:
Corn moisture:
The energy efficiency:
In the process of drying corn with hot air, the heat exchange between the corn particles and hot air, and the heat conduction between the particles can be approximately regarded as the convective heat transfer process between the hot air and corn particles. However, there is no appropriate calculation method for the selection of a convective heat transfer system under the condition of the downward drying tower [10]. Therefore, in this paper, the corresponding range of convective heat transfer coefficient was determined by the experiments.
3. Experimental Test of Convective Heat Transfer Coefficient
3.1. Experimental System
The changes in hot air outlet temperature and moisture content of corn can be accurately calculated by the thermal balance model; however, the total heat transferred to corn particles within a limited residence time depends entirely on the convective heat transfer coefficient. Therefore, tests are needed to determine the convective heat transfer coefficient. This paper designed and built a set of corn drying experiment systems, as shown in Figure 2. The actual photograph of the experimental setup is shown in Figure 3. The dry tower is made of quartz glass with a height of 70 cm and an inner diameter of 50 mm, as shown in Figure 2. Air flows through the flow meter from the forced draft fan. By heating the gas in the preheating system under the dry tower, the hot gas passes the distributor into the dry tower. The flow meter (ENID DN25) (Tianjin Flowmeter Co., Ltd, Tianjin, China) is a metal float type with a value of 2.5 m3/h and resolution of 0.01%.
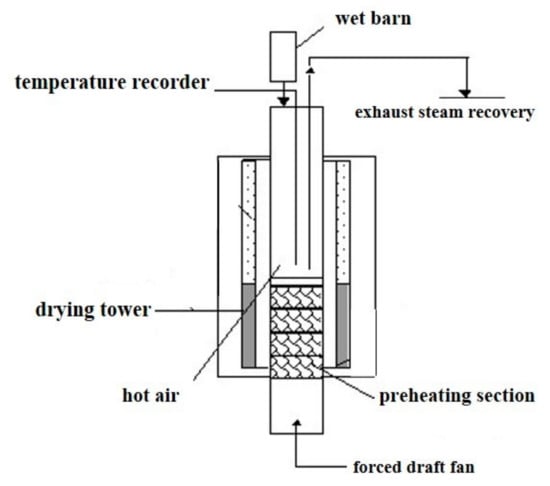
Figure 2.
Experimental system for heat transfer measurement.

Figure 3.
Drying tower experimental equipment.
Through the electric heating of the bottom preheating section, the dry hot air was heated to the predetermined temperature, and different numbers of corn particles were placed on the air distributor. The change in central temperature of corn particles was recorded online by a 0.5-mm J-type thermocouple. Some corn particles were taken out at different time intervals, and the moisture content of corn particles was measured after cooling. The FA1004 (Shanghai Sunyu Hengping Scientific Instruments Co., Ltd., Shanghai, China) weight balance with the value of 100 g and resolution of 0.1 mg was used to measure the weight loss. Each case was repeated two times and the average value was chosen. In the experiments, the humidity was not especially controlled, but the gas was maintained in a dry environment and the relative humidity of the lab was maintained at 10%.
The central temperature and moisture content of corn particles were analyzed, and the results are shown in Figure 4 and Figure 5. Figure 4 shows that under different initial hot air temperatures, the center temperature of corn particles increases rapidly from 0 to 110 s. When the hot air temperature was 160 °C, the temperature of the corn particles’ center changed most dramatically. At 110 s, the temperature of the corn particles’ center increased to 103 °C. However, when the hot air temperature was 110 °C, the temperature at the corn particles’ center remains the same, at about 100 °C. When the hot air temperature was 140 °C, the central temperature of corn particles first remains unchanged at about 110 °C, then continues to rise at 350 s. At hot air temperature of 160 °C, the corn particles’ center temperature continues to rise slowly, since the exhalation rate of corn moisture is associated with the hot air temperature. The higher the temperature of hot air, the faster the rate of moisture released in the corn particles, and the higher the temperature of corn particles’ center. However, at hot air temperature of 110 °C, the temperature is close to the minimum temperature of moisture evaporation after the 110 s. Therefore, the central temperature in corn particles remains unchanged.
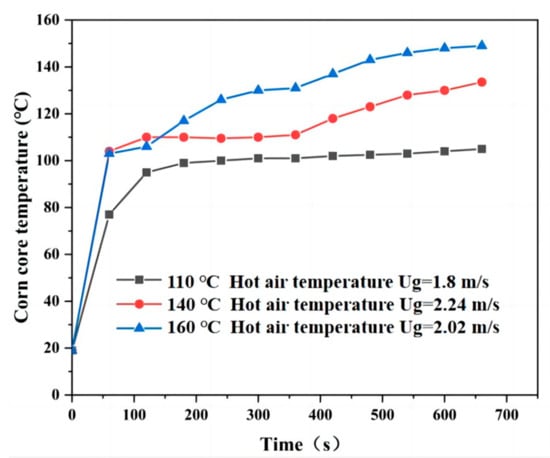
Figure 4.
Temperature change in corn particles’ temperature with time.
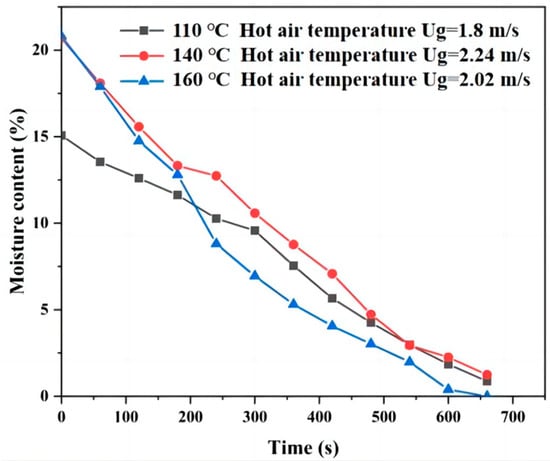
Figure 5.
Moisture content change in corn with time.
The moisture content of corn particles changes with time as shown in Figure 5. Under the different hot air temperatures, the moisture content of corn particles decreases rapidly. When the hot air temperature is 160 °C, the moisture content of corn decreases the fastest, and at 300 s, the moisture content of corn particles is less than 5%. However, when the hot air temperature is 110 °C, the moisture content of corn drops slightly from 15% to 8.75% within 0–300 s. This shows that the higher the temperature of hot air, the faster the evaporation rate of moisture content on the surface of corn, and the higher the temperature of hot air, the faster the decrease in moisture content in the corn.
3.2. Heat Transfer Model of Hot Air Drying Corn Particles
According to the basic theory of heat transfer, the hot-air drying condition of corn particles was simplified, and the basic equation of the drying process model was obtained [11]. High temperature hot air flows through the surface of the corn, due to the temperature difference between the hot air and corn. Herein, the heat is transferred by convection to the surface of the corn, and then by conduction to heat the inside of the corn. After heating and evaporating, the moisture on the surface of the corn is transmitted to the hot air by convection, while the moisture inside of the corn is evaporated and transmitted to the surface by diffusion [12].
Based on the size and shape distribution of corn particles, the following assumptions are proposed: (1) The initial temperature and moisture content of corn was homogeneous and isotropic; (2) the bed thickness and accumulated porosity are always regarded as constant, while neglecting the particle breakage, abrasion, and volume shrinkage during the drying process; (3) the turbulence effect on the gas inside of the corn was neglected due to the fact that Reynolds number is less than 1000; (4) moisture diffuses from the center of corn to the surface, and evaporation mainly takes place on the surface; (5) the hot air first transfers heat to the surface of corn particles by convection, and then transfers heat to the inside of the corn using heat conduction.
Conservation Equation
Based on the above assumptions, the following conservation equations were established to describe the drying process of corn.
- Energy equation for corn particles
During the drying process, heat is transferred from the hot air to the surface of the corn since the temperature of the corn is lower than the hot air. This heat is used partly to provide the energy to change moisture from the liquid phase to the gas phase, and partly to heat the corn itself [13,14,15].
- (1)
- Heat transfer to corn:where h is the convective heat transfer coefficient, ; Sbed* is the convection heat transfer area, which is the effective surface area of corn, m2; Tgas is the hot air temperature, K; and Tbed is the initial temperature of corn, K.
- (2)
- Energy needed to evaporate moisture from the corn into the hot air:where msteam represents the mass of moisture from the particles to the hot air in unit time, kg; Cw is the specific heat at this temperature, ; Cυ is the specific heat of moisture vapor at this tempature, ; and rh is the latent heat of evaporation of moisture at this temperature, .
Under the condition of neglecting the effects of radiation [16,17,18,19,20], the following can be obtained: according to the law of energy conservation, the energy conservation relation of corn can be obtained as follows:
In the formula, Cp-coal is the specific heat of dry corn, , and Yw-bed is the whole average moisture content of corn [21,22,23].
- 2.
- Energy balance of dry hot air
In a closed system for studying hot air and corn particles, the energy lost by hot air is equal to the energy gained by corn Qc and the heat transferred by the system to the surrounding environment Qloss, J/s.
where Yw-gas is the moisture content of the hot air [24].
- 3.
- Mass conservation equation
During the drying process, the mass transfer between the corn particles to the hot air occurs simultaneously with the heat transfer process. During the drying process, moisture mass msteam is evaporated from the corn particles and released into the hot air. Therefore, the mass conservation equation can be expressed by calculating the equation of msteam [25,26,27,28].
The three stages considered in the drying process are the high-speed drying stage, the deceleration drying stage, and the rapid drying stage. The mark that distinguishes the three stages is the critical moisture content Y* of the corn particles.
When the average moisture content of corn particles is Yw-bed ≥ Y*, the corn particles are in a high-speed drying stage. At this stage, the moisture content of the thin hot air layer near the surface of corn particles can be considered as the saturated moisture content at the temperature of the hot air. In the process of moisture evaporation on the surface of corn particles, if the diffusion rate of moisture inside of the corn particles to the surface is equal to or greater than the evaporation rate of moisture on the surface, the heat transferred by the hot air to the corn particles is all used for moisture evaporation [29,30,31].
The mass transfer equation in the high-speed drying stage is obtained as follows:
where Dy-convection is the inverse mass transfer coefficient, kg/(m2 · s).
When the average moisture content of corn particles is Yw-bed ≤ Y*, the corn particles are in a decelerating drying stage. At this stage, the steam pressure generated by the combined moisture is always lower than the saturated steam pressure of moisture at the same temperature. Moreover, the diffusion power of moisture vapor from the corn particles to hot air will become smaller, the mass transfer rate will decrease, and the drying rate will decrease. In the decelerating drying stage, part of the energy provided by the hot air to corn particles is used to evaporate moisture, and the remaining energy is used to raise the temperature of corn particles [32,33,34,35].
The mass transfer equation in the stage of deceleration drying is obtained as follows:
Dy is the moisture diffusion coefficient, kg/(m2 · s), and Y* is the critical moisture content of corn particles.
When the average moisture content of corn particles is Yw-bed << Y*, the corn particles are in a rapid drying stage. In this situation, the high temperature accelerates the decrease in moisture inside of the corn particles, resulting in the rapid drying stage. The mass transfer equation is the same as the high-speed drying stage [36,37,38].
3.3. Calculate the Convective Heat Transfer Coefficient
The convective heat transfer coefficient is an important parameter to describe the heat transfer intensity, and the accurate value of the convective heat transfer coefficient is required to calculate the energy efficiency of the drying tower [39,40]. The variation range of the convective heat transfer coefficient of hot air to corn particles can be obtained through the following calculations.
Dry based wet content M is the ratio of wet component mass to absolute dry material mass:
where mw is the wet component mass of wet material, g, and md is the relative dry material mass, g.
Effective thermal conductivity of corn particles:
where A = −1.74 − 3.56 M, B = 4.72 × 10−3 × (Tbed x − 273.15), C = 6.48 M2 − 1.5 × 0−4 × (Tbed x − 273.15)2, D = 6.72 × 10−2 M × (Tbed x − 273.15).
Tbed x is the central temperature of corn particles at different times.
The true density of corn accumulation:
where Ψ is the corn stacking void fraction, and ρp is the corn particle true density, kg/m3; ρp = 1150 kg/m3.
Specific heat capacity of corn at constant pressure:
where Ψ is the corn accumulation void fraction, Cp, and p is the corn particle specific heat capacity at constant pressure, kJ/kg·K [41].
Heat transfer coefficient between corn particles:
where τ is the residence time of particles, s, and λ is the thermal conductivity of corn particles.
Heat transfer coefficient between hot air gas and particles:
where m is moisture evaporation, kg/s; Cp is the specific heat capacity of moisture, kJ/kg K; Tgas out is the outlet temperature of hot air, °C; Tgas in is the inlet temperature of hot air, °C; A is the area of contact between the corn particles and heat exchange tube, m2; and Tbed is the corn particle central temperature, °C; . Convective heat transfer coefficient:
As can be seen from Figure 6, the convective heat transfer coefficient increased rapidly at the beginning of the heating stage of the drying tower. When the heating reached 200 s, the increase in the convective heat transfer coefficient began to slow down, and after 250 s, the change in the convective heat transfer coefficient gradually leveled. As the temperature increased, the hot air velocity increased from 1.8 to 2.02 m/s, and the convective heat transfer coefficient increased accordingly. As the outlet temperature of hot air is influenced by the change in moisture content of corn, the corn particles enter the slow drying stage after the high-speed drying stage, the moisture in the center of the particles is evaporated by heat, and the temperature increase in the center of corn particles becomes slow; therefore, when the inlet temperature of hot air increases from 110 to 160 °C, the change in hot air outlet temperature is not clear. The hot air entering the drying tower causes the heat transfer temperature difference between the hot air and the pellet to increase from 43.3 to 95 °C, and the convective heat transfer coefficient increases. As the hot air temperature increased, the temperature difference between the center temperature of the corn kernel and the average temperature of the hot air inlet increased from 103.4 to 127.5 °C, increasing the heat transfer coefficient between the hot air gas and the corn kernel. According to the classical heat transfer theory, the faster the flow velocity of the fluid, the larger the convective heat transfer coefficient. When the hot air velocity gradually increases, the temperature corresponding to the hot air velocity similarly increases. However, when the hot air temperature and the hot air speed have a combined effect on the convective heat transfer coefficient, the effect of the hot air speed on the convective heat transfer coefficient is not clear; therefore, when the hot air speed increases from 1.8 to 2.02 m/s and the hot air temperature increases by 50 °C, the convective heat transfer coefficient gradually increases with the increase in the hot air temperature. When the heating time reached 250 s, the change in convective heat transfer coefficient appeared to turn and then gradually leveled, which was due to the fact that the higher the hot air inlet temperature, the more rapidly the water inside of the corn leveled. Moreover, as the heating time proceeded, the evaporation of water in the corn particles decreased, i.e., the volume flow rate of the hot air gas decreased, and thus the convective heat transfer coefficient decreased.
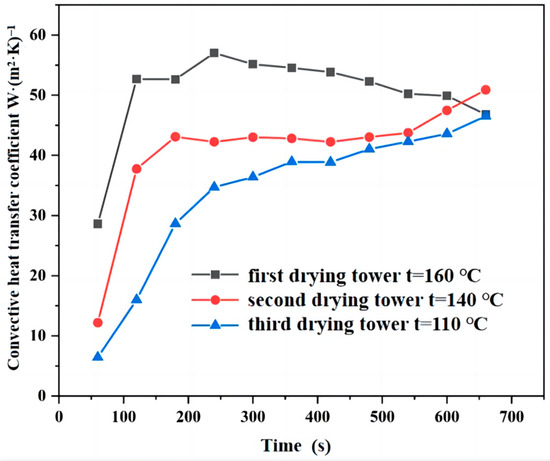
Figure 6.
Change in convective heat coefficient with time.
4. Energy Efficiency Calculation of Drying Tower
Using the heat balance model of the drying tower and the convective heat transfer coefficient in Section 2.3, the values of energy efficiency in each drying zone of the downward drying tower can be calculated. As listed in Table 3, the values in brackets are the measured values of the actual operation of the drying tower. By comparing the limited experimental values, the prediction of the drying tower model is reliable.

Table 3.
Energy efficiency calculation of drying tower.
As listed in Table 3, the values of energy efficiency of the three drying zones are 60.15%, 41.97%, and 44.99%, respectively. When the inlet temperature of hot air in the first drying zone is 160 °C, the energy efficiency is 60.15%. After 250 s, the convective heat transfer coefficient decreases slowly, indicating that the hot air speed is significantly high after 250 s, and thus the appropriate wind speed should be selected to improve the energy efficiency. When the inlet temperature of hot air in the second drying zone is 140 °C, the energy efficiency is only 41.97%, indicating that the inlet temperature in this zone is significantly high. Moreover, it can be observed that the measured outlet temperature actually reaches as high as 84 °C, and the energy efficiency of the drying tower can be improved to the greatest extent by reducing the hot air inlet temperature. If the inlet temperature is reduced to 135 °C and the outlet temperature is reduced to 70 °C, then the energy efficiency increases to 45%, and the product moisture content is 13.68%, which still meets the product quality requirements. Therefore, a reasonable and accurate downward drying tower model has a very important guiding significance for the improvement of the energy efficiency of the drying system.
5. Conclusions
- (1)
- A heat balance model was established to describe the heating process of fresh corn in the downward moving tower with hot air, which has a very important guiding significance for the improvement of the energy efficiency of the drying system.
- (2)
- To determine the convective heat transfer coefficient between the fresh corn and hot air, a corn particle drying system with hot air was established, and the effects of hot air temperature and wind speed were discussed. Utilizing the heat balance model, the total convective heat transfer coefficients were determined in the range of 39.4–53.8 W/m2·K.
- (3)
- Utilizing the convective heat transfer coefficient of 46.7 W/m2·K, the drying energy efficiency in different drying zones in the drying tower was calculated and verified with the operation data. The highest efficiency of the first drying zone was 60.15% due to the high inlet temperature of hot air. When the hot air temperature in the second drying zone is 140 °C, the energy efficiency is only 41.97%. It is recommended that if the inlet hot air temperature can be reduced to 135 °C, then the energy efficiency will be increased to 45%.
Author Contributions
Conceptualization, H.W.; methodology, H.W.; validation, S.Z.; formal analysis, N.H.; investigation, M.Z.; resources, H.F.; data curation, H.W.; writing—original draft preparation, H.W.; writing—review and editing, H.Y.; visualization, M.Z.; supervision, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was financially supported by the Development of Flexible Low Carbon Power Generation Technology for High Proportion Consumption of New Energy.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Development of Flexible Low Carbon Power Generation Technology for High Proportion Consumption of New Energy.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Nomenclatures
| A | m2 |
| Cp | Specific heat capacity of moisture (kJ/kg K) |
| Cp-coal | Specific heat of dry corn (J/kg K) |
| Cp, p | Corn particle specific heat capacity at constant pressure (kJ/kg K) |
| Cv | Specific heat of moisture vapor at this temperature (J\kg K) |
| Cw | Specific heat at this temperature (J/kg K) |
| Dy | Moisture diffusion coefficient, kg/(m2 · s) |
| h | Convective heat transfer coefficient (W/m2 K) |
| L | Height of the drying section (m) |
| m | Moisture evaporation (kg/s) |
| md | Relative dry material mass (g) |
| mw | Wet component mass of wet material (g) |
| rh | Latent heat of evaporation of moisture at this temperature (J/kg) |
| Sbed* | Convection heat transfer area (m2) |
| Tbed | Initial temperature of corn (K) |
| Tbed out | Export temperature of corn (°C) |
| Tbed x | Central temperature of corn particles |
| Tgas | Hot air temperature (K) |
| Tgas in | Inlet temperature of hot air (°C) |
| Tgas out | Outlet temperature of hot air (°C) |
| Y* | Critical moisture content of corn particles (%) |
| Yw-bed | Whole average moisture content of corn (%) |
| Yw-gas | Moisture content of the hot air (%) |
References
- Krissada, N.; Phitsanupong, P.; Witaya, P. Thermal analysis of hot air drying of chicken manure pellets in a modified portable horizontal rotary dryer. Heat Mass Transf. 2022, 58, 1997–2007. [Google Scholar] [CrossRef]
- Borja, H.; Mariano, M.; Prashant, G. Numerical study of airflow regimes and instabilities produced by the swirl generation chamber in counter-current spray dryers. Chem. Eng. Res. Des. 2021, 176, 89–101. [Google Scholar]
- Manimaran, R.; Kumar, M.M.K.; Shankar, V.H. Study on novel nano mahua methyl ester powered DI diesel engine preheated with a thermoelectric waste heat recovery system. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 43, 3251–3265. [Google Scholar]
- Jangam, S.V. Role of Drying Technology in The Promotion of Global Drying R&D. Dry. Technol. 2012, 30, 327. [Google Scholar]
- Kong, N.H. Simulation of Hot Air Drying on Corn Kernel Based on Three Dimension Solid Model; Northeastern University: Shenyang, China, 2013. [Google Scholar]
- Zheng, F. Research and Experiment on Key Technologies and Equipment of Grain Multi-Field Collaborative Drying; South China Agricultural University: Guangzhou, China, 2018. [Google Scholar]
- Chi, G.L. Air Drying Simulation System for Corn Drying; Jilin University: Changchun, China, 2004. [Google Scholar]
- Bishnoi, R.; Aharwal, K.R. Experimental and theoretical analysis of mass transfer in a refrigerated food storage. Heat Mass Transf. 2022, 58, 1845–1855. [Google Scholar] [CrossRef]
- Chokphoemphun, S.; Chokphoemphum, S. Moisture content prediction of paddy drying in a fluidized-bed drier with a vortex flow generator using an artificial neural network. Appl. Therm. Eng. 2018, 145, 630–636. [Google Scholar] [CrossRef]
- Sureshkumar, R.; Kale, S.R.; Dhar, P.L. Heat and mass transfer processes between a water spray and ambient air-I. Exp. Data. Appl. Therm. Eng. 2007, 28, 349–360. [Google Scholar] [CrossRef]
- Lowrey, S.; Sun, Z. Experimental investigation and numerical modelling of a compact wet air-to-air plate heat exchanger. Appl. Therm. Eng. 2017, 131, 89–101. [Google Scholar] [CrossRef]
- Chang, S.J.; Wi, S.; Lee, J.; Kim, S. Thermal performance analysis of phase change materials composed of double layers considering heating and cooling period. J. Ind. Eng. Chem. 2019, 72, 255–264. [Google Scholar] [CrossRef]
- Loo, L.; Maaten, B.; Siirde, A.; Pihu, T.; Konist, A. Experimental analysis of the combustion characteristics of Estonian oil shale in air and oxy-fuel atmospheres. Fuel Process. Technol. 2015, 134, 317–324. [Google Scholar] [CrossRef]
- Chu, Z.; Yang, J.; Li, X.; Song, Y. Heat and mass transfer engorgement of vibrating fluidized bed. J. Therm. Sci. 1994, 3, 257–262. [Google Scholar] [CrossRef]
- Ibrahim, D.; Mehmet, P. The thin-layer drying characteristics of corn. J. Food Eng. 2003, 60, 125–130. [Google Scholar]
- Yin, W.D.; Li, B.; Wu, Y.; Yang, H.; Liu, Q.; Lu, J.; Zhao, J. Model of coal slime combustion behavior in CFB boiler. J. China Coal Soc. 2015, 40, 1628–1633. [Google Scholar]
- Daming, S.; Rainer, N.; Lothar, R. Wall-to-bed heat transfer in circulating fluidized beds. Chem. Eng. Process. Process Intensif. 1998, 37, 287–293. [Google Scholar]
- Liu, Q.; Bakker-Arkema, F.W. A model-predictive controller for grain drying. J. Food Eng. 2001, 49, 321–326. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, J.; Yue, G.; Liu, Q.; Yu, L.; Lin, X.; Li, W.; Tang, Y.; Luo, T.; Ge, R. Method of calculation of heat transfer coefficient of the heater in a circulating fluidized bed furnace. Heat Transf. Asian Res. 2002, 31, 540–550. [Google Scholar] [CrossRef]
- Hao, Z.H. The Development of Baffle Downer Dryer for Lignite Demoisture with High Temperature Flue Gas and the Research of the Key Technologies; Tsinghua University: Beijing, China, 2011. [Google Scholar]
- Syahrul, I.; Dincer, F. Thermodynamic modeling of fluidized bed drying of moist particles. Int. J. Therm. Sci. 2003, 42, 691–701. [Google Scholar] [CrossRef]
- Wu, G.; He, Y.; Luo, L.; Chen, W. Dynamic characterizations of gas–solid flow in a novel multistage fluidized bed via nonlinear analyses. Chem. Eng. J. 2021, 359, 1013–1023. [Google Scholar] [CrossRef]
- Wang, C.T.; Tian, S.X.; An, X.Z. The effects of drying parameters on drying characteristics, colorimetric differences, antioxidant components of sliced Chinese jujube. Heat Mass Transf. 2022, 58, 1561–1571. [Google Scholar] [CrossRef]
- Wang, C. Analysis of Corn Hot Air Drying and Influencing Factors; Northeastern University: Shenyang, China, 2020. [Google Scholar]
- Onwude, D.I.; Hashim, N.; Chen, G. Recent advances of novel thermal combined hot air drying of agricultural crops. Trends Food Sci. Technol. 2016, 57, 132–145. [Google Scholar] [CrossRef]
- Prakash, B.; Pan, Z. Effect of geometry of rice kernels on drying modeling results. Dry. Technol. 2012, 30, 801–807. [Google Scholar] [CrossRef]
- Henrik, T.; Kent, D.; Bo, L. Separation of drying and devolatilization during conversion of solid fuels. Combust. Flame 2004, 137, 242–250. [Google Scholar]
- Perez, J.H.; Tanaka, F.; Uchino, T. Comparative 3D simulation on moisture absorption and hygroscopic swelling in japonica rice grains under various isothermal soaking condition. Food Res. Int. 2011, 44, 2615–2623. [Google Scholar] [CrossRef]
- Huang, K.; Chen, X.F.; Chen, P.X.; Wang, F.H.; Tu, G.; Zhao, Y.; Liu, X.D.; Yang, D.Y. Simulation and experimental analysis of mass transfer drying in maize grains. J. Eng. Thermophys. 2017, 38, 193–198. [Google Scholar]
- Walton, L.R.; White, G.M.; Ross, I.J. A cellular diffusion based drying model for corn. Trans. ASAE 1988, 31, 279–0283. [Google Scholar] [CrossRef]
- Franz, W.; Michael, E.P.; Hermann, H. Temperatures in a fuel particle burning in a fluidized bed: The effect of drying, devolatilization, and char combustion. Combust. Flame 1997, 108, 302–314. [Google Scholar]
- Zhao, L.; Yang, J.; Du, T.; Wu, Z. A 3-Dimensional body fitted simulation of heat and mass transfer in rice kernel during hot air drying Process. Int. J. Food Eng. 2019, 15, 1–11. [Google Scholar] [CrossRef]
- Lu, J.; Tian, Y.; Peng, X.; Yue, G. Analysis of particles motion and convection heat transfer in circulating fluidized bed. J. Chem. Ind. Eng. 2003, 54, 1224–1229. [Google Scholar]
- Gao, K. Study of Heat and Mass Exchange and Energy Consumption of during Grain Drying; North China Electric Power University: Beijing, China, 2019. [Google Scholar]
- Liu, Q.; Bakker-Arkema, F.W. Stochastic modelling of grain drying: Part 2. Model development. J. Agric. Eng. Res. 1997, 66, 275–280. [Google Scholar] [CrossRef]
- Zare, D.; Jayas, D.S.; Singh, C.B. A Generalized Dimensionless Model for Deep Bed Drying of Paddy. Dry. Technol. 2012, 30, 44–51. [Google Scholar] [CrossRef]
- Khatchatourian, O.A.; Vielmo, H.A.; Bortolaia, L.A. Modelling and simulation of cross flow grain dryers. Biosyst. Eng. 2013, 116, 335–345. [Google Scholar] [CrossRef]
- Prommas, R.; Rattanadecho, P.; Cholaseuk, D. Energy and exergy analyses in drying process of porous edia using hot air. Int. Commun. Heat Mass Transf. 2010, 37, 372–378. [Google Scholar] [CrossRef]
- Motevali, A.; Minaei, S.; Khoshtagaza, M.H. Evaluation of energy consumption in different drying methods. Energy Convers. Manag. 2011, 52, 1192–1199. [Google Scholar] [CrossRef]
- Sivakumar, R.; Elayaperumal, A. Studies on combined cooling and drying of agro products using air cooled internal heat recovered vapour absorption system. Appl. Therm. Eng. 2015, 97, 100–108. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Wang, Q.M. Analysis of hot air drying characteristics of corn seeds considering the effect of flow field. Mod. Food 2022, 28, 164–167. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).