This section introduces the features of the developed test vehicle. The experimental setup and the utilized numerical methods are introduced. A detailed comparison of the obtained results is done.
To study the ventilation drag of HDV wheels, a 1:4.5 scale vehicle model was designed, manufactured, and investigated in the Model Scale Wind Tunnel of the University of Stuttgart. Force measurements with the wind tunnel balance and flow filed measurements with a PIV system were done on different HDV wheel configurations. The focus is on the ventilation drag of different treaded tires and rim topologies. The experiments aim to identify the relevant flow features and also provide a database for the validation of the numerical simulation. In a next step, an approach for investigating and quantifying the ventilation drag in CFD is introduced.
2.1. Development of a Test Vehicle
The developed vehicle model generates a flow topology in the vicinity of the wheel that is comparable to a real commercial vehicle. The shape of the vehicle model is based on the generic tractor-trailer of the German Association for Research in Automotive Technology (FAT) [
11,
12].
Since the investigation of the ventilation drag focuses on the forces and moments acting on the wheels, the representation of the flow conditions in the wheel area is of great importance. Therefore, the design of the test vehicle was reduced to a quarter vehicle model, which only covers half of the width and both axles of the tractor. This design also allows to keep the influence of the blockage effects of the wind tunnel as small as possible while at the same time allowing investigations at high Reynolds numbers () making sure the results can be transferred to full scale. The resulting blockage ratio between the cross-section of the wind tunnel nozzle and the vehicle frontal area is 7.8%.
The 1:4.5 scale of the vehicle model is determined due to the necessary quality of the measurements and the boundary conditions of the model-scale wind tunnel. The goal is to achieve a fully developed turbulent boundary layer at
[
8]. Furthermore, the vehicle model has to fit on the five-belt system used simulate the relative motion between vehicle and floor and to rotate the wheels.
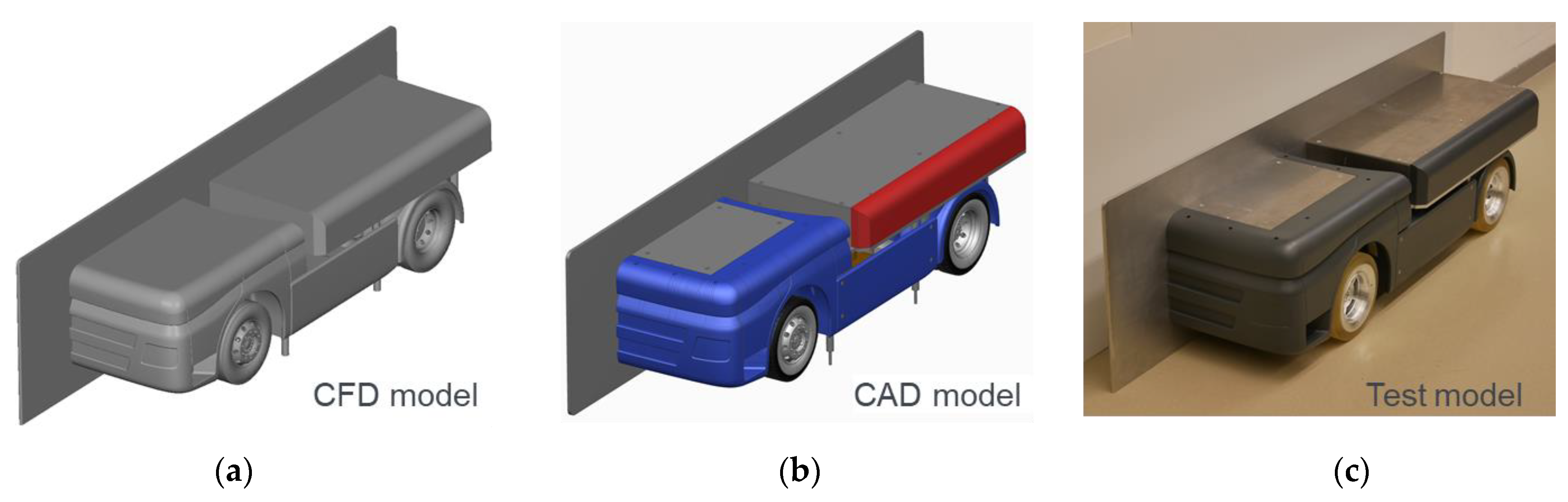
For designing the vehicle model shown in
Figure 1, an iterative process is used. The requirements and specifications are incorporated into the model in different development loops. The design of the vehicle model is fully digital, and it is supported by several CAE programs. First, the commercial CFD software Simulia PowerFLOW is used to develop the outer skin of the model, the geometry of which is intended to reproduce the aerodynamic conditions in the wheel area of a real HDV. In the next step, the geometry of the vehicle model consolidated in the CFD is converted into a CAD model suitable for manufacturing. A detailed description of the development and production of the vehicle model can be found in [
13].
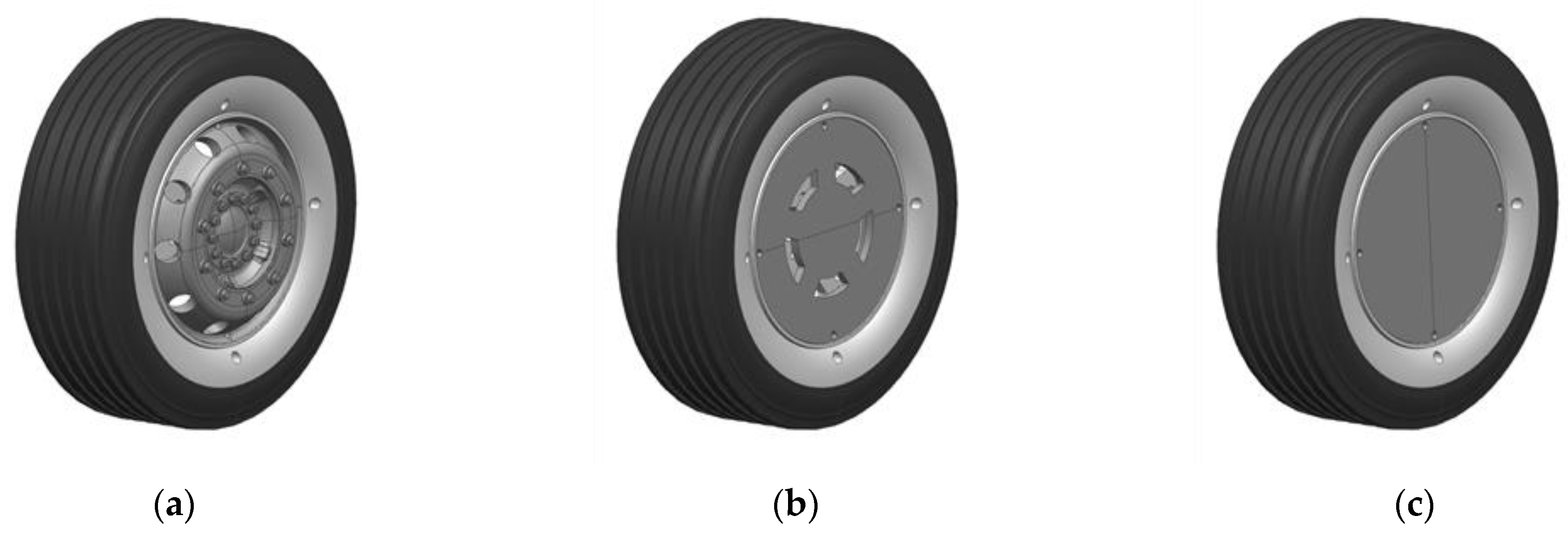
The wheels correspond to a type 315/70 R 22.5 in 1:4.5 scale. The modular design of the wheels, as shown in
Figure 2, enables the investigation of different rim and tread geometries. Both the front wheel and the twin wheels on the rear axle are based on a reference rim from solid aluminum which allows the attachment of different rim shapes and treads from rapid prototyping.
To investigate the ventilation drag, two different treads and three different rim shapes are used.
Figure 3 shows the chosen tread topologies, which are based on a realistic tire geometry from Continental. Furthermore, three different rim covers can be fitted (
Figure 4). While the standard rim (a) represents a conventional front axle rim, the rim covers (b) and (c) represent rim shapes with flat outer surface. The eco rim (b) is based on a design proposed by Vdovin et al. [
10] for passenger cars.
2.2. Experimental Setup for Wind Tunnel Testing
All experimental investigations were carried out in the model scale wind tunnel at the Institute of Automotive Engineering (IFS) of the University of Stuttgart. It is a Göttingen type wind tunnel with an open jet test section. The nozzle cross-sectional area is 1.65 m
2. The wind tunnel is equipped with a turntable and a ground simulation system, including a state of the art five-belt and boundary layer control system. The underfloor balance installed in the test section allows to measure the aerodynamic forces and moments acting on the vehicle [
14].
The force required to overcome the wheel resistance Is applied by the wheel rotation units. This is an internal force of the vehicle-balance system that is not measured in the standard wind tunnel setup. To isolate the forces acting on the wheels, the vehicle model is attached to the test section floor via the rocker panel struts, displayed in
Figure 5. The forces are measured by the underfloor balance since it is directly connected to the wheel rotation units. The total force to be overcome by the wheel which will be measured by the balance represents the superposition of the ventilation drag
, the rolling resistance
, and the aerodynamic forces acting on the belts. To exclude the rolling resistance and the frictional losses from the measurements, a velocity of 5 km/h is chosen as value of tare. At this speed, the aerodynamic forces are negligible, whereas the rolling resistance is supposed to be nearly constant over the whole speed range. Therefore, for low speed, it is possible to evaluate the mechanical and frictional losses on the wheel and subtract them from the final measurements. However, the influence of the aerodynamic forces on the belts are difficult to capture separately from the measurement. Consequently, the measured aerodynamic forces experienced by the wheel stand for the superposed ventilation drag and the aerodynamic effect of the belts. The time-averaged value of this longitudinal force is designated as
.
In addition to the investigation of the aerodynamic forces, the flow field in the vicinity of the rotating wheel is measured by means of Particle Image Velocimetry (PIV). The FlowMaster PIV system from LaVision GmbH was used, consisting of a Nd:YAG-Laser, two SCMOS cameras, as well as a timing and recording computer. The obtained images record the movement of the particles, which are translated into the velocity components of the flow field using a cross-correlation.
The measurements are carried out in several laser sheet positions including the upstream and downstream regions beside the rotating front wheel. The location of four planes oriented normal to the ground plane are shown in
Figure 6. The measured flow fields close to the vehicle can be distorted by laser reflections from nearby surfaces. The reflections cause areas that can shine brighter than the particles on the laser sheet illuminated by the laser. To minimize this phenomenon, all potentially reflective surfaces are covered with low-reflection coatings.
2.3. Numerical Setup for Modeling Wheel Rotation in CFD
The commercial CFD code Simulia PowerFLOW is used for all numerical simulations. PowerFLOW is widely used in the automotive industry, a large number of validation reports can be found in the literature [
15,
16,
17]. The underlying Lattice–Boltzmann Method is based on the mesoscopic kinetic theory that considers particle distribution tracking and is inherently transient. The behavior of the particle distribution function
with position
, velocity
, time
and the collision operator
is described by the Boltzmann equation (Equation (1)). The left side of this equation shows the advection of the particle distribution while the right side represents the redistribution of the particle distribution function due to collisions. Equation (2) shows the collision operator in its Bhatnagar–Gross–Krook form with the relaxation time constant
and the equilibrium distribution
[
18]. For discretizing the Boltzmann equation on a lattice, 3 spatial dimensions and 19 discrete velocities are considered in Simulia PowerFLOW. The fluid–wall interaction is calculated using a volumetric boundary scheme that allows the modeling of no-slip walls, slip walls, and wall functions at each facet particle [
19].
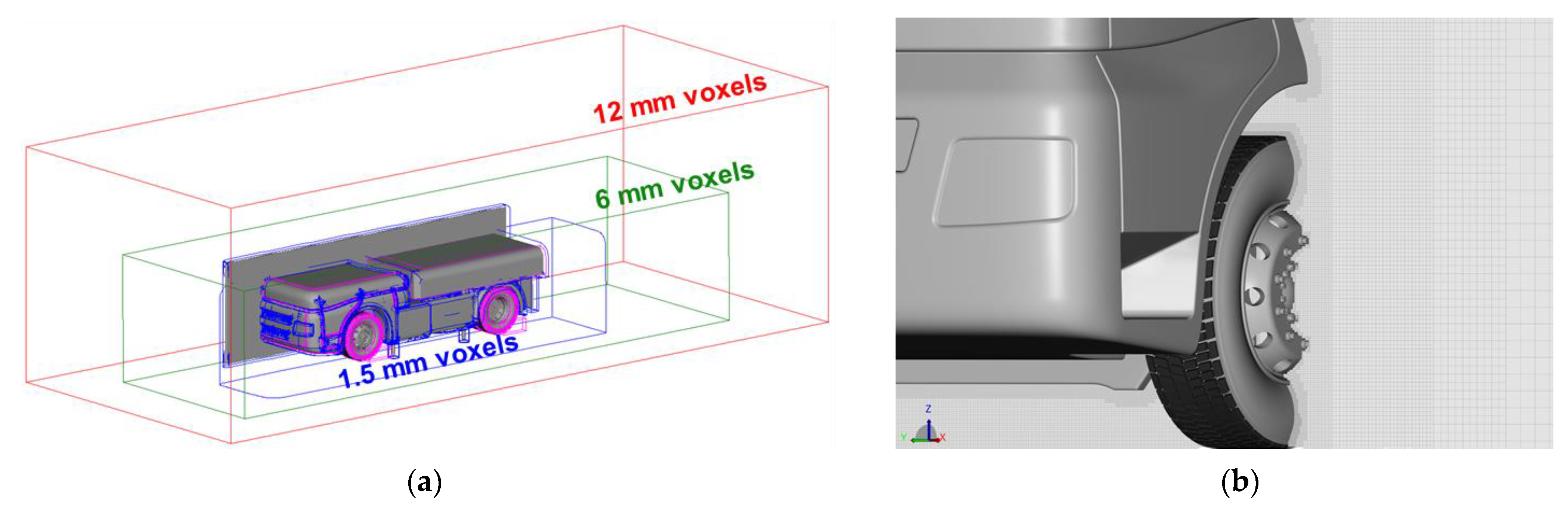
The applied VLES (Very Large Eddy Simulation) turbulence model and an adapted RNG 𝑘-ε model for the unresolved small scales allow to capture the relevant turbulence effects in the highly turbulent flow field. The simulation domain is discretized by using cubic volumetric elements called voxels that are cells of the lattice, where the large-scale turbulence is resolved. Several regions with increased resolution are added to resolve the sensitive flow phenomena on the vehicle following the best practices provided by Simulia. The finest voxels are assigned to the highest resolution level and they have a size of 0.375 mm (
Figure A1). The turbulence is considered in the collision operator by adjusting the relaxation time
to
as shown in Equation (3), where
is the temperature,
is the local strain parameter, and
is a model coefficient. A detailed description of the equations for solving the turbulent kinetic energy
and the turbulent dissipation
can be found in [
20].
The simulation domain is created with dimensions large enough to avoid any blockage or interference effects. The implemented boundary conditions are velocity inlet, pressure outlet, and frictionless boundary conditions for the sidewalls and ceiling. Moreover, the five-belt system, consisting of a central moving belt and four wheel belts, has been implemented. It allows to reproduce the rolling road and the contact patch of the wheels in a realistic way. According to the wind tunnel configuration, a moving wall boundary condition was assigned to each belt.
In general, rotating geometries represent a transient flow situation. However, their representation in the numerical simulation depends on the modeling complexity, the expected accuracy as well as the necessary computing power. While some flow situations can be modeled as steady-state due to their simplicity, other flow problems have to be solved by using complex grid motion techniques to capture the time-dependent nature of the flow, which requires a considerable increase in computing power.
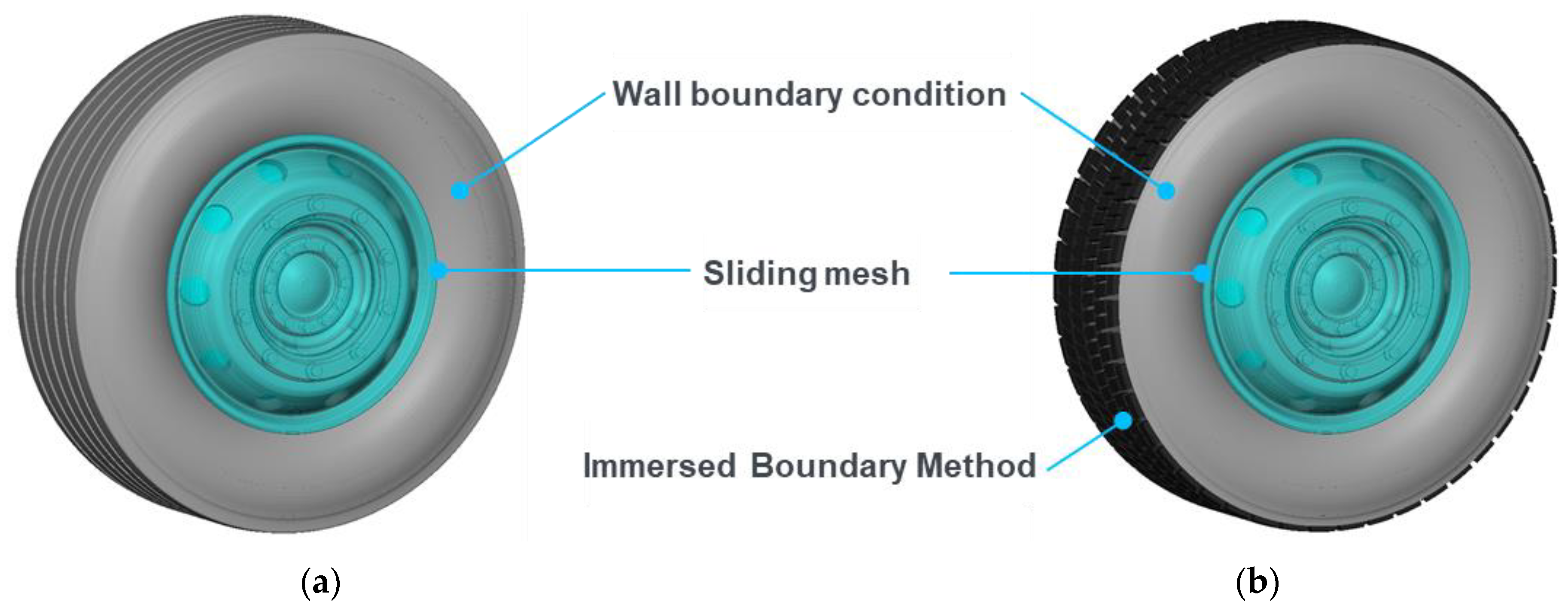
Determining the ventilation drag of a wheel in CFD requires an accurate representation of the wheel as well as a realistic and time-dependent modeling of the rotation. The approach for modeling the rotation of HDV wheels applied in this study combines several methods available in Simulia PowerFLOW. The purpose is to achieve the best possible accuracy while at the same time reducing the necessary computing power. Wall boundary conditions with a given tangential velocity are applied to the axisymmetric regions of the wheel such as the wheel shoulder or the tread with longitudinal grooves. As shown in
Figure 7 the rims are enclosed in isolated volumes which physically rotate when applying the sliding-mesh approach. Here, the calculated flow quantities are transferred between the global static grid and the rotating sub-grid via a rotationally symmetrical interface using interpolation [
21]. On the other hand, the patterns of the treaded tires are modeled by means of the immersed boundary method. This method allows to consider a non-conformal geometry on a computational grid and represents its movement by incorporating the appropriate boundary conditions in the vicinity of the geometry [
22]. Finally, since the experimentally investigated wheels are rigid—they do not deform as in the case of real tires—it is not necessary to consider shape changes on the tire shoulder. To represent the contact patch in the simulation, the tires penetrate the respective belts.
With the used methods for modeling the wheel rotation, the aerodynamic influence of the wheel rotation as well as the influence of the rim and tire geometry can be represented. This approach is thus suited for investigating the time-dependent, aerodynamic forces of rotating wheels. The rotational aerodynamic losses of the wheels due to the pressure and friction forces are captured by the chosen modelling. In that sense, the pressure distribution on the rotating rim and tire treads can be properly represented thanks to the grid motion techniques. The friction losses of the wheel are captured by the used wall boundary modelling.
2.4. Comparison of the Results and Validation
All measurements were carried out at a freestream velocity of . The maximum velocity was limited to ensure the operational safety of the 3D printed treads. The translation speed of the belts of the ground simulation system is also 60 m/s, which results in a wheel rotation velocity of 5090 rpm so that a fully developed turbulent boundary layer with is achieved. The investigated inflow situation thus corresponds to a straight-ahead drive at approximately 50 km/h for a full scale HDV.
The experimental force measurements are recorded over a measuring time of 60 s. The numerical simulations are simulated for 3 s after being initialized with the flow field of a previous coarse discretized simulation. An averaging interval of 1 s is selected to average the forces calculated in the simulation. All other parameters of the simulation analysis correspond to those of the experimental evaluation.
The results of the wind tunnel measurements and the CFD simulations shown in
Table 1 show a good agreement of force values for the individual wheel configurations. The maximum deviation between CFD and WT is 0.15 N and is close to the measurement accuracy of the balance (±0.1 N).
The crosswise position of the treads to the incident flow results in a local increase of the pressure and friction forces acting on the tire. The comparison of the forces between the variants with different tire topology shows that the influence of the treaded pattern leads to an increase of of approximately 180% in the test. However, applying the profiling in the simulation amounts to an increase in the calculated forces of approx. 230%.
The ventilation drag can be reduced when using aerodynamically improved rims. The wind tunnel measurements of the wheel configurations with closed and eco rims show a reduction of the measured force of 10–18% compared to the standard rim. Moreover, the simulation results show a similar reduction (5–16%) of the ventilation drag due to the flat rims. Furthermore, it can be observed that the force measurements performed in the model wind tunnel are more sensitive to the rim shape, while the CFD results of the closed and eco rim differ little from each other.
Table 2 shows the results of the aerodynamic ventilation forces acting on the twin wheels. Analogous to the study of the front wheel, there are moderate deviations between the measured and simulated forces. The maximum deviation between CFD and WT is 0.43 N. However, this deviation is greater than that on the front axle and is particularly noticeable on the twin wheels with longitudinal grooves.
Again, the treaded pattern increases the ventilation drag compared to the longitudinal grooves. This increase amounts to 70% in the wind tunnel tests and approximately 90% in the CFD simulations. However, the observed increase on the rear axle is smaller than that on the front axle. The reason for this is the different inflow situation experienced by the wheels on the front and rear axle. While the single wheel in the front wheel arch is directly exposed to the airflow, the twin wheels are in the wake of the front wheel and under the influence of the underbody airflow.
Fitting flat hub covers to the twin wheels results in a reduction of ventilation drag. The improvement of the aerodynamic properties compared to the standard rim is evaluated similarly in the experiment and in CFD. The difference between the closed and eco covers is minimal due to the characteristics of the underbody airflow at the rear axle.
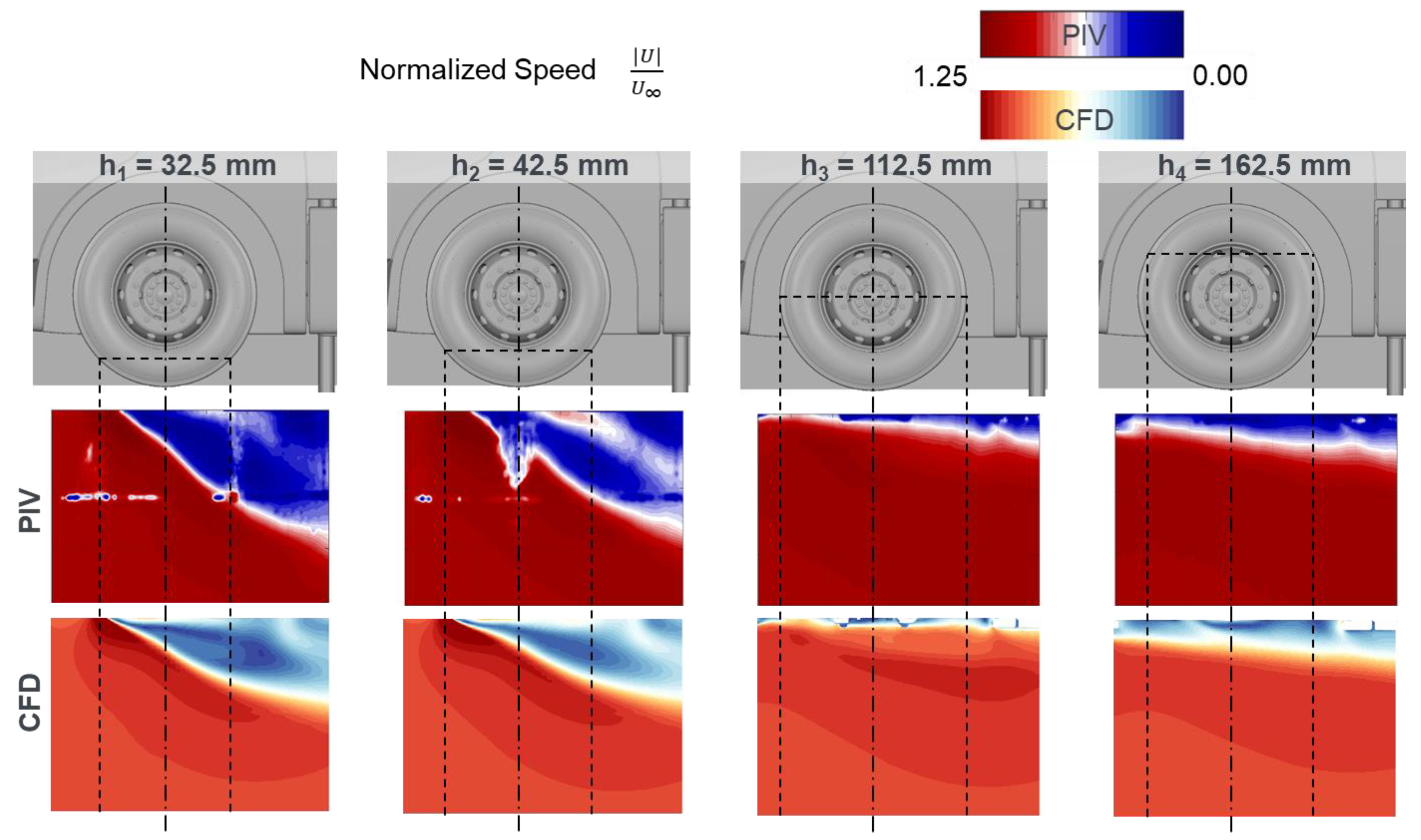
In general, a good agreement between the experimental and the simulated flow field can be observed in
Figure 8. The horseshoe vortex is fully developed at wheel shoulder height (h1) and its size, intensity as well as the flow separation at the flank of the tire are represented in the same way by both results. Likewise, at the height of the lower rim edge (h2), the interactions of the horseshoe vortex and the wheel wake are comparable. The small, detached flow area at wheel hub height (h3) indicates that the wheel is shielded by the wheel housing. Finally, the flank vortex in the upper area of the wheel housing (h4) is reproduced equally by both results.
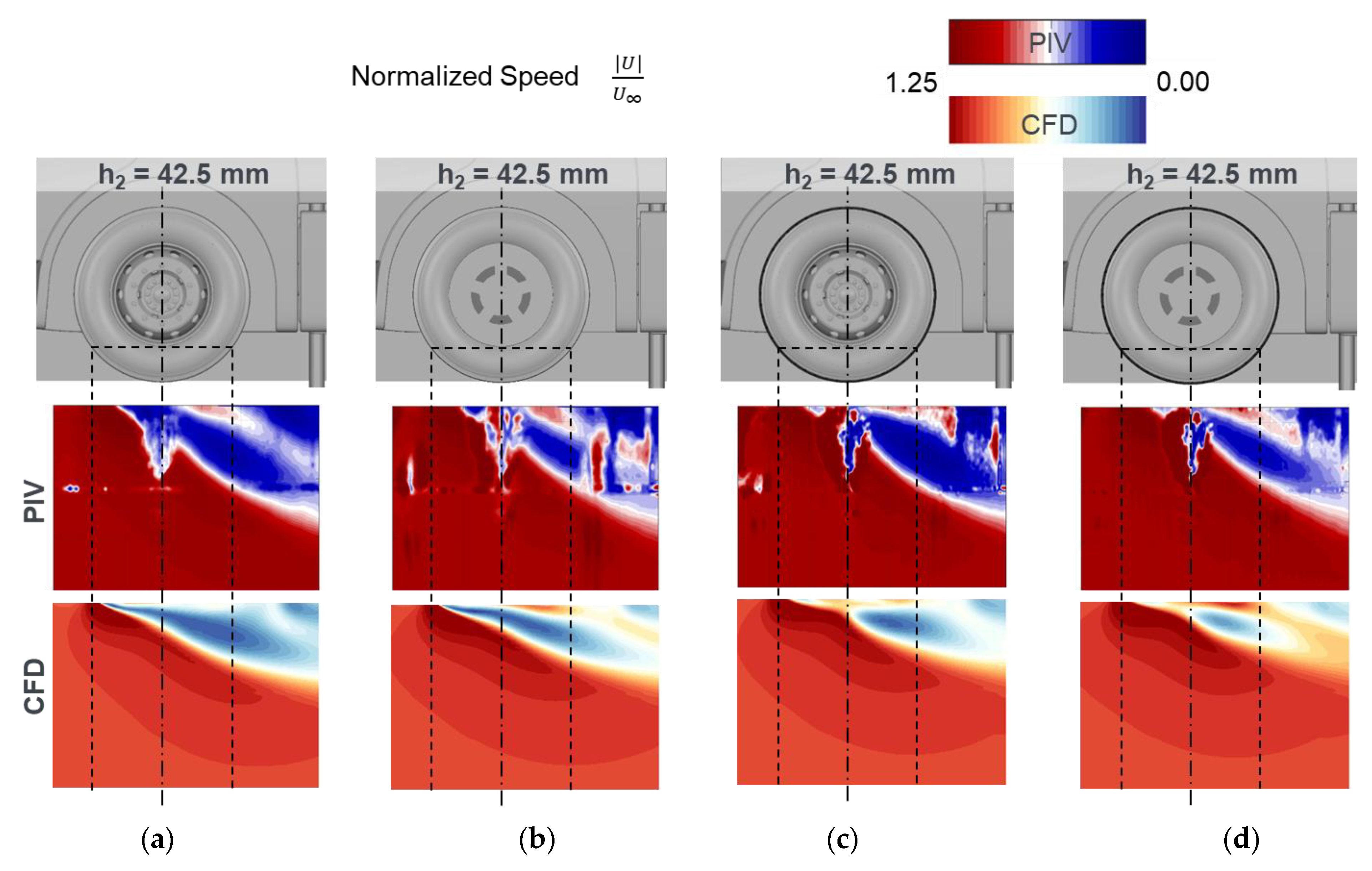
The influence of the thread and the rim shape on the flow topology is illustrated in
Figure 9. The flow field on the lower plane h2 shows that the use of a flat rim, such as the eco rim, reduces the size of the horseshoe vortex, regardless of the tires used. This flow behavior is equally reflected in the simulation results. On the other hand, the treaded pattern of the tire causes a change in shape and displacement of the wheel horseshoe vortex.
To evaluate the quality of the applied CFD procedure with regard to the determination of the ventilation drag, the numerically calculated forces are compared with the measurements obtained in the wind tunnel for each wheel configuration investigated. The percentage deviation of CFD results from the experimental measurements is 5% to 15% regardless of the wheel type, rim type, or topology of the tread. An exception to this is the results of the tests with longitudinal grooves on the rear axle, which show a deviation of up to 30%. The mentioned deviation is independent of the rim shape and indicates that there may be differences in the inflow experienced by the twin wheel. Furthermore, the sensitivity of the CFD procedure with respect to geometrical wheel changes is also evaluated. In this regard, the measured and simulated forces show comparable tendencies due to the different treads and rim shapes.
The methods used to model the wheel rotation in CFD allow a good representation of the flow phenomena observed in the wind tunnel. The introduced CFD approach is able to predict the aerodynamic forces, the flow topology, and the changes in the flow field due to geometric changes on the wheel.