Non-Singular Burton–Miller Boundary Element Method for Acoustics
Abstract
1. Introduction
2. The Burton–Miller Framework
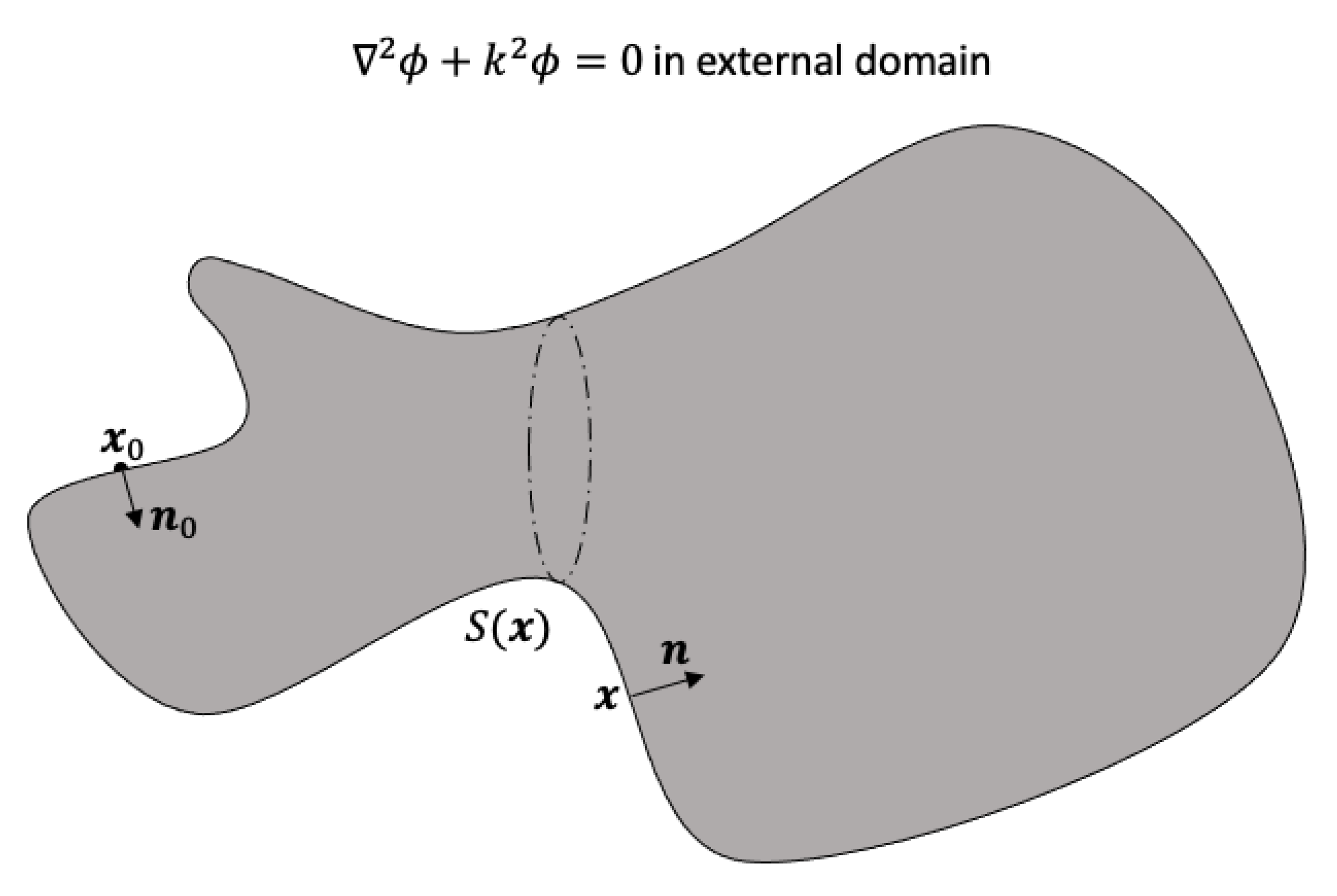
2.1. Overview
2.2. The Standard Boundary Integral Equation
2.3. The Normal Derivative of the Boundary Integral Equation
2.4. The Non-Singular Burton–Miller Formulation
3. Results
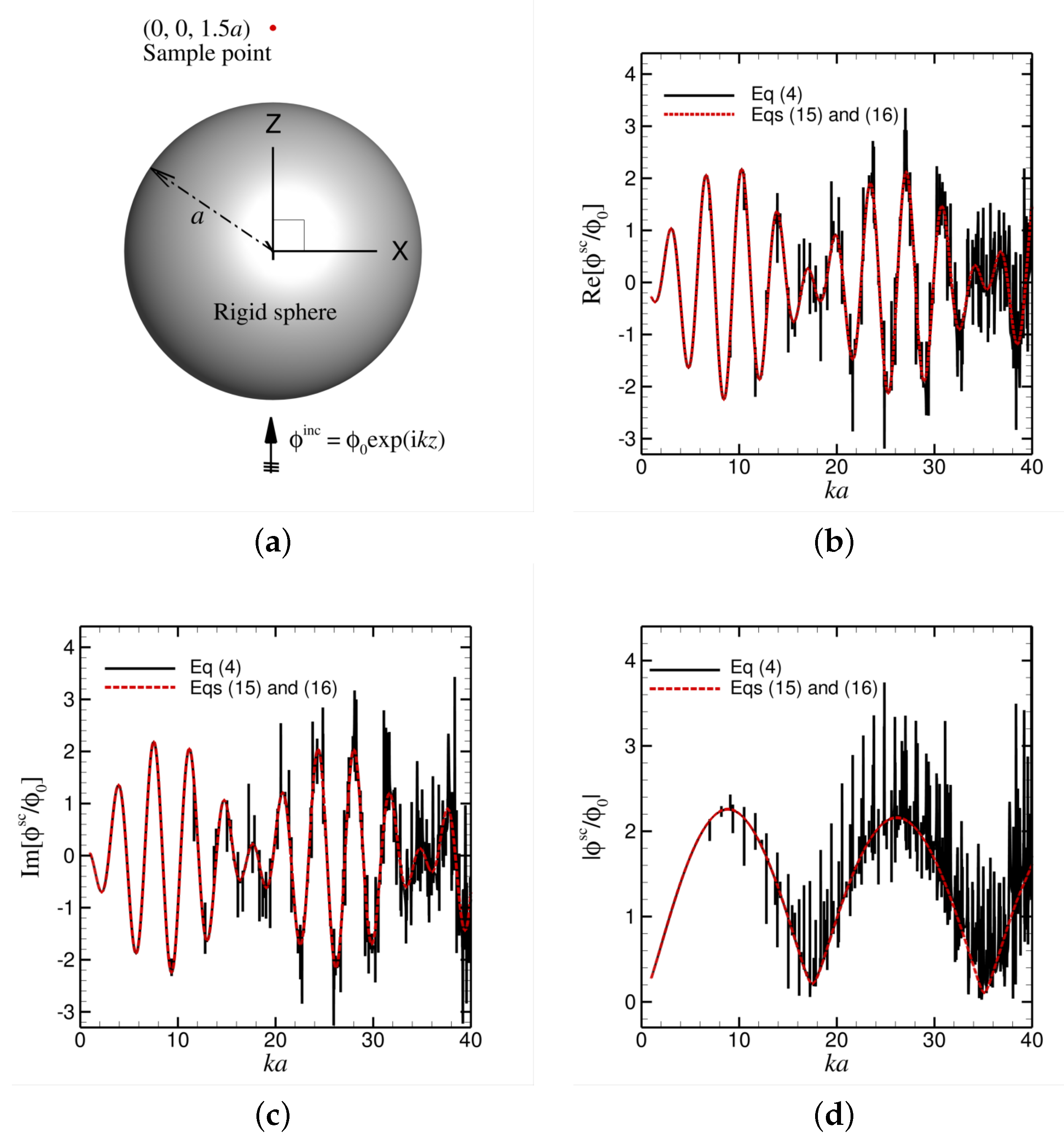
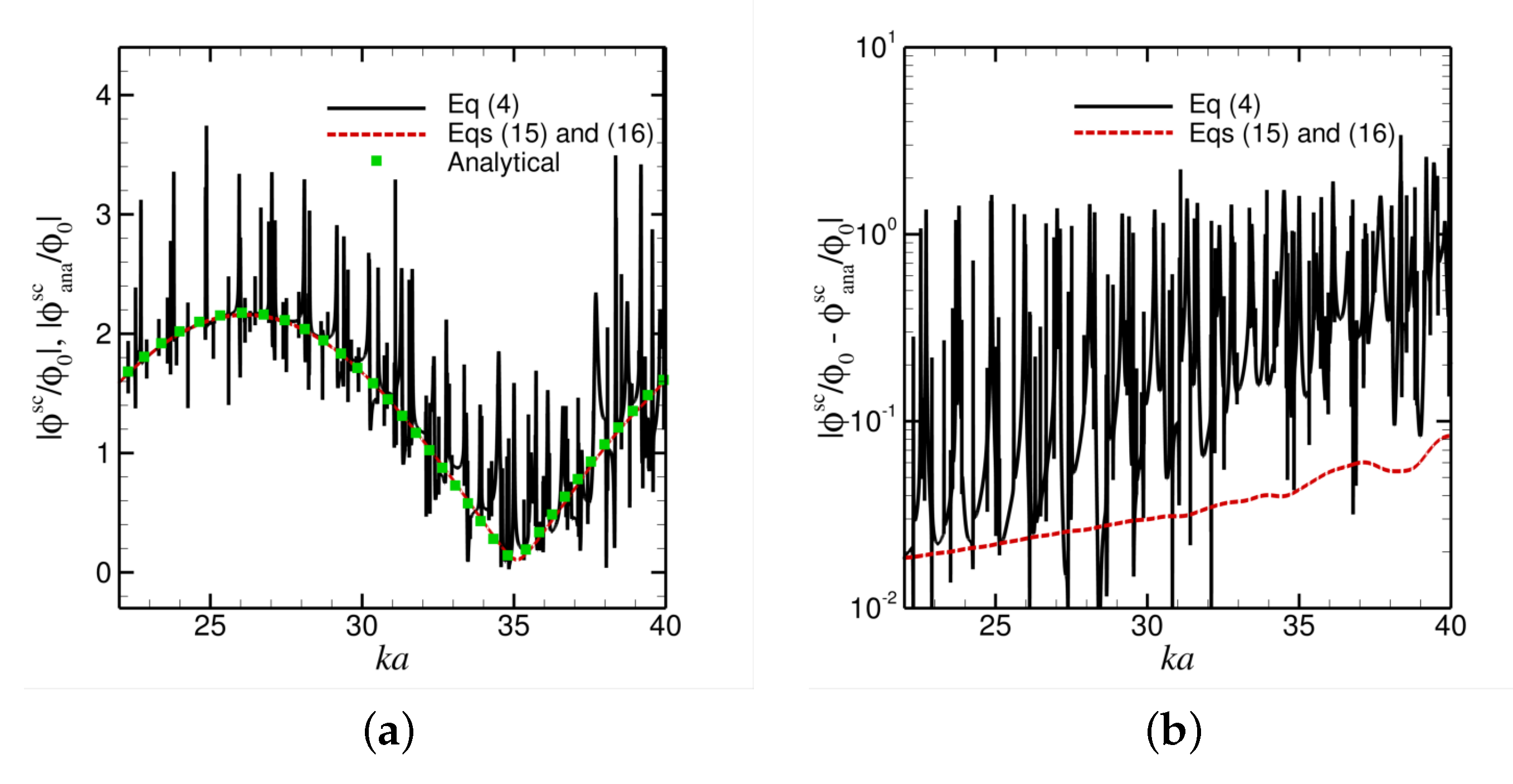
3.1. Scattering from a Rigid Sphere
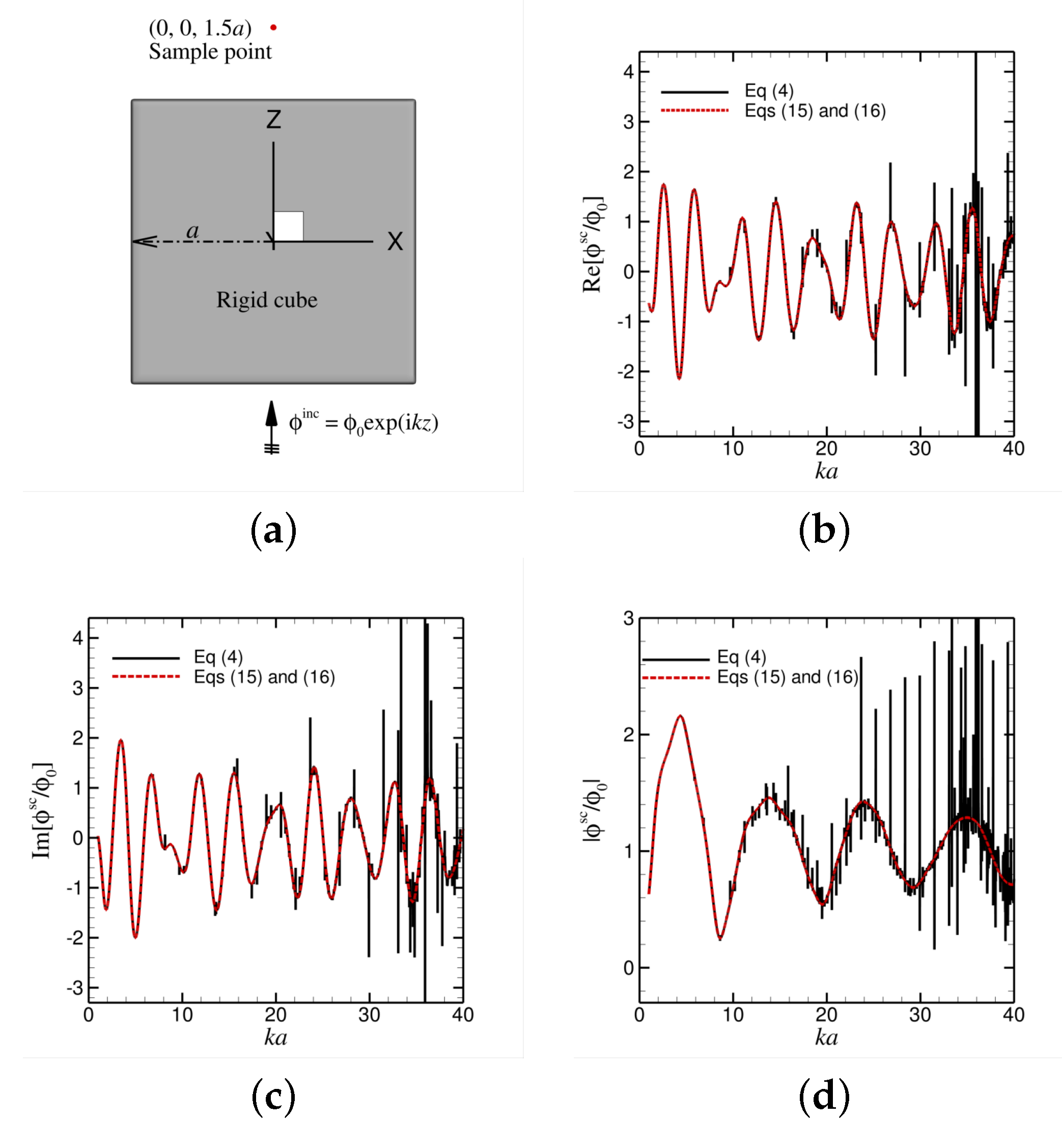
3.2. Scattering from a Rigid Cube
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Singular Behaviour of the Green’s Functions
References
- Rienstra, S.W.; Hirschberg, A. An Introduction to Acoustics; Eindhoven University of Technology: Eindhoven, The Netherlands, 2004. [Google Scholar]
- von Helmholtz, H. Theorie der Luftschwingungen in Röhren mit Offenen Enden; Verlag von Wilhelm Engelmann: Leipzig, Germany, 1896. [Google Scholar]
- Nita, B.G.; Ramanathan, S. Fluids in Music: The Mathematics of Pan’s Flutes. Fluids 2019, 4, 181. [Google Scholar] [CrossRef]
- Kadar, H.; Le Bras, S.; Bériot, H.; de Roeck, W.; Desmet, W.; Schram, C. Trailing-edge noise prediction by solving Helmholtz equation with stochastic source term. AIAA J. 2021, 60, 1–20. [Google Scholar] [CrossRef]
- Smyk, E.; Markowicz, M. Impact of the Soundproofing in the Cavity of the Synthetic Jet Actuator on the Generated Noise. Fluids 2022, 7, 323. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Ostachowicz, W.; Yang, Z. Structural Health Monitoring system based on a concept of Lamb wave focusing by the piezoelectric array. Mech. Syst. Signal Process. 2018, 108, 21–32. [Google Scholar] [CrossRef]
- Lighthill, J. Waves in Fluids; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Pergamon Press: London, UK, 1987. [Google Scholar]
- Rayleigh, R. The Theory of Sound; Macmillan and Co., Ltd.: New York, NY, USA, 1896; Volume 2. [Google Scholar]
- Becker, A.A. The Boundary Element Method in Engineering; McGraw-Hill Book Company: London, UK, 1992. [Google Scholar]
- Brebbia, C.A.; Walker, S. Boundary Element Techniques In Engineering; Newnes-Butterworths: London, UK, 1980. [Google Scholar]
- Amini, S.; Harris, P.J.; Wilton, D.T. Coupled Boundary and Finite Element Methods for the Solution of the Dynamic Fluid-Structure Interaction Problem; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Bai, M.R. Application of BEM (boundary element method)-based acoustic holography to radiation analysis of sound sources with arbitrarily shaped geometries. J. Acoust. Soc. Am. 1992, 92, 533–549. [Google Scholar] [CrossRef]
- Liu, Y. On the BEM for acoustic wave problems. Eng. Anal. Bound. Elem. 2019, 107, 53–62. [Google Scholar] [CrossRef]
- Sommerfeld, A. Die Greensche Funktion der Schwingungsgleichung. Jahresber. Dtsch.-Math.-Ver. 1912, 21, 309–353. [Google Scholar]
- Klaseboer, E.; Charlet, F.D.E.; Khoo, B.C.; Sun, Q.; Chan, D.Y.C. Eliminating the fictitious frequency problem in BEM solutions of the external Helmholtz equation. Eng. Anal. Bound. Elem. 2019, 109, 106–116. [Google Scholar] [CrossRef]
- Schenck, H.A. Improved integral formulation for acoustic radiation problems. J. Acoust. Soc. Am. 1968, 44, 41–58. [Google Scholar] [CrossRef]
- Burton, A.J.; Miller, G.F. The application of integral equation methods to the numerical solution of some exterior boundary-value problems. Proc. R. Soc. A 1971, 323, 201–210. [Google Scholar]
- Marburg, S. The Burton and Miller method: Unlocking another mystery of its coupling parameter. J. Comput. Acoust. 2016, 24, 1550016. [Google Scholar] [CrossRef]
- Langrenne, C.; Garcia, A.; Bonnet, M. Solving the hypersingular boundary integral equation for the Burton and Miller formulation. J. Acoust. Soc. Am. 2015, 138, 3332. [Google Scholar] [CrossRef]
- Klaseboer, E.; Sun, Q.; Chan, D.Y.C. Non-singular boundary integral methods for fluid mechanics applications. J. Fluid Mech. 2012, 696, 468–478. [Google Scholar] [CrossRef]
- Sun, Q.; Klaseboer, E.; Chan, D.Y.C. A robust and accurate formulation of molecular and colloidal electrostatics. J. Chem. Phys. 2016, 145, 054106. [Google Scholar] [CrossRef]
- Sun, Q.; Klaseboer, E.; Khoo, B.C.; Chan, D.Y. A robust and non-singular formulation of the boundary integral method for the potential problem. Eng. Anal. Bound. Elem. 2014, 43, 117–123. [Google Scholar] [CrossRef]
- Klaseboer, E.; Sun, Q. Helmholtz equation and non-singular boundary elements applied to multi-disciplinary physical problems. Commun. Theor. Phys. 2022, 74, 085003. [Google Scholar] [CrossRef]
- Meyer, W.; Bell, W.; Zinn, B.; Stallybrass, M. Boundary integral solutions of three dimensional acoustic radiation problems. J. Sound Vib. 1978, 59, 245–262. [Google Scholar] [CrossRef]
- Chen, K.; Cheng, J.; Harris, P.J. A new study of the Burton and Miller method for the solution of a 3D Helmholtz problem. IMA J. Appl. Math. 2008, 74, 163–177. [Google Scholar] [CrossRef]
- Hwang, W.S. Eliminating the fictitious frequency problem in BEM solutions of the external Helmholtz equation. J. Acoust. Soc. Am. 1997, 101, 3336. [Google Scholar] [CrossRef]
- Sun, Q.; Klaseboer, E.; Khoo, B.C.; Chan, D.Y.C. Boundary regularized integral equation formulation of the Helmholtz equation in acoustics. R. Soc. Open Sci. 2015, 2, 140520. [Google Scholar] [CrossRef]
- Morse, P. Vibration and Sound, 4th ed.; American Institute of Physics: New York, NY, USA, 1991. [Google Scholar]
- Klaseboer, E.; Sun, Q.; Chan, D.Y.C. Non-singular field-only surface integral equations for electromagnetic scattering. IEEE Trans. Antennas Propag. 2017, 65, 972–977. [Google Scholar] [CrossRef]
- Sun, Q.; Klaseboer, E.; Chan, D.Y.C. A Robust Multi-Scale Field-Only Formulation of Electromagnetic Scattering. Phys. Rev. B 2017, 95, 045137. [Google Scholar] [CrossRef]
- Klaseboer, E.; Sun, Q.; Chan, D.Y.C. A field only integral equation method for time domain scattering of electromagnetic pulses. Appl. Opt. 2017, 56, 9377. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Klaseboer, E.; Yuffa, A.J.; Chan, D.Y.C. Field-only surface integral equations: Scattering from a perfect electric conductor. J. Opt. Soc. Am. A 2020, 37, 276–283. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Klaseboer, E.; Yuffa, A.J.; Chan, D.Y.C. Field-only surface integral equations: Scattering from a dielectric body. J. Opt. Soc. Am. A 2020, 37, 284–293. [Google Scholar] [CrossRef]
- Sun, Q.; Klaseboer, E. A Non-Singular, Field-Only Surface Integral Method for Interactions between Electric and Magnetic Dipoles and Nano-Structures. Annal. Phys. 2022, 534, 2100397. [Google Scholar] [CrossRef]
- Klaseboer, E.; Sun, Q. Analytical solution for a vibrating rigid sphere with an elastic shell in an infinite linear elastic medium. Int. J. Solids Struct. 2022, 239, 111448. [Google Scholar] [CrossRef]
- Klaseboer, E.; Sepehrirahnama, S.; Chan, D.Y.C. Space-time domain solutions of the wave equation by a non-singular boundary integral method and Fourier transform. J. Acoust. Soc. Am. 2017, 142, 697–707. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Klaseboer, E. Non-Singular Burton–Miller Boundary Element Method for Acoustics. Fluids 2023, 8, 56. https://doi.org/10.3390/fluids8020056
Sun Q, Klaseboer E. Non-Singular Burton–Miller Boundary Element Method for Acoustics. Fluids. 2023; 8(2):56. https://doi.org/10.3390/fluids8020056
Chicago/Turabian StyleSun, Qiang, and Evert Klaseboer. 2023. "Non-Singular Burton–Miller Boundary Element Method for Acoustics" Fluids 8, no. 2: 56. https://doi.org/10.3390/fluids8020056
APA StyleSun, Q., & Klaseboer, E. (2023). Non-Singular Burton–Miller Boundary Element Method for Acoustics. Fluids, 8(2), 56. https://doi.org/10.3390/fluids8020056






