Abstract
Physics-informed neural networks (PINN) can be used to predict flow fields with a minimum of simulated or measured training data. As most technical flows are turbulent, PINNs based on the Reynolds-averaged Navier–Stokes (RANS) equations incorporating a turbulence model are needed. Several studies demonstrated the capability of PINNs to solve the Naver–Stokes equations for laminar flows. However, little work has been published concerning the application of PINNs to solve the RANS equations for turbulent flows. This study applied a RANS-based PINN approach to a backward-facing step flow at a Reynolds number of 5100. The standard k- model, the mixing length model, an equation-free and an equation-free pseudo-Reynolds stress model were applied. The results compared favorably to DNS data when provided with three vertical lines of labeled training data. For five lines of training data, all models predicted the separated shear layer and the associated vortex more accurately.
1. Introduction
Several methods of artificial intelligence have been developed and applied to the field of fluid dynamics. Among them, physics-informed neural networks (PINNs) are becoming popular, as these networks reduce the requirements for large high-quality datasets [1]. PINNs can be used to solve partial differential Equations (PDEs) and predict nonlinear solution fields. A PINN is a neural network (NN) trained to satisfy given laws of physics. Lagaris et al. [2] were the first to employ a PINN to solve ordinary differential Equations (ODEs), coupled ODEs and PDEs. Later, Raissi et al. [3,4,5] used a PINN to solve the Burgers equation, the Schrödinger equation, and the Allen–Cahn equation for time-dependent one-dimensional problems. The reported predictions agreed well with the exact solutions. These publications showed that PINNs can be used to solve different equations accurately. Hence, PINNs could also be applied to fluid dynamics to solve the Navier–Stokes equations.
The application of PINNs to solve the Navier-Stokes equations was investigated in several publications. Raissi et al. [6] deployed a PINN to predict a two-dimensional (2D) flow past a cylinder, a 2D channel flow over a spherical obstacle, and a three-dimensional (3D) flow through the intercranial aneurysm. The predictions agreed favorably with exact solutions. Sun et al. [7] presented a PINN that was trained using boundary-condition enforcement and adaptive activation functions. They reported good agreement between PINN and CFD simulations for the aneurysmal flow. Zhu et al. [8] used a convolutional PINN to predict the 2D Darcy flow. The results showed more accurate predictions for the PINN than for a data-driven NN. Jin et al. [9] trained a PINN to predict a 2D Kovasznay flow, a 2D cylinder wake, a 3D Beltrami flow, and a turbulent channel flow. The predicted channel flow agreed favorably with DNS results. Zhu et al. [10] applied a PINN to melt pool fluid dynamics using hard boundary-constraint enforcing. Their employed PINN accurately predicted temperature and dynamics using only a moderate number of labeled datasets. Wang et al. [11] deployed a convolutional PINN to predict 2D multiscale turbulent-flow fields based on numerical simulations. Laubscher and Rousseau [12] trained a PINN on an incompressible flow with heat transfer around two sequentially positioned cylinders. They obtained good agreement with CFD results. Wand et al. [13] used a PINN to reconstruct the flow field from PIV measurements and found good agreement with DNS results. In a recent study, Eivazi and Vinuesa [14] trained a PINN to reconstruct a transient flow field from low-resolution and noisy measurements, showing that PINNs can be used to solve unsteady turbulent problems.
In most of the research presented above, PINNs were trained to predict a solution for a single geometry. Wandel et al. [15] trained a convolutional PINN with different 3D shapes, such as boxes, cylinders, or spinning balls, and tested the neural net for geometries not contained in the training dataset.
High-Reynolds-number flows play a major role in many technical problems. For turbulent flows, the velocity and pressure fields are complex in space and time. This imposes challenges on any training attempt with PINNs. As for most engineering applications only stationary information is required, PINN predictions of the Reynolds-averaged Naver–Stokes (RANS) equations are sufficient. To our best knowledge, predictions of the RANS equations have only been presented by Hennigh et al. [16], Eivazi et al. [17] and Xu et al. [18]. Hennigh et al. [16] applied the mixing-length turbulence model to predict a turbulent thermal flow. Eivazi et al. [17] trained a PINN to statisfy the RANS equations without a transport-equation-based model to predict a turbulent boundary layer, the high Reynolds flow in a sub domain on an airfoil, as well as a flow over a periodic hill. Xu et al. [18] used a similar approach and trained a PINN to predict the turbulent viscosity without any imposed equation. They trained the model to CFD data and used it to explore missing flow data inside of a finite area downstream of a backward-facing step. Hence, a comparison of different turbulence modeling approaches for PINN and an extension to transport-equation-based models, such as the k- model, remain an open question.
In this work, we contribute to the question of how different turbulence modeling approaches could be applied and how the prediction accuracy of the different PINNs compares. Therefore, we applied different turbulence models for the flow over a backward-facing step at a Reynolds number of 5100. For our study, we deployed the mixing-length model as used in [16], as well as the two-equation k- model. Additionally, we applied two equation-free turbulence models for PINNs similar to the approaches in [17,18]. These models were developed to evade the training difficulties associated with the PDEs of traditional turbulence models. The predictions obtained with different amounts of labeled training data are compared to the DNS results of Le et al. [19]. Furthermore, we discuss the strengths and weaknesses of the turbulence models regarding the usage for PINN. The scope of our work was to compare the prediction quality of different turbulence models when applied with a fully connected feedfoward PINN that was trained with different amounts of labeled training data. The motivation for this work was to develop a method to use turbulence models for PINNs and to serve as a reference for application and selection of turbulence models in future work.
2. Backward-Facing Step Flow
Several PINNs with different turbulence models were trained to predict the flow around a backward-facing step at a Reynolds number of 5100. Figure 1 schematically illustrates the expected mean flow field. As seen, the flow field exhibits a boundary layer on the channel wall, a separated and reattached shear layer downstream of the step, a recirculative vortex inside of the separation bubble, and a secondary corner vortex in the lower corner of the step. A review of the literature concerning the flow field around the backward-facing step can be found in [20].
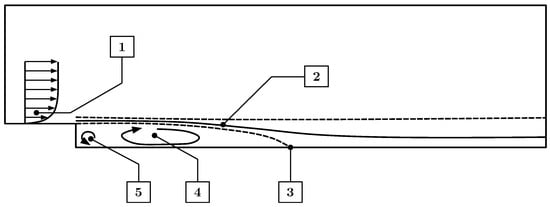
Figure 1.
Backward-facing step flow features. 1: Boundary layer; 2: separated shear layer; 3: reattached flow; 4: recirculative vortex; 5: corner vortex.
The networks were trained with data and compared against DNS results for the backward-facing step flow of Le et al. [19]. They used the mean inlet velocity profile of Spalart [21] for the forced convection boundary condition. The velocity profile was superimposed with random velocity fluctuations. A convective boundary condition was applied for the outlet. In the spanwise dimension, they used a periodic boundary condition. The step had a contraction rate of 1.2. At the considered Reynolds number of 5100, the flow was turbulent [19]. Le et al. [19] reported that the DNS results agreed favorably with experiments.
3. Methodology
3.1. Flow Prediction with PINNs
A feedforward NN was trained to predict the two-dimensional stationary flow field. The network had three input neurons corresponding to coordinates x and y and wall distance d. An output layer displayed the variables of the flow field. In case the NN is trained to solve the Naver–Stokes equations for the variables u, v, and p, the network reads
where represents the trainable parameters (weights) of the NN. Figure 2 shows the corresponding network architecture of the PINN.
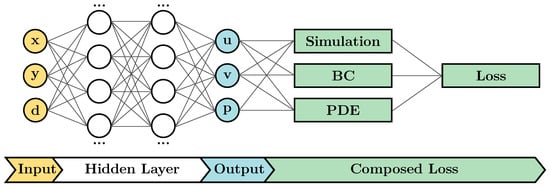
Figure 2.
Neural network architecture of the PINN.
As shown in Figure 2, the output of the NN is fed into a so-called composed loss function which adds several individual losses.
3.2. Composed Loss Function
The pivotal part of a PINN is the composed loss function. Here, several individual losses are added. The composed loss function deployed here reads
where corresponds to the boundary conditions, to the simulated labeled training data, and to the partial differential equation employed.
3.3. Governing Equations
The flow field considered here is governed by the two-dimensional Reynolds-averaged Navier–Stokes (RANS) equations and the continuity equation for an incompressible fluid. Hence, the PDEs considered in the composed loss function read
with averaged velocity components and , averaged pressure , density and kinematic viscosity . The RANS equations contain the following derivations of the Reynolds stress terms:
and
4. Experiments
4.1. Turbulence Modeling
We considered four different turbulence-modeling approaches. According to the Boussinesq hypothesis, for an incompressible flow the Reynolds stresses read as follows:
where k is the turbulent kinetic energy, is the Kronecker delta, and is the turbulent viscosity. The utilization of a turbulent viscosity is based on the gradient diffusion hypothesis. This hypothesis assumes that the turbulent transport is in negative gradient direction of the mean flow and depends on an isotropic turbulent viscosity serving as a diffusion coefficient.
The first model we considered is the standard k- model of Wilcox [22]. For this model, the turbulent viscosity is calculated as follows:
with the specific dissipation rate . The 2D stationary equations for k and read
with , as recommended by Wilcox [22]. Note that for the k- model, the transport equations for k and are added as additional PDEs into the composed loss function. The corresponding PINN reads
The second turbulence model we considered is the mixing-length model by Prandtl as applied in [16]. For this model, the turbulent viscosity is calculated as follows:
For a two-dimensional flow, the modulus of the mean rate of strain tensor G reads
and the mixing length is calculated as follows:
where d is the wall normal distance and its maximal value. As no turbulent kinetic energy is calculated with the mixing-length model, the Reynolds stresses must be computed differently than in Equation (8). Since the 2D case is considered here, this reads
The PINN, then, reads
We applied two additional novel turbulence modeling approaches for PINNs, here referred to as the -model and the pseudo-Reynolds stress model. In both cases, no physics-based equation for the output is imposed.
For the -model, the Reynolds stresses are calculated in the same way as for the mixing length model. The deployed PINN then reads
In the training process, the weights are adjusted such that the predicted values of u, v, p, and satisfy the RANS equations.
In case of the pseudo-Reynolds stress model, the derivations of the Reynolds stresses are calculated directly from the pseudo-turbulent output of the PINN, as follows:
and
where and are pseudo turbulent velocity components. As and represent time-independent velocity components,
Therefore, the model is referred to as the pseudo-Reynolds stress model. The corresponding PINN reads
In the training process, the weights are adjusted such that the predicted u, v, p, and satisfy the RANS Equations (3)–(5).
4.2. Boundary Conditions
For the upper channel wall, a slip wall boundary condition was specified; for the lower channel walls a no-slip wall condition. For the no-slip wall, a smooth surface was considered. Additionally, a Neumann boundary condition was defined for the mean velocities u and v at the inlet edge of the training domain. The DNS data for the mean values of u and v were prescribed for six vertical lines. The lines were positioned at , and . The associated boundary conditions were created using the DNS data of [19], which were taken from the ERCOFTAC database [23] (note the coordinate system was modified for our purposes). Data at specified the inlet boundary condition of the domain. All other vertical lines were positioned inside the domain. For training, a point-wise boundary condition was used for the DNS data. Figure 3 displays the training setup and the associated boundary conditions.
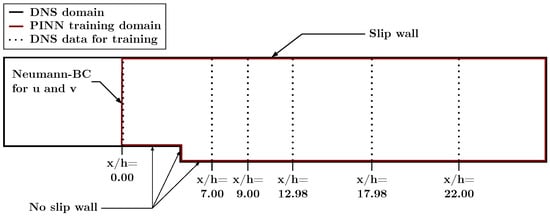
Figure 3.
Boundaries for the PINN training process.
4.3. PINN Training Procedure
We used the Tensorflow-based library DeepXDE to set up and train the model [24]. As mentioned above, the PINN was trained to satisfy the RANS equations together with the turbulence models. Additionally, the model was trained to fulfill the boundary conditions and to match the DNS data. Figure 4 shows the implementation of the algorithm. The automatic differentiation allows to derive the outputs of the PINN depending on the turbulence model with respect to the inputs and to form the loss function of the PDE.
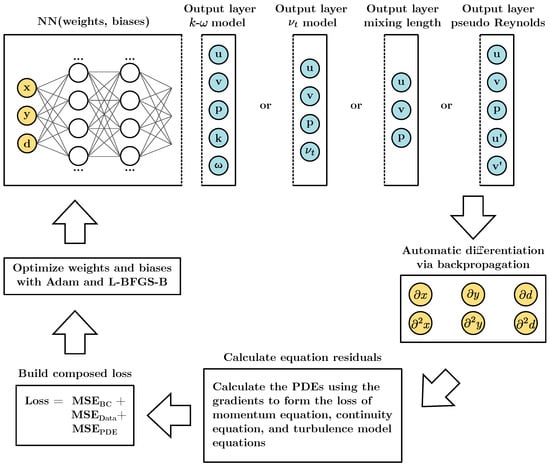
Figure 4.
Flowchart of the applied training algorithm. For supplementary information on residuals of the specific turbulence models, see for the k- model Equations (8)–(11), the mixing-length model Equations (13)–(19), the model Equations (17)–(19), and the pseudo-Reynolds stress model Equations (22) and (23).
The PINN was trained for 30,000 epochs with the Adam optimizer and, afterwards, with the L-BFGS-B optimizer under predefined default settings. The boundary conditions and simulation data were trained at a total of 2000 training points. The PDEs were trained at 2000 training points inside of the domain. The applied number of points was based on a sensitivity analysis. Figure 5 displays the global normalized mean squared error (NMSE) for 1000, 2000, and 4000 points in the domain as well as on the boundaries. As seen, the error was minimal for the case of 2000 points. Consequently, this investigation was conducted with 2000 points. The training points were uniformly (equispaced) distributed.
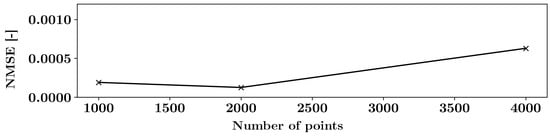
Figure 5.
Global NMSE over the number of training points inside the domain as well as on the boundaries. The results were obtained for the pseudo-Reynolds stress model using three lines of labeled training data.
Table 1 lists the specified training parameters. Every neural net was reinitialized and trained ten times, as the initalization of the weights was shown to have a significant influence on the result [24]. If possible, all samples with physically unrealistic solutions were discarded, and the remaining sample with the lowest global NMSE was selected for further evaluation.

Table 1.
PINN training parameters.
4.4. Comparison with DNS Data
To compare the turbulence models with the DNS data, we evaluated several error metrics. To measure systematic and random errors, the normalized mean squared error (NMSE) was used [25]. The factor of observations (FAC2) was utilized to asses extreme deviations [25]. Systematic errors were measured using the fractional bias (FB) [25]. Additionally, the validation metric V of Oberkampf and Trucano [26] was applied to assess the overall level of validation. Commonly used acceptance limits are: NMSE < 4, FAC2 > 0.5, and FB < 0.2 [27].
4.5. Analyses
An analysis was carried out to investigate the sensitivities of the predictions on turbulence modeling as well as on the quantity of labeled training data.
In the first step, the PINN was trained with DNS training data at = 0 only. This training configuration investigated the training quality without any labeled training data inside of the flow domain. In a second step, the PINN was trained with DNS data at = 0.00, 7.00, 12.98, and 22.00. Both cases were compared with the DNS data to assess the accuracy of the predictions. In a third step, the PINN was trained with all DNS data available.
For all steps, the predictions obtained using the k-, the mixing length model, the proposed model, and the proposed pseudo-Reynolds stress model were compared.
5. Results
In this section, the predictions of the different PINNs are presented in comparison with the DNS data.
5.1. Training without Labeled Training Data Inside of the Domain
Figure 6 presents the magnitudes of fluid velocity predicted by the best-trained neural nets (lowest overal NMSE). The predictions are displayed together with DNS results and the deviations are shown. As seen, for all turbulence models, the training without labeled training data resulted in predictions which deviated significantly from the DNS results. Above the backward-facing step, all models underpredicted the fluid velocity; in the wake of the step, all models overpredicted the length of the recirculating vortex.
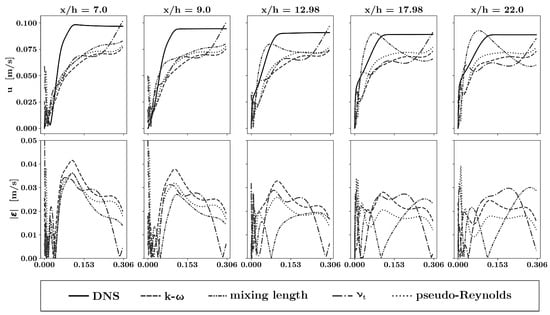
Figure 6.
Comparative PINN predictions of velocity magnitudes (top) and their deviation from DNS results (bottom) for the training without any labeled training data inside of the flow domain. The results are shown at several longitudinal positions. The y-axis of the bottom row is clipped at 0.05.
5.2. Training with Three Lines of Labeled Training Data Inside of the Domain
Figure 7 displays the magnitudes of fluid velocity magnitudes predicted by the best-trained neural nets (lowest overal NMSE). The predictions are compared to the DNS results and the deviations are presented. As seen, all models favorably match the labeled training data. For data belonging to the vertical lines at and , where no DNS data were used for the training, all models agreed favorably with the DNS data. The greatest deviations occured at for the model. The mixing-length model and the model overpredicted the length of the separated shear layer. Above the step, the k- model as well as the mixing-length model exhibited deviations from the DNS results.
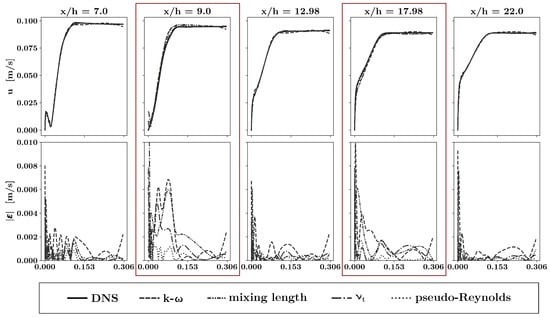
Figure 7.
Comparative PINN predictions of velocity magnitudes (top) and their deviations from DNS results (bottom) for the training with three vertical lines of labeled training data inside of the flow domain. The y axis of the bottom row is clipped at 0.01. The red boxes indicate positions where no labeled training data was used for the training of the PINN.
Table 2 lists error measures for the most accurate PINN sample for the five turbulence models considered. The average NMSEs for the k- model, the mixing length model, the model, and the pseudo-Reynolds-stress model were 2.0 , 1.2 , 2.2 , and 7.5 , respectively. The standard deviations of the NMSEs from ten reinitialized training runs were 66.9%, 48.8%, 37.2%, and 70.0%, which indicated significant variations in accuracy over the runs. The error measures for NMSE, FAC2, FB, and V, presented in Table 2, indicate low random errors, extreme deviations, bias errors and a good overall agreement, respectively.

Table 2.
Error measures of the most accurate PINN sample for the five turbulence models.
Figure 8 displays fluid velocities and streamlines of the flow predicted by the PINN using the k- model. As seen, the neural net predicted the separated shear layer as well as the vortex inside the separation bubble. At the vertical wall of the step, a small flux through the boundary is present (point 1 in Figure 8). The results did not exhibit a corner vortex (point 2 in Figure 8). Above the backward-facing step, a region of high-velocity fluid is present (point 3 in Figure 8). Downstream of the reattached shear layer, flux through the horizontal wall accompanied by an upward fluid motion is visible (compare denotation 4 in Figure 8).
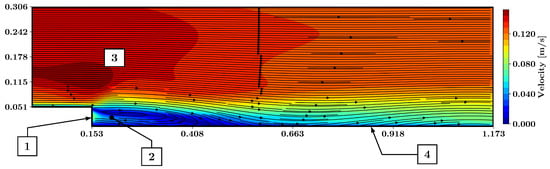
Figure 8.
Predicted flow field around the backward-facing step using the k- model, based on training with three vertical lines of labeled training data. The magnitude of velocity is presented together with the streamlines. 1: Flux through the vertical wall; 2: no corner vortex predicted; 3: thickened shear layer; 4: flux through the horizontal wall accompanied by an upward motion.
Figure 9 shows the velocity as well as the streamlines predicted by the mixing-length model. The model predicted a separated shear layer that reattaches downstream of the step. Flux through the vertical and horizontal wall of the step is visible (point 1 in Figure 9). The PINN did not predict the vortex inside of the separation bubble nor the corner vortex (point 2 in Figure 9). The predicted shearlayer is thickened shortly downstream of the step (point 3 in Figure 9). Additionally, flux passing through the horizontal wall accompanied by an upward fluid motion is visible downstream of the step (point 4 in Figure 9).
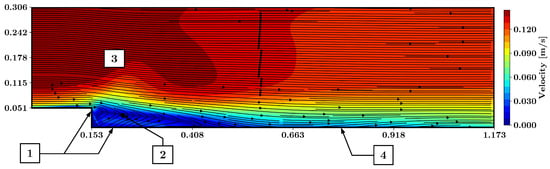
Figure 9.
Predicted flow field around the backward-facing step using the mixing length model, based on training with three vertical lines of labeled training data. The magnitude of velocity is presented together with the streamlines. 1: Flux through the vertical wall; 2: no corner vortex predicted; 3: thickened shear layer; 4: flux through the horizontal wall accompanied by an upward motion.
Figure 10 exhibits the velocity field as well as the streamlines predicted by the PINN model using the model. The separated shear layer and the associated recirculative vortex are present in the results. As for the other models, the streamlines indicate a small flux through the vertical wall of the backward-facing step (point 1 in Figure 10). No corner vortex was predicted (point 2 in Figure 10). Above the separated shear layer and downstream of the step, an area of high-velocity fluid is present (point 3 in Figure 10).
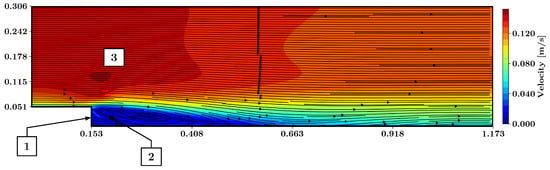
Figure 10.
Predicted flow field around the backward-facing step using the model, based on training with three vertical lines of labeled training data. The magnitude of velocity is presented together with the streamlines. 1: Flux through the vertical wall; 2: no corner vortex predicted; 3: area of high velocity.
Figure 11 displays the velocity as well as the streamlines predicted by the PINN using the pseudo-Reynolds-stress model. Similar to most other models, the pseudo-Reynolds-stress model predicted the separated shear layer and the associated vortex at the backward-facing step. At the corner of the backward facing step, flux passing through the vertical wall exists (point 1 in Figure 11). As for all other turbulence models, no corner vortex was predicted by the PINN using the pseudo-Reynolds-stress model (point 2 in Figure 11).
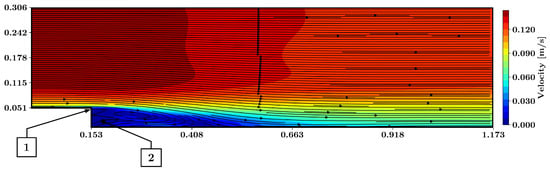
Figure 11.
Predicted flow field around the backward-facing step using the pseudo Reynolds stress model, based on training with three vertical lines of labeled training data. The magnitude of velocity is presented together with the streamlines. 1: Flux through the vertical wall; 2: no corner vortex predicted.
5.3. Training with Five Lines of Labeled Training Data Inside of the Domain
The k- model, the mixing-length model, the model, and the pseudo-Reynolds model yielded global NMSE of 4.0 , 7.7 , 1.1 , and 5.6 as well as standard deviations of 1,196%, 61.8%, 46.2%, and 35.1%, respectively. This, again, indicated that the quality of the predictions obtained from the the ten reinitialized training sets varied significantly.
Figure 12 displays the fluid velocities and streamlines of the flow predicted by the PINN using the k- model. The neural network predicted the separated shear layer as well as the vortex inside of the separation bubble. At the vertical wall of the step, a small flux passing through the boundary is present (point 1 in Figure 12). The results do not exhibit a corner vortex (point 2 in Figure 12).
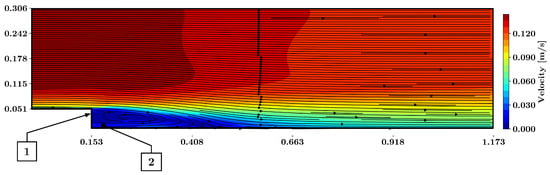
Figure 12.
Predicted flow field around the backward-facing step using the k- model, based on training with five vertical lines of labeled training data. The magnitude of velocity is presented together with the streamlines. 1: Flux through the vertical wall; 2: no corner vortex predicted.
Figure 13 shows the velocity as well as the streamlines predicted by the PINN using the mixing-length model. The model predicted the separation bubble downstream of the backward-facing ramp as well as the vortex. A small flux through the vertical wall of the step is present (point 1 in Figure 13). The PINN did not predict the corner vortex (point 2 in Figure 13). The predicted shearlayer was thickened shortly downstream of the step and a high-velocity region was formed upstream (point 3 in Figure 13).
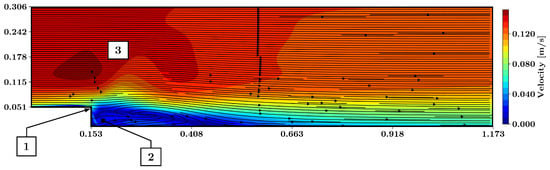
Figure 13.
Predicted flow field around the backward-facing step using the mixing-length model, based on training with five vertical lines of labeled training data. The magnitude of velocity is presented together with the streamlines. 1: Flux through the vertical wall; 2: no corner vortex predicted; 3: thickened shear layer.
Figure 14 exhibits the velocity field as well as the streamlines predicted by the PINN model using the model for the PDE inside of the composed loss function. The separated shear layer and the associated recirculative vortex characterized the flow. As for the other models, the streamlines indicated a small flux passing through the vertical wall of the backward-facing step (point 1 in Figure 14). No corner vortex was predicted (point 2 in Figure 14). Above the separated shear layer and downstream of the step, an area of high-velocity fluid is present (point 3 in Figure 14).
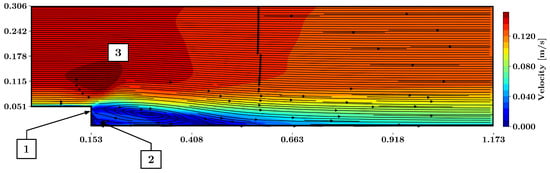
Figure 14.
Predicted flow field around the backward-facing step using the model, based on training with five vertical lines of labeled training data. The magnitude of velocity is presented together with the streamlines. 1: Flux through the vertical wall; 2: no corner vortex predicted; 3: area of high velocity.
Figure 15 displays the velocities as well as streamlines predicted by the best PINN using the pseudo-Reynolds-stress model. Predicted was the separated shear layer and the associated vortex at the backward-facing step. At the corner of the backward-facing step, a flux passing through the vertical wall is present (point 1 in Figure 15). As for all other turbulence models, no corner vortex was predicted by the PINN using the pseudo-Reynolds-stress model (point 2 in Figure 15).
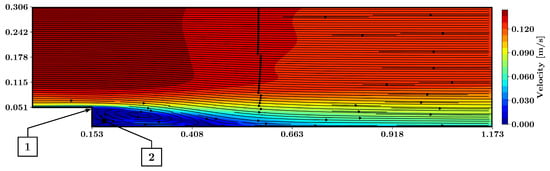
Figure 15.
Predicted flow field around the backward-facing step using the pseudo-Reynolds-stress model, based on training with five vertical lines of labeled training data. The magnitude of velocity is presented together with the streamlines. 1: Flux through the vertical wall; 2: no corner vortex predicted.
6. Discussion
For training without labeled training data inside the domain, predictions of the fully connected feed-forward PINNs disagreed with corresponding DNS data. In part, these deviations were attributable to the spatial and temporal configuration. While the DNS results in [19] were obtained for a three-dimensional backward-facing step, we applied the PINN to a two-dimensional geometry.
Another explanation for the deviation from the DNS results could be the lack of labeled training data inside the domain. In contrast, several authors reported accurate predictions using PINNs that were trained without any labeled training data. However, the associated Reynolds numbers were below 300 and, hence, the flow corresponded to laminar conditions [6,7,9,12,28]. As the flow of our work had a Reynolds number of 5100, we attribute the deviation in the PINN when trained without labeled training data to the high Reynolds number.
For training with five vertical lines of labeled training data, excellent agreement was achieved between the predictions and the DNS results for all turbulence models. The reported error metrics turned out to be well below the acceptance limits for random and bias errors. These results support the claim that PINNs can be trained to yield accurate stationary predictions of turbulent flows.
The predictions were improved when using all available training data. This was especially so when using the k-w and the mixing-length models, which exhibited distinct flaws of the flow field when trained with only three lines (compare Figure 8 and Figure 9 with Figure 12 and Figure 13).
However, these results also demonstrated the limitations of the PINN approach deployed here, as small flux was formed through the boundaries, especially through the vertical step wall. This effect could be attributed to the loss reduction during the training process. Specifically, any violation of the imposed boundary conditions is penalized with an equivalent loss. As these losses cannot be eliminated by the optimizer, a small flux through the walls could remain after the training. These fluxes could accumulate over the boundaries, resulting in mass and momentum losses which deteriorate the flow field inside the domain. As a remedy, loss-specific weighting factors could be considered. Another potential solution is hard boundary constraint enforcement [7,8] or the direct-forcing immersed boundary method [29].
All models predicted the primary separation vortex of the backward-facing step when five vertical lines of training data were used. However, every applied turbulence model failed to predict the secondary corner vortex. Consequently, the shape of the primary corner vortex was flawed. Application of a residual adaptive refinement method (RAR) might have increased the accuracy of the PINN predictions for the backward-facing step flow. When training a PINN with a RAR, training points are added in areas where high residuals are present. This may yield more accurate solutions for the smaller areas, such as the secondary corner vortex. Lu et al. [24] applied this RAR method in the PINN framework DeepXDE.
Our results also indicate that the novel turbulence models considered here are capable of predicting turbulent flows when applied with a PINN. In fact, the PINN using the pseudo-Reynolds-stress model yielded more accurate predictions than the PINNs using the established turbulence models when trained with three lines of training data. In the following, we discuss the strengths and weaknesses of all employed models.
The advantage of the k- model is that two transport equations are employed: one equation to determine the kinetic turbulent energy; the other equation the specific dissipation rate. This model has been proven to yield accurate results for a wide variety of flows, including flows over a backward-facing step [30]. Here, we incorporated this model into a PINN obtaining favorable agreements with DNS results. However, introducing two additional complex PDEs might impede the optimization process in other cases. A too-complex optimization problem could then cause the optimizer failing to approach the global minimum and, hence, provide unrealistic predictions.
For the mixing-length model, no additional PDEs needed to be solved. Hence, the optimizer was expected to more easily solve the associated system of equations. However, as no transport equation for turbulent quantities was considered, the system of PDEs can be assumed to represent the real flow less accurately. This might have caused the overpredicted thickness of the shear layer behind the step, which could have been due to an overestimated turbulent viscosity. The mixing-length model was also applied by Hennigh et al. [16]. They reported good agreement with CFD results. However, no areas of separated flow seem to be present in [16].
For the model, the PINN predicted values for the velocity and pressure as well as the turbulent viscosity field. The Reynolds stress terms were then calculated from the output of the PINN using the Boussinesq hypothesis. In contrast to the established CFD turbulence models discussed above, no equation for needed to be satisfied. This is also the case for the proposed pseudo-Reynolds-stress model, where the Reynolds stresses were computed directly from the pseudo-turbulent output of the PINN. In the training process the weights of the PINN were adjusted such that the predicted u, v, and p, as well as the turbulent variables , and (of the pseudo-Reynolds-stress model) or (of the model) together satisfy the RANS equations. Presumably, as no physics-based equation was prescribed, this method might yield wrong predictions of u, v, and p.
However, in the example presented here, the predictions compared favorably to the DNS results. In fact, the pseudo-Reynolds-stress model and the model yielded more plausible flow fields than the traditional turbulence models, when trained with only three lines of labeled data (compare Figure 8, Figure 9, Figure 10 and Figure 11). Harmening et al. [31] presented a PINN-based surrogate model which predicted the stationary flow and pressure field around a square within a range of high Reynolds numbers using the pseudo-Reynolds-stress model. Their predictions also agreed well with comparable RANS simulations. Eivazi et al. [17] presented a similar approach. They trained a PINN to predict several turbulent flows. The applied neural net was designed to predict velocity, pressure, and pseudo-Reynolds-stress terms. They also reported good agreements with simulations.
In many cases, experimental or simulative data are available. Therefore, the model and the pseudo-Reynolds-stress model could be a viable alternative to the k- model or the mixing-length model. This is especially the case for multidimensional surrogate models of variable geometry.
Data for the turbulent viscosity can be obtained from RANS simulations. Hence, although no equation was designated for the model, the corresponding PINN could be trained with labeled training data for all output variables. This is an advantage of the model when compared to the pseudo-Reynolds-stress model, where no training data can be derived for the pseudo turbulent output. The pseudo-Reynolds-stress model, on the other hand, provides more output variables that can be adjusted to satisfy the RANS equations. In fact, the pseudo-Reynolds-stress model yielded better results for the cases investigated here.
The presented RANS-based PINN method could be applied to a variety of turbulent engineering problems. This accounts for cases for which steady or unsteady solutions are required without resolving the turbulent motions. In this work, the training of the PINN took, on average, 1285 s for the pseudo-Reynolds-stress model and 2155 s for the k- model on a GeForce RTX 2070 GPU. This was 264% or 157% faster than a reference CFD simulation computed using a 120,000-cell computational grid on a i7-9700K CPU with 64 GB DDR4 RAM. However, the CFD simulations would be significantly faster for coarser grids. After training, the model required only 2.84 ms to predict the entire flow field (40,000 data points). This makes PINNs suitable for application as surrogate models for steering or optimization problems or for the generation of initial conditions for CFD calculations. As PINNs do not require a computational grid, they could also be applied as an alternative to CFD calculations to avoid expensive grid generation and errors associated with poor grid quality.
In future studies, we will investigate the capability of PINNs as multidimensional surrogate models for variable geometries. Furthermore, future work should concern improvements in the predicted flow field such that the corner vortex is also predicted by the PINN. The effect of different Reynolds numbers is a question for future studies as well. Additionally, an application of PINNs to the Lagrangian description of the Navier–Stokes equations using the smoothed particle hydrodynamics (SPH) method [32] would be interesting.
7. Conclusions
In this work, we compared four different RANS turbulence-modeling methods to predict an incompressible 2D turbulent backward-facing step flow using a PINN incorporating little labeled training data. The steady-state predictions were compared to averaged DNS results for a Reynolds number of 5100.
The models comprised the standard k- model and the mixing-length model. Additionally, we applied two equation-free models, namely, the model and a pseudo-Reynolds-stress model, which can be used to train a PINN. For the model and the pseudo-Reynolds-stress model, no additional equations needed to be solved. Instead, the PINN was trained to yield predictions that, together, satisfied the RANS equations.
Our predictions compared favorably to DNS results when three or five lines of labeled training data were used. For three lines of labeled training data, the pseudo-Reynolds-stress model produced the lowest errors. For this configuration, all models except the mixing-length model predicted the separated shear layer and the associated primary vortex. When five lines of labeled training data were used, the predicted flow fields were improved and the vortex behind the backward-facing step was predicted by all models. Every model failed to predict the secondary corner vortex.
Our work demonstrated the applicability of the k- model to PINNs. Furthermore, the pseudo-Reynolds-stress model was shown to be a viable alternative to the traditional turbulence models. For the high-Reynolds-number flow considered here, the fully connected feedforward PINN failed to yield acceptable predictions when trained without any labeled training data inside the domain. Our results demonstrated that the incorporation of few lines of training data could solve this issue.
Author Contributions
Conceptualization, F.P. and J.H.H.; methodology, F.P. and J.H.H.; software, F.P., J.H.H. and A.M.M.; validation, F.P. and J.H.H.; formal analysis, J.H.H. and F.P.; investigation, F.P., J.H.H. and A.M.M.; resources, F.-J.P.; data curation, A.M.M.; writing—original draft preparation, J.H.H. and F.P.; writing—review and editing, F.-J.P., O.e.M., D.S. and A.M.M.; visualization, F.P.; supervision, F.-J.P., O.e.M. and D.S.; project administration, F.P. and J.H.H. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge support by the Open Access Publication Fund of the Westphalian University.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sofos, F.; Stavrogiannis, C.; Exarchou-Kouveli, K.K.; Akabua, D.; Charilas, G.; Karakasidis, T.E. Current Trends in Fluid Research in the Era of Artificial Intelligence: A Review. Fluids 2022, 7, 116. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [PubMed]
- Raissi, M. Physics Informed Deep Learning (Part I): Data-Driven Solutions of Nonlinear Partial Differential Equations. 2017. Available online: http://arxiv.org/pdf/1711.10561v1 (accessed on 29 December 2022).
- Raissi, M. Physics Informed Deep Learning (Part II): Data-Driven Discovery of Nonlinear Partial Differential Equations. 2017. Available online: http://arxiv.org/pdf/1711.10566v1 (accessed on 29 December 2022).
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Gao, H.; Pan, S.; Wang, J.X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Jin, X.; Cai, S.; Li, H.; Karniadakis, G.E. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J. Comput. Phys. 2021, 426, 109951. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, Z.; Yan, J. Machine learning for metal additive manufacturing: Predicting temperature and melt pool fluid dynamics using physics-informed neural networks. Comput. Mech. 2021, 67, 619–635. [Google Scholar] [CrossRef]
- Wang, R.; Kashinath, K.; Mustafa, M.; Albert, A.; Yu, R. Towards Physics-informed Deep Learning for Turbulent Flow Prediction. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; Gupta, R., Liu, Y., Shah, M., Rajan, S., Tang, J., Prakash, B.A., Eds.; ACM: New York, NY, USA, 2020; pp. 1457–1466. [Google Scholar] [CrossRef]
- Laubscher, R.; Rousseau, P. Application of a mixed variable physics-informed neural network to solve the incompressible steady-state and transient mass, momentum, and energy conservation equations for flow over in-line heated tubes. Appl. Soft Comput. 2022, 114, 108050. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Wang, S. Dense velocity reconstruction from particle image velocimetry/particle tracking velocimetry using a physics-informed neural network. Phys. Fluids 2022, 34, 017116. [Google Scholar] [CrossRef]
- Eivazi, H.; Vinuesa, R. Physics-informed deep-learning applications to experimental fluid mechanics. arXiv 2022, arXiv:2203.15402. [Google Scholar]
- Wandel, N.; Weinmann, M.; Klein, R. Teaching the incompressible Navier–Stokes equations to fast neural surrogate models in three dimensions. Phys. Fluids 2021, 33, 047117. [Google Scholar] [CrossRef]
- Hennigh, O.; Narasimhan, S.; Nabian, M.A.; Subramaniam, A.; Tangsali, K.; Fang, Z.; Rietmann, M.; Byeon, W.; Choudhry, S. NVIDIA SimNet™: An AI-Accelerated Multi-Physics Simulation Framework. In Computational Science–ICCS 2021; Lecture Notes in Computer Science; Paszynski, M., Kranzlmüller, D., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 12746, pp. 447–461. [Google Scholar] [CrossRef]
- Eivazi, H.; Tahani, M.; Schlatter, P.; Vinuesa, R. Physics-informed neural networks for solving Reynolds-averaged Navier–Stokes equations. Phys. Fluids 2022, 34, 075117. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, W.; Wang, Y. Explore missing flow dynamics by physics-informed deep learning: The parameterized governing systems. Phys. Fluids 2021, 33, 095116. [Google Scholar] [CrossRef]
- Le, H.; Moin, P.; Kim, J. Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 1997, 330, 349–374. [Google Scholar] [CrossRef]
- Nadge, P.M.; Govardhan, R.N. High Reynolds number flow over a backward-facing step: Structure of the mean separation bubble. Exp. Fluids 2014, 55, 1657. [Google Scholar] [CrossRef]
- Spalart, P.R. Direct simulation of a turbulent boundary layer up to Rθ = 1410. J. Fluid Mech. 1988, 187, 61–98. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- European Research Community on Flow, Turbulence and Combustion. Classic Collection Database: Case031 (Backward-Facing Step). Available online: http://cfd.mace.manchester.ac.uk/ercoftac/doku.php?id=cases:case031 (accessed on 9 September 2022).
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Britter, R. (Ed.) Background and Justification Document to Support the Model Evaluation Guidance and Protocol: COST Action 732 Quality Assurance and Improvement of Microscale Meteorological Models; Meteorological Inst: Hamburg, Germany, 2007. [Google Scholar]
- Oberkampf, W.L.; Trucano, T.G. Verification and validation in computational fluid dynamics. Prog. Aerosp. Sci. 2002, 38, 209–272. [Google Scholar] [CrossRef]
- Meroney, R.; Ohba, R.; Leitl, B.; Kondo, H.; Grawe, D.; Tominaga, Y. Review of CFD Guidelines for Dispersion Modeling. Fluids 2016, 1, 14. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Thuerey, N.; Hu, X.; Haidn, O.J. Physics-driven Learning of the Steady Navier-Stokes Equations using Deep Convolutional Neural Networks. 2021. Available online: http://arxiv.org/pdf/2106.09301v1 (accessed on 29 December 2022).
- Huang, Y.; Zhang, Z.; Zhang, X. A Direct-Forcing Immersed Boundary Method for Incompressible Flows Based on Physics-Informed Neural Network. Fluids 2022, 7, 56. [Google Scholar] [CrossRef]
- Kim, J.Y.; Ghajar, A.J.; Tang, C.; Foutch, G.L. Comparison of near-wall treatment methods for high Reynolds number backward-facing step flow. Int. J. Comput. Fluid Dyn. 2005, 19, 493–500. [Google Scholar] [CrossRef]
- Harmening, J.H.; Pioch, F.; Schramm, D. Physics Informed Neural Networks as Multidimensional Surrogate Models of CFD Simulations. In Proceedings of the Machine Learning und Artificial Intelligence in Strömungsmechanik und Strukturanalyse, Wiesbaden, Germany, 16–17 May 2022; pp. 71–80. [Google Scholar]
- Rakhsha, M.; Kees, C.E.; Negrut, D. Lagrangian vs. Eulerian: An Analysis of Two Solution Methods for Free-Surface Flows and Fluid Solid Interaction Problems. Fluids 2021, 6, 460. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).