Intensification of Droplet Disintegration for Liquid–Liquid Systems in a Pulsating Flow Type Apparatus by Adding an Inert Gas

Abstract

Experimental studies have revealed that the introduction of a small amount (0.5% by volume) of permanent and chemically inert gas bubbles leads to the intensification of droplets disintegration in a liquid–liquid system (emulsification) in a pulsating flow type apparatus. The liquids used were water (continuous phase) and oil (dispersed phase) at room temperature, and nitrogen was used as a gas. The gas hold-up ${\mathsf{\phi }}_{in}$ was varied in the range of 0% to 4%. The volume fraction of the dispersed phase (oil) was 1% with respect to the continuous phase. The size of the oil droplets was determined by microphotographs; at least 600 drops were photographed in each experiment. The optimal gas hold-up in terms of the highest interfacial area (for the studied conditions) was found to be 0.5%, at which value the droplets’ Sauter mean diameter d₃₂ decreased 1.88 times, and the maximum droplet size decreased 1.3 times, compared with the case without gas input. The effect of decreasing the average droplet size d₃₂ upon the injection of an inert gas in the continuous phase disappears at φ_in ≈ 2%. The pressure loss at φ_in ≤ 2% within the measurement error remained constant, while at 4%, it increases by only 5.4%. The role of an inert gas is explained by several factors: (i) a redistribution of momentum over the volume of liquid; (ii) the occurrence of microflows near bubbles and drops, which leads to an increase in shear stresses on the surface of the drops; and (iii) gas bubbles act as pseudocavitation bubbles, whereby when they collapse, they break up adjacent droplets.

1. Introduction

Emulsification processes and liquid–liquid systems are widely used in the chemical and petrochemical industry, cosmetics, drugs, fabrics, liquid extraction and homogenization, food products, etc. [1]. Another application of emulsions is the use of droplets as a transporting tool for various types of chemicals within droplets.

The following physical mechanisms are those most studied and applied in industrial practice for droplet disintegration [2,3], specifically laminar shear flows (in devices with rotating disks, rotor-stator mixers) and laminar elongation flows (nozzles and diffusers, microfluidic devices), and for turbulent flows, specifically pressure fluctuation or shear forces (stirred tanks, colloid mills, impinging jet mixers, static mixers) and the cavitation field (cavitation caused by ultrasonication, high velocity flows).

Efficiency enhancement, energy savings, and sustainability problems are the challenges of the modern science and technologies, inspiring research into new paths of process intensification by use of sophisticated and possibly easy methods. One of the trends is to intensify the momentum exchange processes occurring in the fluids by inputting into it additional forms of energy or by redistributing the input energy to activate and receive the necessary effect by spending less [4].

In recent decades, there has been a tendency toward decreasing energy costs versus energy input in the immediate vicinity of the interphase boundary. One scientifically based method is the principle of discrete-pulse energy input [5,6,7]. Obviously, this method of energy conversion should lead to an increase in the efficiency of processes in heterogeneous media, which will be expressed, for example, as a sharp increase in the specific surface area of the dispersed phase at an equal energy dissipation rate. To implement the principle, two conditions must be met: (i) the presence in the system of distributed working elements that play the role of local microsources of energy, and (ii) the presence in the system of significant gradients of thermodynamic or hydrodynamic parameters (temperature, pressure, velocity, etc.) [6].

The approach is known to be implemented by creating vapor–gas bubbles in a heterogeneous system by sharply reducing the pressure to the saturated vapor pressure at a given temperature. With a following sharp increase in pressure, the bubbles collapse with the release of a short powerful pulse. Accompanying this phenomenon, shock waves, microcavitation, cumulative microjets, and vortices cause Rayleigh–Taylor and Kelvin–Helmholtz instabilities on interfacial surfaces, leading to intensive fragmentation during the dispersed phase, an increase in the interface, and an increase in the rate of the mass and heat transfer processes [6,7].

To form the dispersed phase, it is necessary to use sufficiently rigid mechanisms of influence with a high level of specific power (energy dissipation rate) in the pulse, which requires the use of high-speed devices for a sharp change in the hydrodynamic parameters in the system. In this case, such processes should be carried out in flow type devices with intensive exposure in a small working volume, which eliminates the circulation and repeated imposition of effects on the already-processed system and, consequently, additional energy costs. This principle is implemented in a number of elementary devices connected in series, a common feature of which is the design in the form of a pipe with a periodically changing cross-section area. In this case, a change in the channel configuration leads to pulsations of velocity, flow pressure, and shear stresses, as well as enhanced vortex formation caused by the separation of the flow from the walls thanks to sudden expansion. The intentional generation of vortices in some pulsating devices of the tubular type [8,9,10,11] allows for classifying these devices as so-called static mixers. An extensive review by Thakur et al. [12] represents the main types of commercially available static mixers, along with the area on their industrial application for mixing, heat and mass transfer, and emulsification. Several significant reviews have been devoted to more-specific topics: the application of static mixers in organic chemistry [13], the synthesis of pharmaceutical ingredients [14], etc. Current advances in liquid–liquid mixing in static mixers has been presented in a recent review [15].

However, the presence of secondary eddies leads to an increase in hydraulic resistance (in which the most of the mechanical energy is dissipated) and to the formation of stagnant zones in the apparatus, which leads to a broadening of the residence time distribution curve. In order to solve this problem, a new type of apparatus has been elaborated at the Department of Optimization of Chemical and Biotechnological Equipment of SPSIT—a pulsating flow type apparatus (PFA) [16,17,18]. This device has a smoother shape, preventing the detachment of the flow from the walls in the expansion sections, but at the same time, PFA has higher intensity of impact on the fluids to be processed, compared both with commercially available types of static mixers (such as Lightnin and Sulzer SMV) [19] and with tubular type [8] apparatuses (see [20,21]). It was found that there are disintegration mechanisms other than turbulence in the PFA that contribute to a finer dispersion of droplets. It was shown earlier that these mechanisms are high shear stresses and Kelvin–Helmholtz instability [22,23]. On the other hand, in [16], it was first proposed to inject a small amount of gas into the system, into a liquid (not a vapor), and the appearance of cumulative jets when gas bubbles collapse (just like cavitation bubbles do), as a result of periodic changes in the pressure in the system, is called by the author “pseudocavitation”. The dynamics and the pulsation of vapor (vapor–gas) bubbles, as well as the high-frequency radial oscillations of the fluid created by them in the vicinity of these bubbles, are discussed in [24,25].

In this paper, the method of redistributing the introduced energy by introducing a third phase (a gas phase) into the liquid–liquid system is studied. The implementation of the method consists in the gas supply and uniform distribution of gas bubbles in the volume of the treated medium, which would transform the accumulated potential energy into the kinetic energy of the liquid movement in the vicinity of the bubbles. It is assumed that with a sharp change in pressure, high-frequency oscillations of the interphase surface of gas bubbles occur, as well as a change in their volume, accompanied under certain conditions by the emission of a pressure pulse of large amplitude and strong turbulence of the adjacent layers of the liquid. As a result, intense microflows occur in the space between the bubbles with high instantaneous values of local velocity, acceleration, and pressure. Thus, to implement the method, it is necessary to have gas bubbles in the system that act as (secondary) energy microtransformers and to have the presence of significant pressure gradients in the working system. With this in mind, in this work, a pulsating flow type apparatus, a new type of static disperser (see Section 3.1), was used as a disintegration device.

This work is an experimental study of liquid disintegration process intensification in a pulsating flow type apparatus by introducing a gas phase into a liquid–liquid system. The device efficiency is assessed, and the optimal volume fraction of gas bubbles is determined.

2. Theoretical Part

Two main aims of the emulsification process can be distinguished: (i) to disintegrate the dispersed phase to the droplets that have the required size and (ii) to distribute the droplets within the volume of the continuous phase as evenly as possible.

Currently, there is the widely used population balance model that theoretically predicts the average size of droplets dispersed in laminar or turbulent flows [26,27]. The population balance method makes it possible to predict the distribution curves of drops and bubbles. However, to use them, one needs to have reliable information on the following functions, birth and death by breakage and birth and death by coalescence, which creates significant difficulties. Therefore, to assess the efficiency of dispersion, the size of the maximum stable droplet size d_max is traditionally used; under the influence of external stresses τ, a diameter exceeding the forces that keep the drop from disintegration ${\tau }_{coh}\approx 2\sigma /d$ will make the drop become unstable and break up into smaller drops.

To disperse droplets in laminar flow, it is important to consider droplet breakdown in two deformation cases: shear flow and elongation flow. In the first case, with a shear flow, the deformation and subsequent destruction of the drop occurs as a result of shear-stress τ action. This is caused by the shear field (${\tau }_s={\mu }_c\dot{\gamma }$, where $\dot{\gamma }$ is the shear rate s⁻¹), and it happens in the presence of an elongation flow, under the action of tensile stresses determined by the equation ${\tau }_e=2{\mu }_c\dot{\epsilon }$, where $\dot{\epsilon }$ is the elongation deformation rate s⁻¹.

In this case, the maximum stable droplet size can be determined from an expression that includes the capillary number, which is characterized by the ratio of viscous forces promoting droplet fragmentation to the surface tension forces holding the droplet [28,29]:

$$C{a}_{cr}=\frac{\dot{\gamma }{\mu }_c{d}_{max}}{\sigma }$$

(1)

where $\dot{\gamma }$ is the shear rate s⁻¹; μ_c is the dynamic viscosity of the continuous phase Pa·s; d_max is maximum stable droplet size, in m; and σ is interfacial tension, in N/m.

The traditional methods of process intensification in heterogeneous media are based mainly on the concept of local isotropic turbulence, the foundations of which were laid in the works of Kolmogorov [30] and Hinze [31]. According to this theory, the level of intensification depends directly on the turbulent pulsation velocity value $v_t$, which, in the general case, is defined as:

$$v_t\left(d\right)=C{\left(\epsilon d\right)}^{\frac{1}{3}}$$

(2)

where C is a constant; ε is the specific energy dissipation rate W/kg; and d is the diameter of the droplet, in m.

In this case, drops of low viscosity are within the inertial range, i.e., ${\eta }_K<d<L$, where $L$ is the size of large structures (eddies) of energy cascade and ${\eta }_K$ is the Kolmogorov microscale (${\eta }_K={\left({\nu }^3/\epsilon \right)}^{1/4}$). The maximum stable diameter of droplets that resist further dispersion due to confining interfacial tension forces can be related to the local energy dissipation rate by the following expression:

$$d_{max}=C{\left(\frac{\sigma }{{\rho }_c}\right)}^{3/5}{\epsilon }^{-2/5}$$

(3)

where ρ_c is the density of the continuous phase, in kg/m³.

Thus, in accordance with this concept, in order to increase the level of intensification, it is necessary to achieve the maximum values of turbulent pulsations velocity $v_t$. On the other hand, the most effective intensification could be expected in those zones where the greatest energy dissipation is observed. These methods are used to one degree or another to improve the operation of traditional devices, including static mixers. However, any increase in the specific energy dissipation rate ε in the apparatus usually requires an additional increase in the power input. As a consequence, this leads to a decrease in its efficiency because the main part of the energy is not spent on performing useful work in the vicinity of dispersions but is instead unproductively dissipated in the volume of the continuous phase and on the walls of the apparatus.

As mentioned above, an alternative approach to the process intensification in heterogeneous media assumes that the dissipation of the introduced energy should occur mainly in the vicinity of a dispersed particle, and any factors contributing to energy losses outside these local zones should be eliminated as much as possible. The implementation of the method consists in creating vapor or gas bubbles evenly distributed in the working volume, which transform the accumulated potential energy into kinetic energy of liquid movement in the vicinity of the bubble when the volume of bubbles changes.

It is known that the presence of gas bubbles complicates the understanding of both dispersion processes and coalescence [29]. However, there is very little information in the literature on the mechanisms of the gas-phase effect on the emulsification process.

Thus, a particle of a dispersed phase located between two growing bubbles will be subjected to the action of shear stresses due to high velocities. This, in turn, can lead to the development of Kelvin–Helmholtz instability and cause the fragmentation of the dispersed phase. The possible dispersion of such fragmentation can be estimated as [6,32]

$$d_{KH}=\frac{\sigma W{e}_{cr}}{4{\rho }_c{v}_b{}^2}$$

(4)

where $W{e}_{cr}$ is the critical Weber number, equal to $W{e}_{cr}=2\pi \approx 6.28$ [32], and $v_b$ is the radial bubble growth rate, in m/s.

Moreover, impulsive pressure changes during the collapse of gas or vapor bubbles lead to the high-frequency oscillations of the dispersed medium. Such oscillations can cause Rayleigh–Taylor instability for dispersed-phase inclusions with subsequent destruction to a size of the order of [6,32]

$$d_{RT}=\sqrt{\frac{\sigma B{o}_{cr}}{4{\rho }_{c}b}},$$

(5)

where $B{o}_{cr}$ is the critical bond number, equal to $B{o}_{cr}=4{\pi }^2\approx 39.5$ [32]; b is a linear acceleration, $b=1/{\rho }_c\mathrm{C}·dP/d\tau$; and C is the sound velocity in the system.

The presence of gas bubbles in the system can also contributes to the occurrence of the so-called cumulative mechanism of cavitation emulsification. The collapse of the bubble at the interface leads to the formation of a cumulative jet, the entry of which into the nearest drop is accompanied by its fragmentation. Given the characteristics of cumulative jets and the physical properties of liquids, it is possible to estimate the most probable diameter of the formed emulsion droplets from the theory of jet disintegration [33]:

$$d_C={\left(\frac{{\delta }_{cj}}{v_{cj}}\right)}^{2/3 }{\left(\frac{4.5\pi \sigma }{{\rho }_c+{\rho }_d}\right)}^{1/3},$$

(6)

where ${\delta }_{cj}$ is the diameter of the cumulative jet, in m; $v_{cj}$ is the collapse rate of the cumulative jet, in m/s; and ${\rho }_c, {\rho }_d$ are the densities of continuous and dispersed phases, respectively, in kg/m³.

In addition to the direct introduction of cumulative jets with their subsequent disintegration, the formation of shock waves from collapsing bubbles along the interface, leading to its deformation, is also possible. These shock waves are generated by the collapse of a symmetric bubble and then radially propagate outward from the collapse point into the surrounding fluid. In addition, shock waves often accompany an effect known as an acoustic stream [34], which can be observed as a rapid flow of fluid caused by the oscillation of bubbles. Cumulative jets have velocities in the order of 100 m/s [33,35,36] and, together with shock waves and acoustic streams, are extremely effective in the formation of emulsions.

The noted reasons for hydrodynamic fragmentation with a change in the volume of bubbles lead to the micron range of the obtained particles of the dispersed phase.

In addition, other mechanisms explain the role of gas bubbles in the decay of dispersions:

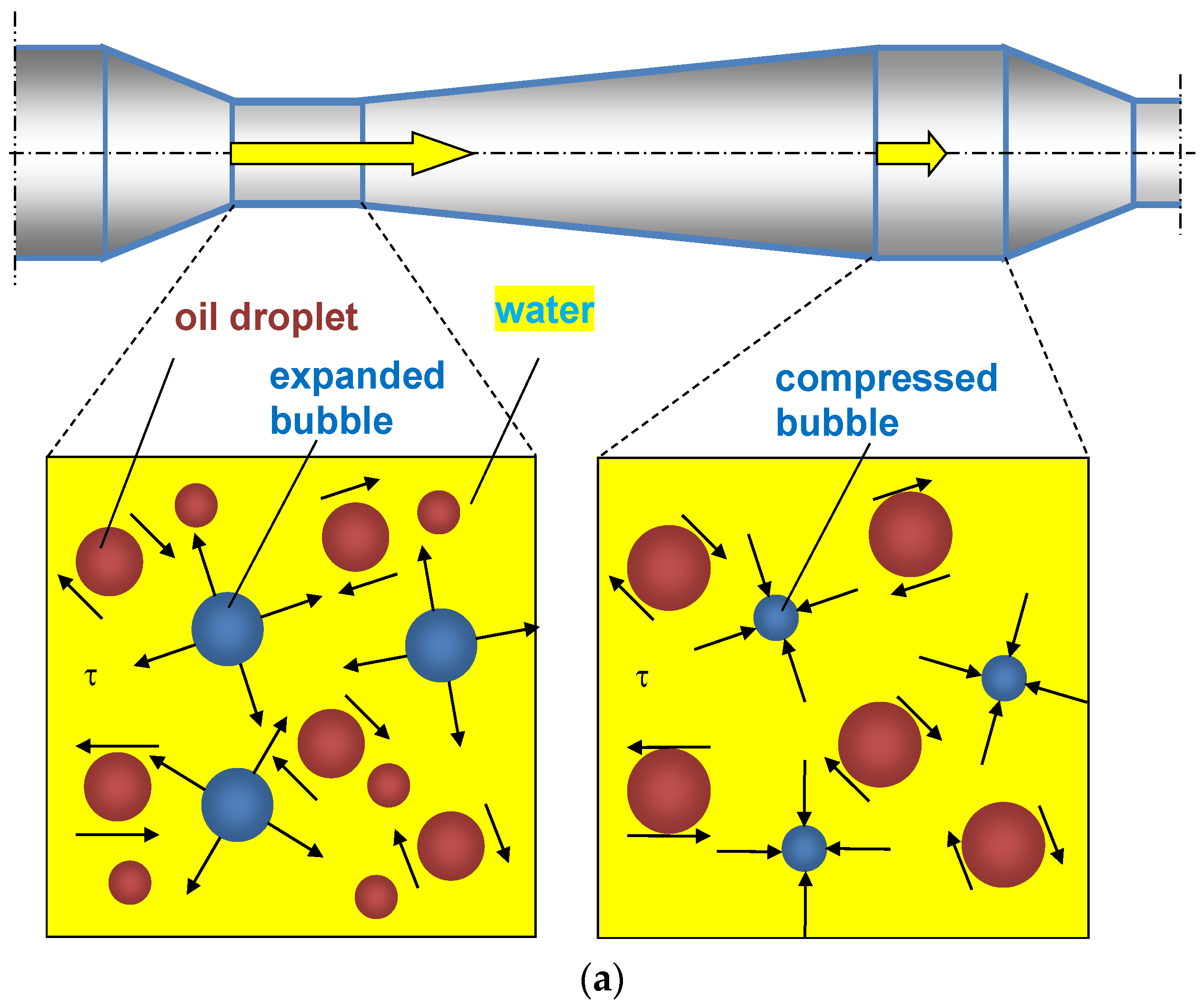
• The oscillations of bubbles cause additional shear stresses and local flows.
• The reduced rigidity of the gas–liquid mixture leads to an increase in the amplitude of droplet oscillations thanks to a decrease in acoustic impedance.
• Bubbles redistribute energy between particles.
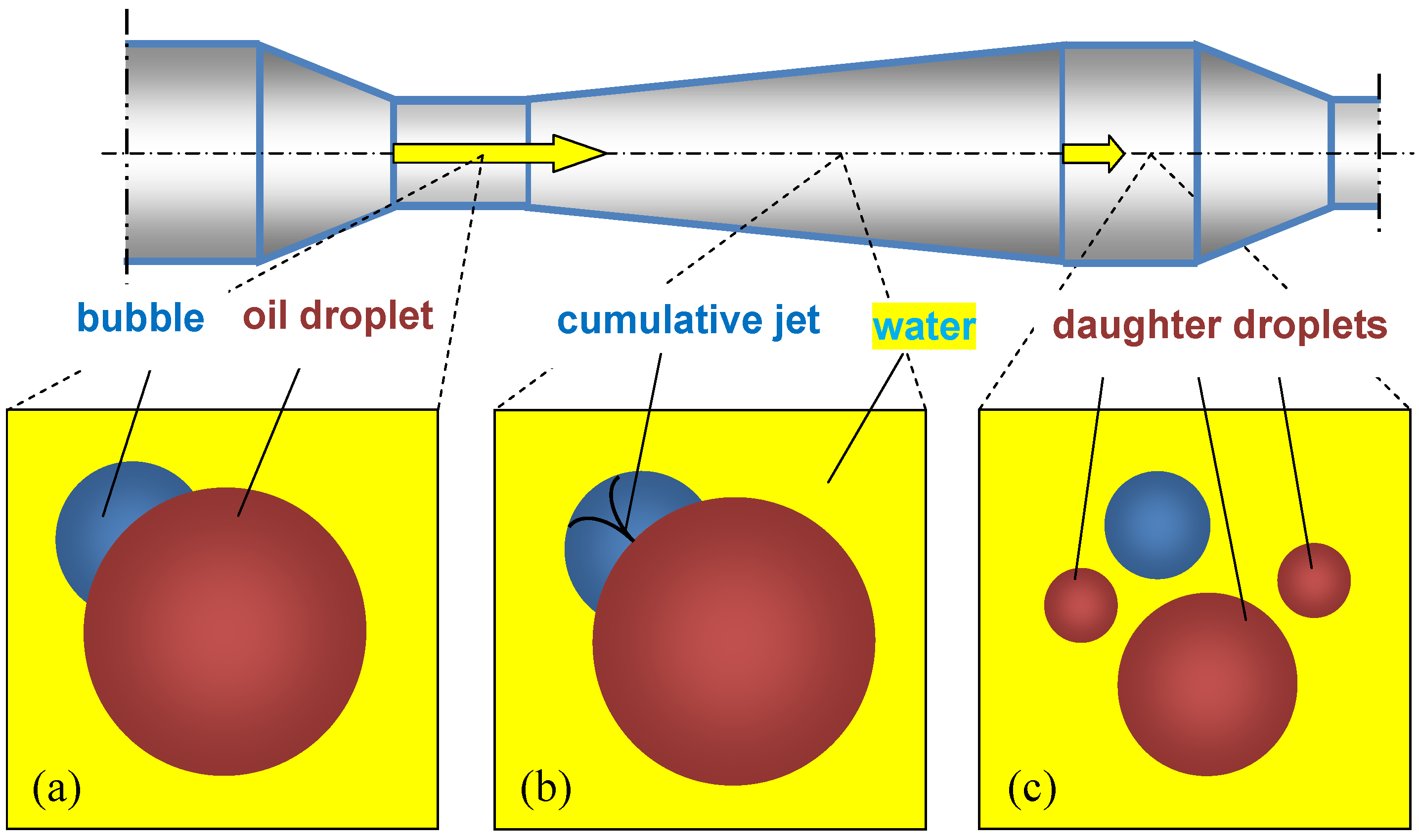
• Gas bubbles act as pseudocavitation bubbles, where collapsed bubbles break up droplets.
• Gas bubbles expand along the axial coordinate of each PFA element, resulting in additional acceleration of the liquid.

Currently, not all mechanisms can be accurately described theoretically. A detailed study of these processes should be the topic of several future theoretical works.

In this article, a theoretical assessment of some mechanisms of the effect of gas bubbles on the dispersed-phase droplets was performed, which made it possible to explain the obtained experimental results.

The aim of this study is to experimentally demonstrate the possibility to increase disintegration efficiency by introducing small amounts of inert gas into a liquid–liquid system and to assess the size of the formed droplets and the additional amount of energy needed for gas–liquid–liquid system transportation through the disintegration device.

3. Experimental Part

3.1. Materials and Methods

To study the liquid–liquid disintegration process intensification in PFA by the addition of a permanent and chemically inert gas as a third phase, an oil-in-water emulsion was used. A permanent gas is regarded as one that cannot be liquefied by pressure alone at normal temperatures; an inert gas is regarded as one that cannot react with either of two liquids. The following liquids were used: tap water as the continuous phase and sunflower oil as the dispersed phase (

Table 1. Physicochemical properties of liquids used in this study (at 20 °C).

Fluids	Density (ρ), kg/m3	Dynamic Viscosity (μ), mPa·s	Interphase Tension (σ), mN/m
Dispersed phase: Sunflower oil	920.3	56	20.6
Continuous phase: Water	998.2	1.0016

contains the physical properties of the liquids used). The flow rate of the continuous phase (water) was fixed at Q_c = 2 m³/h, and the flow rate of the dispersed phase (oil) was 1% (Q_d = 0.02 m³/h). A syringe pump with variable infusion rate was used to supply the dispersed phase into PFA. At the same time, a certain speed was set on the syringe pump to supply oil within a given time slot to ensure the desired volumetric flow. The interfacial liquid–liquid tension was measured by using the Schrodinger method (maximum droplet pressure method [37]), the maximum relative measurement error was 0.6%, and a homemade measuring device was built. The dynamic viscosity of sunflower oil was determined from [38]. High-purity nitrogen as an inert gas injected into the liquid–liquid system was used in this work.

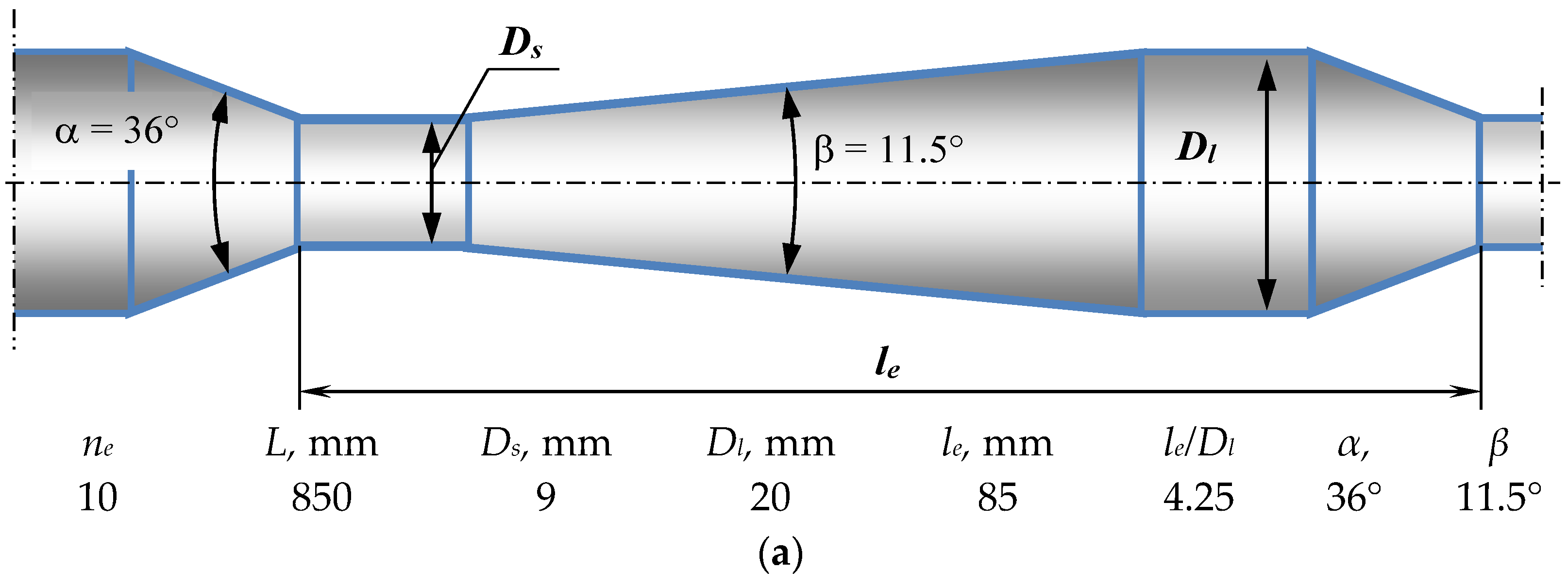
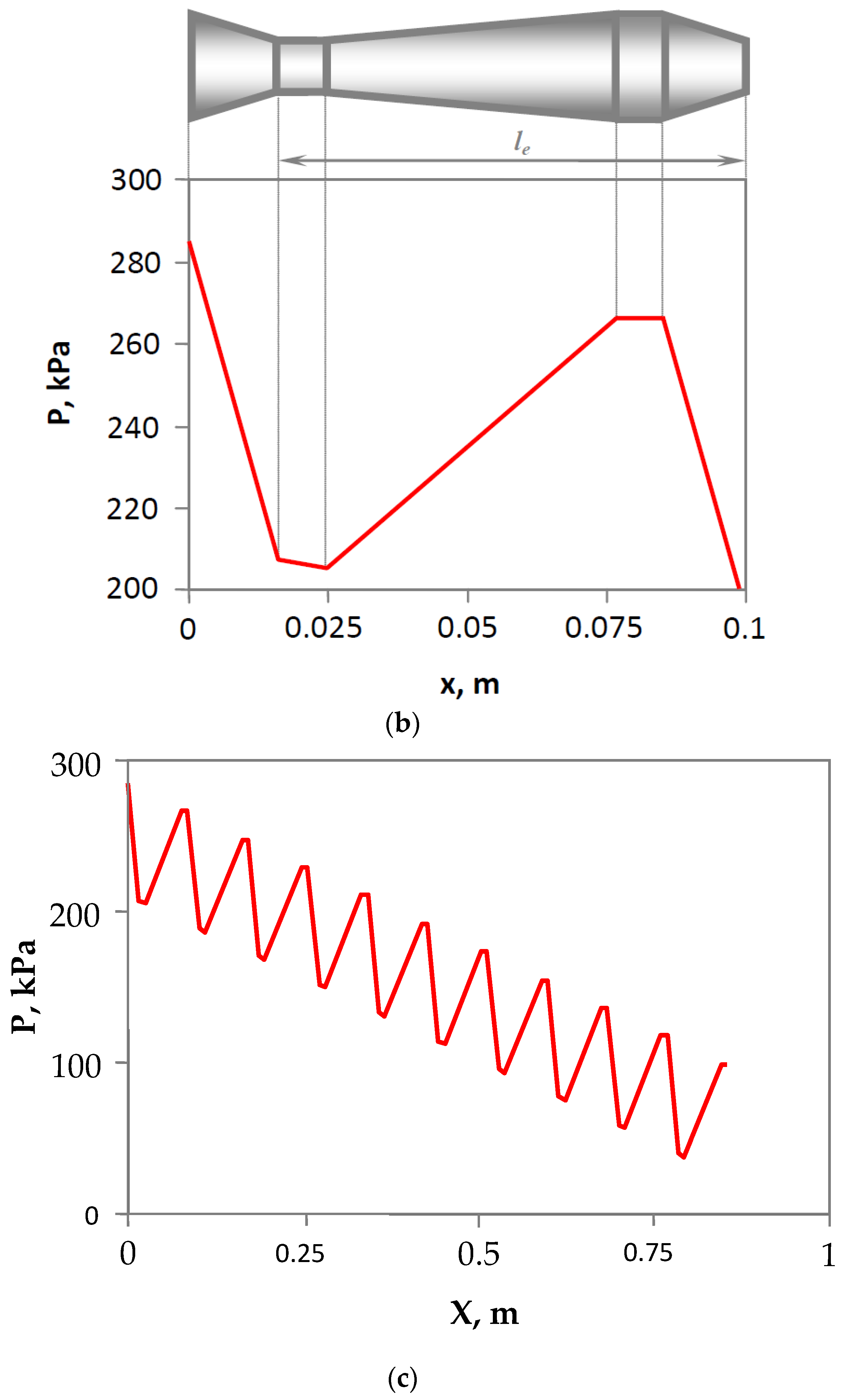
3.2. Design and Operating Principle of Pulsating Flow Type Apparatus

A pulsating flow type apparatus (PFA, see Figure 1) was studied in this work. PFA demonstrates a high level of energy dissipation and could be used in various processes: liquid reactions, absorption, emulsification, etc. [18].

A liquid–liquid two-phase mixture, passing through a PFA having a periodical geometry, is exposed by pulsating velocity, acceleration, and pressure appearing thanks to the cross-section variation along streamlines. As it has been revealed earlier [22], disintegration of droplets in PFA occurs mainly thanks to two factors: shear stresses in the neck area and Kelvin–Helmholtz instability. Additionally, our previous studies, which were devoted to the study of the carbon nanotubes deagglomeration [39] and droplet dispersion [23] with a subsequent comparison with static mixers [19], showed the high efficiency of PFA for solid–liquid dispersion and liquid–liquid dispersion.

In this study, a PFA with a diameter of the neck at D_s = 10 mm; D_s/D_l = 1/2 and l_e/D_l = 4.25 ratio, the angles of confuser and diffuser at 36° and 11.5°, respectively; and the number of dispersing elements at n_e = 10 was used (see Figure 1a). Laboratory-scale PFAs were made of Pyrex glass tubes having a wall thickness of approx. 2–2.5 mm (see Figure 1b).

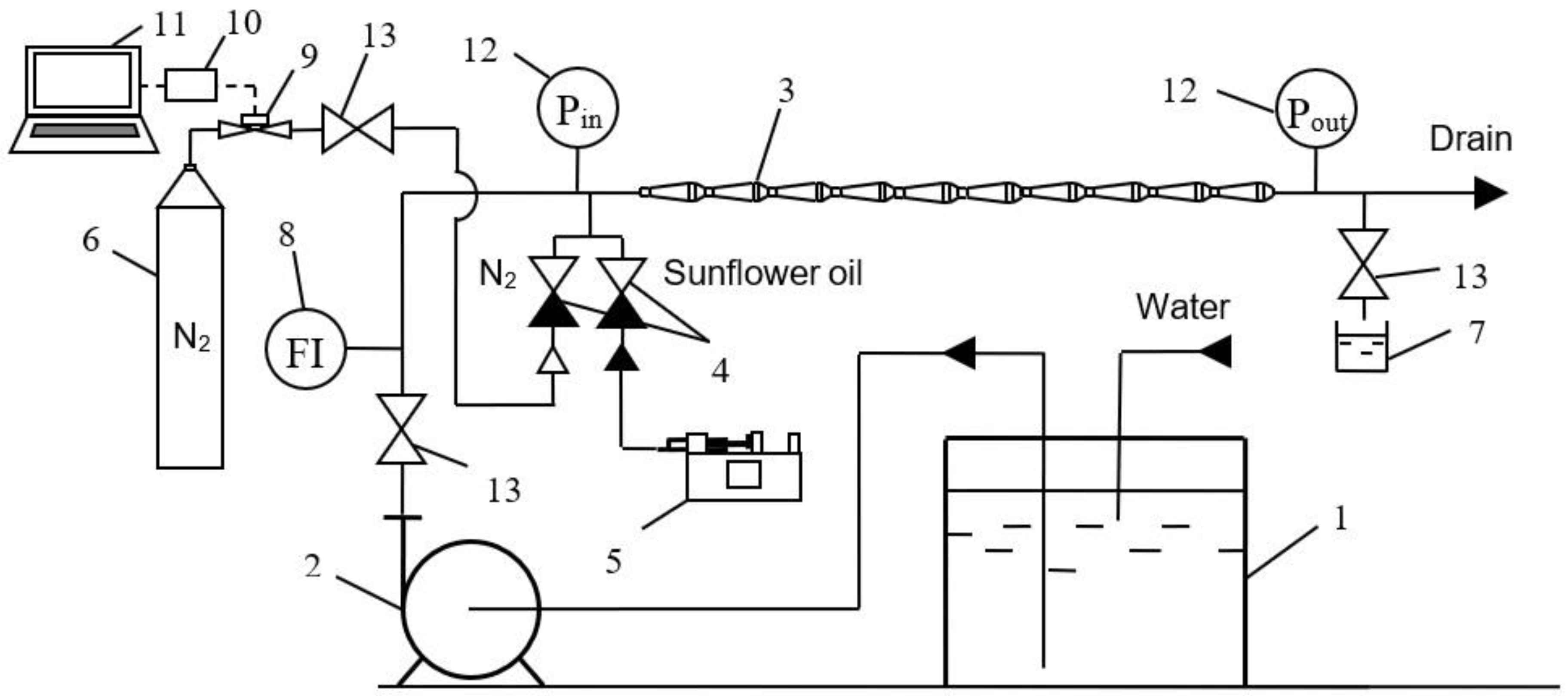
3.3. Experimental Rig

An experimental setup for the study of the liquid disintegration process intensification by means of additional injection of the gas phase into a two-phase liquid–liquid system in a PFA is shown in Figure 2. The continuous phase was supplied from the tank 1 by a centrifugal pump 2 (Wilo MVIE414 (Wilo, Dortmund, Germany), head H = 160 m, maximal flow rate Q = 8 m³/h) into the horizontal PFA 3—a thick-walled glass tube consisting of n_e = 10, dispersing elements of the “Venturi tube” (linear dimensions of the structural elements are shown in Figure 1a). The inner diameter of feeding and discharging lines of PFA was 16 mm. The dispersed and gas phases were fed into the cross-section center in the initial part of the stabilization section: pipeline between pressure gauge and the first Venturi element, through a straight tube (OD = 3.5 mm, ID = 2.5 mm) and a check valve 4. The dispersed phase was supplied using a syringe pump 5 with adjustable flow rate and was equipped by two syringes of 22 mL each. Two syringes were used to provide a given volumetric flow rate of the dispersed phase. The gas phase (nitrogen) used in the work was supplied to the apparatus through the check valve 4 from the high-pressure cylinder 6. At the outlet of the PFA, there was a nipple to take samples to the 60 mL glass sampler 7, prefilled with surfactant (a water solution of sodium dodecylsulfate, SDS). The volume ratio of 1:10 was used to ensure total blocking of droplets surface by surfactant molecules (5 mL of surfactant per 50 mL of the emulsion obtained in the sample). Electromagnetic flow meter 8 Vzlyot ER ERSV-540M (Vzlyot, Russia) with a relative error of ±2.0% was used for the mixture’s flow rate measurements.

The volumetric gas flow rate in the system was registered using a nitrogen flow sensor 9 Honeywell AWM5101VN (Honeywell, Freeport, IL, USA) with a relative measurement error of ±0.5%. The signal acquisition from the sensor was performed using an analog-to-digital converter 10 L-Card E14-140 (L-Card, Moscow, Russia) and recorded using a laptop 11 with a PowerGraph software package for information collecting and processing. To determine the friction factor of the apparatus at the stabilization part with known dimensions, the pressure was measured before and after the apparatus by means of pressure gauges 12 Elemer AIR-20/M2-DI (Elemer, Moscow, Russia) with a relative error of measurement of ±0.6%.

In this paper, a volumetric flow-rate-defined gas hold-up reduced to standard conditions for temperature and pressure was used. After taking into account the pressure and temperature of gas at which the experiments were conducted, the volumetric flow rate of the gas (Q_G.in)-defined gas hold-up under standard conditions at the inlet of the apparatus was determined:

$$Q_{G.in}=\frac{(Q_c+Q_d)·{\phi }_{in}}{100}·\frac{P_G}{T_G}·\frac{273.15}{101325}$$

(7)

where ${\phi }_{in}$ is the gas hold-up in the inlet of PFA; $P_G$ is the gas pressure, in Pa; $T_G$ is temperature, in K; Q_c is the volumetric flow rate of the continuous phase (water), in m³/s; and Q_d is the volumetric flow rate of the dispersed phase (oil), in m³/s. The gas pressure was taken to be equal to the pressure measured by the pressure gauge before the PFA ($P_G=P_{in}$) (see Figure 2). In this case, the gas temperature was taken to be equal to the room temperature measured in the immediate vicinity of the nitrogen cylinder. Volumetric flow-rate-defined gas hold-up was subsequently set during the experiment by the output voltage from the flow sensor datasheet [40]. Then, the value of gas hold-up at the PFA inlet is as follows:

$${\phi }_{in}=\frac{Q_{G.in}}{Q_L+Q_{G.in}}$$

(8)

At the same time, it is obvious that owing to the change in pressure along the length of the PFA, the gas hold-up values will also change. The equations for calculating the real average volume gas hold-up, which take into account the expansion of the gas, are presented in the Appendix A.

3.4. Droplets Diameters Measurements

Microphotographs gained by means of an optical microscope MBS-10 (LOMO, Russia, a total magnification of ×56) were used for drop-size measurements. The SLR camera Nikon D3100 SLR with Zoom NIKKOR 18–55 mm f/3.5-5.6G AF-S VR DX lens (resolution 4608 × 3072 = 14.2 million pixels) was attached to the microscope. The resolution of pictures (2.3 pixels/μm) was high enough to identify the droplets with a size ~5 μm or larger (see Figure 3: an example of a microphotograph).

Two samples were taken during each experiment to check the reproducibility. This was repeated twice; i.e., for each set of input parameters, 4 samples were taken. Thus, the diameters reported below were obtained from the average values of the 4 assays performed at each gas hold-up tested. CAD Kompas software (Russia) was used to measure the droplets’ size in microphotographs. In addition, a visual control on the monitor allowed for avoiding counting the same droplet twice. The minimal number of droplets to be measured was experimentally found for an amount of sampling from n = 100 to n = 800 (with a step of 100 drops). The empirical method included the calculation of the standard deviation σ_n for the droplet diameter, and then the normalized standard deviation (scaling function) ${\sigma }_N$ was calculated:

$${\sigma }_N=\frac{{\sigma }_n-{\sigma }_{n.min}}{{\sigma }_{n.max}-{\sigma }_{n.min}}$$

(9)

where ${\sigma }_n$ is the standard deviation of the sample with a volume of n, in μm, and ${\sigma }_{n.min}, {\sigma }_{n.max}$ is the standard deviation for the minimum and the maximum amount of sampling, respectively (n = 100 and 800), in μm.

The influence of the amount of sampling on the normalized standard deviation of droplet sizes is shown in Figure 4. From what follows, the normalized standard deviation value is stabilized with an amount of sampling of 600 drops. This amount of sampling (n = 600) was used as the minimum for further analysis of the obtained emulsions. All the droplets in the sample were numbered.

One of the most used parameters characterizing droplet size is their mean diameter d₁₀. However, the more appropriate average size for mass transfer is the average surface-to-volume diameter (Sauter diameter) d₃₂ [41], which is defined as $d_{32}=m_3/m_2$, where $m_q$ is the moment of the qth order (q = 2, 3) of a particle’s size density function $f_n\left(d\right)$ [42]:

$$m_q={{\displaystyle \int }}_{d_{min}}^{d_{max}}{d}^q{f}_n\left(d\right)\mathrm{d}d .$$

(10)

For the experimental data on droplet sizes presented for the ith fractions, the Sauter diameter is defined as follows:

$$d_{32}=\frac{m_3}{m_2}=\frac{{{\displaystyle \sum }}_i{n}_i·d_i{}^3}{{{\displaystyle \sum }}_i{n}_i·d_i{}^2},$$

(11)

where $n_i$ is the number of droplets in the range of sizes from $d_i$ to $d_{i+1}$.

4. Results and Discussion

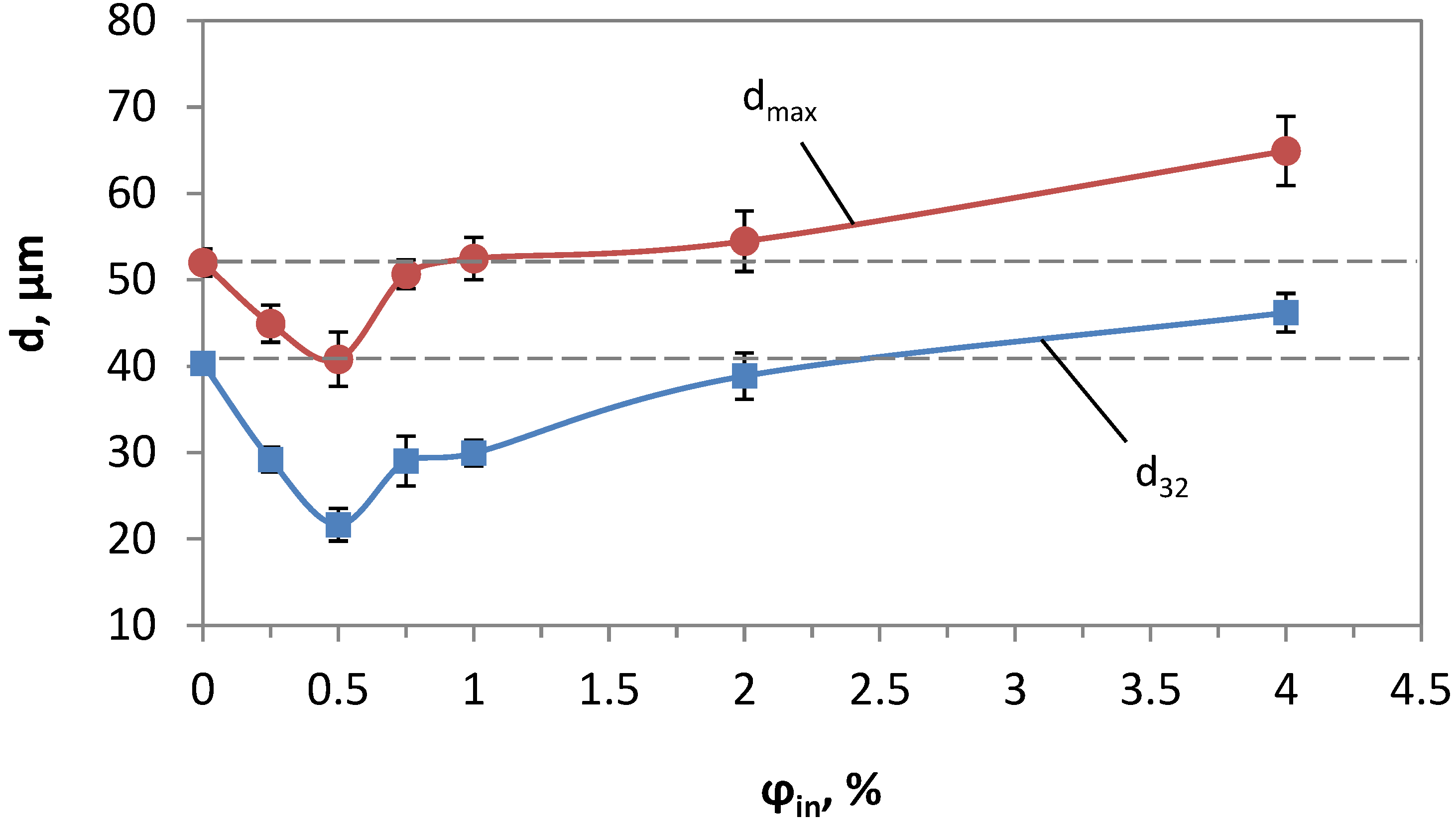
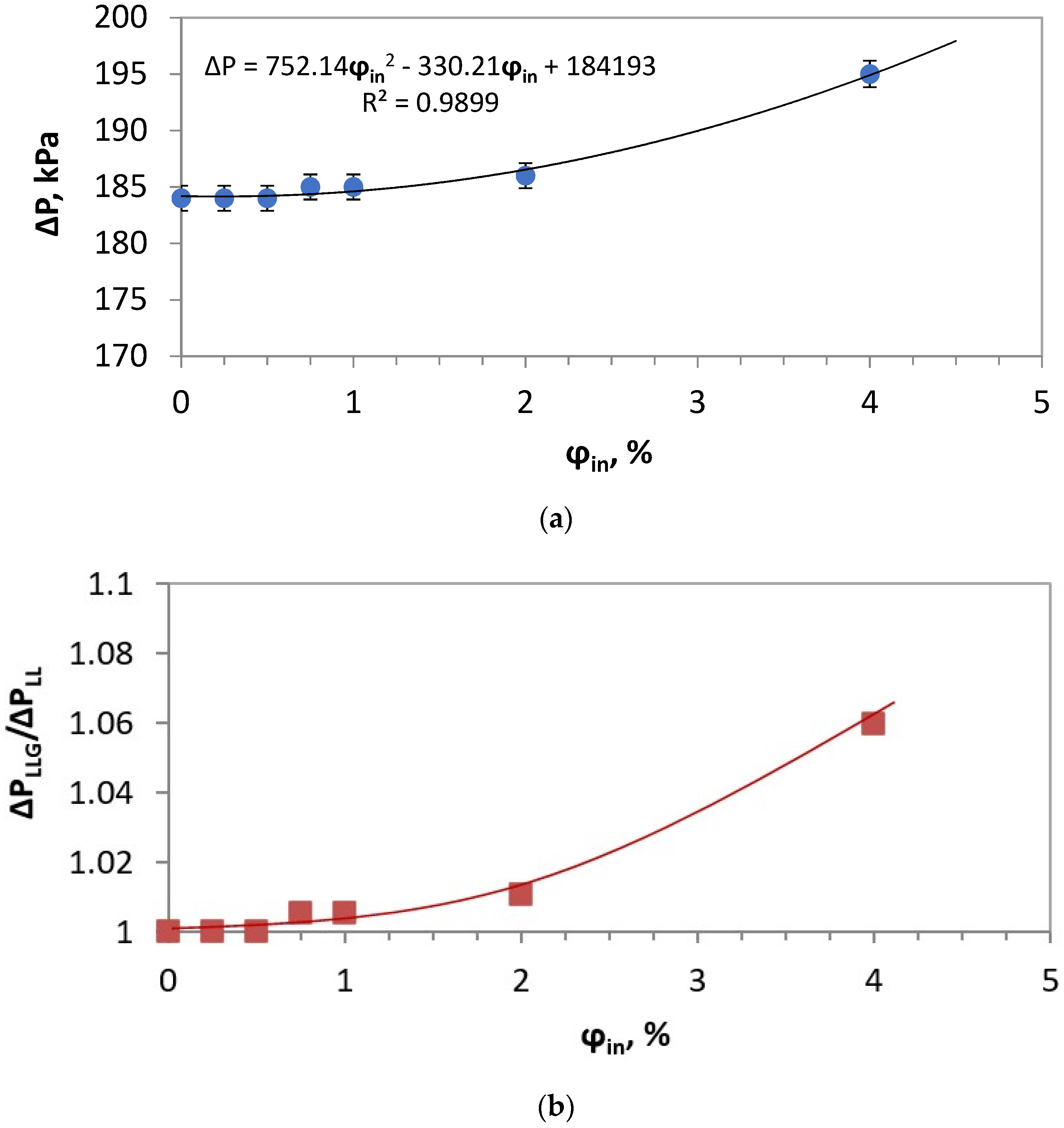
4.1. Estimation of Droplet-Size Distribution and the Mean Droplet Size for Various Gas Hold-Up Values

Our experimental results show that the introduction of the gas phase into the PFA generally has a positive effect on the quality of dispersion at a ${\phi }_{in}\le$ 2%. With a value of gas hold-up of 0.25% to 2.0%, the maximum size of the obtained droplets is 2.6% to 21.5% smaller than the droplets obtained under the same conditions without any gas supply (see Figure 5). The average diameter of the droplets for the case of injected gas is 1.8 times smaller and is 21.7 microns against 40.7 microns. The values of the average volume of gas hold-up ${\phi }_{avg}$ (see Equation (A5)), which take into account the expansion of the gas, for the corresponding ${\phi }_{in}$ are given in

Table 2. Dependence of the pressure drop in PFA, the maximum and average droplet size on the gas hold-up.

${\mathsf{\phi }}_{\mathit{i}\mathit{n}}, \%$	0	0.25	0.5	0.75	1	2	4
${\mathsf{\phi }}_{out}$, %	0	0.71	1.42	2.14	2.87	5.72	11.29
${\mathsf{\phi }}_{avg}$, %	0	0.40	0.80	1.20	1.59	3.13	6.04
ΔP, kPa	184	184	184	185	184	185	195
dmax, µm	52	44.93	40.82	50.64	52.47	54.47	64.92
d32, µm	40.69	33.94	21.67	28.36	29.49	38.87	46.20

.

It can also be concluded from Figure 5 that the optimum volume gas hold-up at which the smallest droplets are achieved is 0.5% (${\phi }_{avg}=0.8\%$). Figure 6 shows microphotographs of the obtained emulsions without gas injection ${\phi }_{in}$ = 0%, with an average droplet size equal to d₃₂ = 40.7 µm (see Figure 6a), as well as at a gas flow rate of ${\phi }_{in}$ = 0.5%, at which the average droplet size is d₃₂ = 21.7 µm (see Figure 6b).

Moreover, Figure 6 illustrates the droplet-size distribution on the volume gas hold-up (see Figure 6c). It is clear that the distribution curves shift to the smaller droplet size at volume gas hold-up ${\phi }_{in}$ = 0.5%. The droplet-size distribution f_n was calculated according to Equation (12):

$$f_n=\frac{\Delta n}{n·\Delta d},$$

(12)

where $\Delta n$ is the number of drops in the nth range of sizes [d, d + Δd] and n is the total number of droplets.

It was also found that pressure losses along the length of the apparatus for volume gas hold-up in the PFA in the range from 0% to 2% remain unchanged (they are within an experimental error), and an increase in resistance is observed when the gas hold-up is larger than 2% (see Figure 7a, Table 2). For clarity, the dependence of the pressure drop for the L–L–G system to the two-phase L–L system ratio on the gas hold-up was also obtained (see Figure 7b).

The equation for approximating the experimental dependence of the pressure drop (in Pa) on the gas hold-up in the PFA is in Equation (13), as follows (φ_in is expressed in %):

$$\Delta P=752.14{\phi }_{in}{}^2-330.21{\phi }_{in}+1.84·{10}^5$$

(13)

Thus, the effect of the injected gas on the droplet size theoretically predicted earlier [16,24] has been experimentally confirmed: introducing a small amount of gas into the liquid–liquid system reduces the average drop size by almost two times, without increasing the energy cost of pumping the liquid.

4.2. Mechanisms Explaining the Role of Gas Bubbles in the Intensified Emulsification in PFA

Consider the possible reasons for which an additional intensification of the emulsification process occurs when gas is introduced into the PFA. The fact is that the bubbles are uniformly distributed over the volume of the apparatus, and they intensively expand when the pressure falls (in the neck zone) and when there is a fluctuation in the interface surface, in which case a rapid transformation of kinetic energy occurs in the vicinity of the bubbles with the release of a short powerful pulse. In this case, in the continuous phase, nonstationary microflows are formed in the vicinity of the bubbles, which have a dynamic effect on the dispersed liquid phase. Thus, the introduction of the gas phase leads to the fact that bubble oscillations induce additional shear stresses and local flows; bubbles reduce the stiffness of the gas–liquid mixture, resulting in the amplitude increase in droplet oscillations; and the bubbles redistribute energy among the oil droplets (see Figure 8a).

Let us evaluate the possible effect of droplet fragmentation under the condition of the Kelvin–Helmholtz and Rayleigh–Taylor instabilities, according to Equations (4) and (5), respectively. Under the given experimental conditions for the calculated $v_b$ = 0.2 m/s and b = 125 m/s² ($dP/d\tau$ = 2.5·10⁷ Pa/s, $C$ = 200 m/s), the possible droplet sizes caused by the Kelvin–Helmholtz and Rayleigh–Taylor instabilities are $d_{KH}$ = 1.26 mm and $d_{RT}$ = 1.6 mm, respectively. Thus, under the conditions under consideration, the Kelvin–Helmholtz and Rayleigh–Taylor instabilities are not the predominant droplet-fragmentation mechanisms; at least, they can work in the first stages of crushing large droplets. During the final stages, crushing is carried out, apparently owing to the collapse of gas bubbles, which is reminiscent of cavitation. We call this mechanism “pseudocavitation”.

In PFA, thanks to the special shape of the apparatus’s longitudinal section, periodic nonstationary motion occurs, in which favorable conditions are created for the formation of the dispersed phase. In addition, the necessary conditions are implemented in the PFA for their increases and decreases in size, as well as high-frequency oscillations of the interface. Figure 8b shows the dependence of the pressure along the axial coordinate of one PFA element. According to calculations, the double amplitude (span) of pressure pulsations in one PFA element for the studied flow rate is 0.4 bar. Relative to the average pressure on an absolute scale of 2.45 bar (abs.), this is 16.3%. Hence, the amplitude of the pulsations of the volume of the bubbles is A_V = 0,163/2 = 0.0815. The amplitude of the pulsations of the bubble’s diameter is A_d ∝ (1 + A_V)^1/3−1 ≈ 0.052, which seems to be not very large.

Indeed, the estimate of the probable droplet diameter by the cumulative mechanism of cavitation emulsification (see Equation (6)) with a cumulative jet diameter ${\delta }_{cj}$ = 50 μm (for drops of approximately 0.5 mm [33]) and a cumulative jet collapse velocity $v_{cj}$ = 100 m/s gives us a result in the order of $d_C$ = 4–5 µm.

Thus, significant pressure pulsations in the PFA element contribute to the fact that gas bubbles act as pseudocavitation bubbles (see Figure 9). Thus, with a sharp pressure jump in the diffuser of the PFA dispersing element, cumulative jets are formed (see Figure 9b), which contribute to the intensification of drop disintegration in the apparatus (see Figure 9c).

In addition, it is necessary to take into account the fact that, on average, the pressure decreases along the length of the apparatus, which leads to the expansion of bubbles and to the additional acceleration of the emulsion toward the exit from the apparatus. Therefore, under experimental conditions, the pressure decreases along the length of the apparatus from 280 to 100 kPa (see Figure 8c). In this case, the volume of gas bubbles, in view of the decrease in pressure, will increase by an average of ${\phi }_{out}/{\phi }_{in}\approx 2.85$ times by the end of the apparatus. This leads to an increase in the emulsion velocity in the PFA neck toward the end of the apparatus—for example, at ${\phi }_{in}$ = 1% by 0.12 m/s.

However, the effect of the expansion–compression process of the bubbles along the length of one PFA element is more significant. First, the local pressure gradients along the length of one element are much higher than the average pressure gradient in PFA (see Figure 9a). Thus, during the passage of one PFA element, gas bubbles in the confuser and neck of the apparatus first sharply expand by 42% of the initial size, and then they are compressed by 31% in the diffuser and wide part of the PFA. Second, the expansion–compression process occurs in each element of the PFA; i.e., the impact on the bubbles (and droplets) is repeated n_e times. In addition, owing to the repeated effects on the PFA emulsion, the probability that all the volumes of a heterogeneous medium will fall into the zone of the most intensive energy conversion near the walls of the neck and small areas adjacent to it [19,23] increases; thus, spatial discretization is realized. Therefore, along the length of the apparatus, when gas is introduced, the efficiency of the droplet crushing increases, in addition to the imposition of the effect of the bubbles.

Thus, the introduction of an inert gas into the apparatus allows for increasing the efficiency of the liquid–liquid dispersion process thanks to a more uniform input of energy into the heterogeneous system. When passing through areas with a periodically changing cross section, the bubbles distributed in the volume of the processed emulsion serve as secondary oscillation emitters, significantly improving the hydrodynamic condition in the apparatus.

This effect is most pronounced in the range of gas hold-up from 0.25% to 2% (see Figure 5). With an increase in the gas hold-up of the injected gas above 2%–4%, the distance between the bubbles becomes comparable with their diameter; with pressure pulsations, the force of hydrodynamic long-range action (Bjerknes force) arises, under the influence of which the bubbles come closer and coalesce, as a result of which they become larger, their buoyancy increases, and the uniformity of their distribution in the volume decreases. This explains why, with an increase in the gas hold-up over the value ${\phi }_{in}$ = 2%, the effect of gas bubbles diminishes and then completely disappears.

As could be seen from the calculations presented in

Table 3. Influence of the gas hold-up φ on sonic speed C in liquid–gas mixture (liquid—water, gas—nitrogen) at P = 1.85 bar. C₀ = 1483 m/s is a sonic speed in pure water.

${\mathsf{\phi }}_{\mathit{i}\mathit{n}}, \%$	0.25	0.5	0.75	1.0
C, m/s	338.1	239.3	195.7	169.7
C/C0	0.228	0.161	0.132	0.114

, the sound velocity rapidly decreases with growing φ, even in the range from 0.25% to 1.0%. For ${\phi }_{in}$ = 0.25%, C/C₀ = 0.228 (related to the pure water sound velocity C₀), and for ${\phi }_{in}$ = 0.5%, C/C₀ = 0.161. For higher gas hold-up values, the C/C₀ is even smaller.

5. Conclusions

Experimental studies have shown that the input of a small amount of inert gas bubbles leads to an intensification of disintegration in the liquid–liquid system (emulsification) in a pulsation flow type apparatus. A range of gas hold-up ${\mathsf{\phi }}_{in}$ from 0% to 4% was investigated in the paper. The volume fraction of the dispersed phase (oil) was 1% with respect to the continuous phase. During the study, it was found that the optimal gas hold-up was φ_opt = 0.5%.

The average droplet size according to Sauter decreased by 1.88 times, and the maximum droplet size decreased by 1.30 times. The effect of a decrease in the average droplet size upon the input of the inert gas decreases with an increase in its volume fraction (with respect to φ_opt = 0.5%) and completely disappears at ${\mathsf{\phi }}_{in}$ ≈ 2%–2.5%. At the same time, the pressure loss at ${\mathsf{\phi }}_{in}$ ≤ 2% within the measurement error remained constant, and at 4%, it increased by only 5.4%.

In the course of the work, the reasons for the intensification of the process of droplet dispersion (emulsification) when inert gas was introduced were considered and discussed. It was proposed that in the presence of gas bubbles in the system, the dispersed phase (oil) is influenced by the following factors: the redistribution of the momentum over the volume of the liquid; the occurrence of microflows near bubbles and drops, which leads to an increase in shear stresses on the surface of the drops; gas bubbles act as pseudocavitation bubbles; and when gas bubbles collapse on the surface of the droplets, they are dispersed. The listed factors contribute to the occurrence of such droplet-fragmentation mechanisms as the Kelvin–Helmholtz and Rayleigh–Taylor instabilities and the so-called cumulative mechanism of cavitation emulsification.

It was found in this paper that the Kelvin–Helmholtz and Rayleigh–Taylor instabilities, under the conditions under consideration, are not the dominant droplet-fragmentation mechanisms. However, at the same time, they can work at the first stages of crushing large droplets (in the order of several millimeters). The final stages of fragmentation, down to micron sizes, appear to be due to the cumulative mechanism caused by the collapse of gas bubbles.

Thus, this paper gives experimental proof of the idea that the introduction of gas bubbles could improve hydrodynamics in liquids and liquid–liquid systems.

Though not all the obtained results could be now exactly described theoretically, a detailed study of these processes should be the topic of future theoretical papers.

The method of introducing inert gas with a small flow rate (just 0.5%) could be recommended as a promising tool for the intensification of emulsification process.