Numerical Investigation of Critical Hydraulic Parameters Using FLOW-3D: A Case Study of Taunsa Barrage, Pakistan
Abstract
1. Introduction
1.1. Significance of Hydraulic Jumps (HJs)
1.2. Role of Stilling Basins
1.3. Computational Fluid Dynamic and Hydraulic Modelling
1.4. Research Motives and Problem Statement
- To calibrate and validate a 3D model under the field conditions of a full-scale hydraulic structure using data from Taunsa Barrage.
- To identify the critical hydraulic parameters (CHPs) that play a crucial role in the design of graded control structures.
- To investigate the flow patterns of CHPs for stilling basins at various tailwater levels using the data from the old Taunsa Barrage.
- To study the effects of different tailwater levels on the locations of the HJs and compare them with relevant field and numerical data.
- To provide an overview of HJ locations in various basins of a barrage for different tailwater and discharge levels (a case study for Taunsa Barrage).
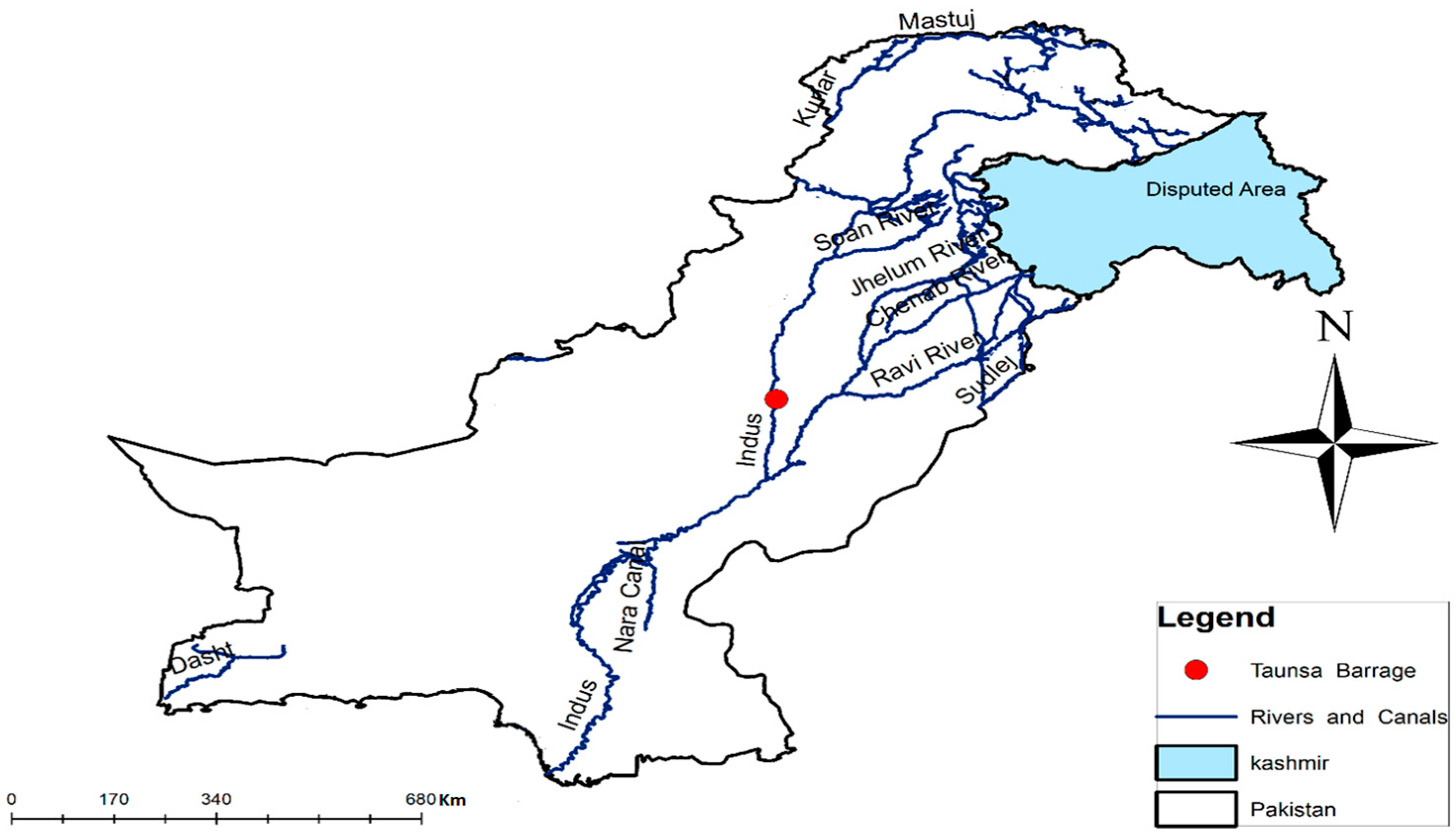
2. Study Area
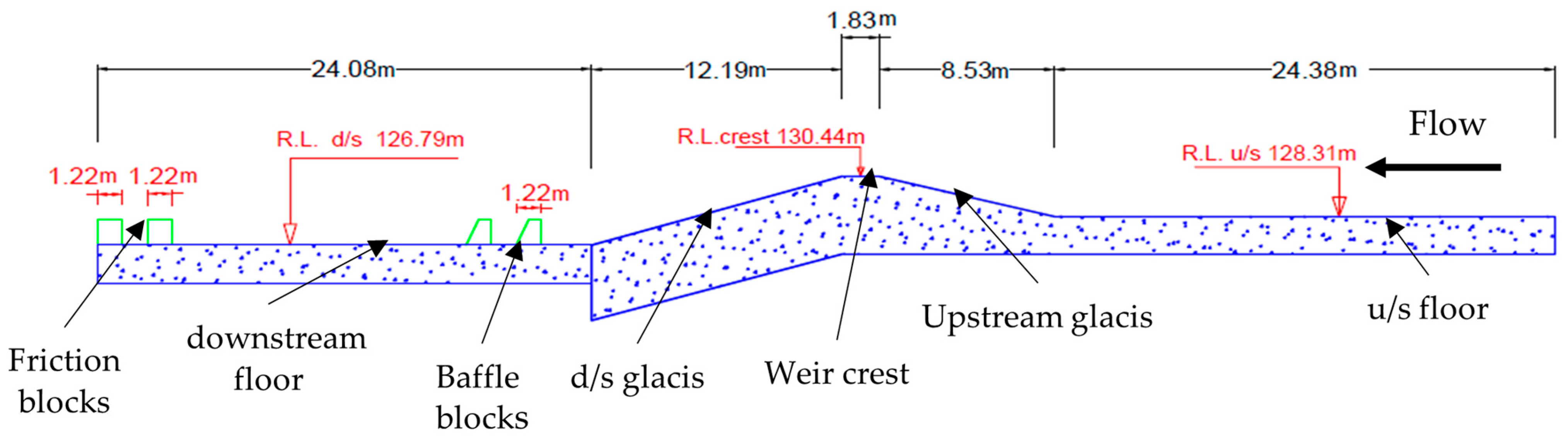
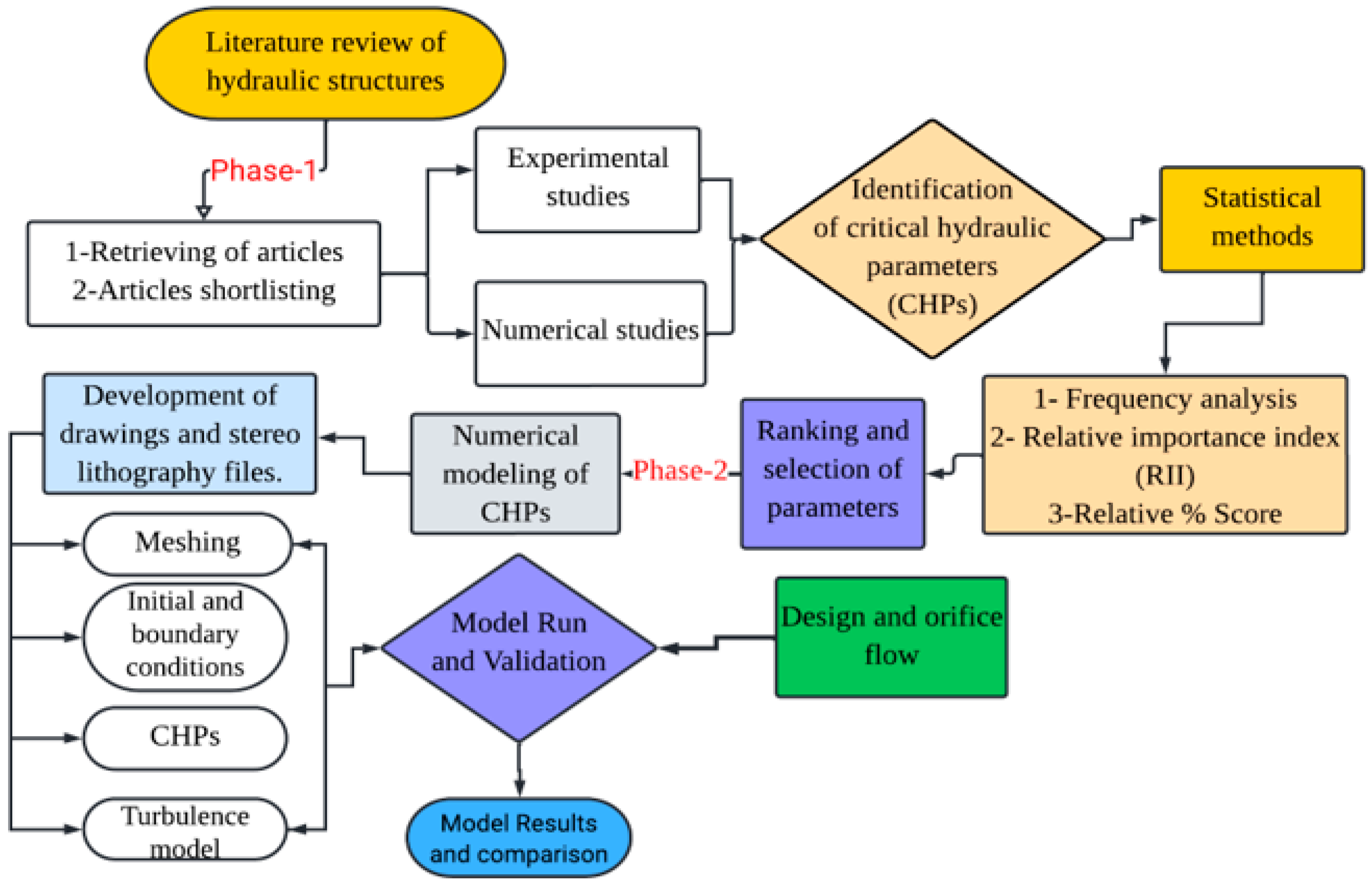
3. Material and Methods
3.1. Phase 1: Identification of the Critical Hydraulic Parameters
3.2. Phase 2: Numerical Model Implementation
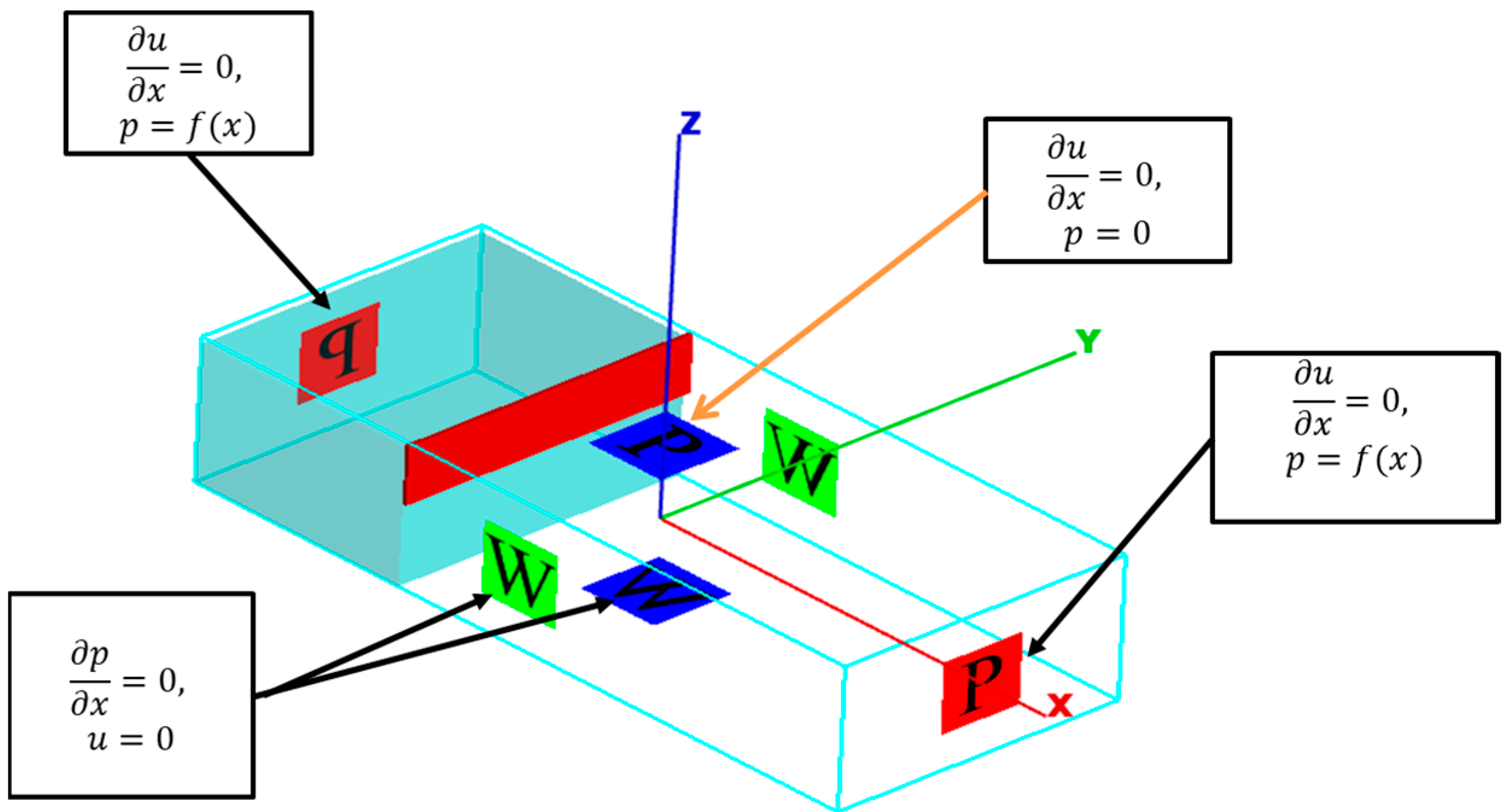
3.2.1. Model Meshing and the Initial and Boundary Conditions
3.2.2. Turbulence Modelling and Free Surface Tracking
- If F approaches 0, the cell is considered as empty;
- When F reaches 1, the cell is believed to be occupied by fluid;
- If 0 < F < 1, the cell represents a surface between the two fluids.
3.3. Model Verification and Validation
4. Results
4.1. Identification of Critical Hydraulic Parameters (CHPs)
4.2. Phase 2: Results for Critical Hydraulic Parameters (CHPs) Using Numerical Models
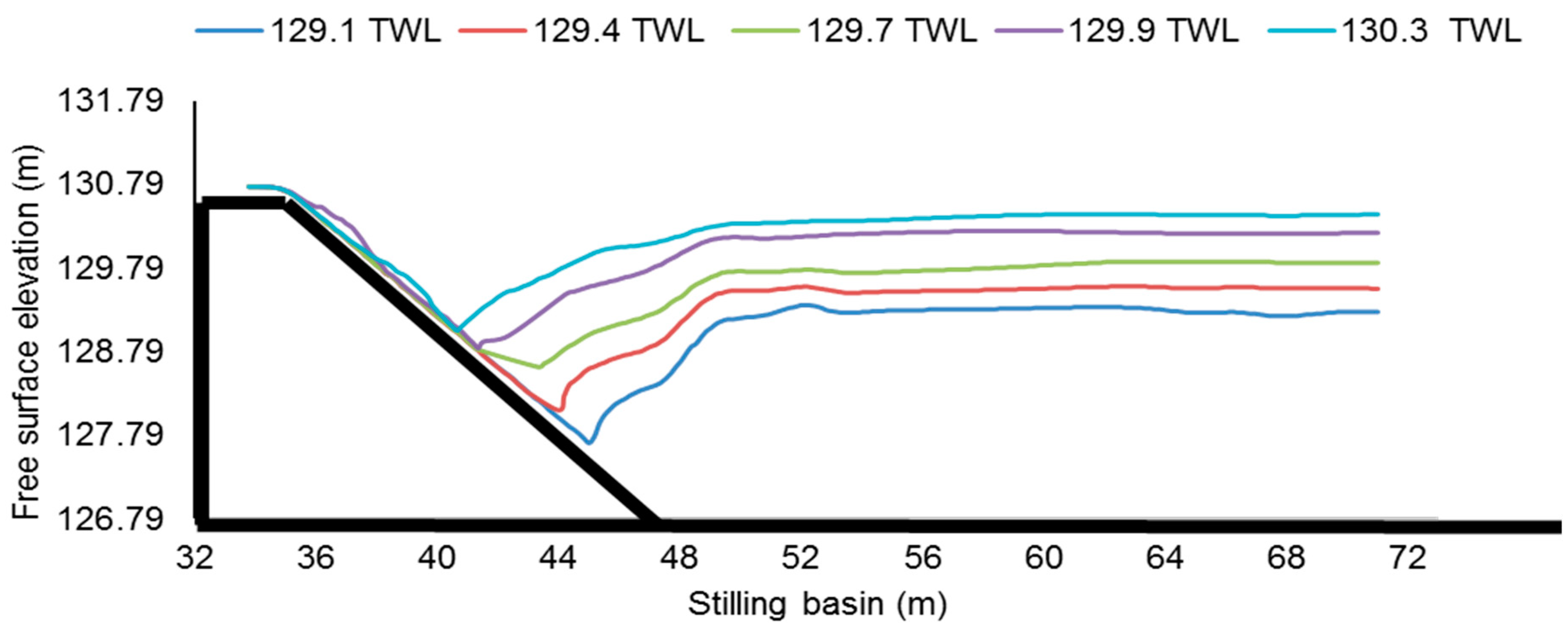
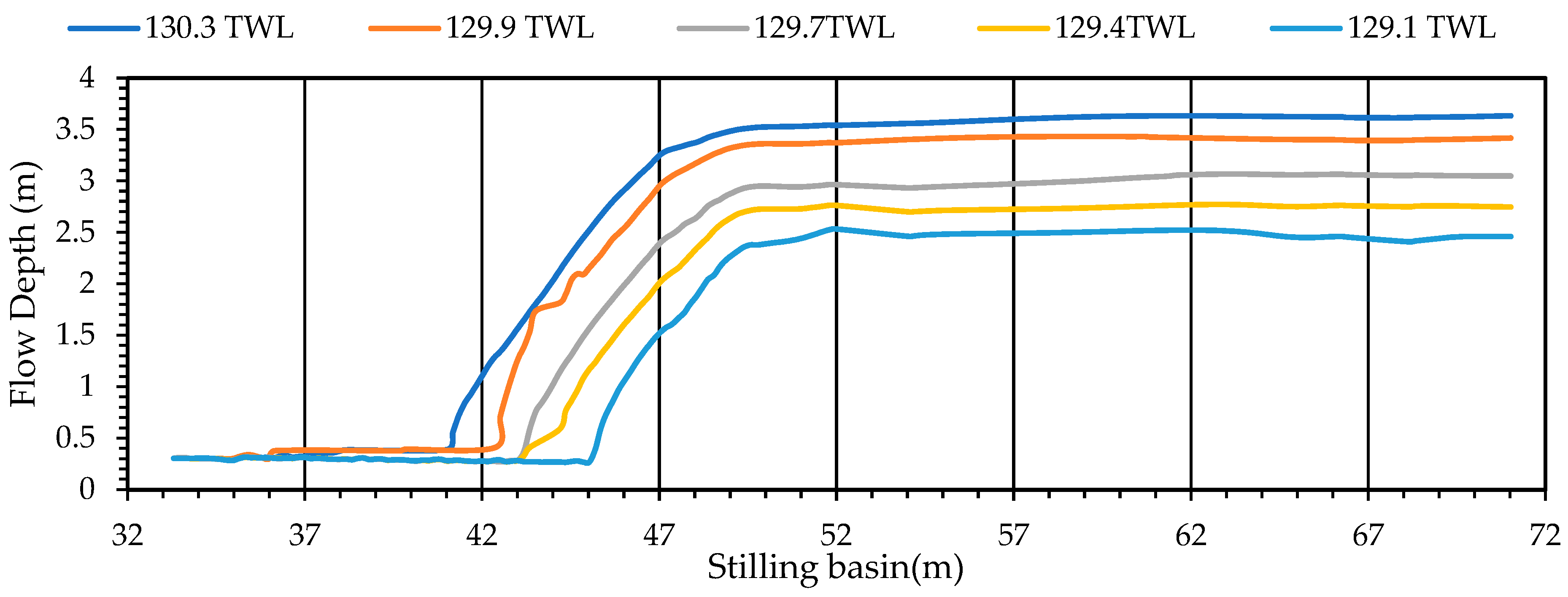
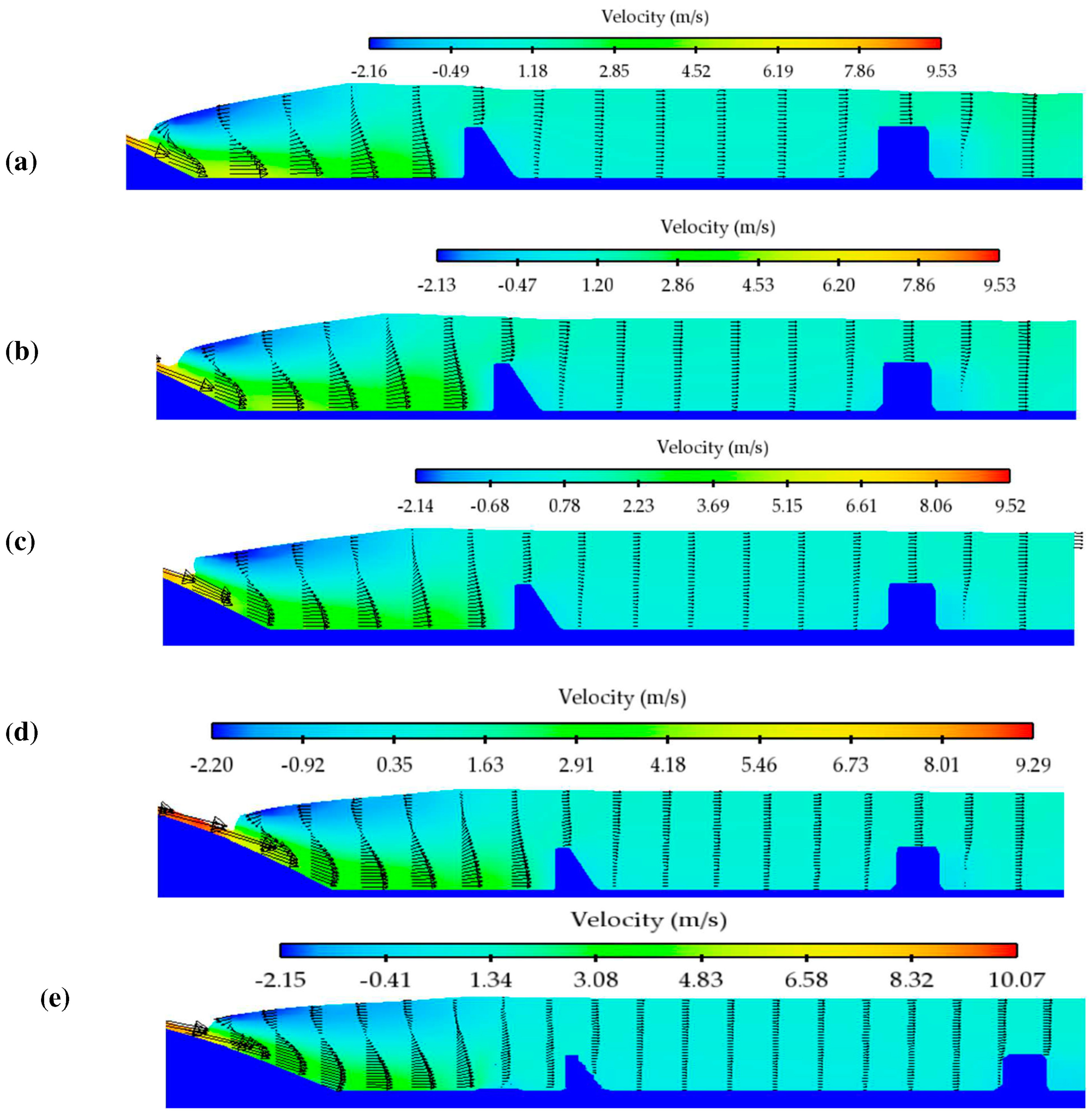
4.2.1. Free Surface Profiles
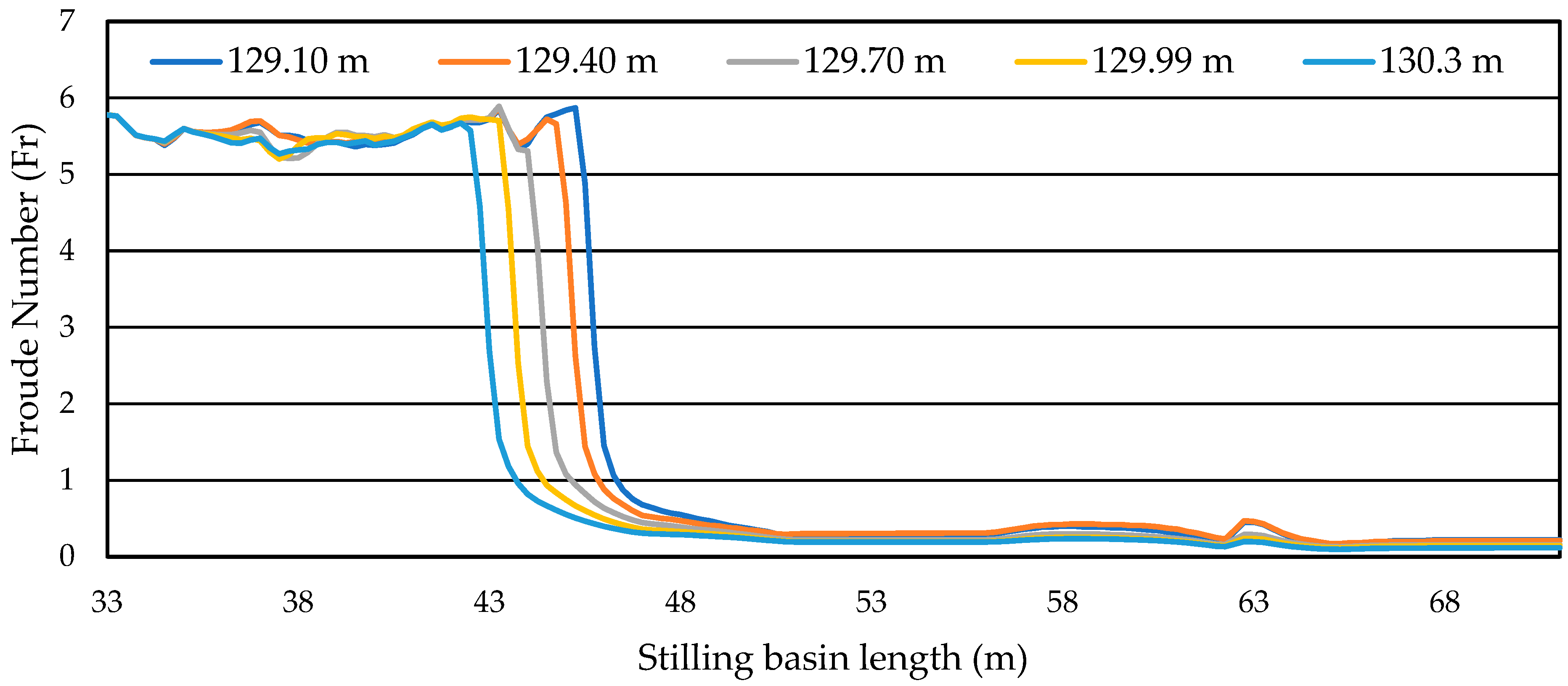
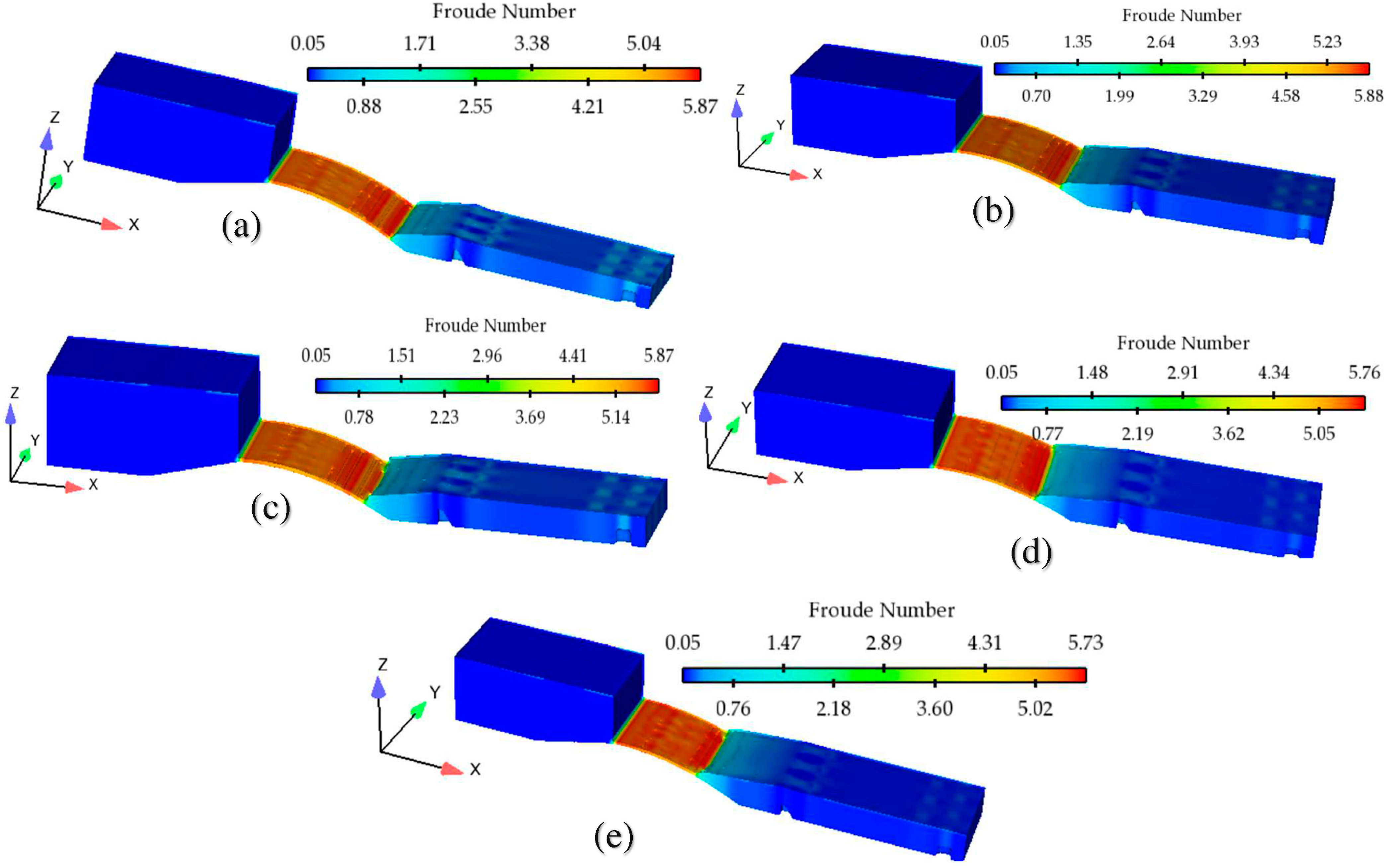
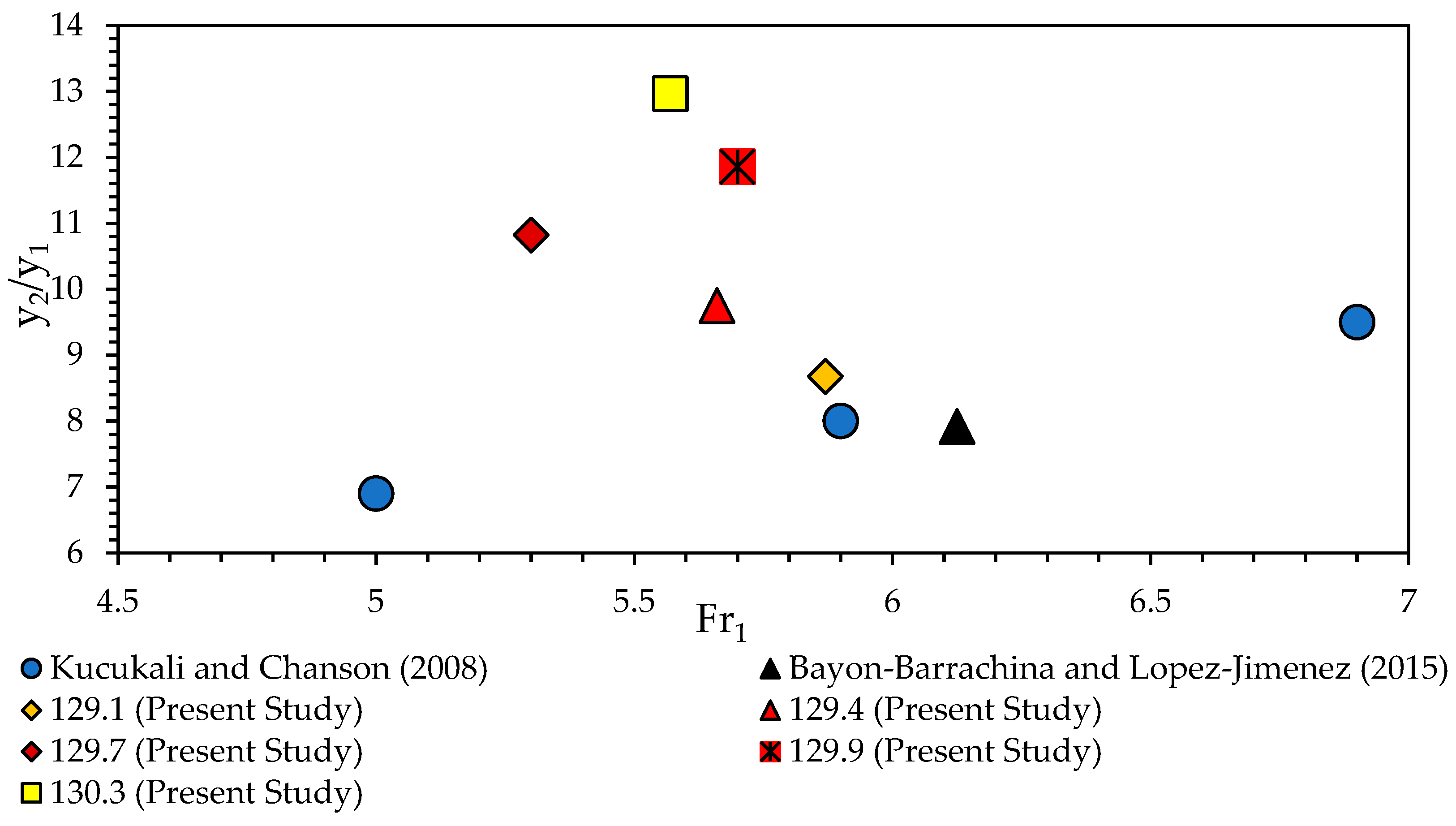
4.2.2. Froude Number
4.2.3. Flow Depths
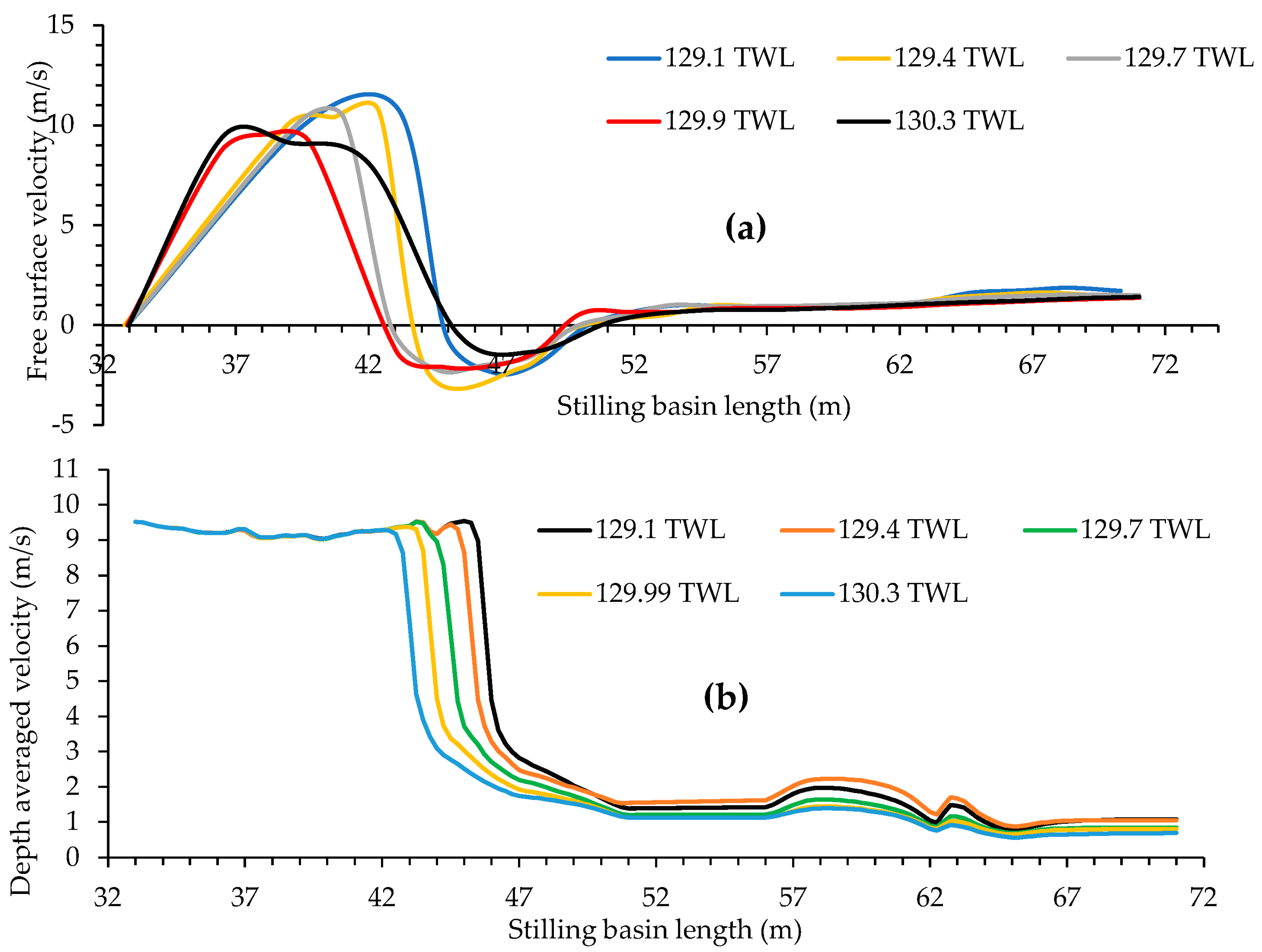
4.2.4. Free-Surface and Depth-Averaged Velocities
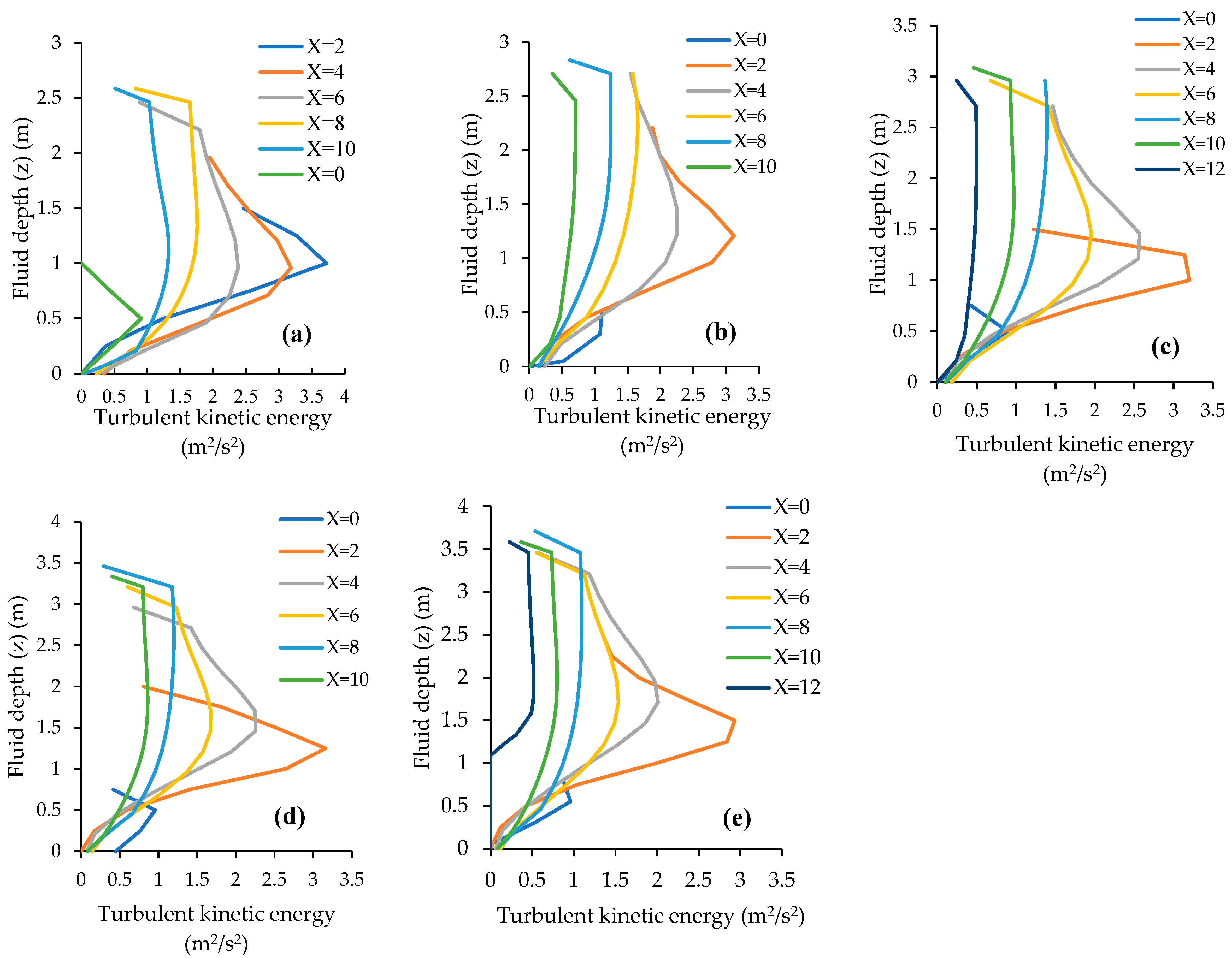
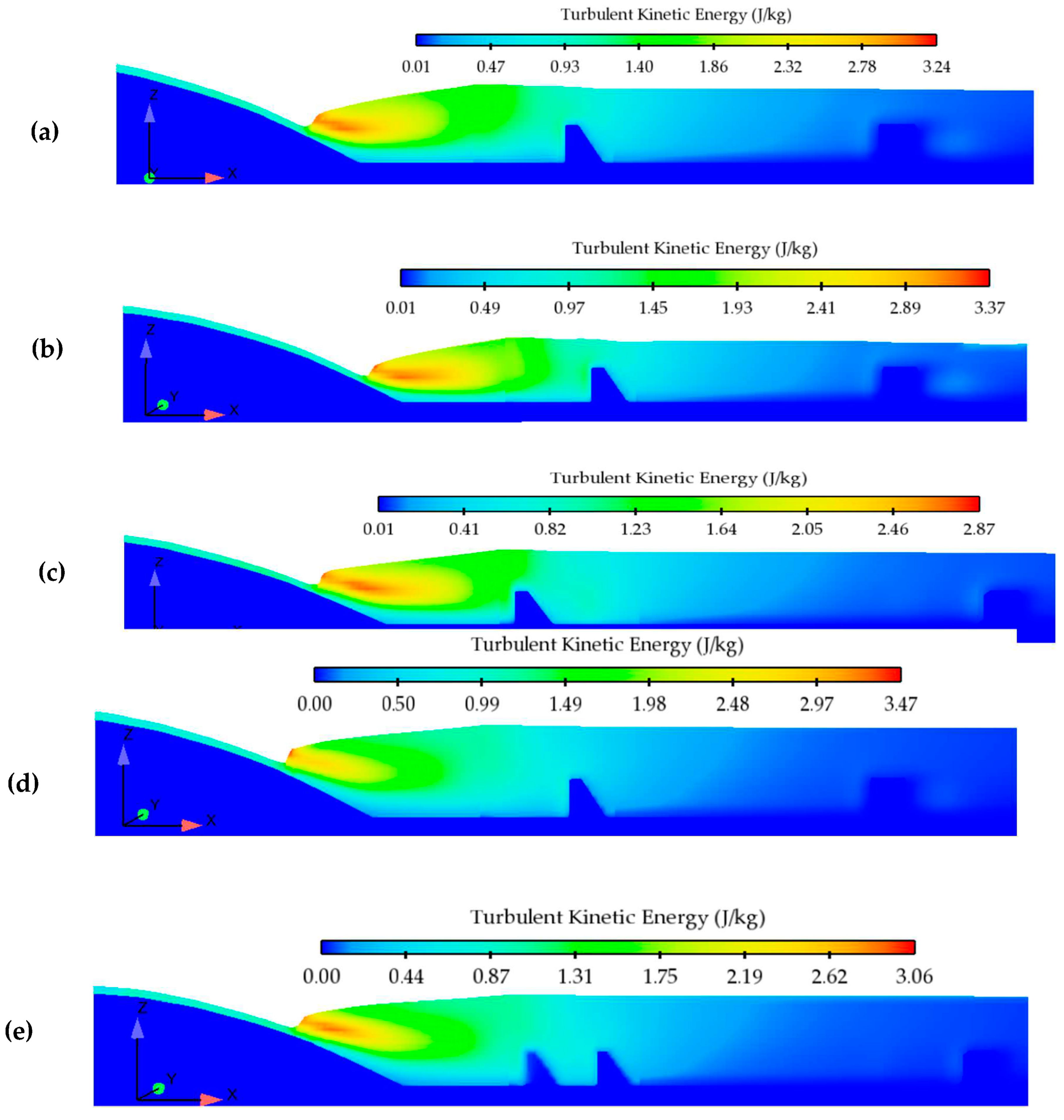
4.2.5. Turbulent Kinetic Energies (TKEs)
5. Discussion and Real-World Implications
6. Conclusions
- The literature review outlined thirty-three hydraulic parameters; out of those, the velocity profile, Froude number, free surface profile, shape of stilling basin, tailwater, and turbulent kinetic energy were the highly significant hydraulic parameters in the literature that were studied downstream of hydraulic structures.
- At all the investigated tailwater levels, no sweeping of the HJ was observed as reported in the previous studies. The location and elevation of HJs were observed to be different compared with a previous HEC-RAS one-dimensional hydraulic study. Upon comparison with the HJ results of the designed and downstream of a prototype barrage (i.e., remodeled basin), the distance of the HJ from the glacis toe was found to be higher, which further revealed the old basin (i.e., studied presently) was efficiently holding the HJ at the investigated discharge and TWLs.
- Non-linear trends for the Froude number and sequent depths were observed as the tailwater levels varied. On comparison with previous studies, the present models showed higher values for the Froude number and sequent depths, which showed deviation at higher tailwater levels.
- At lower tailwater levels, the vertical velocity profiles in the developing region of the HJ near the floor were found to be higher than the results at higher tailwater levels. At the investigated tailwater levels, jet-like velocity profiles were obtained in the HJ regions that levelled off as the distance from the HJ was increased.
- The maximum turbulent kinetic energy was found in the developing region of the HJ at the minimum tailwater level. After the impact and baffle blocks, the kinetic energy gradually reduced, and the minimum kinetic energy was observed at higher tailwater levels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Hydraulic Parameters from the Numerical Studies and Their Sources
| Sr.No. | Hydraulic Parameters | Articles Cited |
| 1 | Velocity profile (VP) | [4,24,27,37,43,44,46,47,49,52,55,71,74,75,76,77] |
| 2 | Free surface profile (FSP) | [4,9,24,27,37,44,45,47,49,71,75,76,77,78] |
| 3 | Pressure profile (PP) | [4,24,44,45,49,50,72,73,74,76,78] |
| 4 | Turbulent kinetic energy (TKE) | [4,27,37,46,47,55,75,76] |
| 5 | Air volume value (AV) | [4,24,27,37,44,45,75] |
| 6 | Discharge measurement (DM) | [24,72,73,76,77,78] |
| 7 | Shape of stilling basin (SS) | [16,18,47,72] |
| 8 | Froude number (Fr1) | [24,37,43,50,75,79] |
| 9 | HJ efficiency (ɳ) | [24,44,50,74,76] |
| 10 | Reynolds shear stress (RSS) | [4,46,49] |
| 11 | Tailwater level (TWL) | [75] |
| 12 | Contraction coefficient (CC) | [55] |
| 13 | Head loss (HL) | [55] |
| 14 | Frictional forces (FF) | [55] |
| 15 | Momentum coefficient (MC) | [55] |
| 16 | Energy coefficient (EC) | [47] |
| 17 | Discharge coefficient (DC) | [47] |
| 18 | Wall shear stress (WSS) | [4,74] |
| 19 | Sequent depth of HJ (SDHJ) | [4,49,71,74] |
| 20 | Length of HJ (LHJ) | [49,71,74] |
| 21 | Scour profile (SP) | [9] |
| 22 | Bed profile (BP) | [37] |
| 23 | Energy dissipation (ED) | [47] |
| 24 | Bed shear stress (BSS) | [47,74] |
Appendix B. Hydraulic Parameters from the Experimental Studies and Their Sources
| Sr.No. | Hydraulic Parameters | Articles Cited |
| 1 | Velocity profile (VP) | [2,3,8,9,10,14,15,18,21,22,23,24,25,26,32,48,73,80,81,82,83,84,85,86] |
| 2 | Froude number (Fr1) | [2,3,8,11,13,17,18,19,20,21,22,24,25,28,32,73,82,83,84,88,90,95] |
| 3 | Tailwater level (TWL) | [3,12,13,15,20,22,32,43,72,73,74,81,84,85,86,87,89,90,91,92] |
| 4 | Shape of stilling basin (SS) | [12,19,20,24,25,26,28,72,73,79,81,85,88,90,91,93] |
| 5 | Free surface profile (FSP) | [3,8,9,11,12,14,16,22,23,24,32,80,81,84,87,89,90,92,94] |
| 6 | Bed profile (BP) | [3,11,12,16,22,23,24,32,73,80,84,90,94,95] |
| 7 | Scour profile (SP) | [3,15,32,45,76,84,87,88,90,91,93,94] |
| 8 | Energy dissipation (ED) | [14,20,22,23,24,82,83,87,91] |
| 9 | Turbulence kinetic energy (TKE) | [14,20,22,23,24,73] |
| 10 | Pressure profile (PP) | [14,24,32,80,81,92] |
| 11 | Bed shear stress (BSS) | [2,11,17,22,48,73,85] |
| 12 | Reynolds shear stress (RSS) | [17,18,21,85,90] |
| 13 | Turbulence intensity (TI) | [17,18,21,81,85] |
| 14 | Submergence (SM) | [3,19,25,89] |
| 15 | Retrogression (RG) | [73,80,89] |
| 16 | HJ efficiency (ɳ) | [22,23,29] |
| 17 | Momentum flux (MF) | [11,13] |
| 18 | Volume flux (VF) | [11,13] |
| 19 | Length of HJ (LHJ) | [8,26,86,92] |
| 20 | Turbulence production (TP) | [23] |
| 21 | Power spectra (PS) | [18] |
| 22 | Sequent depth of HJ (SDHJ) | [9,74] |
| 23 | Relative energy loss (∆E/E1) | [22] |
References
- Mahtabi, G.; Chaplot, B.; Azamathulla, H.M.; Pal, M. Classification of hydraulic jump in rough beds. Water 2020, 12, 2249. [Google Scholar] [CrossRef]
- Maleki, S.; Fiorotto, V. Hydraulic Jump Stilling Basin Design over Rough Beds. J. Hydraul. Eng. 2021, 147, 04020087. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, A. Response of velocity and turbulence in submerged wall jets to abrupt changes from smooth to rough beds and its application to scour downstream of an apron. J. Fluid Mech. 2006, 556, 387–419. [Google Scholar] [CrossRef]
- Bayon-Barrachina, A.; Lopez-Jimenez, P.A. Numerical analysis of hydraulic jumps using OpenFOAM. J. Hydroinform. 2015, 17, 662–678. [Google Scholar] [CrossRef]
- Bai, R.; Ning, R.; Liu, S.; Wang, H. Hydraulic Jump on a Partially Vegetated Bed. Water Resour. Res. 2022, 58, e2022WR032013. [Google Scholar] [CrossRef]
- Li, P.; Zhu, D.Z.; Xu, T.; Zhang, J. Air Demand of a Hydraulic Jump in a Closed Conduit. J. Hydraul. Eng. 2022, 148, 04021058. [Google Scholar] [CrossRef]
- Bantacut, A.Y.; Azmeri, A.; Jemi, F.Z.; Ziana, Z.; Muslem, M. An experiment of energy dissipation on USBR IV stilling basin—Alternative in modification. J. Water Land Dev. 2022, 53, 68–72. [Google Scholar] [CrossRef]
- Mazumder, S. Hydraulic jump control using stilling basin with Adverse slope and positive step. ISH J. Hydraul. Eng. 2020, 28, 18–20. [Google Scholar] [CrossRef]
- Macián-Pérez, J.F.; Bayón, A.; García-Bartual, R.; López-Jiménez, P.A.; Vallés-Morán, F.J. Characterization of Structural Properties in High Reynolds Hydraulic Jump Based on CFD and Physical Modeling Approaches. J. Hydraul. Eng. 2020, 146, 04020079. [Google Scholar] [CrossRef]
- Elsayed, H.; Helal, E.; El-Enany, M.; Sobeih, M. Impacts of multi-gate regulator operation schemes on local scour downstream. ISH J. Hydraul. Eng. 2018, 27, 51–64. [Google Scholar] [CrossRef]
- Ead, S.A.; Rajaratnam, N. Hydraulic Jumps on Corrugated Beds. J. Hydraul. Eng. 2002, 128, 656–663. [Google Scholar] [CrossRef]
- Ead, S.A.; Rajaratnam, N. Plane Turbulent Wall Jets on Rough Boundaries with Limited Tailwater. J. Eng. Mech. 2004, 130, 1245–1250. [Google Scholar] [CrossRef]
- Ead, S.A.; Rajaratnam, N. Plane turbulent surface jets in shallow tailwater. J. Fluids Eng. 2000, 123, 121–127. [Google Scholar] [CrossRef]
- Chen, J.-G.; Zhang, J.-M.; Xu, W.-L.; Wang, Y.-R. Numerical simulation of the energy dissipation characteristics in stilling basin of multi-horizontal submerged jets. J. Hydrodyn. 2010, 22, 732–741. [Google Scholar] [CrossRef]
- Balachandar, R.; Kells, J.; Thiessen, R.; Gunal, M.; Guven, A.; Kells, J.A.; Hagel, K.P. The effect of tailwater depth on the dynamics of local scour. Can. J. Civ. Eng. 2000, 27, 138–150. [Google Scholar] [CrossRef]
- Sarker, M.; Rhodes, D. Calculation of free-surface profile over a rectangular broad-crested weir. Flow Meas. Instrum. 2004, 15, 215–219. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, A. Characteristics of Turbulent Flow in Submerged Jumps on Rough Beds. J. Eng. Mech. 2008, 134, 599. [Google Scholar] [CrossRef]
- Liu, M.; Rajaratnam, N.; Zhu, D.Z. Turbulence Structure of Hydraulic Jumps of Low Froude Numbers. J. Hydraul. Eng. 2004, 130, 511–520. [Google Scholar] [CrossRef]
- Habibzadeh, A.; Loewen, M.R.; Rajaratnam, N. Performance of Baffle Blocks in Submerged Hydraulic Jumps. J. Hydraul. Eng. 2012, 138, 902–908. [Google Scholar] [CrossRef]
- Pagliara, S.; Lotti, I.; Palermo, M. Hydraulic jump on rough bed of stream rehabilitation structures. J. Hydro-Environ. Res. 2008, 2, 29–38. [Google Scholar] [CrossRef]
- Zobeyer, A.H.; Jahan, N.; Islam, Z.; Singh, G.; Rajaratnam, N. Turbulence characteristics of the transition region from hydraulic jump to open channel flow. J. Hydraul. Res. 2010, 48, 395–399. [Google Scholar] [CrossRef]
- Abbaspour, A.; Dalir, A.H.; Farsadizadeh, D.; Sadraddini, A.A. Effect of sinusoidal corrugated bed on hydraulic jump characteristics. J. Hydro-Environ. Res. 2009, 3, 109–117. [Google Scholar] [CrossRef]
- Mignot, E.; Cienfuegos, R. Energy Dissipation and Turbulent Production in Weak Hydraulic Jumps. J. Hydraul. Eng. 2010, 136, 116–121. [Google Scholar] [CrossRef]
- Babaali, H.; Shamsai, A.; Vosoughifar, H. Computational Modeling of the Hydraulic Jump in the Stilling Basin with Convergence Walls Using CFD Codes. Arab. J. Sci. Eng. 2014, 40, 381–395. [Google Scholar] [CrossRef]
- Habibzadeh, A.; Wu, S.; Ade, F.; Rajaratnam, N.; Loewen, M.R. Exploratory Study of Submerged Hydraulic Jumps with Blocks. J. Hydraul. Eng. 2011, 137, 706–710. [Google Scholar] [CrossRef]
- Ali, A.M.; Mohamed, Y.A. Effect of stilling basin shape on the hydraulic characteristics of the flow downstream radial gates. Alex. Eng. J. 2010, 49, 393–400. [Google Scholar] [CrossRef]
- Mishra, K. 3DNumerical Modelling of Energy Dissipation in Flexible Apron of Barrages. J. Inst. Eng. Ser. A 2015, 96, 47–56. [Google Scholar] [CrossRef]
- Alikhani, A.; Behrozi-Rad, R.; Fathi-Moghadam, M. Hydraulic jump in stilling basin with vertical end sill. Int. J. Phys. Sci. 2010, 5, 25–29. [Google Scholar]
- Elsaeed, G.; Ali, A.; Abdelmageed, N.; Ibrahim, A. Effect of End Step Shape in the Performance of Stilling Basins Downstream Radial Gates. J. Sci. Res. Rep. 2016, 9, 1–9. [Google Scholar] [CrossRef]
- Tiwari, H.L.; Panwar, A.; Gehlot, B.; Singh, J. Study of Shape of Intermediate Sill on the Design of Stilling Basin Model. Int. J. Res. Eng. Technol. 2014, 3, 133–138. [Google Scholar] [CrossRef]
- Tiwari, H.L.; Gehlot, V.K.; Tiwari, S. Effect of Height of Triangular Siil on the Performance of Stilling Basin Model. Int. J. Res. Eng. Technol. 2014, 3, 868–873. [Google Scholar] [CrossRef]
- Hager, W.H.; Li, D. Sill-controlled energy dissipator. J. Hydraul. Res. 1992, 30, 181. [Google Scholar] [CrossRef]
- Herrera-Granados, O.; Kostecki, S.W. Numerical and physical modeling of water flow over the ogee weir of the new Niedów barrage. J. Hydrol. Hydromechanics 2016, 64, 67–74. [Google Scholar] [CrossRef]
- Zulfiqar, C.; Kaleem, S.M. Launching/Disappearance of Stone Apron, Block Floor Downstream of the Taunsa Barrage and Unprecedent Drift of the River towards Kot Addu Town. Sci. Technol. Dev. 2015, 34, 60–65. [Google Scholar] [CrossRef][Green Version]
- Chaudary, Z.A.; Sarwar, M.K.; Barrage, R.T. Rehabilitated Taunsa Barrage: Prospects and Concerns. Sci. Technol. Dev. 2014, 33, 127–131. [Google Scholar]
- Chaudhry, Z.A. Surface Flow Hydraulics of Taunsa Barrage: Before and after Rehabilitation. Pak. J. Sci. 2010, 62, 116–119. [Google Scholar]
- Witt, A.; Gulliver, J.; Shen, L. Simulating air entrainment and vortex dynamics in a hydraulic jump. Int. J. Multiph. Flow 2015, 72, 165–180. [Google Scholar] [CrossRef]
- Yoo, S.; Hong, M.; Wang, H. 3-Dimensional numerical study of a flow patterns around a multipurpose dam. In Proceedings of the International Conference on Hydro Informatics, Cardiff, UK, 1–5 July 2002; pp. 353–357. [Google Scholar]
- Aydogdu, M.; Gul, E.; Dursun, O.F. Experimentally Verified Numerical Investigation of the Sill Hydraulics for Abruptly Expanding Stilling Basin. Arab. J. Sci. Eng. 2022, 48, 4563–4581. [Google Scholar] [CrossRef]
- Mukha, T.; Almeland, S.K.; Bensow, R.E. Large-Eddy Simulation of a Classical Hydraulic Jump: Influence of Modelling Parameters on the Predictive Accuracy. Fluids 2022, 7, 101. [Google Scholar] [CrossRef]
- El Azim, N.A.; Saleh, O.; Tohamy, E.; Mahgoub, S.; Ghany, S. Effect of Vertical Screen on Energy Dissipation and Water Surface Profile Using Flow 3D. Egypt. Int. J. Eng. Sci. Technol. 2022, 38, 20–25. [Google Scholar]
- Kosaj, R.; Alboresha, R.S.; Sulaiman, S.O. Comparison between Numerical Flow3d Software and Laboratory Data, for Sediment Incipient Motion. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Baghdad, Iraq, 3–4 November 2022; p. 961. [Google Scholar] [CrossRef]
- Mirzaei, H.; Tootoonchi, H. Experimental and numerical modeling of the simultaneous effect of sluice gate and bump on hydraulic jump. Model. Earth Syst. Environ. 2020, 6, 1991–2002. [Google Scholar] [CrossRef]
- Macián-Pérez, J.F.; García-Bartual, R.; Bayon, B.H.A.; Vallés-Morán, F.J. Analysis of the flow in a typified USBR II stilling basin through a numerical and physical modeling approach. Water 2020, 12, 227. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Ghader, A. Numerical Investigation of Inverse Curvature Ogee Spillway. Civ. Eng. J. 2017, 3, 1146. [Google Scholar] [CrossRef]
- Anjum, N.; Ghani, U.; Pasha, G.A.; Rashid, M.U.; Latif, A.; Rana, M.Z.Y. Reynolds stress modeling of flow characteristics in a vegetated rectangular open channel. Arab. J. Sci. Eng. 2018, 43, 5551–5558. [Google Scholar] [CrossRef]
- Dargahi, B. Experimental Study 3DNumerical Simulations for a Free-Overflow Spillway. J. Hydraul. Eng. 2006, 132, 899–907. [Google Scholar] [CrossRef]
- Karim, O.A.; Ali, K.H.M. Prediction of flow patterns in local scour holes caused by turbulent water jets. J. Hydraul. Res. 2000, 38, 279–287. [Google Scholar] [CrossRef]
- Liu, X.; García, M.H. Three-Dimensional Numerical Model with Free Water Surface and Mesh Deformation for Local Sediment Scour. J. Waterw. Port Coast. Ocean. Eng. 2008, 134, 203–217. [Google Scholar] [CrossRef]
- Bayon, A.; Valero, D.; García-Bartual, R.; Vallés-Morán, F.J.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Bayon-Barrachina, A.; Valles-Moran, F.J.; Lopes-Jiménez, P.A.; Bayn, A.; Valles-Morn, F.J.; Lopes-Jimenez, P.A. Numerical Analysis and Validation of South Valencia Sewage Collection System. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 2015; Volume 17, pp. 1–11. [Google Scholar]
- Nguyen, V.T.; Nestmann, F.; Scheuerlein, H. Three-dimensional computation of turbulent flow in meandering channels and rivers. J. Hydraul. Res. 2007, 45, 595–609. [Google Scholar] [CrossRef]
- Riad, P.; Roelvink, D.J.A.; Ahmed, A.; Boeru, P. Use of Mathematical Models to Improve the Design of the Stilling Basin. Available online: https://doi.org/10.13140/RG.2.2.34562.94409 (accessed on 27 September 2022).
- Chatila, J.; Tabbara, M. Computational modeling of flow over an ogee spillway. Comput. Struct. 2004, 82, 1805–1812. [Google Scholar] [CrossRef]
- Cassan, L.; Belaud, G. Experimental and Numerical Investigation of Flow under Sluice Gates. J. Hydraul. Eng. 2012, 138, 367–373. [Google Scholar] [CrossRef]
- Carvalho, R.F.; Lemos, C.M.; Ramos, C.M. Numerical computation of the flow in hydraulic jump stilling basins. J. Hydraul. Res. 2008, 46, 739–752. [Google Scholar] [CrossRef]
- World Bank. Announcement of World Bank Provides United States (U.S.) One Hundred Twenty-Three Million Dollars Loan to Rehabilitate and Modernize Taunsa Barrage in Pakistan on 15 March 2005 (English). Available online: http://documents.worldbank.org/curated/en/099915203252274440/IDU01bcc88300a93504d270b1a20dbc553c584df (accessed on 25 March 2022).
- Zaidi, S.; Khan, M.A.; Rehman, S.U. Planning and Design of Taunsa Barrage Rehabilitation Project. In Proceedings of the Pakistan Engineering Congress, 71st Annual Session Proceedings, Pakistan, Lahore, 2004; Paper No. 687. pp. 228–286. [Google Scholar]
- Aloini, D.; Dulmin, R.; Mininno, V.; Ponticelli, S. Supply chain management: A review of implementation risks in the construction industry. Bus. Process Manag. J. 2012, 18, 735–761. [Google Scholar] [CrossRef]
- Ullah, F.; Ayub, B.; Siddiqui, S.Q.; Thaheem, M.J. A review of public-private partnership: Critical factors of concession period. J. Financ. Manag. Prop. Constr. 2016, 21, 269–300. [Google Scholar] [CrossRef]
- Ayub, B.; Thaheem, M.J.; Din, Z.U. Dynamic Management of Cost Contingency: Impact of KPIs and Risk Perception. Procedia Eng. 2016, 145, 82–87. [Google Scholar] [CrossRef]
- Muneeswaran, G.; Manoharan, P.; Awoyera, P.O.; Adesina, A. A statistical approach to assess the schedule delays and risks in Indian construction industry. Int. J. Constr. Manag. 2020, 20, 450–461. [Google Scholar] [CrossRef]
- Gündüz, M.; Nielsen, Y.; Özdemir, M. Quantification of Delay Factors Using the Relative Importance Index Method for Construction Projects in Turkey. J. Manag. Eng. 2013, 29, 133–139. [Google Scholar] [CrossRef]
- Ahmad, Z.; Thaheem, M.J.; Maqsoom, A. Building information modeling as a risk transformer: An evolutionary insight into the project uncertainty. Autom. Constr. 2018, 92, 103–119. [Google Scholar] [CrossRef]
- Siddiqui, S.Q.; Ullah, F.; Thaheem, M.J.; Gabriel, H.F. Six Sigma in construction: A review of critical success factors. Int. J. Lean Six Sigma 2016, 7, 171–186. [Google Scholar] [CrossRef]
- Sciences, F. FLOW 3D User Manual, Version 10.1; Flow Sciences: Santa Fe, NM, USA, 2013. [Google Scholar]
- Yakhot, V.; Thangam, S.; Gatski, T.B.; Orszag, S.A.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A 1991, 4, 1510–1520. [Google Scholar] [CrossRef]
- Training, E. Water & Environment Training Guide 1: CFD Project Workflow Guide, n.d. Available online: https://www.flow3d.com/wp-content/uploads/2017/03/cfd-project-workflow-guide-v112.pdf (accessed on 7 August 2021).
- Kometa, S.T.; Olomolaiye, P.O.; Harris, F.C. Attributes of UK construction clients influencing project consultants’ performance. Constr. Manag. Econ. 1994, 12, 433–443. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Nikmehr, S.; Aminpour, Y. Numerical simulation of hydraulic jump over rough beds, Period. Polytech. Civ. Eng. 2020, 64, 396–407. [Google Scholar] [CrossRef]
- Savage, B.M.; Johnson, M.C. Flow over Ogee Spillway: Physical and Numerical Model Case Study. J. Hydraul. Eng. 2001, 127, 640–649. [Google Scholar] [CrossRef]
- Johnson, M.C.; Savage, B.M. Physical and Numerical Comparison of Flow over Ogee Spillway in the Presence of Tailwater. J. Hydraul. Eng. 2006, 132, 1353–1357. [Google Scholar] [CrossRef]
- Ebrahimiyan, S.; Hajikandi, H.; Bejestan, M.S.; Jamali, S.; Asadi, E. Numerical Study on the Effect of Sediment Concentration on Jump Characteristics in Trapezoidal Channels. Iran. J. Sci. Technol.—Trans. Civ. Eng. 2021, 45, 1059–1075. [Google Scholar] [CrossRef]
- Bricker, J.D.; Nakayama, A. Contribution of Trapped Air Deck Superelevation, and Nearby Structures to Bridge Deck Failure during a Tsunami. J. Hydraul. Eng. 2014, 140, 05014002. [Google Scholar] [CrossRef]
- Soori, S.; Babaali, H.; Soori, N. An Optimal Design of the Inlet and Outlet Obstacles at USBR II Stilling Basin. Int. J. Sci. Eng. Appl. 2017, 6, 134–142. [Google Scholar] [CrossRef]
- Nguyen, V.T. 3D numerical simulation of free surface flows over hydraulic structures in natural channels and rivers. Appl. Math. Model 2015, 39, 6285–6306. [Google Scholar] [CrossRef]
- Geun, K.D.; Jae Hyun, P. Analysis of Flow Structure over Ogee-Spillway in Consideration of Scale and Roughness Effects by Using CFD Model. KSCE J. Civ. Eng. 2005, 9, 161–169. [Google Scholar]
- D’Agostino, V.; Ferro, V. Scour on Alluvial Bed Downstream of Grade-Control Structures. J. Hydraul. Eng. 2004, 130, 24–37. [Google Scholar] [CrossRef]
- Chen, Q.; Dai, G.; Liu, H. Volume of Fluid Model for Turbulence Numerical Simulation of Stepped Spillway Overflow. J. Hydraul. Eng. 2002, 128, 683–688. [Google Scholar] [CrossRef]
- Lin, P.; Xu, W. NEWFLUME: A numerical water flume for two-dimensional turbulent free surface flows NEWFLUME: Un canal numérique hydraulique pour écoulements bidimensional à surface libre turbulents. J. Hydraul. Res. 2006, 44, 79–93. [Google Scholar] [CrossRef]
- Chaudhry, Z.A. Performance Assessment of Taunsa Barrage Subsidiary Weir for Long Term Rehabilitation Planning. Pak. J. Engg. Appl. Sci. 2010, 7, 65–70. [Google Scholar]
- Adduce, C.; Sciortino, G. Scour due to a horizontal turbulent jet: Numerical and experimental investigation. J. Hydraul. Res. 2006, 44, 663–673. [Google Scholar] [CrossRef]
- Guan, D.; Melville, B.W.; Friedrich, H. Flow Patterns and Turbulence Structures in a Scour Hole Downstream of a Submerged Weir. J. Hydraul. Eng. 2014, 140, 68–76. [Google Scholar] [CrossRef]
- Neisi, M.; Sajjadi, S.M.; Shafai Bejestan, M. Experimental Investigation of Discharge and Flow Energy Dissipation of Elliptical Lopac Gate in Free Flow Condition. Irrig. Sci. Eng. 2020, 46, 91–101. [Google Scholar] [CrossRef]
- Grimaldi, C.; Gaudio, R.; Cardoso, F.C.A.H. Control of Scour at Bridge Piers by a Downstream Bed Sill. J. Hydraul. Eng. 2009, 135, 13–21. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.; Ansari, A.; Borghei, S.M. Hydraulic behaviour of flow over an oblique weir. J. Hydraul. Res. 2010, 48, 669–673. [Google Scholar] [CrossRef]
- Gaudio, R.; Marion, A. Time evolution of scouring downstream of bed sills. J. Hydraul. Res. 2003, 41, 271–284. [Google Scholar] [CrossRef]
- Stojnic, I.; Pfister, M.; Matos, J.; Schleiss, A.J. Hydraulic jump downstream of a stepped chute: An experimental study. In Proceedings of the E-Proceedings 38th IAHR World Congr, Panama City, Panama, 1–6 September 2019; pp. 2056–2065. [Google Scholar] [CrossRef]
- Wüthrich, D.; Chamoun, S.; De Cesare, G.; Schleiss, A.J. Behaviour of a scour protection overlay with randomly distributed concrete prisms in plunge pools downstream of mobile barrages for exceptional operation conditions. In Proceedings of the 7th IAHR International Symposium Hydraulic Structures, ISHS 2018, Aachen, Germany, 15–18 May 2018; pp. 150–158. [Google Scholar] [CrossRef]
- Marion, A.; Lenzi, M.A.; Comiti, F. Effect of sill spacing and sediment size grading on scouring at grade-control structures. Earth Surf. Process. Landforms 2004, 29, 983–993. [Google Scholar] [CrossRef]
- Goel, A.; Pal, M. Application of support vector machines in scour prediction on grade-control structures. Eng. Appl. Artif. Intell. 2009, 22, 216–223. [Google Scholar] [CrossRef]
- Goel, A. Design of stilling basin for circular pipe outlets Can. J. Civ. Eng. 2008, 35, 1365–1374. [Google Scholar] [CrossRef]
- Kucukali, S.; Chanson, H. Turbulence measurements in the bubbly flow region of hydraulic jumps. Exp. Therm. Fluid Sci. 2008, 33, 41–53. [Google Scholar] [CrossRef]
- Zaidi, S.M.A.; Amin, M.; Ahmadani, M.A. Performance Evaluation of Taunsa Barrage Emergency Rehabilitation and Modernization Project. Paper No. 705. 2011, pp. 650–682. Available online: https://pecongress.org.pk/images/upload/books/PERFORMANCE%20EVALUATION%20OF%20TAUNSA%20BARRAGE%20EMERGENCY%20REHABILIT.pdf (accessed on 3 October 2023).


| Reference | Numerical Codes | Modelling Approach | Turbulence Scheme |
|---|---|---|---|
| Chaudhry [36] | HEC-RAS | Energy equation | 1-D model |
| Aydogdu et al. [39] | ANSYS-FLUENT | RANS | RNG K-ε |
| Mukha et al. [40] | Open Foam | Large Eddy Simulation (LES) | LES-VOF |
| Abd El Azim et al. [41] | FLOW-3D | RANS | RNG K-ε |
| Kosaj et al. [42] | FLOW-3D | RANS | RNG K-ε |
| Mirzaei and Tootoonchi [43] | FLOW-3D | RANS | Standard K-ε, LES, RNG K-ε, |
| Macián-Pérez et al. [44] | FLOW-3D | RANS | Standard K-ε, K-ω, RNG K-ε, |
| Daneshfaraz and Ghaderi [45] | FLUENT | RANS | RNG K-ε |
| Anjum et al. [46] | FLUENT | RANS | Reynolds Stress Model (RSM) |
| Dargahi [47] | FLUENT | RANS | RSM, Standard K-ε, RNG K-ε |
| Karim and Ali [48] | FLUENT | RANS | RSM, Standard K-ε, RNG K-ε |
| Liu and García [49] | Open Foam | RANS | Standard K-ε |
| Bayon et al. [50] | Open Foam, FLOW-3D | RANS | RNG K-ε |
| Bayon-Barrachina et al. [51] | Open Foam | RANS | Standard K-ε, SST K-ω, RNG K-ε |
| Nguyen et al. [52] and Riad et al. [53] | Finite Element Model (FEM) | RANS | Standard K-ε, Prandtl Mixing Length |
| Chatila and Tabbara [54] | ADINA-F | RANS | Standard K-ε |
| Cassan and Belaud [55] | FLUENT | RANS | RSM, Standard K-ε, RNG K-ε |
| Carvalho et al. [56] | FLOW-3D | RANS | RNG K-ε |
| Discharge (m3/s) | Minimum Tailwater Required for HJ (m) | Maximum Tailwater Required for HJ (m) | Upstream Water Level Maintained (m) | Turbulence Model | Models Operation |
|---|---|---|---|---|---|
| 44 | 129.10 | 132.28 | 136.24 | RNG K-ε | Gated Flow |
| 444 | 133.8 | ----- | 135.93 | RNG K-ε | Free Designed Flow |
| Parameters | Frequency | RII | Rank | Parameters | Frequency | RII | Rank |
|---|---|---|---|---|---|---|---|
| VP | 16 | 0.155 | 1st | WSS | 2 | 0.019 | 10th |
| FSP | 15 | 0.146 | 2nd | BSS | 2 | 0.019 | |
| PP | 11 | 0.107 | 3rd | TWL | 1 | 0.010 | 11th |
| TKE | 8 | 0.078 | 4th | CC | 1 | 0.010 | |
| AV | 7 | 0.068 | 5th | HL | 1 | 0.010 | |
| DM | 6 | 0.058 | 6th | FF | 1 | 0.010 | |
| Fr1 | 6 | 0.058 | MC | 1 | 0.010 | ||
| ɳ | 5 | 0.049 | 7th | EC | 1 | 0.010 | |
| SS | 4 | 0.039 | 8th | DC | 1 | 0.010 | |
| SDHJ | 4 | 0.039 | SP | 1 | 0.010 | ||
| RSS | 3 | 0.029 | 9th | BP | 1 | 0.010 | |
| LHJ | 3 | 0.029 | ED | 1 | 0.010 |
| Parameters | Frequency | RII | Rank | Parameters | Frequency | RII | Rank |
|---|---|---|---|---|---|---|---|
| VP | 24 | 0.125 | 1st | TI | 5 | 0.026 | 11th |
| Fr1 | 24 | 0.125 | SM | 4 | 0.021 | 12th | |
| TWL | 20 | 0.104 | 2nd | LHJ | 4 | 0.021 | |
| FSP | 19 | 0.099 | 3rd | RG | 3 | 0.016 | 13th |
| SS | 17 | 0.089 | 4th | ɳ | 3 | 0.016 | |
| BP | 14 | 0.073 | 5th | MF | 2 | 0.010 | 14th |
| SP | 13 | 0.068 | 6th | VF | 2 | 0.010 | |
| ED | 9 | 0.047 | 7th | SDHJ | 2 | 0.010 | |
| BSS | 7 | 0.036 | 8th | TP | 1 | 0.005 | 15h |
| TKE | 6 | 0.031 | 9th | PS | 1 | 0.005 | |
| PP | 6 | 0.031 | ∆E/E1 | 1 | 0.005 | ||
| RSS | 5 | 0.026 | 10th |
| Parameters | Frequency | RII | Rank | Parameters | Frequency | RII | Rank |
|---|---|---|---|---|---|---|---|
| VP | 40 | 0.140 | 1st | SDHJ | 6 | 0.021 | 14th |
| FSP | 31 | 0.110 | 2nd | TI | 5 | 0.017 | 15th |
| Fr1 | 30 | 0.100 | 3rd | SM | 4 | 0.014 | 16th |
| SS | 21 | 0.080 | 4th | RG | 3 | 0.010 | 17th |
| TWL | 21 | 0.070 | 5th | MF | 2 | 0.007 | 18th |
| PP | 17 | 0.050 | 6th | VF | 2 | 0.007 | |
| BP | 15 | 0.060 | 7th | WSS | 2 | 0.007 | |
| TKE | 14 | 0.060 | CC | 1 | 0.003 | 19th | |
| SP | 14 | 0.060 | HL | 1 | 0.003 | ||
| ED | 10 | 0.040 | 8th | FF | 1 | 0.003 | |
| BSS | 9 | 0.030 | 9th | MC | 1 | 0.003 | |
| RSS | 8 | 0.030 | EC | 1 | 0.003 | ||
| ɳ | 8 | 0.020 | 10th | DC | 1 | 0.003 | |
| AV | 7 | 0.030 | 11th | ES | 1 | 0.003 | |
| LHJ | 7 | 0.010 | 12th | TP | 1 | 0.003 | |
| DM | 6 | 0.020 | 13th | PS | 1 | 0.003 | |
| (∆E/E1) | 1 | 0.003 |
| Parameters | Frequency | Relative Frequency | PA | RPA | % Score | R % Score | Parameters | Frequency | Relative Frequency | PA | RPA | % Score | R % Score |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VP | 40 | 0.137 | 2 | 1 | 0.137 | 14.71% | TI | 5 | 0.017 | 1 | 0.34 | 0.006 | 0.63% |
| FSP | 31 | 0.106 | 2 | 1 | 0.106 | 11.40% | SM | 4 | 0.014 | 1 | 0.34 | 0.005 | 0.50% |
| Fr1 | 30 | 0.103 | 2 | 1 | 0.103 | 11.04% | RG | 3 | 0.010 | 1 | 0.34 | 0.003 | 0.38% |
| SS | 21 | 0.072 | 2 | 1 | 0.072 | 7.72% | MF | 2 | 0.007 | 1 | 0.34 | 0.002 | 0.25% |
| TWL | 21 | 0.072 | 2 | 1 | 0.072 | 7.72% | VF | 2 | 0.007 | 1 | 0.34 | 0.002 | 0.25% |
| PP | 17 | 0.058 | 2 | 1 | 0.058 | 6.25% | WSS | 2 | 0.007 | 1 | 0.66 | 0.005 | 0.49% |
| BP | 15 | 0.051 | 2 | 1 | 0.051 | 5.52% | CC | 1 | 0.003 | 1 | 0.66 | 0.002 | 0.24% |
| TKE | 14 | 0.048 | 2 | 1 | 0.048 | 5.15% | HL | 1 | 0.003 | 1 | 0.66 | 0.002 | 0.24% |
| SP | 14 | 0.048 | 2 | 1 | 0.048 | 5.15% | FF | 1 | 0.003 | 1 | 0.66 | 0.002 | 0.24% |
| ED | 10 | 0.034 | 2 | 1 | 0.034 | 3.68% | MC | 1 | 0.003 | 1 | 0.66 | 0.002 | 0.24% |
| BSS | 9 | 0.031 | 2 | 1 | 0.031 | 3.31% | EC | 1 | 0.003 | 1 | 0.66 | 0.002 | 0.24% |
| RSS | 8 | 0.027 | 2 | 1 | 0.027 | 2.94% | DC | 1 | 0.003 | 1 | 0.66 | 0.002 | 0.24% |
| ɳ | 8 | 0.027 | 2 | 1 | 0.027 | 2.94% | ES | 1 | 0.003 | 1 | 0.66 | 0.002 | 0.24% |
| AV | 7 | 0.024 | 1 | 0.66 | 0.016 | 1.70% | TP | 1 | 0.003 | 1 | 0.34 | 0.001 | 0.13% |
| LHJ | 7 | 0.024 | 2 | 1 | 0.024 | 2.57% | PS | 1 | 0.003 | 1 | 0.34 | 0.001 | 0.13% |
| DM | 6 | 0.021 | 1 | 0.66 | 0.014 | 1.46% | ∆E/E1 | 1 | 0.003 | 1 | 0.34 | 0.001 | 0.13% |
| SDHJ | 6 | 0.021 | 2 | 1 | 0.021 | 2.21% |
| Parameters | Ranking Extracted from Table 2 | Ranking Extracted from Table 3 | Ranking Extracted from Table 4 | Ranking Extracted from Table 5 | Overall Occurrence |
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) = (2) + (3) + (4) + (5) |
| VP | 1st | 1th | 1th | 1th | 4 |
| Fr1 | 6th | 1th | 3rd | 3rd | 4 |
| FSP | 2nd | NA | 2nd | 2nd | 3 |
| SS | NA * | 4th | 4th | 4th | 3 |
| TKE | 4th | NA | 7th | 8th | 3 |
| TWL | NA | 2nd | 5th | 5th | 3 |
| Q (m3/s) | TWLs (m) | Present Study 3D Models | Chaudhry [36] HEC-RAS | Zaidi et al. [95] | |||
|---|---|---|---|---|---|---|---|
| HJ Elevation (m) | HJ Distance from Glacis Toe (m) | HJ Elevation (m) | HJ Distance from Glacis Toe (m) | Designed HJ Location(m) | HJ Location Obserevd at Prototype (m) | ||
| 44 | 129.10 | 127.91 | 2.97 | 128 | 3.20 | ………. | ………. |
| 129.40 | 128.33 | 4.17 | ………. | ………. | ………. | ………. | |
| 129.70 | 128.60 | 5.92 | ………. | ………. | ………. | ………. | |
| 129.9 | 128.87 | 6.15 | ………. | ………. | ………. | ………. | |
| 130.30 | 129.03 | 6.03 | 129.5 | 6.5 | 1.22 | 1.22 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaffar, M.W.; Haasan, I.; Ghumman, A.R. Numerical Investigation of Critical Hydraulic Parameters Using FLOW-3D: A Case Study of Taunsa Barrage, Pakistan. Fluids 2023, 8, 310. https://doi.org/10.3390/fluids8120310
Zaffar MW, Haasan I, Ghumman AR. Numerical Investigation of Critical Hydraulic Parameters Using FLOW-3D: A Case Study of Taunsa Barrage, Pakistan. Fluids. 2023; 8(12):310. https://doi.org/10.3390/fluids8120310
Chicago/Turabian StyleZaffar, Muhammad Waqas, Ishtiaq Haasan, and Abdul Razzaq Ghumman. 2023. "Numerical Investigation of Critical Hydraulic Parameters Using FLOW-3D: A Case Study of Taunsa Barrage, Pakistan" Fluids 8, no. 12: 310. https://doi.org/10.3390/fluids8120310
APA StyleZaffar, M. W., Haasan, I., & Ghumman, A. R. (2023). Numerical Investigation of Critical Hydraulic Parameters Using FLOW-3D: A Case Study of Taunsa Barrage, Pakistan. Fluids, 8(12), 310. https://doi.org/10.3390/fluids8120310








