Effect of a Control Mechanism on the Interaction between a Rectangular Jet and a Slotted Plate: Experimental Study of the Aeroacoustic Field
Abstract
:1. Introduction
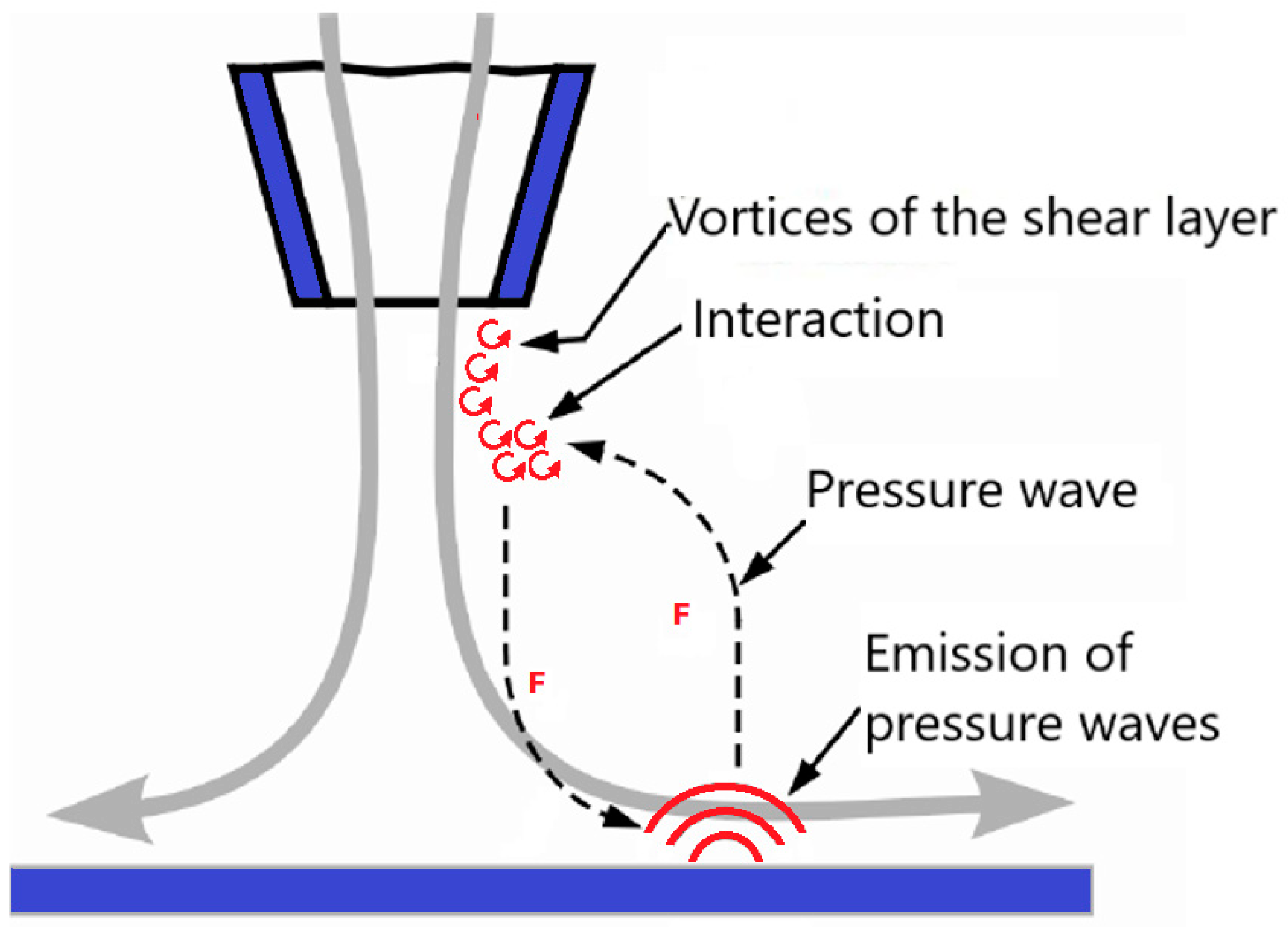
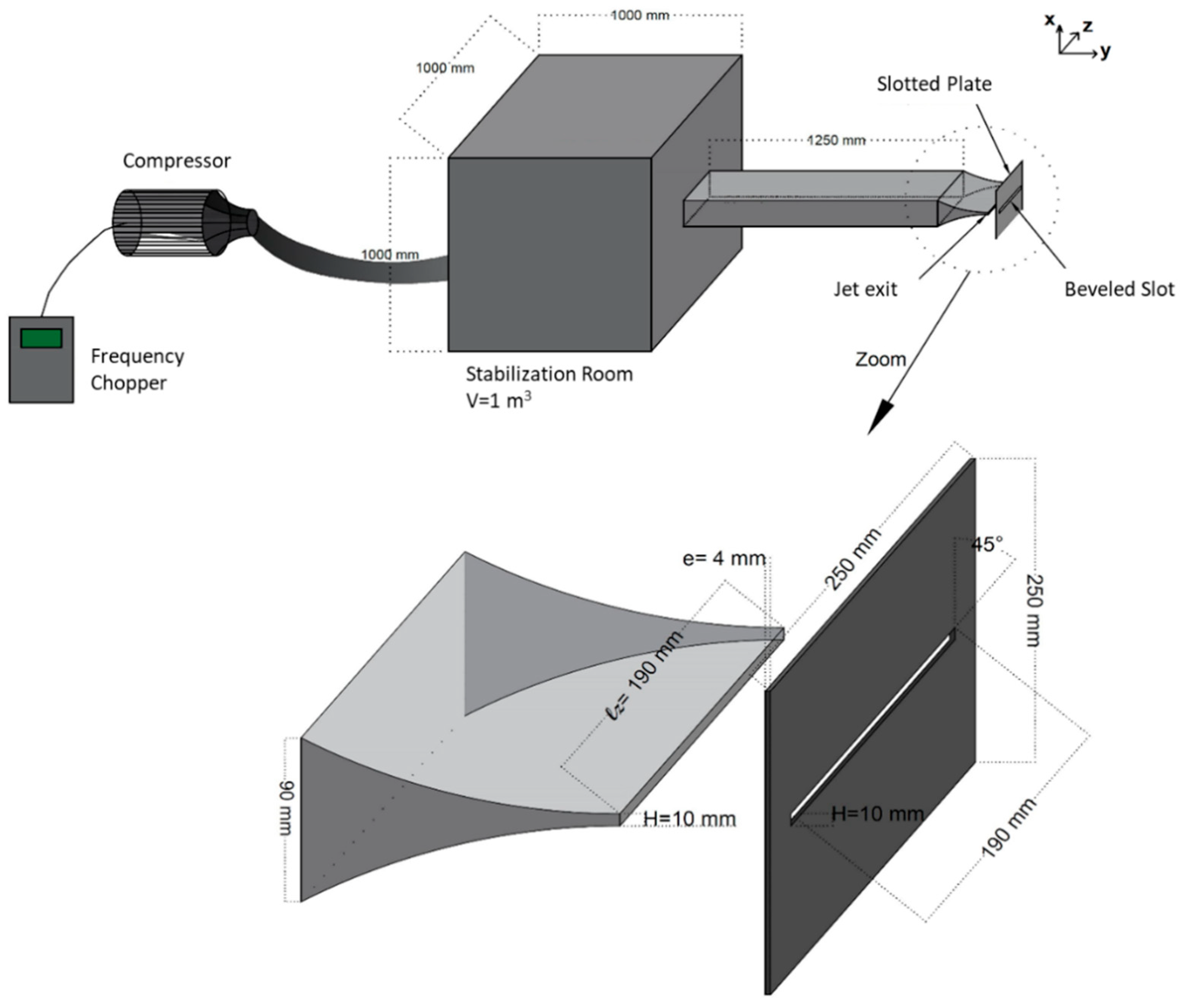
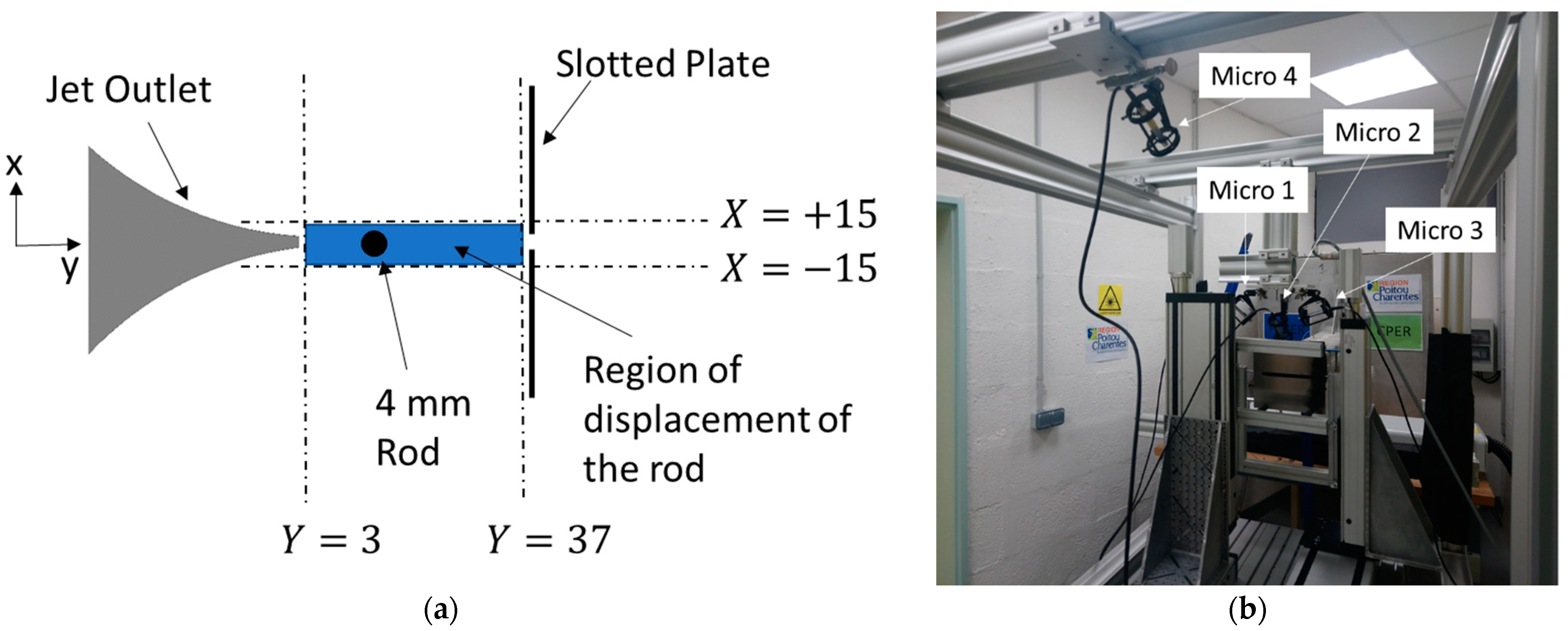
2. Materials and Methods
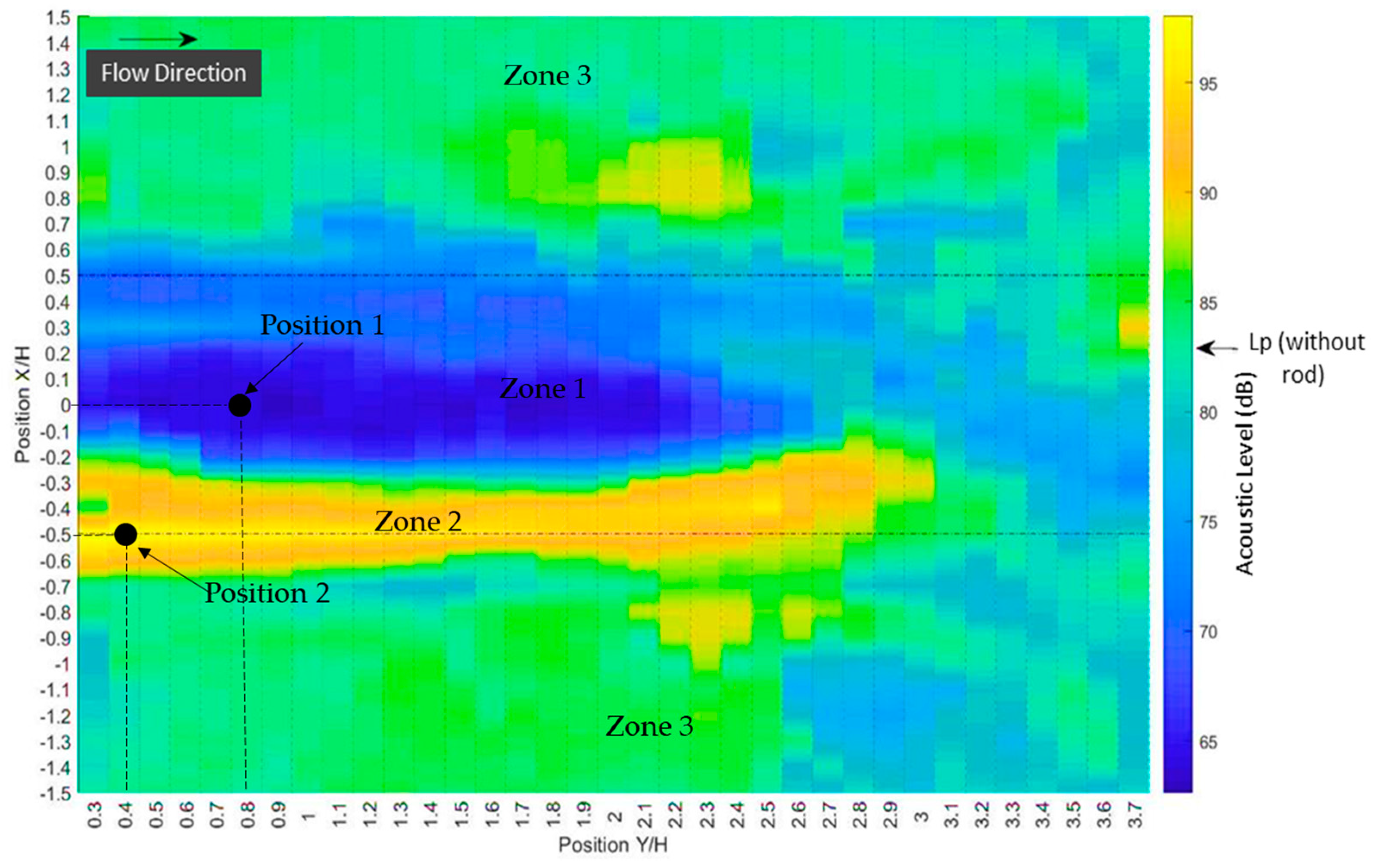
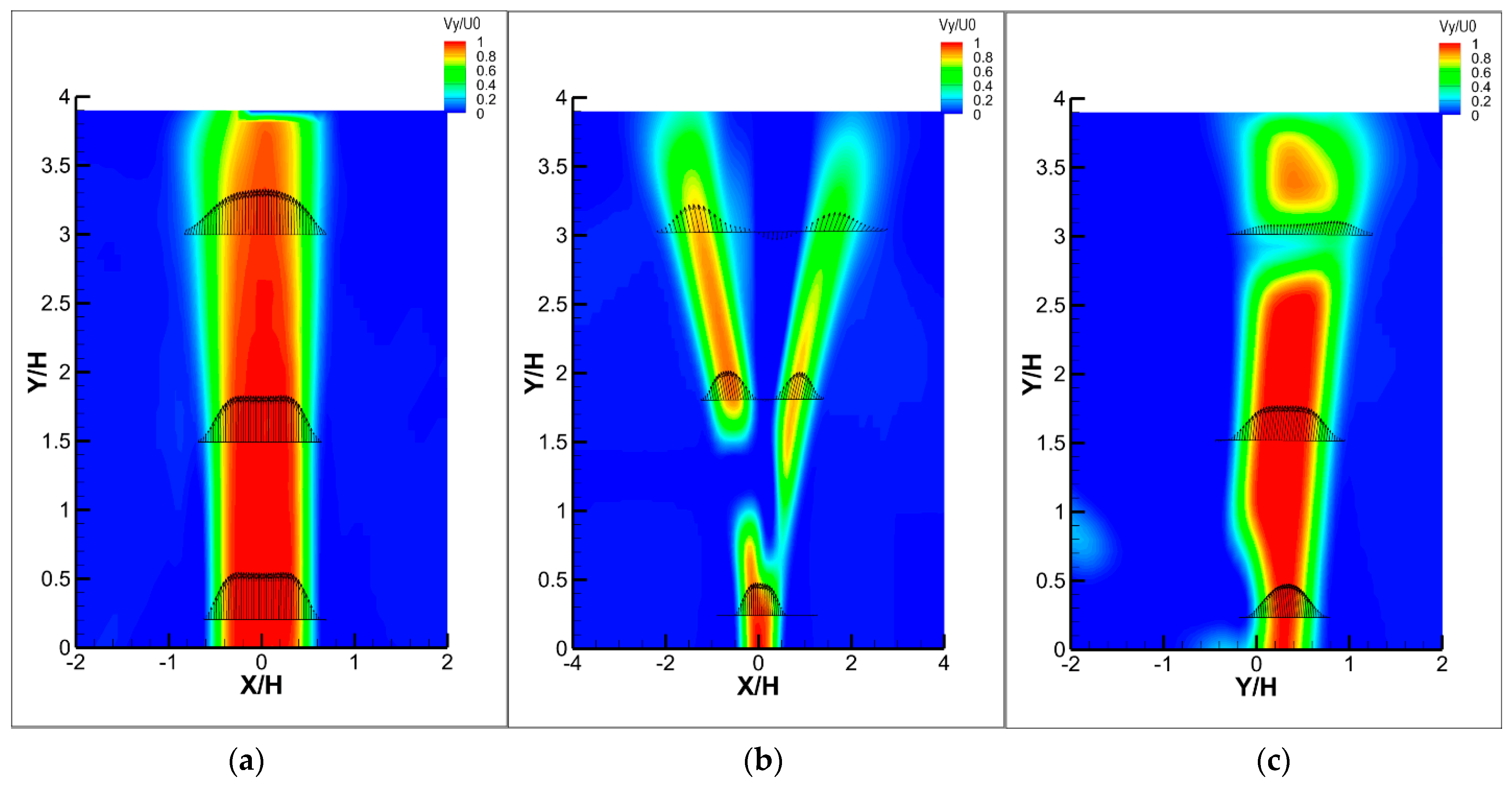
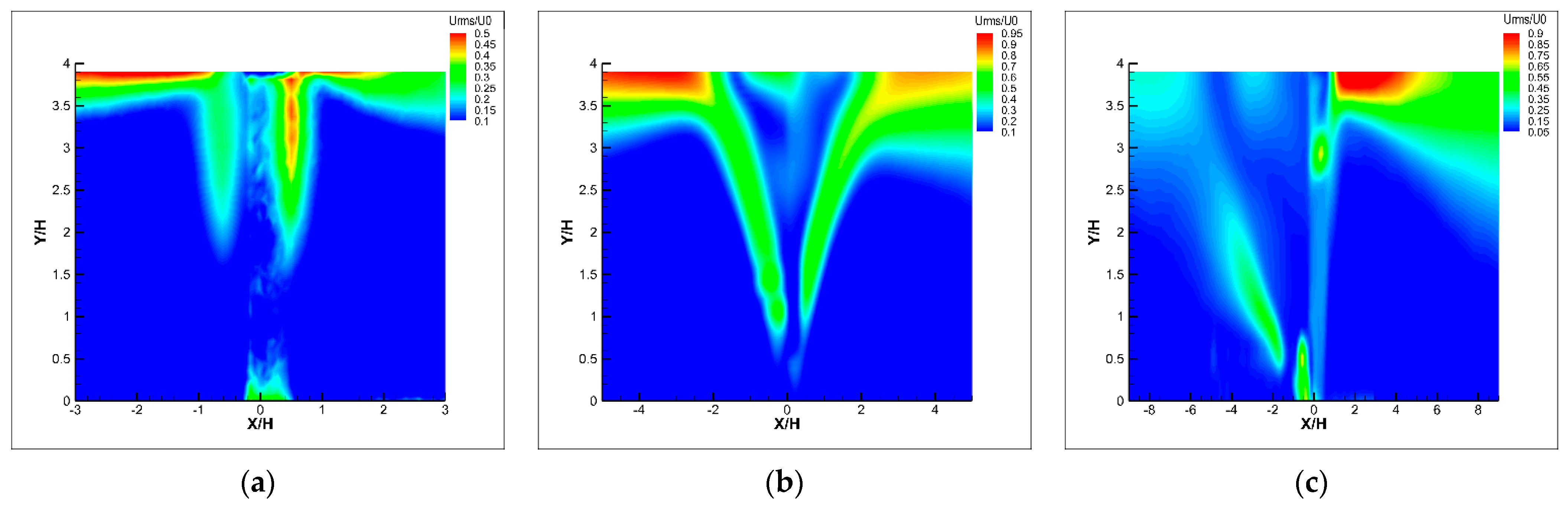
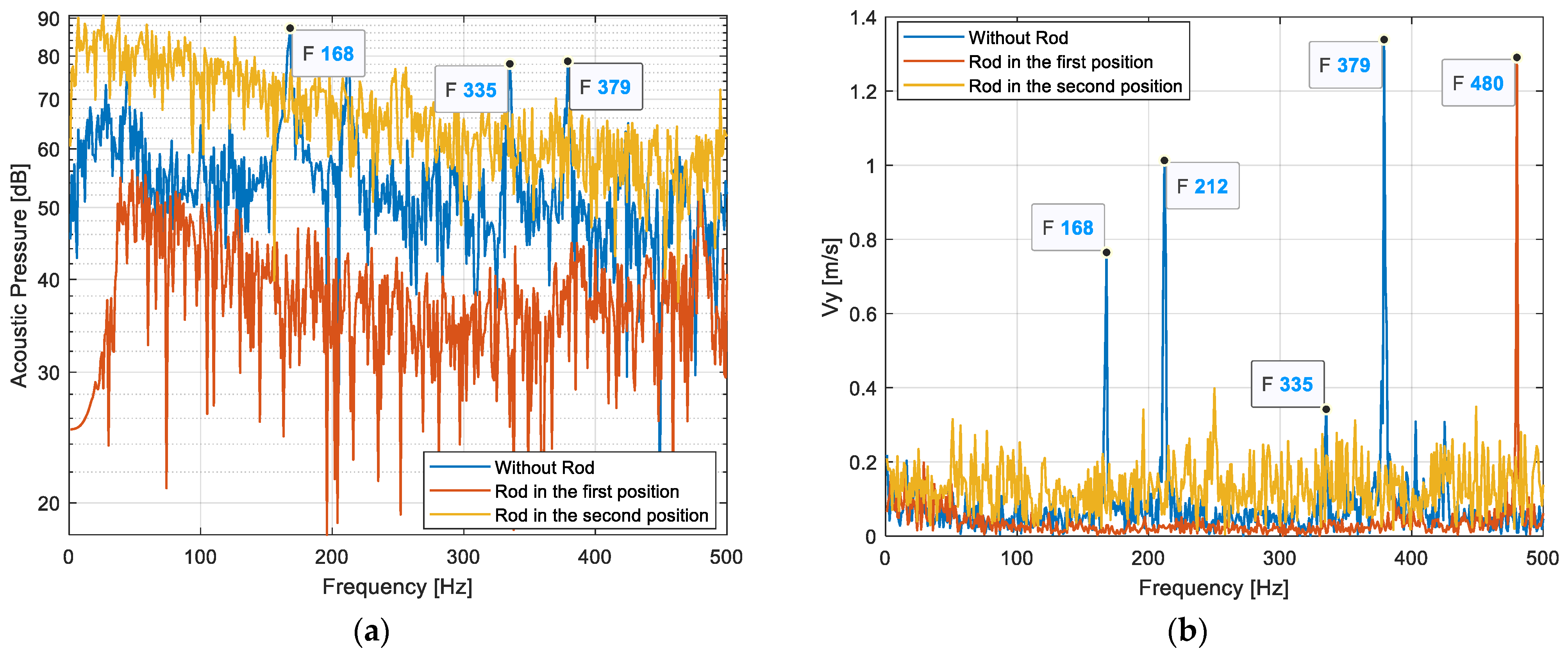
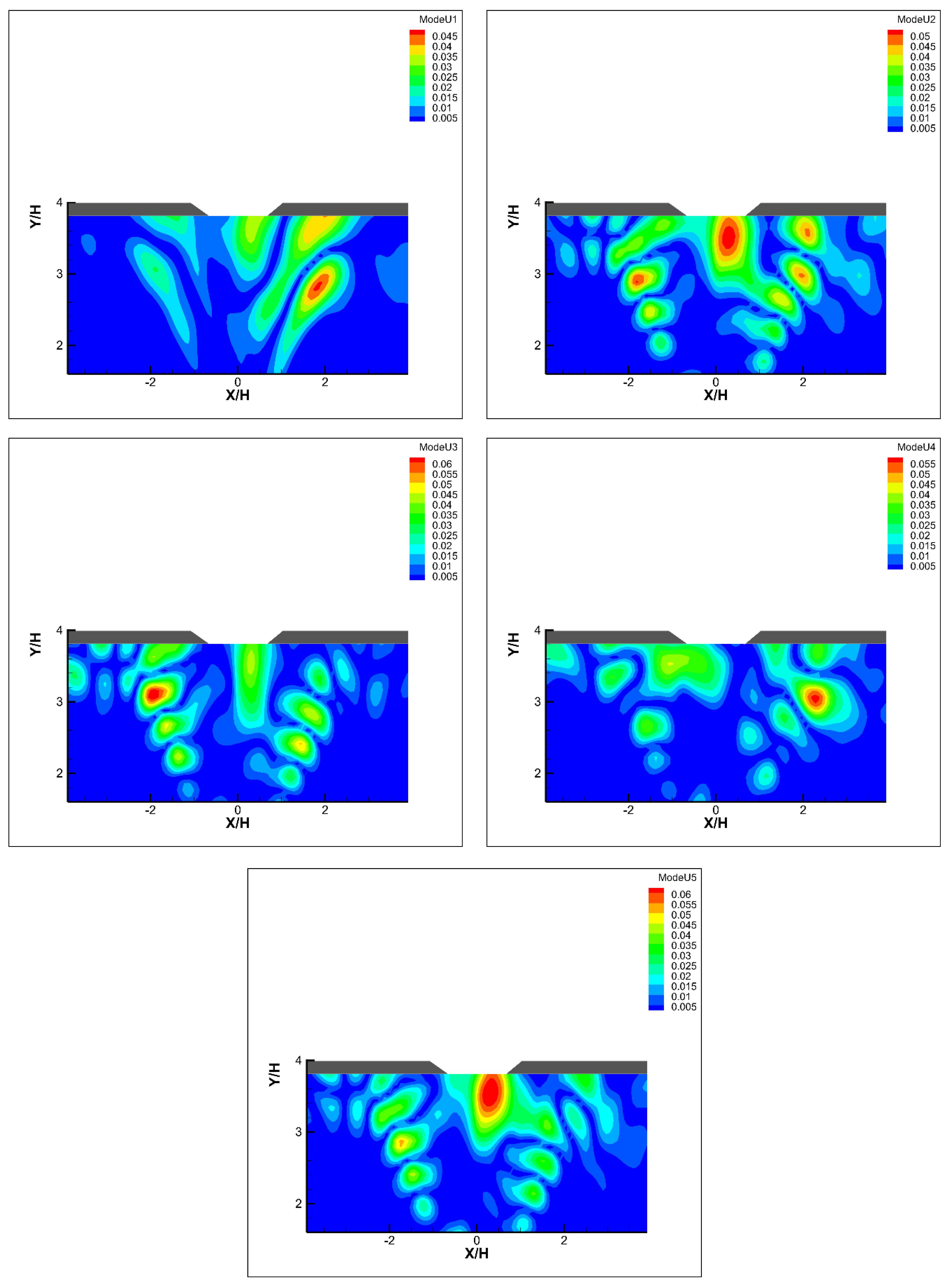
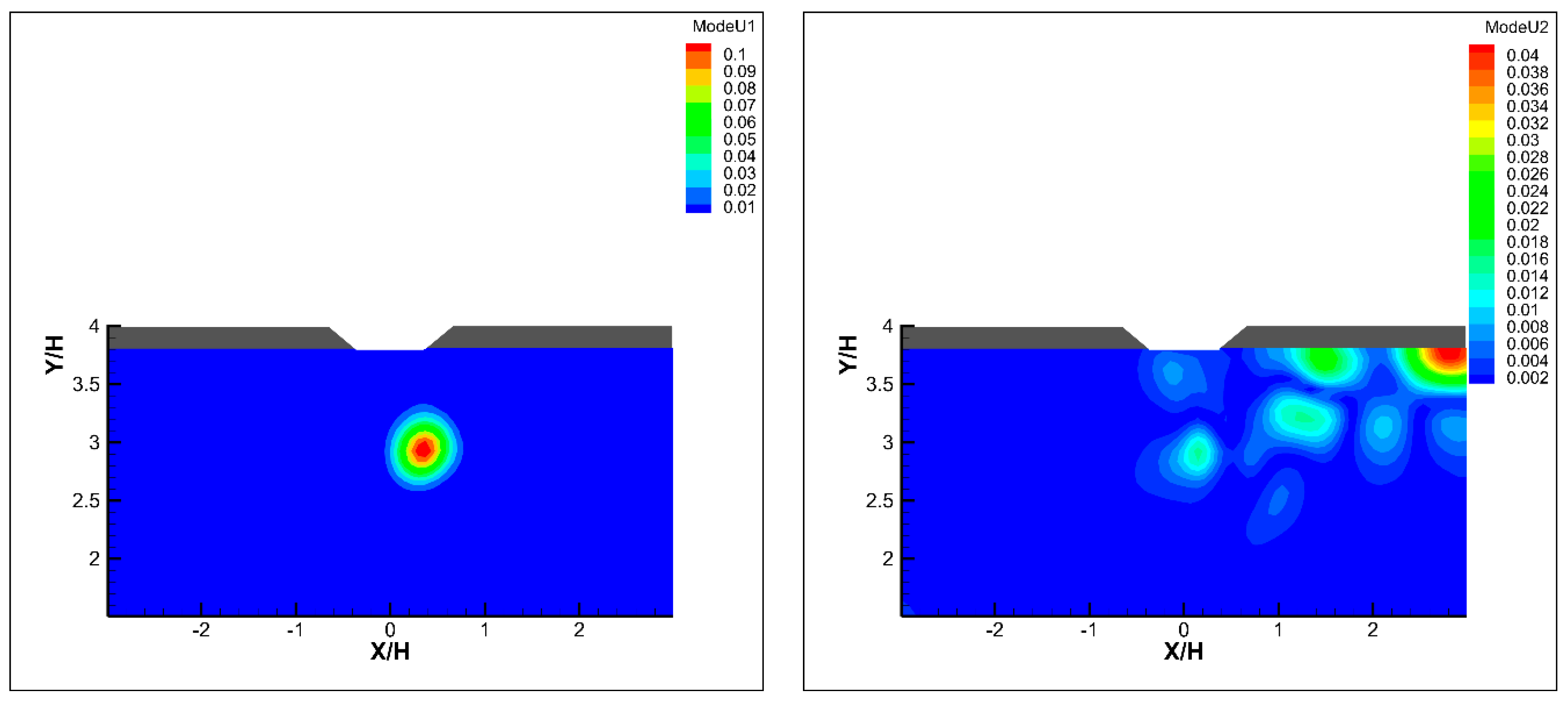
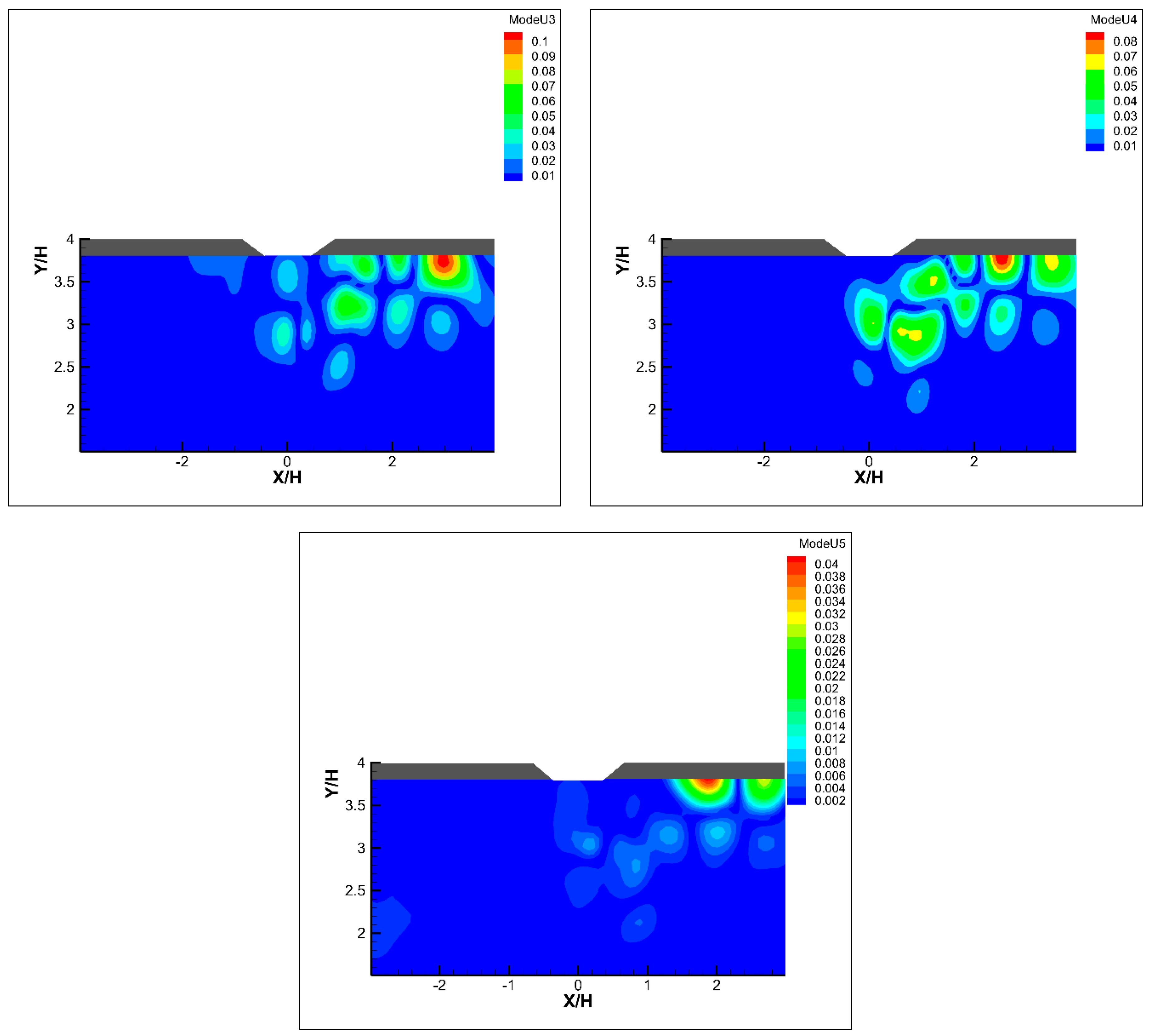
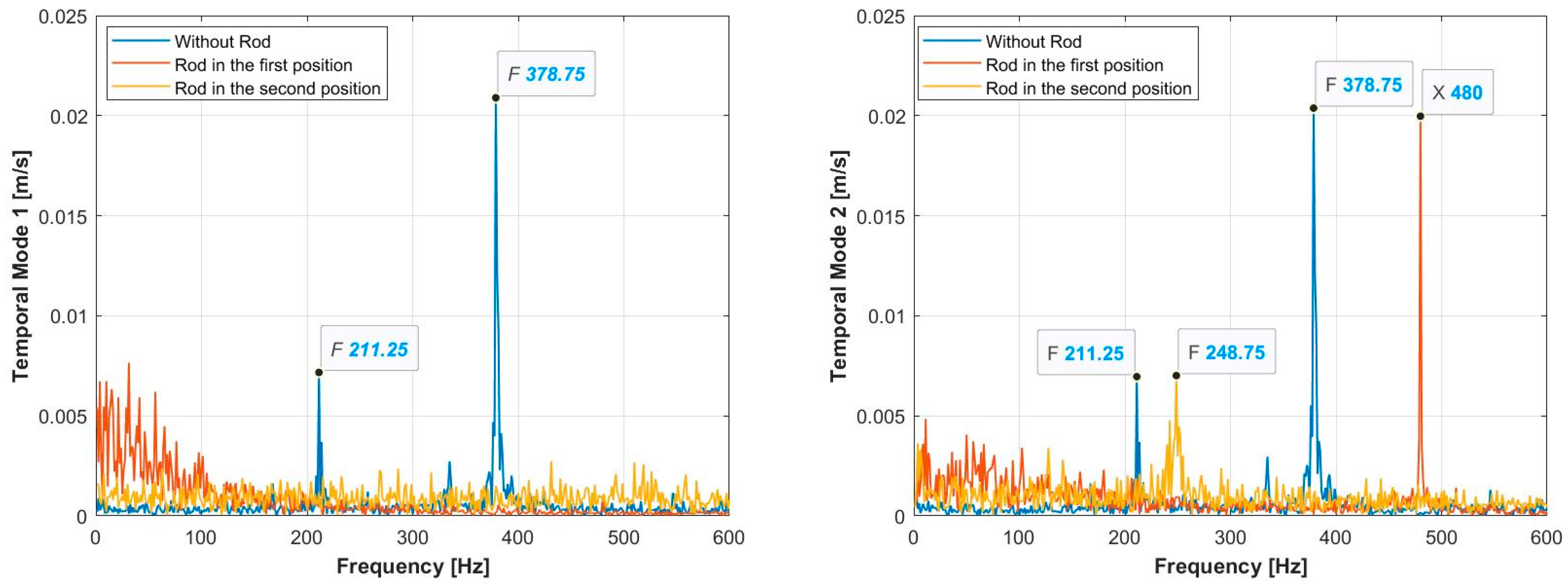
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vejrazka, J. Experimental Study of a Pulsating Round Impinging Jet. Ph.D. Thesis, INPG, Grenoble, France, 2002. Available online: https://www.theses.fr/2002INPG0160 (accessed on 12 July 2023).
- Sondhauss, C. Ueber die beim Ausströmen der Luft entstehenden Töne. Ann. Phys. Chem. 1854, 167, 126–147. [Google Scholar] [CrossRef]
- Rayleigh, J.W. Strutt, Baron. The Theory of Sound, Volume 2. 1986. Available online: http://archive.org/details/in.ernet.dli.2015.22520 (accessed on 28 February 2020).
- Powell, A. Theory of Vortex Sound. J. Acoust. Soc. Am. 1964, 36, 177–195. [Google Scholar] [CrossRef]
- Powell, A. The sound-producing oscillations of round underexpanded jets impinging on normal plates. J. Acoust. Soc. Am. 1988, 83, 515–533. [Google Scholar] [CrossRef]
- Powell, A. On Edge Tones and Associated Phenomena. Available online: https://www.ingentaconnect.com/search/article?option2=author&value2=Powell%2c+Alan&pageSize=10&index=7 (accessed on 28 February 2020).
- Ho, C.-M.; Nosseir, N.S. Large coherent structures in an impinging turbulent jet. In Proceedings of the 2nd Symposium on Turbulent Shear Flows, London, UK, 2–4 July 1979; pp. 7.26–7.31. Available online: http://adsabs.harvard.edu/abs/1979stsf.procR...7H (accessed on 4 April 2017).
- Powell, A. On the Edgetone. J. Acoust. Soc. Am. 1961, 33, 395–409. [Google Scholar] [CrossRef]
- Lighthill, M.J. On Sound Generated Aerodynamically I. General theory. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically II. Turbulence as a source of sound. Proc. R. Soc. Lond. A 1954, 222, 1–32. [Google Scholar] [CrossRef]
- Lighthill, M.J. Jet Noise. AIAA J. 1963, 1, 1507–1517. [Google Scholar] [CrossRef]
- Chanaud, R.C.; Powell, A. Some Experiments concerning the Hole and Ring Tone. J. Acoust. Soc. Am. 1965, 37, 902–911. [Google Scholar] [CrossRef]
- Rockwell, D.; Naudascher, E. Self-Sustained Oscillations of Impinging Free Shear Layers. Annu. Rev. Fluid Mech. 1979, 11, 67–94. [Google Scholar] [CrossRef]
- Ho, C.-M.; Nosseir, N.S. Dynamics of an impinging jet. Part 1. The feedback phenomenon. J. Fluid Mech. 1981, 105, 119. [Google Scholar] [CrossRef]
- Krothapalli, A.; Rajkuperan, E.; Alvi, F.; Lourenco, L. Flow field and noise characteristics of a supersonic impinging jet. Fluid Mech. 1999, 392, 155–181. [Google Scholar] [CrossRef]
- Zhang, Y. Experimental studies of the turbulence structures of impinging reacting jets using time-resolved particle image velocimetry visualisation, hot wire anemometry and acoustic signal processing. Exp. Fluids 2000, 29, S282–S290. [Google Scholar] [CrossRef]
- Uzun, A.; Kumar, R.; Hussaini, M.Y.; Alvi, F.S. Prediction of supersonic impinging jet noise using computational aeroacoustics. In Proceedings of the INTER-NOISE, Osaka, Japan, 4–7 September 2011. [Google Scholar]
- El Hassan, M.; Assoum, H.H.; Sobolik, V.; Vétel, J.; Abed-Meraim, K.; Garon, A.; Sakout, A. Experimental investigation of the wall shear stress and the vortex dynamics in a circular impinging jet. Exp. Fluids 2012, 52, 1475–1489. [Google Scholar] [CrossRef]
- Assoum, H.H.; Hamdi, J.; Abed-Meraïm, K.; El Hassan, M.; Hammoud, A.; Sakout, A. Experimental investigation the turbulent kinetic energy and the acoustic field in a rectangular jet impinging a slotted plate. Energy Procedia 2017, 139, 398–403. [Google Scholar] [CrossRef]
- Assoum, H.H.; El Hassan, M.; Hamdi, J.; Alkheir, M.; Meraim, K.A.; Sakout, A. Turbulent Kinetic Energy and self-sustaining tones in an impinging jet using High Speed 3D Tomographic-PIV. Energy Rep. 2020, 6, 802–806. [Google Scholar] [CrossRef]
- Assoum, H.H.; Hamdi, J.; El Hassan, M.; Abed-Meraim, K.; El Kheir, M.; Mrach, T.; El Asmar, S.; Sakout, A. Turbulent kinetic energy and self-sustaining tones: Experimental study of a rectangular impinging jet using high Speed 3D tomographic Particle Image Velocimetry. J. Mech. Eng. Sci. 2020, 14, 6322–6333. [Google Scholar] [CrossRef]
- Assoum, H.H.; Hamdi, J.; Alkheir, M.; Abed Meraim, K.; Sakout, A.; Obeid, B.; El Hassan, M. Tomographic Particle Image Velocimetry and Dynamic Mode Decomposition (DMD) in a Rectangular Impinging Jet: Vortex Dynamics and Acoustic Generation. Fluids 2021, 6, 429. [Google Scholar] [CrossRef]
- Assoum, H.H.; Hamdi, J.; Abed-Meraïm, K.; El Hassan, M.; Ali, M.; Sakout, A. Correlation between the acoustic field and the transverse velocity in a plane impinging jet in the presence of self-sustaining tones. Energy Procedia 2017, 139, 391–397. [Google Scholar] [CrossRef]
- Assoum, H.H.; Hamdi, J.; Abed-Meraïm, K.; Al Kheir, M.; Mrach, T.; El Soufi, L.; Sakout, A. Spatio-Temporal Changes in the Turbulent Kinetic Energy of a Rectangular Jet Impinging on a Slotted Plate Analyzed with High Speed 3D Tomographic-Particle Image Velocimetry Spatio-Temporal Changes in the Turbulent Kinetic Energy of a Rectangular Jet. Int. J. Heat Technol. 2019, 37, 1071–1079. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Lucas, N.; Doty, M.; Taubert, L.; Wygnanski, I. Reducing the noise emanating from a twin jet nozzle using flexible filaments. Exp. Fluids 2013, 54, 1504. [Google Scholar] [CrossRef]
- Geyer, T.F. Experimental evaluation of cylinder vortex shedding noise reduction using porous material. Exp. Fluids 2020, 61, 153. [Google Scholar] [CrossRef]
- Alvi, F.S.; Shih, C.; Elavarasan, R.; Garg, G.; Krothapalli, A. Control of Supersonic Impinging Jet Flows Using Supersonic Microjets. AIAA J. 2003, 41, 1347–1355. [Google Scholar] [CrossRef]
- Choi, J.J.; Annaswamy, A.M.; Lou, H.; Alvi, F.S. Active control of supersonic impingement tones using steady and pulsed microjets. Exp. Fluids 2006, 41, 841–855. [Google Scholar] [CrossRef]
- Kopiev, V.F.; Bityurin, V.A.; Belyaev, I.V.; Godin, S.M.; Zaitsev, M.Y.; Klimov, A.I.; Kopiev, V.A.; Moralev, I.A.; Ostrikov, N.N. Jet noise control using the dielectric barrier discharge plasma actuators. Acoust. Phys. 2012, 58, 434–441. [Google Scholar] [CrossRef]
- Gomez Carrasco, F.J. Matrix-Free Time-Stepping Methods for the Solution of TriGlobal Instability Problems. Ph.D. Thesis, School of Aeronautics, Universidad Politécnica de Madrid, Madrid, Spain, 2013. [Google Scholar]
- Dipankar, A.; Sengupta, T.K.; Talla, S.B. Suppression of vortex shedding behind a circular cylinder by another control cylinder at low Reynolds numbers. J. Fluid Mech. 2007, 573, 171–190. [Google Scholar] [CrossRef]
- Strykowski, P.J.; Sreenivasan, K.R. On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 1990, 218, 71. [Google Scholar] [CrossRef]
- Favier, J.; Dauptain, A.; Basso, D.; Bottaro, A. Passive separation control using a self-adaptive hairy coating. J. Fluid Mech. 2009, 627, 451–483. [Google Scholar] [CrossRef]
- Hœpffner, J.; Bottaro, A.; Favier, J. Mechanisms of non-modal energy amplification in channel flow between compliant walls. J. Fluid Mech. 2010, 642, 489–507. [Google Scholar] [CrossRef]
- Skillen, A.; Revell, A.; Pinelli, A.; Piomelli, U.; Favier, J. Flow over a Wing with Leading-Edge Undulations. AIAA J. 2015, 53, 464–472. [Google Scholar] [CrossRef]
- BenChiekh, M.; Bera, J.-C.; Michard, M.; Sunyach, M. Contrôle par jet pulsé de l’écoulement dans un divergent court à grand angle. Comptes Rendus Académie Sci. Ser. II B Mech. 2000, 328, 749–756. [Google Scholar] [CrossRef]
- Lecordier, J.C.; Hamma, L.; Paranthoen, P. The control of vortex shedding behind heated circular cylinders at low Reynolds numbers. Exp. Fluids 1991, 10, 224–229. [Google Scholar] [CrossRef]
- Wan, H.; Patnaik, S.S. Suppression of vortex-induced vibration of a circular cylinder using thermal effects. Phys. Fluids 2016, 28, 123603. [Google Scholar] [CrossRef]
- Korkischko, I.; Meneghini, J.R. Suppression of vortex-induced vibration using moving surface boundary-layer control. J. Fluids Struct. 2012, 34, 259–270. [Google Scholar] [CrossRef]
- Patino, G.A.; Gioria, R.S.; Meneghini, J.R. Evaluating the control of a cylinder wake by the method of sensitivity analysis. Phys. Fluids 2017, 29, 044103. [Google Scholar] [CrossRef]
- Chapin, V.G.; Boulanger, N.; Chassaing, P. Improvement of the jet-vectoring through the suppression of a global instability. In Proceedings of the IUTAM Symposium on Flow Control and MEMS, London, UK, 19–22 September 2026; Morrison, J.F., Birch, D.M., Lavoie, P., Eds.; Springer: Dordrecht, The Netherlands, 2008; Volume 7, pp. 393–396. [Google Scholar] [CrossRef]
- Gioria, R.S.; Jabardo, P.J.S.; Carmo, B.S.; Meneghini, J.R. Floquet stability analysis of the flow around an oscillating cylinder. J. Fluids Struct. 2009, 25, 676–686. [Google Scholar] [CrossRef]
- Blackburn, H.M.; Sheard, G.J. On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 2010, 22, 031701. [Google Scholar] [CrossRef]
- Hill, C. A theoretical approach for analyzing the restabilization of wakes. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; American Institute of Aeronautics and Astronautics: Reno, NV, USA, 1992; Volume 92. [Google Scholar]
- Marquet, O.; Sipp, D.; Jacquin, L. Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 2008, 615, 221–252. [Google Scholar] [CrossRef]
- Pralits, J.O.; Brandt, L.; Giannetti, F. Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 2010, 650, 513–536. [Google Scholar] [CrossRef]
- Assoum, H. Étude Expérimentale des Couplages Entre La Dynamique d’un Jet Qui Heurte Une Plaque Fendue et L’émission Sonore Générée. Ph.D. Thesis, Université de La Rochelle, La Rochelle, France, 2013. [Google Scholar]
- Arroyo, M.P.; Greated, C.A. Stereoscopic particle image velocimetry. Meas. Sci. Technol. 1991, 2, 1181. [Google Scholar] [CrossRef]
- Calluaud, D.; David, L. Stereoscopic particle image velocimetry measurements of the flow around a surface-mounted block. Exp. Fluids 2004, 36, 53–61. [Google Scholar] [CrossRef]
- Watanabe, R.; Gono, T.; Yamagata, T.; Fujisawa, N. Three-dimensional flow structure in highly buoyant jet by scanning stereo PIV combined with POD analysis. Int. J. Heat Fluid Flow 2015, 52, 98–110. [Google Scholar] [CrossRef]
- Wieneke, B. Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 2008, 45, 549–556. [Google Scholar] [CrossRef]
- Kähler, C.J.; Kompenhans, J. Fundamentals of multiple plane stereo particle image velocimetry. Exp. Fluids 2000, 29, S070–S077. [Google Scholar] [CrossRef]
- Alkheir, M.; Assoum, H.H.; Afyouni, N.E.; Abed Meraim, K.; Sakout, A.; El Hassan, M. Combined Stereoscopic Particle Image Velocimetry Measurements in a Single Plane for an Impinging Jet around a Thin Control Rod. Fluids 2021, 6, 430. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.; Scarano, F.; Christian, K.; Wereley, S.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide (PDF Download Available), SpringerLink. Available online: https://link.springer.com/book/10.1007/978-3-319-68852-7 (accessed on 3 April 2018).
- Chen, Q.; Zhong, Q.; Qi, M.; Wang, X. Comparison of vortex identification criteria for planar velocity fields in wall turbulence. Phys. Fluids 2015, 27, 085101. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Miron, P.; Vétel, J.; Garon, A.; Delfour, M.; Hassan, M.E. Anisotropic mesh adaptation on Lagrangian Coherent Structures. J. Comput. Phys. 2012, 231, 6419–6437. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Humley, J.L. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Ann. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Chatterjee, A. An Intronduction to the Propper Orthogonal Decomposition. Curr. Sci. 2000, 10, 808–817. [Google Scholar]
- Pedersen, J.; Meyer, K. POD analysis of flow structures in a scale model of a ventilated room. Exp. Fluids 2002, 33, 940–949. [Google Scholar] [CrossRef]
- Kostas, J.; Soria, J.; Chong, M.S. A comparison between snapshot POD analysis of PIV velocity and vorticity data. Exp. Fluids 2005, 38, 146–160. [Google Scholar] [CrossRef]
- Hammad, K.J.; Milanovic, I.M. A POD study of an impinging jet flowfield. In Proceedings of the Fluids Engineering Division Summer Meeting, Vail, CO, USA, 2 August 2009; Volume 1: Symposia, Parts A, B and C; ASMEDC: Vail, CO, USA, 2009; pp. 1477–1485. [Google Scholar] [CrossRef]
- Podvin, B.; Sergent, A. Proper orthogonal decomposition investigation of turbulent Rayleigh-Bénard convection in a rectangular cavity. Phys. Fluids 2012, 24, 105106. [Google Scholar] [CrossRef]
- Graftieaux, L.; Michard, M.; Grosjean, N. Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 2001, 12, 1422. [Google Scholar] [CrossRef]
- Vernet, R.; Thomas, L.; David, L. Analysis and reconstruction of a pulsed jet in crossflow by multi-plane snapshot POD. Exp. Fluids 2009, 47, 707. [Google Scholar] [CrossRef]
- Bernero, S.; Fiedler, H.E. Application of particle image velocimetry and proper orthogonal decomposition to the study of a jet in a counterflow. Exp. Fluids 2000, 29, S274–S281. [Google Scholar] [CrossRef]
- Delville, J. Characterization of the organization in shear layers via the Proper Orthogonal Decomposition. Appl. Sci. Res. 1994, 53, 263–281. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Wang, S. The identification of coherent structures using proper orthogonal decomposition and dynamic mode decomposition. J. Fluids Struct. 2014, 49, 53–72. [Google Scholar] [CrossRef]
- Druault, P.; Guibert, P.; Alizon, F. Use of proper orthogonal decomposition for time interpolation from PIV data. Exp. Fluids 2005, 39, 1009–1023. [Google Scholar] [CrossRef]
- Hamdi, J.; Assoum, H.H.; Alkheir, M.; Abed-Meraïm, K.; Cauet, S.; Sakout, A. Analysis of the 3D flow of an impinging jet on a slotted plate using TR-Tomo PIV and Proper Orthogonal Decomposition. Energy Rep. 2020, 6, 158–163. [Google Scholar] [CrossRef]
- Hamdi, J.; Assoum, H.; Abed-Meraïm, K.; Sakout, A. Analysis of the effect of the 3C kinematic field of a confined impinging jet on a slotted plate by stereoscopic PIV. Eur. J. Mech. B Fluids 2019, 76, 243–258. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afyouni, N.E.; Alkheir, M.; Assoum, H.; El Zohbi, B.; Abed-Meraim, K.; Sakout, A.; El Hassan, M. Effect of a Control Mechanism on the Interaction between a Rectangular Jet and a Slotted Plate: Experimental Study of the Aeroacoustic Field. Fluids 2023, 8, 309. https://doi.org/10.3390/fluids8120309
Afyouni NE, Alkheir M, Assoum H, El Zohbi B, Abed-Meraim K, Sakout A, El Hassan M. Effect of a Control Mechanism on the Interaction between a Rectangular Jet and a Slotted Plate: Experimental Study of the Aeroacoustic Field. Fluids. 2023; 8(12):309. https://doi.org/10.3390/fluids8120309
Chicago/Turabian StyleAfyouni, Nour Eldin, Marwan Alkheir, Hassan Assoum, Bilal El Zohbi, Kamel Abed-Meraim, Anas Sakout, and Mouhammad El Hassan. 2023. "Effect of a Control Mechanism on the Interaction between a Rectangular Jet and a Slotted Plate: Experimental Study of the Aeroacoustic Field" Fluids 8, no. 12: 309. https://doi.org/10.3390/fluids8120309
APA StyleAfyouni, N. E., Alkheir, M., Assoum, H., El Zohbi, B., Abed-Meraim, K., Sakout, A., & El Hassan, M. (2023). Effect of a Control Mechanism on the Interaction between a Rectangular Jet and a Slotted Plate: Experimental Study of the Aeroacoustic Field. Fluids, 8(12), 309. https://doi.org/10.3390/fluids8120309





