A Computational Fluid Dynamics Study to Compare Two Types of Arterial Cannulae for Cardiopulmonary Bypass
Abstract
:1. Introduction
2. Materials and Methods
2.1. Anatomical Model
2.2. Mathematical Model, Boundary Conditions, and Simulation Details
- (a)
- Case I: Straight Tip Arterial Cannula;
- (b)
- Case II: Angled Tip Arterial Cannula.
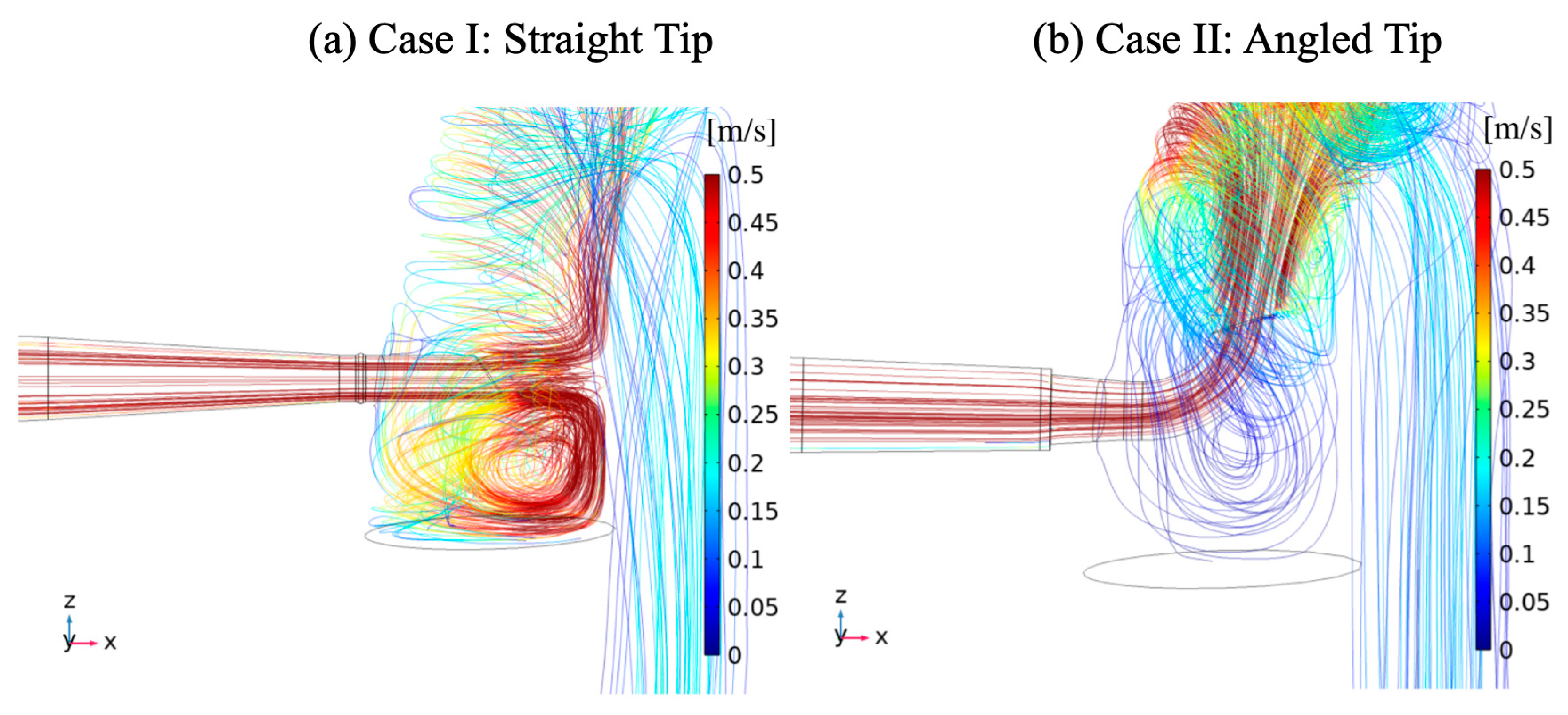
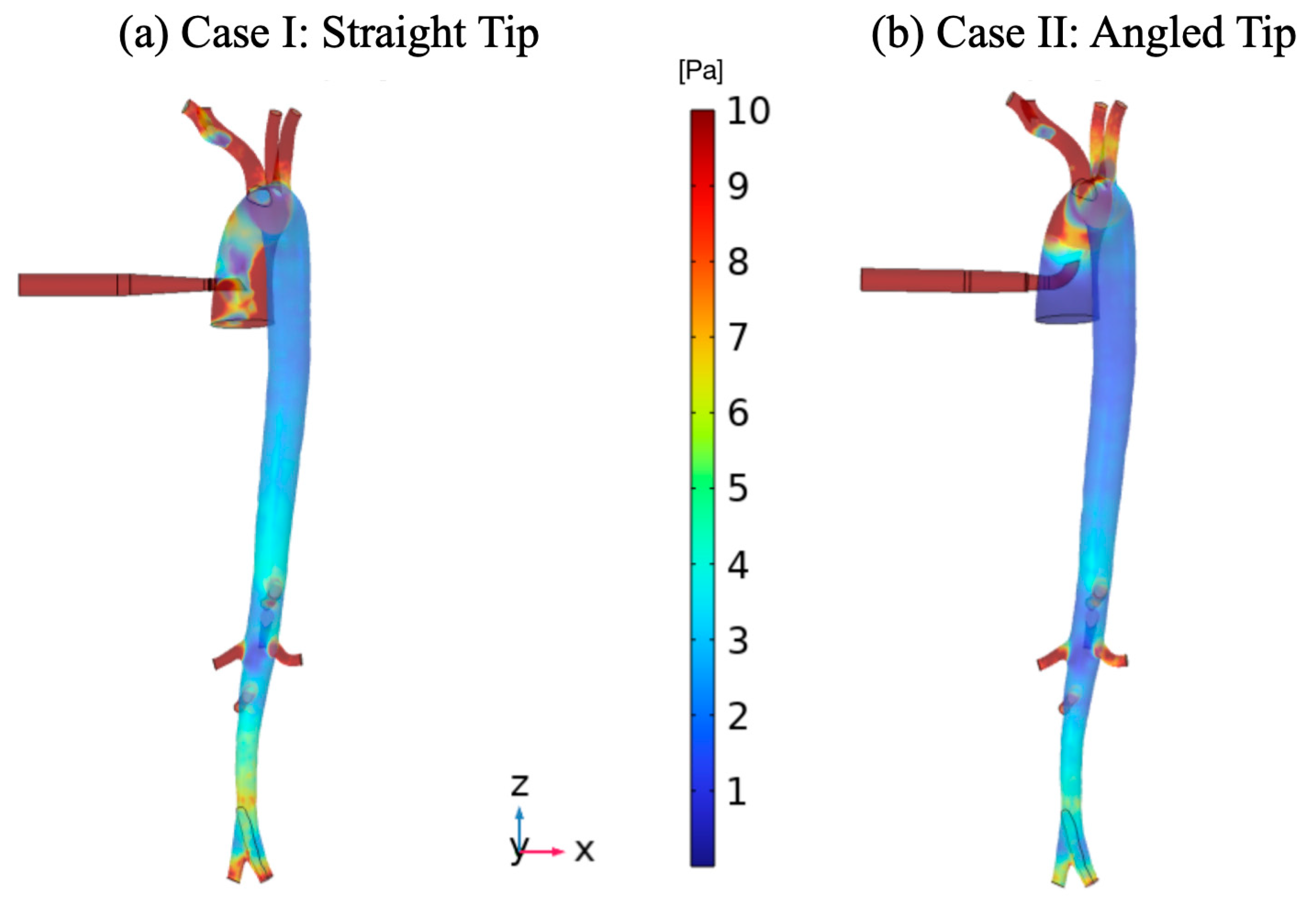
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, K.; Alshehry, A.S.; Aljahdaly, N.H.; Shah, R.; Shah, N.A.; Ali, M.R. Efficient computational approaches for fractional-order Degasperis-Procesi and Camassa–Holm equations. Results Phys. 2023, 50, 106549. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Probing Families of Optical Soliton Solutions in Fractional Perturbed Radhakrishnan–Kundu–Lakshmanan Model with Improved Versions of Extended Direct Algebraic Method. Fractal Fract. 2023, 7, 512. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Investigating Families of Soliton Solutions for the Complex Structured Coupled Fractional Biswas–Arshed Model in Birefringent Fibers Using a Novel Analytical Technique. Fractal Fract. 2023, 7, 491. [Google Scholar] [CrossRef]
- Schwarz, E.L.; Pegolotti, L.; Pfaller, M.R.; Marsden, A.L. Beyond CFD: Emerging methodologies for predictive simulation in cardiovascular health and disease. Biophys. Rev. 2023, 4, 011301. [Google Scholar] [CrossRef]
- Basri, E.I.; Basri, A.A.; Riazuddin, V.N.; Shahwir, S.F.; Zuber, M.; Ahmad, K.A. Computational fluid dynamics study in biomedical applications: A review. Int. J. Fluids Heat Transf. 2016, 1, 2–14. [Google Scholar]
- Kumar, N.; Ganesha, A.; Girish, H.; Kumar, S.; Shenoy, B.G. Advances in the application of computational fluid dynamics in cardiovascular flow. Cogent Eng. 2023, 10, 2178367. [Google Scholar] [CrossRef]
- Costache, V.S.; Yeung, K.K.; Solomon, C.; Popa, R.; Melnic, T.; Sandu, M.; Bucurenciu, C.; Candea, G.; Santa, A.; Costache, A. Aortic Remodeling After Total Endovascular Aortic Repair With Multilayer Stents: Computational Fluid Dynamics Analysis of Aortic Remodeling Over 3 Years of Follow-up. J. Endovasc. Ther. 2018, 25, 760–764. [Google Scholar] [CrossRef]
- Candreva, A.; Nisco, G.D.; Rizzini, M.L.; D’Ascenzo, F.; Ferrari, G.M.D.; Gallo, D.; Morbiducci, U.; Chiastra, C. Current and Future Applications of Computational Fluid Dynamics in Coronary Artery Disease. RCM 2022, 23, 377. [Google Scholar] [CrossRef]
- Andelovic, K.; Winter, P.; Jakob, P.M.; Bauer, W.R.; Herold, V.; Zernecke, A. Evaluation of plaque characteristics and inflammation using magnetic resonance imaging. Biomedicines 2021, 9, 185. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, J.; Li, M. Non-invasive assessment of intracranial wall shear stress using high-resolution magnetic resonance imaging in combination with computational fluid dynamics technique. Fundam. Res. 2021, 2, 329–334. [Google Scholar] [CrossRef]
- Le, T.; Borazjani, I.; Sotiropoulos, F. A Computational Fluid Dynamic (CFD) Tool for Optimization and Guided Implantation of Biomedical Devices. J. Med. Devices 2009, 3, 27553. [Google Scholar] [CrossRef]
- Sotiropoulos, F. Computational Fluid Dynamics for Medical Device Design and Evaluation: Are We There Yet? Cardiovasc. Eng. Technol. 2012, 3, 137–138. [Google Scholar] [CrossRef]
- Han, D.; Leibowitz, J.L.; Han, L.; Wang, S.; He, G.; Griffith, B.P.; Wu, Z.J. Computational fluid dynamics analysis and experimental hemolytic performance of three clinical centrifugal blood pumps: Revolution, Rotaflow and CentriMag. Med. Nov. Technol. Devices 2022, 15, 100153. [Google Scholar] [CrossRef] [PubMed]
- Gramigna, V.; Caruso, M.V.; Rossi, M.; Serraino, G.F.; Renzulli, A.; Fragomeni, G. A numerical analysis of the aortic blood flow pattern during pulsed cardiopulmonary bypass. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1574–1581. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Qin, H.; Guan, Z.; Mu, Q.; Xia, Q.; Wang, M.; Huang, W.H.; Gu, K. Computational numerical analysis of different cannulation methods during cardiopulmonary bypass of type A aortic dissection model based on computational fluid dynamics. Ann. Transl. Med. 2021, 9, 667. [Google Scholar] [CrossRef]
- Hugenroth, K.; Borchardt, R.; Ritter, P.; Groß-Hardt, S.; Meyns, B.; Verbelen, T.; Steinseifer, U.; Kaufmann, T.A.S.; Engelmann, U.M. Optimizing cerebral perfusion and hemodynamics during cardiopulmonary bypass through cannula design combining in silico, in vitro and in vivo input. Sci. Rep. 2021, 11, 16800. [Google Scholar] [CrossRef]
- Caruso, M.V.; Gramigna, V.; Serraino, G.F.; Renzulli, A.; Fragomeni, G. Influence of Aortic Outflow Cannula Orientation on Epiaortic Flow Pattern During Pulsed Cardiopulmonary Bypass. J. Med. Biol. Eng. 2015, 35, 455–463. [Google Scholar] [CrossRef]
- Malvindi, P.G.; Pasta, S.; Raffa, G.M.; Livesey, S. Computational fluid dynamics of the ascending aorta before the onset of type A aortic dissection. Eur. J. Cardiothorac. Surg. 2017, 51, 597–599. [Google Scholar] [CrossRef]
- Xu, H.; Piccinelli, M.; Leshnower, B.G.; Lefieux, A.; Taylor, W.R.; Veneziani, A. Coupled Morphological-Hemodynamic Computational Analysis of Type B Aortic Dissection: A Longitudinal Study. Ann. Biomed. Eng. 2018, 46, 927–939. [Google Scholar] [CrossRef]
- Blauth, C.I.; Cosgrove, D.M.; Webb, B.W.; Ratliff, N.B.; Boylan, M.; Piedmonte, M.R.; Lytle, B.W.; Loop, F.D. Atheroembolism from the ascending aorta. An emerging problem in cardiac surgery. J. Thorac. Cardiovasc. Surg. 1992, 103, 1104–1112. [Google Scholar] [CrossRef]
- Rossi, M.; Caruso, M.V.; Fragomeni, G.; Serraino, G.F.; Renzulli, A. Comparative study of different left ventricular assist device outflow graft placement on patient haemodynamics. Interact. Cardio Vasc. Thorac. Surg. 2013, 17 (Suppl. S2), S83. [Google Scholar] [CrossRef]
- Formaggia, L.; Perktold, K.; Quarteroni, A. Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System; Springer: Milan, Italy, 2009; Volume 1. [Google Scholar]
- Moon, J.H.; Kim, D.Y.; Lee, S.H. Spreading and receding characteristics of a non-Newtonian droplet impinging on a heated surface. Exp. Therm. Fluid Sci. 2014, 57, 94–101. [Google Scholar] [CrossRef]
- Johnston, B.M.; Johnston, P.R.; Corney, S.; Kilpatrick, D. Non-Newtonian blood flow in human right coronary arteries: Transient simulations. J. Biomech. 2006, 39, 1116–1128. [Google Scholar] [CrossRef] [PubMed]
- Hippelheuser, J.E.; Lauric, A.; Cohen, A.D.; Malek, A.M. Realistic non-Newtonian viscosity modelling highlights hemodynamic differences between intracranial aneurysms with and without surface blebs. J. Biomech. 2014, 47, 3695–3703. [Google Scholar] [CrossRef]
- Rabby, M.G.; Shupti, S.P.; Molla, M.M. Pulsatile Non-Newtonian Laminar Blood Flows through Arterial Double Stenoses. J. Fluids 2014, 2014, 757902. [Google Scholar] [CrossRef]
- Husain, I.; Labropulu, F.; Langdon, C.; Schwark, J. A comparison of Newtonian and non-Newtonian models for pulsatile blood flow simulations. J. Mech. Behav. Mater. 2013, 21, 147–153. [Google Scholar] [CrossRef]
- Comsol. COMSOL-Software for Multiphysics Simulation. Available online: https://www.comsol.com/ (accessed on 4 April 2023).
- Stalder, A.F.; Russe, M.F.; Frydrychowicz, A.; Bock, J.; Hennig, J.; Markl, M. Quantitative 2D and 3D phase contrast MRI: Optimized analysis of blood flow and vessel wall parameters. Magn. Reson. Med. 2008, 60, 1218–1231. [Google Scholar] [CrossRef]
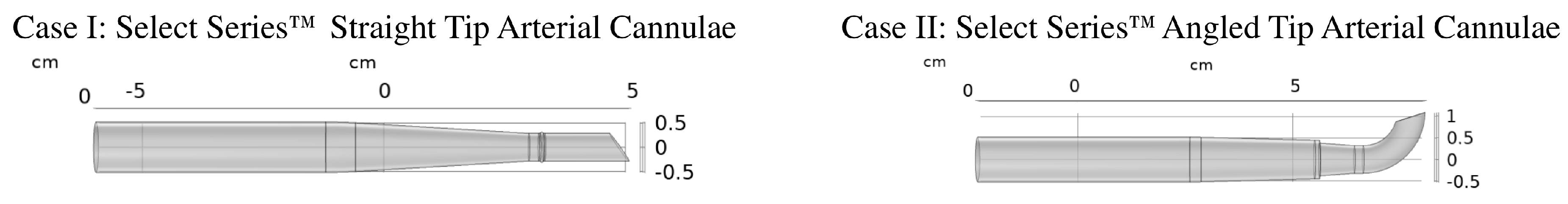


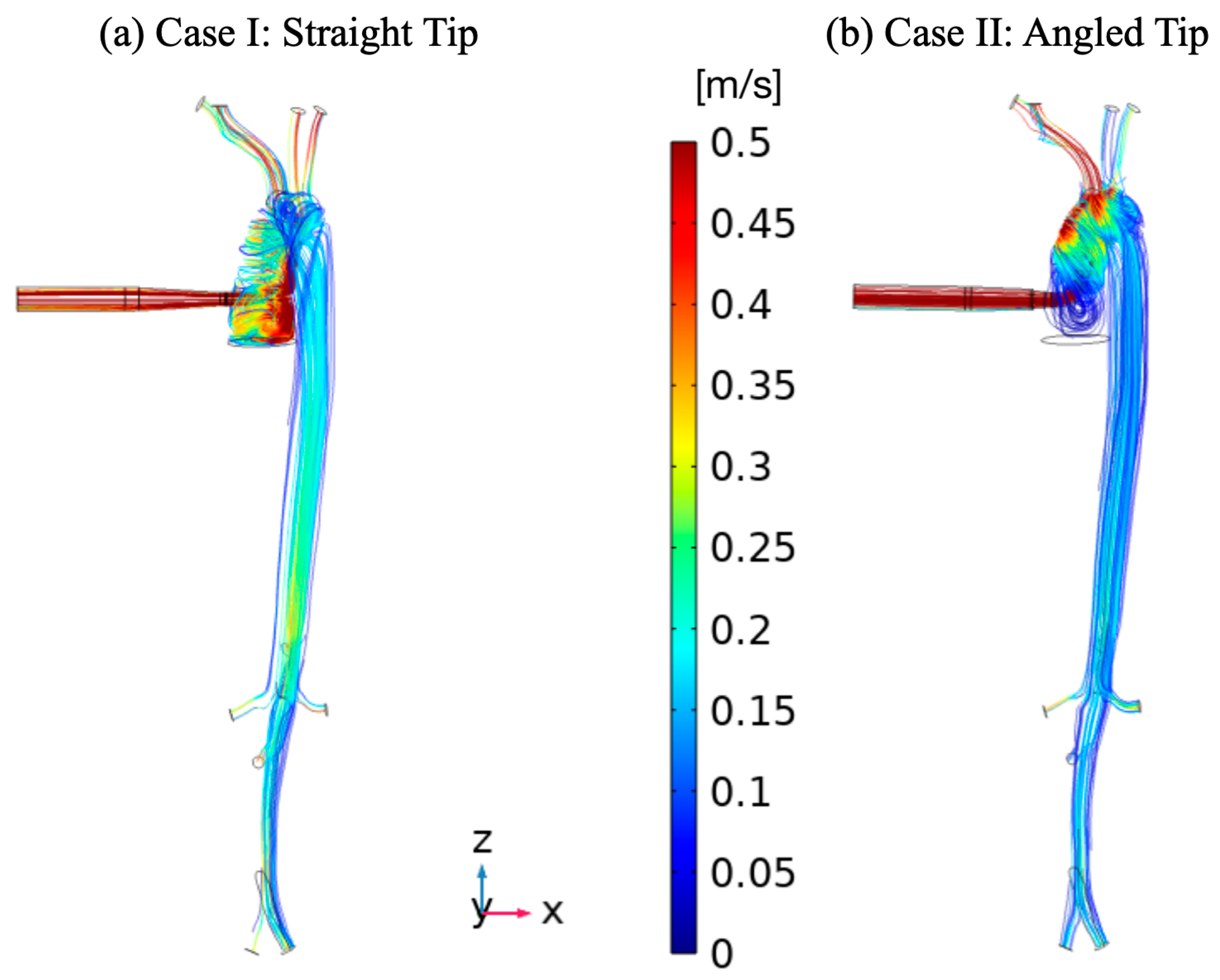
| Vessel | Case I (Straight Tip) | Case II (Angled Tip) | ||
|---|---|---|---|---|
| Mean Flow (L/min) | % Mean Flow | Mean Flow (L/min) | % Mean Flow | |
| Cannula | 5.00 | 100 | 5.00 | 100 |
| Thoracic aorta | 2.30 | 46 | 1.70 | 34 |
| Epiaortic vessels | 2.70 | 54 | 3.30 | 66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gramigna, V.; Palumbo, A.; Rossi, M.; Fragomeni, G. A Computational Fluid Dynamics Study to Compare Two Types of Arterial Cannulae for Cardiopulmonary Bypass. Fluids 2023, 8, 302. https://doi.org/10.3390/fluids8110302
Gramigna V, Palumbo A, Rossi M, Fragomeni G. A Computational Fluid Dynamics Study to Compare Two Types of Arterial Cannulae for Cardiopulmonary Bypass. Fluids. 2023; 8(11):302. https://doi.org/10.3390/fluids8110302
Chicago/Turabian StyleGramigna, Vera, Arrigo Palumbo, Michele Rossi, and Gionata Fragomeni. 2023. "A Computational Fluid Dynamics Study to Compare Two Types of Arterial Cannulae for Cardiopulmonary Bypass" Fluids 8, no. 11: 302. https://doi.org/10.3390/fluids8110302
APA StyleGramigna, V., Palumbo, A., Rossi, M., & Fragomeni, G. (2023). A Computational Fluid Dynamics Study to Compare Two Types of Arterial Cannulae for Cardiopulmonary Bypass. Fluids, 8(11), 302. https://doi.org/10.3390/fluids8110302








