Abstract
This article takes insights from a previously derived mathematical framework for the free settling velocity of particles of any shape to model analytical constructs to solve the hindered settling velocity of hard particles of any shape. Because the geometry of the physical environment and continuity can be strictly enforced in the construct model, the relative velocity of the fluid front pumped upward by the settling particles can be found, thus allowing for calculation by subtracting the front velocity from the calculated velocity.
1. Introduction
This article concerns the physical environment formed by small solid particles suspended in a Newtonian fluid, and with how the quantitative volume–mass relationships between the phase of solid particles and the fluid phase influence the settling velocity of the suspended particles. The dispersed phase settles at a rate that is reduced or hindered when the relative volume of particles is higher.
The ratio of hindered settling velocity to the settling velocity of an isolated particle can be defined as . The pursuit of this article is to find a ratio that is directly based on a single mathematical framework that captures the magnitude of both velocities.
The mathematical framework is summarized in [1] where it was evaluated to solve analytically the effect of shape on in the context of the sedimentation of a single particle in quiescent fluid, and in the context of the motion of a particle that settles in a fluid that moves horizontally as a whole. The part of the above pursuit concerned with the denominator of the ratio was assumed to have been met.
The numerator part of the ratio is fundamental in multiphase flow, but yet not well-understood. Much research has been performed over the course of many years to elucidate the intricate relationships controlling . A set of comparable work could be obtained by applying the following filters:
- Reynolds number: the maximal particle Reynolds number calculated on the spheres of naturally occurring materials is approximately 0.2. However, the maximal Reynolds number for mineral particles of a high aspect ratio (up to 15) can be as high as 2.
- When considering datasets, the concentration of solids is at least 5% for natural minerals in water.
- The examined problem is for hard particles without surface roughness.
- Where the particles influence neighboring particles, only the effect of voidage (or its inverse) is considered, and the problem is studied on the physics of a single particle. Voidage within the range of the validity of the Richarson and Zaki (RZ) equation [2], in the range from 0.5 to 0.9, is generally acceptable. This filter generally removes batch sedimentation under Kynch theory because “The settling process is then determined entirely by a continuity equation, without knowing the details of the forces on the particle” [3].
- When comparing the experimental data, the particle’s geometry was characterized with sufficient detail.
These filters were applied with a degree of flexibility here. The flexibility was mostly related to the Reynolds number, as indicated by Hinch [4]: “Note that the Reynolds number for the bulk macro-scale flow need not be small, because at the macro-scale the velocity differences and length scales are much larger than at the micro-scale around the particles”. As such, some studies involving microscale flow in fluidization and transport are permissibly comparable. For instance, the flow of a suspension through a funnel-like structure can have a large , while the magnitude of the velocity difference between the fluid phase and the particles can be very small.
The mathematical framework presented in this paper can be considered to be part of the discussions in the set that falls within the following categories:
- (A)
- Recent research: It is useful to note how active this area of research is today.
- (B)
- Analytical studies concerning the hindered settling velocity of spheres.
- (C)
- Empirical studies concerning the hindered settling velocity of spheres.
- (D)
- Analytical studies concerning the hindered settling velocity of NSPs.
- (E)
- Empirical studies concerning the hindered settling velocity of NSPs.
Some recent studies on this topic (Category A) are those by Ghatage et al. [5], who conducted Eulerian–Eulerian simulations using a dynamic mesh approach to study the impact of turbulence on the motion of a settling particle in a monodisperse solid–liquid fluidized bed. Comparing the obtained results via simulations with those of an earlier experimental study [6] revealed that this numerical model can properly predict the settling velocity for low-voidage fluidization in 2D and 3D simulations. Ardekani et al. [7] conducted direct numerical simulations to investigate the impact of vertical density gradients on the sedimentation of particles in water columns. They discovered that stratification significantly affects the settling dynamics of a particle, the interaction between a pair of particles, settling rates, and the microstructure of the suspension of particles.
George Batchelor (8 March 1920–30 March 2000) is the most influential figure in the analytical treatment of the physics controlling the settling behavior of the suspensions of fine particles (Categories B and D). His work is mostly theoretical [4] and has found application in computer simulations involving calculations on the scores of spherical particles [8,9,10]. These theoretical advances have attracted interest in the interpretation of unresolved phenomena involving the low Reynolds number of the flow around particles such as settling velocity fluctuations [11,12,13,14], particle- and bubble-induced drag reduction [15,16], and skin friction reduction [17]. For instance, Cunha et al. [12] implemented a computational scheme to calculate the average hindered settling velocity, velocity fluctuations, and particle velocity correlations. His implementation involved far-field interactions via mobility tensors, an artificial short-range force, a restoring force for collisions, the calculation of the particle’s trajectories, and appropriate boundary conditions for the velocity components to reach a general form of the velocity of the particle. Then, they validated the model using the empirical correlations of Sangani and Acrivos [18], and Richardson and Zaki [2], and the analytical solutions by Batchelor and Wen [19], and Davis and Hatice [20].
Batchelor’s work involving non-Brownian spheres and polydisperse systems [19,21] was also consistent with the empirical correlation by Richardson and Zaki. Some additional developments in the theoretical treatment of hindered suspensions of nonspherical particles (Category D) are those of Hinch and Leal [22], and Koch and Shaqfeh [23].
Some empirical approaches to the hindered settling velocity of spheres (Categories C and E) were published by Steinour H. H. [24], Barnea and Mizrahi [25], Sangani and Acrivos [18], and Takacs et al. [26]. However, the approach by Richardson and Zaki [27] is the most widely used. In fact, numerous studies sought to improve its accuracy by developing expressions for the exponent in the RZ equation [28,29,30,31,32]. Davis and Acrivos [33] discussed some of these developments. Empirical approaches to NSPs (Category E) were published in [34,35,36,37,38]. These approaches focus on the effect of the particle shape on hindered settling exponents envisioned in the RZ equation. The RZ equation for spheres is presented below:
where is the hindered settling velocity, is the settling velocity at infinite dilution from Stokes’ law, is the ratio of the volume of solids divided by the total volume of the suspension of fluids and solids . The exponent m of 4.6 is generally used for spheres in the Reynolds number considered in this study.
Equation (1) was considered to be a valid benchmark, as many of the most rigorous analyses mentioned above have sought validation on the basis of its calculation and the deviations found in experimental studies. Even under some of the most rigorous of Batchelor’s analytical developments, the end result suggests a form that is very similar to that of Equation (1) and no additional variables. The developments in this article reference the results to the output of (1) and the deviations reported in the literature as many other previous studies.
In spite of the research effort briefly overviewed above, Silva et al. [39], regarding settling suspensions, note: “their inherent complexity has yet to be properly predicted by a unified numerical model or empirical correlation”. This article proposes an examination of the potential of this mathematical framework to reduce the burden of this deficiency. The framework is unified in a coherent analytical connection between the physics controlling the terminal settling velocity of spheres to the physics controlling the settling velocity of nonspherical particles and the transport mechanisms for any particle shape with relatively minimal assumptions. The framework also highlights the deficiency resulting from the omission of the accurate characterization of the specific surface area of particles as the most influential physical quantity in processes undoubtedly connected with the dynamics of viscosity. Future experimental work may well benefit from the establishment of the specific surface area as a fundamental measure of the of the driving forces influencing the behavior of settling particles.
2. Mathematical Framework
This article is not concerned with developing the mathematical framework; it is concerned with the application of the framework to present solutions to the hindered settling velocity of particles, and to subject the solutions to validations on the basis of published data. Although a thorough explanation of the framework was presented in [1], the development of equations can be better understood from [40,41], and the reader is encouraged to become familiar with those developments. Thus, the subsections below are intended to summarize the framework, as this single article is insufficient to present the entirety of the developments forming the framework.
2.1. Spheres
Consider a sphere of radius settling in quiescent fluid as a sphere influencing a spherical portion of the radius r of the ambient fluid concentric with the settling sphere. The fluid is quiescent beyond this sphere of influence. Consider a rational construction defining the radius R of this sphere of influence. A boundary limit. Equation (1) captures the computation of the velocity u profile due to the dynamics of viscosity in the spherical ambient expansion to mobilize the driving force exerted by the particle to the fluid. Because the sphere is sufficiently small, its submerged weight is transferred to the fluid via its . is simply its submerged weight divided by its area.
is not explicitly expressed in Equation (2). Potential pressure gradient results from the fraction defined by divided by the volume of fluid per square meter that is due to mobilize it as follows:
can also be derived from the fluid properties (viscosity and density ) as follows:
with the tributary mass per unit velocity gradient calculated to be (kg-s)/m2 at different temperatures in water and put to further validation in water, cyclohexane, and toluene [41].
Because in Equation (2) can be obtained from Equation (4) and R also in Equation (2) can be obtained from Equation (3), the velocity profile from Equation (2) can be computed.
The value of the velocity at the wall is the settling velocity . Thus,
This can also be written in the following form:
because the volumetric relationships in Equation (2) imply that a dimensionless maximal tributary ratio , defined as the volume of the ambient fluid divided by the volume of the particle, is related to the radius of the particle and the ambient fluid via the following relationships:
Hence:
and
The equilibrium of forces in the fluid with the forces mobilized by the particle also implies that can be obtained as follows:
On the basis of some insights provided in [1,41], the limit of applicability of these relationships was estimated to be a 155 velocity gradient () and 0.01126 viscosity.
2.2. Nonspherical Particles (NSP)
The mathematical volume and area relationships defining a NSP are necessarily based on at least two physical dimensions. It is simple to define a sphere of radius having the same area as that of the NSP. The problem with this is that a sphere so defined holds a much greater volume (and weight) than the original volume of the NSP. For the sphere so defined, it is, however, simple to define a density that makes it weigh as much as the NSP. In essence, the goal of the framework is to use Equation (6) to compute the velocity of a NSP by transforming the NSP into a sphere having the same area and weight (and, thus, the same ) as those of the NSP. This transformation is much more than it seems. Consider Figure 1 as a cross-section of a spherical cone identical on two perpendicular planes.
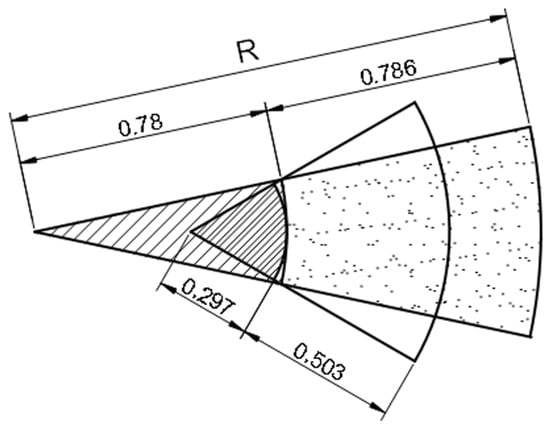
Figure 1.
Tributary volumes of same magnitude and different shape (microns) for same .
The transformation tells us what the effect of changing the shape is. does not by itself define the velocity. The “flatter” tributary volume of the NSP due to its large area increases the velocity with respect to a sphere having the same . This was validated with experimental measurements for high NSPs.
The equivalent sphere is, thus, implemented by defining from the area of the NSP as follows:
and by extracting the equivalent density from the following relationship:
The volumetric relationship between the ambient spherical expansion and the volume of the equivalent sphere also changes, so that turns into as follows:
Equation (6) for the settling velocity is used for the settling velocity of the NSP in the following form:
can also be obtained for an NSP of volume as follows:
3. The Hindered Settling Velocity of Spheres
Consider settling velocity in a quiescent Newtonian fluid of a sphere of radius falling within an ambient expansion of volume times the volume of the settling sphere:
From the standpoint of the mechanics leading to Equation (6), one can be tempted to use Equation (6) to model the dynamics of hindered settling velocity with a reasoned adjustment of the mechanics. Such an ambition does not appear to be unjustified: the velocity profile implied in it bears a volumetric relationship with the solid particle, in a sense that it is very similar to in Equation (1). The challenges that are visible do not seem difficult to overcome, but the displaced fluid moves upwards, so that if a successful attempt is performed, the value of the calculated velocity from the construction of the mechanics using Equation (6) would be with reference to a fluid front that is moving upward at velocity . If so, one can expect that the real hindered settling velocity with respect to a fixed point is the difference between and :
The constructions leading to these velocities are presented below, and the results are compared with Equation (1).
Because solid volume fraction is defined as the volume of solids divided by the total volume, one can define for a single particle of volume within fluid of volume as , and since is defined as the volume of fluid in the bulk fluid region divided by the volume of the solid particle , can be expressed as follows:
for a single particle. One can, thus, define a hindered tributary ratio as
associated with , which simply defines a spherical tributary volume in which a velocity profile exists whose boundary value of velocity at the wall of the solid sphere can be calculated using Equation (6). As is physically limited externally due to the limited space where the solid concentration increases, Equation (10), written as
computes pressure gradient in the limited space. is, thus,
which can be verified to compute a value of greater than Equation (1), confirming that the ambition that triggered this discussion is justified. Hindered pressure gradient is, in fact, an increased pressure gradient. Subscript h and the term “hindered” are maintained below for view of the context in which they occurs.
The task of reaching reasoned mechanics to derive a construction to compute either separately or by means of mechanics to be captured in Equation (20) seemed daunting at some point. In essence, Equation (20) tests a hypothesis: with the understanding that there is of the mechanics, the constructions leading to Equation (20) should calculate a slightly greater velocity than that suggested by Equation (1). If this failed, a real daunting challenge would have been imposed; if it succeeded, continuity would be able to supply a relatively easy answer for : because of continuity when a spherical particle settles a distance , it pumps a volume that is exactly the volume of the particle back behind the particle. This fact leads to the constructions presented below to compute .
From the standpoint of this work, is the only velocity there is to calculate from the mechanics. There is a fact that needs to be examined from Equation (2), written as follows:
for free settling particles or as follows:
for the calculation of the boundary value of the settling velocity . There exists a tributary volume of radius for which Equation (20) calculates the boundary value of the velocity at the wall of the solid sphere and for which the flow can be computed [42]. The flow occurs through equatorial area enclosed by radius and radius , which can be calculated from the volumetric relationships as follows:
The requirement of continuity for a particle that settles a distance is that it strictly pumps upward through A. Regardless of the dynamics, where is the average velocity upward, the front advances upward a distance as
when the particle settles the distance. At the same time during which the front t advances , the particle advances the real distance. is, thus,
and
If not obvious, which renders and available from Equations (16) and (25), respectively, and the ratio is also available from Equations (6) and (16).
Comparison with the R. Z. Equation
Equation (1) yields 0.62 and 0.27 for with equal to 0.1 and 0.25, respectively, whereas using Equations (6) and (16) yields 0.67 and 0.34, respectively, for a 2.65 specific gravity particle 10 μm diameter in water at 20 degrees. Any correlation for spheres via Equation (1) would have been performed using Stokes’ relationship. To render the reported observations comparable with the calculation of from Equation (16), must be the value computed from Stoke’s law. The calculations, thus, yield 0.5 and 0.25 for , equal to 0.1 and 0.25, respectively. This is an interesting result when noting that the experimental hindered settling velocity was reported [30,31,43] to be less than that predicted under the RZ equation. It is fair to say that the correlation in Equation (1) has all the merits of the correlations that could be performed with the limited number of quantities accounted for in it; however, the mechanics here derived are a robust approach to the problem that lends meaningful insight to embrace the hindered settling velocity for the NSPs presented below.
4. Hindered Settling Velocity of Nonspherical Particles
Consider the goals established in developing Equation (16) to be the same for NSPs. The development of relationships defining the hindered settling velocity of NSPs follows a similar logic as that of spheres, with the difference that it builds on the relationships for NSPs. Summarized steps with some distinct remarks are presented below.
Where the surface area of the NSP is , is
because is defined by the real volume of the NSPs, and is simply , as defined by Equation (18), copied below for ease of reference.
The same applies to the hindered pressure gradient for the NSP for the same reason. The hindered pressure gradient for the NSP is, thus, from Equation (19) as follows:
The hindered equivalent tributary ratio for the NSP having volume given the construction of the radius particle from Equation (15) can be written as follows:
which yields the following equation to solve :
and the geometry of the NSP can be verified to be considered in Equation (31) from
As proposed above, the aim is to compute , the dimension defining the passing of the entire particle (and its entire volume) across a horizontal plane is ; however, such a dimension is not defined for a NSP. As there are many falling particles, it is not unreasonable to assume that the average dimension defining the passing of the entire volume of the NSP is that of a sphere having the same volume of the NSP. Radius so defined can be
where defines the distance that the particle travels to displace a volume of fluid equal to of the NSP, and the displacement of fluid occurs through the interstice of the ambient fluid defined by areas and . Such an interstice is, thus, defined by the area of the equatorial ring around the particle of radius and the volumetric relationship as
The displacement of the front velocity of the NSP when the particle settles is, thus,
The time t for the displacement becomes
to compute the front velocity for the NSP as follows:
and the hindered settling velocity of the NSP is found as follows:
As an example, with equal to 0.1, a disklike particle with an aspect ratio of 8 having the same specific gravity and as those of the 10 μm particle above yields (as opposed to 0.67 for the sphere). For a given specific gravity, NSPs with equal to a sphere are heavier particles with flatter tributary volumes, so they settle faster. As such. the disk mentioned above settles faster at m/s (compared to m/s for the sphere). The lesser ratio is because of the greater value of and the relationships.
On the basis of directly derived constructs from the framework, the difference of the ratio between spheres and any nonspherical particle can be rationalized and established without the need to create exponents for the R. Z. equation or other relationships.
5. Conclusions
The mathematical framework presented in this article enabled a unification of concepts to predict not only the hindered settling velocity of particles, but also the magnitude of the back-flow by means of a simple application of the principle of continuity. The calculated predicted velocities were less than those predicted with the RZ equation, which is consistent with the reported observation that the experimental velocities are less than those predicted by the RZ equation.
A key aspect of the capabilities enabled by this framework is its ability to provide a rationalization to develop constructs to establish the difference of the ratio between spheres and any nonspherical particle. Establishing this difference via empirical correlations remains a challenging task in this field.
The concepts in the framework could be useful in reducing deficiencies in the predictions of other problems such as polydisperse suspensions, the translational motion of particles, and the sedimentation of aggregates.
Funding
This research was funded by its author.
Acknowledgments
The author would like to thank Kevin Slatttery Bouchey, P.E. for the feedback provided during the production of this article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Mendez, Y. The Single Particle Motion of Non-Spherical Particles in Low Reynolds Number Flow. Fluids 2022, 7, 320. [Google Scholar] [CrossRef]
- Richarson, J.; Zaki, W. Sedimentation and fluidisation, Part 1. Trans. Ins. Chem. Engrs 1954, 31, 35–53. [Google Scholar]
- Kynch, G.J. A theory of sedimentation. Trans. Faraday Soc. 1952, 48, 166–176. [Google Scholar] [CrossRef]
- Hinch, J. A perspective of Batchelor’s research in micro-hydrodynamics. J. Fluid Mech. 2010, 663, 8–17. [Google Scholar] [CrossRef]
- Ghatage, S.V.; Khan, M.S.; Peng, Z.; Doroodchi, E.; Moghtaderi, B.; Padhiyar, N.; Joshi, J.B.; Evans, G.; Mitra, S. Settling/rising of a foreign particle in solid-liquid fluidized beds: Application of dynamic mesh technique. Chem. Eng. Sci. 2017, 170, 139–153. [Google Scholar] [CrossRef]
- Ghatage, S.V.; Sathe, M.J.; Doroodchi, E.; Joshi, J.B.; Evans, G.M. Effect of turbulence on particle and bubble slip velocity. Chem. Eng. Sci. 2013, 100, 120–136. [Google Scholar] [CrossRef]
- Ardekani, A.; Doostmohammadi, A.; Desai, N. Transport of particles, drops, and small organisms in density stratified fluids. Phys. Rev. Fluids 2017, 2, 100503. [Google Scholar] [CrossRef]
- Brady, J.F.; Bossis, G. Stokesian dynamics. Annu. Rev. Fluid Mech. 1988, 20, 111–157. [Google Scholar] [CrossRef]
- Loewenberg, M.; Hinch, E.J. Numerical simulation of a concentrated emulsion in shear flow. J. Fluid Mech. 1996, 321, 395–419. [Google Scholar] [CrossRef]
- Ladd, A.J. Hydrodynamic screening in sedimenting suspensions of non-Brownian spheres. Phys. Rev. Lett. 1996, 76, 1392. [Google Scholar] [CrossRef]
- Guazzelli, E. Evolution of particle-velocity correlations in sedimentation. Phys. Fluids 2001, 13, 1537–1540. [Google Scholar] [CrossRef]
- Cunha, F.R.; Abade, G.C.; Sousa, A.J.; Hinch, E.J. Modeling and Direct Simulation of Velocity Fluctuations and Particle-Velocity Correlations in Sedimentation. J. Fluids Eng. 2002, 124, 957–968. [Google Scholar] [CrossRef]
- Mucha, P.J.; Tee, S.Y.; Weitz, D.A.; Shraiman, B.I.; Brenner, M.P. A model for velocity fluctuations in sedimentation. J. Fluid Mech. 2004, 501, 71–104. [Google Scholar] [CrossRef]
- Boschan, A.; Ocampo, B.; Annichini, M.; Gauthier, G. Velocity fluctuations and population distribution in clusters of settling particles at low Reynolds number. Phys. Fluids 2016, 28, 063301. [Google Scholar] [CrossRef]
- Madavan, N.K.; Merkle, C.L.; Deutsch, S. Numerical Investigations Into the Mechanisms of Microbubble Drag Reduction. J. Fluids Eng. 1985, 107, 370–377. [Google Scholar] [CrossRef]
- Ouyang, K.; Wu, S.J.; Huang, H.H. Optimum Parameter Design of Microbubble Drag Reduction in a Turbulent Flow by the Taguchi Method Combined With Artificial Neural Networks. J. Fluids Eng. 2013, 135, 111301. [Google Scholar] [CrossRef]
- Fontaine, A.A.; Deutsch, S. The influence of the type of gas on the reduction of skin friction drag by microbubble injection. Exp. Fluids 1992, 13, 128–136. [Google Scholar] [CrossRef]
- Sangani, A.S.; Acrivos, A. Slow flow through a periodic array of spheres. Int. J. Multiph. Flow 1982, 8, 343–360. [Google Scholar] [CrossRef]
- Batchelor, G.; Wen, C.S. Sedimentation in a dilute polydisperse system of interacting spheres. Part 2. Numerical results. J. Fluid Mech. 1982, 124, 495–528. [Google Scholar] [CrossRef]
- Davis, R.H.; Gecol, H. Hindered settling function with no empirical parameters for polydisperse suspensions. AIChE J. 1994, 40, 570–575. [Google Scholar] [CrossRef]
- Batchelor, G. Sedimentation in a dilute polydisperse system of interacting spheres. Part 1. General theory. J. Fluid Mech. 1982, 119, 379–408. [Google Scholar] [CrossRef]
- Hinch, E.; Leal, L. The effect of Brownian motion on the rheological properties of a suspension of non-spherical particles. J. Fluid Mech. 1972, 52, 683–712. [Google Scholar] [CrossRef]
- Koch, D.L.; Shaqfeh, E.S. The instability of a dispersion of sedimenting spheroids. J. Fluid Mech. 1989, 209, 521–542. [Google Scholar] [CrossRef]
- Steinour, H.H. Rate of sedimentation. Nonflocculated suspensions of uniform spheres. Ind. Eng. Chem. 1944, 36, 618–624. [Google Scholar] [CrossRef]
- Barnea, E.; Mizrahi, J. A generalized approach to the fluid dynamics of particulate systems: Part 1. General correlation for fluidization and sedimentation in solid multiparticle systems. Chem. Eng. J. 1973, 5, 171–189. [Google Scholar] [CrossRef]
- Takács, I.; Patry, G.G.; Nolasco, D. A dynamic model of the clarification-thickening process. Water Res. 1991, 25, 1263–1271. [Google Scholar] [CrossRef]
- Richardson, J.; Zaki, W. The sedimentation of a suspension of uniform spheres under conditions of viscous flow. Chem. Eng. Sci. 1954, 3, 65–73. [Google Scholar] [CrossRef]
- Garside, J.; Al-Dibouni, M.R. Velocity-voidage relationships for fluidization and sedimentation in solid-liquid systems. Ind. Eng. Chem. Process. Des. Dev. 1977, 16, 206–214. [Google Scholar] [CrossRef]
- Chien, N.; Wan, Z. Sediment Transport Mechanics; ASCE: Reston, VA, USA, 1983. [Google Scholar]
- Cheng, N.S. Effect of concentration on settling velocity of sediment particles. J. Hydraul. Eng. 1997, 123, 728–731. [Google Scholar] [CrossRef]
- Pal, D.; Ghoshal, K. Hindered settling with an apparent particle diameter concept. Adv. Water Resour. 2013, 60, 178–187. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, H.; Peng, D.; Dou, J. Modelling the Hindered Settling Velocity of a Falling Particle in a Particle-Fluid Mixture by the Tsallis Entropy Theory. Entropy 2019, 21, 55. [Google Scholar] [CrossRef] [PubMed]
- Davis, R.H.; Acrivos, A. Sedimentation of noncolloidal particles at low Reynolds numbers. Annu. Rev. Fluid Mech. 1985, 17, 91–118. [Google Scholar] [CrossRef]
- Chong, Y.S.; Ratkowsky, D.A.; Epstein, N. Effect of particle shape on hindered settling in creeping flow. Powder Technol. 1979, 23, 55–66. [Google Scholar] [CrossRef]
- Turney, M.A.; Cheung, M.K.; Powell, R.L.; McCarthy, M.J. Hindered settling of rod-like particles measured with magnetic resonance imaging. AIChE J. 1995, 41, 251–257. [Google Scholar] [CrossRef]
- Lau, R.; Chuah, H.K.L. Dynamic shape factor for particles of various shapes in the intermediate settling regime. Adv. Powder Technol. 2013, 24, 306–310. [Google Scholar] [CrossRef]
- Dogonchi, A.; Hatami, M.; Hosseinzadeh, K.; Domairry, G. Non-spherical particles sedimentation in an incompressible Newtonian medium by Padé approximation. Powder Technol. 2015, 278, 248–256. [Google Scholar] [CrossRef]
- Paul, N.; Biggs, S.; Shiels, J.; Hammond, R.B.; Edmondson, M.; Maxwell, L.; Harbottle, D.; Hunter, T.N. Influence of shape and surface charge on the sedimentation of spheroidal, cubic and rectangular cuboid particles. Powder Technol. 2017, 322, 75–83. [Google Scholar] [CrossRef]
- Silva, R.; Garcia, F.A.; Faia, P.M.; Rasteiro, M.G. Settling suspensions flow modelling: A review. KONA Powder Part. J. 2015, 32, 2015009. [Google Scholar] [CrossRef]
- Mendez, Y. A Flow Model for the Settling Velocities of non Spherical Particles in Creeping Motion. J. Appl. Fluid Mech. 2011, 4, 65–75. [Google Scholar] [CrossRef]
- Mendez, Y. A Flow Model for the Settling Velocities of non Spherical Particles in Creeping Motion, Part II. J. Appl. Fluid Mech. 2012, 5, 123–129. [Google Scholar] [CrossRef]
- Mendez, Y. A Flow Model for the Settling Velocities of Non Spherical Particles in Creeping Motion. Part III. Slender Bodies, the Stream Functions, the Flow and the Momentum Equation. J. Appl. Fluid Mech. 2015, 8, 391–398. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Kundu, S.; Ghoshal, K. Hindered settling velocity in particle-fluid mixture: A theoretical study using the entropy concept. J. Hydraul. Eng. 2017, 143, 06017019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).