Note on the Early Thermoelastic Stage Preceding Rayleigh–Bénard Convection in Soft Materials
Abstract
:1. Introduction
1.1. Rayleigh–Bénard Convection in a Yield–Stress Fluid: Literature Review
1.2. Objectives, Methodology and Outline of the Paper
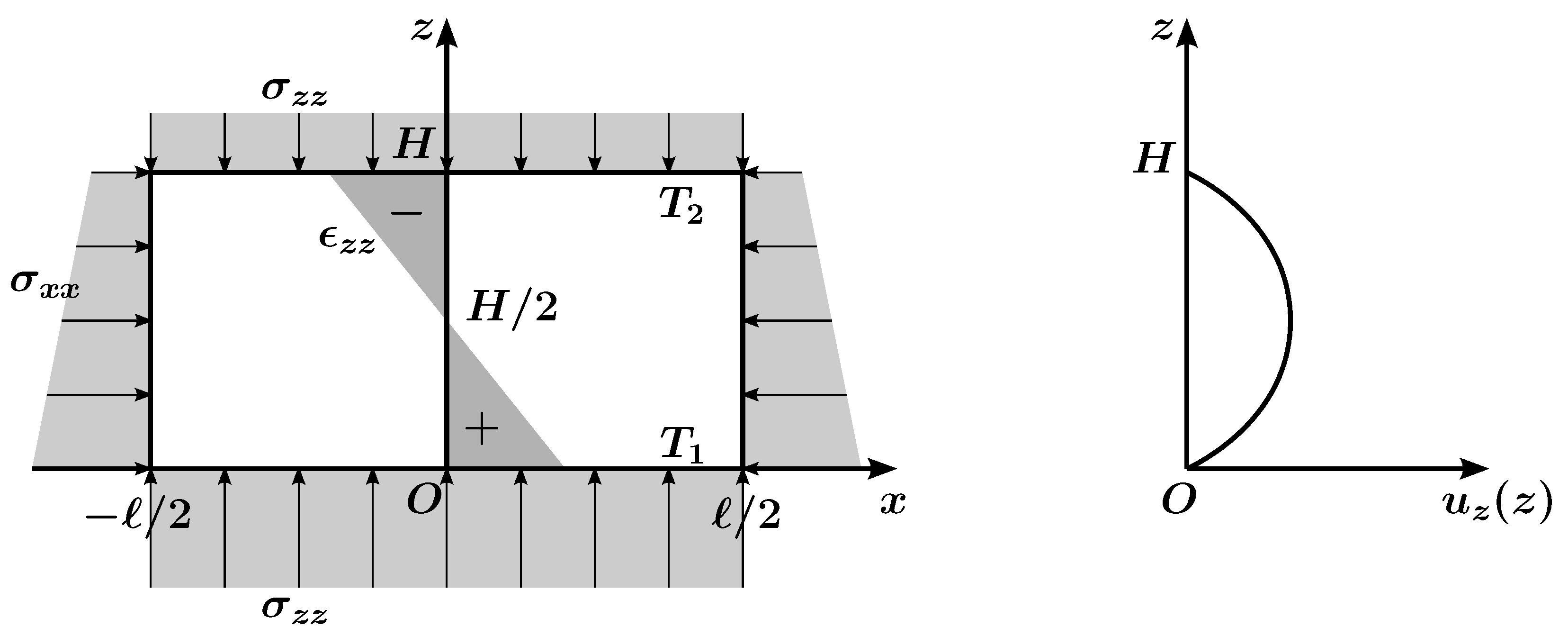
2. Problem Formulation
2.1. Governing Equations
2.2. Boundary Conditions
3. Thermal Stresses and Strains Induced by a Temperature Gradient
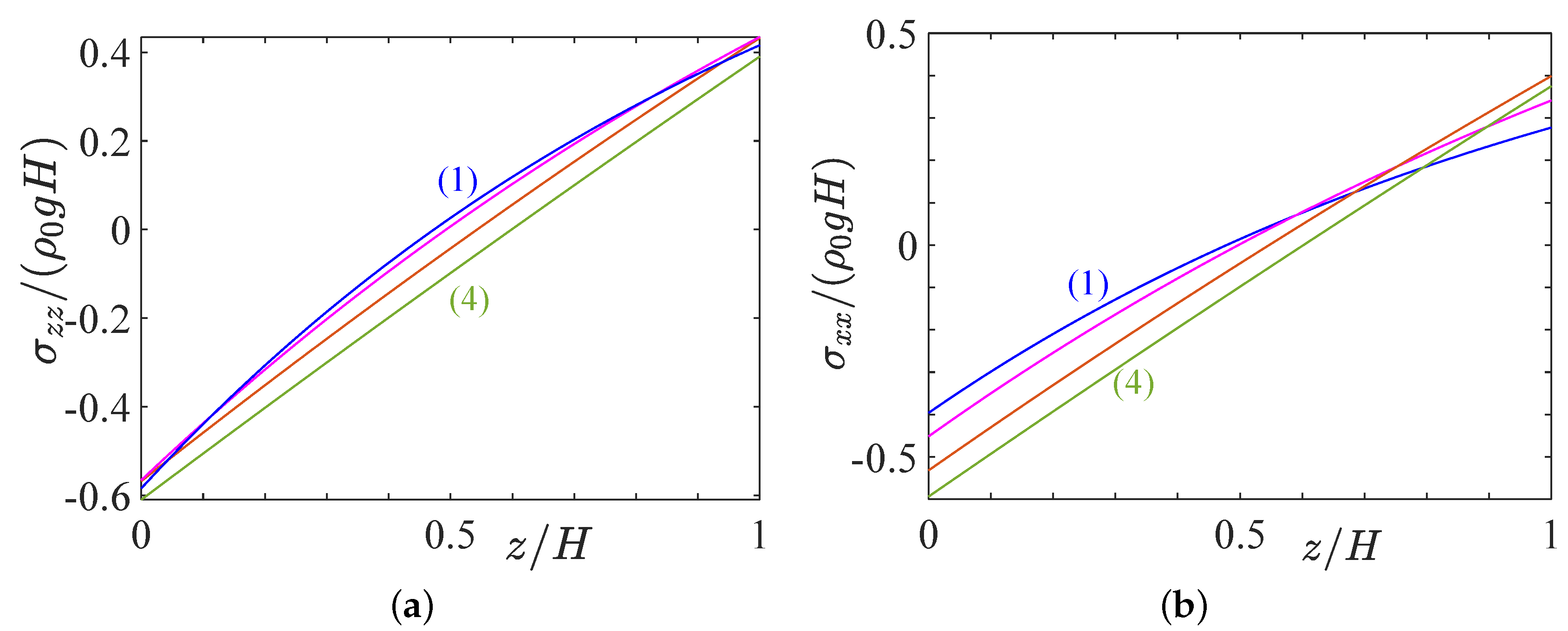
4. Strain and Stress Fields Induced by Gravity Combined with a Temperature Gradient
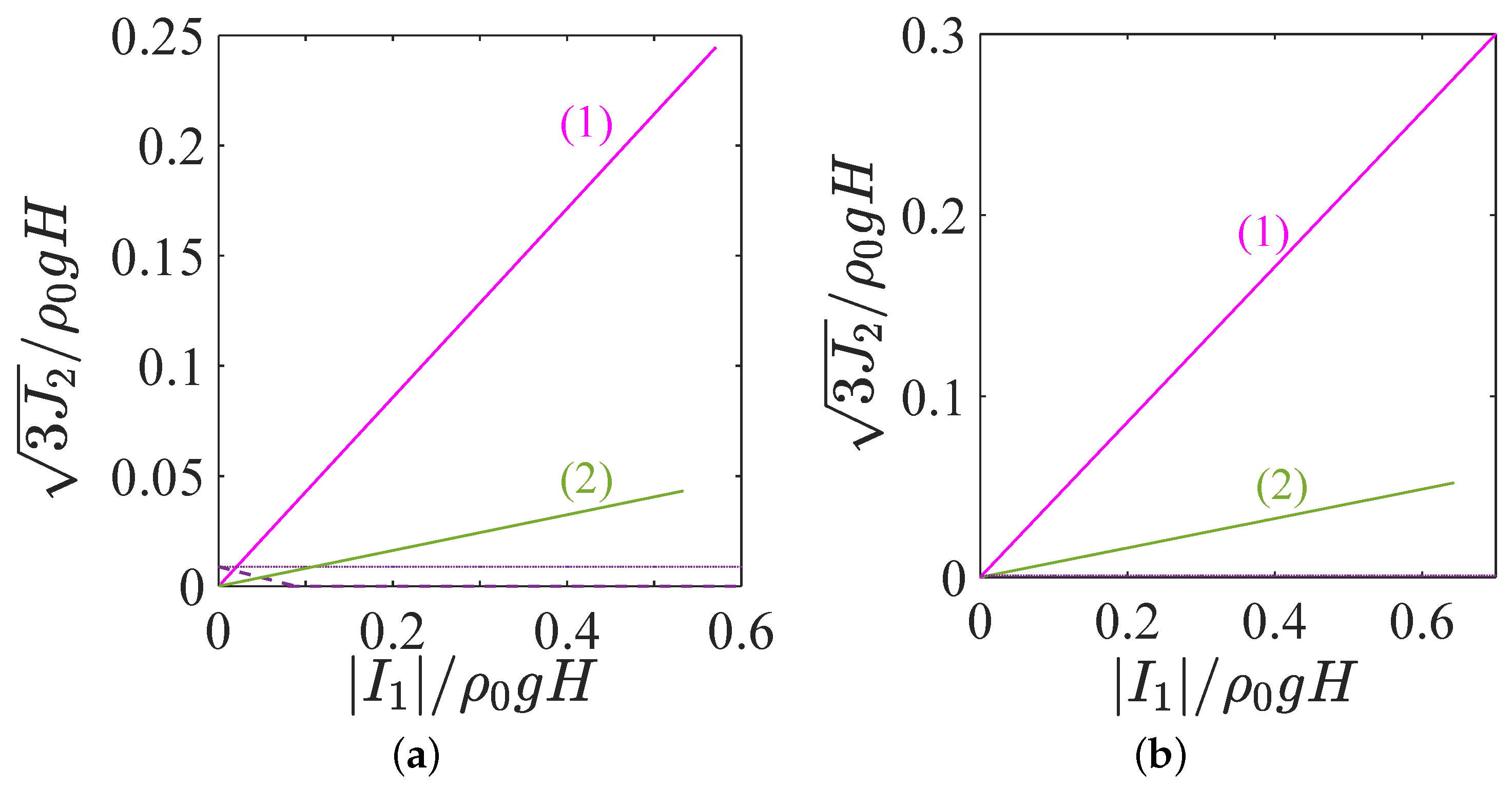
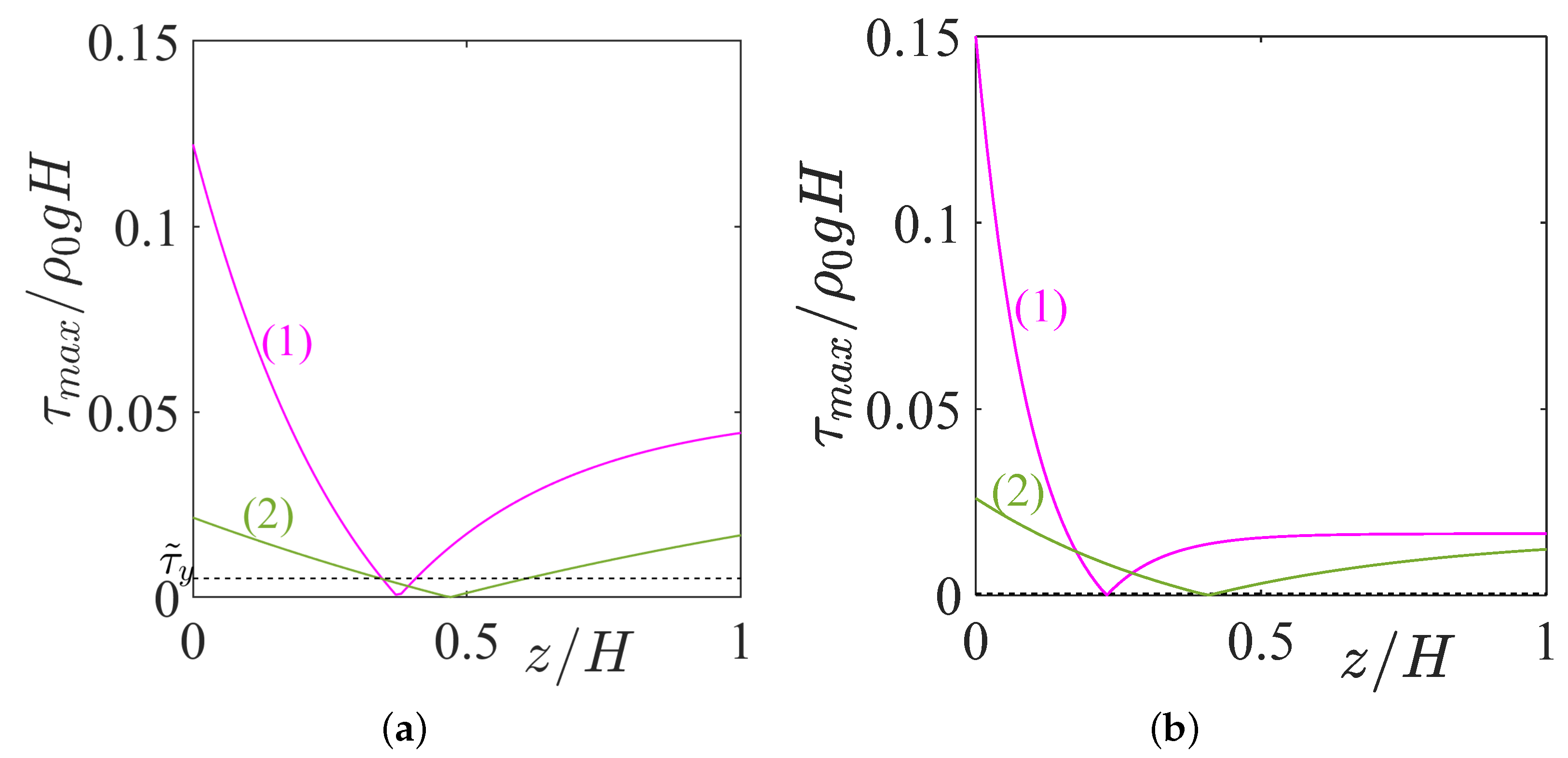
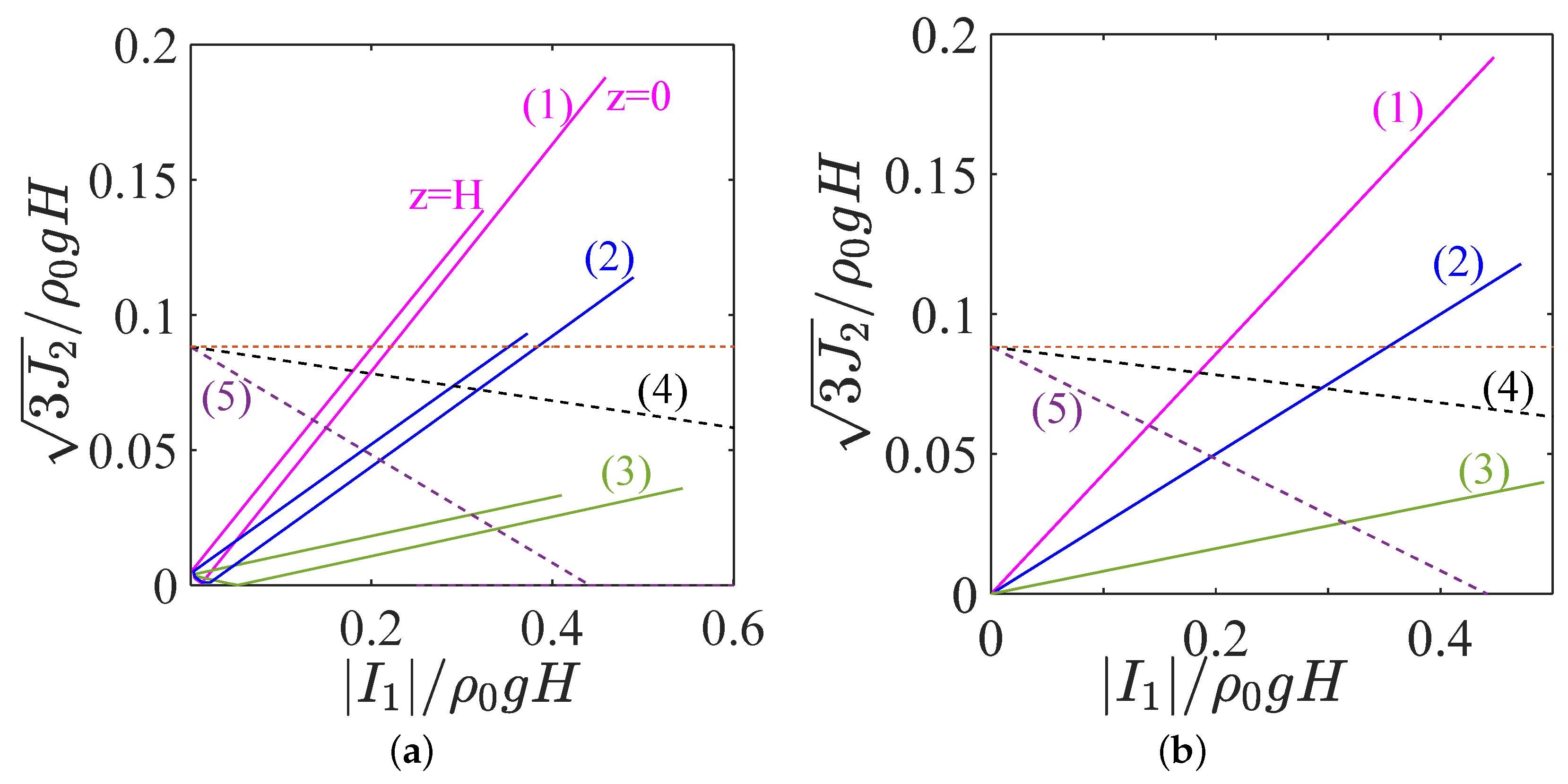
5. Onset of Plastic Deformation: Main Yield Criteria
5.1. Tresca Criterion
5.2. Von Mises Yield Criterion
5.3. Drucker–Prager Yield Criterion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| specific heat constant volume | ||
| thermal diffusivity | ||
| E | Young’s modulus | Pa |
| g | acceleration of gravity | |
| H | thickness of the viscoplastic fluid layer | |
| first invariant of the Cauchy stress tensor | ||
| second invariant of the deviatoric stress tensor | ||
| K | thermal conductivity | |
| T | temperature | |
| temperature difference between top and bottom walls | ||
| displacement vector | ||
| z | vertical coordinate | |
| volume expansion coefficient | ||
| strain tensor | ||
| dynamic viscosity | ||
| first Lamé’s parameter | ||
| second Lamé’s parameter | ||
| Poisson’s ratio | ||
| fluid density | ||
| reference value of the fluid density | ||
| maximum value of shear-stress | ||
| Cauchy stress tensor | ||
| yield stress |
References
- Balmforth, N.; Frigaard, I.; Ovarlez, G. Yielding to stress: Recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 2014, 46, 121–146. [Google Scholar] [CrossRef]
- Coussot, P. Bingham’s heritage. Rheol. Acta 2017, 56, 163–176. [Google Scholar] [CrossRef]
- Bonn, D.; Denn, M.; Berthier, L.; Divoux, T.; Manneville, S. Yield stress materials in soft condensed matter. Rev. Mod. Phys. 2017, 89, 035005. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Vola, D.; Frigaard, I. Yield stress effects on Rayleigh–Bénard convection. J. Fluid Mech. 2006, 566, 389–419. [Google Scholar] [CrossRef]
- Balmforth, N.; Rust, A. Weakly nonlinear viscoplastic convection. J. Non–Newton. Fluid Mech. 2009, 158, 36–45. [Google Scholar] [CrossRef]
- Vikhansky, A. Thermal convection of a viscoplastic liquid with high Rayleigh and Bingham numbers. Phys. Fluids 2009, 21, 103103. [Google Scholar] [CrossRef]
- Turan, O.; Poole, R.; Chakraborty, N. Influences of boundary conditions on laminar natural convection in rectangular enclosures with differentially heated side walls. Int. J. Heat Fluid Flow 2012, 33, 131–146. [Google Scholar] [CrossRef]
- Turan, O.; Yigit, S.; Chakraborty, N. Critical condition for Rayleigh-Bénard convection of Bingham fluids in rectangular enclosures. Int. Commun. Heat Mass Transf. 2017, 86, 117–125. [Google Scholar] [CrossRef] [Green Version]
- Aghighi, M.; Ammar, A.; Masoumi, H.; Lanjabi, A. Rayleigh–Bénard convection of a viscoplastic liquid in a trapezoidal enclosure. Int. J. Mech. Sci. 2020, 180, 105630. [Google Scholar] [CrossRef]
- Aghighi, M.; Ammar, A. Aspect ratio effects in Rayleigh–Bénard convection of Herschel–Bulkley fluids. Eng. Comput. 2017. [Google Scholar] [CrossRef]
- Aghighi, M.; Ammar, A.; Metivier, C.; Gharagozlu, M. Rayleigh-Bénard convection of Casson fluids. Int. J. Therm. Sci. 2018, 127, 79–90. [Google Scholar] [CrossRef] [Green Version]
- Darbouli, M.; Métivier, C.; Piau, J.M.; Magnin, A.; Abdelali, A. Rayleigh-Bénard convection for viscoplastic fluids. Phys. Fluids 2013, 25, 023101. [Google Scholar] [CrossRef] [Green Version]
- Kebiche, Z.; Castelain, C.; Burghelea, T. Experimental investigation of the Rayleigh–Bénard convection in a yield stress fluid. J. Non–Newton. Fluid Mech. 2014, 203, 9–23. [Google Scholar] [CrossRef]
- Hurle, D.; Jakeman, E.; Pike, E. On the solution of the Bénard problem with boundaries of finite conductivity. Proc. R. Soc. Lond. A Math Phys. Sci. 1967, 296, 469–475. [Google Scholar]
- Piau, J. Carbopol gels: Elastoviscoplastic and slippery glasses made of individual swollen sponges: Meso-and macroscopic properties, constitutive equations and scaling laws. J. Non–Newton. Fluid Mech. 2007, 144, 1–29. [Google Scholar] [CrossRef]
- Cloitre, M.; Bonnecaze, R. A review on wall slip in high solid dispersions. Rheol. Acta 2017, 56, 283–305. [Google Scholar] [CrossRef]
- Cerisier, P.; Rahal, S.; Cordonnier, J.; Lebon, G. Thermal influence of boundaries on the onset of Rayleigh-Bénard convection. Int. J. Heat Mass Transf. 1998, 41, 3309–3320. [Google Scholar] [CrossRef]
- Bouteraa, M.; Nouar, C.; Plaut, E.; Métivier, C.; Kalck, A. Weakly nonlinear analysis of Rayleigh-Bénard convection in shear-thinning fluids: Nature of the bifurcation and pattern selection. J. Fluid. Mech 2015, 767, 696–734. [Google Scholar] [CrossRef]
- Davaille, A.; Gueslin, B.; Massmeyer, A.; Giuseppe, E.D. Thermal instabilities in a yield stress fluid: Existence and morphology. J. Non–Newton. Fluid Mech. 2013, 193, 144–153. [Google Scholar] [CrossRef]
- Jadhav, K.; Rossi, P.; Karimfazli, I. Motion onset in simple yield stress fluids. J. Fluid Mech. 2021, 912. [Google Scholar] [CrossRef]
- Ahmadi, A.; Olleik, H.; Karimfazli, I. Rayleigh–Bénard convection of carbopol microgels: Are viscoplastic models adequate? J. Non–Newton. Fluid Mech. 2022, 300, 104704. [Google Scholar] [CrossRef]
- Metivier, C.; Li, C.; Magnin, A. Origin of the onset of Rayleigh-Bénard convection in a concentrated suspension of microgels with a yield stress behavior. Phys. Fluids 2017, 29, 104102. [Google Scholar] [CrossRef] [Green Version]
- Horton, C.; Rogers, J. Convection currents in a porous medium. J. Appl. Phys. 1945, 16, 367–370. [Google Scholar] [CrossRef]
- Lapwood, E. Convection of a fluid in a porous medium. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, MA, USA, 1948; Volume 44, pp. 508–521. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3. [Google Scholar]
- Tiu, C.; Guo, J.; Uhlherr, P.; Heinz, T. Yielding behaviour of viscoplastic materials. J. Ind. Eng. Chem. 2006, 12, 653–662. [Google Scholar]
- Salençon, J. Mécanique des Milieux Continus: Thermoélasticité Linéaire; Editions Ecole Polytechnique: Paris, France, 2000; Volume 2. [Google Scholar]
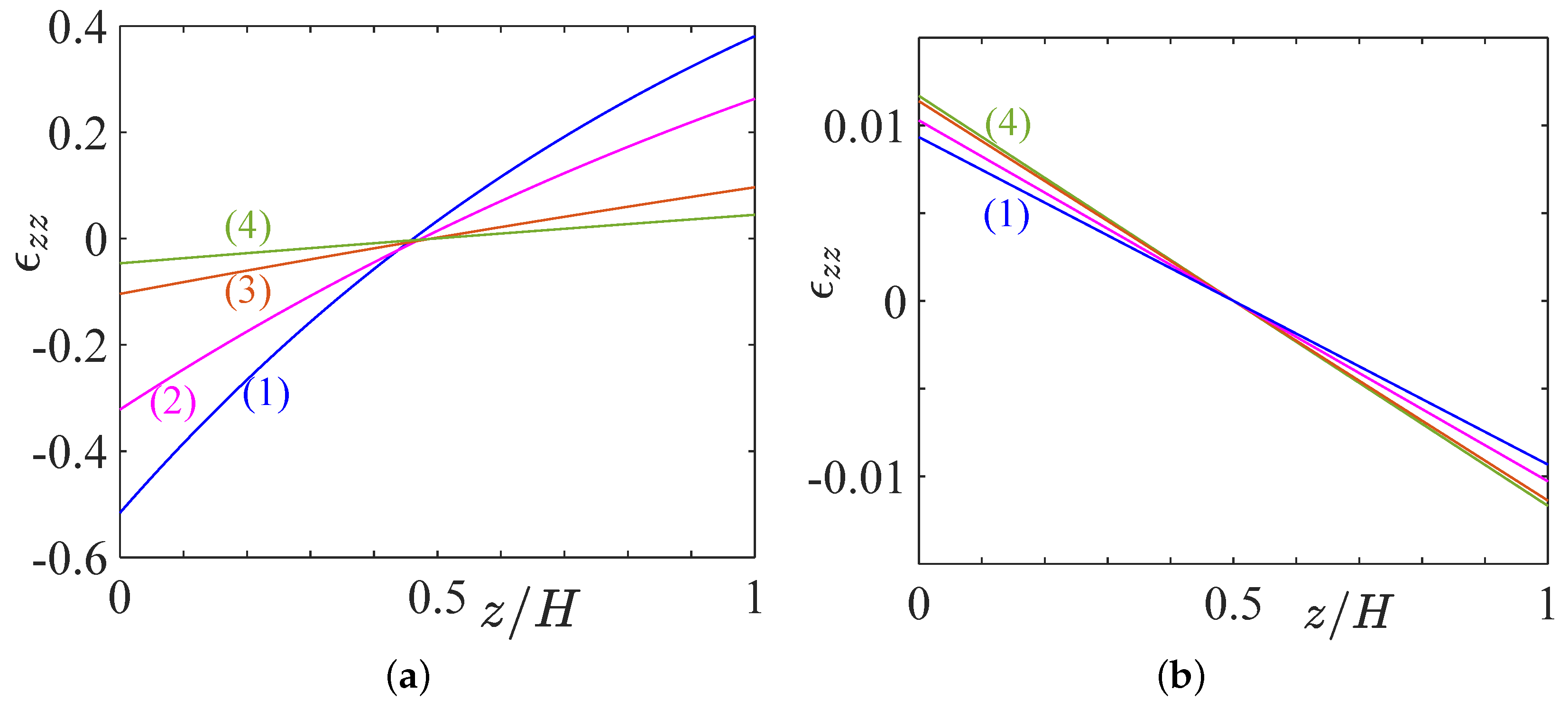

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahouadj, R.; Nouar, C.; Pereira, A. Note on the Early Thermoelastic Stage Preceding Rayleigh–Bénard Convection in Soft Materials. Fluids 2022, 7, 231. https://doi.org/10.3390/fluids7070231
Rahouadj R, Nouar C, Pereira A. Note on the Early Thermoelastic Stage Preceding Rayleigh–Bénard Convection in Soft Materials. Fluids. 2022; 7(7):231. https://doi.org/10.3390/fluids7070231
Chicago/Turabian StyleRahouadj, Rachid, Chérif Nouar, and Antonio Pereira. 2022. "Note on the Early Thermoelastic Stage Preceding Rayleigh–Bénard Convection in Soft Materials" Fluids 7, no. 7: 231. https://doi.org/10.3390/fluids7070231