Hydrodynamic Interaction of Two Self-Propelled Fish Swimming in a Tandem Arrangement
Abstract
:1. Introduction
2. Problem Description and Methods
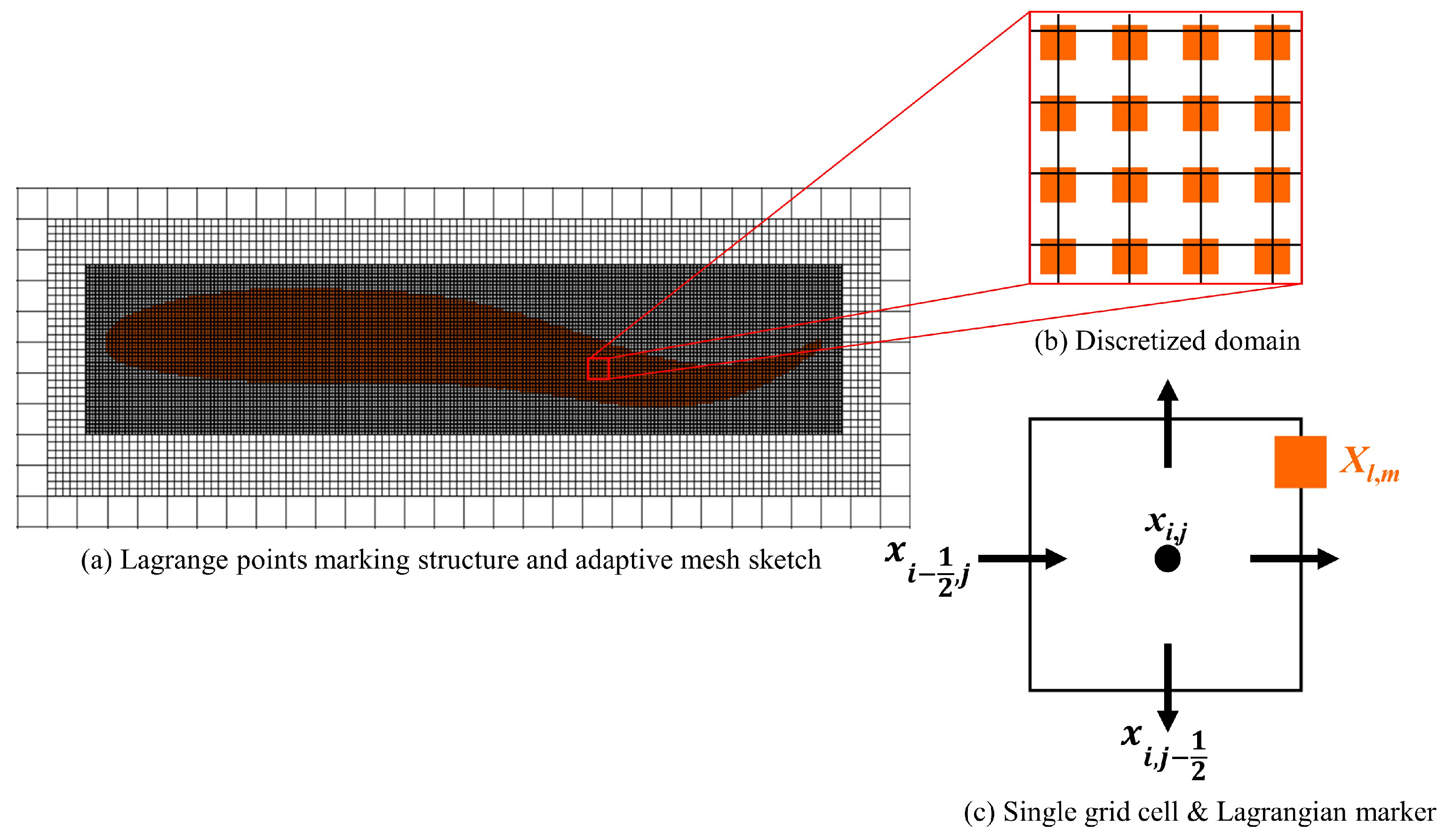
2.1. Fish Body Kinematics and Computational Details
2.2. Calculation of Hydrodynamic Arguments and Correlation Formula
2.3. Numerical Method
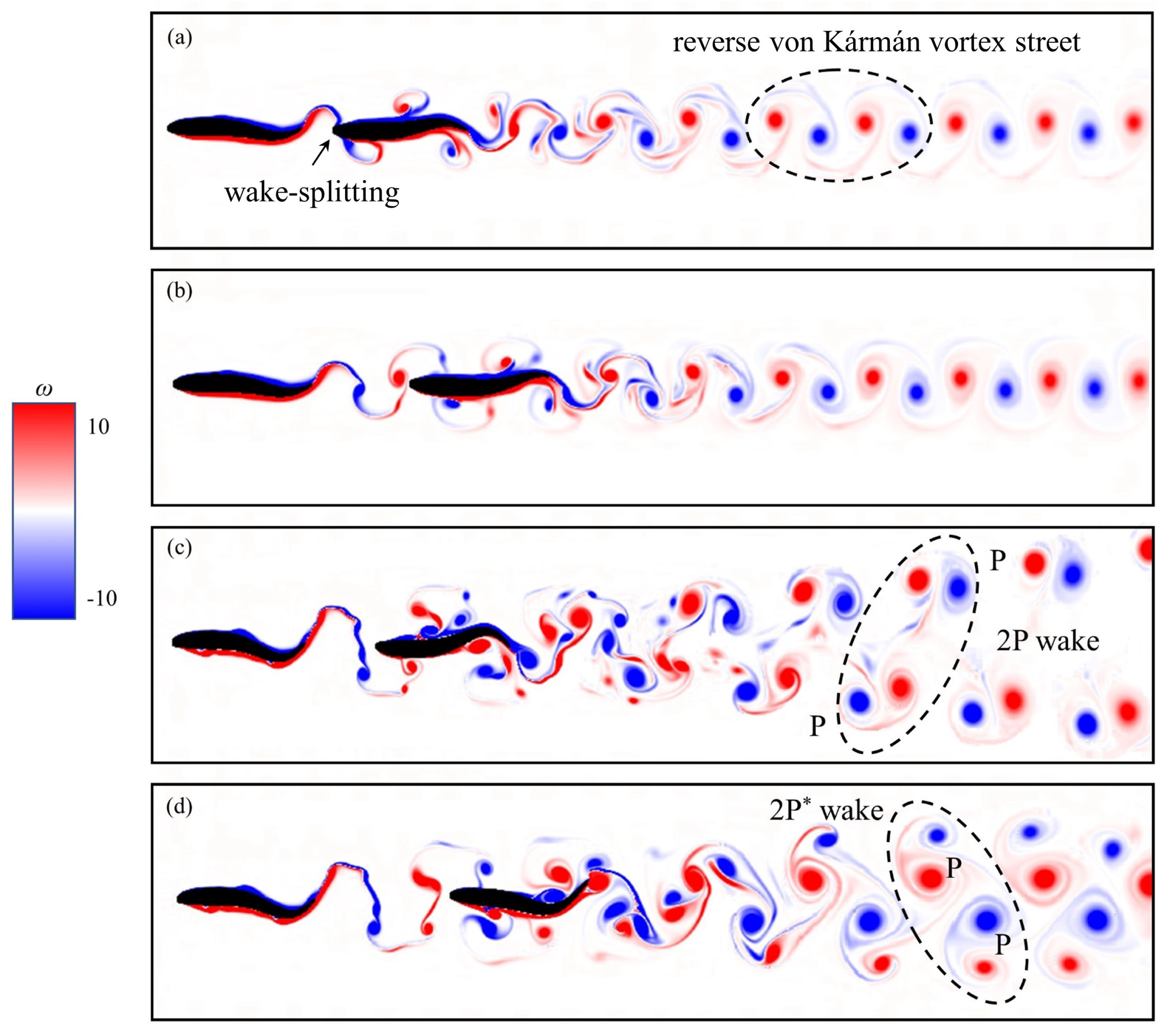
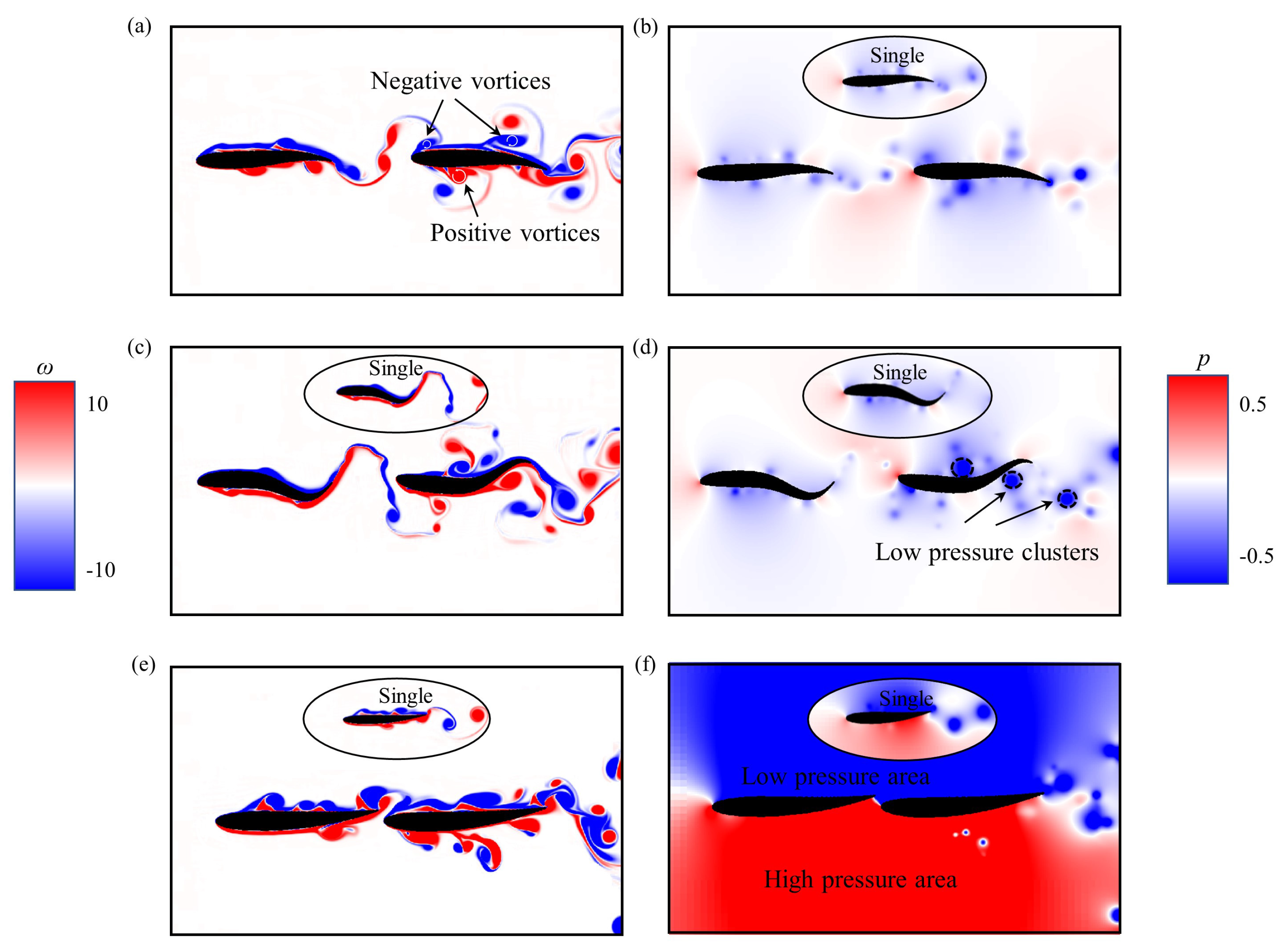
3. Results and Discussion
3.1. Effects of Swimming Parameters on Hydrodynamics
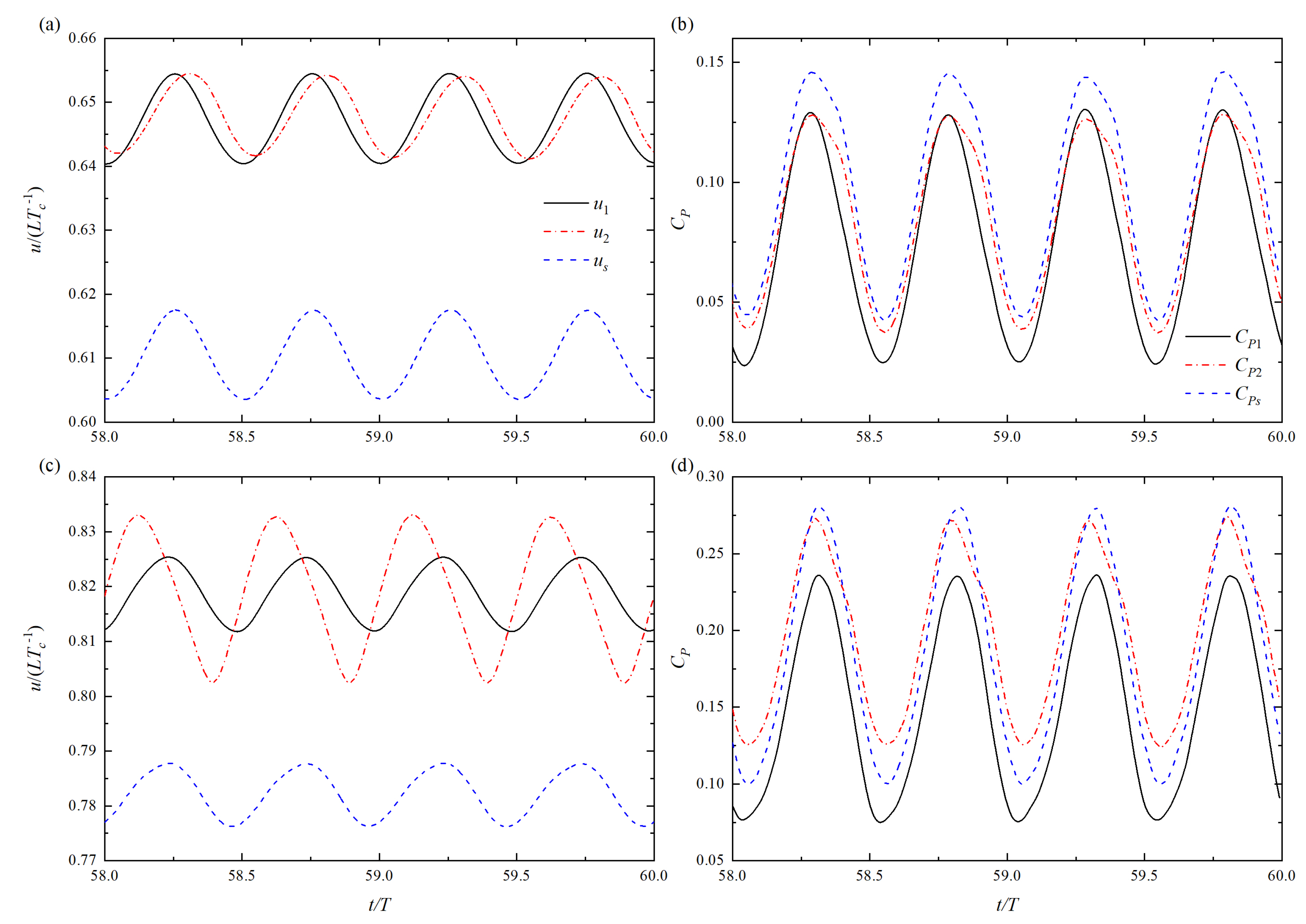
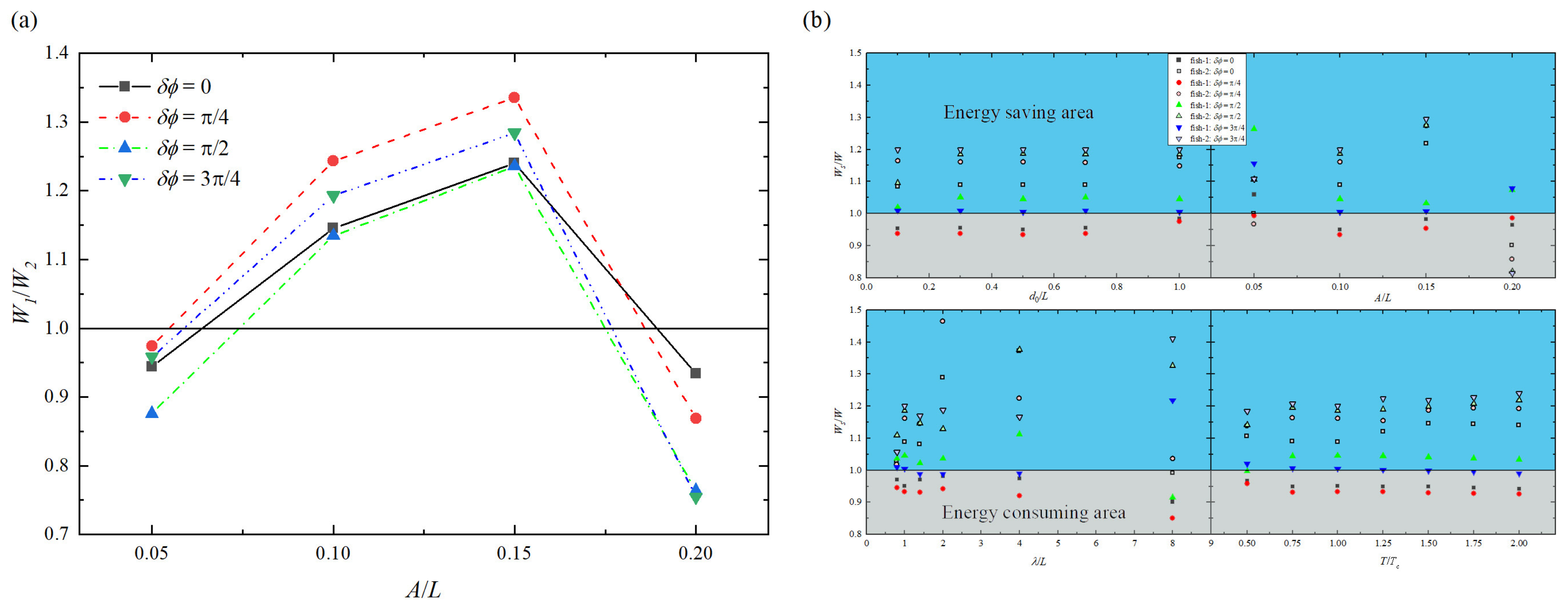
3.1.1. Effect on Swimming Speed
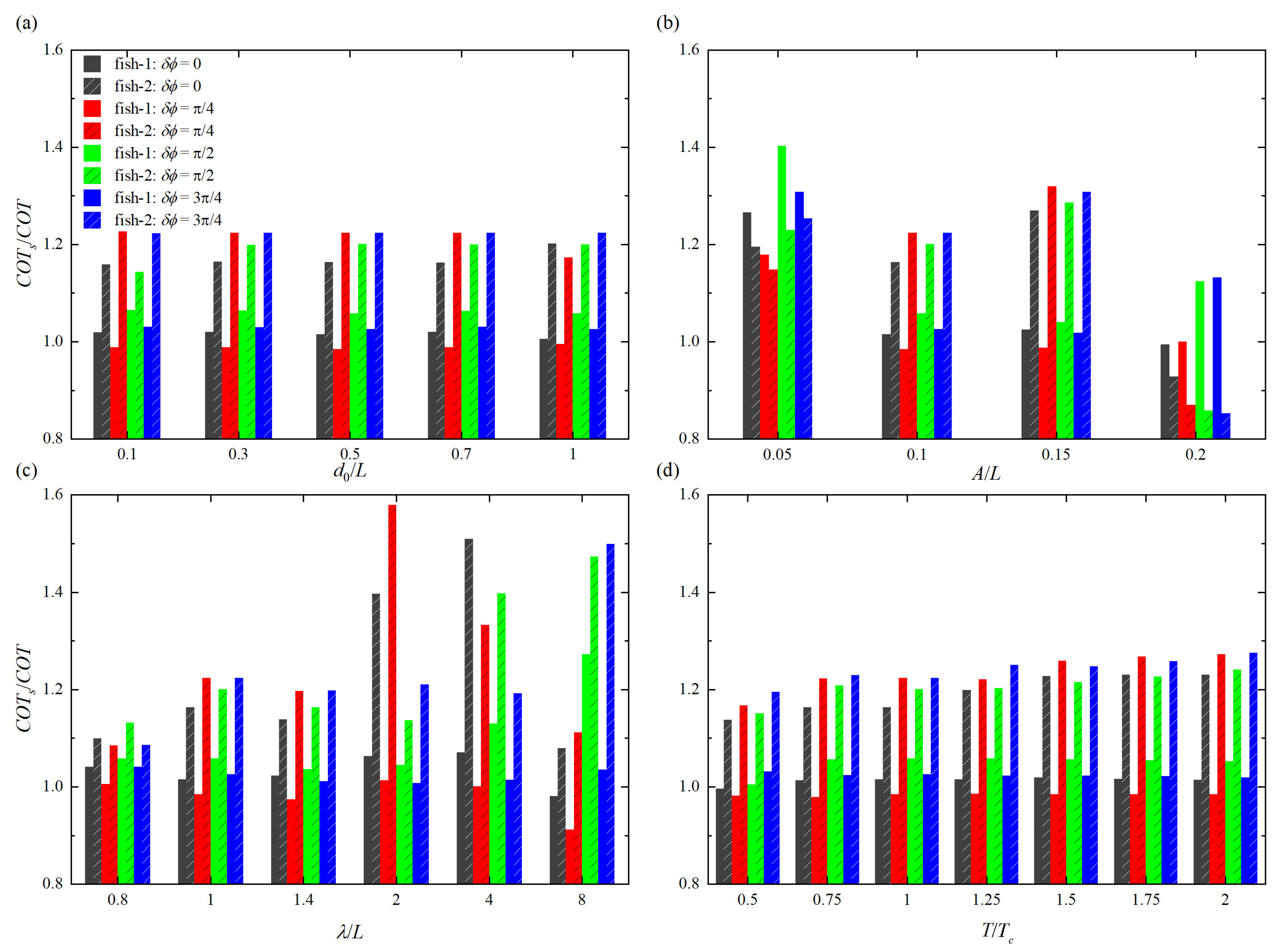
3.1.2. Effect on Energy-Saving Efficiency
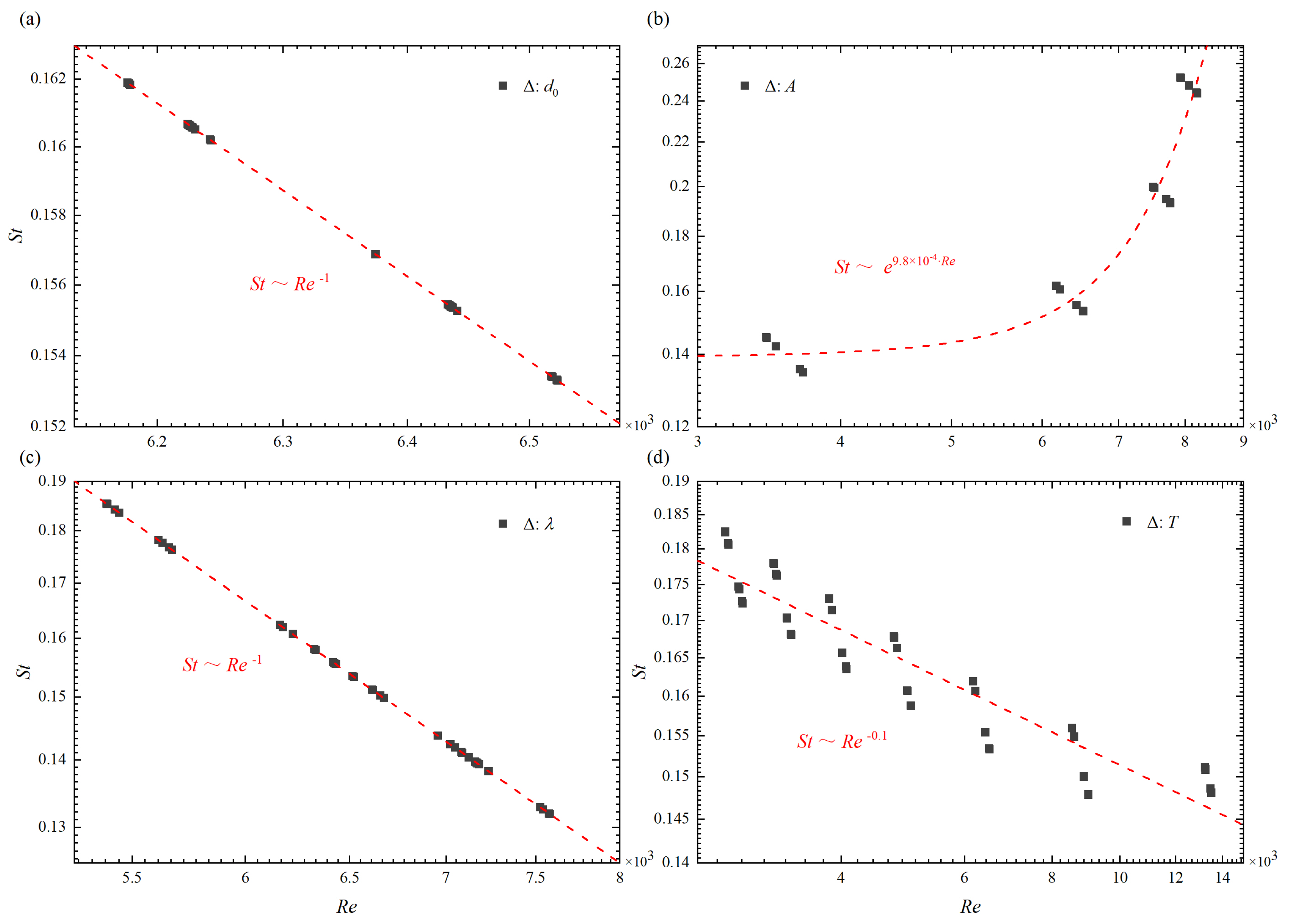
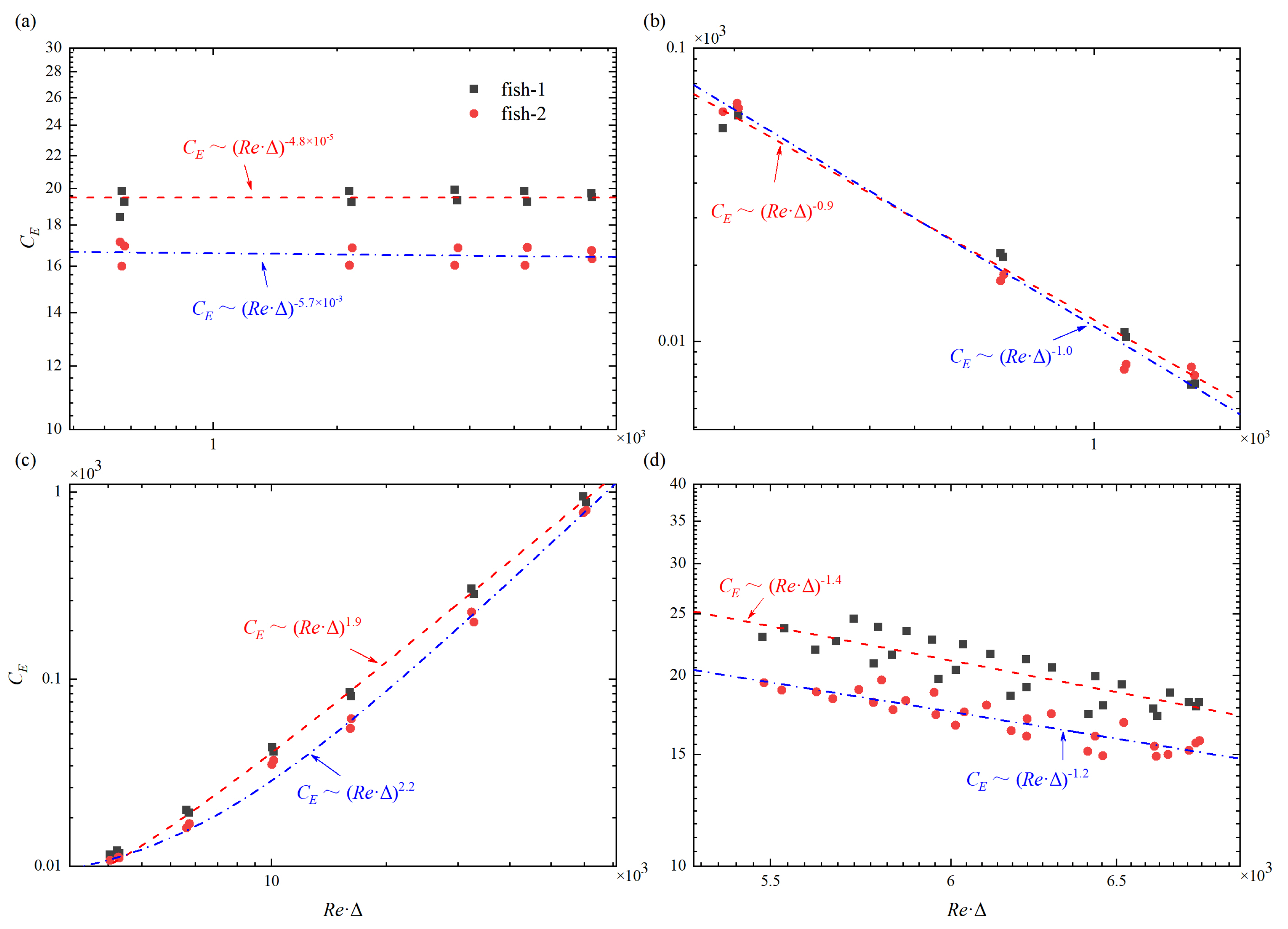
3.2. Scaling Laws for Re, St, and
4. Conclusions
- In most cases, the swimming speed gain in the anti-phase swimming is smaller than that in other phases, and the speed gain shows a fixed trend under different phase differences. When the initial separation distance is larger, the speed gain is smaller. In addition, high swimming speed does not mean high speed gain.
- The rear fish is not always more energy-saving-efficient than the upstream fish. When the tail beat amplitude is either large or small, the energy consumption of the rear fish is higher than that of the upstream fish. Except for either large or small tail beat amplitude, the rear fish is more energy-saving-efficient than the upstream fish in most cases.
- Swimming in a tandem arrangement is not always more energy-saving-efficient than an isolated fish.
- The higher tail beat amplitude is the least friendly to the rear fish, while the lower tail beat amplitude is better for the upstream fish.
- For energy-saving efficiency, the optimal wavelength depends on the phase difference between two fish.
- There are scaling laws related to body kinematics (tail beat amplitude, period of oscillation, and wavelength), arrangement of formation (initial separation distance), and fluid property (kinematic viscosity).
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Value | Unit | Full Name |
| 1 × 10 | m/s | kinematic viscosity of fluid | |
| P | — | N·m/s | power of swimming |
| 1 × 10 | kg/m | fish body density | |
| V | 0.822 × 10 | m | fish body volume |
| — | m/s | constrained Lagrangian body velocity field | |
| — | N/m | constraint force density | |
| 1 × 10 | kg/m | fluid density | |
| f | 0.5-2 | s | tail beat frequency |
| — | s | angular frequency | |
| L | 0.1 | m | fish body length |
| 0.00026 | m | mesh size | |
| 0.0005 | s | time step | |
| m | 0.822 | kg | mass of fish |
| — | N | net force on the fish body in the x-direction | |
| — | N·m/s | mean net power spent | |
| — | N·m/s | mean lateral power spent | |
| u | — | m/s | forward swimming speed |
| — | m/s | mean swimming speed | |
| — | m/s | fluctuation of swimming speed | |
| — | N | cost and transport | |
| — | — | energy-consumption coefficient | |
| W | — | N·m | mean work done of fish swimming |
| 0.01–0.1 | m | initial separation distance | |
| A | 0.005–0.02 | m | tail beat amplitude |
| 0.08–0.8 | m | body wavelength | |
| T | 0.5–2.0 | s | period of oscillation |
| 1 | s | characteristic period of oscillation | |
| t | — | s | time |
| — | rad | phase difference | |
| 2897–13,513 | — | Reynolds number | |
| 0.13–0.25 | — | Strouhal number | |
| — | — | index of scaling law | |
| — | — | variable of swimming parameters | |
| — | — | power coefficient | |
| — | — | cell center of the grid | |
| — | — | position of a marker point |
References
- Weihs, D. Hydromechanics of fish schooling. Nature 1973, 241, 290–291. [Google Scholar] [CrossRef]
- Shaw, E. Schooling fishes. Am. Sci. 1978, 66, 166–175. [Google Scholar] [CrossRef]
- Pitcher, T.J.; Parrish, J.K. Functions of shoaling behavior in teleosts. In The Behaviour of Teleost Fishes; Springer: Boston, MA, USA, 1993; pp. 363–439. [Google Scholar]
- Godin, J.G.J.; Morgan, M.J. Predator avoidance and school size in a cyprinodontid fish, the banded killifish (Fundulus diaphanous lesueur). Behav. Ecol. Sociobiol. 1985, 16, 105–110. [Google Scholar] [CrossRef]
- Magurran, A.E.; Higham, A. Information transfer across fish shoals under predator threat. Ethology 1988, 78, 153–158. [Google Scholar] [CrossRef]
- Pitcher, T.J.; Magurran, A.E.; Winfield, I.J. Fish in larger shoals find food faster. Behav. Ecol. Sociobiol. 1982, 10, 149–151. [Google Scholar] [CrossRef]
- Fish, F.E. Energetics of swimming and flying in formation. Comments Theor. Biol. 1999, 5, 283–304. [Google Scholar]
- Killen, S.S.; Marras, S.; Steffensen, J.F.; McKenzie, D.J. Aerobic capacity influences the spatial position of individuals within fish schools. Biol. Sci. 2012, 279, 357–364. [Google Scholar] [CrossRef] [Green Version]
- Hemelrijk, C.K.; Reid, D.A.P.; Hildenbrandt, H.; Padding, J.T. The increased efficiency of fish swimming in a school. Fish Fish. 2015, 16, 511–521. [Google Scholar] [CrossRef] [Green Version]
- Chao, L.; Pan, G.; Zhang, D.; Yan, G. On the two staggered swimming fish. Chaos Solitons Fractals 2019, 129, 260–262. [Google Scholar] [CrossRef]
- Park, S.; Sung, H. Hydrodynamics of flexible fins propelled in tandem, diagonal, triangular and diamond configurations. J. Fluid Mech. 2018, 840, 154–189. [Google Scholar] [CrossRef]
- Deng, J.; Shao, X.; Yu, Z. Hydrodynamic Studies on Two Traveling Wavy Foils in Tandem Arrangement. Phys. Fluids 2007, 19, 113104. [Google Scholar] [CrossRef]
- Kang, L.; Peng, Z.; Huang, H.; Lu, X.; Cui, W. Active external control effect on the collective locomotion of two tandem self-propelled flapping plates. Phys. Fluids 2021, 33, 101901. [Google Scholar] [CrossRef]
- Novati, G.; Verma, S.; Alexeev, D.; Rossinelli, D.; van Rees, W.M.; Koumoutsakos, P. Synchronisation through learning for two self-propelled swimmers. Bioinspir. Biomimetics 2017, 12, 036001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, X.; Wu, J.; Zhang, T.; Yang, L. Flow-mediated organization of two freely flapping swimmers. J. Fluid Mech. 2021, 912, A37. [Google Scholar] [CrossRef]
- Lin, X.; Wu, J.; Zhang, T.; Yang, L. Self-organization of multiple self-propelling flapping foils: Energy saving and increased speed. J. Fluid Mech. 2020, 884, R1. [Google Scholar] [CrossRef]
- Lin, X.; Wu, J.; Yang, L.; Dong, H. Two-dimensional hydrodynamic schooling of two flapping swimmers initially in tandem formation. J. Fluid Mech. 2022, 941, A29. [Google Scholar] [CrossRef]
- Herskin, J.; Steffensen, J.F. Energy savings in sea bass swimming in a school: Measurements of tail beat frequency and oxygen consumption at different swimming speeds. J. Fish Biol. 1998, 53, 366–376. [Google Scholar] [CrossRef]
- Marras, S.; Killen, S.S.; Lindstrom, J.; Mckenzie, D.J.; Steffensen, J.F.; Domenici, P. Fish swimming in schools save energy regardless of their spatial position. Behav. Ecol. Sociobiol. 2015, 69, 219–226. [Google Scholar] [CrossRef] [Green Version]
- Svendsen, J.C.; Skov, J.; Bildsoe, M.; Steffensen, J.F. Intra-school positional preference and reduced tail beat frequency in trailing positions in schooling roach under experimental conditions. J. Fish Biol. 2003, 32, 834–846. [Google Scholar] [CrossRef] [Green Version]
- Bhalla, A.P.S.; Rahul, B.; Griffith, B.E.; Neelesh, A.P. A unified mathematical framework and an adaptive numerical method for fluid–structure interaction with rigid, deforming, and elastic bodies. J. Comput. Phys. 2013, 250, 446–476. [Google Scholar] [CrossRef]
- Griffith, B.E.; Hornung, D.; McQueen, D.M.; Peskin, C.S. An adaptive, formally second order accurate version of the immersed boundary method. J. Comput. Phys. 2007, 223, 10–49. [Google Scholar] [CrossRef]
- Zhao, H.; Freund, J.B.; Moser, R.D. A fixed-mesh method for incompressible flow-structure systems with finite solid deformations. J. Comput. Phys. 2008, 227, 3114–3140. [Google Scholar] [CrossRef]
- Herschlag, G.; Miller, L. Reynolds number limits for jet propulsion: A numerical study of simplified jellyfish. J. Theor. Biol. 2011, 285, 84–95. [Google Scholar] [CrossRef] [Green Version]
- Tytell, E.D.; Hsu, C.Y.; Williams, T.L.; Cohen, A.H.; Fauci, L.J. Interactions between internal forces, body stiffness, and fluid environment in a neuromechanical model of lamprey swimming. Proc. Natl. Acad. Sci. USA 2010, 107, 19832–19837. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Wu, C. An adaptive version of ghost-cell immersed boundary method for incompressible flows with complex stationary and moving boundaries. Sci. China Phys. Mech. Astron. 2010, 53, 923–932. [Google Scholar] [CrossRef]
- Borazjani, I.; Sotiropoulos, F. On the role of form and kinematics on the hydrodynamics of self-propelled body/caudal fin swimming. J. Exp. Biol. 2010, 213, 89–107. [Google Scholar] [CrossRef] [Green Version]
- Tytell, E.D.; Lauder, G.V. The hydrodynamics of eel swimming. I: Wake structure. J. Exp. Biol. 2004, 207, 1825–1841. [Google Scholar] [CrossRef] [Green Version]
- Videler, J.J.; Hess, F. Fast continuous swimming of two pelagic predators, saithe (Pollachius virens) and mackerel (Scomber scombrus): A kinematic analysis. J. Exp. Biol. 1984, 109, 209–228. [Google Scholar] [CrossRef]
- Pedley, T.J.; Hill, S.J. Large-amplitude undulatory fish swimming: Fluid mechanics coupled to internal mechanics. J. Exp. Biol. 1999, 202, 3431–3438. [Google Scholar] [CrossRef]
- Tytell, E.D. Do trout swim better than eels? Challeges for estimating performance based on the wake of self-propelled bodies. Exp. Fluids. 2007, 43, 701–712. [Google Scholar] [CrossRef]
- Bale, R.; Hao, M.; Bhalla, A.P.S.; Patankar, N.A. Energy efficiency and allometry of movement of swimming and flying animals. Proc. Natl Acad. Sci. USA 2014, 111, 7517–7521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Griffith, B.E.; Bhalla, A.P.S. IBAMR: An Adaptive and Distributed-memory Parallel Implementation of the Immersed Boundary Method. Available online: https://ibamr.github.io/ (accessed on 9 August 2020).
- Lauder, G.V. Function of the caudal fin during locomotion in fishes: Kinematics, flow visualization, and evolutionary patterns. Am. Zool. 2000, 40, 101–122. [Google Scholar] [CrossRef] [Green Version]
- Lauder, G.V.; Nauen, J.C.; Drucker, E.G. Experimental hydrodynamics and evolution: Function of median fins in ray-finned fishes. Integr. Comput. Biol. 2002, 42, 1009–1017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dabiri, J.O.; Gharib, M. Sensitivity analysis of kinematic approximations in dynamic medusan swimming models. J. Exp. Biol. 2003, 206, 3675–3680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Curet, O.M.; Patankar, N.A.; Lauder, G.V.; MacIver, M.A. Aquatic manoeuvering with counter-propagating waves: A novel locomotive strategy. J. R. Soc. Interface 2011, 8, 1041–1050. [Google Scholar] [CrossRef] [Green Version]
- Curet, O.M.; Patankar, N.A.; Lauder, G.V.; MacIver, M.A. Mechanical properties of a bio-inspired robotic knifefish with an undulatory propulsor. Bioinspir. Biomimetics 2011, 6, 026004. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Torres, R.; Curet, O.M.; Lauder, G.V.; MacIver, M.A. Kinematics of the ribbon fin in hovering and swimming of the electric ghost knifefish. J. Exp. Biol. 2013, 216, 823–834. [Google Scholar]
- Nangia, N.; Johansen, H.; Patankar, N.A.; Bhalla, A.P.S. A moving control volume approach to computing hydrodynamic forces and torques on immersed bodies. J. Comput. Phys. 2017, 347, 437–462. [Google Scholar] [CrossRef] [Green Version]
- Hornung, R.D.; Kohn, S.R. Managing application complexity in the SAMRAI object-oriented framework. Concurr. Comput. 2002, 14, 347–368. [Google Scholar] [CrossRef]
- Hornung, R.D.; Wissink, A.M.; Kohn, S.R. Managing complex data and geometry in parallel structured AMR applications. Eng. Comput. 2006, 22, 181–195. [Google Scholar] [CrossRef]
- SAMRAI: Structured Adaptive Mesh Refinement Application Infrastructure. Available online: http://www.llnl.gov/CASC/SAMRAI (accessed on 9 August 2020).
- Berger, M.J.; Rigoutsos, I. An algorithm for point clustering and grid generation. IEEE. Trans. Syst. Man. Cybern. 1991, 21, 1278–1286. [Google Scholar] [CrossRef]
- Griffith, B.E. An accurate and efficient method for the incompressible Navier-Stokes equations using the projection method as a preconditioner. J. Comput. Phys. 2009, 228, 7565–7595. [Google Scholar] [CrossRef]
- Griffith, B.E.; Patankar, N.A. Immersed methods for fluid-structure interaction. Annu. Rev. Fluid Mech. 2020, 52, 421–448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balay, S.; Buschelman, K.; Gropp, W.D.; Kaushik, D.; Knepley, M.G.; McInnes, L.C.; Smith, B.F.; Zhang, H. PETSc Web Page 2009. Available online: http://www.mcs.anl.gov/petsc (accessed on 9 August 2020).
- Bale, R.; Bhalla, A.P.S.; Neveln, I.D.; MacIver, M.A.; Patankar, N.A. Convergent evolution of mechanically optimal locomotion in aquatic invertebrates and vertebrates. PLoS Biol. 2015, 13, 1002123. [Google Scholar] [CrossRef] [Green Version]
- Bhalla, A.P.S.; Griffith, B.E.; Patankar, N.A. A forced damped oscillation framework for undulatory swimming provides new insights into how propulsion arises in active and passive swimming. PLoS Comput. Biol. 2013, 9, 100309. [Google Scholar] [CrossRef] [Green Version]
- Dombrowski, T.; Jones, S.K.; Bhalla, A.P.S.; Katsikis, G.; Griffith, B.E.; Klotsa, D. Transition in swimming direction in a model self-propelled inertial swimmer. Phys. Rev. Fluid 2019, 4, 021101. [Google Scholar] [CrossRef]
- Hoover, A.P.; Tytell, E. Decoding the Relationships between Body Shape, Tail Beat Frequency, and Stability for Swimming Fish. Fluids 2020, 5, 215. [Google Scholar] [CrossRef]
- Patel, N.K.; Bhalla, A.P.S.; Patankar, N.A. A new constraint-based formulation for hydrodynamically resolved computational neuromechanics of swimming animals. J. Comput. Phys. 2018, 375, 684–716. [Google Scholar] [CrossRef]
- Voesenk, C.J.; Li, G.; Muijres, F.T.; van Leeuwen, J.L. Experimental–numerical method for calculating bending moments in swimming fish shows that fish larvae control undulatory swimming with simple actuation. PLoS Biol. 2020, 18, 3000462. [Google Scholar] [CrossRef]
- Zhang, D.; Pan, G.; Chao, L.; Zhang, Y. Effects of Reynolds number and thickness on an undulatory self-propelled foil. Phys. Fluids 2018, 30, 071902. [Google Scholar] [CrossRef]
- Nangia, N.; Patankar, N.A.; Bhalla, A.P.S. A DLM immersed boundary method based wave-structure interaction solver for high density ratio multiphase flows. J. Comput. Phys. 2019, 398, 108804. [Google Scholar] [CrossRef] [Green Version]
- Khalid, M.; Imran, A.; Dong, H. Hydrodynamics of a Tandem Fish School with Asynchronous Undulation of Individuals. J. Fluids Struc. 2016, 66, 19–35. [Google Scholar] [CrossRef] [Green Version]
- Diana, R.G.; Aider, J.L.; Wesfreid, J.E. Transitions in the wake of a flapping foil. Phys. Rev. E 2008, 77, 016308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schnipper, T.; Andersen, A.; Bohr, T. Vortex wakes of a flapping foil. J. Fluid Mech. 2009, 633, 411–423. [Google Scholar] [CrossRef] [Green Version]
- Williamson, C.H.K.; Roshko, A. Vortex formation in the wake of an oscillating cylinder. J. Fluids Struc. 1988, 2, 355–381. [Google Scholar] [CrossRef]
- Han, P.; Pan, Y.; Liu, G.; Dong, H. Propulsive performance and vortex wakes of multiple tandem foils pitching in-line. J. Fluids Struc. 2022, 108, 103422. [Google Scholar] [CrossRef]
- Ramananarivo, S.; Fang, F.; Oza, A.; Zhang, J.; Ristroph, L. Flow interactions lead to orderly formations of flapping wings in forward flight. Phys. Rev. Fluids 2016, 1, 071201. [Google Scholar] [CrossRef]
- Williams, T.M.; Friedl, W.A.; Haun, J. Balancing power and speed in bottlenose dolphins (Tursiops truncatus). Symp. Zool. Soc. Lond. 1993, 66, 383–394. [Google Scholar]
- Novati, G.; Verma, S.; Alexeev, D.; Rossinelli, D.; van Rees, W.M.; Koumoutsakos, P. Synchronised Swimming of Two Fish. arXiv 2016, arXiv:1610.04248. [Google Scholar]
- Gazzola, M.; Argentina, M.; Mahadevan, L. Scaling macroscopic aquatic locomotion. Nat. Phys. 2014, 10, 758–761. [Google Scholar] [CrossRef] [Green Version]


| (( − )/) × 100% | |||||
|---|---|---|---|---|---|
| 0 | /4 | /2 | 3/4 | ||
| d0 | 0.10L | 6.8% | 5.4% | 4.4% | 2.0% |
| 0.30L | 6.8% | 5.4% | 1.2% | 2.0% | |
| 0.50L | 6.8% | 5.4% | 1.2% | 2.0% | |
| 0.70L | 6.8% | 5.4% | 1.2% | 2.0% | |
| 1.00L | 2.3% | 2.1% | 1.2% | 2.0% | |
| A | 0.05L | 19.5% | 18.7% | 11.0% | 13.1% |
| 0.10L | 6.8% | 5.4% | 1.2% | 2.0% | |
| 0.15L | 4.4% | 3.5% | 0.8% | 1.1% | |
| 0.20L | 3.1% | 1.4% | 4.7% | 4.9% | |
| 0.80L | 7.3% | 6.2% | 2.2% | 3.1% | |
| 1.00L | 6.8% | 5.4% | 1.2% | 2.0% | |
| 1.40L | 5.4% | 4.7% | 1.4% | 2.4% | |
| 2.00L | 8.4% | 7.6% | 0.8% | 1.9% | |
| 4.00L | 9.9% | 8.7% | 1.5% | 2.4% | |
| 8.00L | 8.8% | 7.2% | 4.4% | 13.1% | |
| T | 0.50 | 2.9% | 2.5% | 0.8% | 0.9% |
| 0.75 | 6.6% | 5.2% | 1.1% | 1.8% | |
| 1.00 | 6.8% | 5.4% | 1.2% | 2.0% | |
| 1.25 | 7.0% | 5.7% | 1.3% | 2.2% | |
| 1.50 | 7.4% | 5.9% | 1.5% | 2.4% | |
| 1.75 | 7.5% | 6.2% | 1.6% | 2.6% | |
| 2.00 | 7.7% | 6.4% | 1.8% | 2.8% | |
| (( − )/) × 100% | ||||||
|---|---|---|---|---|---|---|
| 0 | /4 | /2 | 3/4 | |||
| d0 | 0.10L | fish-1 | 1.9% | −1.1% | 6.1% | 2.9% |
| fish-2 | 13.7% | 18.3% | 12.5% | 1832% | ||
| 0.30L | fish-1 | 2.0% | −1.1% | 6.0% | 2.9% | |
| fish-2 | 14.1% | 18.3% | 16.7% | 18.3% | ||
| 0.50L | fish-1 | 1.5% | −1.6% | 5.5% | 2.5% | |
| fish-2 | 14.1% | 18.3% | 16.7% | 18.3% | ||
| 0.70L | fish-1 | 1.9% | −1.1% | 6.0% | 2.9% | |
| fish-2 | 14.0% | 18.3% | 16.7% | 18.3% | ||
| 1.00L | fish-1 | 0.6% | −0.5% | 5.5% | 2.5% | |
| fish-2 | 16.8% | 14.7% | 16.7% | 18.3% | ||
| A | 0.05L | fish-1 | 21.0% | 15.1% | 28.7% | 23.5% |
| fish-2 | 16.3% | 12.9% | 18.6% | 20.2% | ||
| 0.10L | fish-1 | 1.5% | −1.6% | 5.5% | 2.5% | |
| fish-2 | 14.1% | 18.3% | 16.7% | 18.3% | ||
| 0.15L | fish-1 | 2.5% | −1.2% | 3.9% | 1.8% | |
| fish-2 | 21.2% | 24.2% | 22.2% | 23.5% | ||
| 0.20L | fish-1 | −0.6% | 0.1% | 11.1% | 11.7% | |
| fish-2 | −7.7% | −15.0% | −16.5% | −17.2% | ||
| 0.80L | fish-1 | 4.0% | 0.5% | 5.5% | 3.9% | |
| fish-2 | 9.1% | 7.8% | 11.6% | 7.9% | ||
| 1.00L | fish-1 | 1.5% | −1.6% | 5.5% | 2.5% | |
| fish-2 | 14.1% | 18.3% | 16.7% | 18.3% | ||
| 1.40L | fish-1 | 2.3% | −2.7% | 3.5% | 1.1% | |
| fish-2 | 12.2% | 16.4% | 14.0% | 16.5% | ||
| 2.00L | fish-1 | 5.9% | 1.3% | 4.3% | 0.7% | |
| fish-2 | 28.4% | 36.7% | 12.0% | 17.4% | ||
| 4.00L | fish-1 | 6.6% | 0.1% | 11.5% | 1.4% | |
| fish-2 | 33.8% | 25.0% | 28.5% | 16.1% | ||
| 8.00L | fish-1 | −2.0% | −9.7% | 21.4% | 3.4% | |
| fish-2 | 7.4% | 10.1% | 32.1% | 33.3% | ||
| T | 0.50 | fish-1 | −0.4% | −1.8% | 0.5% | 3.0% |
| fish-2 | 12.1% | 14.3% | 13.1% | 16.3% | ||
| 0.75 | fish-1 | 1.3% | −2.2% | 5.3% | 2.4% | |
| fish-2 | 14.0% | 18.2% | 17.2% | 18.7% | ||
| 1.00 | fish-1 | 1.5% | −1.6% | 5.5% | 2.5% | |
| fish-2 | 14.1% | 18.3% | 16.7% | 18.3% | ||
| 1.25 | fish-1 | 1.5% | −1.5% | 5.5% | 2.3% | |
| fish-2 | 16.6% | 18.1% | 16.9% | 20.0% | ||
| 1.50 | fish-1 | 1.9% | −1.6% | 5.3% | 2.3% | |
| fish-2 | 18.6% | 20.6% | 17.7% | 19.8% | ||
| 1.75 | fish-1 | 1.6% | −1.5% | 5.2% | 2.1% | |
| fish-2 | 18.7% | 21.1% | 18.5% | 20.5% | ||
| 2.00 | fish-1 | 1.4% | −1.6% | 5.0% | 1.9% | |
| fish-2 | 18.7% | 21.4% | 19.4% | 21.6% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Wu, J. Hydrodynamic Interaction of Two Self-Propelled Fish Swimming in a Tandem Arrangement. Fluids 2022, 7, 208. https://doi.org/10.3390/fluids7060208
Yang D, Wu J. Hydrodynamic Interaction of Two Self-Propelled Fish Swimming in a Tandem Arrangement. Fluids. 2022; 7(6):208. https://doi.org/10.3390/fluids7060208
Chicago/Turabian StyleYang, Dewu, and Jie Wu. 2022. "Hydrodynamic Interaction of Two Self-Propelled Fish Swimming in a Tandem Arrangement" Fluids 7, no. 6: 208. https://doi.org/10.3390/fluids7060208
APA StyleYang, D., & Wu, J. (2022). Hydrodynamic Interaction of Two Self-Propelled Fish Swimming in a Tandem Arrangement. Fluids, 7(6), 208. https://doi.org/10.3390/fluids7060208







