Parameterization of the Model of Artificial Clay Freezing Considering the Effect of Pore Water Salinity
Abstract
:1. Introduction
2. Experimental Study
2.1. Methods
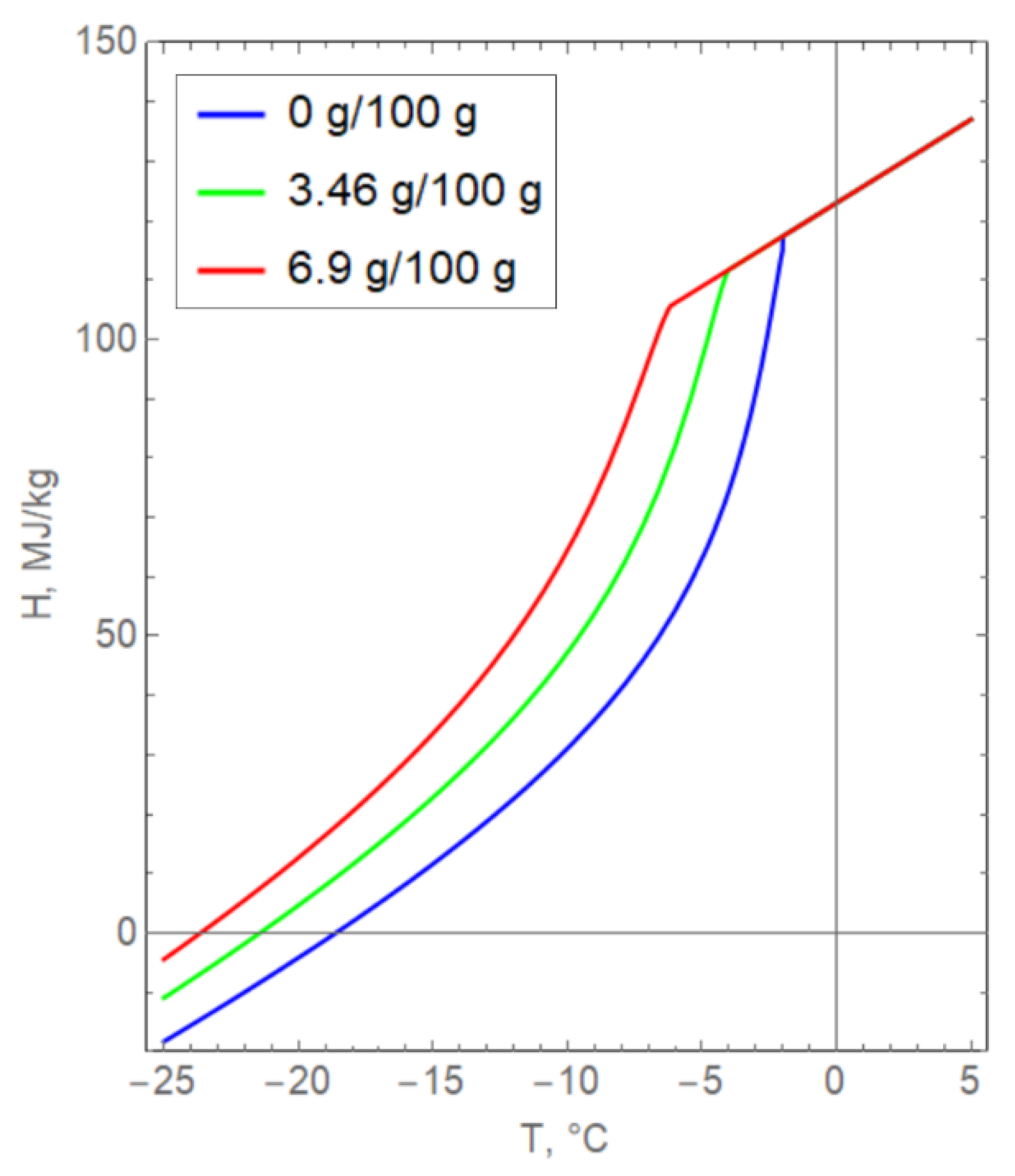
2.2. Results
3. Mathematical Model
- The increments of the soil specific enthalpy ΔH in the internal nodes are calculated from Formula (3).
- The corresponding increments of nodal temperatures ΔT, volume fractions of unfrozen water Δγ, and salinity Δs are determined from the given enthalpy increment ΔH:
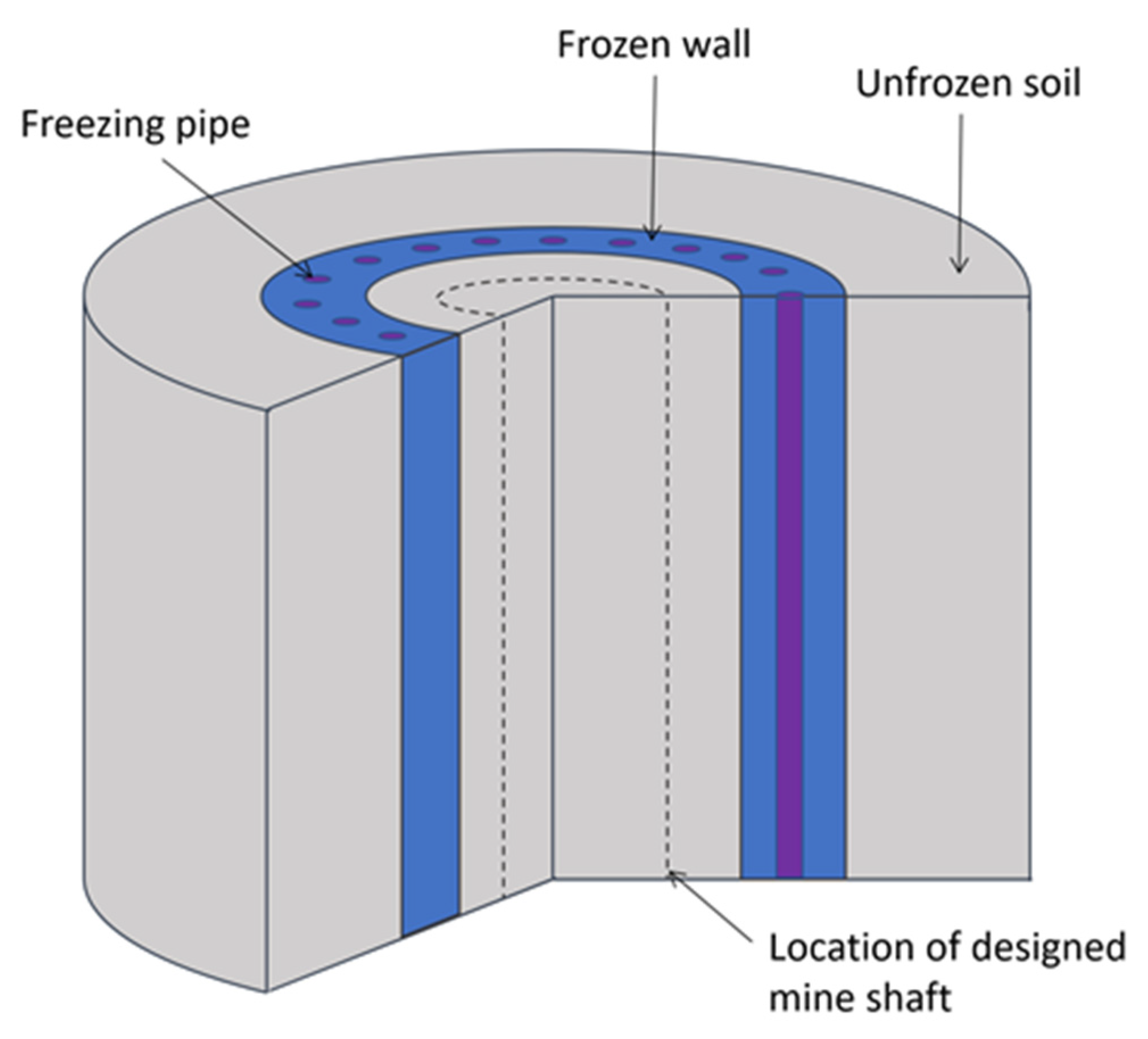
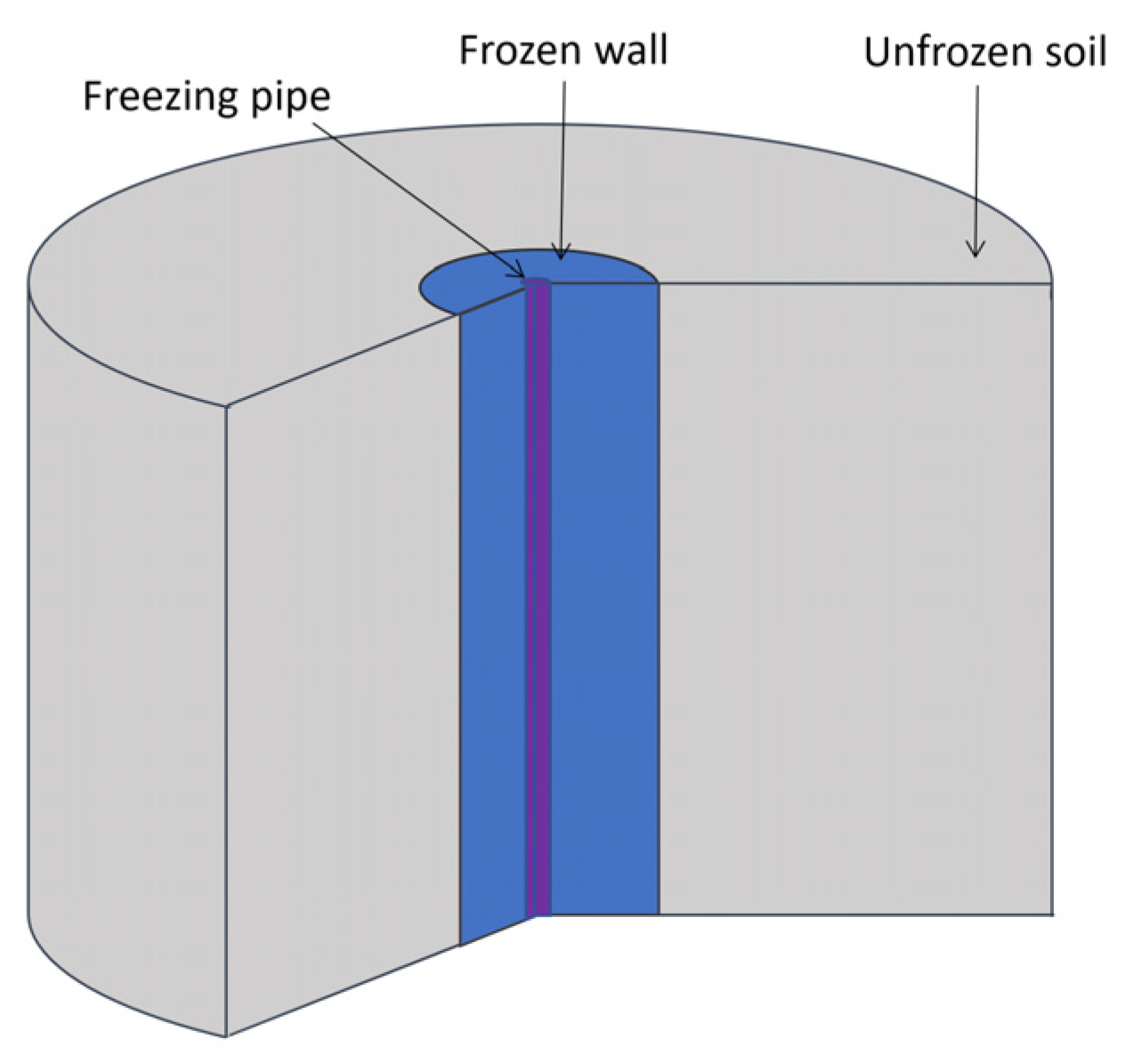
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Levin, L.Y.; Semin, M.A.; Parshakov, O.S. Improving methods of frozen wall state prediction for mine shafts under con-struction using distributed temperature measurements in test wells. J. Min. Inst. 2019, 237, 268–274. [Google Scholar] [CrossRef]
- Olkhovikov; Yu, P. Support of Permanent Openings of Potash and Salt Mines; Nedra: Moscow, Russia, 1984; 238p. (In Russian) [Google Scholar]
- Semin, M.A.; Zaitsev, A.V.; Levin, L.Y. Numerical Solution of the Inverse Stefan Problem in the Analysis of the Artificial Freezing of a Rock Mass. Math. Model. Comput. Simul. 2021, 13, 877–886. [Google Scholar] [CrossRef]
- Banin, A.; Anderson, D.M. Effects of Salt Concentration Changes During Freezing on the Unfrozen Water Content of Porous Materials. Water Resour. Res. 1974, 10, 124–128. [Google Scholar] [CrossRef]
- Bing, H.; Ma, W. Laboratory investigation of the freezing point of saline soil. Cold Reg. Sci. Technol. 2011, 67, 79–88. [Google Scholar] [CrossRef]
- Wan, X.; Lai, Y.; Wang, C. Experimental Study on the Freezing Temperatures of Saline Silty Soils. Permafr. Periglac. Process. 2015, 26, 175–187. [Google Scholar] [CrossRef]
- Chuvilin, E.M.; Bukhanov, B.A.; Mukhametdinova, A.Z.; Grechishcheva, E.S.; Sokolova, N.S.; Alekseev, A.G.; Istomin, V.A. Freezing point and unfrozen water contents of permafrost soils: Estimation by the water potential method. Cold Reg. Sci. Technol. 2022, 196, 103488. [Google Scholar] [CrossRef]
- Yong, R.N.; Cheung, C.H.; Sheeran, D.E. Prediction of Salt Influence on Unfrozen Water Content in Frozen Soils. Dev. Geotech. Eng. 1979, 137–155. [Google Scholar] [CrossRef]
- Xiao, Z.; Lai, Y.; Zhang, M. Study on the freezing temperature of saline soil. Acta Geotechnica 2018, 13, 195–205. [Google Scholar] [CrossRef]
- Wang, C.; Lai, Y.; Yu, F.; Li, S. Estimating the freezing-thawing hysteresis of chloride saline soils based on the phase transition theory. Appl. Therm. Eng. 2018, 135, 22–33. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, J.; Wang, S.; Xu, J.; Yang, Y. Effect of freeze-thaw on freezing point of a saline loess. Cold Reg. Sci. Technol. 2019, 170, 102922. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, J.; Shi, X.-Y.; Zhou, G.-Q. Practical models describing hysteresis behavior of unfrozen water in frozen soil based on similarity analysis. Cold Reg. Sci. Technol. 2018, 157, 215–223. [Google Scholar] [CrossRef]
- Liu, J.; Yang, P.; Yang, Z.J. Water and salt migration mechanisms of saturated chloride clay during freeze-thaw in an open system. Cold Reg. Sci. Technol. 2021, 186, 103277. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, S.; Wang, Q.; Wang, G.; Liu, Y.; Peng, W.; Liu, Y. Experimental investigation of water migration characteristics for saline soil. Pol. J. Environ. Stud. 2019, 28, 1495–1505. [Google Scholar] [CrossRef] [Green Version]
- Jochem, M.; Körber, C. A numerical solution of the coupled heat and mass transfer problem of non-planar solidification and melting of aqueous solutions. Warmeund Stoffubertrag. 1993, 28, 195–204. [Google Scholar] [CrossRef]
- Vasil’Ev, V.I.; Maksimov, A.M.; Petrov, E.E.; Tsypkin, G.G. Mathematical model of the freezing-thawing of saline frozen soil. J. Appl. Mech. Technol. Phys. 1995, 36, 689–696. [Google Scholar] [CrossRef]
- Lucas, T.; Chourot, J.; Bohuon, P.; Flick, D. Freezing of a porous medium in contact with a concentrated aqueous freezant: Numerical modelling of coupled heat and mass transport. Int. J. Heat Mass Transf. 2001, 44, 2093–2106. [Google Scholar] [CrossRef]
- Watanabe, K.; Mizoguchi, M. Amount of unfrozen water in frozen porous media saturated with solution. Cold Reg. Sci. Technol. 2002, 34, 103–110. [Google Scholar] [CrossRef]
- Qin, B.; Rui, D.; Ji, M.; Chen, X.; Wang, S. Research on influences of groundwater salinity and flow velocity on artificial frozen wall. Transp. Geotech. 2022, 34, 100739. [Google Scholar] [CrossRef]
- Plekhov, O.; Panteleev, I.; Kostina, A.; Levin, L. The effect of cryogenic suction on the monitoring data of ice barrier for-mation in a porous water-saturated soil. Procedia Struct. Integr. 2019, 17, 602–609. [Google Scholar] [CrossRef]
- Rouabhi, A.; Jahangir, E.; Tounsi, H. Modeling heat and mass transfer during ground freezing taking into account the salinity of the saturating fluid. Int. J. Heat Mass Transf. 2018, 120, 523–533. [Google Scholar] [CrossRef]
- Tounsi, H.; Rouabhi, A.; Jahangir, E. Thermo-hydro-mechanical modeling of artificial ground freezing taking into account the salinity of the saturating fluid. Comput. Geotech. 2019, 119, 103382. [Google Scholar] [CrossRef]
- Lade, P.V.; De Boer, R. The concept of effective stress for soil, concrete and rock. Geotechnique 1997, 47, 61–78. [Google Scholar] [CrossRef]
- Zhelnin, M.; Kostina, A.; Prokhorov, A.; Plekhov, O.; Semin, M.; Levin, L. Coupled thermo-hydro-mechanical modeling of frost heave and water migration during artificial freezing of soils for mineshaft sinking. J. Rock Mech. Geotech. Eng. 2021, 14, 537–559. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.; Yu, T.; Wang, G.; Wang, W. Numerical study on the multifield mathematical coupled model of hydraulic-thermal-salt-mechanical in saturated freezing saline soil. Int. J. Geomech. 2018, 18, 04018064. [Google Scholar] [CrossRef]
- Wu, D.; Lai, Y.; Zhang, M. Thermo-hydro-salt-mechanical coupled model for saturated porous media based on crystallization kinetics. Cold Reg. Sci. Technol. 2017, 133, 94–107. [Google Scholar] [CrossRef]
- Zhang, J.; Lai, Y.; Zhao, Y.; Li, S. Study on the mechanism of crystallization deformation of sulfate saline soil during the unidirectional freezing process. Permafr. Periglac. Process. 2020, 32, 102–118. [Google Scholar] [CrossRef]
- Brovka, A.G.; Brovka, G.P.; Dedyulya, I.V. The influence of salt concentration in a detached water of claystone-like clay on the ground freezing point and the dependence of the amount of unfrozen water on temperature. Min. Mech. Eng.-Ing Mach.-Build. 2022, 1, 14–23. [Google Scholar]
- Azmatch, T.F.; Sego, D.C.; Arenson, L.U.; Biggar, K.W. Using soil freezing characteristic curve to estimate the hydraulic conductivity function of partially frozen soils. Cold Reg. Sci. Technol. 2012, 83–84, 103–109. [Google Scholar] [CrossRef]
- Pardo Lara, R.; Berg, A.A.; Warland, J.; Parkin, G. Implications of measurement metrics on soil freezing curves: A simulation of freeze–thaw hysteresis. Hydrol. Processes 2021, 35, e14269. [Google Scholar] [CrossRef]
- Zhelnin, M.S.; Plekhov, O.A.; Semin, M.A.; Levin, L.Y. Numerical solution for an inverse problem about determination of volumetric heat capacity of rock mass during artificial freezing. PNRPU Mech. Bull. 2017, 4, 56–75. [Google Scholar]
- Voller, V.R.; Swaminathan, C.R.; Thomas, B.G. Fixed grid techniques for phase change problems: A review. Int. J. Numer. Methods Eng. 1990, 30, 875–898. [Google Scholar] [CrossRef]
- Nishimura, S.; Gens, A.; Olivella, S.; Jardine, R.J. THM-coupled finite element analysis of frozen soil: Formulation and application. Géotechnique 2009, 59, 159–171. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.M.; Meschke, G. A three-phase thermo-hydro-mechanical finite element model for freezing soils. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 3173–3193. [Google Scholar] [CrossRef]
- Tsytovich, N.A. The Mechanics of Frozen Ground; McGraw-Hill: New York, NY, USA, 1975; 426p. [Google Scholar]
- Panteleev, I.; Kostina, A.; Zhelnin, M.; Plekhov, A.; Levin, L. Intellectual monitoring of artificial ground freezing in the flu-id-saturated rock mass. Procedia Struct. Integr. 2017, 5, 492–499. [Google Scholar] [CrossRef]
- Xiao, Z.; Hou, Z.; Zhu, L.; Dong, X. Experimental investigation of the influence of salt on the phase transition temperature in saline soil. Cold Reg. Sci. Technol. 2021, 183, 103229. [Google Scholar] [CrossRef]
- Wang, M.; Zhu, Y.; Zhao, T.; Cui, L.; Mao, W.; Ye, M.; Yang, J. Chemical characteristics of salt migration in frozen soils during the freezing-thawing period. J. Hydrol. 2022, 606, 127403. [Google Scholar] [CrossRef]
- Leys, J.; Losada-Pérez, P.; Glorieux, C.; Thoen, J. The melting behaviour of water and water–sodium chloride solutions studied by high-resolution Peltier-element-based adiabatic scanning calorimetry. J. Therm. Anal. 2017, 129, 1727–1739. [Google Scholar] [CrossRef]
- Tsai, T.-L.; Chiang, S.-W.; Yang, J.-C. Examination of characteristics method with cubic interpolation for advection–diffusion equation. Comput. Fluids 2006, 35, 1217–1227. [Google Scholar] [CrossRef]
- Semin, M.; Golovatyi, I.; Pugin, A. Analysis of Temperature Anomalies during Thermal Monitoring of Frozen Wall Formation. Fluids 2021, 6, 297. [Google Scholar] [CrossRef]
- Alzoubi, M.A.; Xu, M.; Hassani, F.P.; Poncet, S.; Sasmito, A.P. Artificial ground freezing: A review of thermal and hydraulic aspects. Tunn. Undergr. Space Technol. 2020, 104, 103534. [Google Scholar] [CrossRef]
- Wells, A.J.; Hitchen, J.R.; Parkinson, J.R. Mushy-layer growth and convection, with application to sea ice. Philos. Trans. R. Soc. A 2019, 377, 20180165. [Google Scholar] [CrossRef] [PubMed]
- Castellazzi, G.; De Miranda, S.; Grementieri, L.; Molari, L.; Ubertini, F. Multiphase model for hygrothermal analysis of porous media with salt crystallization and hydration. Mater. Struct. 2016, 49, 1039–1063. [Google Scholar] [CrossRef]

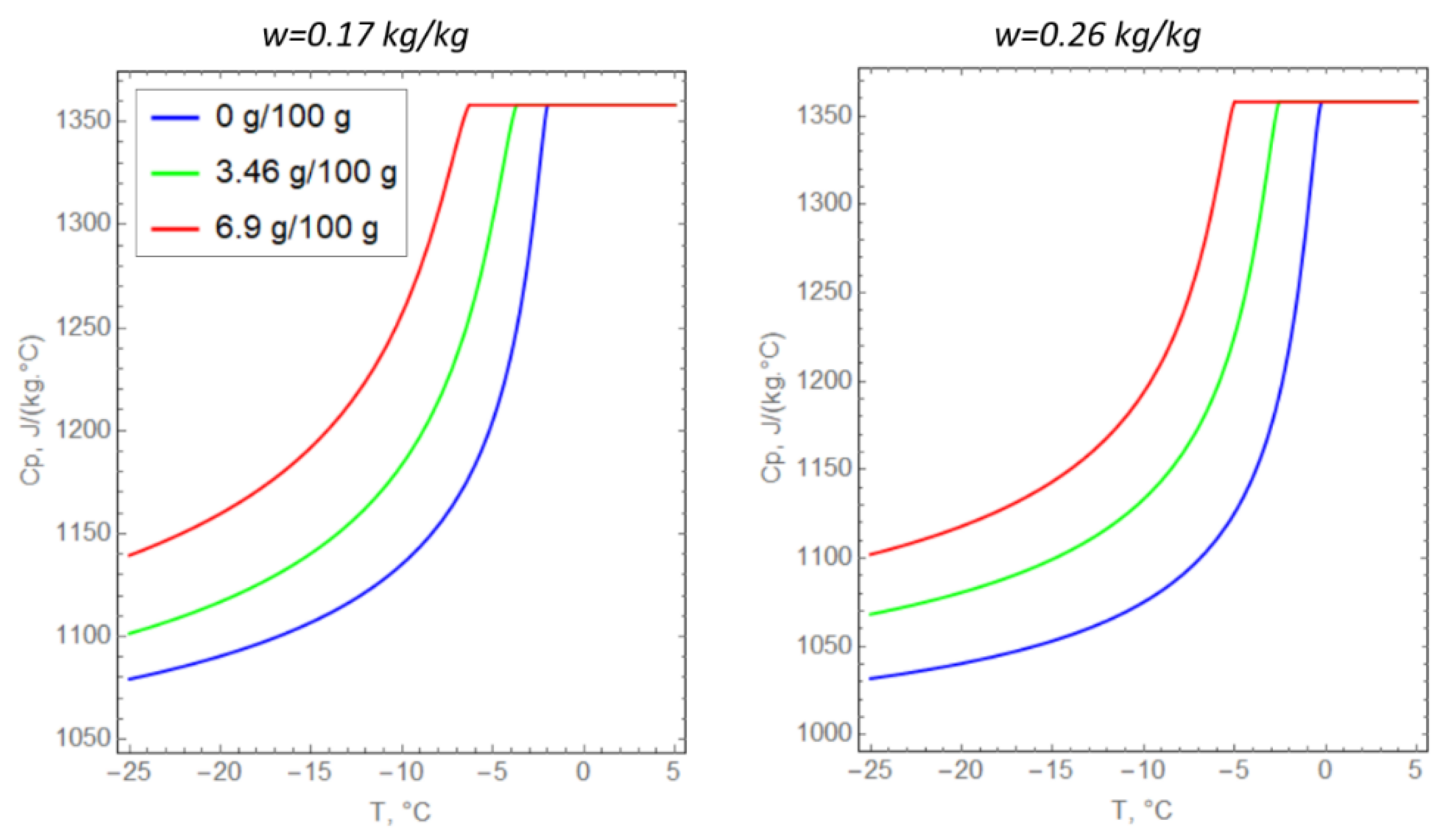
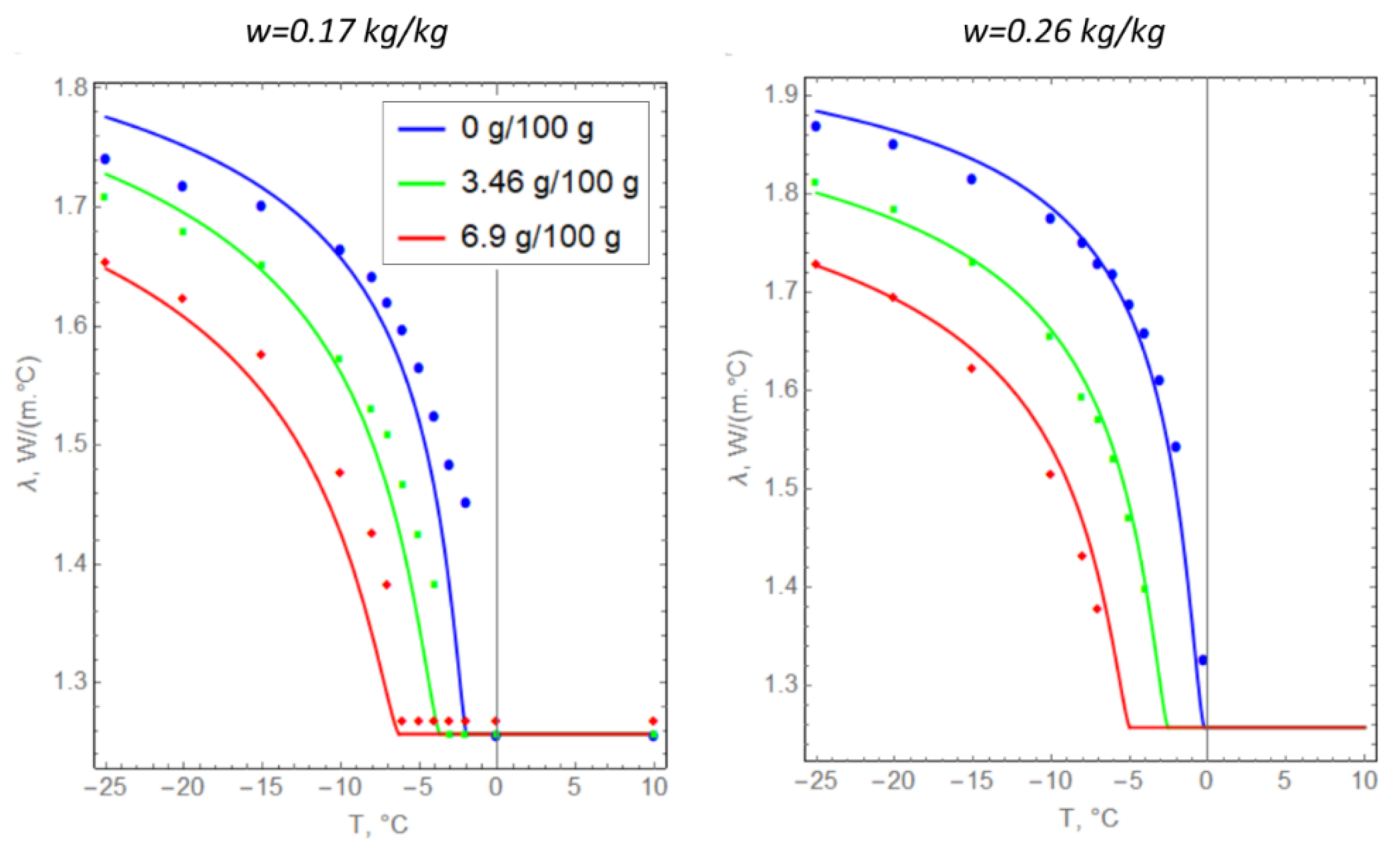


| T, °C | W = 0.17 kg/kg | W = 0.26 kg/kg | ||||
|---|---|---|---|---|---|---|
| NaCl Content, g/100 g of Water | NaCl Content, g/100 g of Water | |||||
| 0 | 3.46 | 6.90 | 0 | 3.46 | 6.90 | |
| −0.5 | – | – | – | 0.255 | – | – |
| −1 | – | – | – | 0.271 | – | – |
| −2 | 0.17 | – | – | 0.169 | – | – |
| −3 | 0.137 | – | – | 0.136 | 0.229 | – |
| −4 | 0.119 | 0.165 | 0.116 | 0.197 | – | |
| −5 | 0.105 | 0.148 | – | 0.101 | 0.174 | 0.251 |
| −6 | 0.094 | 0.133 | – | 0.090 | 0.155 | 0.251 |
| −7 | 0.086 | 0.120 | 0.154 | 0.083 | 0.139 | 0.197 |
| −8 | 0.079 | 0.111 | 0.145 | 0.077 | 0.126 | 0.181 |
| −10 | 0.071 | 0.096 | 0.127 | 0.068 | 0.107 | 0.154 |
| −15 | 0.059 | 0.076 | 0.098 | 0.058 | 0.084 | 0.116 |
| −20 | 0.053 | 0.065 | 0.082 | 0.053 | 0.071 | 0.095 |
| −25 | 0.050 | 0.059 | 0.071 | 0.048 | 0.063 | 0.085 |
| Freezing point, °C | ||||||
| −2.00 | −3.69 | −6.30 | −0.23 | −2.55 | −5.00 | |
| T, °C | W = 0.17 kg/kg | W = 0.26 kg/kg | ||||
|---|---|---|---|---|---|---|
| NaCl Content, g/100 g of Water | NaCl Content, g/100 g of Water | |||||
| 0 | 3.46 | 6.90 | 0 | 3.46 | 6.90 | |
| 10 | 1.254 | 1.254 | 1.267 | 1.104 | 1.104 | 1.117 |
| 0 | 1.254 | 1.254 | 1.267 | – | – | – |
| −0.23 | – | – | – | 1.324 | 1.104 | 1.117 |
| −2 | 1.451 | 1.254 | 1.267 | 1.541 | 1.104 | 1.117 |
| −3 | 1.482 | 1.254 | 1.267 | 1.609 | 1.125 | 1.117 |
| −4 | 1.523 | 1.381 | 1.267 | 1.656 | 1.395 | 1.117 |
| −5 | 1.564 | 1.423 | 1.267 | 1.686 | 1.467 | 1.121 |
| −6 | 1.596 | 1.465 | 1.267 | 1.717 | 1.527 | 1.129 |
| −7 | 1.618 | 1.506 | 1.382 | 1.728 | 1.568 | 1.377 |
| −8 | 1.640 | 1.528 | 1.425 | 1.749 | 1.590 | 1.430 |
| −10 | 1.663 | 1.570 | 1.476 | 1.773 | 1.652 | 1.514 |
| −15 | 1.700 | 1.649 | 1.575 | 1.813 | 1.728 | 1.621 |
| −20 | 1.716 | 1.677 | 1.622 | 1.848 | 1.781 | 1.693 |
| −25 | 1.740 | 1.707 | 1.653 | 1.867 | 1.809 | 1.727 |
| w0, kg/kg | s, g/100 g | Tliq, °C | m | ω, °C |
|---|---|---|---|---|
| 0.17 | 0 | −2 | 0.286 | 0.988 |
| 0.17 | 3.46 | −3.69 | 0.300 | 1.735 |
| 0.17 | 6.9 | −6.3 | 0.279 | 2.282 |
| 0.21 | 0 | −0.91 | 0.305 | 0.777 |
| 0.21 | 3.46 | −3.05 | 0.313 | 1.514 |
| 0.21 | 6.9 | −5.45 | 0.288 | 1.882 |
| 0.26 | 0 | −0.23 | 0.357 | 0.978 |
| 0.26 | 3.46 | −2.55 | 0.323 | 1.278 |
| 0.26 | 6.9 | −5.00 | 0.290 | 1.460 |
| Parameter | Value |
|---|---|
| Freezing pipe radius, m | 0, 1 |
| Radius of the outer boundary of the computational domain, m | 3 |
| Number of spatial nodes | 27 |
| Aspect ratio for neighboring cells | 1.1 |
| Minimum cell size at the freezing pipe, m | 0.026 |
| Initial water content, kg/kg | 0.17 |
| Initial temperature of clay, °C | 10 |
| Coolant temperature in the freezing pipe, °C | −30 |
| Heat transfer coefficient at the boundary near the freezing pipe, W/(m2·°C) | 150 |
| Specific heat capacity of dry soil particles, J/(kg·°C) | 776 |
| Specific heat capacity of water, J/(kg·°C) | 4200 |
| Specific heat capacity of ice, J/(kg·°C) | 2100 |
| Specific latent heat of water crystallization, J/kg | 333,600 |
| Thermal conductivity of dry soil particles, W/(m·°C) | 1.95 |
| Thermal conductivity of water, W/(m·°C) | 0.56 |
| Thermal conductivity of ice, W/(m·°C) | 2.2 |
| Density of wet rocks, kg/m3 | 2070 |
| Simulation time, days | 50 |
| Diffusion coefficient of dissolved salt, m2/s | 0, 10−8, and 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semin, M.; Levin, L.; Bublik, S.; Brovka, G.; Brovka, A.; Agutin, K. Parameterization of the Model of Artificial Clay Freezing Considering the Effect of Pore Water Salinity. Fluids 2022, 7, 186. https://doi.org/10.3390/fluids7060186
Semin M, Levin L, Bublik S, Brovka G, Brovka A, Agutin K. Parameterization of the Model of Artificial Clay Freezing Considering the Effect of Pore Water Salinity. Fluids. 2022; 7(6):186. https://doi.org/10.3390/fluids7060186
Chicago/Turabian StyleSemin, Mikhail, Lev Levin, Sergey Bublik, Gennadiy Brovka, Andrey Brovka, and Kirill Agutin. 2022. "Parameterization of the Model of Artificial Clay Freezing Considering the Effect of Pore Water Salinity" Fluids 7, no. 6: 186. https://doi.org/10.3390/fluids7060186
APA StyleSemin, M., Levin, L., Bublik, S., Brovka, G., Brovka, A., & Agutin, K. (2022). Parameterization of the Model of Artificial Clay Freezing Considering the Effect of Pore Water Salinity. Fluids, 7(6), 186. https://doi.org/10.3390/fluids7060186








