An Analytical Study on the Mechanism of Grouping of Droplets

Abstract

The condition for the formation of droplet groups in liquid sprays is poorly understood. This study looks at a simplified model system consisting of two iso-propanol droplets of equal diameter, $D_{d0}$, in tandem, separated initially by a center-to-center distance, $a_{20}$, and moving in the direction of gravity with an initial velocity, $V_{d0}>V_t$, where $V_t$ is the terminal velocity of an isolated droplet from Stokes flow analysis. A theoretical analysis based on Stokes flow around this double-droplet system is presented, including an inertial correction factor in terms of drag coefficient to account for large Reynolds numbers (≫1). From this analysis, it is observed that the drag force experienced by the leading droplet is higher than that experienced by the trailing droplet. The temporal evolutions of the velocity, $V_d\left(t\right)$, of the droplets, as well as their separation distance, $a_2\left(t\right)$, are presented, and the time $t_o$ at which the droplets come in contact with each other and their approach velocity at this time, $\Delta V_{d0}$, are calculated. The effects of the droplet diameter, $D_{d0}$, the initial droplet velocity, $V_{d0}$, and the initial separation, $a_{20}$ on $t_o$ and $\Delta V_{d0}$ are reported. The agreement between the theoretical predictions and experimental data in the literature is good.

1. Introduction

A liquid spray, defined as a collection of liquid droplets moving in an ambient fluid, is commonly seen in many practical applications. Biofuel sprays in engines [1] and aqueous urea solution sprays in automotive Selective Catalytic Reduction (SCR) DeNOx systems [2,3,4] to control pollutant emissions, spray coating of surfaces in solar cell fabrication [5,6], pesticide sprays in agriculture [7], the role of ocean sprays in global climate [8], 3D ink-jet printing of biological entities (bio-printing) [9], nasal sprays to treat critical ailments [10], dynamics of pathogen-bearing droplets ejected while sneezing or coughing [11], and spray-on skin cells for burn treatment [12] are a few examples where liquid sprays play a key role in determining the outcome of emerging technologies as well as public health and environmental issues. In many of these cases, it may not be possible to modify the ambient fluid or the solid surface with which the liquid spray interacts to achieve the desired outcome. Hence, control of the liquid spray is needed, and this requires a deep understanding of the motion of the droplets comprising the liquid spray, leading to a ‘multi-body’ physical problem.

The motion of a collection of droplets is governed by the flow field around the droplets, which, in turn, is affected by the motion of the droplets, leading to coupled flow mechanics. This, in combination with the initial conditions, which can be specified by the size, the velocity, and the initial separation of the droplets upon injection into the ambient fluid, gives a model for predicting the motion of a collection of droplets. In the present study, we are broadly interested in understanding the conditions that lead to a localized formation of droplet clusters/groups due to the motion of a collection of droplets in liquid sprays. This phenomenon is referred to as ‘droplet grouping’ or ‘droplet clustering’. Such clustering of droplets in a spray leads to an unsteady spray structure and could be caused due to the inherent unsteadiness in the injection of droplets into the ambient medium and/or the interaction among the spray droplets mediated by the flow in the ambient medium [13].

Droplet grouping could potentially lead to collision among the droplets, which, in turn, could lead to coalescence, separation (bouncing, reflexive, or stretching), or shattering of the colliding droplets depending on the conditions under which they collide [14,15]. This, inevitably, leads to an alteration in the droplet size and velocity distribution of the liquid spray. Such an alteration of the liquid spray characteristics could be either beneficial or detrimental depending on the system/application under consideration. For example, an increase in droplet size is detrimental to combustion in aircraft and internal combustion engines due to less efficient vaporization and mixing of fuel droplets with an oxidizer, whereas it could be beneficial to filter out pollutant particles in exhaust systems [16]. In addition to this indirect effect, droplet grouping can directly alter evaporation/mixing characteristics of droplets/vapor [17], thereby affecting the combustion regime of the spray [18]. Hence, to control the droplet grouping process in order to benefit a particular application, a deeper understanding of the droplet grouping phenomenon is required.

Even though the configuration of a single droplet/sphere falling under gravity has been studied extensively (see, for example, the review article [19]), configurations involving two or more droplets/spheres have not been explored to a similar extent. Earlier studies focused on the motion of a pair of solid spheres, in a spatial arrangement similar to the one shown in Figure 1, falling from rest under gravity in a viscous ambient medium (see, for example, Refs. [20,21,22] and the references therein). These studies reported a reduction in the drag force experienced by the trailing sphere compared to that experienced by the leading sphere. This is in line with the analysis reported by Oseen [23]; however, the drag force experienced by the trailing sphere is not independent of the Reynolds number as predicted by Oseen [22,23]. An interesting numerical study on the motion of a pair of porous solid spheres in air reported the dependence of drag forces on leading and trailing spheres on the size and porosity of the spheres [24]. More recently, Katoshevski et al. [25,26] studied droplet grouping in an oscillating flow. A non-dimensional parameter was proposed in this study [25] to differentiate the conditions that lead to the grouping and non-grouping of droplets in an oscillating flow field. The authors reported that droplet grouping is dominantly seen for smaller droplets, evaporating droplets tend to group because of this, and the droplet-ambient coupling tends to inhibit droplet grouping [26]. Furthermore, since bigger droplets tend not to group, their evaporation rates are similar to that of smaller droplets that tend to form groups, resulting in less sensitivity of spray vaporization on droplet size [26]. To understand the physical principles governing droplet grouping phenomena, a fundamental experimental study on trains of double- and triple-droplet systems of iso-propanol droplets injected in tandem at high velocities into quiescent ambient air was reported by Roth et al. [27,28]. A direct numerical simulation was also reported by Roth et al. [28], which captures the motion of groups of two droplets observed in experiments when a wider computational domain is employed.

Even though the phenomenon of droplet–droplet collision has been studied quite extensively through experimental, theoretical, and numerical approaches [14], the conditions that lead to the collision of droplets as well as the calculation of the initial conditions at which droplets collide are not sufficiently addressed in the current literature. This is where the current study on droplet grouping becomes relevant. At this point, it is worth re-emphasizing that the current study explores the mechanism through which two droplets come closer together through a simple analytical study.

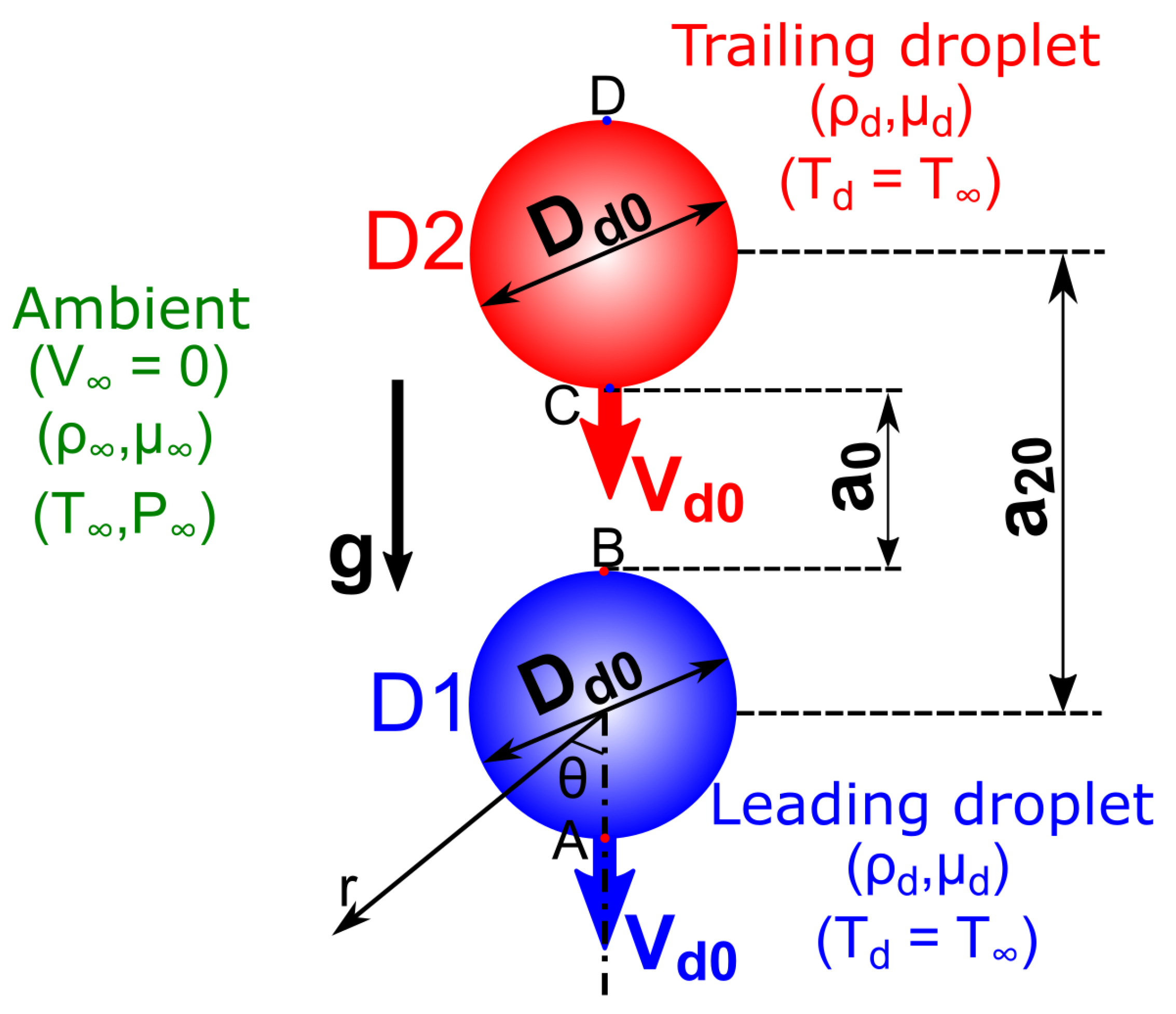
As a first step, we consider a simple one-dimensional model system of two droplets each of diameter $D_{d0}$ in tandem, separated by a center-to-center distance of $a_{20}$, injected with an initial velocity $V_{d0}$ in the direction of gravitational acceleration g into quiescent ambient air (see Figure 1). Such double-droplet systems are relevant in one-dimensional droplet streams in typical ink-jet printing applications. Note that here we consider the injection velocity $V_{d0}$ to be much larger than the terminal velocity $V_t$ attained by an isolated droplet freely falling under gravity; this is in contrast to the earlier studies that considered spheres either freely falling from rest or moving at equal and constant velocities [20,21]. The theoretical formulation for the motion of this double-droplet system in a Stokes flow regime is detailed in Section 2, listing the assumptions made. The theoretical formulation is validated by comparing with limited experimental data available in the literature. This is followed by Section 3 on the predictions of (i) the temporal evolution of the velocities and separation of the droplets, (ii) the time at which the droplet surfaces come in contact with each other, and (iii) the relative velocity with which the droplets contact each other, as well as the effects of $D_{d0}$, $V_{d0}$, and $a_{20}$ on these predictions. The concluding remarks from the present investigation and directions for further exploration are outlined in Section 4.

2. Theoretical Methodology

This section describes the theoretical approach followed to understand/predict the motion of the individual droplets in a double-droplet system, as shown in Figure 1. Both the leading and trailing droplets are assumed to have the same diameter $D_{d0}$ and are injected into the ambient air at $t=0$ with the same initial velocity $V_{d0}$. The initial center-to-center separation between the droplets is denoted by $a_{20}$ (surface-to-surface separation, $a_0=a_{20}-D_{d0}$). The underlying assumptions of this theoretical approach are listed below.

• The ambient pressure, temperature, and physical properties (density, viscosity, and surface tension) are assumed to be constant.
• Any effect due to droplet evaporation is assumed to be negligible (for example, the droplet diameter at any instant of time, $D_d\left(t\right)=D_{d0}$).
• The flow around the droplets is assumed to be Stokes flow, with the inertial effects incorporated through an expression for the coefficient of drag, $C_D$, valid for a wide range of Reynolds numbers.
• Any deviation in the droplets’ shape from spherical, due to deformation, is assumed to be negligible. In general, this is valid at conditions of a low aerodynamic Weber number, $W{e}_{\infty }={\rho }_{\infty }{V}_d^2{D}_{d0}/{\sigma }_d$ (${\rho }_{\infty }$ and ${\sigma }_d$ are, respectively, the density of the ambient fluid and the surface tension of the droplet liquid, $V_d$ is the instantaneous velocity of the droplet). For example, the transition from ‘no deformation’ to ‘non-oscillatory deformation’, characterized by a 10% change in the cross-stream droplet diameter, occurs at $W{e}_{\infty }=1.1$ for an Ohnesorge number, $Oh={\mu }_d/\sqrt{{\rho }_d{\sigma }_d{D}_{d0}}<0.1$ [29]; ${\rho }_d$ and ${\mu }_d$ being the density and the dynamic viscosity of the droplet liquid, respectively.
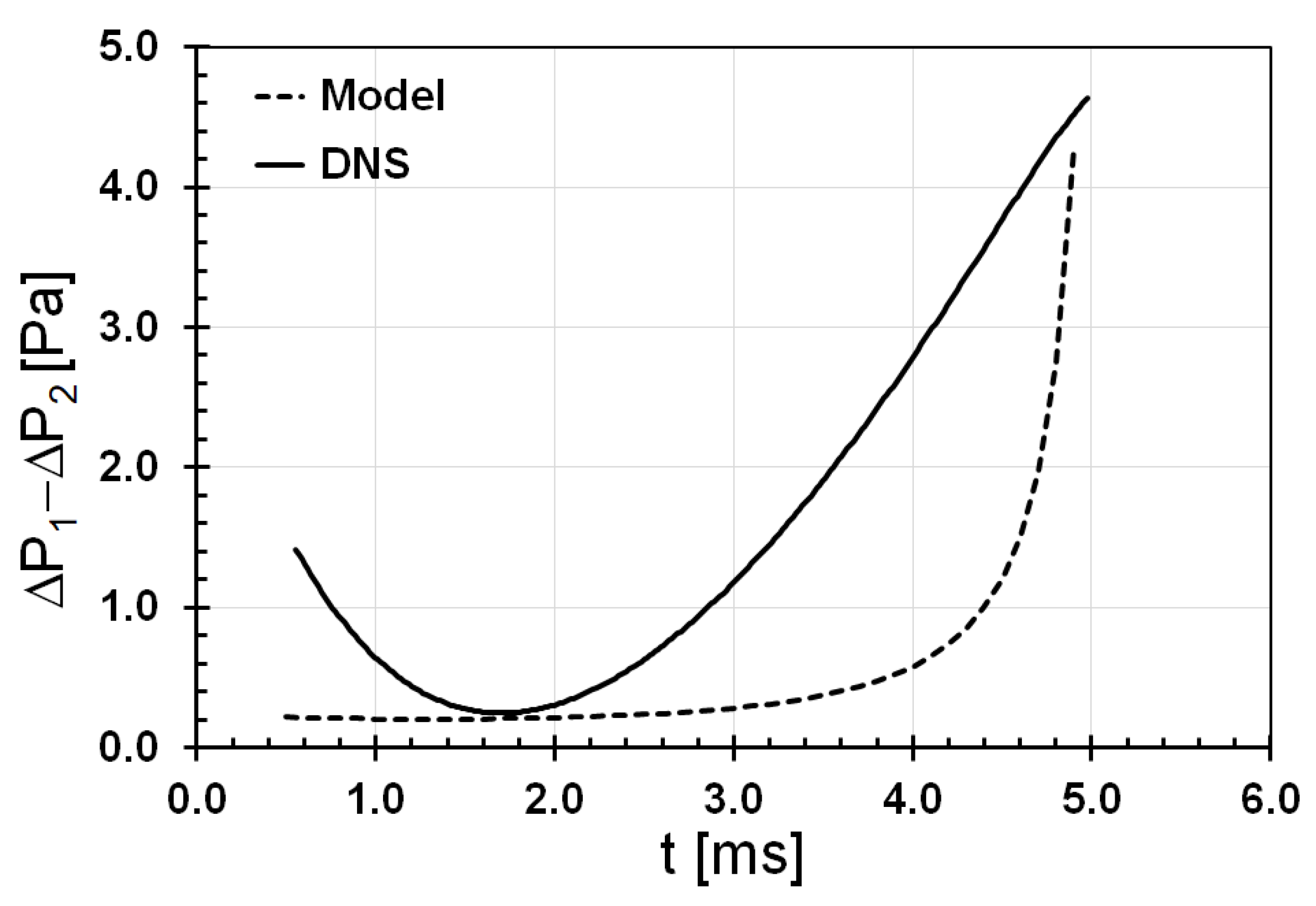
• The effect of the skin friction component of the drag force on the motion of the droplets is neglected. Please refer to Appendix A.1 for a discussion on the importance of this assumption, with the help of direct numerical simulations (DNS) at typical flow conditions.
• The pressure field around the leading droplet is assumed to affect the motion of the trailing droplet, whereas the effect of the pressure field around the trailing droplet on the motion of the leading droplet is neglected. In other words, the effect of a two-way mutual interaction between the pressure fields around the leading and trailing droplets is neglected. Such mutual interaction effects have been studied for spheres/droplets moving at very low Reynolds numbers (≈O(1) and below) [20]; this leads to very complex mathematical equations that need to be solved with a strenuous computational effort [30,31]. Please refer to Appendix A.2 for a discussion on the importance of this assumption, with the help of DNS at typical flow conditions.
• The effect of the presence of other droplets around the double-droplet system, as in the case of a typical spray, on the motion of this system is neglected.

Within the framework of these assumptions, the theoretical approach is formulated. The pressure field for Stokes flow around a single isolated sphere is given as follows [32]:

$$P(r,\theta )=P_{\infty }+\frac{3{\mu }_{\infty }{V}_d{D}_{d0}cos\theta }{4r^2}.$$

(1)

Here, r and $\theta$ are the radial and azimuthal coordinates measured from the droplet’s center and from the direction of motion of the droplet, respectively (see Figure 1). $P_{\infty }$ and ${\mu }_{\infty }$ are, respectively, the ambient pressure far away from the droplets and the dynamic viscosity of the ambient fluid, $V_d$ is the instantaneous droplet velocity, and $D_{d0}$ is the droplet diameter. This form of the pressure field, as predicted by Stokes flow, is adopted for the case of the double-droplet system considered in the present study. At any instant of time, the pressure difference across the leading droplet (D1 in Figure 1) $\Delta P_1$ is approximated as the pressure difference between the points A and B. Note that this is the maximum pressure difference acting on the surface of the droplet, whereas the viscous drag at the points A and B is zero. We further make a simplifying assumption that this maximum pressure difference acts all over the effective cross-sectional area of the droplet normal to the direction of its motion, $A_d=\pi D_d^2/4$. The instantaneous pressures at A$(D_d/2,0^{\circ })$ and B$(D_d/2,{180}^{\circ })$ ($P_A$ and $P_B$, respectively) can be calculated from Stokes flow approximation (Equation (1)) as follows:

$$P_A=P_{\infty }+\frac{3{\mu }_{\infty }{V}_{d1}}{D_{d0}},$$

(2)

$$P_B=P_{\infty }-\frac{3{\mu }_{\infty }{V}_{d1}}{D_{d0}}.$$

(3)

Here, $V_{d1}$ is the instantaneous velocity of the leading droplet. Hence, the pressure difference, $\Delta P_1=P_A-P_B$ acting on the leading droplet can be calculated from Equations (2) and (3) as follows:

$$\Delta P_1=\frac{6{\mu }_{\infty }{V}_{d1}}{D_{d0}}.$$

(4)

Similarly, the pressure difference acting on the trailing droplet (D2 in Figure 1) at any instant of time $\Delta P_2$ is approximated as the instantaneous pressure difference between the points C and D. The pressures at C and D ($P_C$ and $P_D$, respectively) are calculated from Stokes flow approximation under the assumption of ‘linear superposition’. In other words, the pressure at C (or D) is expressed as the sum of the pressure at C (or D) due to flow over the leading droplet, $P_{C1}$ (or $P_{D1}$) and that at C (or D) due to the presence of the trailing droplet, $P_{C2}$ (or $P_{D2}$). Such an approach of superposition is somewhat similar to the one discussed by Smoluchowski [33]. This leads to

$$\begin{array}{cc}\hfill P_C=P_{C1}+P_{C2}& =\left[P_{\infty }-\frac{3{\mu }_{\infty }{V}_{d1}{D}_{d0}}{{(D_{d0}+2a)}^2}\right]+\left[P_{\infty }+\frac{3{\mu }_{\infty }{V}_{d2}}{D_{d0}}\right]\hfill \\ \hfill & =2P_{\infty }+\frac{3{\mu }_{\infty }{V}_{d2}}{D_{d0}}\left[1-\frac{V_{d1}}{V_{d2}}\frac{{D_{d0}}^2}{{(D_{d0}+2a)}^2}\right],\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill P_D=P_{D1}+P_{D2}& =\left[P_{\infty }-\frac{3{\mu }_{\infty }{V}_{d1}{D}_{d0}}{{(3D_{d0}+2a)}^2}\right]+\left[P_{\infty }-\frac{3{\mu }_{\infty }{V}_{d2}}{D_{d0}}\right]\hfill \\ \hfill & =2P_{\infty }-\frac{3{\mu }_{\infty }{V}_{d2}}{D_{d0}}\left[1+\frac{V_{d1}}{V_{d2}}\frac{{D_{d0}}^2}{{(3D_{d0}+2a)}^2}\right].\hfill \end{array}$$

(6)

In the above equations, $a=a_2-D_{d0}$ is the instantaneous surface-to-surface separation between the droplets. Now, the instantaneous pressure difference acting on the trailing droplet, $\Delta P_2=P_C-P_D$ can be calculated from Equations (5) and (6) as follows:

$$\Delta P_2=\frac{6{\mu }_{\infty }{V}_{d2}}{D_{d0}}\left[1-\frac{4}{9}\frac{V_{d1}}{V_{d2}}\frac{\left(1+\frac{a}{D_{d0}}\right)}{{\left(1+\frac{2a}{3D_{d0}}\right)}^2{\left(1+\frac{2a}{D_{d0}}\right)}^2}\right].$$

(7)

Comparing Equations (4) and (7), it is evident that at any instant of time, the pressure difference acting on the trailing droplet, $\Delta P_2$ is less than that on the leading droplet, $\Delta P_1$. Now, it is assumed that both $\Delta P_1$ and $\Delta P_2$ act over an effective droplet surface area of $\pi D_d^2/4$. Applying a force balance on the leading and trailing droplets gives the following equations of motion for them.

For the leading droplet:

$$m\frac{d{V}_{d1}}{dt}=mg-\frac{\pi D_{d0}^3}{6}{\rho }_{\infty }g-(\Delta P_1\frac{\pi D_{d0}^2}{4})\left(\frac{C_{D1}R{e}_1}{24}\right)$$

(8)

For the trailing droplet:

$$m\frac{d{V}_{d2}}{dt}=mg-\frac{\pi D_{d0}^3}{6}{\rho }_{\infty }g-(\Delta P_2\frac{\pi D_{d0}^2}{4})\left(\frac{C_{D2}R{e}_2}{24}\right)$$

(9)

m is the mass of each droplet, the dependence of $C_D$ on $Re$ is assumed to be the same for both the leading and trailing droplets, and equal to that for an isolated droplet of the same diameter and velocity falling vertically down, and $g=9.81$ m/s² is the acceleration due to gravity. In the above equations, the term on the left-hand side is the net force acting on the droplet, and on the right-hand side, the first term is the weight of the droplet, the second term is the buoyancy force acting on the droplet, and the third term is the drag force acting on the droplet corrected for inertial effects through the coefficient of drag, $C_D$ (more details are given below). Note that the inertial correction factor (also referred to as the ‘drag factor’ [32]), ($C_{Di}R{e}_i/24$) tends to unity for Stokes flow conditions at which $C_{Di}=24/R{e}_i$ (where $R{e}_i={\rho }_{\infty }{V}_{di}{D}_{d0}/{\mu }_{\infty }$ (i = 1 or 2)). The coefficient of drag is, in general, a function of the Reynolds number. There are many correlations available for the dependence of $C_D$ on the Reynolds number [34]. Among the relations that do not diverge at low to moderate values of $Re$, the one reported by Mikhailov and Freire [34], given by Equation (10), is appropriate for the range of Reynolds numbers (≈O(100)) considered here. Note that Equation (10) is a modification of the Stokes drag coefficient, given by $C_D=24/Re$, by taking inertial terms into account. Hence, even though the governing equations are formulated from Stokes flow assumption, the inertial effect is incorporated in the calculation of $C_D$ using Equation (10), which is suitable at higher Reynolds number conditions (≫1, up to ${10}^5$) too. Mikhailov and Freire [34] showed that Equation (10) closely agrees with the experimental data on the coefficient of drag for an isolated solid sphere reported by Roos and Willmarth [35] and Brown and Lawler [36]. Please refer to Appendix B for a comparison between the drag coefficient given by Equation (10) and the Stokesian drag coefficient.

$$C_{Di}=\frac{3808((1617933/2030)+(178861/1063)R{e}_i+(1219/1084)R{e}_i^2)}{681R{e}_i((77531/422)+(13529/976)R{e}_i-(1/71154)R{e}_i^2)};i=1,2$$

(10)

Using Equations (4) and (7) in Equations (8) and (9) gives the following equations for the rate of change of velocity of the leading and trailing droplets, respectively.

$$\frac{d{V}_{d1}}{dt}=(1-\frac{{\rho }_{\infty }}{{\rho }_d})g-\left(\frac{C_{D1}R{e}_1}{24}\right)\frac{9{\mu }_{\infty }{V}_{d1}}{{\rho }_d{D}_{d0}^2}$$

(11)

$$\frac{d{V}_{d2}}{dt}=(1-\frac{{\rho }_{\infty }}{{\rho }_d})g-\left(\frac{C_{D2}R{e}_2}{24}\right)\frac{9{\mu }_{\infty }{V}_{d2}}{{\rho }_d{D}_{d0}^2}\left[1-\frac{4}{9}\frac{V_{d1}}{V_{d2}}\frac{\left(1+\frac{a}{D_{d0}}\right)}{{\left(1+\frac{2a}{3D_{d0}}\right)}^2{\left(1+\frac{2a}{D_{d0}}\right)}^2}\right]$$

(12)

The time evolution of velocity of the leading and trailing droplets can be computed using Equations (11) and (12), respectively. Now, the time evolution of center-to-center separation of the droplets, $a_2\left(t\right)$ at the nth time step ($n\in \mathbb{N}$) can be calculated from the above equations as follows.

$${\left(a_2\right)}_{t=n\Delta t}={\left(a_2\right)}_{t=(n-1)\Delta t}+(\Delta t){(V_{d1}-V_{d2})}_{t=(n-1)\Delta t}+\frac{{(\Delta t)}^2}{2}{(\frac{d{V}_{d1}}{dt}-\frac{d{V}_{d2}}{dt})}_{t=(n-1)\Delta t}$$

(13)

Equation (13) is solved, together with Equations (11) and (12), by a forward marching in time with a time step $\Delta t$ = 0.1 ms, and the initial conditions $D_{d0}$, ${\left(a_2\right)}_{t=0}=a_{20}$, ${\left(V_{d1}\right)}_{t=0}=V_{d0}$, and ${\left(V_{d2}\right)}_{t=0}=V_{d0}$. It was observed from our calculations that decreasing the time step from 0.1 to 0.001 ms resulted in a maximum deviation of ≈1.09% in the parameters of motion ($V_d\left(t\right)$, $a_2\left(t\right)$, $t_o$, and $\Delta V_{do}$).

Validation of the Theoretical Approach

As mentioned in Section 1, there are very few experiments reported in the literature on double-/triple-droplet systems falling down vertically along their line of centers, especially at injection velocities much greater than the terminal velocity of free fall. This poses a constraint on the breadth of comparison of theoretical predictions with experimental data in terms of the number and range of parameters. Keeping this restriction in mind, the current theoretical predictions are compared with the very limited experimental data reported in the literature [27,28], as shown in Figure 2.

Note that, in experiments, the droplets form a stream (see Figure 3), whereas in the model, an isolated double-droplet system is considered (see Figure 1). It should be noted here that the model double-droplet system is a special case of the droplet stream when $a_1\gg a_2$ (see Figure 3). Moreover, in the experiments, the initial velocities of leading and trailing droplets are different since they are not injected at the same time. However, the model presented in Section 2 assumes that the droplets are injected at the same velocity $V_{d0}$ at $t=0$ ms. In reality, the velocity of the leading droplet will change when it travels a distance corresponding to the initial separation between the droplets $a_{20}$. It can be shown using Equation (11) that, for the experimental conditions used for comparison here, this change in velocity of the leading droplet from the assumed velocity is only around 0.13%. For experimental conditions where the initial separation and/or the drag force is much larger, this deviation of assumed initial velocity from the actual velocity of the leading droplet could be larger. Keeping the above-mentioned points in mind, the comparison between theoretical predictions and experimental data, as shown in Figure 2, is discussed below.

The predictions obtained using Equations (11)–(13) seem to capture the overall trend of the experimental data. Even though the equations governing the droplet motion were formulated based on Stokes flow ($Re<1$), their predictions capture the trend of the experimental data at a value of $Re$ (110.6), which is two orders of magnitude larger than the typical values of $Re$ in the Stokes flow regime. A similar observation was reported in a recent study of the same problem using the homotopy analysis method [30]. The inclusion of inertial effects through an empirical drag coefficient in this study (Equation (10)) and through higher-order terms in $Re$ in the previous study (see Equation (7) in [30]) could be potential reasons for the apparently surprising match between the predictions and the experimental data. The predictions, however, underestimate the temporal evolution of $a_2\left(t\right)$ at larger values of t, and this leads to an underprediction of the time taken by the droplets to come in contact with each other, $t_o$. The error in the prediction of $t_o$ for this experimental case is around 7.4%. The time-averaged error in the predictions relative to the experimental data presented in Figure 2 is 4.84%; this is 9.97% for $t>3.1$ ms, and close to $t=t_o=4.91$ ms, it is around 24.37 %.

Neglecting the skin friction drag component in the analysis could be one of the potential reasons for this under-prediction. Please refer to Appendix A.1 for a more detailed discussion on this matter. Another possible reason for the deviation of the prediction from experimental data is neglecting the ‘non-oscillatory deformation’ in the analysis. The aerodynamic Weber number at the experimental flow condition (1.38) is slightly larger than the critical value for the transition from ‘no deformation’ to ‘non-oscillatory deformation’ for an isolated droplet in an ambient flow (1.1) [29]. A third possibility is the difference in the configuration of the droplets between the experiments (droplet stream) and the model (double-droplet), as indicated before (compare Figure 1 and Figure 3). Results from DNS, where a droplet stream is considered (similar to that in experiments), showed that with an increase in the distance between the double-droplet and its neighboring droplets ($a_1$ increases), droplet grouping happens faster ($t_o$ decreases). This is qualitatively in line with the theoretical predictions in Figure 2, which correspond to a very large separation between the double-droplet and its neighboring droplets ($a_1\gg a_2$) and show a faster grouping than in the experiments.

The critical droplet Weber number for coalescence without further (‘stretching’) separation when two identical droplets undergo head-on collision is given by the following semi-empirical relation [37].

$$W{e}_{d,c}=30O{h}_d+15$$

(14)

In Equation (14), $O{h}_d=16\sqrt{2}{\mu }_d/\sqrt{{\rho }_d{\sigma }_d{D}_d}$ is the droplet Ohnesorge number as defined in [37], and $W{e}_{d,c}$ is the critical value of droplet collision Weber number, $W{e}_d={\rho }_d\Delta V_{do}^2{D}_{d0}/{\sigma }_d$ [38], calculated based on the approach velocity of the droplets at the instant they come in contact for the first time, $\Delta V_{do}$; for $W{e}_d<W{e}_{d,c}$, the approaching droplets will coalesce without further undergoing separation due to shape oscillations associated with the coalescence process (‘stretching separation’) [14,38]. The approach velocity of the droplets at the instant $t=t_o$ for the experimental condition presented in Figure 2 is ≈0.14 m/s (see Figure 7). The corresponding value of $W{e}_d$ is ≈0.080, which is much less than $W{e}_{d,c}=52$ (from Equation (14)) and seems to be less than the critical Weber number above-which a transition from coalescence to ‘reflexive separation’ takes place [39,40,41]. The images close to the time $t_o$ corresponding to the experimental data in Figure 2 are shown in Figure 3. Indeed, the approaching droplets undergo coalescence and remain as one bigger droplet afterward.

3. Results and Discussion

The predictions from the simple model, as described in Section 2, are presented and discussed in this section. The effects of (i) initial droplet diameter, $D_{d0}$, (ii) initial droplet velocity, $V_{d0}$, and (iii) initial separation between the droplets, $a_{20}$ on (a) the temporal evolution of velocity of leading and trailing droplets, (b) the temporal evolution of the separation between the leading and trailing droplets, (c) the time taken for the droplet surfaces to come in contact with each other, and (d) the velocity of approach of droplets at the time of their first contact are looked into.

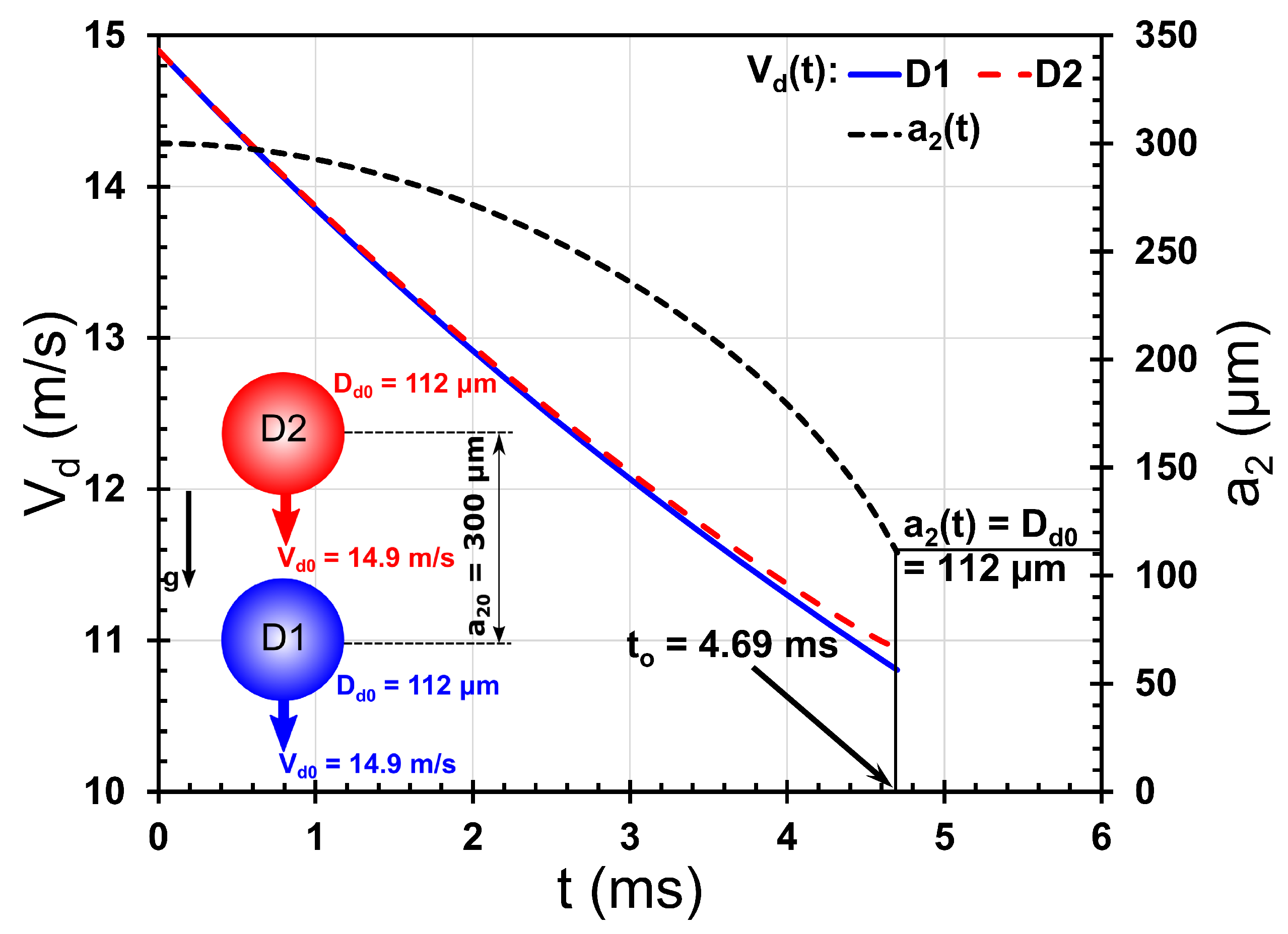
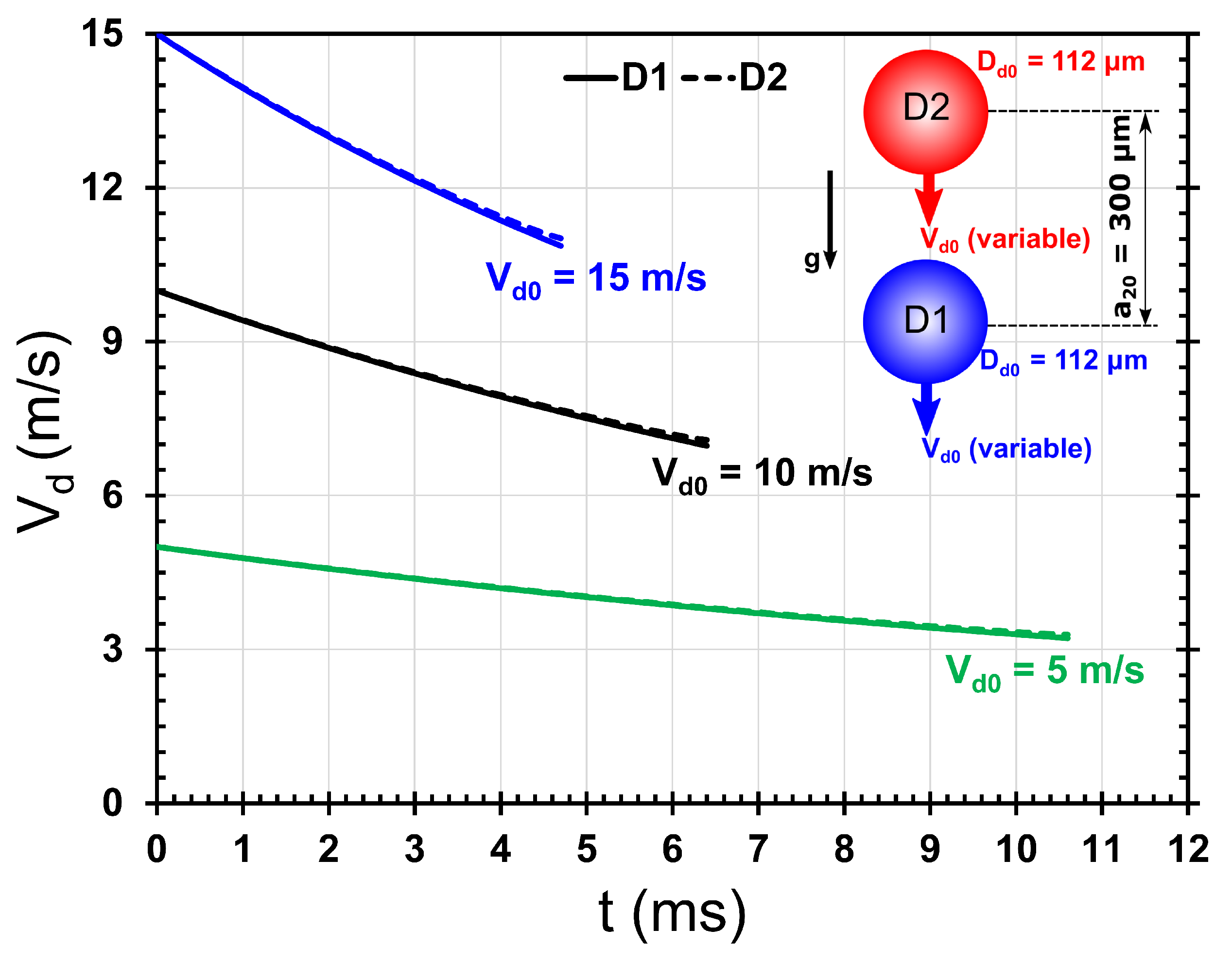
Figure 4 shows a typical time evolution of velocities of the leading (D1) and trailing (D2) iso-propanol (${\rho }_d$ = 786 kg/m³, ${\mu }_d$ = 2.38 mPa·s, ${\sigma }_d$ = 21.7 mN/m) droplets of initial diameter, $D_{d0}$ = 112 $\mathsf{\mu }$m, injected into ambient air (${\rho }_{\infty }$ = 1.2 kg/m³; ${\mu }_{\infty }$ = 1.81$\times$${10}^{-5}$ Pa·s) at the same initial velocity, $V_{d0}$ = 14.9 m/s. The corresponding time evolution of the center-to-center separation between the droplets, $a_2\left(t\right)$, is also shown in Figure 4. It is evident that as time progresses, the velocity of the leading droplet deviates from that of the trailing droplet, with the former decreasing faster than the latter. This clearly indicates that the drag force acting on the leading droplet is greater than that acting on the trailing droplet. This difference in velocity, which increases with time, leads to a decrease in the separation between the droplets with time, as shown by the temporal variation of $a_2\left(t\right)$. When the separation between the droplets becomes equal to the droplet diameter ($a_2\left(t\right)=D_{d0}$), the droplets meet at their surface. This instant of time, $t_o$, can be extracted from plots similar to Figure 4. The approach velocity of the droplets at this instant of time, $\Delta V_{d0}={\left(V_d(t=t_o)\right)}_2-{\left(V_d(t=t_o)\right)}_1$, together with the droplet diameter and physical properties of the liquid and ambient, provide information to predict whether the droplets will undergo coalescence, bouncing, reflexive separation, stretching separation, or shattering after this instant.

3.1. Effect of Initial Droplet Diameter, $D_{d0}$

Figure 5 shows the time evolution of the velocities of the leading (D1) and trailing (D2) droplets for three typical cases of droplet diameters. Other initial conditions remain the same as in Figure 4. The difference in the time evolution of the velocities of leading and trailing droplets, as seen in Figure 4, is also observed at different droplet diameters in Figure 5. Injected at the same initial velocity with the same initial separation, smaller droplets experience a higher rate of change in their velocities with time (higher deceleration), as evident from the different slopes of curves in Figure 5. This is due to an interplay of the effects of the drag coefficient, Reynolds number, and droplet diameter on the deceleration due to the drag force experienced by the droplet (see the second term on the right-hand side of Equations (11) and (12)). A decrease in droplet diameter leads to a decrease in Reynolds number and a corresponding increase in drag coefficient, as given by Equation (10). Both of these effects counter-act, resulting in a net increase in drag force term in Equations (11) and (12) when the droplet diameter decreases. Furthermore, a decrease in droplet diameter directly results in an increase in deceleration due to the drag force term in Equations (11) and (12). Overall, decreasing the droplet diameter results in an increase in the deceleration due to the drag force experienced by the droplet, as observed in Figure 5.

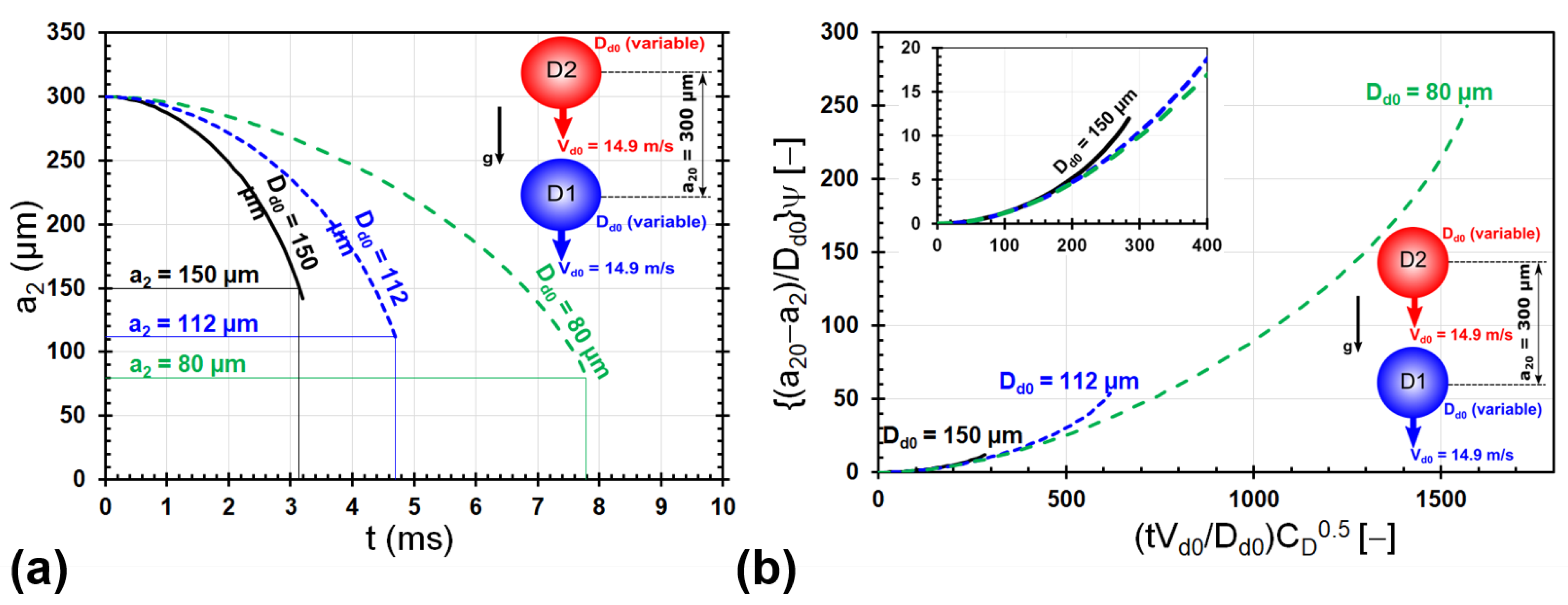
Figure 6a shows the time evolution of the center-to-center separation of the droplets for the cases shown in Figure 5. For smaller droplets, with other initial conditions remaining the same, the time evolution of the separation between them is slower, and it takes longer for the droplets to come in contact with each other (as indicated by the vertical lines in Figure 6a). This is due to the combined effect of the time evolution of their relative velocities and the smaller center-to-center separation at contact (due to smaller droplet diameters). The trends shown in Figure 6a are normalized using the non-dimensionalization discussed in Appendix C; the corresponding non-dimensional plot is shown in Figure 6b. It is clear that the non-dimensionalization is able to collapse the trends into one curve, except for the instants of time when the droplets are very close to each other (larger values of time in each case of $D_{d0}$).

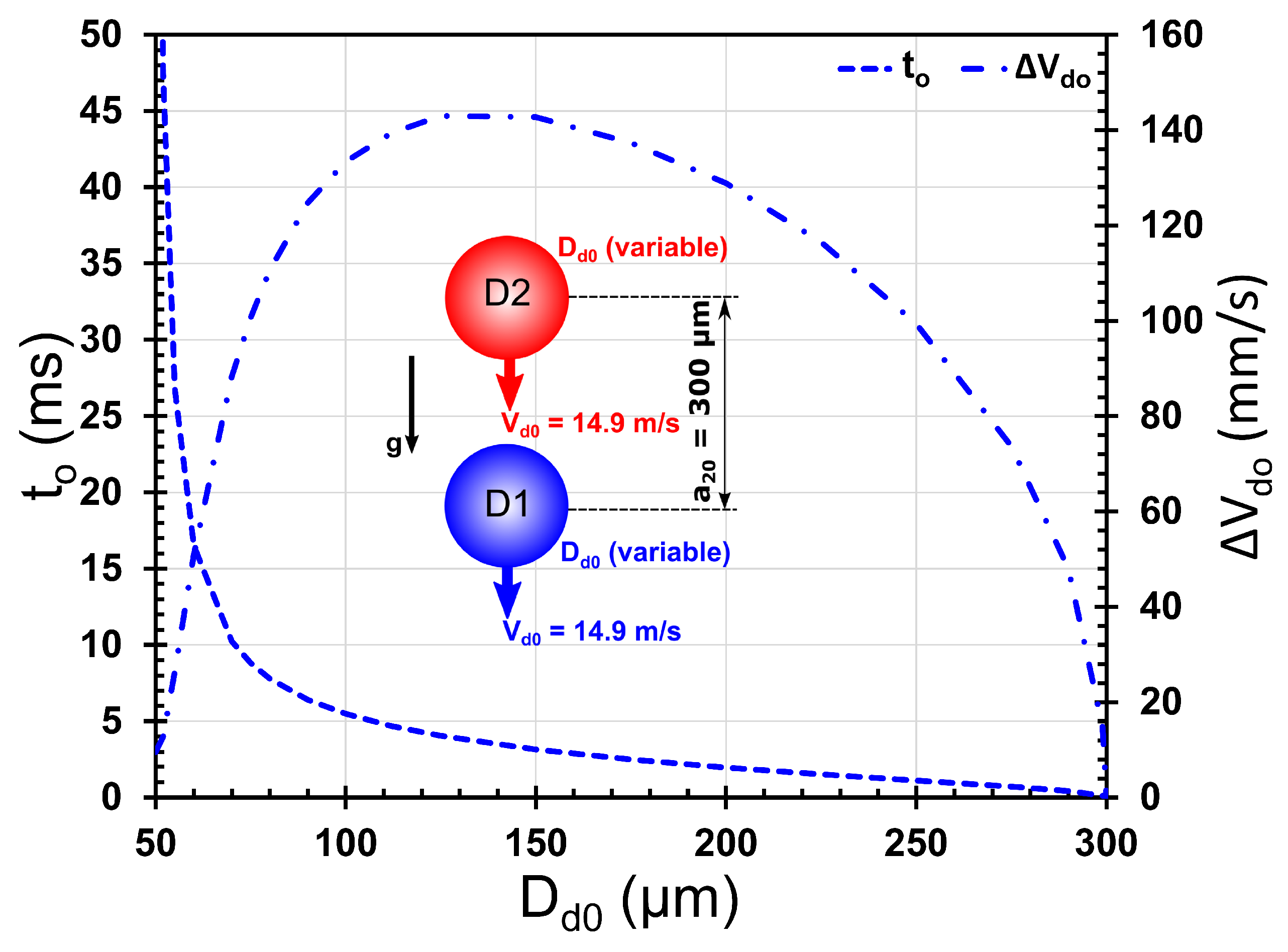
Figure 7 shows the effect of the initial droplet diameter on the time taken by the droplets to come in contact with each other for the first time and their approach velocity at this instant of time. The initial values of the droplet center-to-center separation and velocities are the same as in Figure 4. Both $t_o$ and $\Delta V_{d0}$ have a non-linear dependence on the initial droplet diameter. For smaller droplets, $t_o$ decreases drastically with a small increase in droplet size, with a corresponding steep increase in the approach velocity. For droplets of size larger than a critical value, the approach velocity decreases with an increase in droplet diameter. Considering the extreme cases of droplet size: for very small droplets, $t_o$ is very large (compared to the time scale of flow around the droplets), resulting in an overall reduction in the velocity of the double-droplet system at a large $t_o$, and hence, the approach velocity of droplets is also quite small; for very large droplets (of diameter the same as their center-to-center separation), $t_o$ vanishes, and hence, the relative velocity of the approach also becomes zero. This is a possible explanation for the non-linear trend of $\Delta V_{d0}$ with $D_{d0}$ exhibiting a maximum in Figure 7.

It should be noted here that, at higher values of $D_{d0}$, the quantitative values of $t_o$ and $\Delta V_{d0}$ in Figure 7 should be treated with caution since the aerodynamic Weber number calculated at $t=0$ could be significant enough to cause a ‘non-oscillatory deformation’ of the droplet [29]. For example, the range of aerodynamic Weber numbers, $W{e}_{\infty }$, in which ‘non-oscillatory deformation’ is observed for an isolated droplet exposed to an ambient air flow, is ∼1.1–5.0 for the range of Ohnesorge numbers 0.03–0.08 corresponding to the variation of $D_{d0}$ from 50 to 300 $\mathsf{\mu }$m in Figure 7 (see Figure 1 in [29]). The range of aerodynamic Weber numbers, corresponding to the parameter range in Figure 7, is 0.61–3.68; for $D_{d0}>$∼90 $\mathsf{\mu }$m, $W{e}_{\infty }>1.1$, where ‘non-oscillatory deformation’ of the droplets may become increasingly significant [29]. Furthermore, in the range of Reynolds numbers shown in Figure 7 (49.4–296.4), it is known that for flow over an isolated sphere, the ring vortex in its wake starts oscillating for $Re>$∼130 [32], and hence, wake unsteadiness could become increasingly relevant as $Re$ increases beyond 130. Hence, the predictions under these conditions should be treated with caution.

3.2. Effect of Initial Droplet Velocity, $V_{d0}$

Figure 8 shows the effect of the initial droplet velocity, $V_{d0}$, on the time evolution of velocities of the leading and trailing droplets in the double-droplet system. The diameter and center-to-center separation of the droplets are kept the same as in Figure 4. The difference in the time evolution of the velocities of leading and trailing droplets, as seen in Figure 4, is also observed at different initial droplet velocities in Figure 8. Droplets injected at higher velocities tend to decelerate faster, as seen by an increase in the overall slope of the curves with an increase in $V_{d0}$. This can be explained in a similar manner as the trend of deceleration with droplet diameter, discussed in relation to Figure 5, where it was seen that smaller droplets exhibit a larger deceleration. Here, droplets injected at a higher velocity will experience a larger deceleration due to the combined influence of the factors in $C_{D}Re{V}_d$ in the deceleration due to the drag term in Equations (11) and (12).

Figure 9a shows the effect of the initial droplet velocity, $V_{d0}$, on the time evolution of the center-to-center separation of the droplets in the double-droplet system. Other initial conditions remain the same as in Figure 8. Droplets injected at lower velocities tend to take more time to come in contact with each other as highlighted by the vertical lines in Figure 9a. The trends shown in Figure 9a are normalized using the non-dimensionalization discussed in Appendix C; the corresponding non-dimensional plot is shown in Figure 9b. It is clear that the non-dimensionalization is able to collapse the trends into one curve, except for the instants of time when the droplets are very close to each other (larger values of time in each case of $V_{d0}$).

Figure 10 shows the effect of the initial droplet velocity, $V_{d0}$, on the time taken by the droplets to come in contact with each other for the first time and their approach velocity at this time instant. The initial conditions are the same as in Figure 8. Droplets injected at higher velocities tend to take less time to come in contact with each other, and when they do so, their approach velocity is higher. Similar to the case of large droplet diameters in Figure 7, it should be noted here that the conditions at which $V_{d0}$ is large in Figure 10 could lead to a significant ‘non-oscillatory deformation’ of the droplets during the initial stages of their motion. The aerodynamic Weber number lies in the range 1.39 ×${10}^{-4}$–3.87 for $V_{d0}$ varying between 0.15 and 25 m/s in Figure 10; for $V_{d0}>13.3$ m/s, $W{e}_{\infty }>1.1$, where ‘non-oscillatory deformation’ of the droplets may become increasingly significant [29]. As discussed in Figure 7, the wake unsteadiness at Reynolds numbers larger than ∼130 should be kept in mind while interpreting the predictions under these conditions in Figure 10.

3.3. Effect of Initial Droplet Separation, $a_{20}$

Figure 11 shows the effect of the initial center-to-center droplet separation, $a_{20}$, on the time evolution of velocities of the leading and trailing droplets in the double-droplet system. Other initial conditions are the same as in Figure 4. It is interesting to see that the initial separation between the droplets does not seem to have a significant influence on the time evolution of droplet velocities. However, the difference in the time evolution between the velocities of the leading and trailing droplets is still observed at a given value of initial separation.

Figure 12a shows the effect of the initial center-to-center droplet separation, $a_{20}$, on the time evolution of center-to-center separation of the droplets in the double-droplet system. Droplets that are initially separated by a larger distance tend to take a longer time to come in contact with each other (see Figure 12a and Figure 13). The trends shown in Figure 12a are normalized using the non-dimensionalization discussed in Appendix C; the corresponding non-dimensional plot is shown in Figure 12b. It is clear that the non-dimensionalization is able to collapse the trends into one curve, except for the instants of time when the droplets are very close to each other (larger values of time in each case of $a_{20}$).

The approach velocity of droplets at the instant they contact each other seems to have a non-monotonic dependence on their initial separation (see Figure 13). For initial droplet separations greater than two times the droplet diameter, the approach velocity decreases with an increase in their initial separation, whereas for initial separations less than this value, the approach velocity increases sharply with increasing the initial separation. A possible explanation for the non-linear trend of $\Delta V_{d0}$ with $a_{20}$ is similar to the one discussed for a similar trend observed in Figure 7 for the effect of droplet diameter.

4. Conclusions

A simple theoretical approach based on the superposition of pressure fields due to Stokes flow around two droplets in a double-droplet system was developed to derive the equations governing the motion of a double-droplet system. The effect of inertial terms, neglected in the Stokes flow model, was incorporated through the use of a drag coefficient reported in the literature that fits the experimental data for an isolated sphere falling under gravity at Reynolds numbers ranging from 0.1 to 10⁵. The developed model contains the dependence of the motion of droplets in the double-droplet system on the initial values of the droplet diameter, the center-to-center droplet separation, and the velocity of droplets.

A comparison of the model predictions with limited experimental data showed a good agreement between the experiments and predictions. The predicted time at which the droplets come in contact with each other showed a deviation of 7.4% from the experimental data. The time-averaged error in the predictions relative to the experimental data was 4.84%, with a higher error of 9.97% for the data at later times during the grouping process.

The predictions indicated that the trailing droplet experiences a reduced drag force compared to that experienced by the leading droplet. From the solution of the equations of motion of the droplets, the time required for them to come in contact with each other and their approach velocity at this instant were extracted. The dependence of these parameters on the initial conditions (diameter, center-to-center separation, and velocity) was discussed. Using appropriate normalizations involving these initial conditions, it was shown that the temporal variation of the inter-droplet distance during the grouping process collapsed into one single trend for parametric studies involving initial droplet diameter, initial droplet velocity, and initial inter-droplet separation. The time taken for the droplets to come in contact with each other ($t_o$) was seen to be a non-monotonous function of the initial droplet diameter ($D_{d0}$) and the initial inter-droplet distance ($a_{20}$), exhibiting a maximum in both the cases at $a_{20}/D_{d0}\approx 2$; whereas $t_o$ was seen to decrease monotonously with the initial droplet velocity.

Using the conditions at which the droplets contact each other, the criterion for droplet coalescence was checked, and this seemed to agree with the limited experimental observation. Further experiments at different values of initial conditions are needed to judge the validity of assumptions made in the current theoretical approach. In addition to this, data from direct numerical simulations were used to understand the validity of the pressure field assumptions made in the theoretical approach reported here.