RANS Modelling of a NACA4412 Wake Using Wind Tunnel Measurements
Abstract
1. Introduction
2. Numerical and Experimental Setups
2.1. Simulation
2.2. Experiment
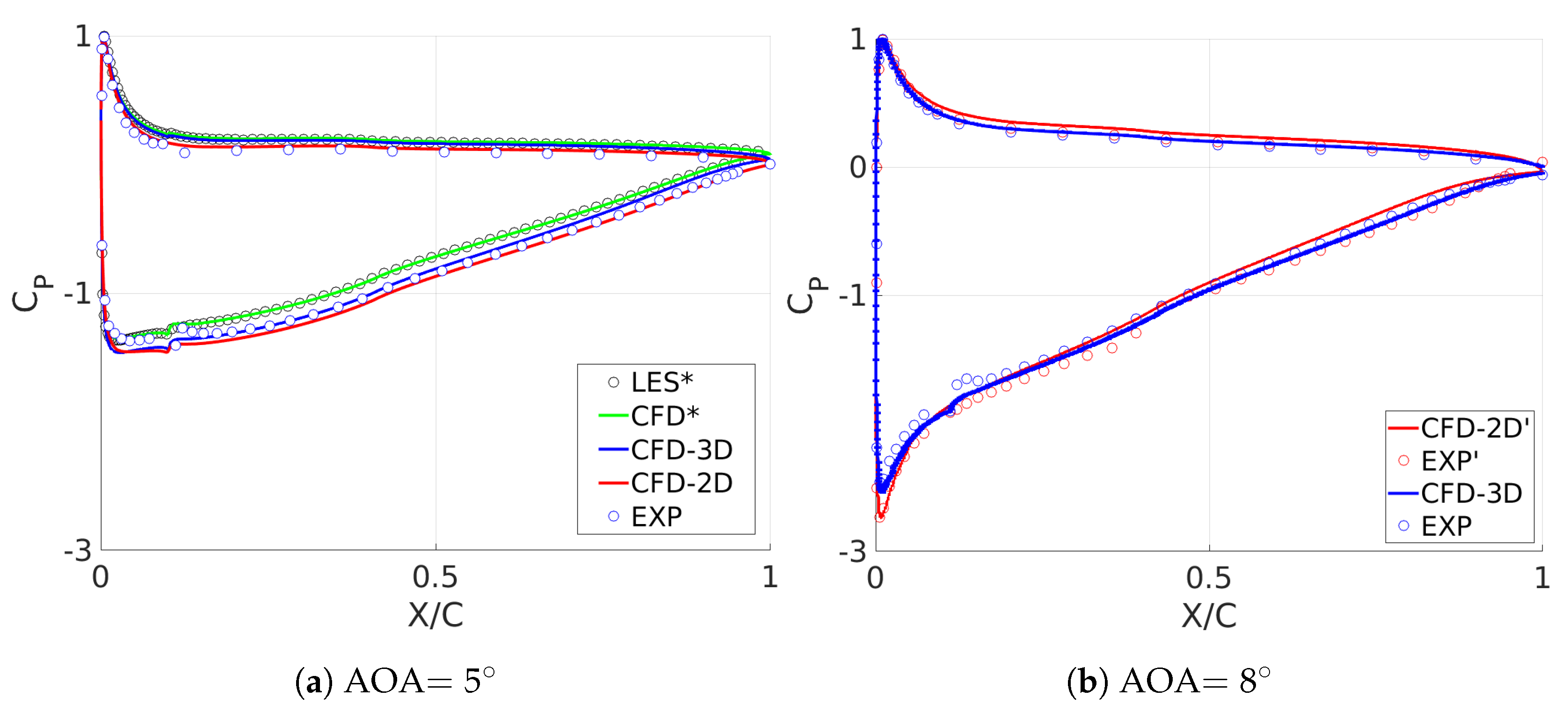
2.2.1. Pressure Scans
2.2.2. Tuft Visualization
2.2.3. Hot-Wire Measurements
3. Setup Sensitivity
4. Wake Analysis
4.1. Multiple Aspects Analysis
4.2. Results at the Mid-Span Section
4.2.1. Mean Velocity Field
4.2.2. Velocity Fluctuation Field
4.2.3. Instantaneous Wake
4.3. Spanwise Variation
4.4. Spanwise Blockage
5. Wake Characteristics and Similarity Analysis
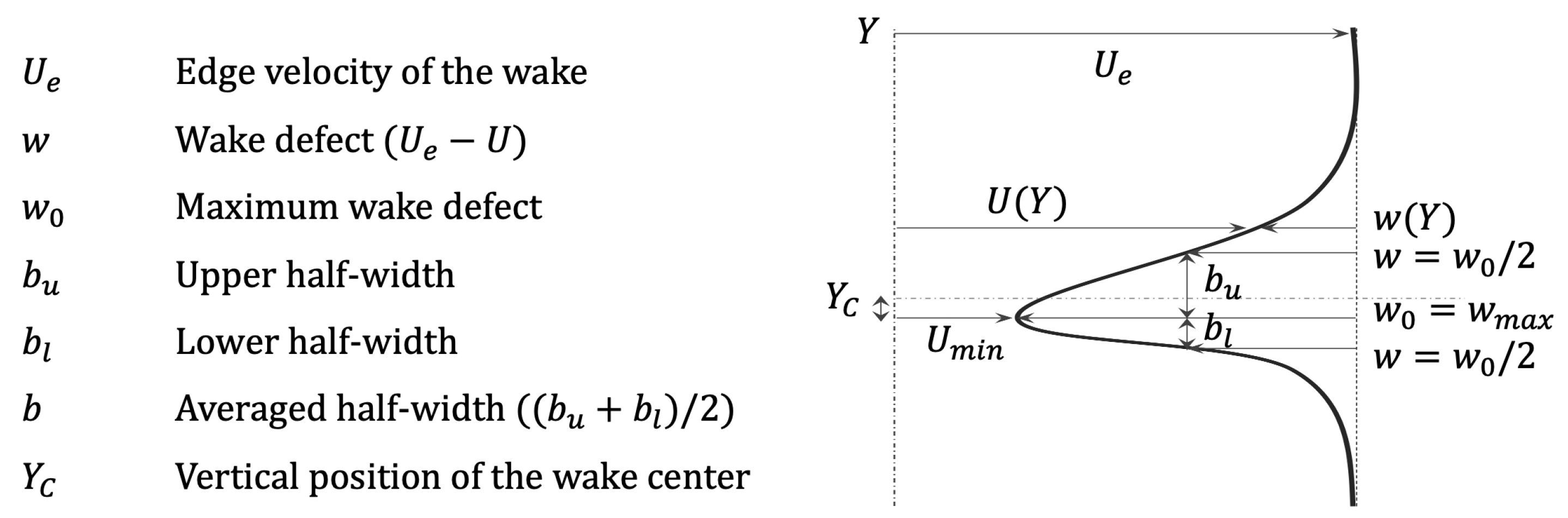
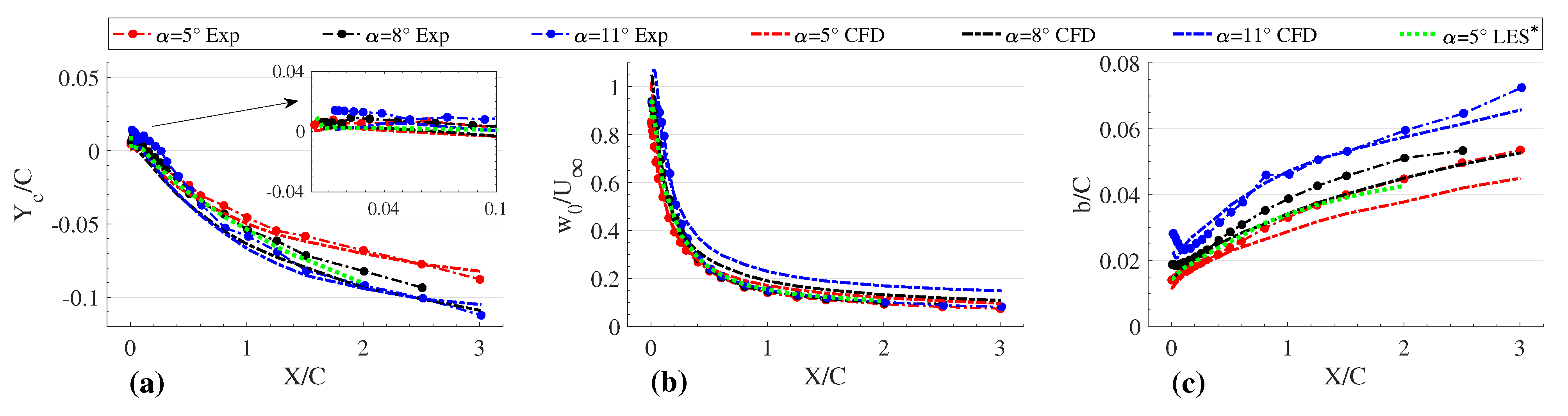
5.1. Wake Characteristics
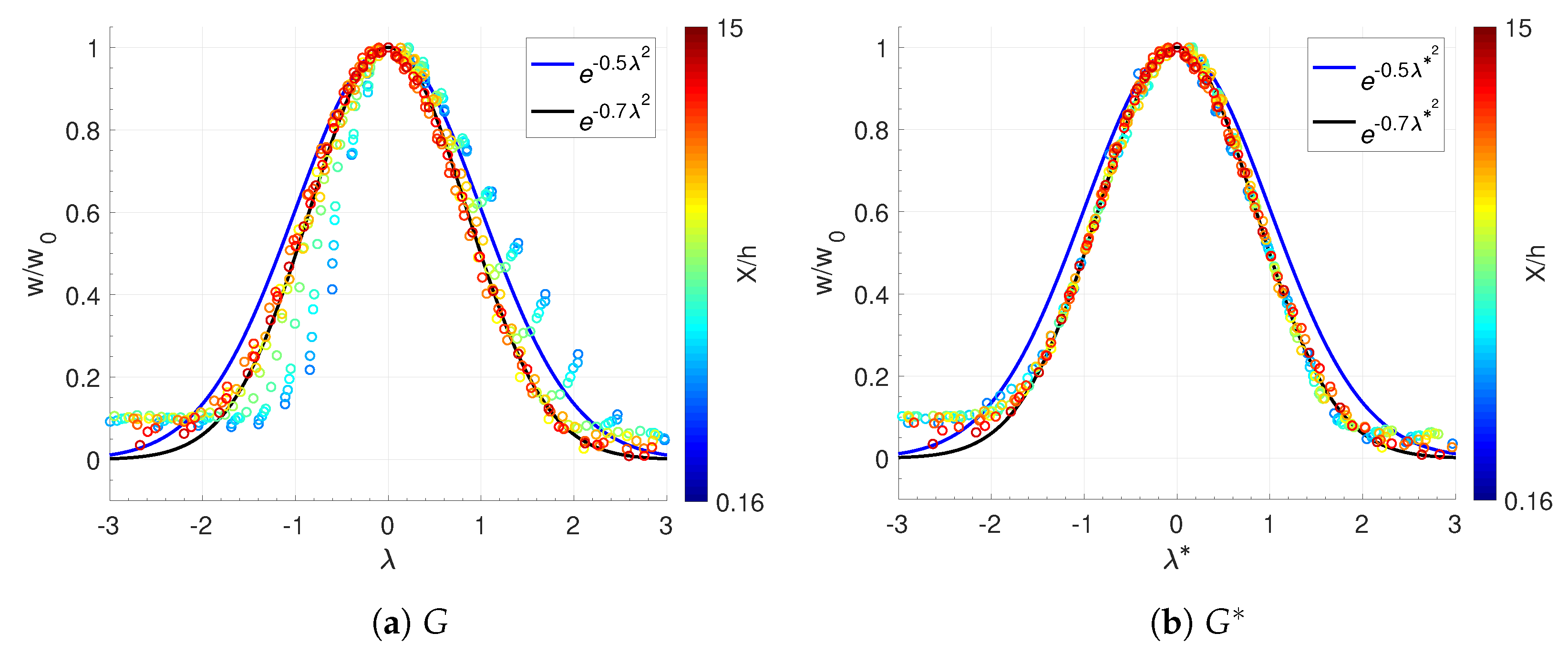
5.2. Self-Similarity
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Williamson, C.H.K. Vortex Dynamics in the Wake of a Cylinder. In Fluid Vortices; Springer: Dordrecht, The Netherlands, 1995; pp. 155–234. [Google Scholar] [CrossRef]
- Rossow, V.; Hardy, G.; Meyn, L. Models of Wake-Vortex Spreading Mechanisms and Their Estimated Uncertainties. In Proceedings of the AIAA 5th ATIO and 16th Lighter-Than-Air Sys Technology and Balloon Systems Conferences, Arlington, VA, USA, 26–28 September 2005; p. 7353. [Google Scholar] [CrossRef]
- Dimotakis, P.E. Turbulent Mixing. Annu. Rev. Fluid Mech. 2005, 37, 329–356. [Google Scholar] [CrossRef]
- Davidson, L. An Introduction to Turbulence Models; Chalmers University of Technology: Goteborg, Sweden, 2018. [Google Scholar]
- Creese, T.; Brogan, C. Digital wind Tunnels Could Help Develop More Fuel Efficient Aeroplanes; Imperial College London: London, UK, 2021. [Google Scholar]
- Bennetsen, J.C. Know Which Way the Wind Blows. Ramboll Group A/S. 2021. Available online: https://ramboll.com/digital-solutions/buildings/cfd-technology/digital-wind-tunnel (accessed on 15 March 2022).
- Tabatabaei, N. Impact of Icing on Wind Turbines Aerodynamic. Ph.D. Thesis, Luleå University of Technology, Fluid and Experimental Mechanics, Luleå, Sweden, 2018. [Google Scholar]
- Tabatabaei, N.; Vinuesa, R.; Örlü, R.; Schlatter, P. Techniques for turbulence tripping of boundary layers in RANS simulations. Flow Turbul. Combust. 2021. [Google Scholar] [CrossRef]
- Tabatabaei, N.; Örlü, R.; Vinuesa, R.; Schlatter, P. Aerodynamic Free-Flight Conditions in Wind Tunnel Modelling through Reduced-Order Wall Inserts. Fluids 2021, 6, 265. [Google Scholar] [CrossRef]
- Yoder, D.A.; DeBonis, J.R.; Georgiadis, N.J. Modeling of Turbulent Free Shear Flows. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; pp. 1–30. [Google Scholar] [CrossRef][Green Version]
- Yoder, D.; DeBonis, J.; Georgiadis, N. Modeling of turbulent free shear flows. Comput. Fluids 2015, 117, 212–232. [Google Scholar] [CrossRef]
- Johnson, P.B.; Jonsson, C.; Achilleos, S.; Eames, I. On the spread and decay of wind turbine wakes in ambient turbulence. J. Phys. Conf. Ser. 2014, 555, 012055. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Schlatter, P.; Örlü, R. Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 2010, 659, 116–126. [Google Scholar] [CrossRef]
- Lindgren, B.; Johansson, A.V. Evaluation of the Flow Quality in the MTL Wind-Tunnel; Technical Report TRITA-MEK 2002:13; Deparment of Mechanics, KTH: Stockholm, Sweden, 2002. [Google Scholar]
- Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware, Inc.: Clifton Park, NY, USA, 2015. [Google Scholar]
- Greenshields, C.J. OpenFOAM User Guide; Version 7; Foundation Ltd.: Tokyo, Japan, 2019. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Bardina, J.; Huang, P.; Coakley, T. Turbulence Modeling Validation, Testing, and Development. NASA Tech. Memo. 1997, 110446, 147. [Google Scholar]
- Ansys, I. ICEM CFD User Manual; Release 14.0; Ansys Inc.: Pune, India, 2011. [Google Scholar]
- Steinfurth, B.; Cura, C.; Gehring, J.; Weiss, J. Tuft deflection velocimetry: A simple method to extract quantitative flow field information. Exp. Fluids 2020, 61, 146. [Google Scholar] [CrossRef]
- Bailey, S.C.C.; Hultmark, M.; Monty, J.P.; Alfredsson, P.H.; Chong, M.S.; Duncan, R.D.; Fransson, J.H.M.; Hutchins, N.; Marusic, I.; McKeon, B.J.; et al. Obtaining accurate mean velocity measurements in high Reynolds number turbulent boundary layers using Pitot tubes. J. Fluid Mech. 2013, 715, 642–670. [Google Scholar] [CrossRef]
- Vinuesa, R.; Negi, P.; Atzori, M.; Hanifi, A.; Henningson, D.; Schlatter, P. Turbulent boundary layers around wing sections up to Rec=1,000,000. Int. J. Heat Fluid Flow 2018, 72, 86–99. [Google Scholar] [CrossRef]
- Wallin, S.; Johansson, A.V. An explicit algebraic Reynolds stress model for incompressible and compressible turbulent flows. J. Fluid Mech. 2000, 403, 89–132. [Google Scholar] [CrossRef]
- Kalpakli Vester, A.; Sattarzadeh, S.S.; Örlü, R. Combined hot-wire and PIV measurements of a swirling turbulent flow at the exit of a 90 degree pipe bend. J. Vis. 2016, 19, 261–273. [Google Scholar] [CrossRef]
- Parker, R.; Welsh, M. Effects of sound on flow separation from blunt flat plates. Int. J. Heat Fluid Flow 1983, 4, 113–127. [Google Scholar] [CrossRef]
- Morgenthal, G. Fluid-Structure Interaction in Bluff-Body Aerodynamics and Long-Span Bridge Design: Phenomena and Methods; University of Cambridge: Cambridge, UK, 2001. [Google Scholar]
- Nedić, J.; Vassilicos, J.C. Vortex Shedding and Aerodynamic Performance of Airfoil with Multiscale Trailing-Edge Modifications. AIAA J. 2015, 53, 3240–3250. [Google Scholar] [CrossRef]
- Yarusevych, S.; Sullivan, P.E.; Kawall, J.G. On vortex shedding from an airfoil in low-Reynolds-number flows. J. Fluid Mech. 2009, 632, 245–271. [Google Scholar] [CrossRef]
- Lee, H.W.; Huang, R.F. frequency Selection of Wake Flow Behind a NACA 0012 Wing. J. Mar. Sci. Technol. 1998, 6, 29–37. [Google Scholar] [CrossRef]
- Kurtulus, D. On the wake pattern of symmetric airfoils for different incidence angles at Re = 1000. Int. J. Micro Air Veh. 2016, 8, 109–139. [Google Scholar] [CrossRef]
- Koca, K.; Genç, M.S.; Açıkel, H.H.; Çağdaş, M.; Bodur, T.M. Identification of flow phenomena over NACA 4412 wind turbine airfoil at low Reynolds numbers and role of laminar separation bubble on flow evolution. Energy 2018, 144, 750–764. [Google Scholar] [CrossRef]
- Rojratsirikul, P.; Genc, M.; Wang, Z.; Gursul, I. Flow-induced vibrations of low aspect ratio rectangular membrane wings. J. Fluids Struct. 2011, 27, 1296–1309. [Google Scholar] [CrossRef]
- Ramjee, V.; Neelakandan, D. Curvature effects on the wake of an airfoil and other bodies. Fluid Dyn. Res. 1990, 6, 1. [Google Scholar] [CrossRef]
- Yao, C.; Paschal, K. PIV measurements of airfoil wake-flow turbulence statistics and turbulent structures. In Proceedings of the 32nd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 1994; p. 85. [Google Scholar]
- Duda, D.; Uruba, V.; Yanovych, V. Wake Width: Discussion of Several Methods How to Estimate It by Using Measured Experimental Data. Energies 2021, 14, 4712. [Google Scholar] [CrossRef]
- Marble, E.; Morton, C.; Yarusevych, S. Spanwise wake development of a pivoted cylinder undergoing vortex-induced vibrations with elliptic trajectories. Exp. Fluids 2019, 60, 81. [Google Scholar] [CrossRef]
- Abdalla, H.A. Boundary layer-tripping studies on characteristics of near-wake behind a cambered airfoil. ERJ. Eng. Res. J. 1999, 22, 115–133. [Google Scholar] [CrossRef]
- Abkar, M.; Dabiri, J.O. Self-similarity and flow characteristics of vertical-axis wind turbine wakes: An LES study. J. Turbul. 2017, 18, 373–389. [Google Scholar] [CrossRef]
- Lyu, P.; Chen, W.L.; Li, H.; Shen, L. A Numerical Study on the Development of Self-Similarity in a Wind Turbine Wake Using an Improved Pseudo-Spectral Large-Eddy Simulation Solver. Energies 2019, 12, 643. [Google Scholar] [CrossRef]
- Mayes, C.; Schlichting, H.; Krause, E.; Oertel, H.; Gersten, K. Boundary-Layer Theory; Physic and Astronomy; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Johansson, P.B.V.; George, W.K.; Gourlay, M.J. Equilibrium similarity, effects of initial conditions and local Reynolds number on the axisymmetric wake. Phys. Fluids 2003, 15, 603–617. [Google Scholar] [CrossRef]
- Wei, T. Self-Similarity Analysis of Turbulent Wake Flows. J. Fluids Eng. 2017, 139, 051203. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modeling for CFD; Number v. 1 in Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 2006. [Google Scholar]
- Fage, A.; Falkner, V.M.; Taylor, G.I. Note an experiments on the temperature and velocity in the wake of a heated cylindrical obstacle. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1932, 135, 702–705. [Google Scholar]
- Qian, J. Non-Gaussian self-similarity in the inertial range of turbulence. J. Hydrodyn. Ser. B 2006, 18, 232–236. [Google Scholar] [CrossRef]
- Xie, S.; Archer, C. Self-similarity and turbulence characteristics of wind turbine wakes via large-eddy simulation. Wind Energy 2014, 18, 1815–1838. [Google Scholar] [CrossRef]


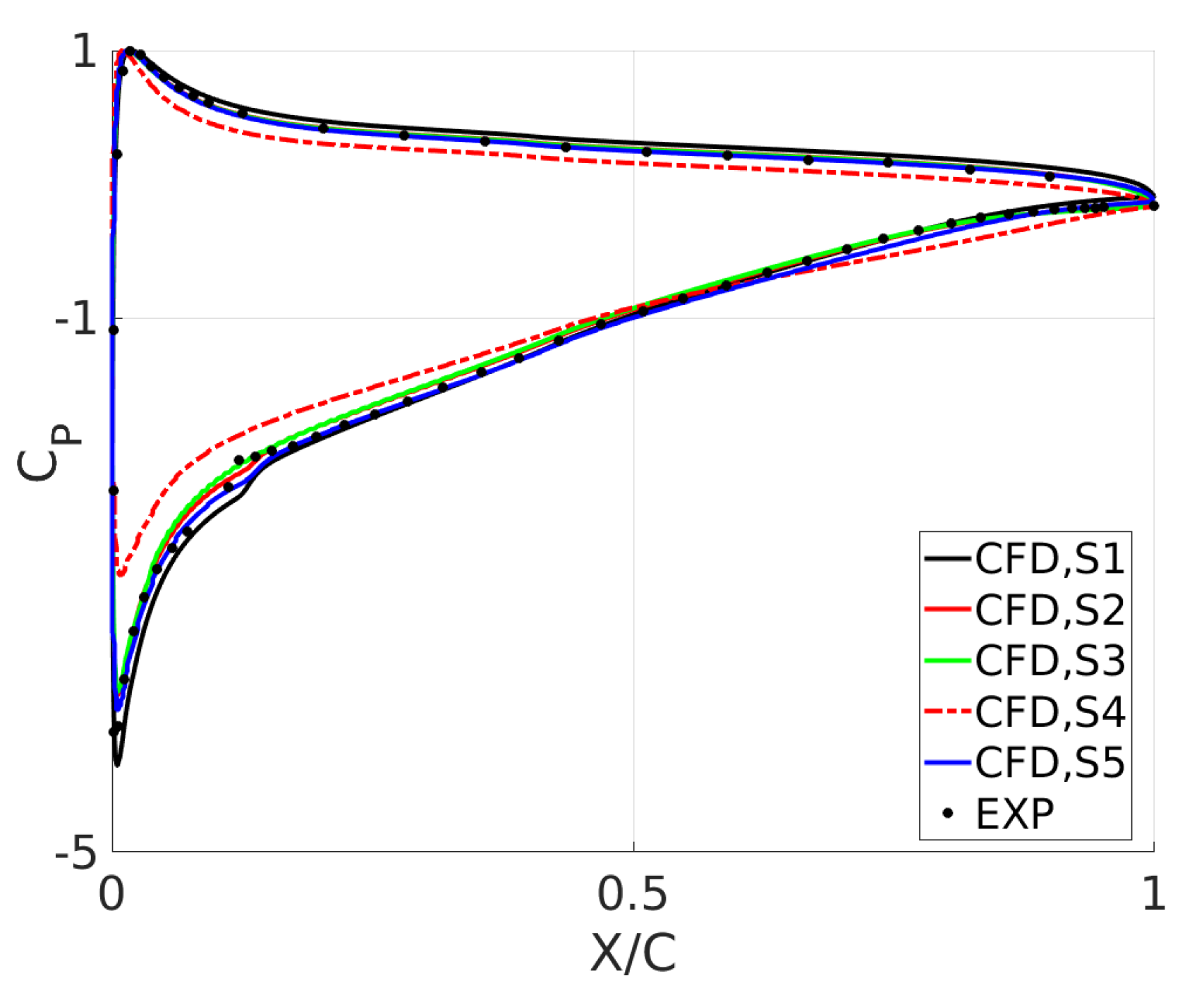

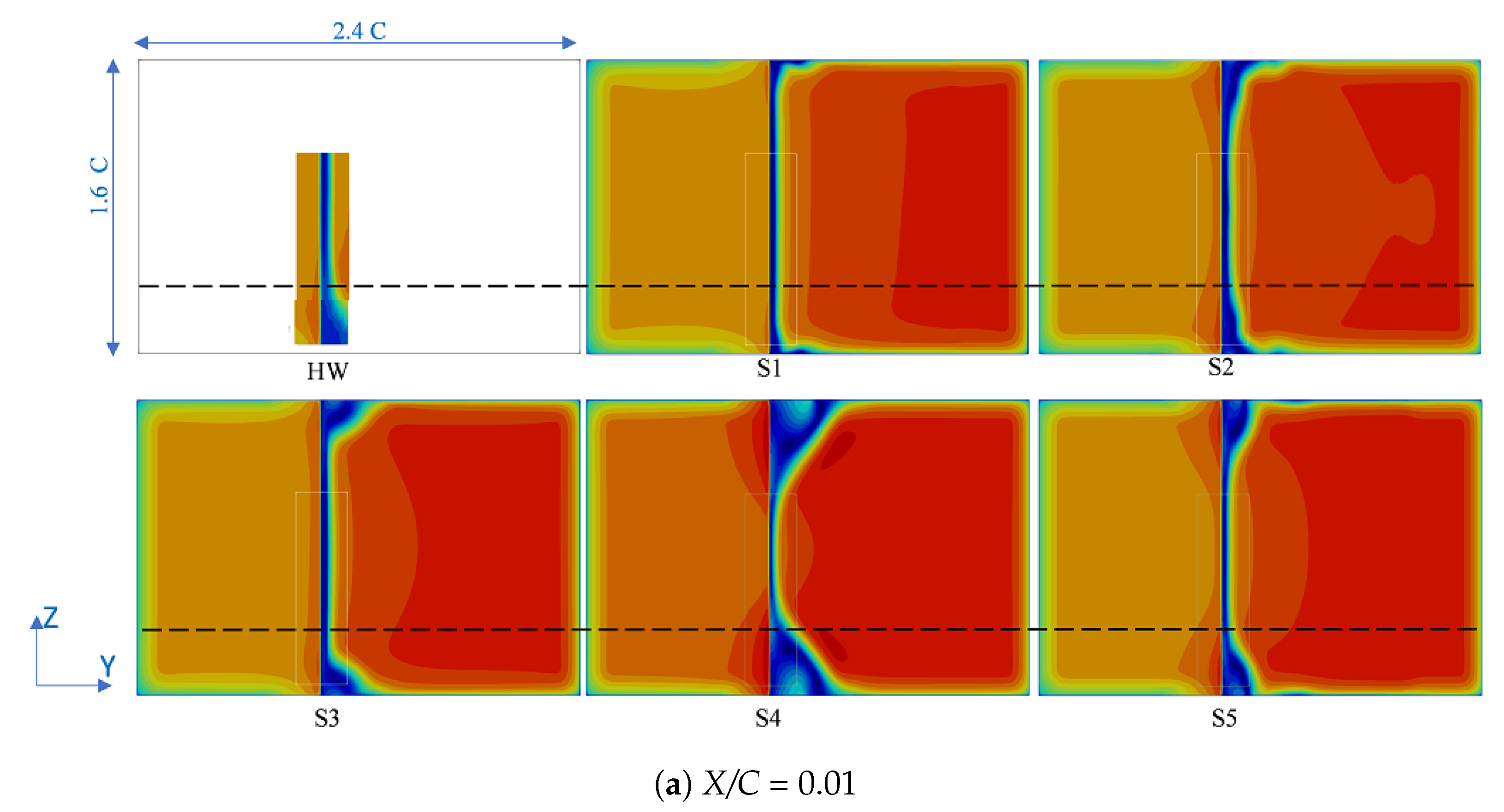
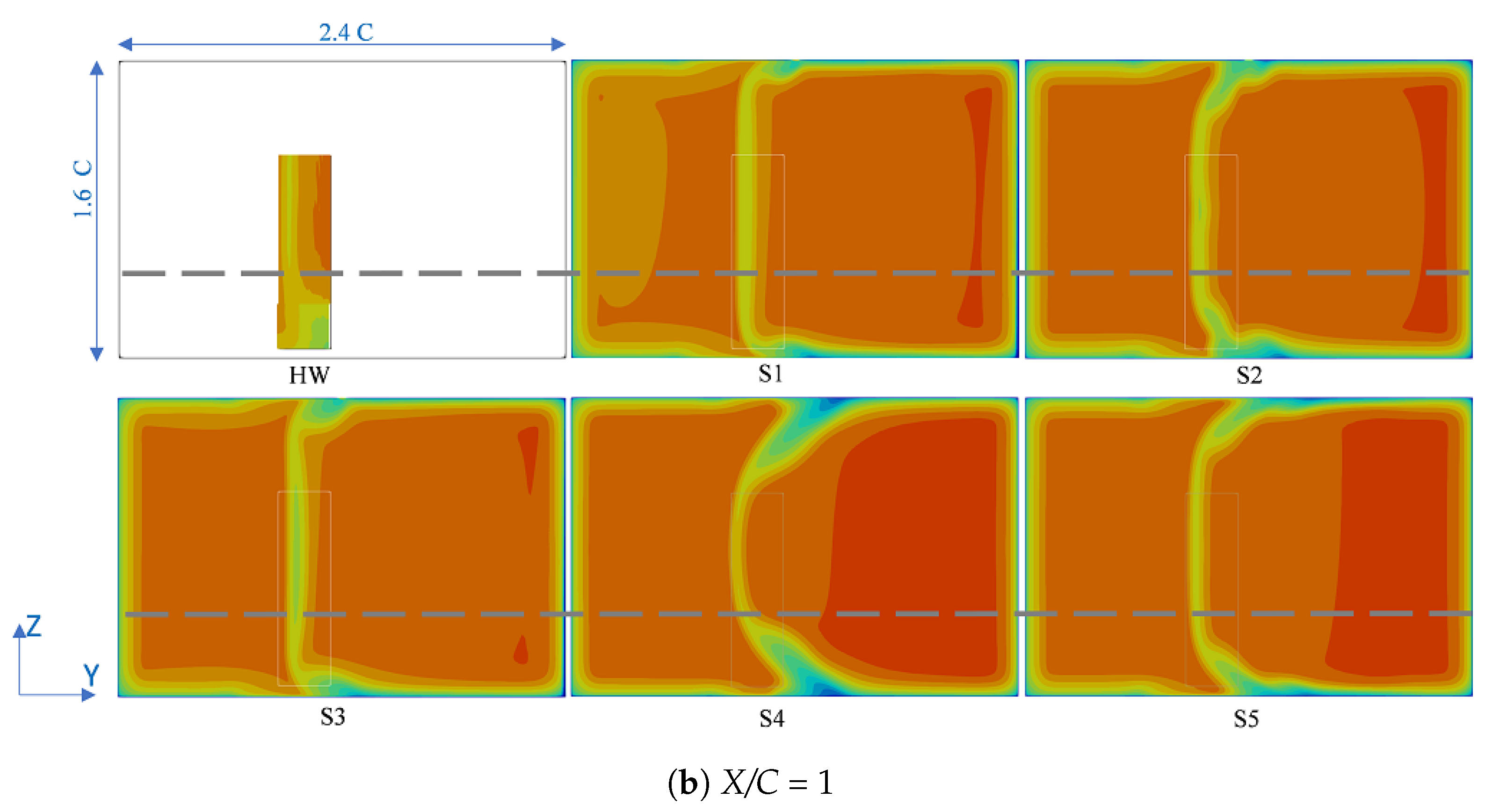

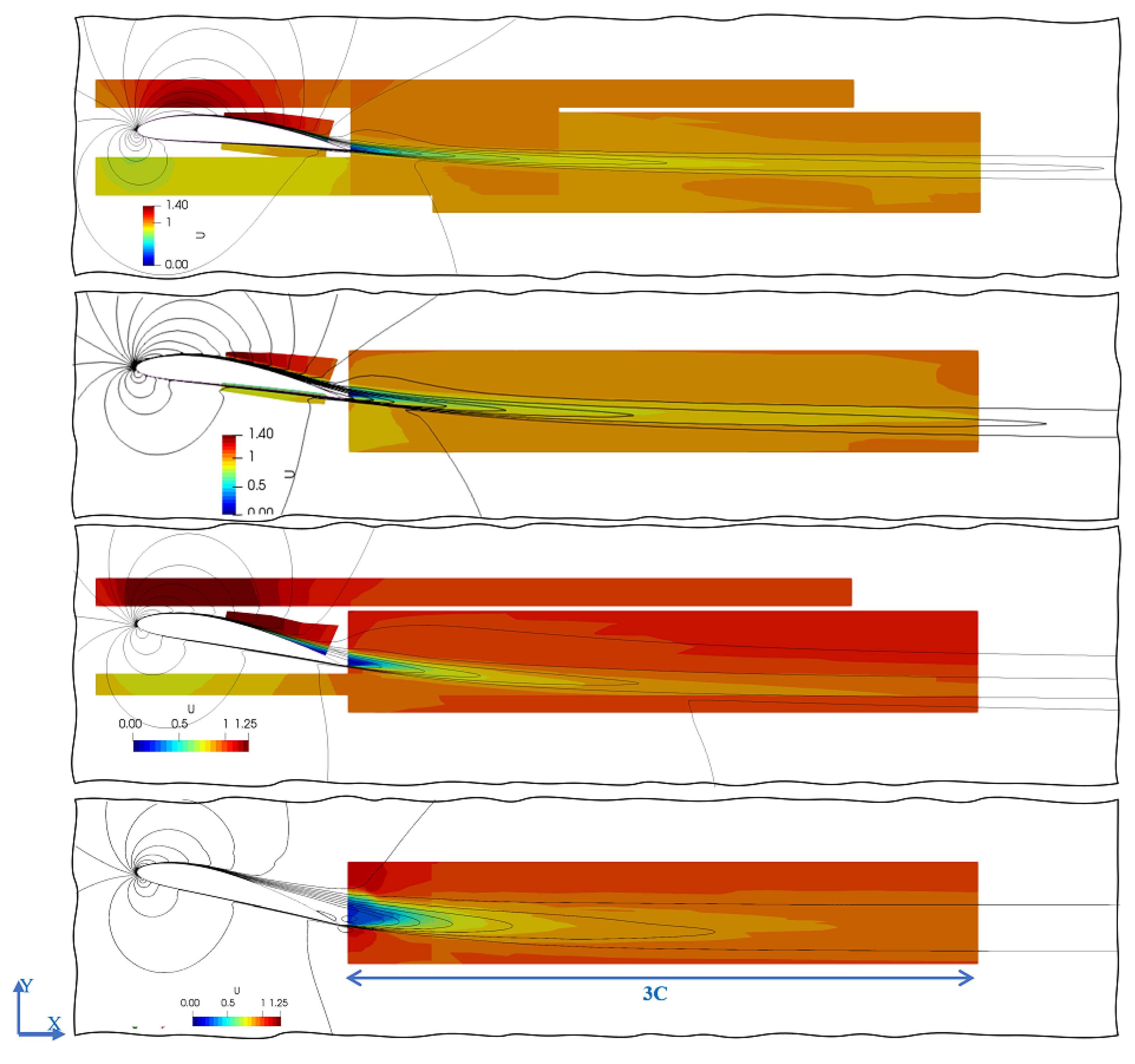
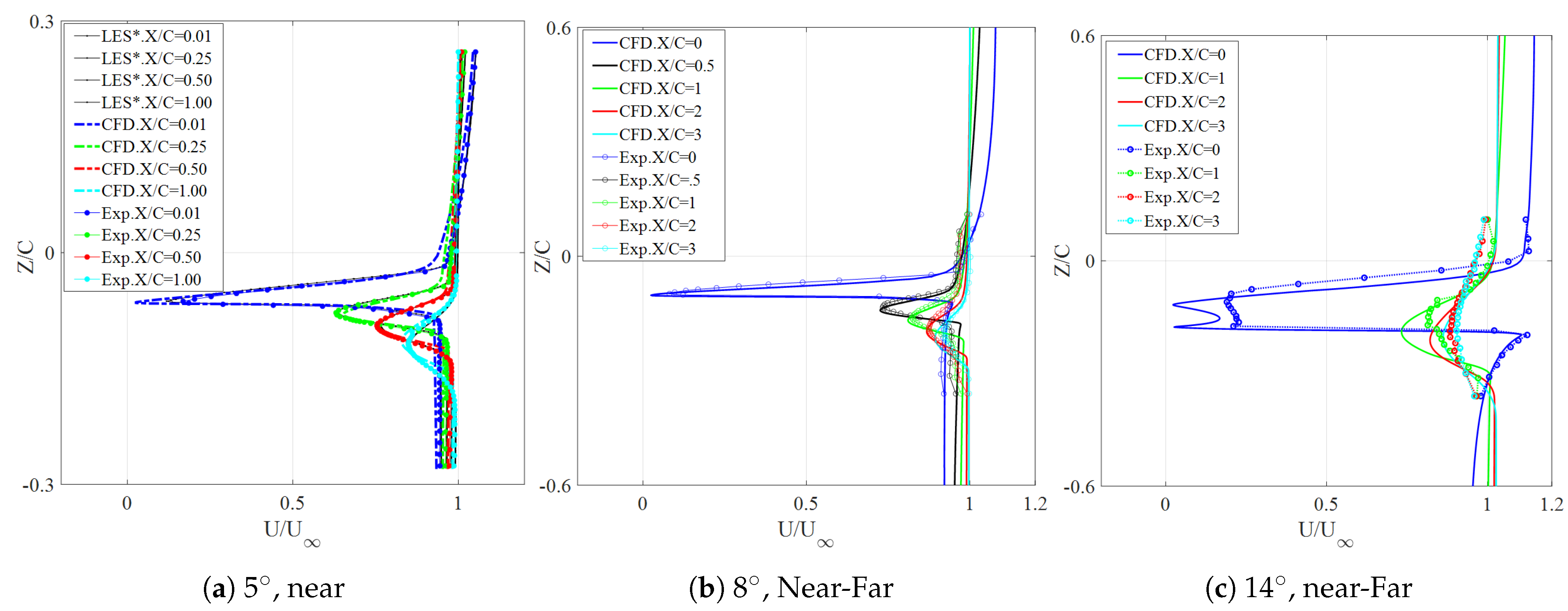
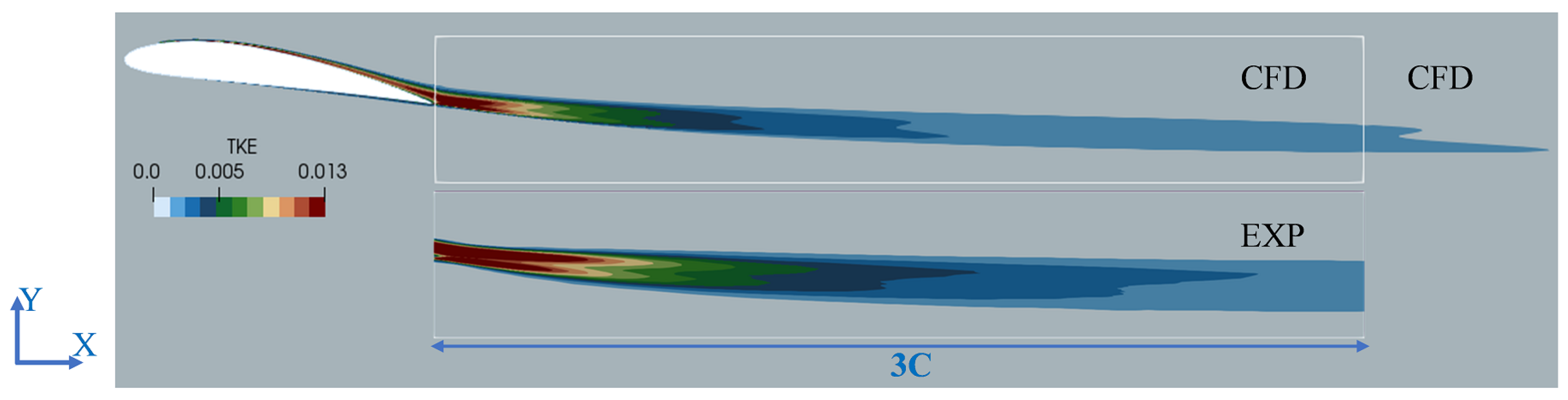

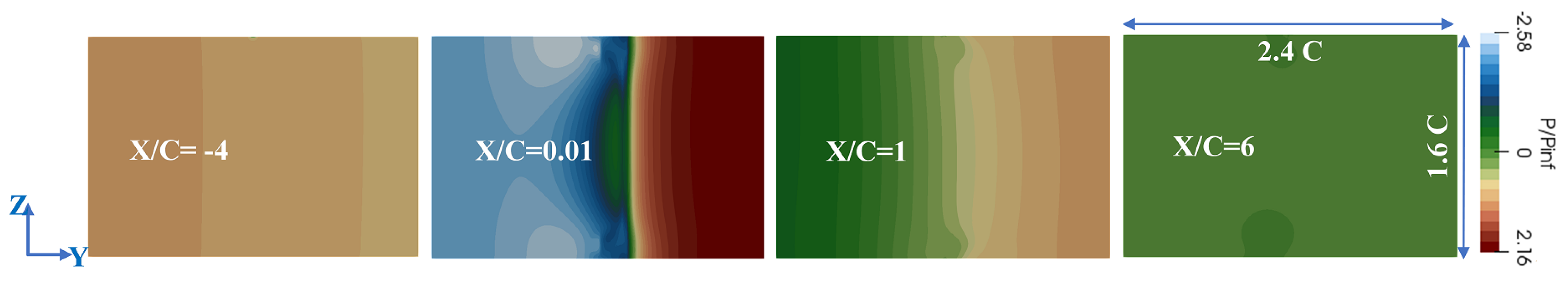


| Configuration | Description |
|---|---|
| S1 | Open slot, BL control (2-cm away from the walls) |
| S2 | Open slot, BL control (10-cm away from the walls) |
| S3 | Open slot, No BL control |
| S4 | Closed slot, No BL control |
| S5 | Closed slot, BL control (all through) |
| Parameter | Region | Technique | Section in the Paper | |
|---|---|---|---|---|
| 1 | Chordwise distribution | Wing surface at mid-height section | Scanivalve | Section 3 |
| 2 | Wake velocity profile | Mid-height plane (XY) | HW | Section 4 |
| 3 | Instantaneous wake | Mid-height plane (XY) | HW | Section 4.2.1 |
| 4 | Spanwise wake velocity profile | Normal plane (YZ) at different X | HW | Section 3 and Section 4.3 |
| 5 | Surface streamlines | Over the wing upstream of TE | Tuft | Section 4.3 |
| Reference | ||
|---|---|---|
| CFD | 0.20 | 0.73 |
| EXP | 0.22 | 0.78 |
| Ref. [26,27] | 0.22 | - |
| Ref. [28] | 0.19–0.21 | - |
| Ref. [29] | 0.20 | - |
| Ref. [32,33] | - | 0.71 |
| Spreading Rate Criteria | Cylinder | Airfoil | ||||||
|---|---|---|---|---|---|---|---|---|
| Formulation | Method | Pope [13] | Bardina [19] | Fage [45] | Pope [13] | |||
| = | EXP | - | - | 0.37 | 0.28 | 0.30 | 0.33 | - |
| CFD | - | 0.26 | - | 0.25 | 0.25 | 0.26 | - | |
| EXP | 0.08 | - | - | 0.11 | 0.10 | 0.12 | 0.10 | |
| CFD | - | - | - | 0.07 | 0.07 | 0.05 | - | |
| LES | - | - | - | 0.07 | - | - | - | |
| Self-Similarity Criteria | Onset | Onset | |||||
|---|---|---|---|---|---|---|---|
| Formulation | Method | AOA = | AOA = | AOA = | AOA = | AOA = | AOA = |
| EXP | 0.1 | 0.2 | 0.2 | 0.8 | 0.9 | 0.9 | |
| CFD | 0.3 | 0.2 | 0.2 | 0.9 | 0.9 | 1.0 | |
| LES* | 0.1 | - | - | 0.9 | - | - | |
| () | EXP | 2.5 | 1.6 | 0.9 | 0.3 | 0.3 | 0.5 |
| CFD | 9.5 | 15.2 | 23.0 | 0.1 | 0.1 | 0.1 | |
| LES* | 3.2 | - | - | 0.3 | - | - | |
| S | EXP | 5.1 | 5.1 | 5.3 | 0.2 | 0.1 | 0.1 |
| CFD | 6.3 | 6.3 | 6.3 | 0.2 | 0.2 | 0.2 | |
| LES* | 7.9 | - | - | 0.1 | - | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabatabaei, N.; Hajipour, M.; Mallor, F.; Örlü, R.; Vinuesa, R.; Schlatter, P. RANS Modelling of a NACA4412 Wake Using Wind Tunnel Measurements. Fluids 2022, 7, 153. https://doi.org/10.3390/fluids7050153
Tabatabaei N, Hajipour M, Mallor F, Örlü R, Vinuesa R, Schlatter P. RANS Modelling of a NACA4412 Wake Using Wind Tunnel Measurements. Fluids. 2022; 7(5):153. https://doi.org/10.3390/fluids7050153
Chicago/Turabian StyleTabatabaei, Narges, Majid Hajipour, Fermin Mallor, Ramis Örlü, Ricardo Vinuesa, and Philipp Schlatter. 2022. "RANS Modelling of a NACA4412 Wake Using Wind Tunnel Measurements" Fluids 7, no. 5: 153. https://doi.org/10.3390/fluids7050153
APA StyleTabatabaei, N., Hajipour, M., Mallor, F., Örlü, R., Vinuesa, R., & Schlatter, P. (2022). RANS Modelling of a NACA4412 Wake Using Wind Tunnel Measurements. Fluids, 7(5), 153. https://doi.org/10.3390/fluids7050153








