Blood Flow Simulation to Determine the Risk of Thrombosis in the Fontan Circulation: Comparison between Atriopulmonary and Total Cavopulmonary Connections
Abstract
1. Introduction
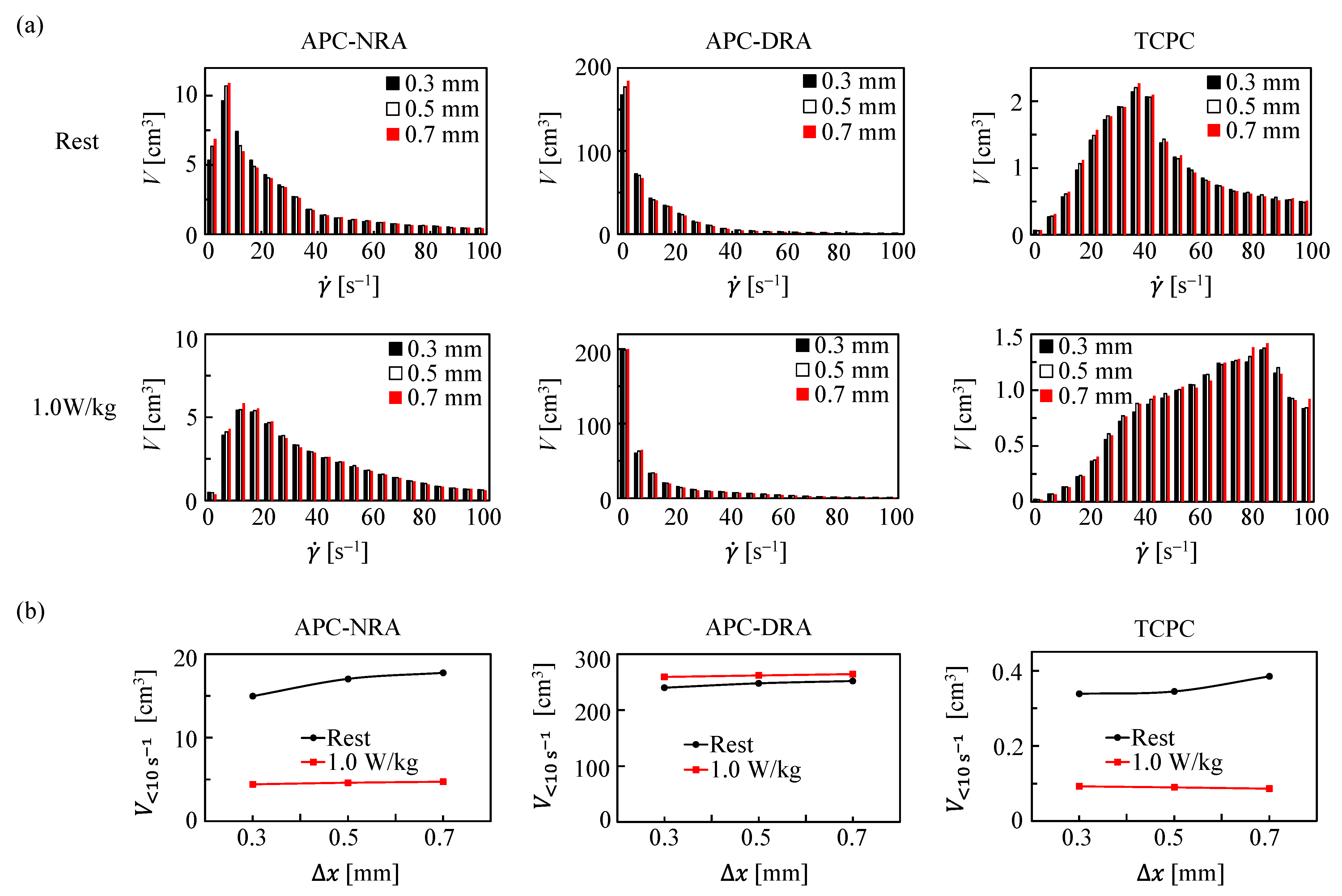
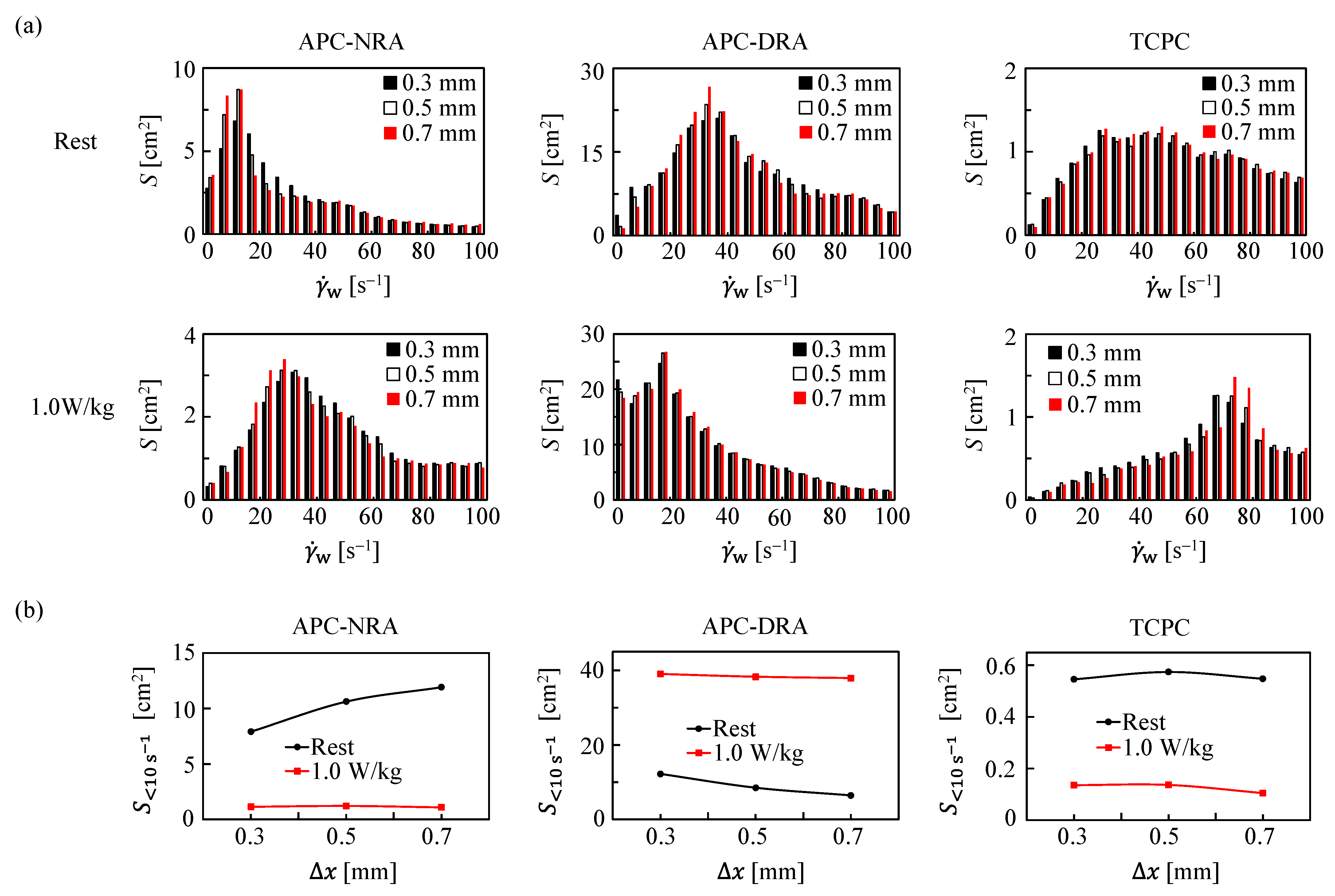
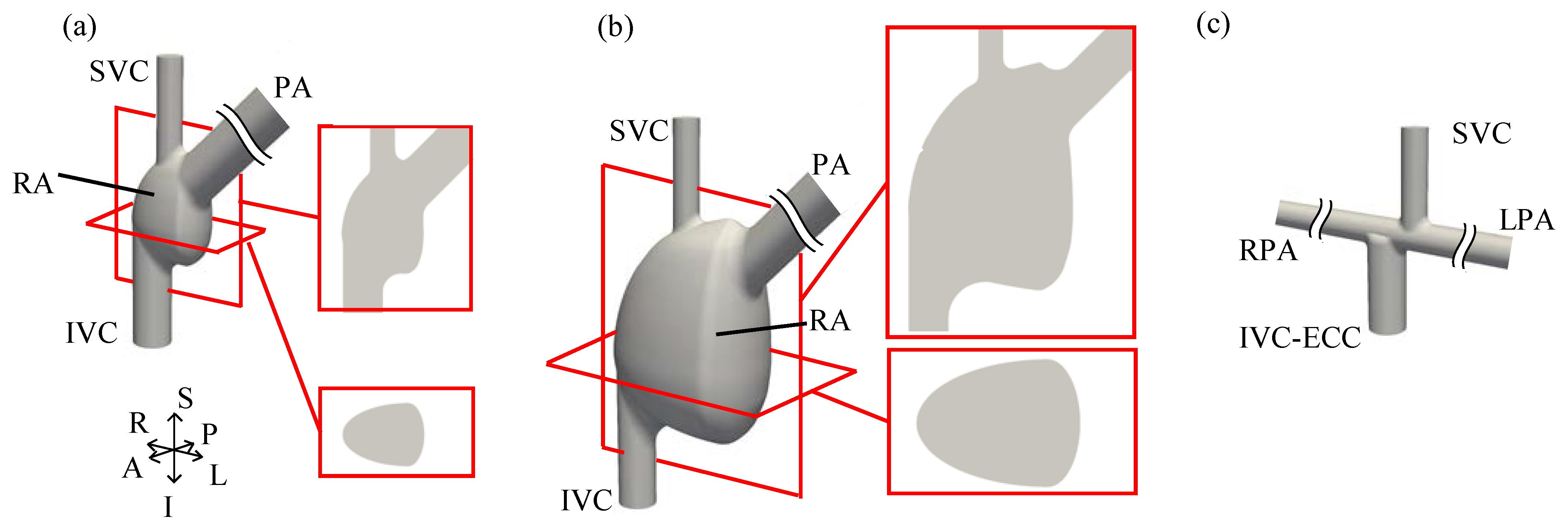
2. Methods
3. Results
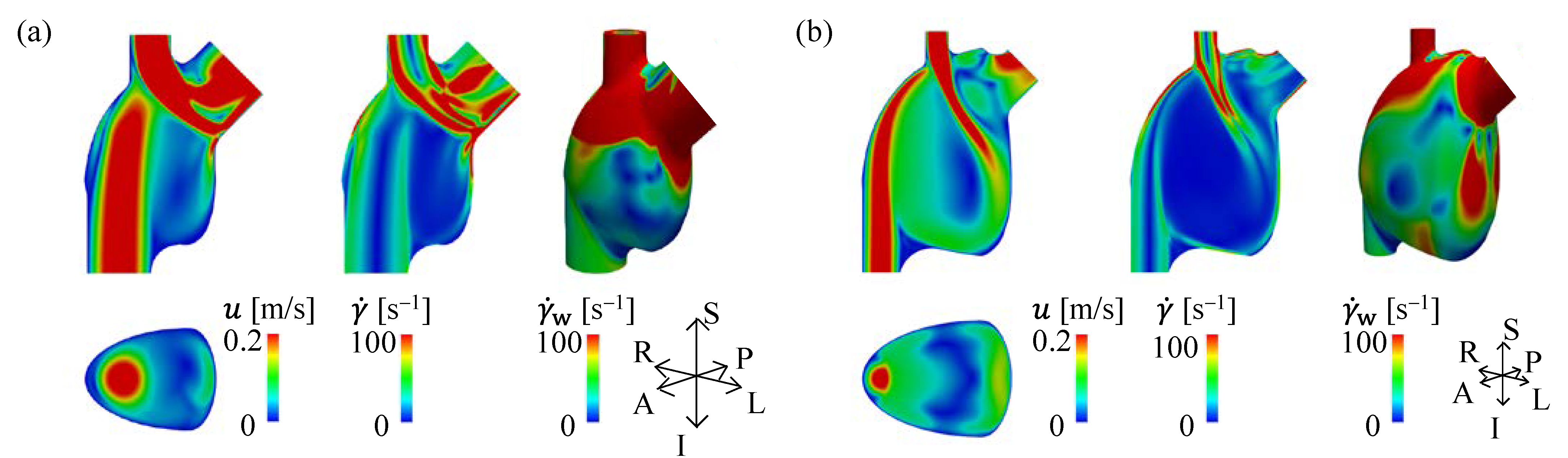
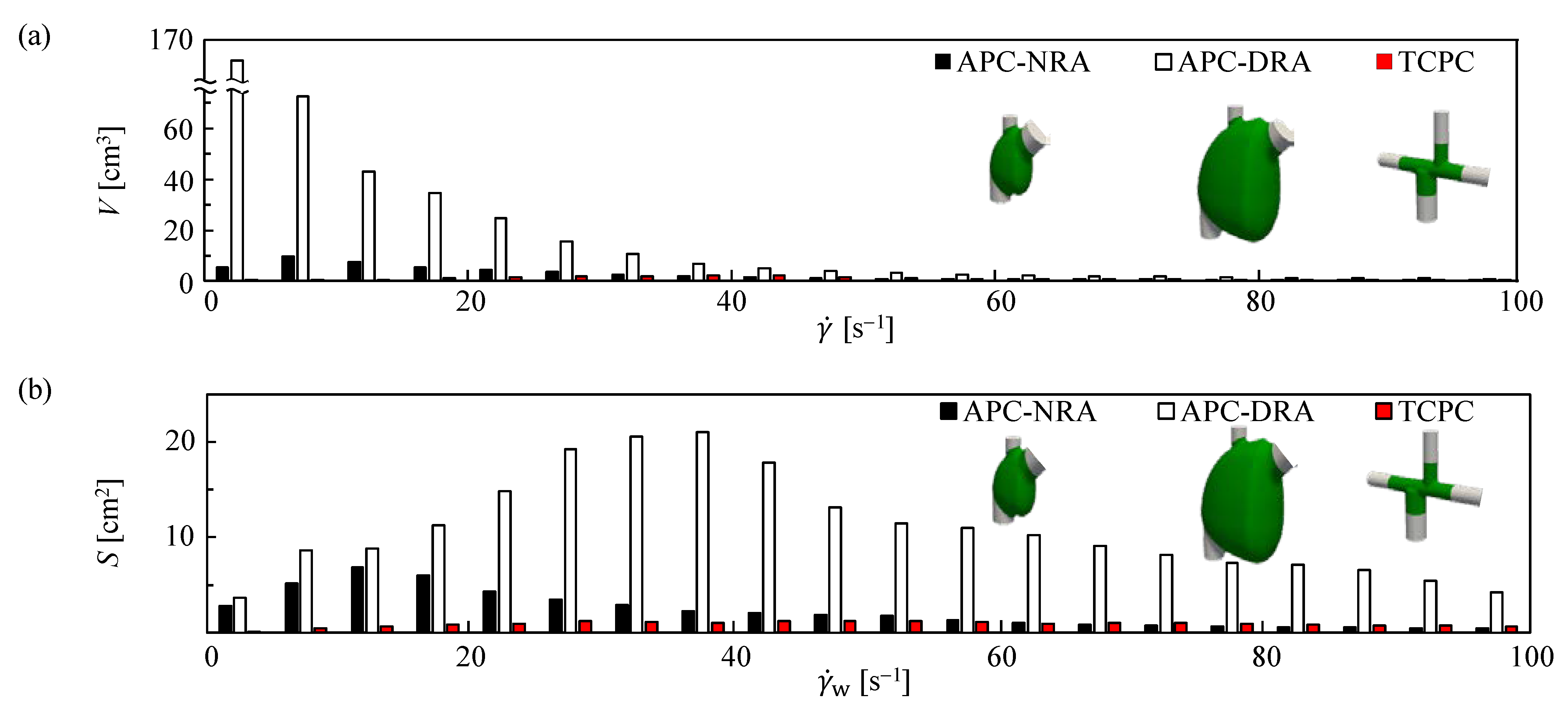
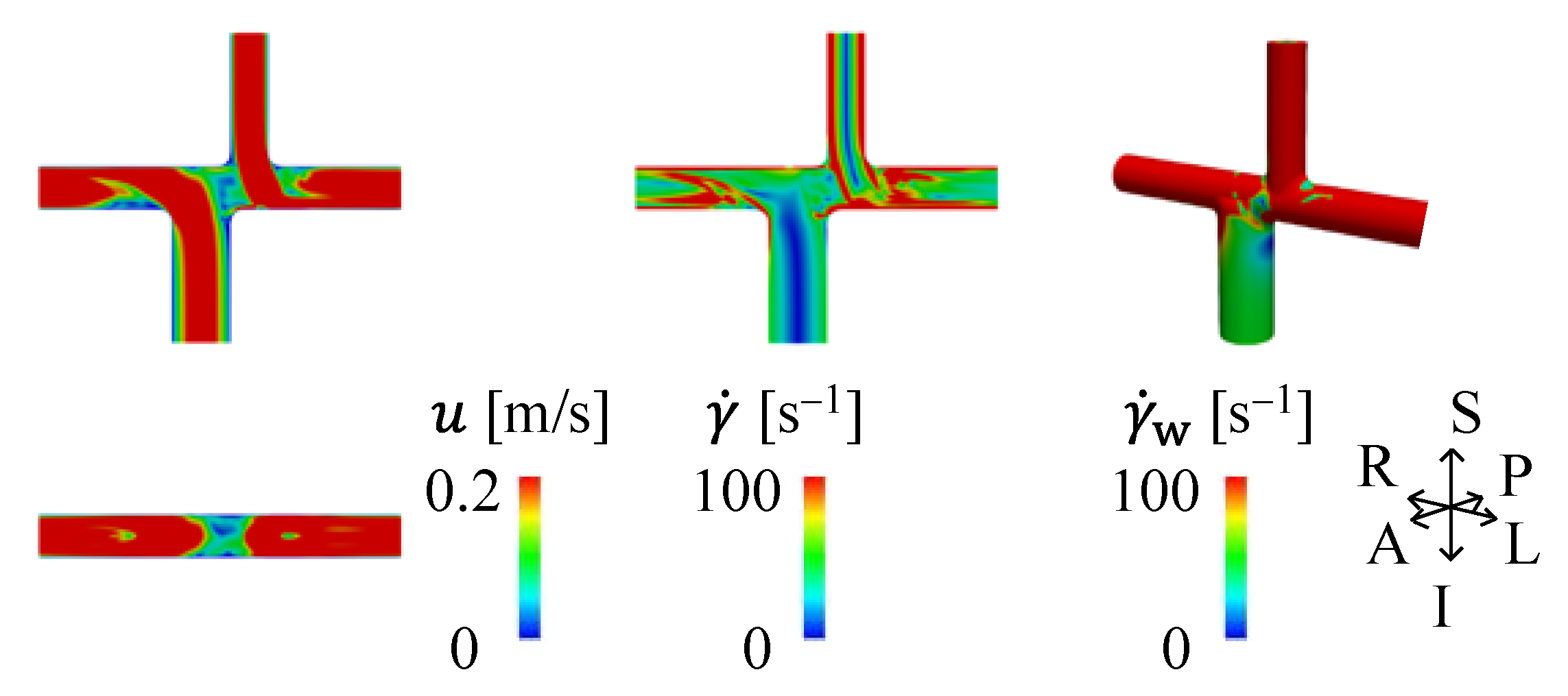
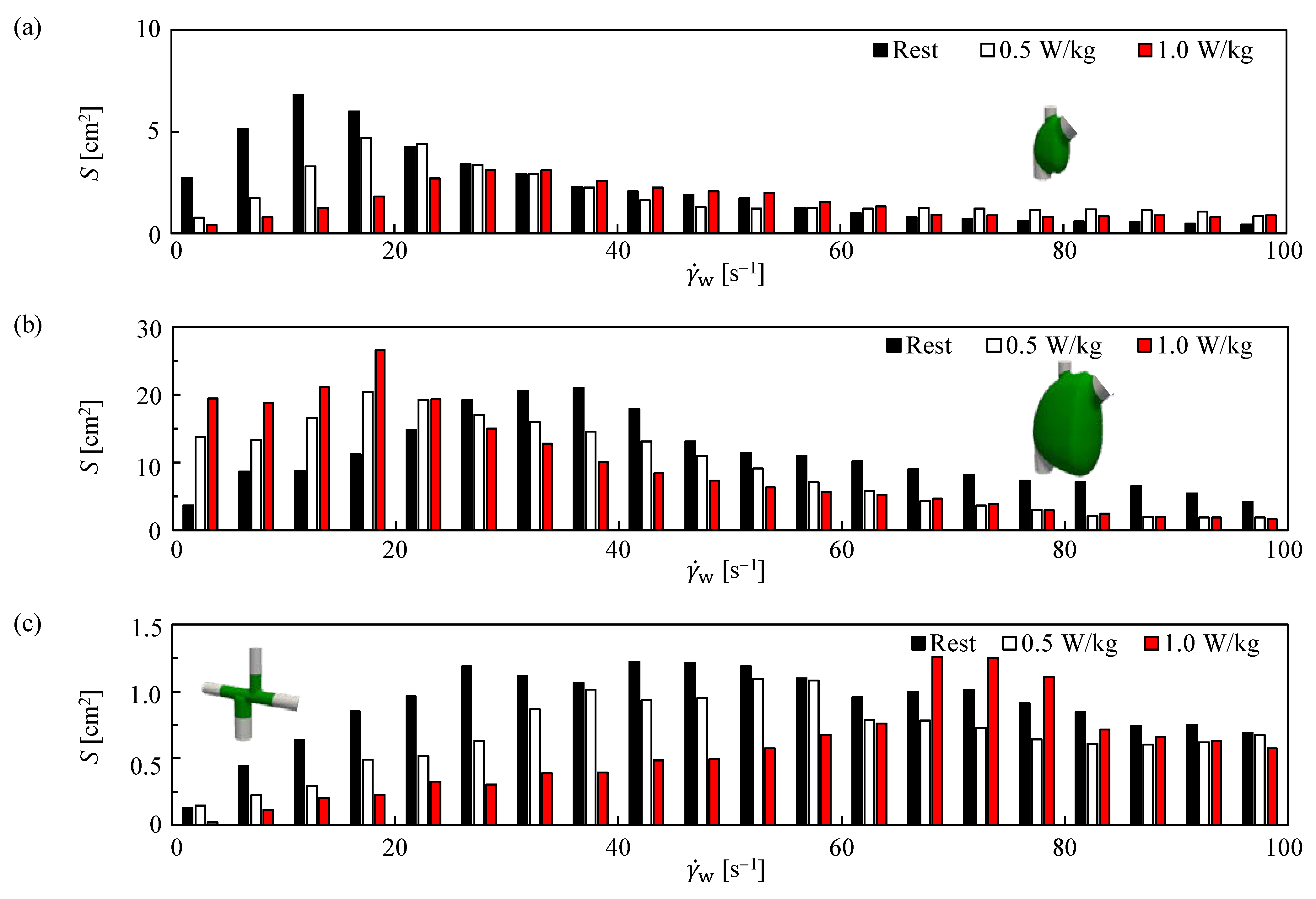
3.1. Velocity and SR in APC and TCPC at Rest
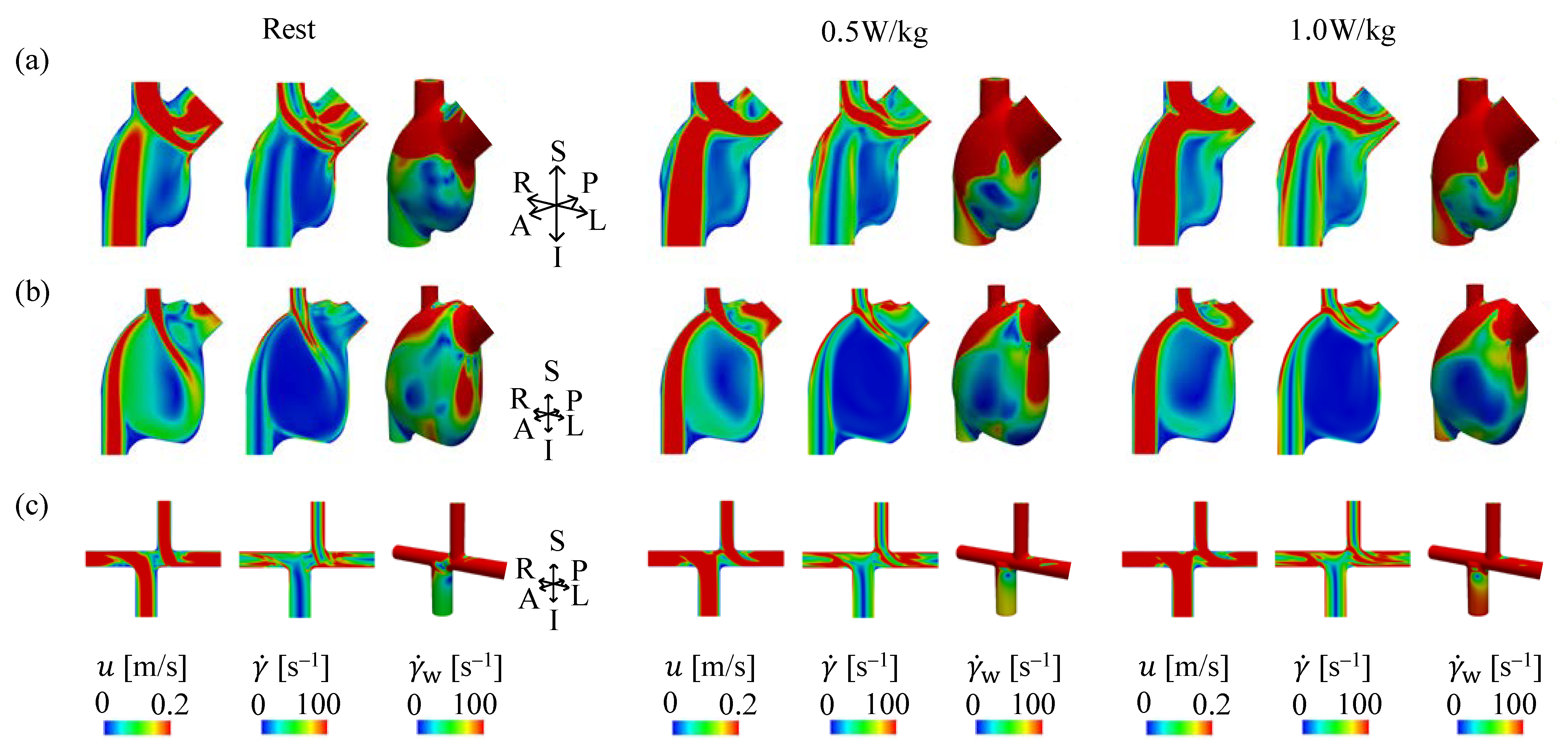
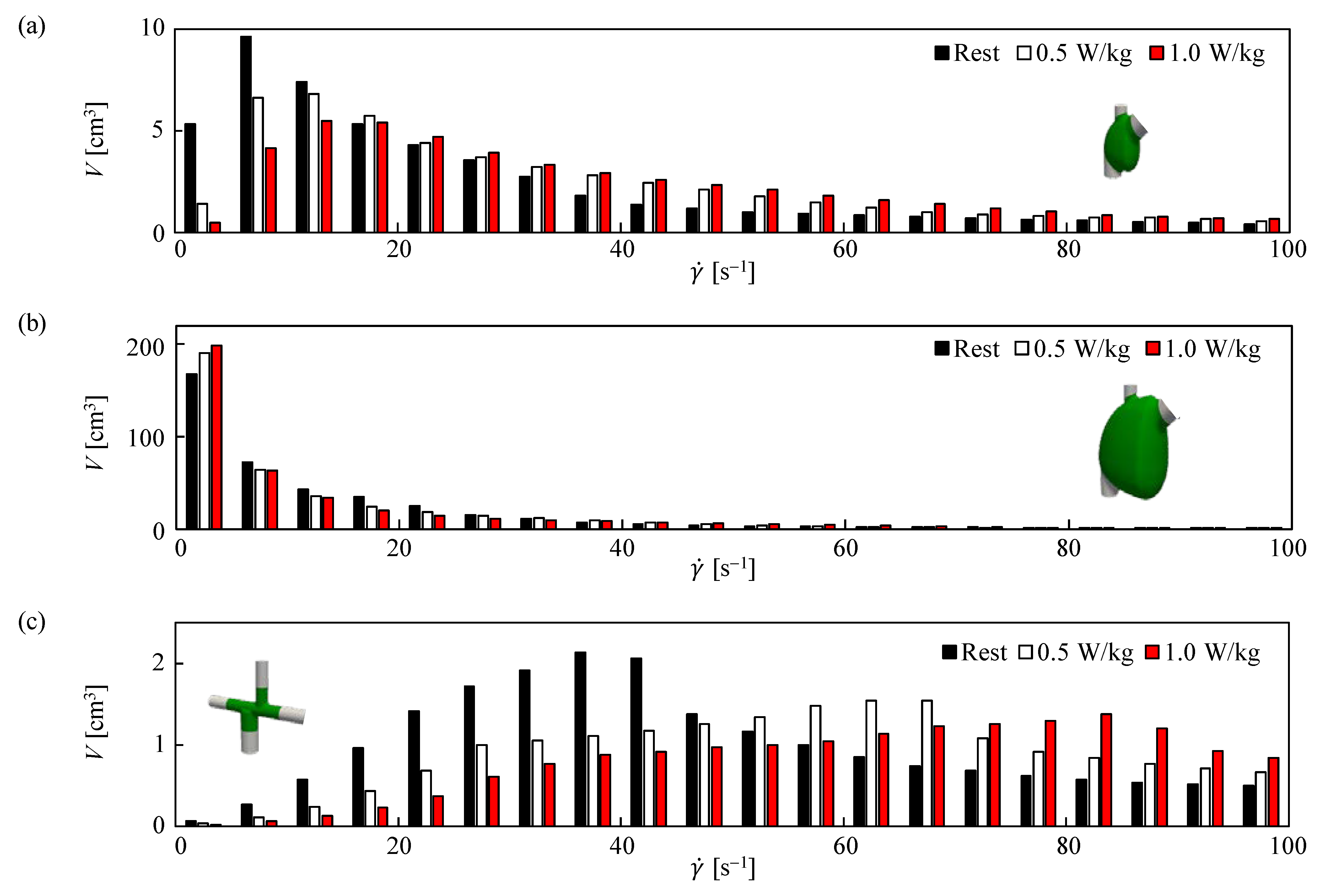
3.2. Velocity and SR in APC and TCPC during Exercise
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- de Leval, M.R.; Deanfield, J.E. Four decades of Fontan palliation. Nat. Rev. Cardiol. 2010, 7, 520–527. [Google Scholar] [CrossRef] [PubMed]
- Rychik, J.; Atz, A.M.; Celermajer, D.S.; Deal, B.J.; Gatzoulis, M.A.; Gewillig, M.H.; Hsia, T.Y.; Hsu, D.T.; Kovacs, A.H.; McCrindle, B.W.; et al. Evaluation and management of the child and adult with Fontan circulation: A scientific statement from the American Heart Association. Circulation 2019, 140, e234–e284. [Google Scholar] [CrossRef] [PubMed]
- Kosmidis, D.; Arvanitaki, A.; Kartas, A.; Karvounis, H.; Giannakoulas, G. Thrombosis and thromboprophylactic strategies in the adult with Fontan circulation. Int. J. Cardiol. Congenit. Heart Dis. 2020, 1, 100054. [Google Scholar] [CrossRef]
- Monagle, P.; Karl, T.R. Thromboembolic problems after the Fontan operation. Semin. Thorac. Cardiovasc. Surg. Pediatr. Card. Surg. Annu. 2002, 5, 36–47. [Google Scholar] [CrossRef] [PubMed]
- Mittal, R.; Seo, J.H.; Vedula, V.; Choi, Y.J.; Liu, H.; Huang, H.H.W.; Jain, S.; Younes, L.; Abraham, T.; George, R.T. Computational modeling of cardiac hemodynamics: Current status and future outlook. J. Comput. Phys. 2016, 305, 1065–1082. [Google Scholar] [CrossRef]
- Haggerty, C.M.; de Zelicourt, D.A.; Restrepo, M.; Rossignac, J.; Spray, T.L.; Kanter, K.R.; Fogel, M.A.; Yoganathan, A.P. Comparing pre- and post-operative Fontan hemodynamic simulations: Implications for the reliability of surgical planning. Ann. Biomed. Eng. 2012, 40, 2639–2651. [Google Scholar] [CrossRef]
- Hammer, P.E.; Hoganson, D.M.; del Nido, P.J. A tribute to Ajit Yoganathan’s Cardiovascular Fluid Mechanics Lab: A survey of its contributions to our understanding of the physiology and management of single-ventricle patients. Cardiovasc. Eng. Technol. 2021, 12, 631–639. [Google Scholar] [CrossRef]
- Kung, E.; Baretta, A.; Baker, C.; Arbia, G.; Biglino, G.; Corsini, C.; Schievano, S.; Vignon-Clementel, I.E.; Dubini, G.; Pennati, G.; et al. Predictive modeling of the virtual Hemi-Fontan operation for second stage single ventricle palliation: Two patient-specific cases. J. Biomech. 2013, 46, 423–429. [Google Scholar] [CrossRef]
- Sughimoto, K.; Okauchi, K.; Zannino, D.; Brizard, C.P.; Liang, F.Y.; Sugawara, M.; Liu, H.; Tsubota, K. Total cavopulmonary connection is superior to atriopulmonary connection Fontan in preventing thrombus formation: Computer simulation of flow-related blood coagulation. Pediatr. Cardiol. 2015, 36, 1436–1441. [Google Scholar] [CrossRef]
- D’Oronzio, U.; Senn, O.; Biaggi, P.; Gruner, C.; Jenni, R.; Tanner, F.C.; Greutmann, M. Right heart assessment by echocardiography: Gender and body size matters. J. Am. Soc. Echocardiogr. 2012, 25, 1251–1258. [Google Scholar] [CrossRef]
- Moreno, J.; de Isla, L.P.; Campos, N.; Guinea, J.; Dominguez-Perez, L.; Saltijeral, A.; Lennie, V.; Quezada, M.; de Agustin, A.; Marcos-Alberca, P.; et al. Right atrial indexed volume in healthy adult population: Reference values for two-dimensional and three-dimensional echocardiographic measurements. Echocardiography 2013, 30, 667–671. [Google Scholar] [CrossRef] [PubMed]
- Peluso, D.; Badano, L.P.; Muraru, D.; Dal Bianco, L.; Cucchini, U.; Kocabay, G.; Kovacs, A.; Casablanca, S.; Iliceto, S. Right atrial size and function assessed with three-dimensional and speckle-tracking echocardiography in 200 healthy volunteers. Eur. Heart J. Cardiovasc. Imaging 2013, 14, 1106–1114. [Google Scholar] [CrossRef] [PubMed]
- Zuckerman, W.A.; Richmond, M.E.; Singh, R.K.; Chen, J.M.; Addonizio, L.J. Use of height and a novel echocardiographic measurement to improve size-matching for pediatric heart transplantation. J. Heart Lung. Transpl. 2012, 31, 896–902. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.J.; Dong, J.; Zhou, J.R.; Chen, D.; Chen, J. Dynamic assessment of the central vein throughout the cardiac cycle in adults with no right heart disease by cardiac CT. Clin. Imaging 2021, 69, 120–125. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, Y.J.; Lee, H.J.; Kim, H.Y.; Kang, Y.A.; Park, M.S.; Kim, Y.S.; Kim, S.K.; Chang, J.; Jung, J.Y. Comparison of CT-determined pulmonary artery diameter, aortic diameter, and their ratio in healthy and diverse clinical conditions. PLoS ONE 2015, 10, e0126646. [Google Scholar] [CrossRef]
- Restrepo, M.; Mirabella, L.; Tang, E.; Haggerty, C.M.; Khiabani, R.H.; Fynn-Thompson, F.; Valente, A.M.; McElhinney, D.B.; Fogel, M.A.; Yoganathan, A.P. Fontan pathway growth: A quantitative evaluation of lateral tunnel and extracardiac cavopulmonary connections using serial cardiac magnetic resonance. Ann. Thorac. Surg. 2014, 97, 916–923. [Google Scholar] [CrossRef]
- Restrepo, M.; Tang, E.; Haggerty, C.M.; Khiabani, R.H.; Mirabella, L.; Bethel, J.; Valente, A.M.; Whitehead, K.K.; McElhinney, D.B.; Fogel, M.A.; et al. Energetic implications of vessel growth and flow changes over time in Fontan patients. Ann Thorac. Surg. 2015, 99, 163–170. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Turbulence, Heat and Mass Transfer 4: Proceedings of the Fourth International Symposium on Turbulence, Heat and Mass Transfer, Antalya, Turkey, 12–17 October, 2003; Hanjalić, K., Nagano, Y., Tummers, M.J., Eds.; Begell House: Danbury, CT, USA, 2003; pp. 625–632. [Google Scholar]
- Kenner, T. The measurement of blood density and its meaning. Basic Res. Cardiol. 1989, 84, 111–124. [Google Scholar] [CrossRef]
- Nader, E.; Skinner, S.; Romana, M.; Fort, R.; Lemonne, N.; Guillot, N.; Gauthier, A.; Antoine-Jonville, S.; Renoux, C.; Hardy-Dessources, M.D.; et al. Blood rheology: Key parameters, impact on blood flow, role in sickle cell disease and effects of exercise. Front. Physiol. 2019, 10, 1329. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Hjortdal, V.E.; Emmertsen, K.; Stenbog, E.; Frund, T.; Schmidt, M.R.; Kromann, O.; Sorensen, K.; Pedersen, E.M. Effects of exercise and respiration on blood flow in total cavopulmonary connection-A real-time magnetic resonance flow study. Circulation 2003, 108, 1227–1231. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.S.; Liao, W.; Low, H.T. Numerical simulation of turbulent flow through series stenoses. Int. J. Numer. Methods Fluids 2003, 42, 717–740. [Google Scholar] [CrossRef]
- Linge, F.; Hye, M.A.; Paul, M.C. Pulsatile spiral blood flow through arterial stenosis. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 1727–1737. [Google Scholar] [CrossRef] [PubMed][Green Version]
- de Zelicourt, D.A.; Marsden, A.; Fogel, M.A.; Yoganathan, A.P. Imaging and patient-specific simulations for the Fontan surgery: Current methodologies and clinical applications. Prog. Pediatr. Cardiol. 2010, 30, 31–44. [Google Scholar] [CrossRef]
- Sughimoto, K.; Ueda, T.; Fujiwara, T.; Kabasawa, M.; Liu, H. Impact of atrial fibrillation on Fontan circulation: Fontan computational model. Ann. Thorac. Surg. 2021; in press. [Google Scholar] [CrossRef]
- Wolberg, A.S.; Aleman, M.M.; Leiderman, K.; Machlus, K.R. Procoagulant activity in hemostasis and thrombosis: Virchow’s triad revisited. Anesth. Analg. 2012, 114, 275–285. [Google Scholar] [CrossRef]
- Kaibara, M. Thrombus formation and blood flow-Focusing on venous thrombus. J. Jpn. Soc. Biorheol. 2004, 18, 82–90. (In Japanese) [Google Scholar] [CrossRef]
- Neeves, K.B.; Illing, D.A.R.; Diamond, S.L. Thrombin flux and wall shear rate regulate fibrin fiber deposition state during polymerization under flow. Biophys. J. 2010, 98, 1344–1352. [Google Scholar] [CrossRef]
- Caro, C.G.; Pedley, T.J.; Schroter, R.C.; Seed, W.A. The Mechanics of the Circulation; Oxford University Press: Oxford, UK, 1978. [Google Scholar]
- Bosi, G.M.; Cook, A.; Rai, R.; Menezes, L.J.; Schievano, S.; Torii, R.; Burriesci, G. Computational fluid dynamic analysis of the left atrial appendage to predict thrombosis risk. Front. Cardiovasc. Med. 2018, 5, 34. [Google Scholar] [CrossRef]
- Garcia-Villalba, M.; Rossini, L.; Gonzalo, A.; Vigneault, D.; Martinez-Legazpi, P.; Duran, E.; Flores, O.; Bermejo, J.; McVeigh, E.; Kahn, A.M.; et al. Demonstration of patient-specific simulations to assess left atrial appendage thrombogenesis risk. Front. Physiol. 2021, 12, 596596. [Google Scholar] [CrossRef] [PubMed]
- Otani, T.; Al-Issa, A.; Pourmorteza, A.; McVeigh, E.R.; Wada, S.; Ashikaga, H. A Computational framework for personalized blood flow analysis in the human left atrium. Ann. Biomed. Eng. 2016, 44, 3284–3294. [Google Scholar] [CrossRef] [PubMed]
- Koizumi, R.; Funamoto, K.; Hayase, T.; Kanke, Y.; Shibata, M.; Shiraishi, Y.; Yambe, T. Numerical analysis of hemodynamic changes in the left atrium due to atrial fibrillation. J. Biomech. 2015, 48, 472–478. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.D.; Li, D.; Wu, P.; Li, X.Q.; Zheng, T.H. A two-fluid blood stasis model for false lumen thrombosis after type B dissection repair. Comput. Methods Biomech. Biomed. Eng. 2021. published online. [Google Scholar] [CrossRef]
| IVC and IVC-ECC | SVC | |||
|---|---|---|---|---|
| Flow Rate [μm3/s] | Mean Velocity [m/s] | Flow Rate [μm3/s] | Mean Velocity [m/s] | |
| rest | 49.1 | 0.129 | 38.6 | 0.251 |
| 0.5 W/kg | 79.1 | 0.208 | 38.9 | 0.253 |
| 1.0 W/kg | 99.7 | 0.262 | 38.9 | 0.253 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsubota, K.-i.; Sonobe, H.; Sughimoto, K.; Liu, H. Blood Flow Simulation to Determine the Risk of Thrombosis in the Fontan Circulation: Comparison between Atriopulmonary and Total Cavopulmonary Connections. Fluids 2022, 7, 138. https://doi.org/10.3390/fluids7040138
Tsubota K-i, Sonobe H, Sughimoto K, Liu H. Blood Flow Simulation to Determine the Risk of Thrombosis in the Fontan Circulation: Comparison between Atriopulmonary and Total Cavopulmonary Connections. Fluids. 2022; 7(4):138. https://doi.org/10.3390/fluids7040138
Chicago/Turabian StyleTsubota, Ken-ichi, Hidetaka Sonobe, Koichi Sughimoto, and Hao Liu. 2022. "Blood Flow Simulation to Determine the Risk of Thrombosis in the Fontan Circulation: Comparison between Atriopulmonary and Total Cavopulmonary Connections" Fluids 7, no. 4: 138. https://doi.org/10.3390/fluids7040138
APA StyleTsubota, K.-i., Sonobe, H., Sughimoto, K., & Liu, H. (2022). Blood Flow Simulation to Determine the Risk of Thrombosis in the Fontan Circulation: Comparison between Atriopulmonary and Total Cavopulmonary Connections. Fluids, 7(4), 138. https://doi.org/10.3390/fluids7040138







