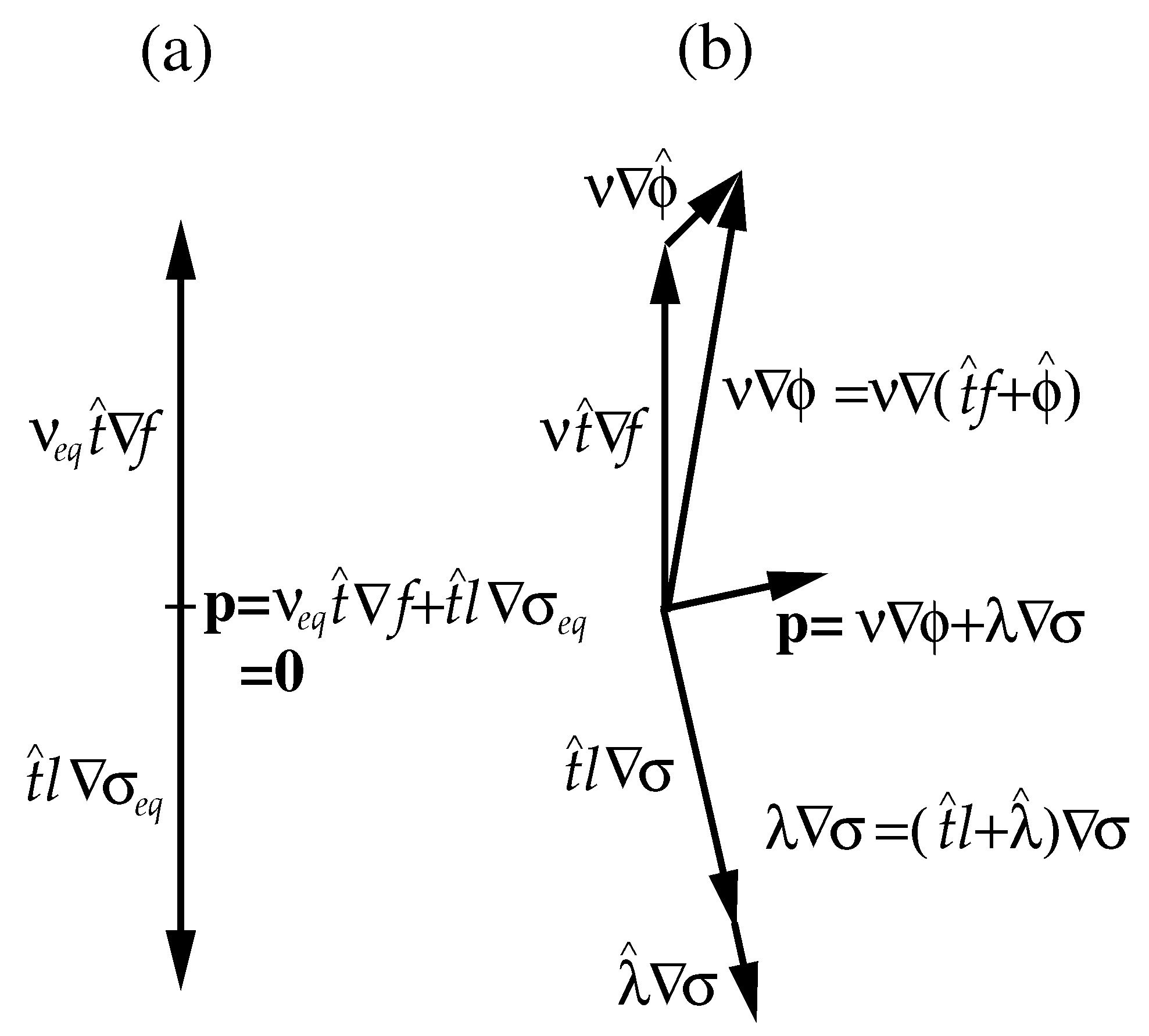Generalized Clebsch Variables for Compressible Ideal Fluids: Initial Conditions and Approximations of the Hamiltonian

Abstract

Clebsch variables provide a canonical representation of ideal flows that is, in practice, difficult to handle: while the velocity field is a function of the Clebsch variables and their gradients, constructing the Clebsch variables from the velocity field is not trivial. We introduce an extended set of Clebsch variables that circumvents this problem. We apply this method to a compressible, chemically inhomogeneous, and rotating ideal fluid in a gravity field. A second difficulty, the secular growth of canonical variables even for stationary states of stratified fluids, makes expansions of the Hamiltonian in Clebsch variables problematic. We give a canonical transformation that associates a stationary state of the canonical variables with the stationary state of the fluid; the new set of variables permits canonical approximations of the dynamics. We apply this to a compressible stratified ideal fluid with the aim to facilitate forthcoming studies of wave turbulence of internal waves.

1. Introduction

Like a variety of Hamiltonian systems, inviscid flows may be represented by noncanonical variables (including the velocity governed by the Euler equation), or by canonical variables, namely Clebsch variables and their generalizations [1,2,3,4,5]. Clebsch variables express the velocity or momentum field of a fluid as a sum of gradient fields each of which is multiplied by a scalar field. Each scalar factor field and the potential of the associated gradient field are conjugate variables. A simple illustration is a potential flow $\mathbf{u}=\nabla \varphi$ of a gas of noninteracting particles: $\varphi$ and the mass density $\rho$ are a pair of Clebsch variables for the momentum density $\mathbf{p}=\rho \nabla \varphi$, $H[\varphi ,\rho ]={\int \rho |\nabla \varphi |}^2/2d^3\mathbf{r}$ is a kinetic energy Hamiltonian. The first canonical equation $\dot{\rho }=\delta H/\delta \varphi =-\nabla ·(\rho \nabla \varphi )$ is the continuity equation, the second canonical equation $\dot{\varphi }=-\delta H/\delta \rho =-{(\nabla \varphi )}^2/2$ yields the Euler equation $\dot{\mathbf{u}}+(\mathbf{u}·\nabla )\mathbf{u}=0$ without pressure or external forces. Equivalent equations of motion follow from the variations [6]

$$\delta \int \int \mathcal{L}(\mathbf{u},\rho )+\varphi [\dot{\rho }+\nabla \left(\rho \mathbf{u}\right)]d^3\mathbf{r}dt=0$$

with the kinetic energy Lagrangian density $\mathcal{L}(\mathbf{u},\rho )=\rho {\mathbf{u}}^2/2$. $\varphi$ is a Lagrange multiplier that ensures the conservation of mass, i.e., the continuity equation for $\rho$ follows from the $\varphi$-variation. The $\mathbf{u}$-variation yields the gradient flow $\mathbf{u}=\nabla \varphi$ and the $\rho$-variation yields again $\dot{\varphi }=-{\mathbf{u}}^2/2$.

Describing a less specific flow requires additional terms in the Hamiltonian (e.g., the potential energy of gravity) and additional Clebsch variables. Representing an arbitrary momentum field requires three pairs of Clebsch variables [5], e.g., $\mathbf{p}=\nu \nabla \varphi +\lambda \nabla \sigma +\alpha \nabla \beta$ (Figure 1). The three gradients $\nabla \varphi$, $\nabla \sigma$, $\nabla \beta$ locally form a trihedron that is adjusted to the local momentum field by the three scalar fields $\nu$, $\lambda$, $\alpha$. The Euler equations may describe the same flow with fewer variables, e.g., four variables $\mathbf{u}$ and $\rho$. This reduction of the number of variables in the Euler equations compared to the canonical Clebsch variables is a consequence of the relabeling symmetry [6,7,8,9,10], i.e., the invariance of the Hamiltonian under displacements of the fluid that leave its chemical and thermodynamical properties unchanged. The conserved quantities (Casimirs) associated with these symmetries are generators of identical canonical transformations of the canonical variables, their Poisson-brackets with any functional (including the Hamiltonian) are zero. While the velocity field and the density in the noncanonical description are unchanged under a relabeling transformation, a complete set of canonical variables distinguishes fluid particles even if they have the same properties (“particles” refers to small fluid volumes, and not to molecules). The noncanonical description is handier by exploiting the relabeling symmetry, while canonical descriptions can maintain the symplectic structure through approximations of the Hamiltonian and specializations of the initial conditions; this may be advantageous for applications in wave turbulence theory [11,12,13,14,15,16,17,18]. Fluids that have additional conserved quantities (e.g., a space-dependent solute density and the entropy per mass), in general, do not possess this relabeling symmetry; consequently the Euler equations need to be extended by an advection equation for each of these quantities so that canonical and noncanonical descriptions require the same number of variables.

Figure 1. (a) Small fluid parcel with surfaces of constant $\varphi$, $\beta$, and $\sigma$. (b) The gradients $\nabla \varphi$, $\nabla \sigma$, and $\nabla \beta$ are adjusted by scalars $\nu$, $\lambda$, and $\alpha$ to yield the local momentum density $\mathbf{p}=\nu \nabla \varphi +\lambda \nabla \sigma +\alpha \nabla \beta$.

Canonical descriptions of interacting waves have been successfully applied to internal wave dynamics described with Clebsch variables [15,19] and with isopycnal variables in analogy to the Hamiltonian description of surface waves [16,20]. Spherical Clebsch maps for incompressible flows allow to transform a complex two-component wave function into knotted velocity fields [21,22,23,24]. This allows the direct identification and visualization of vortex tubes [24].

This paper discusses a variety of Clebsch maps for a rotating compressible ideal fluid with a space-dependent solute concentration in a gravity field in Section 2. A practical problem in handling Clebsch variables is their representation as functions of the velocity field. We suggest several methods to determine Clebsch variables from the initial conditions. We show that introducing one or two auxiliary pairs of Clebsch variables allows the explicit construction of all Clebsch variables.

A difficulty in perturbation expansions is the secular growth of canonical variables, e.g., for a stratified flow in a gravity field [25]. Even elementary problems like finding canonical equations that are equivalent to linearized Euler equations turn out to be nontrivial. One complication is that maintaining the canonical structure requires refraining from any non-canonical transformations or approximations. In Section 3 we discuss this for a simplified flow, namely a stratified non-rotating ideal fluid in a gravity field. We introduce a canonical transformation that eliminates the secular growth of the Clebsch variables for the stationary state of the fluid. Linear and nonlinear canonical approximations are obtained on the basis of this transformation.

2. Canonical Equations for Compressible Nonhomogeneous Fluids

In this section we discuss two alternative sets of Clebsch variables for compressible nonhomogeneous fluids. Taking the compressibility of the fluid into account has the advantage that the thermodynamical conjugate of the pressure (namely the volume) can be represented by a canonical variable (in our case the normalized inverse volume). We first note that the state equation for the pressure in water can be approximated as a function of the ratio of the actual mass density $\rho$ and the mass density $\sigma$ of the same fluid parcel at a reference pressure. For example, refs. [26,27,28] discuss a variety of approximate equations of state for the pressure such as $P(\rho ,\sigma )=(P_r+K/\gamma ){(\rho /\sigma )}^{\gamma }-K/\gamma$ with $\gamma \approx 7$, K is the bulk modulus and $\sigma$ is the mass density at atmospheric pressure $P_r$. $\rho /\sigma$ equals the normalized inverse volume $V_r/V$ of a fluid parcel that has a reference volume $V_r$ at $P_r$. While $\rho$ and $\sigma$ depend on the entropy and the concentration of any solutes, the state equation for $P(V_r/V)$ depends on these variables only weakly [26,28] within a range that is relevant e.g., in internal waves. This suggests to use $V_r/V$ as a dynamical variable. The pressure can then be derived from an internal energy density $e(V_r/V)$. We introduce this approach in Section 2.1 and use it in particular in Section 3.

A dependence of the state equation on the entropy per mass s and solute mass percentage c may be taken into account either by starting from an internal energy density $e(V_r/V,s,c)$ or alternatively from $e(\rho ,s,c)$. In the latter case the pressure differential $dp=\rho d(\partial e/\partial \rho )-(\partial e/\partial s)ds-(\partial e/\partial c)dc$ depends on these three variables, and these variables may be used as dynamical Clebsch variables. We discuss this approach in Section 2.2.

2.1. Clebsch Variables for a State Equation $P(V_r/V)$

We introduce a set of three Clebsch variables [3] for an inviscid, compressible, and diffusionless rotating fluid with an inhomogeneous solute concentration in a homogeneous gravity field and discuss their relation to Ertel’s potential vorticity [29]. We assume that the fluid compressibility is a function of the pressure only with no explicit dependence on the salinity or entropy. Let V be the actual volume of a small fluid parcel at the pressure P, and $V_r$ be the volume of the parcel at a fixed reference pressure $P_r$. The mass density $\rho =m/V$ is governed by continuity equation $\dot{\rho }=-\nabla ·\left(\rho \mathbf{u}\right)$. The mass density at the reference pressure $P_r$ is again denoted as $\sigma =m/V_r$. This quantity is in general a function of any solute mass percentages and the entropy per mass, and it is materially conserved, i.e., $D\sigma /Dt=0$. The Euler equations for this system are

$$\begin{array}{ccc}\hfill \frac{D\mathbf{u}}{Dt}& =& -g{\mathbf{e}}_z-{\rho }^{-1}\nabla P+2\mathbf{u}\times \Omega \hfill \\ \hfill \dot{\rho }+\nabla ·\left(\rho \mathbf{u}\right)& =& 0\hfill \\ \hfill \dot{\sigma }+\mathbf{u}·\nabla \sigma & =& 0\hfill \end{array}$$

(1)

To exploit the state equation of the form $P(V_r/V)$ we introduce the normalized inverse volume of the fluid parcel $\nu =V_r/V=\rho /\sigma$ with $\nu \left(P_r\right)=1$, which is governed by the continuity equation $\dot{\nu }=-\nabla ·\left(\nu \mathbf{u}\right)$. We use $\nu$ and $\sigma$ as independent variables. The pressure gradient follows from an internal energy per volume (written as as a function of $\nu$ using $V=V_r/\nu$) as $\nabla P=\nu \nabla \frac{\partial e}{\partial \nu }$ with $d\frac{\partial e}{\partial \nu }={\nu }^{-1}dP.$ Note that $\sigma$ may be influenced by the entropy per mass as well as any solutes of the fluid; it is only required that the compressibility can be expressed as a function of $\nu$ only. The equations of motion and the Hamilton function can be obtained from the variation of the action that is constrained by the conservation laws [3,6,7,8]. The constrained action is

$$\int \int \mathcal{L}(\mathbf{u},\mathbf{r},\nu ,\sigma )-\lambda (\dot{\sigma }+\mathbf{u}·\nabla \sigma )+\varphi [\dot{\nu }+\nabla \left(\nu \mathbf{u}\right)]-\alpha (\dot{\beta }+\mathbf{u}·\nabla \beta )d^3\mathbf{r}dt,$$

(2)

where $\mathcal{L}=\mathcal{T}-\mathcal{V}$ is the Lagrangian density with the kinetic energy density

$$\mathcal{T}(\mathbf{u},\mathbf{r},\nu ,\sigma )=\nu \sigma {\mathbf{u}}^2/2+\nu \sigma \mathbf{u}·\mathbf{A}$$

and the potential energy density

$$\mathcal{V}(\mathbf{r},\nu ,\sigma )=e\left(\nu \right)+\nu \sigma gz.$$

$\mathbf{A}\left(\mathbf{r}\right)$ is a vector potential for the Coriolis force. $\varphi (\mathbf{r},t)$, $\lambda (\mathbf{r},t)$, $\alpha (\mathbf{r},t)$ are Lagrange multipliers of the continuity equation for $\nu (\mathbf{r},t)$ and the advection equations of $\sigma (\mathbf{r},t)$ and $\beta (\mathbf{r},t)$. $\beta (\mathbf{r},t)$ may be a formal fluid particle label, or (as discussed below) it may be identified with the potential vorticity. Applying Hamilton’s principle to Equation (2), the $\mathbf{u}$-variation yields (Figure 1)

$$\mathbf{u}={\sigma }^{-1}{\nu }^{-1}(\lambda \nabla \sigma +\nu \nabla \varphi +\alpha \nabla \beta )-\mathbf{A}.$$

(3)

Variations of the multipliers $\varphi$, $\lambda$, $\alpha$ and the variables $\nu$, $\sigma$, $\beta$ give the equations of motion

$$\begin{array}{ccc}\hfill \dot{\nu }+\nabla ·\left(\nu \mathbf{u}\right)& =& 0\hfill \\ \hfill \dot{\varphi }+\mathbf{u}·\nabla \varphi & =& \partial \mathcal{L}/\partial \nu \hfill \\ \hfill \dot{\lambda }+\nabla ·\left(\lambda \mathbf{u}\right)& =& -\partial \mathcal{L}/\partial \sigma \hfill \\ \hfill \dot{\sigma }+\mathbf{u}·\nabla \sigma & =& 0\hfill \\ \hfill \dot{\alpha }+\nabla ·\left(\alpha \mathbf{u}\right)& =& 0\hfill \\ \hfill \dot{\beta }+\mathbf{u}·\nabla \beta & =& 0\hfill \end{array}$$

(4)

with

$$\begin{array}{ccc}\hfill \partial \mathcal{L}/\partial \nu & =& \sigma \mathbf{u}·(\mathbf{u}/2+\mathbf{A})-\sigma gz-\partial e/\partial \nu \hfill \\ \hfill \partial \mathcal{L}/\partial \sigma & =& \nu \mathbf{u}·(\mathbf{u}/2+\mathbf{A})-\nu gz.\hfill \end{array}$$

Equation (4) is equivalent to the canonical equations $\dot{\mathbf{P}}=-\delta H/\delta \mathbf{Q}$ and $\dot{\mathbf{Q}}=\delta H/\delta \mathbf{P}$ for $\mathbf{P}=(\varphi ,\sigma ,\beta )$ and $\mathbf{Q}=(\nu ,\lambda ,\alpha )$ for the Hamiltonian

$$H[\nu ,\varphi ,\lambda ,\sigma ,\alpha ,\beta ]=\int (\nu \sigma {\mathbf{u}}^2/2+\nu \sigma gz+e)d^3\mathbf{r}.$$

(5)

The velocity $\mathbf{u}$ in Equation (5) is expressed as the function (3) of the Clebsch variables, while it is an independent variable in the variation of Equation (2). The canonical momentum density is $\mathbf{p}=\lambda \nabla \sigma +\nu \nabla \varphi +\alpha \nabla \beta$, the kinetic momentum density is $\nu \sigma \mathbf{u}=\mathbf{p}-\nu \sigma \mathbf{A}$.

Expressing $\dot{\mathbf{u}}$ by Equation (4) yields the Euler equation

$$\frac{D\mathbf{u}}{Dt}=-g{\mathbf{e}}_z-{\sigma }^{-1}{\nu }^{-1}\nabla P+2\mathbf{u}\times \Omega$$

(6)

after a straightforward calculation. $\Omega =\nabla \times \mathbf{A}/2$ is the angular velocity of the Coriolis force, e.g., the vector potential $\mathbf{A}=(-y\Omega ,x\Omega ,0)$ yields $\Omega =\Omega {\mathbf{e}}_z$. A Hamiltonian formalism for inertial waves in rotating fluids was introduced in [15].

We observe that a stationary state of the Euler Equation (6) is not a stationary state of the Clebsch variables Equation (4): a stratified equilibrium state $\mathbf{u}=\mathbf{0}$, $\sigma ={\sigma }_{eq}\left(z\right)$, $\nu ={\nu }_{eq}\left(z\right)$ of the Euler equation satisfies

$${\sigma }_{eq}{\nu }_{eq}g+{\nu }_{eq}\frac{d}{dz}\frac{\partial e}{\partial {\nu }_{eq}}=0.$$

(7)

The variables $\lambda$ and $\varphi$ grow at constant rates $\dot{\varphi }=-{\sigma }_{eq}gz-\partial e/\partial {\nu }_{eq}$ and $\dot{\lambda }={\nu }_{eq}gz$ by Equation (4) for the stationary state of the fluid. These equations together with $\dot{\nu }=\dot{\sigma }=\dot{\alpha }=\dot{\beta }=0$ are canonical equations for a Hamiltonian with no kinetic energy.

For the limit of an incompressible fluid $\nu =1$, $\partial e/\partial \nu \to \infty$, $\dot{\varphi }$ diverges and $(\nu ,\varphi )$ are not a pair of canonical variables. In this case the potential $\varphi$ in $\mathbf{p}=\lambda \nabla \sigma +\nabla \varphi +\alpha \nabla \beta$ needs to be determined from $\nabla ·\mathbf{u}=0$ and the boundary conditions [15,19].

The conservation of potential vorticity follows directly from the conservation laws of Clebsch variables. The Jacobian determinant of the three materially conserved quantities $\sigma$, $\beta$, $\alpha /\nu$

$$\begin{array}{ccc}\hfill detW& =& det[\nabla \sigma ,\nabla \beta ,\nabla (\alpha /\nu \left)\right]\hfill \\ \hfill & =& \sigma \nabla \sigma ·[\nabla \times (\mathbf{u}+\mathbf{A}\left)\right]\hfill \end{array}$$

(8)

is a locally conserved density, i.e., it is governed by the continuity equation

$$\frac{\partial detW}{\partial t}+\nabla ·(\mathbf{u}detW)=0.$$

With ${\sigma }^2\nu$ being another locally conserved quantity, we note that the ratio of $detW$ and ${\sigma }^2\nu$ is materially conserved; this yields Ertel’s potential vorticity conservation [29]

$$\frac{D}{Dt}\frac{detW}{{\sigma }^2\nu }=\frac{D}{Dt}\frac{\nabla \sigma ·[\nabla \times (\mathbf{u}+\mathbf{A}\left)\right]}{\sigma \nu }=0.$$

(9)

We note that $\alpha =0$ or $\beta =0$ yields a zero potential vorticity which again shows that two pairs of Clebsch variables are insufficient for a general velocity field. The potential vorticity conservation is associated with the relabeling symmetry [6,7,8,9,10], which is, in this case, the invariance of the Hamiltonian under displacements of the fluid on surfaces with constant $\sigma$ while keeping $\nu \left(\mathbf{r}\right)$ unchanged. Both $\beta$ and the potential vorticity are materially conserved; this suggests to represent the potential vorticity by the variable $\beta$: setting the initial condition of $\beta$ as $\beta ={\sigma }^{-1}{\nu }^{-1}\nabla \sigma ·[\nabla \times (\mathbf{u}+\mathbf{A})]$ ensures that $\beta$ matches the potential vorticity throughout the time evolution.

$\beta$ can be used for other purposes depending on the type of fluid. It can represent an additional materially conserved quantity of the fluid, e.g., the entropy per mass or a solute mass percentage. In this case, the potential energy $\mathcal{V}$ depends on $\beta$ so that $\alpha$ is not governed by a continuity equation. Correspondingly, $\alpha /\nu$ and the potential vorticity are not materially conserved in this case. This reflects that the Hamiltonian of such a system is in general not invariant under continuous displacements of fluid particles on surfaces $\sigma =const.$: such displacements change the entropy distribution of the fluid unless the surfaces $\sigma =const.$ coincide with surfaces $\beta =const.$

2.2. Clebsch Variables for More General State Equations

We now give a generalization for fluids whose compressibility depends also on the entropy per mass $s(\mathbf{r},t)$ and the mass percentage (mass of a solute per mass of the fluid) $c(\mathbf{r},t)$. The internal energy per volume is $e(\rho ,s,c)$. With $\rho$ being locally conserved and s and c being materially conserved, the Euler equations are

$$\begin{array}{ccc}\hfill \frac{D\mathbf{u}}{Dt}& =& -g{\mathbf{e}}_z-{\rho }^{-1}\nabla P+2\mathbf{u}\times \Omega \hfill \\ \hfill \dot{\rho }+\nabla ·\left(\rho \mathbf{u}\right)& =& 0\hfill \\ \hfill \dot{s}+\mathbf{u}·\nabla s& =& 0\hfill \\ \hfill \dot{c}+\mathbf{u}·\nabla c& =& 0.\hfill \end{array}$$

(10)

The pressure gradient is $\nabla P=\rho \nabla \frac{\partial e}{\partial \rho }-\frac{\partial e}{\partial s}\nabla s-\frac{\partial e}{\partial c}\nabla c.$ The constrained action becomes

$$\int \int \mathcal{L}(\mathbf{u},\mathbf{r},\nu ,\sigma )-\lambda (\dot{s}+\mathbf{u}·\nabla s)+\varphi [\dot{\rho }+\nabla \left(\rho \mathbf{u}\right)]-\alpha (\dot{c}+\mathbf{u}·\nabla c)d^3\mathbf{r}dt,$$

(11)

with $\mathcal{L}=\mathcal{T}-\mathcal{V}$,

$$\mathcal{T}(\mathbf{u},\mathbf{r},\rho )=\rho {\mathbf{u}}^2/2+\rho \mathbf{u}·\mathbf{A}$$

and the potential energy density

$$\mathcal{V}(\mathbf{r},\rho ,s,c)=e(\rho ,s,c)+\rho gz.$$

$\varphi (\mathbf{r},t)$, $\lambda (\mathbf{r},t)$, $\alpha (\mathbf{r},t)$ are now Lagrange multipliers of the continuity equation for $\rho (\mathbf{r},t)$ and the advection equations of $s(\mathbf{r},t)$ and $c(\mathbf{r},t)$. The $\mathbf{u}$-variation yields

$$\mathbf{u}={\rho }^{-1}(\lambda \nabla s+\rho \nabla \varphi +\alpha \nabla c)-\mathbf{A}.$$

(12)

Variations of the multipliers $\varphi$, $\lambda$, $\alpha$ and the variables $\rho$, s, c give the equations of motion

$$\begin{array}{ccc}\hfill \dot{\rho }+\nabla ·\left(\rho \mathbf{u}\right)& =& 0\hfill \\ \hfill \dot{\varphi }+\mathbf{u}·\nabla \varphi & =& \mathbf{u}·(\mathbf{u}/2+\mathbf{A})-gz-\partial e/\partial \rho \hfill \\ \hfill \dot{\lambda }+\nabla ·\left(\lambda \mathbf{u}\right)& =& \partial e/\partial s\hfill \\ \hfill \dot{s}+\mathbf{u}·\nabla s& =& 0\hfill \\ \hfill \dot{\alpha }+\nabla ·\left(\alpha \mathbf{u}\right)& =& \partial e/\partial c\hfill \\ \hfill \dot{c}+\mathbf{u}·\nabla c& =& 0.\hfill \end{array}$$

(13)

These equations together with Equation (12) again yield the Euler Equation (10) for an internal energy $e(\rho ,s,c)$. It is straightforward to extend this to several solute mass percentages $c_i$, each of which will be governed by an advection equation. Each solute will require one new pair of Clebsch variables $({\alpha }_i,c_i)$ in the definition of the momentum, which then involves more Clebsch variables than needed for representing an arbitrary velocity field. These contributions may be neutralized with respect to the initial conditions by setting the scalar factor fields ${\alpha }_i$ equal to zero initially.

A fundamental difference between Equations (4) and (13) is that $\alpha$ is not locally conserved in Equation (13), so $\alpha /\rho$ is not materially conserved. Fluid particles with different values of s and c are physically distinguishable, and Ertel’s potential vorticity (Equation (9)) is not conserved. Describing fluids whose pressure depends only on $\rho /\sigma$ with Equation (13) is possible, but unnecessarily complicated. In contrast to this, the description (4) can be reduced to only four Clebsch variables for certain initial conditions, which is not possible for Equation (13). We will take advantage of that in Section 3.

2.3. Computing Clebsch Variables from the Initial Conditions: One Auxiliary Pair of Clebsch Variables

While it is desirable to construct the Clebsch variables from the momentum field $\mathbf{p}$ (e.g., for determining the initial conditions of the Clebsch variables), there are some difficulties in this step. Evidently the Clebsch variables (4) are not uniquely determined by the momentum density, for example $\mathbf{p}$ is invariant under canonical gauge transformations like $\widehat{\varphi }=\varphi -ϵ\sigma$, $\lambda =\widehat{\lambda }-ϵ\widehat{\nu }$, $\widehat{\nu }=\nu$, $\widehat{\sigma }=\sigma$. We now consider the optimal situation where the vectors $(\nabla \varphi$, $\nabla \sigma$, $\nabla \beta )$ are linearly independent everywhere in space. For the given trihedron $(\nabla \varphi ,\nabla \sigma ,\nabla \beta )$ the set of coefficients $(\nu ,\lambda ,\alpha )$ can be determined directly and uniquely in order to adjust $\nu \nabla \varphi +\lambda \nabla \sigma +\alpha \nabla \beta =\mathbf{p}$ to a given momentum field (Figure 1). However, the coefficient $\nu$ is a physical property of the fluid that is determined by its own initial condition, so $\nu$ is not available as an arbitrary parameter for representing a particular momentum field. Instead, it is the leg $\nabla \varphi$ that is arbitrary and therefore available for adjusting to the momentum density. This leaves us with the much harder task of finding a potential $\varphi$ that represents an arbitrary vector field $\mathbf{p}$ as $\nu \nabla \varphi +\lambda \nabla \sigma +\alpha \nabla \beta$. A trivial example may illustrate this difficulty: the initial conditions of the momentum field may be given by $\mathbf{p}(\mathbf{x},t_0)=(1,z,-y)$ with $\sigma \left(x\right)$, $d\sigma /dx>0$. Clebsch variables that yield this field are e.g., $\varphi =y$, $\nu =z$, $\alpha =-y$, $\beta =z$, $\lambda =1/(d\sigma /dx)$. However, the initial condition $\nu (\mathbf{x},t_0)$ will in general be an arbitrary function, so it is necessary to solve $\lambda \nabla \sigma \left(x\right)+\nu \left(\mathbf{x}\right)\nabla \varphi +\alpha \nabla \beta =(1,z,y)$ for $\lambda$, $\varphi$, $\alpha$, $\beta$.

This problem can be circumvented with additional (and redundant) Clebsch variables: introducing a fourth pair of variables ${\alpha }_2$, ${\beta }_2$ and defining the momentum as

$$\mathbf{p}=\lambda \nabla \sigma +\nu \nabla \varphi +\sum _{i=1}^2{\alpha }_i\nabla {\beta }_i$$

(14)

allows us to construct all Clebsch variables explicitly. The variables ${\alpha }_i$ and ${\beta }_i$ are multipliers and fluid labels in Hamilton’s principle that are governed by the canonical equations

$$\begin{array}{ccc}\hfill {\dot{\beta }}_i& =& \frac{\delta H}{\delta {\alpha }_i}\hfill \\ \hfill & =& -\mathbf{u}·\nabla {\beta }_i\hfill \\ \hfill {\dot{\alpha }}_i& =& -\frac{\delta H}{\delta {\beta }_i}\hfill \\ \hfill & =& -\nabla ·\left({\alpha }_i\mathbf{u}\right).\hfill \end{array}$$

(15)

In other words, ${\beta }_2$ is an additional passive tracer with no influence on the dynamics of $\mathbf{u}$. Computing $\dot{\mathbf{u}}$ confirms that the projection (14) reduces the dynamics of four pairs of Clebsch variables to the Euler equation. The initial conditions of these Clebsch variables may be expressed explicitly in terms of the initial conditions of the momentum density. We give two approaches for constructing the initial conditions.

A first way is to set ${\alpha }_2(\mathbf{r},t_0)=-1$ and ${\beta }_2(\mathbf{r},t_0)=\nu (\mathbf{r},t_0)\varphi (\mathbf{r},t_0)$, which leads to the initial momentum density $\mathbf{p}=\lambda \nabla \sigma -\varphi \nabla \nu +{\alpha }_1\nabla {\beta }_1$ at ($\mathbf{r},t_0$). This switches the term $\nu \nabla \varphi$ to $-\varphi \nabla \nu$ at $t_0$, so that $\varphi$ is now an adjustable scalar coefficient of the gradient field $\nabla \nu$. If the three gradients $\nabla \sigma$, $\nabla \nu$,$\nabla {\beta }_1$ are linearly independent everywhere in space, the coefficient $\lambda (\mathbf{r},t_0)$ may be computed directly as

$$\lambda =\frac{\mathbf{p}·(\nabla \nu \times \nabla {\beta }_1)}{\nabla \sigma ·(\nabla \nu \times \nabla {\beta }_1)}.$$

(16)

Similar projections yield $\varphi (\mathbf{r},t_0)$ and ${\alpha }_1(\mathbf{r},t_0)$. The materially conserved variables ${\alpha }_i/\nu$ and ${\beta }_i$ may be combined into new conserved quantities, for example $det{W}_i=\nabla \sigma ·(\nabla {\beta }_i\times \nabla ({\alpha }_i/\nu ))$ is locally conserved. In analogy to Equation (9), the potential vorticity is now

$$\frac{\nabla \sigma ·[\nabla \times (\mathbf{u}+\mathbf{A}\left)\right]}{\sigma \nu }=\frac{det{W}_1+det{W}_2}{{\sigma }^2\nu }.$$

(17)

Again, we may identify ${\beta }_1$ with the potential vorticity via the initial conditions so that the vectors $(\nabla \sigma ,\nabla \nu ,\nabla {\beta }_1)$ at $t_0$ have a clear physical meaning. A limitation of this approach is that $\nabla \sigma$, $\nabla \nu$, and $\nabla {\beta }_1$ can represent an arbitrary velocity field only if they are linearly independent everywhere in space.

A second way of constructing the initial conditions is to set $\varphi =0$ at $t_0$. ${\beta }_1$, ${\beta }_2$ are chosen in a way that $\nabla \sigma$, $\nabla {\beta }_1$, $\nabla {\beta }_2$ are linearly independent everywhere. For a stratified fluid with $\partial \sigma /\partial z<0$, the choice ${\beta }_1=x$, ${\beta }_2=y$ yields $\nabla {\beta }_1={\mathbf{e}}_x$ and $\nabla {\beta }_2={\mathbf{e}}_y$. An alternative is to define $\nabla {\beta }_i$ as tangent vectors on surfaces $\sigma =const$. The coefficients $\lambda$, ${\alpha }_1$, ${\alpha }_2$ are computed in analogy to Equation (16). This requires again that $\nabla \sigma$ is nonzero, but it can be applied to initial conditions where $\nabla \sigma$ and $\nabla \nu$ are linearly dependent.

2.4. Two Auxiliary Pairs of Clebsch Variables

A versatile representation of the momentum density field using five pairs of Clebsch variables is

$$\mathbf{p}=\lambda \nabla \sigma +\nu \nabla \varphi +\sum _{i=1}^3{\alpha }_i\nabla {\beta }_i.$$

(18)

In Hamilton’s principle this merely extends the number of constraints that are governed by Equation (15), the remaining Equation (4) is changed only by the definition of the momentum (18). Again it is straightforward to check that these equations lead to the Euler Equation (6). Initial conditions of these Clebsch variables can be expressed explicitly in terms of the initial conditions of the momentum field: $\lambda (\mathbf{r},t_0)=0$, $\varphi (\mathbf{r},t_0)=0$ lead to $\mathbf{p}(\mathbf{r},t_0)=\sum {\alpha }_i(\mathbf{r},t_0)\nabla {\beta }_i(\mathbf{r},t_0)$. The initial conditions $({\beta }_1,{\beta }_2,{\beta }_3)\left(t_0\right)=\mathbf{r}$ are the initial Cartesian coordinates of fluid parcels; $\nabla {\beta }_1={\mathbf{e}}_x$, $\nabla {\beta }_2={\mathbf{e}}_y$, $\nabla {\beta }_3={\mathbf{e}}_z$ is a standard basis at $t_0$. The variables $({\alpha }_1,{\alpha }_2,{\alpha }_3)=\mathbf{p}$ are the Cartesian components of the initial momenta at $t=t_0$. The advantage of this representation is that it can be used for any initial conditions, in particular, $\nabla \sigma$ and $\nabla \nu$ may be parallel or zero. The simplicity of the initial conditions is traded for additional Clebsch variables that are governed by continuity and advection equations.

The additional variables are redundant in the sense that they are not necessary for representing an arbitrary vector field. It has been shown in [5] that an arbitrary vector field in three dimensions can be represented with two pairs of Clebsch variables plus one gradient field, e.g., dividing Equation (14) by $\nu$ and dropping $\lambda$ the representation $\mathbf{p}/\nu =\nabla \varphi +{\sum }_{i=1}^2({\alpha }_i/\nu )\nabla {\beta }_i$ is possible. The Clebsch variables are not uniquely defined in this representation. If the boundary conditions of the Clebsch variables need to be controlled, an additional pair of Clebsch variables $\mathbf{p}/\nu =\nabla \varphi +{\sum }_{i=1}^3({\alpha }_i/\nu )\nabla {\beta }_i$) is required [5].

3. Expansions of the Hamiltonian

3.1. Secular Growth of Clebsch Variables

We now discuss the relationship of linear and nonlinear approximations of the canonical dynamics and the Euler equation while maintaining the canonical structure through all transformations. To simplify the equations we constrain the flow to zero potential vorticity $\nabla \sigma ·(\nabla \times \mathbf{u})=0$ by omitting the Clebsch variables $\alpha$, $\beta$ or ${\alpha }_i$, ${\beta }_i$; the vector potential $\mathbf{A}$ is dropped; the internal energy density is still specified as a function $e\left(\nu \right)$, $e^{\left(n\right)}\left(\nu \right)=d^{n}e\left(\nu \right)/d{\nu }^n$.

By Equation (4) the Clebsch variables $\lambda$ and $\varphi$ grow secularly even for a stratified equilibrium state $\mathbf{u}=\mathbf{0}$. This raises the question of how the Equation (4) can be expanded about the secularly growing variables. A tentative and unsuccessful approach would be to expand the Hamiltonian or equivalently the Lagrangian and the constraints in terms of the velocity and the deviations $\widehat{\nu }=\nu -{\nu }_{eq}$, $\widehat{\sigma }=\sigma -{\sigma }_{eq}$ of the physical variables $\nu$ and $\sigma$ from their equilibrium values: The quadratic approximation for the Lagrangian density is then ${\mathcal{T}}_2-{\mathcal{V}}_0-{\mathcal{V}}_1-{\mathcal{V}}_2$ with ${\mathcal{T}}_2={\nu }_{eq}{\sigma }_{eq}{\mathbf{u}}^2/2$ and

$${\mathcal{V}}_0+{\mathcal{V}}_1+{\mathcal{V}}_2=({\nu }_{eq}+\widehat{\nu })({\sigma }_{eq}+\widehat{\sigma })gz+e\left({\nu }_{eq}\right)+e^{\left(1\right)}\left({\nu }_{eq}\right)\widehat{\nu }+e^{\left(2\right)}\left({\nu }_{eq}\right){\widehat{\nu }}^2/2.$$

Approximating the constraints as $\dot{\widehat{\sigma }}+\mathbf{u}·\nabla {\sigma }_{eq}=0$ and $\dot{\widehat{\nu }}+\nabla \left({\nu }_{eq}\mathbf{u}\right)=0$, Hamilton’s principle yields $\mathbf{u}=(\lambda \nabla {\sigma }_{eq}+{\nu }_{eq}\nabla \varphi )/\left({\nu }_{eq}{\sigma }_{eq}\right)$ and the linear equations

$$\begin{array}{ccc}\hfill \dot{\varphi }& =& -({\sigma }_{eq}+\widehat{\sigma })gz-e^{\left(1\right)}\left({\nu }_{eq}\right)-\widehat{\nu }{e}^{\left(2\right)}\left({\nu }_{eq}\right)\hfill \\ \hfill \dot{\lambda }& =& ({\nu }_{eq}+\widehat{\nu })gz.\hfill \end{array}$$

These are the canonical equations that follow from the Hamiltonian $H=\int {\mathcal{T}}_2+{\mathcal{V}}_0+{\mathcal{V}}_1+{\mathcal{V}}_2{d}^3\mathbf{r}$. While they are linear in $\widehat{\nu }$, $\widehat{\sigma }$ and $\mathbf{u}$, inserting them in $\dot{\mathbf{u}}$ does not yield the linearized Euler equations.

To find relevant approximations of the canonical equations we first apply a canonical transformation to the Clebsch variables and subsequently expand the Hamiltonian or Lagrangian. This canonical transformation $(\nu ,\varphi ,\sigma ,\lambda )\to (\widehat{\nu },\widehat{\varphi },\widehat{\sigma },\widehat{\lambda })$ associates the stationary state $\mathbf{u}=\mathbf{0}$ with a fixed point $\widehat{\nu }=\widehat{\varphi }=\widehat{\sigma }=\widehat{\lambda }=0$ of the new variables (see Figure 2a) and turns the Hamiltonian into a form that is suitable for expansions.

Figure 2. (a) Stationary state of a stratified fluid: the growing variables $\varphi =\widehat{t}f$ and $\lambda =\widehat{t}l$ yield a zero momentum field $\mathbf{p}={\nu }_{eq}\widehat{t}\nabla f+\widehat{t}l\nabla {\sigma }_{eq}=\mathbf{0}$. (b) Nonstationary state: the terms $\widehat{t}f$ and $\widehat{t}l$ are separated from the canonical variables as $\varphi =\widehat{t}f+\widehat{\varphi }$, $\lambda =\widehat{t}l+\widehat{\lambda }$, the momentum is $\mathbf{p}=\nu \nabla (\widehat{t}f+\widehat{\varphi })+(\widehat{t}l+\widehat{\lambda })\nabla \sigma$.

The generating functional

$$F[\varphi ,\widehat{\nu },\sigma ,\widehat{\lambda },\widehat{t}]=\int [({\nu }_{eq}+\widehat{\nu })(\widehat{t}f-\varphi )+({\sigma }_{eq}-\sigma )(\widehat{\lambda }+\widehat{t}l)]d^3\mathbf{r}$$

with time-independent functions ${\nu }_{eq}\left(\mathbf{r}\right)$, ${\sigma }_{eq}\left(\mathbf{r}\right)$, $f\left(\mathbf{r}\right)$, $l\left(\mathbf{r}\right)$, and $\widehat{t}=t-t_0$ generates the transformations

$$\begin{array}{ccccc}\nu \hfill & =& -\frac{\delta F}{\delta \varphi }& =& {\nu }_{eq}+\widehat{\nu }\hfill \\ \widehat{\varphi }\hfill & =& -\frac{\delta F}{\delta \widehat{\nu }}& =& \varphi -\widehat{t}f\hfill \\ \lambda \hfill & =& -\frac{\delta \tilde{F}}{\delta \sigma }& =& \widehat{\lambda }+\widehat{t}l\hfill \\ \widehat{\sigma }\hfill & =& -\frac{\delta \tilde{F}}{\delta \widehat{\lambda }}& =& \sigma -{\sigma }_{eq}.\hfill \end{array}$$

(19)

The new Hamiltonian for the canonical variables $\widehat{\nu },\widehat{\varphi },\widehat{\lambda },\widehat{\sigma }$ is

$$\begin{array}{ccc}\hfill \widehat{H}& =& H+\partial F/\partial \widehat{t}\hfill \\ \hfill & =& \int ({\nu }_{eq}+\widehat{\nu })({\sigma }_{eq}+\widehat{\sigma })({\widehat{\mathbf{u}}}^2/2+gz)+e\left({\widehat{\nu }}_{eq}+\widehat{\nu }\right)+({\nu }_{eq}+\widehat{\nu })f-\widehat{\sigma }l{d}^3\mathbf{r}\hfill \end{array}$$

(20)

with the velocity (Figure 2b)

$$\widehat{\mathbf{u}}=\frac{({\nu }_{eq}+\widehat{\nu })\nabla (\widehat{t}f+\widehat{\varphi })+(\widehat{t}l+\widehat{\lambda })\nabla ({\sigma }_{eq}+\widehat{\sigma })}{({\sigma }_{eq}+\widehat{\sigma })({\nu }_{eq}+\widehat{\nu })}.$$

(21)

Noting that the force density can be expressed as $-\nu \sigma g{\mathbf{e}}_z+\nabla e^{\left(1\right)}\left(\nu \right)=-\nu \nabla \frac{\partial \mathcal{V}}{\partial \nu }+\frac{\partial \mathcal{V}}{\partial \sigma }\nabla \sigma$, the choice

$$\begin{array}{ccccc}\hfill f\left(z\right)& =& \hfill -\frac{\partial \mathcal{V}({\nu }_{eq},{\sigma }_{eq})}{\partial {\nu }_{eq}}& =& -{\sigma }_{eq}gz-e^{\left(1\right)}\left({\nu }_{eq}\right),\hfill \\ \hfill l\left(z\right)& =& \hfill \frac{\partial \mathcal{V}({\nu }_{eq},{\sigma }_{eq})}{\partial {\sigma }_{eq}}& =& {\nu }_{eq}gz\hfill \end{array}$$

(22)

satisfies ${\nu }_{eq}\nabla f\left(z\right)+l\left(z\right)\nabla {\sigma }_{eq}=\mathbf{0}$ and associates the equilibrium $\widehat{\mathbf{u}}=\mathbf{0}$ with a fixed point $\dot{\widehat{\varphi }}=\dot{\widehat{\lambda }}=\dot{\widehat{\nu }}=\dot{\widehat{\sigma }}=0$ of the canonical equations

$$\begin{array}{ccc}\hfill \dot{\widehat{\nu }}& =& -\nabla ·\left(({\nu }_{eq}+\widehat{\nu })\widehat{\mathbf{u}}\right)\hfill \\ \hfill \dot{\widehat{\varphi }}& =& \widehat{\mathbf{u}}·(({\sigma }_{eq}+\widehat{\sigma })\widehat{\mathbf{u}}/2-\widehat{t}\nabla f-\nabla \widehat{\varphi })-\widehat{\sigma }gz-e^{\left(1\right)}({\nu }_{eq}+\widehat{\nu })+e^{\left(1\right)}\left({\nu }_{eq}\right)\hfill \\ \hfill \dot{\widehat{\lambda }}& =& -\nabla ·\left[(\widehat{\lambda }+\widehat{t}l)\widehat{\mathbf{u}}\right]-({\nu }_{eq}+\widehat{\nu })\widehat{\mathbf{u}}·\widehat{\mathbf{u}}/2+\widehat{\nu }gz\hfill \\ \hfill \dot{\widehat{\sigma }}& =& -\widehat{\mathbf{u}}·\nabla ({\sigma }_{eq}+\widehat{\sigma }).\hfill \end{array}$$

Equation (21) maps these canonical equations again on the Euler equation $D\widehat{\mathbf{u}}/Dt=-g{\mathbf{e}}_z-{\sigma }^{-1}\nabla e^{\left(1\right)}\left(\nu \right)$. The constrained action for these equations is

$$\begin{array}{cc}\hfill \int \int & \mathcal{T}-\mathcal{V}\hfill \\ & -(\widehat{t}l+\widehat{\lambda })[\dot{\widehat{\sigma }}+\widehat{\mathbf{u}}·\nabla ({\sigma }_{eq}+\widehat{\sigma })]\hfill \\ & +(\widehat{t}f+\widehat{\varphi })\{\dot{\widehat{\nu }}+\nabla ·\left[({\nu }_{eq}+\widehat{\nu })\widehat{\mathbf{u}}\right]\}{d}^3\mathbf{r}dt\hfill \end{array}$$

where the multipliers $\varphi$ and $\lambda$ are replaced by $\widehat{t}f+\widehat{\varphi }$ and $\widehat{t}l+\widehat{\lambda }$, the energy densities $\mathcal{T}=({\sigma }_{eq}+\widehat{\sigma })({\nu }_{eq}+\widehat{\nu }){\mathbf{u}}^2/2$ and $\mathcal{V}=e({\nu }_{eq}+\widehat{\nu })+({\sigma }_{eq}+\widehat{\sigma })({\nu }_{eq}+\widehat{\nu })gz$ are functions of the independent variables $\widehat{\nu }$, $\widehat{\sigma }$, and $\widehat{\mathbf{u}}$.

The transformation (19) removes the secular growth of $\varphi$ and $\lambda$ for the stationary state of the fluid, but introduces explicit time-dependencies in $\widehat{\mathbf{u}}$ (21), the canonical Equation (19) and in $\widehat{H}$, where the identities $\partial \widehat{H}/\partial \widehat{t}=d\widehat{H}/d\widehat{t}=d(\partial F/\partial \widehat{t})/d\widehat{t}$ give

$$\partial \widehat{H}/\partial \widehat{t}=\int l\widehat{\mathbf{u}}·\nabla ({\sigma }_{eq}+\widehat{\sigma })-f\nabla ·\left(({\nu }_{eq}+\widehat{\nu })\widehat{\mathbf{u}}\right)d^3\mathbf{r}.$$

3.2. Canonical Approximations of the Linear Dynamics

We expand the Hamiltonian $\widehat{H}=\partial F/\partial t+{\widehat{T}}_0+{\widehat{V}}_0+{\widehat{T}}_1+{\widehat{V}}_1+{\widehat{T}}_2+{\widehat{V}}_2+\dots$ in powers of the variables $\widehat{\varphi },\widehat{\lambda },\widehat{\nu },\widehat{\sigma }$. The momentum vanishes in the lowest order

$$\begin{array}{ccc}{\widehat{\mathbf{p}}}_0\hfill & =& l\left(z\right)\nabla {\sigma }_{eq}+{\nu }_{eq}\nabla f\left(z\right)\hfill \\ & =& [g+{\sigma }_{eq}^{-1}\frac{d}{dz}{e}^{\left(1\right)}\left({\nu }_{eq}\right)]{\mathbf{e}}_z\hfill \\ & =& 0.\hfill \end{array}$$

The first order

$$\begin{array}{ccc}{\widehat{\mathbf{p}}}_1\hfill & =& \widehat{\lambda }\nabla {\sigma }_{eq}+{\nu }_{eq}\nabla \widehat{\varphi }+(\widehat{\nu }\nabla f+l\nabla \widehat{\sigma })\widehat{t},\hfill \end{array}$$

(23)

is explicitly time-dependent. The expansion of the kinetic energy in terms of ${\widehat{\mathbf{p}}}_1$, $\widehat{\nu }$, $\widehat{\sigma }$ up to second order is

$$\begin{array}{ccc}\hfill {\widehat{T}}_0& =& 0\hfill \\ \hfill {\widehat{T}}_1& =& 0\hfill \\ \hfill {\widehat{T}}_2& =& \int {\widehat{\mathbf{p}}}_1^2/\left(2{\sigma }_{eq}{\nu }_{eq}\right)d^3\mathbf{r},\hfill \end{array}$$

(24)

where the zeroth and first order vanish by ${\mathbf{p}}_0=\mathbf{0}$. The potential energy and generating function are

$$\begin{array}{ccc}\hfill {\widehat{V}}_0+\partial F_0/\partial \widehat{t}& =& \int e\left({\nu }_{eq}\right)-{\nu }_{eq}{e}^{\left(1\right)}\left({\nu }_{eq}\right)d^3\mathbf{r}\hfill \\ \hfill {\widehat{V}}_1+\partial F_1/\partial \widehat{t}& =& 0\hfill \\ \hfill {\widehat{V}}_2& =& \int \widehat{\sigma }\widehat{\nu }gz+e^{\left(2\right)}\left({\nu }_{eq}\right){\widehat{\nu }}^2/2d^3\mathbf{r}.\hfill \end{array}$$

(25)

${\widehat{H}}_2={\widehat{T}}_2+{\widehat{V}}_2$ yields explicitly time-dependent equations

$$\begin{array}{ccc}\hfill \dot{\widehat{\varphi }}& =& -\widehat{t}{\widehat{\mathbf{u}}}_1·\nabla f-\widehat{\sigma }gz-e^{\left(2\right)}\left({\nu }_{eq}\right)\widehat{\nu }\hfill \\ \hfill \dot{\widehat{\lambda }}& =& -\widehat{t}\nabla ·\left({\widehat{\mathbf{u}}}_{1}l\right)+\widehat{\nu }gz\hfill \\ \hfill \dot{\widehat{\nu }}& =& -\nabla ·\left({\nu }_{eq}{\widehat{\mathbf{u}}}_1\right)\hfill \\ \hfill \dot{\widehat{\sigma }}& =& -{\widehat{\mathbf{u}}}_1·\nabla {\sigma }_{eq}\hfill \end{array}$$

(26)

for the linear dynamics where ${\widehat{\mathbf{u}}}_1={\widehat{\mathbf{p}}}_1/\left({\nu }_{eq}{\sigma }_{eq}\right)$. While the canonical transformation (19) eliminates the growth of $\varphi$ and $\lambda$ for the stationary state of the fluid, the terms $\sim \widehat{t}\widehat{\mathbf{u}}$ in $\dot{\widehat{\varphi }}$ and $\dot{\widehat{\lambda }}$ grow secularly if $\widehat{\mathbf{u}}\ne \mathbf{0}$. Inserting the canonical Equation (26) in ${\dot{\widehat{\mathbf{u}}}}_1$ yields

$${\nu }_{eq}{\sigma }_{eq}{\dot{\widehat{\mathbf{u}}}}_1={\nu }_{eq}\nabla \dot{\widehat{\varphi }}+\dot{\widehat{\lambda }}\nabla {\sigma }_{eq}+\widehat{t}\dot{\widehat{\nu }}\nabla f+\widehat{t}l\nabla \dot{\widehat{\sigma }}+\widehat{\nu }\nabla f+l\nabla \widehat{\sigma }.$$

(27)

The first two terms contain growing contributions $\sim \widehat{t}$ from the dynamics (26) of $\widehat{\varphi }$ and $\widehat{\lambda }$, the next two terms contain $\widehat{t}$ as a factor. A straightforward calculation with Equations (7) and (22) shows that the terms $\sim \widehat{t}$ (not including the $\widehat{t}$ from the definition (23) of ${\widehat{\mathbf{u}}}_1$) add up to zero

$${\nu }_{eq}\nabla ({\widehat{\mathbf{u}}}_1·\nabla f)+\nabla ·\left(l{\widehat{\mathbf{u}}}_1\right)\nabla {\sigma }_{eq}+\nabla ·\left({\nu }_{eq}{\widehat{\mathbf{u}}}_1\right)\nabla f+l\nabla ({\widehat{\mathbf{u}}}_1·\nabla {\sigma }_{eq})=0.$$

The remaining terms in Equation (27) can be collected and simplified as

$$\begin{array}{c}-{\nu }_{eq}\nabla \left[\widehat{\sigma }gz{e}^{\left(2\right)}\left({\nu }_{eq}\right)\widehat{\nu }\right]+\widehat{\nu }gz\nabla {\sigma }_{eq}+\widehat{\nu }\nabla f+l\nabla \widehat{\sigma }\hfill \\ =-{\nu }_{eq}\widehat{\sigma }g{\mathbf{e}}_z-{\nu }_{eq}\nabla \left[e^{\left(2\right)}\left({\nu }_{eq}\right)\widehat{\nu }\right].\hfill \end{array}$$

Equation (26) includes the nontrivial linearization of the canonical variables that is correct in the sense that they yield the linearized Euler equation

$$\begin{array}{ccc}\hfill {\dot{\widehat{\mathbf{u}}}}_1& =& -{\sigma }_{eq}^{-1}\{\widehat{\sigma }g{\mathbf{e}}_z+\nabla \left[e^{\left(2\right)}\left({\nu }_{eq}\right)\widehat{\nu }\right]\}.\hfill \end{array}$$

(28)

This corresponds to a direct linearization of the Euler equation $\sigma \nu \frac{D\mathbf{u}}{Dt}=-g\sigma \nu {\mathbf{e}}_z-\nu \nabla \frac{de}{d\nu }$ where the left side is replaced by ${\sigma }_{eq}{\nu }_{eq}{\dot{\mathbf{u}}}_1$ and the right side is linearized in $\widehat{\sigma }$ and $\widehat{\nu }$. The variables $\widehat{\varphi }$ and $\widehat{\lambda }$ can be eliminated as

$$\begin{array}{ccc}\hfill \ddot{\widehat{\nu }}& =& \frac{\partial }{\partial z}\left(\frac{{\nu }_{eq}}{{\sigma }_{eq}}\right)\left(g\widehat{\sigma }+\frac{\partial }{\partial z}\left(e^{\left(2\right)}\left({\nu }_{eq}\right)\widehat{\nu }\right)\right)\hfill \\ & +& \frac{{\nu }_{eq}}{{\sigma }_{eq}}\left(g\frac{\partial }{\partial z}\widehat{\sigma }+{\nabla }^2\left(e^{\left(2\right)}\left({\nu }_{eq}\right)\widehat{\nu }\right)\right)\hfill \\ \hfill \ddot{\widehat{\sigma }}& =& \frac{1}{{\sigma }_{eq}}\frac{\partial {\sigma }_{eq}}{\partial z}\left(\frac{\partial }{\partial z}\left(e^{\left(2\right)}\left({\nu }_{eq}\right)\widehat{\nu }\right)+g\widehat{\sigma }\right).\hfill \end{array}$$

While the canonical variables grow, their projection on the velocity field has acoustic and internal wave solutions. For computing wave dispersion relations, we assume that $\widehat{\nu }$ and $\widehat{\sigma }$ vary at a length scale $k_z^{-1}\propto \mathcal{O}\left(1\right)$ that is small compared to the length scales ${\nu }_{eq}/(\partial {\nu }_{eq}/\partial z)$ and ${\sigma }_{eq}/(\partial {\sigma }_{eq}/\partial z)$ of the z-dependence of ${\nu }_{eq}$ and ${\sigma }_{eq}$; this yields two small parameters ${ϵ}_{\nu }=k_z^{-1}{\nu }_{eq}^{-1}\partial {\nu }_{eq}/\partial z$ and ${ϵ}_{\sigma }=k_z^{-1}{\sigma }_{eq}^{-1}\partial {\sigma }_{eq}/\partial z$ and the sound speed $c^2=\frac{{\nu }_{eq}}{{\sigma }_{eq}}{e}^{\left(2\right)}\left({\nu }_{eq}\right)=-{\nu }_{eq}g/\frac{\partial {\nu }_{eq}}{\partial z}$. In the lowest order of these parameters, linear waves

$$\left(\begin{array}{c}\widehat{\nu }(\mathbf{r},\widehat{t})\\ \widehat{\sigma }(\mathbf{r},\widehat{t})\end{array}\right)=\mathbf{w}exp(i\Omega \widehat{t}-i\mathbf{k}·\mathbf{r})+c.c.$$

yield the eigenvalue problem $-{\Omega }^2\mathbf{w}=A\mathbf{w}$ with

$$A=\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right).$$

The entries of the matrix in the lowest order scale as

$$\begin{array}{ccccc}\hfill a_{11}& =& -c^2{k}^2\hfill & =& O\left({ϵ}_{\nu }^{-1}\right)\hfill \\ \hfill a_{12}& =& -i\frac{{\nu }_{eq}g{k}_z}{{\sigma }_{eq}}\hfill & =& O\left(1\right)\hfill \\ \hfill a_{21}& =& -i\frac{c^2{k}_z}{{\nu }_{eq}}\frac{\partial {\sigma }_{eq}}{\partial z}\hfill & =& O\left({ϵ}_{\nu }^{-1}{ϵ}_{\sigma }\right)\hfill \\ \hfill a_{22}& =& \frac{g}{{\sigma }_{eq}}\frac{\partial {\sigma }_{eq}}{\partial z}\hfill & =& O\left({ϵ}_{\sigma }\right)\hfill \end{array}$$

so that ${tr}^{2}A\gg |detA|$. The first root of the eigenvalues ${\Omega }_{1/2}^2=-\frac{trA\pm \sqrt{{tr}^{2}A-4detA}}{2}$ yields the dispersion of sound waves ${\Omega }_1^2\approx -a_{11}\approx c^2{k}^2.$ The second root is the dispersion of internal waves ${\Omega }_2^2\approx \frac{a_{12}{a}_{21}-a_{11}{a}_{22}}{a_{11}}\approx N^2\frac{k_x^2+k_y^2}{k^2}$ with the Brunt–Väisälä frequency $N^2=-\frac{g}{{\sigma }_{eq}}\frac{\partial {\sigma }_{eq}}{\partial z}=-\frac{g}{{\rho }_{eq}}\frac{\partial {\rho }_{eq}}{\partial z}-\frac{g^2}{c^2}$ where ${\rho }_{eq}={\sigma }_{eq}{\nu }_{eq}$ is the equilibrium density.

3.3. Nonlinear Canonical Approximations

Nonlinear canonical equations of motion can be obtained from a third-order approximation of the Lagrangian density ${\sum }_{n=1}^3{\mathcal{L}}_n(\widehat{\nu },\widehat{\sigma },{\widehat{\mathbf{u}}}_{\mathbf{2}})$

$$\begin{array}{ccc}\hfill {\mathcal{L}}_1& =& -e^{\left(1\right)}\left({\nu }_{eq}\right)\widehat{\nu }-(\widehat{\nu }{\sigma }_{eq}+{\nu }_{eq}\widehat{\sigma })gz\hfill \\ \hfill {\mathcal{L}}_2& =& {\sigma }_{eq}{\nu }_{eq}{{\widehat{\mathbf{u}}}_{\mathbf{2}}}^2/2-e^{\left(2\right)}\left({\nu }_{eq}\right){\widehat{\nu }}^2/2-\widehat{\nu }\widehat{\sigma }gz\hfill \\ \hfill {\mathcal{L}}_3& =& ({\sigma }_{eq}\widehat{\nu }+\widehat{\sigma }{\nu }_{eq}){{\widehat{\mathbf{u}}}_{\mathbf{2}}}^2/2-e^{\left(3\right)}\left({\nu }_{eq}\right){\widehat{\nu }}^3/6.\hfill \end{array}$$

The ${\widehat{\mathbf{u}}}_{\mathbf{2}}$-variation of the constrained action in third-order

$$\begin{array}{cc}\hfill \int \int & \sum _{n=1}^3{\mathcal{L}}_n(\widehat{\nu },\widehat{\sigma },{\widehat{\mathbf{u}}}_{\mathbf{2}})\hfill \\ \hfill & -\lambda [\dot{\widehat{\sigma }}+{\widehat{\mathbf{u}}}_{\mathbf{2}}·\nabla ({\sigma }_{eq}+\widehat{\sigma })]\hfill \\ \hfill & +\varphi \{\dot{\widehat{\nu }}+\nabla ·\left[({\nu }_{eq}+\widehat{\nu }){\widehat{\mathbf{u}}}_{\mathbf{2}}\right]\}{d}^3\mathbf{r}dt\hfill \end{array}$$

(29)

yields the velocity

$${\widehat{\mathbf{u}}}_{\mathbf{2}}={({\nu }_{eq}{\sigma }_{eq}+\widehat{\nu }{\sigma }_{eq}+{\nu }_{eq}\widehat{\sigma })}^{-1}[({\nu }_{eq}+\widehat{\nu })\nabla \varphi +\lambda \nabla ({\sigma }_{eq}+\widehat{\sigma })].$$

(30)

The canonical equations

$$\begin{array}{ccc}\hfill \dot{\varphi }+{\widehat{\mathbf{u}}}_{\mathbf{2}}·\nabla \varphi & =& {\sigma }_{eq}{{\widehat{\mathbf{u}}}_{\mathbf{2}}}^2/2-({\sigma }_{eq}+\widehat{\sigma })gz-\sum _{n=0}^2{e}^{(n+1)}\left({\nu }_{eq}\right){\widehat{\nu }}^n/n!\hfill \\ \hfill \dot{\lambda }+\nabla ·\left(\lambda {\widehat{\mathbf{u}}}_{\mathbf{2}}\right)& =& -{\nu }_{eq}{{\widehat{\mathbf{u}}}_{\mathbf{2}}}^2/2+({\nu }_{eq}+\widehat{\nu })gz\hfill \\ \hfill \dot{\widehat{\nu }}+\nabla ·\left[({\nu }_{eq}+\widehat{\nu }){\widehat{\mathbf{u}}}_{\mathbf{2}}\right]& =& 0\hfill \\ \hfill \dot{\widehat{\sigma }}+{\widehat{\mathbf{u}}}_{\mathbf{2}}·\nabla ({\sigma }_{eq}+\widehat{\sigma })& =& 0\hfill \end{array}$$

follow from the variations of Equation (29), or from the Hamiltonian

$$H[\widehat{\nu },\varphi ,\widehat{\sigma },\lambda ]=\int ({\sigma }_{eq}{\nu }_{eq}+{\sigma }_{eq}\widehat{\nu }+\widehat{\sigma }{\nu }_{eq}){{\widehat{\mathbf{u}}}_{\mathbf{2}}}^2/2+{\mathcal{V}}_1+{\mathcal{V}}_2+{\mathcal{V}}_3{d}^3\mathbf{r}.$$

Here the the original untransformed Clebsch variables $\varphi$ and $\lambda$ are used to keep the equations simple. This system represents the Euler equation $D{\widehat{\mathbf{u}}}_2/Dt=-{\sigma }_{eq}^{-1}\{\widehat{\sigma }g{\mathbf{e}}_z+\nabla \left[e^{\left(2\right)}\left({\nu }_{eq}\right)\widehat{\nu }\right]\}+\mathcal{O}\left(3\right)$ where $\mathcal{O}\left(3\right)$ is the cubic order in $\widehat{\nu }$, $\widehat{\sigma }$ and ${\widehat{\mathbf{u}}}_2$. This canonical expansion can describe the interaction of weakly nonlinear waves, e.g., in the context of weak turbulence.

4. Conclusions

Several technical difficulties hamper the use of canonical Clebsch variables for describing inviscid fluids: a first one is the non-unique and in most cases nontrivial dependence of Clebsch variables on the velocity field. We have introduced Clebsch maps with, respectively, one and two pairs of auxiliary variables that allow a simple construction of the initial conditions from the velocity field. These additional degrees of freedom are governed by simple equations (continuity and advection equations). A second problem is the secular growth of the Clebsch variables $\varphi$ and $\lambda$ in Equation (4) in the stratified flow. The growing terms make expansions of the equations of motion difficult, it is not even trivial to identify the canonical equations that are associated with the linearized Euler equations. We have introduced a canonical transformation that associates a stationary state of the fluid with a fixed point of the Clebsch variables; an expansion in these variables leads to correct approximations of the dynamics.

On the other hand, there are various advantages of Clebsch variables: quantities of particular interest like the vorticity can be represented by one of the canonical equations; incomplete sets of Clebsch variables can be chosen to represent specific flows, e.g., flows with zero helicity and potential flows; Liouville’s theorem and its many applications in statistical mechanics can be used. This requires that the canonical structure is preserved through all transformations. The work that we have presented can facilitate canonical perturbative descriptions of weakly interacting waves, in particular for studying wave turbulence of internal waves.