Abstract
The objective of this study was to simulate the flow of graphene oxide (GO) dispersions, a discotic nematic liquid crystal (DNLC), using the Ericksen-Leslie (EL) theory. GO aqueous suspension, as a lubricant, effectively reduces the friction between solid surfaces. The geometry considered in this study was two cylinders with a small gap size, which is the preliminary geometry for journal bearings. The Leslie viscosity coefficients calculated in our previous study were used to calculate the stress tensor in the EL theory. The behavior of GO dispersions in the concentration range of 15 mg/mL to 30 mg/mL, shown in our recent experiments to be in the nematic phase, was investigated to obtain the orientation and the viscosity profile. The viscosities of GO dispersions obtained from numerical simulations were compared with those from our recent experimental study, and we observed that the values are within the range of experimental uncertainty. In addition, the alignment angles of GO dispersions at different concentrations were calculated numerically using EL theory and compared with the respective theoretical values, which were within 1% error. The anchoring angles corresponding to viscosity values closest to the experimental results were between 114 and 118 degrees. Moreover, a sensitivity analysis was performed to determine the effects of different ratios of the elasticity coefficients in EL theory. Using this procedure, the same study could be extended for other DNLCs in different geometries.
1. Introduction
The liquid crystalline phase is mesomorphic, which has properties intermediate of solids and liquids, shows the long-range ordering of orientation, and can have the long-range ordering of the positional degrees of freedom. Liquid crystal (LC) molecules can diffuse, and viscous flow occurs like liquids [1]. There are multiple ways of classifying LCs [2,3,4]. They can be classified based on their shape, phase, or order. Categorizing based on shape leads to calamitic (rod-like) and discotic (disk-like) LCs. Based on the different types of mesophase ordering, they can be classified as nematic, smectic, or cholesteric LCs. Nematics are achiral substances with a high degree of long-range orientational order but have no long-range translational order, and the molecules are aligned in a preferred direction. Based on how the transition to liquid crystalline phase occurs, LCs are divided into thermotropic, where the phase transition occurs due to a temperature change [5], and lyotropic LCs, where the phase transition occurs due to the concentration of the amphiphilic molecule [6]. Other factors such as molecule shape, size, and charge affect the transition.
In the present work, the study is restricted to a nematic, lyotropic, discotic LC. An example of a nanoparticle solution that forms discotic nematic liquid crystal (DNLC) is graphene oxide (GO) aqueous solution. GO has attracted significant attention due to its specific rheological properties [7,8,9,10,11,12]. The chemical structure and physical properties of GOs were investigated in [8], showing the challenges and opportunities in this field. GO forms stable dispersions in aqueous mediums as GO flakes produce large repulsion forces.
As the concentration of discotic GO flakes increases in water, the particles form ordered structures and become lyotropic LCs [7,13,14,15]. In our previous experimental study, the formation of GO dispersions was studied by the polarized light imaging technique, and it was shown that the fully nematic phase of GO dispersions starts at a concentration of 15 mg/mL [7]. Nikzad et al. [7] found that at low concentrations (less than 15 mg/mL), no birefringence is observed, while at higher concentrations of GO dispersions, the birefringence within an image of light scattering appeared. In the previous study, the rheological behavior was investigated, and it was shown that at low concentrations (less than 15 mg/mL), the shear viscosity of the dispersions possesses Newtonian behavior. However, at higher concentrations, shear-thinning behavior was exhibited. In this study, the same GO dispersions with the same characteristics were used.
The rheological properties of GO dispersions at high shear rates and the calculated viscosity coefficients for GO dispersions from the previous study were used to simulate the flow of nematic GO dispersions.
Due to its invaluable properties, GO has been used in a wide range of applications. In order to commercialize GO, developing a cost-effective synthesis process applicable to the bulk scale is essential. There are studies that modeled a Couette–Taylor reactor to improve the GO synthesis process [16,17], where the mixture of an aqueous colloidal suspension of GO and an additive was injected into the gap between the two concentric cylinders.
Furthermore, due to multifunctional properties of graphene-related materials, they have been considered in different studies as self-lubricating solids [18,19,20] and as additives in oils or water [21,22]. GO performance as a water-based lubricant has been evaluated and was shown to effectively reduce the friction and wear of sliding surfaces [23]. Kinoshita et al. [24] and Elomaa et al. [25] investigated the tribological properties of water-based GO suspensions, showing the remarkable improvement in friction reductions and evaluating the protective coating on surfaces. Elomaa et al. [25] showed that the friction coefficient decreased by 57% compared to pure water. Therefore, the understanding of the rheological and tribological properties of GO and its derivatives in water would have a significant impact in the future.
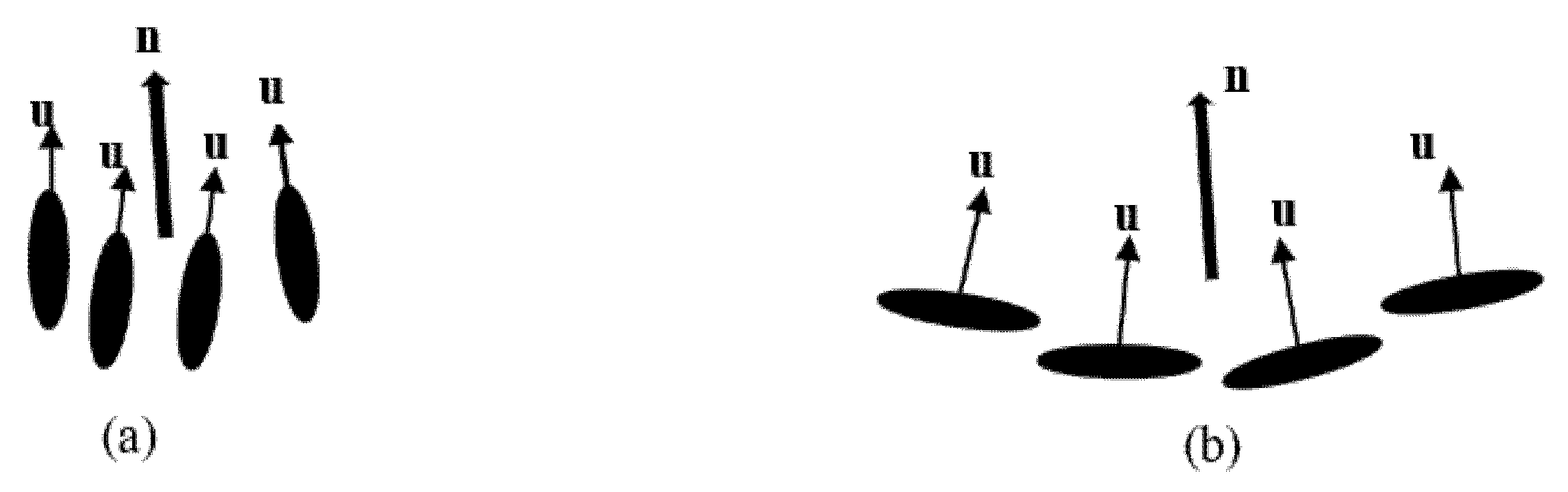
Extensive research has been performed on the theoretical and computational front to understand the morphology of LCs. In this study, the modeling of LCs was performed using a continuum-based approach, the Ericksen–Leslie (EL) theory. Figure 1 represents the director and the molecular orientations (which are represented by u) for discotic LCs.
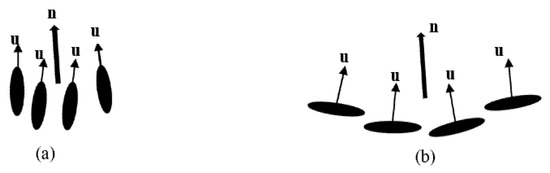
Figure 1.
Schematic representation of director n for (a) calamitic, (b) discotic LCs.
Considering the symmetry of the director and taking it to be of unit magnitude, Leslie simplified the equations based on Ericksen’s theory of anisotropic fluids [26]. The constitutive equations were developed incorporating Frank’s theory to model the elasticity of the LCs [27]. The basis of Frank’s elasticity coefficients is that LCs tend to resist and recover from distortion, analogous to the tendency of elastic solids to resist strain [27]. The EL theory is suitable for cases of slow-moving flows, where the flow time scale is slower than the internal one, in which the orientation dominates the rheology and the gradients of the director of LC do not deviate by a large amount from the equilibrium position [28,29].
The shear flow behavior of nematic LCs depends on the magnitude of the reactive parameter, or tumbling parameter λ, which is the ratio of the flow-aligning effect of shear and the tumbling effect of vorticity. The value of the reactive parameter governs whether an LC is flow aligning (|λ| > 1) or tumbling (|λ| < 1). The theory has been used to study flow-aligning LCs and tumbling LCs to understand the behavior at different shear rates [30]. Moreover, the EL theory is known to provide multiple solutions based on the anchoring angle (the orientation at the boundaries in case of confined flows) and the flow conditions. Lima and Rey [31] studied the Poiseuille flow of DNLCs and reported the existence of multiple solutions based on the anchoring angle and the flow conditions. The Couette flow of nematic LCs using the EL theory for a fixed velocity profile has been previously implemented [32]. Similar implementations employing a fixed velocity profile have been used to study Poiseuille flow [31,32] and Jeffrey-Hamel flow [33], as well. The two-dimensional channel flow has been studied for tumbling nematic LC flows [34] under the application of a magnetic field [35]. Furthermore, Cruz et al. [35] studied the three-dimensional pressure-driven flow under the effect of a magnetic field. Anderson et al. [36] studied the two-dimensional channel flow considering the assumption of unidirectional flow. They explained the existence of multiple solutions and the energy requirements for the stability of the flow solutions. Furthermore, shear and pressure-driven flows of nematic LCs were studied by [37] under the thin-film approximation. Recently, GO aqueous alkaline dispersion with and without shear flow was studied by [38], which showed that the orientational dynamics play a critical role in the rheology of GO dispersions.
In the EL theory, the modified stress tensor is a function of rheological properties. The viscous stress tensor is calculated based on six viscosity coefficients called the Leslie viscosity coefficients, (i = 1:6) [39]. Nikzad et al. [7] defined a method to calculate for disc-like liquid crystalline materials and these coefficients can be used to simulate the flow of GO dispersions using the EL theory.
The main objective of this study is to investigate the rheological properties and the orientation of the molecules in GO dispersions as DNLC. Since GO aqueous suspension, an environmentally friendly lubricant, effectively reduces the friction between solid surfaces, the geometry considered in this study is two cylinders with a small gap size, which is the preliminary geometry for journal bearings. The results are validated by experimental results. This study is a continuation of a previous article [7] where the viscosity coefficients for DNLC, with GO as a case study, were calculated. The viscosity coefficients for the EL theory were validated using rheological experimental data in the previous study [7].
The organization of the article is as follows. The method, the governing equations, and the numerical setup are described in the next section. The results and discussion are presented in the following section. Finally, the paper is concluded in the last section.
2. Methods
In this study, the EL theory is used to analyze the Couette flow of GO dispersions in water as DNLC. The flow in this simulation is steady, incompressible, and isothermal, with no gravity or external field.
2.1. EL Theory
The constitutive equations in the EL theory combine the effects of anisotropic viscous properties and elasticity present in the LCs through modification of the stress tensor in the Navier-Stokes equations. The EL theory consists of Equations (1)–(6), which govern the flow and development of the orientation of LCs. These equations include the mass conservation, linear momentum conservation, angular momentum conservation equations, and the required constitutive equations. The mass conservation equation is as shown below.
where u is the velocity vector and ρ is density.
The conservation of linear momentum equation is as shown below.
where p is pressure, is elastic energy, τ is the viscous stress tensor, g is the internal body force vector, n is the unit vector representing the orientation, G is the force vector due to an external body moment, and F is the external body force per unit mass.
The angular momentum conservation equation is represented as shown below.
where φ is the Lagrange multiplier, which simplifies the balance of elastic and viscous torques [40]. The elastic effects of the LCs are modeled using Frank’s theory, and the term representing the elastic energy is as shown below.
where , , and are known as Frank’s elasticity coefficients for the splay, twist, and bend, respectively [27].
In the present case, the LC orientation is affected only by the hydrodynamic field. The stress tensor due to viscous forces is as shown below.
where represents the Leslie viscosity coefficients (i = 1…6), which are unique to each liquid crystalline material. The Leslie coefficients are subject to certain thermodynamic constraints, and these constraints can be found in any introductory material on LCs [2,40]. The internal body force can be evaluated using the equation shown below.
The rotational viscosities () are defined as and . In Equations (5) and (6), the term , which describes the angular velocity of the director relative to the fluid velocity. is the vorticity tensor and is the rate of deformation tensor.
Flow alignment is a property of the LCs, which means that the LC molecules in the bulk of the domain orient at a fixed angle compared to the direction of the velocity, and that it is dependent on the Leslie viscosities and is therefore a material property [3]. The flow alignment angle can be calculated using , where λ is the reactive parameter and is calculated as . The value of the reactive parameter governs whether a given LC is flow aligning (|λ| > 1) or tumbling (|λ| < 1). For discotic LCs, λ < 0.
2.2. Simplified Equations of Couette Flow
The equations for Couette flow in this study are in polar coordinates, which were derived by Atkins and Leslie [41]. As mentioned earlier, r is the radial distance, and θ represents the angle of a given point from the horizontal in the anti-clockwise sense. These equations were used by Noroozi and Grecov [42] to further study different nematic LCs.
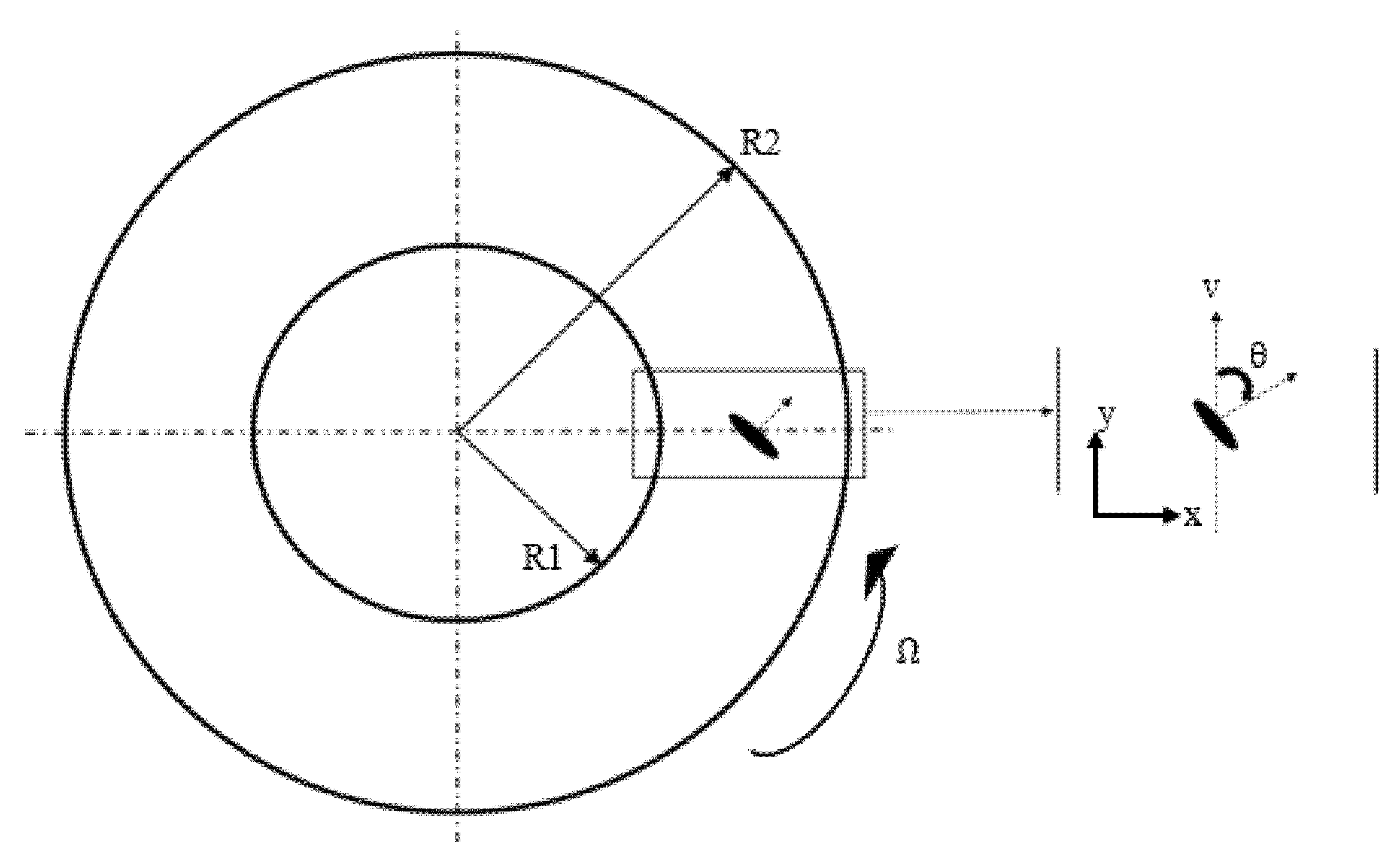
Figure 2 represents the typical Couette flow geometry. The inner and outer surfaces are at radii R1 and R2, respectively. The outer surface is provided with an anti-clockwise angular velocity ω. The enlarged image shows the flow direction along with the orientation θ of a discotic liquid crystal molecule.
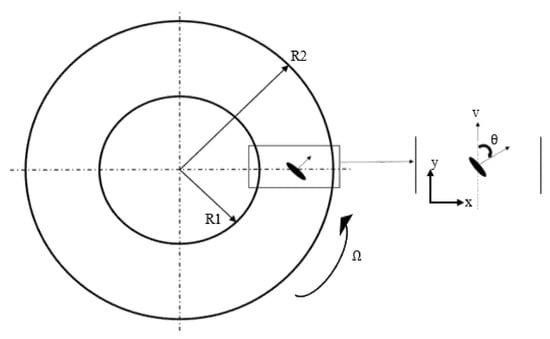
Figure 2.
Couette flow geometry with R1 and R2 representing the radius of the inner and outer surfaces, respectively.
Furthermore, the orientation of a discotic LC molecule is shown along with the orientation angle. Equations (1)–(6) can be simplified by choosing the velocity vector u as (0,rω(r),0) and the director n as . The resulting equations in the dimensionless form are as shown in Equations (7) and (8).
The terms and are defined as shown in Equations (9) and (10), respectively.
In Equations (7)–(10), the tilde represents that the parameters are non-dimensionalized. The parameter and the terms are non-dimensionalized as per Table 1.

Table 1.
Non-dimensionalized variables for Couette flow.
In Table 1, L represents the difference between the radii and , and represents the average of the Miesowicz viscosities , , and . These viscosities are calculated as:
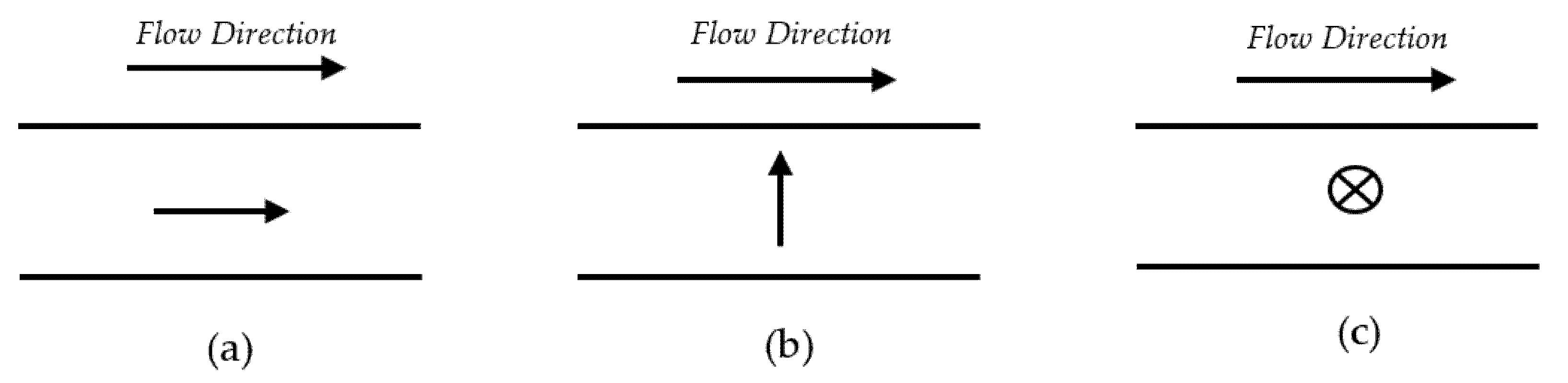
The three Miesowicz viscosities represent the viscosities of the LCs in a shear flow when the LCs are aligned along the flow direction, along the velocity gradient direction, and the vorticity direction. Figure 3 represents these different arrangements.
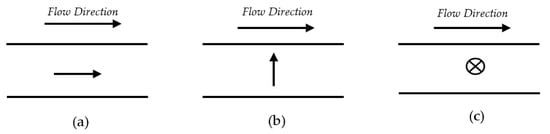
Figure 3.
Miesowicz viscosities in the direction of (a) velocity, (b) velocity gradient, and (c) vorticity.
Recent developments have been achieved to obtain these anisotropic viscosity coefficients based on the rheological measurements without the application of magnetic or electric fields [29]. Miesowicz introduced a technique to calculate the orientation in three perpendicular directions of the LCs, and thereby, the viscosities measured are termed as Miesowicz viscosities [43]. Based on the applications considered as a motivation for this study, the focus is to study the behavior of flows of LCs. The stable planar solution branches of nematic LCs under the application of shear flow are the in-plane elastic state, the in-plane tumbling–wagging state, the in-plane viscous-driven state, and the in-plane wagging state [44]. There are stable out-of-plane mode solution branches, as well [44]. In this study, we focus on the in-plane elastic state and the in-plane viscous-driven state, and the other solution branches are not discussed here.
2.3. Numerical Setup
In this section, the scheme to solve the EL theory’s equations is described. In the EL theory, Equations (7) and (8) are non-linear, non-homogeneous, and second-order one-dimensional ODEs. They can be solved numerically using either shooting or relaxation methods. Since the LC system is prone to multiple solutions, using the relaxation method to numerically solve these equations is preferable. This method was implemented by Noroozi and Grecov [42] to model the flow of nematic LCs between concentric cylinders, and the solution was computed on a mesh of 500 elements, representing a gap of m. The mesh independency study was conducted by comparing the change in the orientation profile with mesh refinement. The relaxation method was used to obtain the solution of the boundary value problem of a system of first-order differential equations. Therefore, Equations (7) and (8) are re-written into a system of four equations, and the variables that are solved are θ, ω, ∂θ/∂r, and ∂ω/∂r. In this method, the spatial derivatives of θ and ω are calculated during the solution procedure. The methodology involves selecting an initial guess of the solution, based on which the solution branch is selected. The finite difference form of the equations is obtained to numerically solve the system of equations. The infinity norm of the change in the solution was selected as the convergence criterion, and the value of tolerance was set as The solution methodology was previously implemented by Noroozi and Grecov [42], and the scheme was validated using nematic liquid crystalline materials DDA9 and AZA9.
In the governing Equations (7)–(10), two sets of material coefficients, namely, Leslie viscosity coefficients and Frank’s elasticity coefficients, are present. In order to implement the EL theory, Leslie viscosity coefficients are required. The viscosity coefficients of GO were obtained using a model based on the rheological data of GO suspensions in water [7] and are shown in Table 2. As shown, the coefficients are different for different concentrations of GO. The elastic coefficients of GO suspensions in water are not available in the literature, and therefore, a sensitivity study was conducted to determine the impact of the elastic coefficients on the orientation of the LCs. The values of the elastic coefficients were chosen to have the order 10 pN, which is the value typically observed for Frank’s elasticity coefficients of nematic LCs. The results of the sensitivity analysis are presented in the results section for EL theory.

Table 2.
Dimensionless Leslie coefficients ) of nematic GO dispersions at different concentrations.
3. Results and Discussions
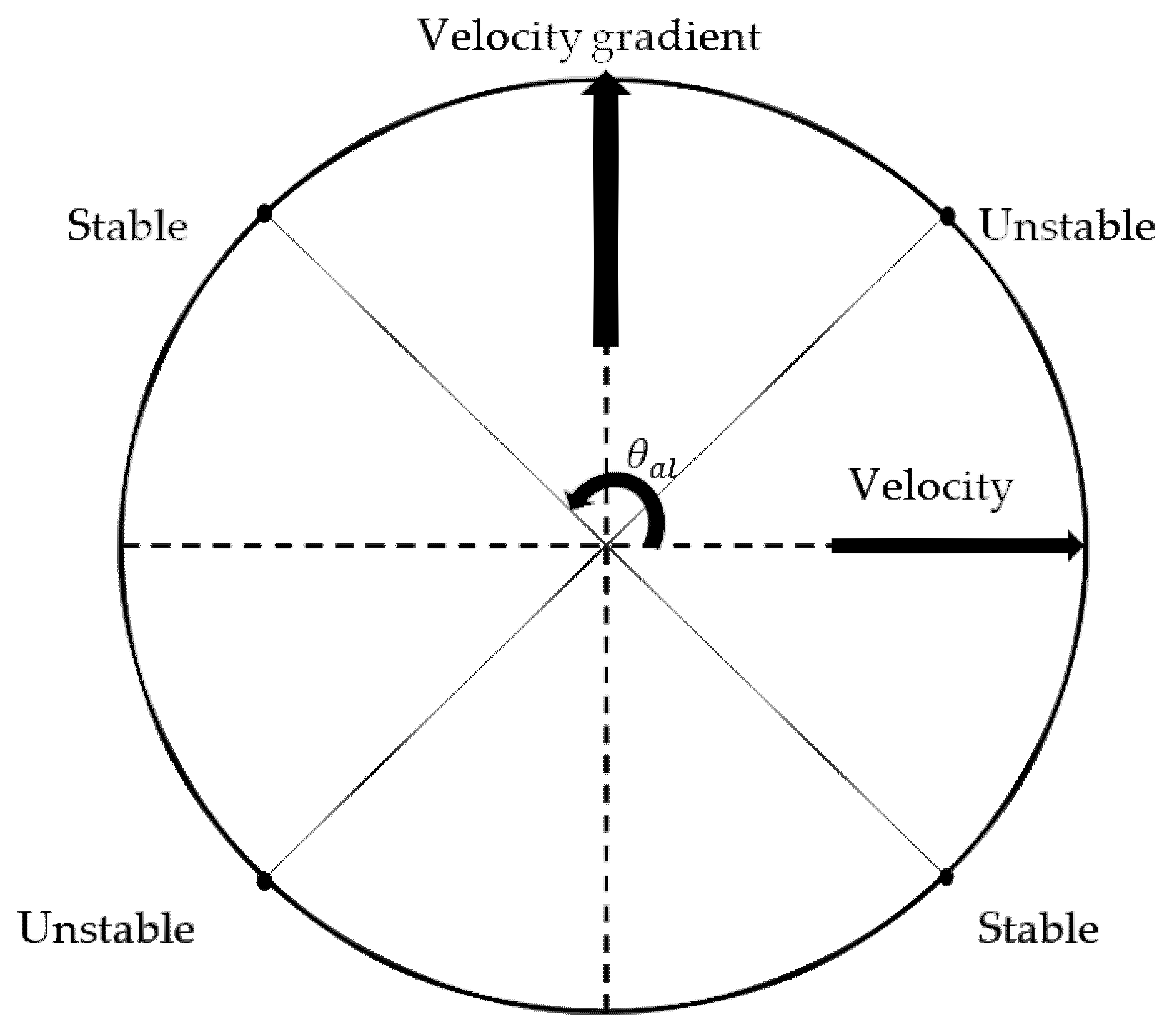
This section presents the results obtained from the study of Couette flow of GO dispersion. Before the in-depth discussion of the results obtained, it is essential to look at the stability diagram of the LC orientation for discotic LCs, shown in Figure 4 [28]. The figure represents the stable and unstable alignment angles of the director. The alignment angle is the angle that the director makes with respect to the primary direction of flow. All the nematic LCs are uniaxial and the director states n and −n cannot be distinguished [2]. Therefore, a 180° rotation of the LC molecule results in the same orientation, which explains both the stable and unstable alignment angles being 180° apart from each other.
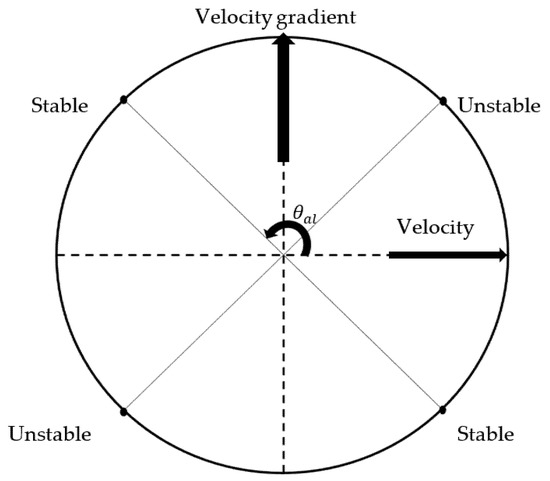
Figure 4.
Schematic showing the stable and unstable alignment angles for nematic discotic liquid crystals based on the direction of the velocity and the velocity gradient.
3.1. Orientation Profile of GO
This orientation of LCs depends on the balance of elastic and viscous forces. The elastic forces are dominant at lower shear rates, and then as the shear rate increases, the contribution of the viscous forces increases [45]. At low rotational velocities, due to the dominance of the elastic forces, the orientation in the bulk of the domain is dependent on the anchoring angle. With the increase in the velocity, a larger part of the molecules in the domain reaches the alignment angle. At high shear rates, the viscous forces are dominant, and except for a boundary layer where the orientation is at the anchoring angle, the bulk of the domain reaches flow alignment. This has been previously reported for calamitic liquid crystals [29].
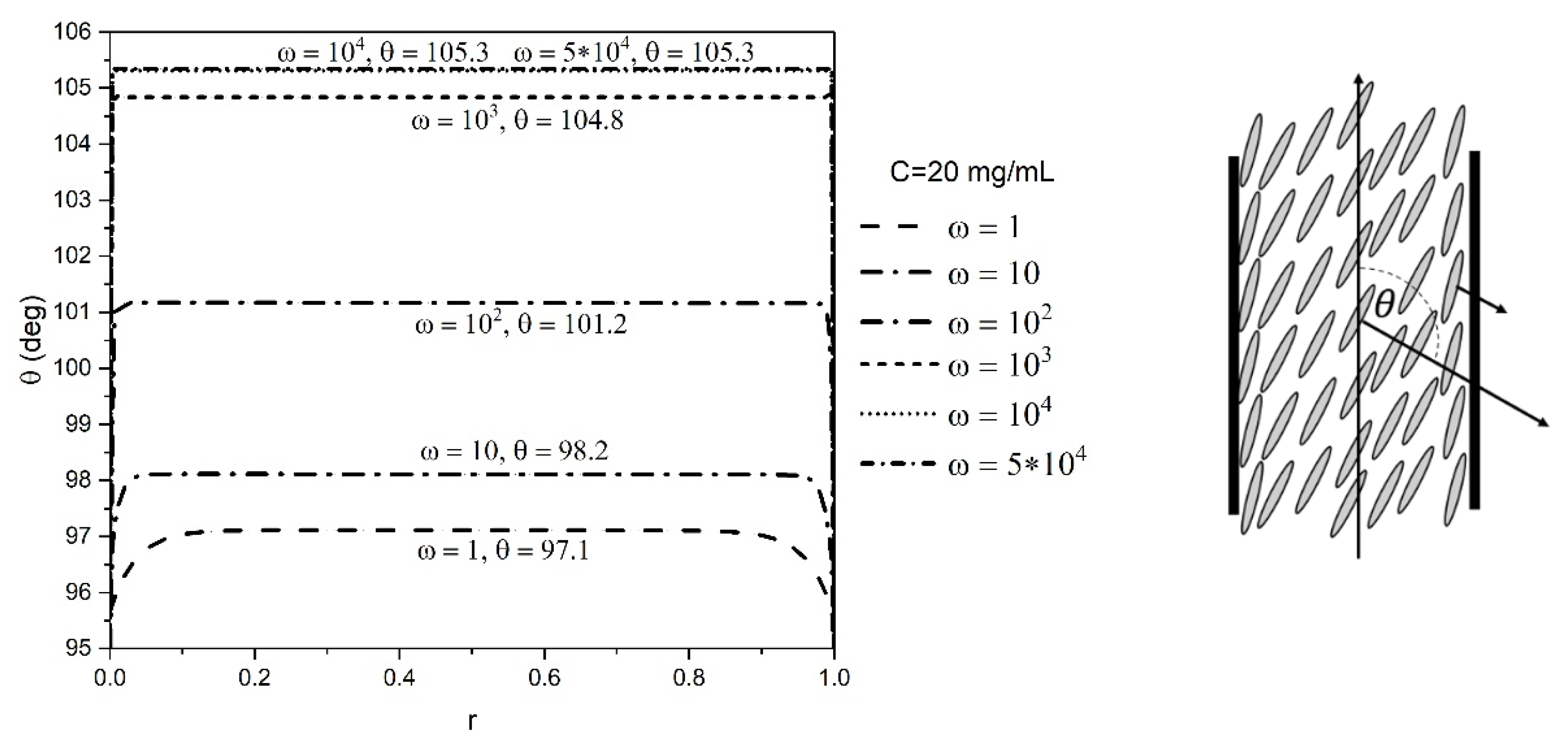
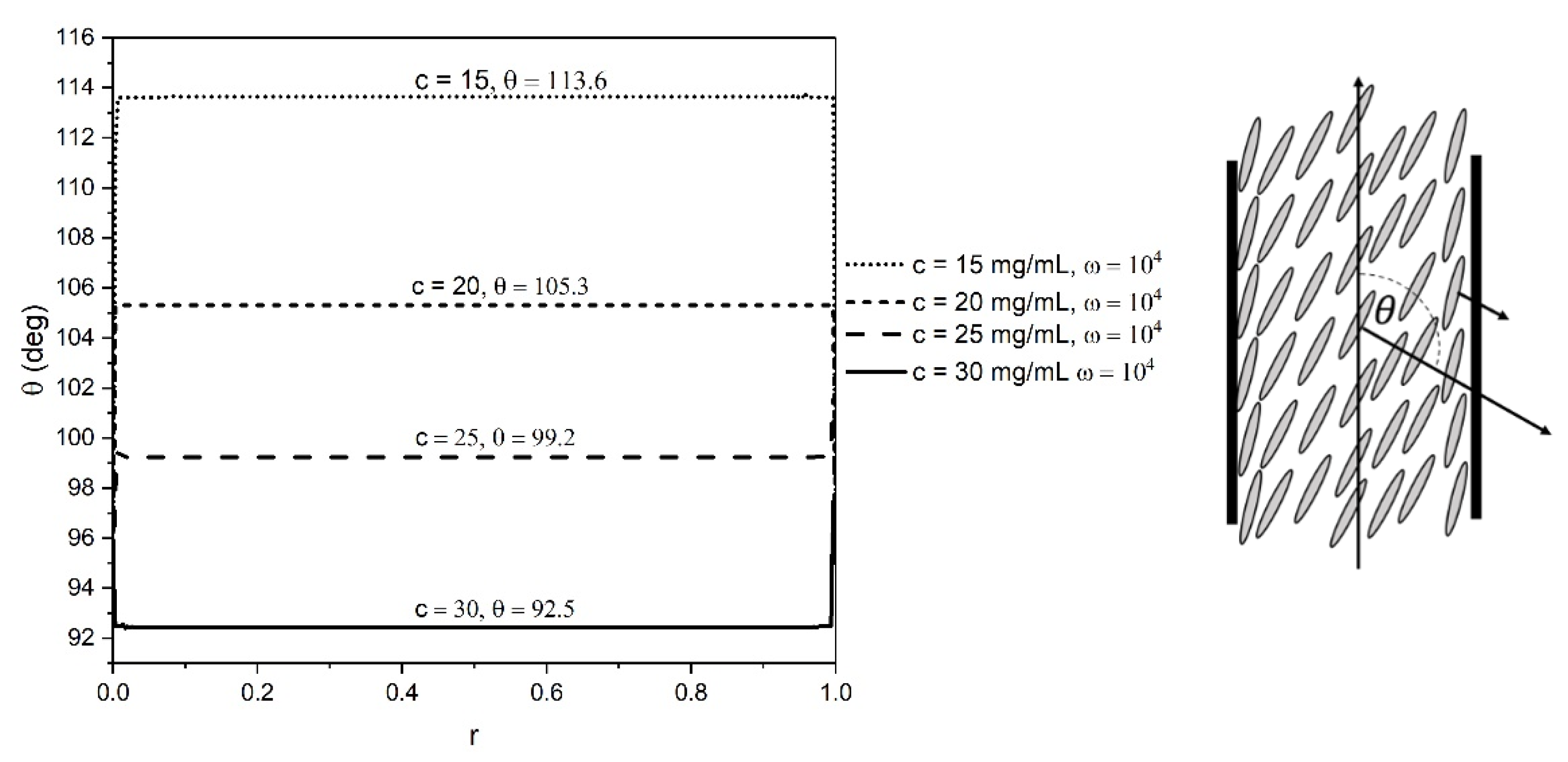
In the present study, the orientation profile of GO is obtained for different concentrations of GO dispersions at a range of shear rates using the EL theory. The numerically obtained orientation angle in the bulk of the domain is compared with the theoretical value of the alignment angle. Flow alignment of LCs is observed at higher shear rates, and if the orientation in bulk reaches the flow alignment angle, it can be concluded that the numerical solution is validated. Figure 5 shows the orientation profile of GO dispersion at a concentration of 20 mg/mL obtained by the EL theory, across the dimensionless gap at different dimensionless shear rates at ϵ = 0.5. This figure shows that the flow alignment is obtained at high shear rates. The anchoring angle in the EL theory is considered as 0.53π = 95°. The choice of anchoring angle is not arbitrary and was selected based on the study performed to compare the numerically obtained viscosity with the theoretical value, and the discussion is provided in the upcoming sections. The initial guess of the orientation was selected as a value between the orientation angle and the anchoring angle. The initial guesses of the velocity and the gradient were set as the typical Couette flow profile. Figure 6 demonstrates the orientation profile for all the concentrations obtained by the numerical solution of EL theory at a high shear rate, . The numerical values of the alignment angle are in good agreement with the theoretically calculated value, which can be obtained as . Table 3 represents the comparison of the alignment value obtained from the numerical solution with the theoretical alignment value of the orientation angle for each concentration. The table confirms that the value of flow alignment angle is obtained for all the concentrations, and the error for the simulation is less than 1% for each concentration.
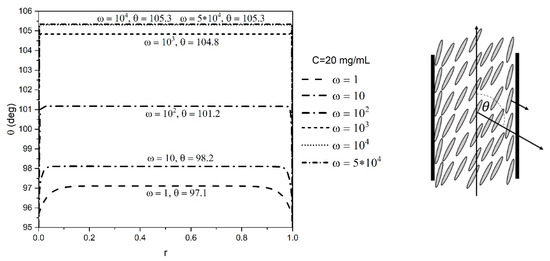
Figure 5.
Orientation profiles for 20 mg/mL GO dispersion across the dimensionless gap at different dimensionless shear rates using the EL theory.
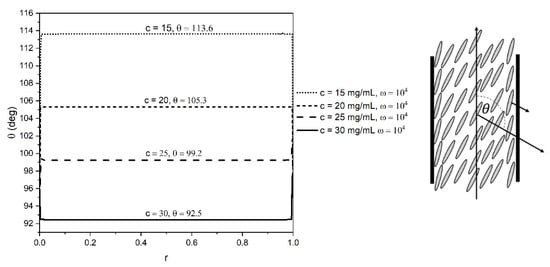
Figure 6.
Orientation profiles for 15, 20, 25, and 30 mg/mL GO dispersions across the dimensionless gap at different dimensionless shear rates using the EL theory.

Table 3.
Comparison of theoretical and numerically obtained values for orientation angles at alignment.
3.2. Multi-Stability and Multiplicity of Solutions
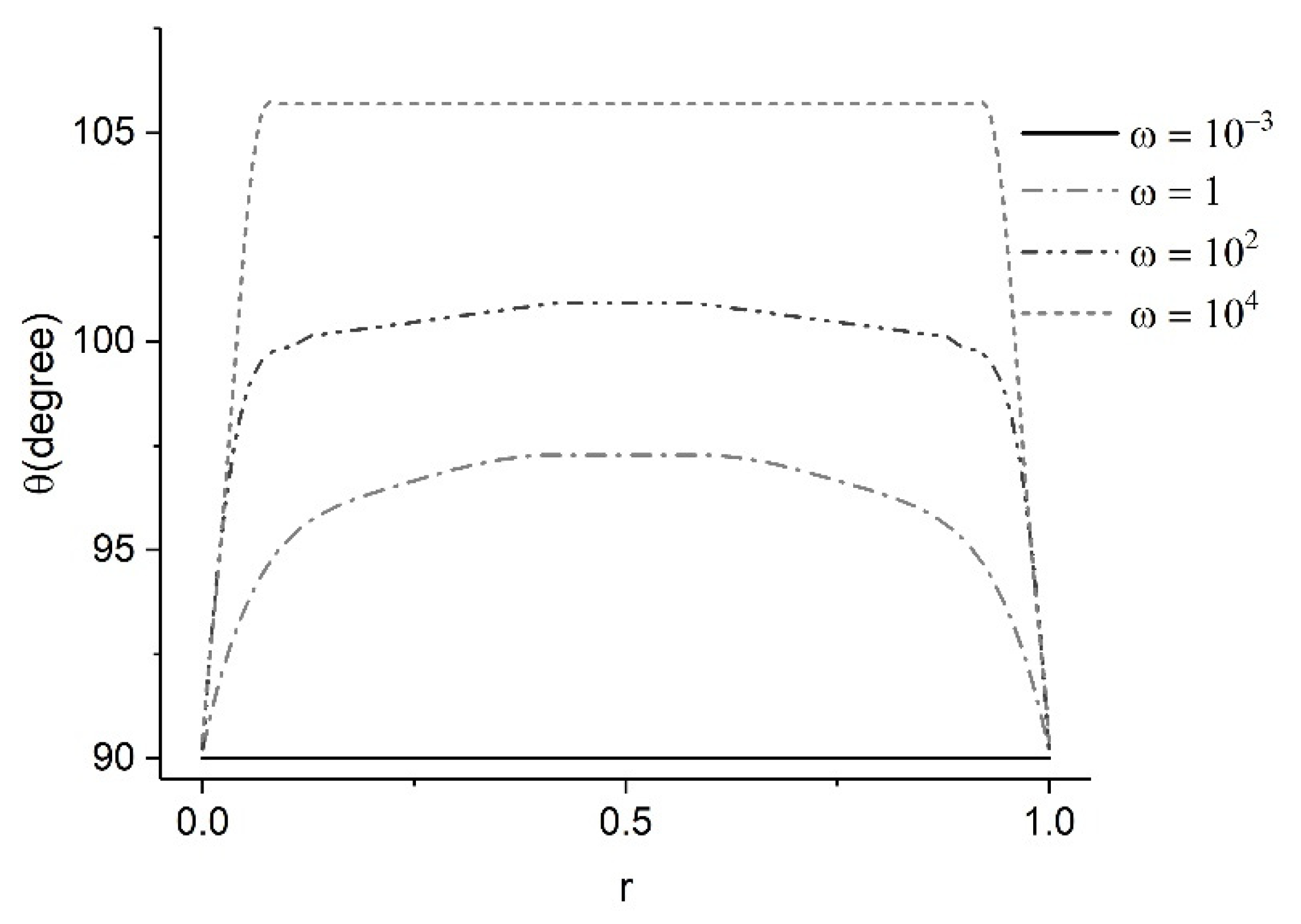
The LCs are prone to having multiple orientation solutions and the solution branch selected depends on the initial guess given to the solver [38,42]. In this section, studies have been performed to show the stable and unstable branches of the solution. To highlight the difference between the solution branch selection, the anchoring angle was chosen as π/2 = 90°. The study was performed using ϵ = 0.5. To obtain the stable branch of the solution, the initial guess was above 90°, and to obtain the unstable branch, the initial guess was lower than 90°. The stark contrast between the stable and unstable branches of the solution are highlighted in Figure 7 and Figure 8. The stable branch solutions are similar to the cases studied in the previous section. At low ω, elasticity is dominant, and as it increases, there is a competition between the elastic and the viscous term to dominate the orientation of molecules. At high ω, a significant part of the domain reaches flow alignment. The elasticity of GO is a combination of splay, bend, and twist as it is implemented by Frank constants. Dietrich et al. showed that splay and bend elastic constants for lyotropic LCs are similar, while the twist is much lower, which is true for LCs in general [46]. However, to the best of our knowledge, there is no complete set of elastic constants for lyotropic nematics.
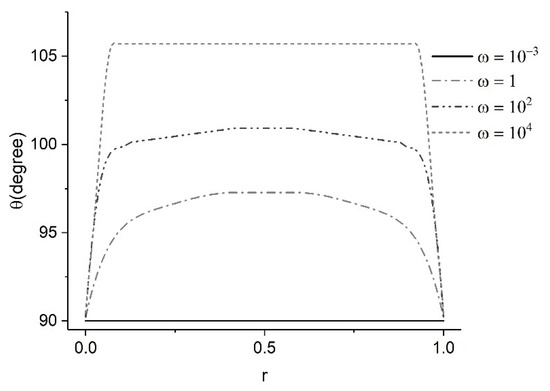
Figure 7.
Stable solution branch for 20 mg/mL GO showing the increase in non-dimensionless shear rate results in orientation reaching alignment value using the EL theory.
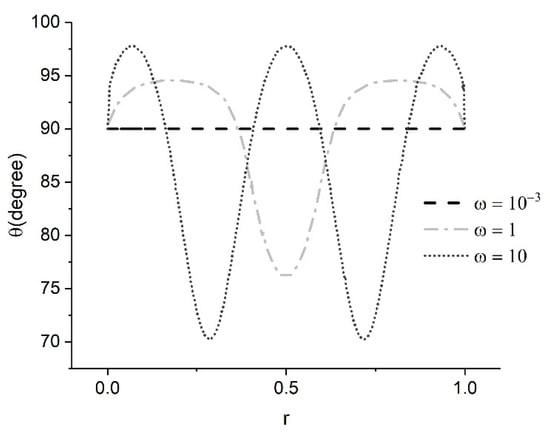
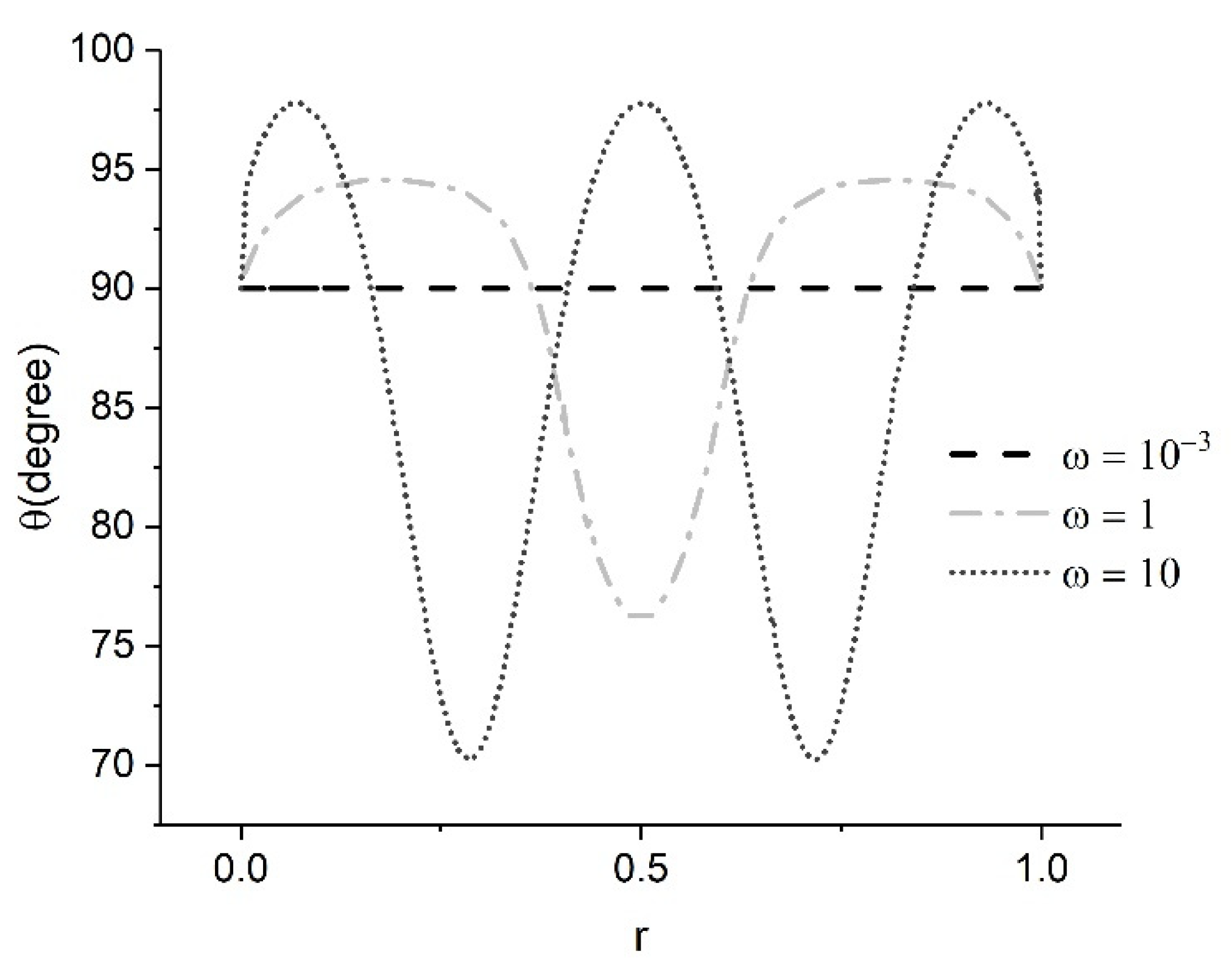
Figure 8.
Unstable solution branch for 20 mg/mL GO at different shear rates showing the increase in non-dimensionless shear rate results in oscillations within the orientation using the EL theory.
In the unstable branch, the solution develops oscillations, and the orientation does not reach the alignment value with the increase in the shear rate. It was observed that the initial guess for the orientational angle can make the results unstable and even diverge at higher ω, which was seen by other authors [31,42]. An initial guess lower than 90° showed a higher chance of reaching the unstable solution, while an initial guess above 90° showed a better chance of reaching the stable solution.
At low ω, the contribution of the anchoring angle is more significant, and as ω increases, the contribution of the viscous term increases, and unstable alignment is reached. With a further increase in the ω, the fluctuations propagate with higher frequencies.
3.3. Viscosity Response of Graphene Oxide
In the previous section, it was observed that the orientation angle reaches the alignment value at higher shear rates. The next step was to examine the viscosity obtained at different shear rates using the EL theory. In the study, the apparent viscosity is calculated, and it is defined as the viscosity of a Newtonian fluid under the same conditions. The apparent viscosity can be evaluated using Equation (12) [41].
In Equation (12), the function g(θ) is based on the definition shown in Equation (10). Equation (12) is based on a function for nematic LCs and therefore applies to a discotic LC such as GO. However, its applicability can be easily tested by ensuring that the calculated Miesowicz viscosities match with the values obtained using Equation (11). Since the scheme is planar, only the values of and can be tested for. Table 4 and Table 5 represent the theoretical and calculated values of and using the EL theory. To obtain the theoretical value, Equation (11) was used, and the value was compared with those obtained from Equation (12). was calculated using the value of orientation set to 90° in the entire domain, and to calculate , the value was set to 180°. It is evident that the difference in values is minimal, which justifies the use of Equation (11).

Table 4.
Comparison of dimensionless theoretical values of and calculated from the EL at different concentrations.

Table 5.
Comparison of dimensionless theoretical values of and calculated from the EL at different concentrations.
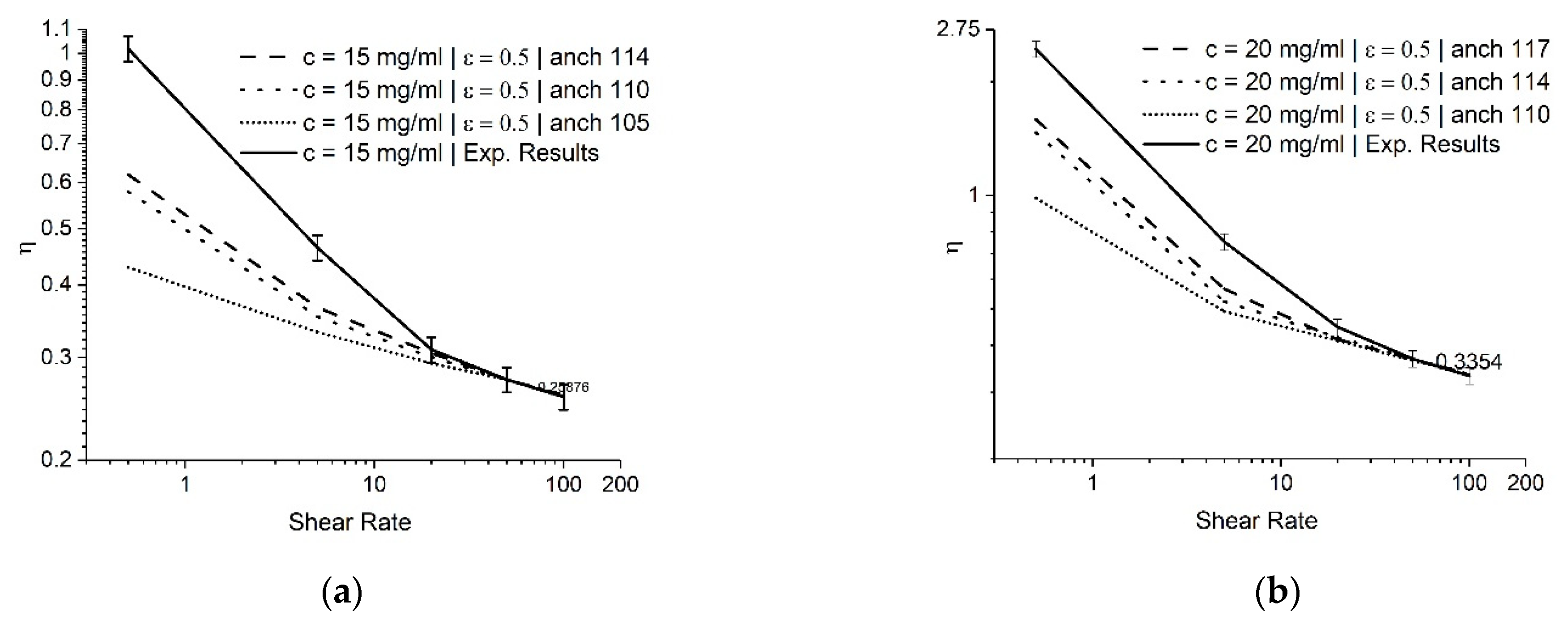
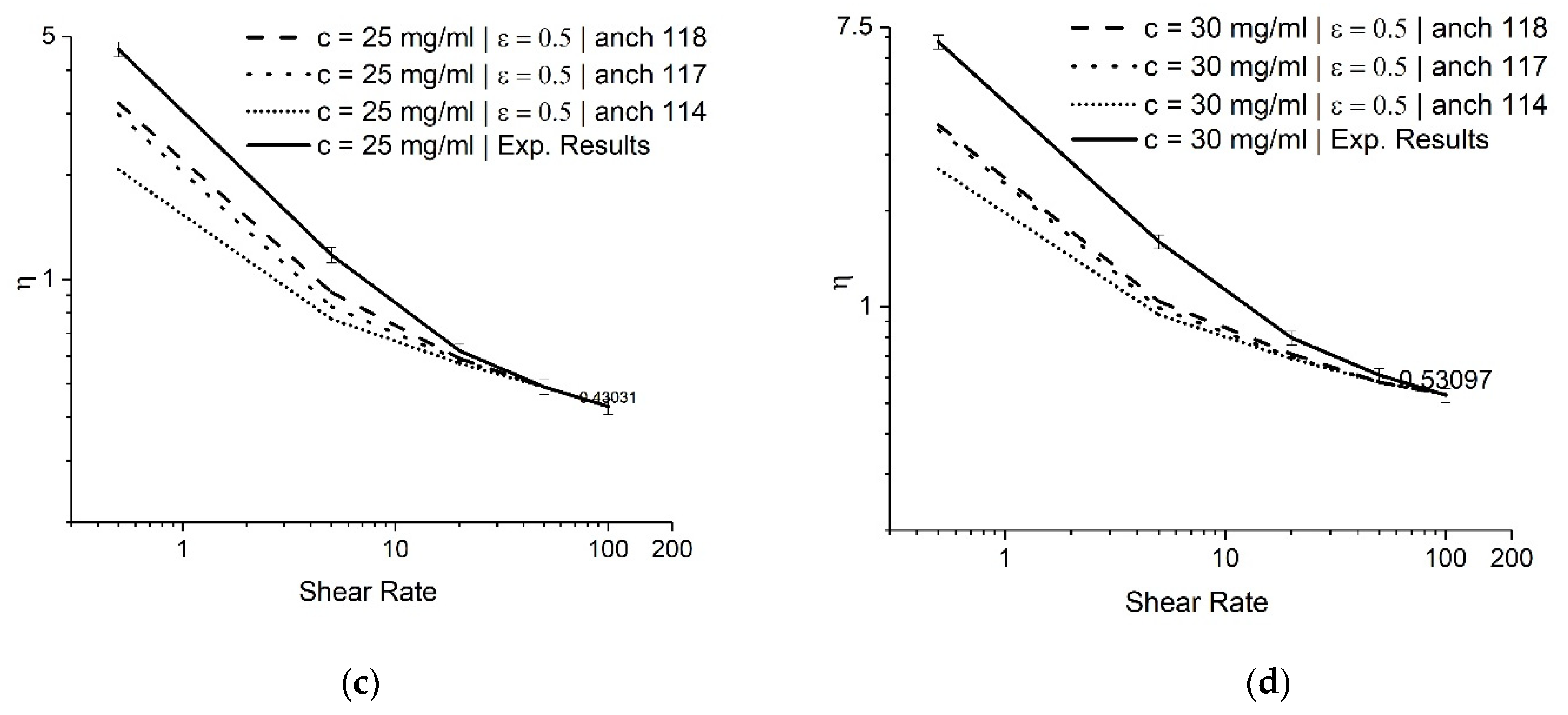
In this study, we investigated the effect of anchoring angles at different concentrations. Figure 9 shows that at lower shear rates, the anchoring angle results in different viscosity values, while at higher shear rates, the anchoring angle effect becomes less significant. Different anchoring angles do not affect the value at flow alignment. However, at low shear rates, the anchoring angle affects the value of viscosity. For all the concentrations, the viscosity values at a higher shear rate converged to their respective experimental values. Higher anchoring angles led the viscosity to be closer to the experimental values but had a numerical limitation. The anchoring angles corresponding to the viscosity values closest to the experimental results [7] at concentrations of 15, 20, 25, and 30 mg/mL are 114, 117, 118, and 118 degrees, respectively. Figure 10 represents the viscosity variation for GO at different anchoring angles from the EL theory. It is evident that the increase in concentration results in a higher viscosity at flow alignment.
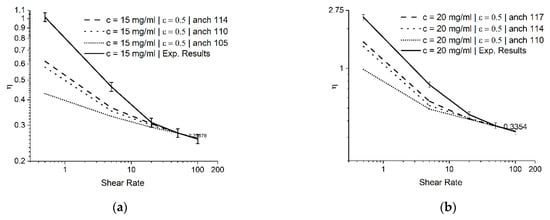
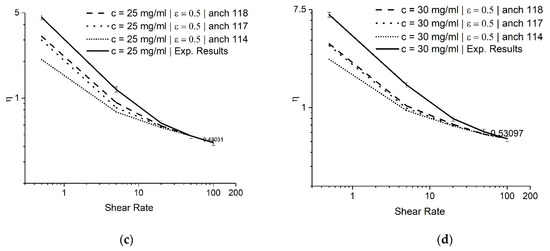
Figure 9.
Dimensionless viscosity vs. shear rate at different anchoring angles for ϵ = 0.5 at (a) 15, (b) 20, (c) 25, and (d) 30 mg/mL concentrations using the EL theory.
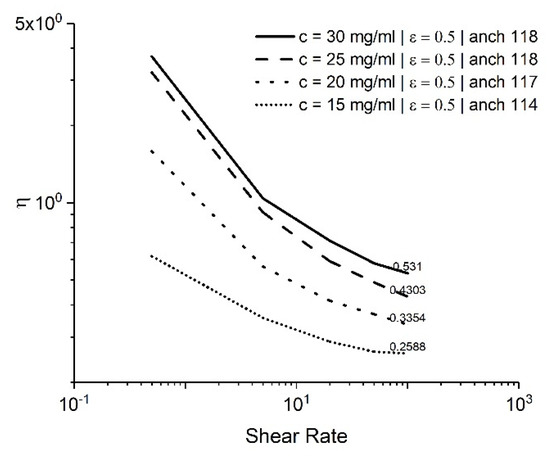
Figure 10.
Dimensionless viscosity vs. shear rate obtained at different concentrations for ϵ = 0.5 at different anchoring angles using the EL theory.
The results from the numerical simulation using the EL theory have been compared with the experimental viscosities, as shown in Table 6, which indicates the excellent agreement at different concentrations.

Table 6.
Comparison of the dimensionless experimental values of alignment viscosity and calculated from EL at different concentrations.
Both observations can be explained based on the Miesowicz viscosities and the orientation angle in the domain. It was shown that when the orientation angle is 90°, the value of viscosity is expected to be equal to , and when the value of orientation angle increases towards 180°, the viscosity can be expected to be closer to . From Table 4 and Table 6, it can be understood that value of , along with the value of the alignment angle, results in increasing values of viscosity when the concentration increases. Similarly, the trend of a higher anchoring angle resulting in a higher viscosity can be explained by the orientation in the domain becoming closer to the orientation representing .
The shear-thinning behavior has previously been reported for flow-aligning nematic LCs and GO suspensions [38,47,48]. Choi et al. [38] and Adnan et al. [49] investigated the viscosity of GO suspensions for shear rates up to 10 s−1 and showed that it increased for different concentrations of GO from the isotropic to discotic phase. Giudice and Shen [48] explored GO aqueous suspensions viscosity further, considering the higher shear rate of , and showed that the shear-thinning behavior becomes more noticeable at higher concentrations. Tesfai et al. [50] investigated the rheology of GO suspensions in the higher range of shear rates (up to for various concentrations (from 0.05 g/L to 0.5 g/L). They showed that at high shear rates, the shear-thinning behavior of the viscosity is followed by a shear-independent region (plateau). The viscosity behavior of GO suspensions from these studies is qualitatively consistent with our results. The quantitative differences between our study and other studies are due to different factors, such as dimensions and the size distribution of the GO sheets.
3.4. Sensitivity Analysis of Frank’s Elasticity Coefficients
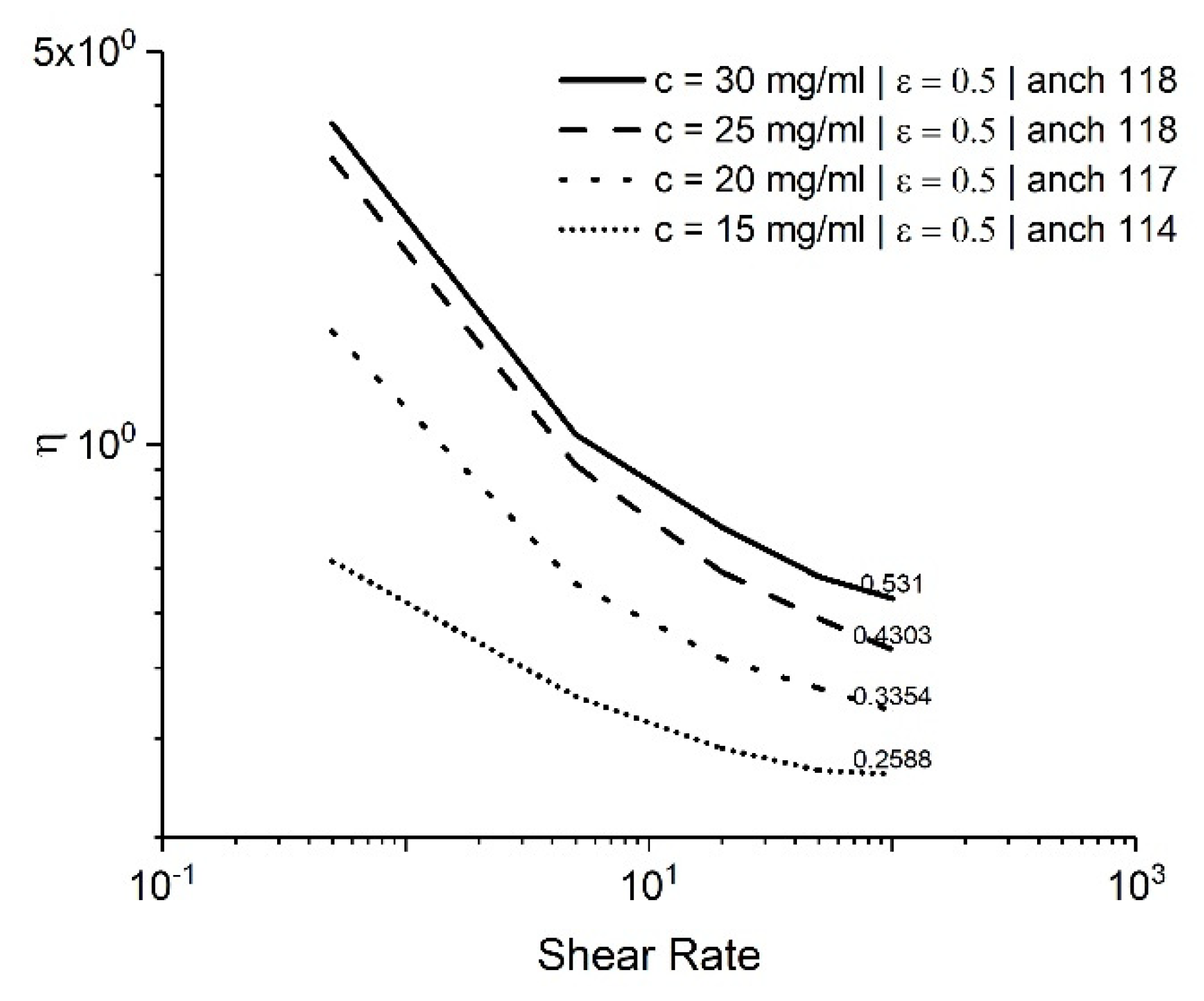
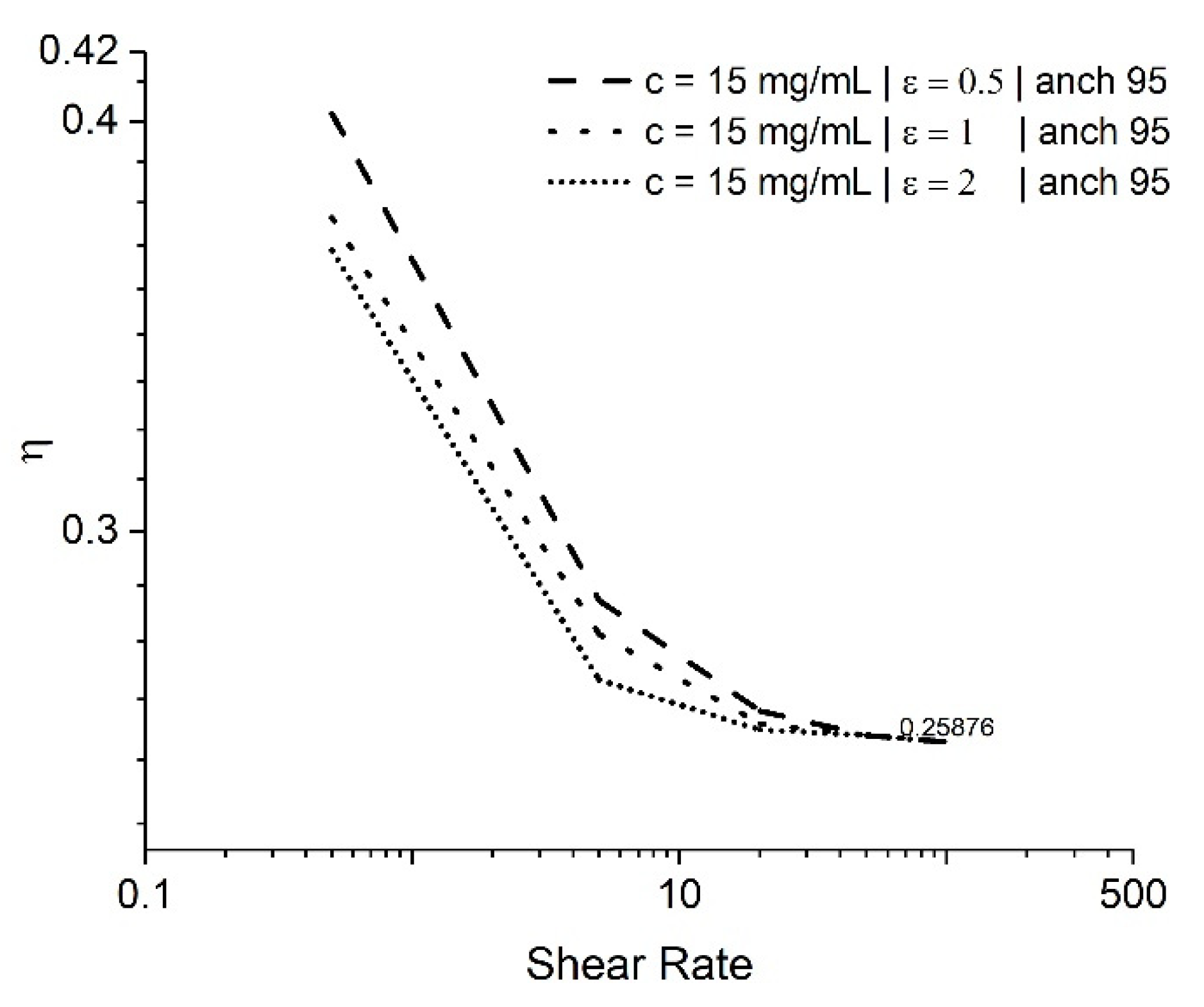
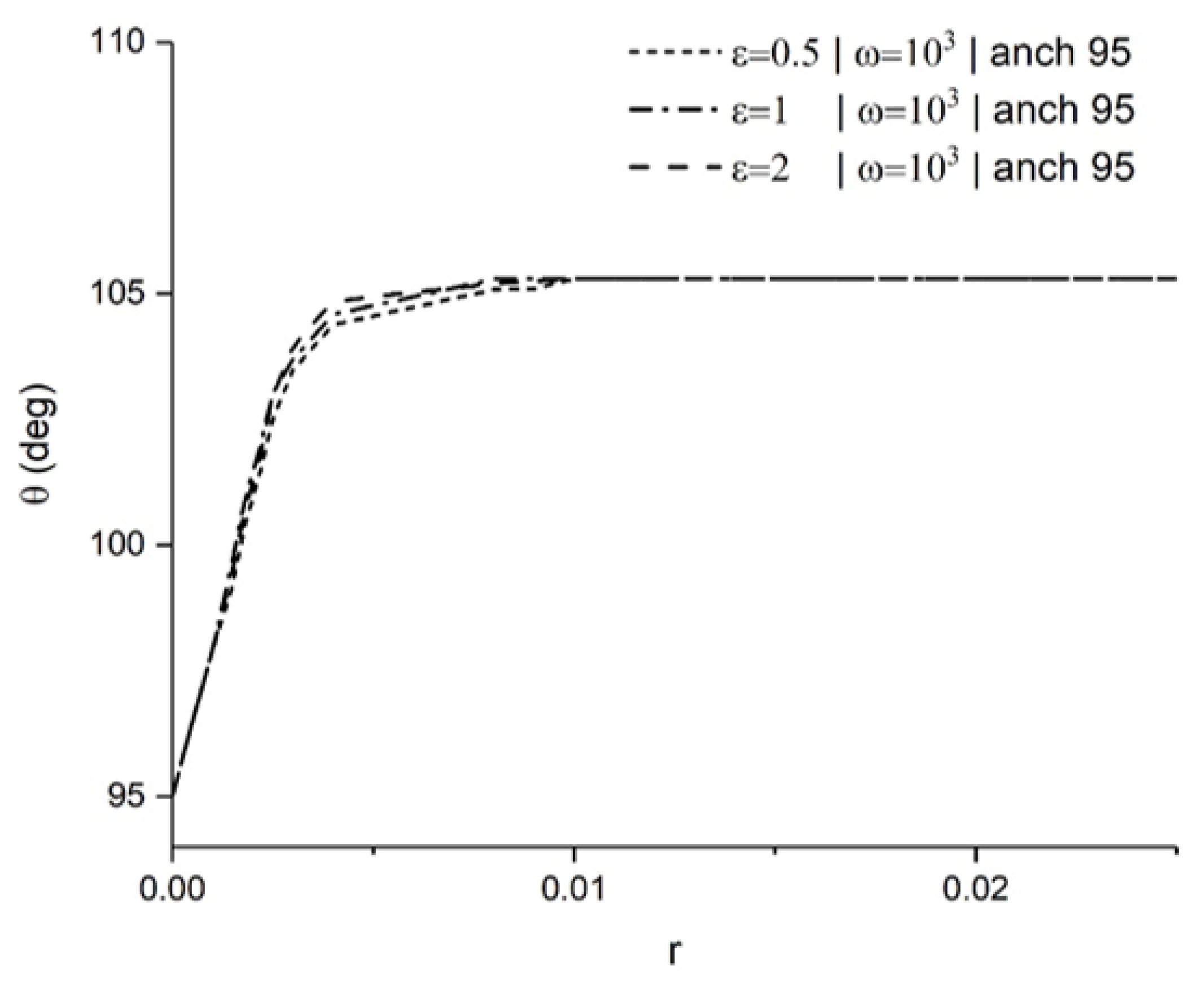
As mentioned previously, there is no literary source available containing the elasticity coefficients of GO suspensions. Dietrich et al. suggested an extremely low value for k22 and a similar order of magnitude for and [46]. To remedy this, a sensitivity analysis was performed using different ratios of ε = . The tested values are ϵ = 0.5, 1, and 2, which lie in the range of values typically expected in nematic LCs [33,51,52]. GO dispersions at 15 mg/mL with the anchoring angle of 0.53π = 95° were studied. It is important to note that the value of k22 does not affect the simulations, except for the value of the average of the elastic coefficients, and is maintained constant across the test cases. This value only affects the dimensional value of the shear rate. Figure 11 represents the variation in the viscosity with the shear rate for the different values of ϵ. It is evident that the changes in ϵ do not change the overall trend for viscosity, and the final value of alignment viscosity is the same.
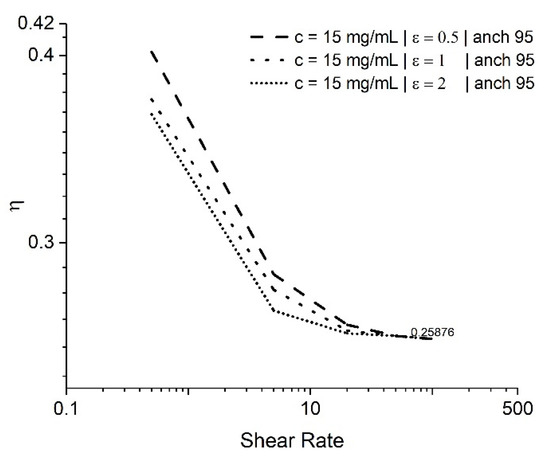
Figure 11.
Dimensionless viscosity vs. shear rate in the sensitivity study of Frank coefficients using the EL theory.
The next step is to examine the changes that the ratio causes in the orientation. It is known that at higher shear rates, the effect of the elasticity is limited to a boundary layer, while the orientation in the domain is primarily dominated by viscous forces [33]. Figure 12. shows the overlap of orientation angles of the LCs close to the boundary from numerical solutions using the LE theory. The orientation profile is compared at different values of at the anchoring angle and the same non-dimensional shear rate . The difference in the profile suggests that the ratio influences the transition from the anchoring angle to the alignment angle.
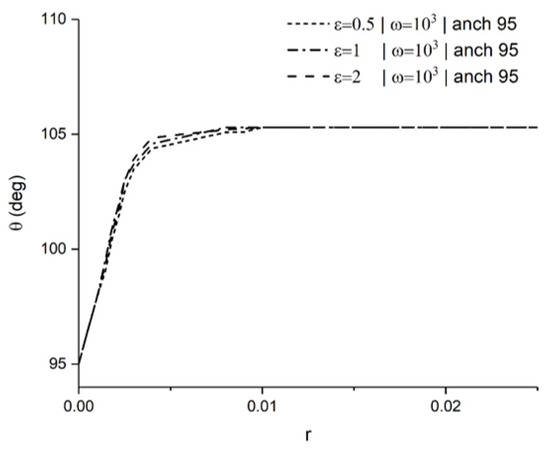
Figure 12.
Variation in orientation angle for different coefficients of elasticity.
4. Conclusions
In this study, the numerical simulations of GO dispersion as a DNLC between two cylinders with a small gap size, which is a preliminary geometry for journal bearing, were performed to characterize the orientation of flow-aligning particles in GO dispersions and its effect on the viscosity response, i.e., the rheology, In our previous study, the Leslie viscosity coefficients of GO dispersions at concentrations of 15, 20, 25, and 30 mg/mL were calculated. At these concentrations, GO dispersions are in the nematic phase of LC. In this study, the calculated coefficients were used to perform the simulations using the EL theory. Applying this theory, the behavior of the molecule under a wide range of shear rates, from to , was studied. In the study, the numerically obtained values of alignment viscosity showed agreement with the theoretical values. The flow alignment behavior of molecules at high shear rates was obtained. Consequently, the shear-thinning behavior of the flow-aligned LCs was observed. The orientation profiles obtained at different shear rates showed that at lower shear rates, the elastic forces dominate the orientation profile of the director, and as the shear rate increases, the viscous forces become predominant and the orientation in the bulk of the domain reaches the alignment angle. The effect of the anchoring angle on viscosity was explained and it was seen that the value of the viscosity at a high shear rate is independent of the anchoring angle. Moreover, it was observed that the solution’s stability depended on the initial guess, which indicates the presence of multiple branches of solutions that the LC could take in the EL theory. Since Frank’s elastic constants for GO were not available in the literature, a sensitivity analysis was performed to determine the effect of different ratios of the elasticity coefficients in the EL theory. The results showed that the alignment angle is not dependent on Frank’s elastic constants in the considered range of 0.5 to 2. Besides understanding the GO suspensions, the successful implementation of a simple model is a stepping stone towards studies of GO in complex geometries and under different flow conditions. Therefore, the simulation of GO suspensions in more complex geometries using the EL theory can be considered as future work.
Author Contributions
Conceptualization, D.G., A.N. and S.B.; methodology, D.G., A.N. and S.B.; software, A.N. and S.B.; validation, A.N.; formal analysis, A.N.; investigation, A.N.; resources, D.G.; data curation, D.G., A.N. and S.B.; writing—original draft preparation, A.N.; writing—review and editing, D.G., A.N. and S.B.; visualization, A.N.; supervision, D.G.; project administration, D.G.; funding acquisition, D.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science and Engineering Research Council (NSERC) of Canada, grant number GR001525.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledges financial support from the Natural Science and Engineering Research Council (NSERC) of Canada, Discovery Grant and financial support from the MITACS Globalink Graduate Fellowship.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Care, C.M.; Cleaver, D.J. Computer simulation of liquid crystals. Rep. Prog. Phys. 2005, 68, 2665–2700. [Google Scholar] [CrossRef]
- De Gennes, P.; Prost, J. The Physics of Liquid Crystals, 3rd ed.; Oxford University Press: Oxford, UK, 1996; ISBN 019851882X. [Google Scholar]
- Larson, R.G. The Structure and Rheology of Complex Fluids; Oxford University Press: Oxford, UK, 1999; ISBN 9780195121971. [Google Scholar]
- Chandrasekhar, S. Liquid Crystals; Cambridge University Press: Cambridge, UK, 1992; ISBN 9780521427418. [Google Scholar]
- Axenov, K.V.; Laschat, S. Thermotropic Ionic Liquid Crystals. Materials 2011, 4, 206–259. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, G.A. Geometric features in lyotropic liquid crystalline phase transitions observed in aqueous surfactant systems. J. Dispers. Sci. Technol. 2021. [Google Scholar] [CrossRef]
- Nikzad, A.; Akbari, A.; Grecov, D. Rheological properties of discotic nematic liquid crystals: Graphene oxide dispersions study. Liq. Cryst. 2021, 48, 1685–1698. [Google Scholar] [CrossRef]
- Akbari, A.; Sheath, P.; Martin, S.T.; Shinde, D.B.; Shaibani, M.; Banerjee, P.C.; Tkacz, R.; Bhattacharyya, D.; Majumder, M. Large-area graphene-based nanofiltration membranes by shear alignment of discotic nematic liquid crystals of graphene oxide. Nat. Commun. 2016, 7, 10891. [Google Scholar] [CrossRef]
- Liu, B.; Wang, C.; Muhuo, Y. The effect of liquid crystalline graphene oxide compared with non-liquid crystalline graphene oxide on the rheological properties of polyacrylonitrile solution. High Temp. Mater. Process. 2021, 40, 428–438. [Google Scholar] [CrossRef]
- Mahalingam, D.K.; Wang, S.; Nunes, S.P. Graphene Oxide Liquid Crystal Membranes in Protic Ionic Liquid for Nanofiltration. ACS Appl. Nano Mater. 2018, 1, 4661–4670. [Google Scholar] [CrossRef] [Green Version]
- Shim, Y.H.; Ahn, H.; Lee, S.; Kim, S.O.; Kim, S.Y. Universal Alignment of Graphene Oxide in Suspensions and Fibers. ACS Nano 2021, 15, 13453–13462. [Google Scholar] [CrossRef]
- Kulyk, B.; Freitas, M.A.; Santos, N.F.; Mohseni, F.; Carvalho, A.F.; Yasakau, K.; Fernandes, A.J.S.; Bernardes, A.; Figueiredo, B.; Silva, R.; et al. A critical review on the production and application of graphene and graphene-based materials in anti-corrosion coatings. Crit. Rev. Solid State Mater. Sci. 2021. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, C. Aqueous Liquid Crystals of Graphene Oxide. ACS Nano 2011, 5, 2908–2915. [Google Scholar] [CrossRef]
- Shao, Y.; Iliut, M.; Dierking, I.; Vijayaraghavan, A. Hybrid molecular/mineral lyotropic liquid crystal system of CTAB and graphene oxide in water. Carbon N. Y. 2021, 173, 105–114. [Google Scholar] [CrossRef]
- Abedin, M.J.; Gamot, T.D.; Martin, S.T.; Ali, M.; Hassan, K.I.; Mirshekarloo, M.S.; Tabor, R.F.; Green, M.J.; Majumder, M. Graphene Oxide Liquid Crystal Domains: Quantification and Role in Tailoring Viscoelastic Behavior. ACS Nano 2019, 13, 8957–8969. [Google Scholar] [CrossRef] [PubMed]
- Nam, K.-H.; Kim, U.J.; Jeon, M.H.; Lee, T.-R.; Yu, J.; You, N.-H.; Kim, Y.-K.; Suk, J.W.; Ku, B.-C. Green, fast, and scalable production of reduced graphene oxide via Taylor vortex flow. Chem. Eng. J. 2020, 391, 123482. [Google Scholar] [CrossRef]
- Alamer, M.; Lim, A.R.; Joo, Y.L. Continuous Synthesis of Structurally Uniform Graphene Oxide Materials in a Model Taylor–Couette Flow Reactor. Ind. Eng. Chem. Res. 2018, 58, 1167–1176. [Google Scholar] [CrossRef]
- Berman, D.; Erdemir, A.; Sumant, A.V. Reduced wear and friction enabled by graphene layers on sliding steel surfaces in dry nitrogen. Carbon N. Y. 2013, 59, 167–175. [Google Scholar] [CrossRef]
- Li, P.F.; Zhou, H.; Cheng, X. Investigation of a hydrothermal reduced graphene oxide nano coating on Ti substrate and its nano-tribological behavior. Surf. Coat. Technol. 2014, 254, 298–304. [Google Scholar] [CrossRef]
- Berman, D.; Erdemir, A.; Sumant, A.V. Few layer graphene to reduce wear and friction on sliding steel surfaces. Carbon N. Y. 2013, 54, 454–459. [Google Scholar] [CrossRef]
- Sarno, M.; Senatore, A.; Cirillo, C.; Petrone, V.; Ciambelli, P. Oil lubricant tribological behaviour improvement through dispersion of few layer graphene oxide. J. Nanosci. Nanotechnol. 2014, 14, 4960–4968. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Pan, G.; Luo, J. A comparative study between graphene oxide and diamond nanoparticles as water-based lubricating additives. Sci. China Technol. Sci. 2013, 56, 152–157. [Google Scholar] [CrossRef]
- Su, F.; Chen, G.; Huang, P. Lubricating performances of graphene oxide and onion-like carbon as water-based lubricant additives for smooth and sand-blasted steel discs. Friction 2018, 8, 47–57. [Google Scholar] [CrossRef] [Green Version]
- Kinoshita, H.; Nishina, Y.; Alias, A.A.; Fujii, M. Tribological properties of monolayer graphene oxide sheets as water-based lubricant additives. Carbon N. Y. 2014, 66, 720–723. [Google Scholar] [CrossRef]
- Elomaa, O.; Singh, V.K.; Iyer, A.; Hakala, T.J.; Koskinen, J. Graphene oxide in water lubrication on diamond-like carbon vs. stainless steel high-load contacts. Diam. Relat. Mater. 2015, 52, 43–48. [Google Scholar] [CrossRef]
- Ericksen, J.L. Anisotropic fluids. Arch. Ration. Mech. Anal. 1959, 4, 231–237. [Google Scholar] [CrossRef]
- Frank, F.C. Liquid Crystals: On the theory of liquid crystals. Discuss. Faraday Soc. 1958, 25, 19–28. [Google Scholar] [CrossRef]
- Grecov, D.; Rey, A.D. Theoretical and Computational Rheology for Discotic Nematic Liquid Crystals. Mol. Cryst. Liq. Cryst. 2003, 391, 57–94. [Google Scholar] [CrossRef]
- Noroozi, N.; Grecov, D.; Shafiei-Sabet, S. Estimation of viscosity coefficients and rheological functions of nanocrystalline cellulose aqueous suspensions. Liq. Cryst. 2014, 41, 56–66. [Google Scholar] [CrossRef]
- Park, M.; Lee, H.S. Rotational motions of repulsive graphene oxide domains in aqueous dispersion during slow shear flow. J. Rheol. (N. Y.) 2019, 64, 29–41. [Google Scholar] [CrossRef]
- De Andrade Lima, L.R.P.; Rey, A.D. Poiseuille flow of Leslie-Ericksen discotic liquid crystal: Solution multiplicity, multistability, and non-Newtonian rheology. J. Non-Newton. Fluid Mech. 2003, 110, 103–142. [Google Scholar] [CrossRef]
- Atkin, R.J. Poiseuille flow of liquid crystals of the nematic type. Arch. Ration. Mech. Anal. 1970, 38, 224–240. [Google Scholar] [CrossRef]
- Ho, A.S.K.; Rey, A.D. Orienting properties of discotic nematic liquid crystals in Jeffrey-Hamel flows. Rheol. Acta 1991, 30, 77–88. [Google Scholar] [CrossRef]
- Chono, S.; Tsuji, T.; Denn, M.M. Spatial development of director orientation of tumbling nematic liquid crystals in pressure-driven channel flow. J. Nonnewton. Fluid Mech. 1998, 79, 515–527. [Google Scholar] [CrossRef]
- Cruz, P.A.; Tomé, M.F.; Stewart, I.W.; McKee, S. A numerical method for solving the dynamic three-dimensional Ericksen–Leslie equations for nematic liquid crystals subject to a strong magnetic field. J. Non-Newton. Fluid Mech. 2010, 165, 143–157. [Google Scholar] [CrossRef]
- Anderson, T.G.; Mema, E.; Kondic, L.; Cummings, L.J. Transitions in Poiseuille flow of nematic liquid crystal. Int. J. Non-Linear Mech. 2015, 75, 15–21. [Google Scholar] [CrossRef] [Green Version]
- Carou, J.Q.; Duffy, B.R.; Mottram, N.J.; Wilson, S.K. Shear-driven and pressure-driven flow of a nematic liquid crystal in a slowly varying channel. Phys. Fluids 2006, 18, 027105. [Google Scholar] [CrossRef] [Green Version]
- Choi, G.M.; Park, M.; Jeong, S.Y.; Lee, H.S. Orientation effect on the rheology of graphene oxide dispersions in isotropic phase, ordered isotropic biphase, and discotic phase. J. Rheol. (N. Y.) 2021, 65, 791–806. [Google Scholar] [CrossRef]
- Ericksen, J.L. Conservation laws for liquid crystals conservation laws for liquid crystals. Cit. Trans. Soc. Rheol. J. Chem. Phys. I Interfacial Free Energy J. Chem. Phys. J. Rheol. 1961, 5, 1205–1959. [Google Scholar] [CrossRef]
- Leslie, F.M. Some constitutive equations for liquid crystals. Arch. Ration. Mech. Anal. 1968, 28, 265–283. [Google Scholar] [CrossRef]
- Atkin, R.J.; Leslie, F.M. Couette flow of nematic liquid crystals. Q. J. Mech. Appl. Math. 1970, 23, 3–24. [Google Scholar] [CrossRef]
- Noroozi, N.; Grecov, D. Flow modelling and rheological characterization of nematic liquid crystals between concentric cylinders. Liq. Cryst. 2013, 40, 871–883. [Google Scholar] [CrossRef]
- Miesowicz, M. The three coefficients of viscosity of anisotropic liquids. Nature 1946, 158, 27. [Google Scholar] [CrossRef]
- Rey, A.D.; Tsuji, T. Recent advances in theoretical liquid crystal rheology. Macromol. Theory Simul. 1998, 7, 623–639. [Google Scholar] [CrossRef]
- de Kort, G.W.; Leoné, N.; Stellamanns, E.; Auhl, D.; Wilsens, C.H.R.M.; Rastogi, S. Effect of Shear Rate on the Orientation and Relaxation of a Vanillic Acid Based Liquid Crystalline Polymer. Polymers 2018, 10, 935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dietrich, C.F.; Collings, P.J.; Sottmann, T.; Rudquist, P.; Giesselmann, F. Extremely small twist elastic constants in lyotropic nematic liquid crystals. Proc. Natl. Acad. Sci. USA 2020, 117, 27238–27244. [Google Scholar] [CrossRef] [PubMed]
- Del Giudice, F.; Cunning, B.V.; Ruoff, R.S.; Shen, A.Q. Filling the gap between transient and steady shear rheology of aqueous graphene oxide dispersions. Rheol. Acta 2018, 57, 293–306. [Google Scholar] [CrossRef]
- Del Giudice, F.; Shen, A.Q. Shear rheology of graphene oxide dispersions. Curr. Opin. Chem. Eng. 2017, 16, 23–30. [Google Scholar] [CrossRef]
- Adnan, A.M.; Lü, C.; Luo, X.; Wang, J. Impact of Graphene Oxide on Zero Shear Viscosity, Fatigue Life and Low-Temperature Properties of Asphalt Binder. Materials 2021, 14, 3073. [Google Scholar] [CrossRef]
- Tesfai, W.; Singh, P.; Shatilla, Y.; Iqbal, M.Z.; Abdala, A.A. Rheology and microstructure of dilute graphene oxide suspension. JNR J. Nanoparticle Res. 2013, 15, 1989. [Google Scholar] [CrossRef]
- Straley, J.P. Frank elastic constants of the hard-rod liquid crystal. Phys. Rev. A 1973, 8, 2181. [Google Scholar] [CrossRef]
- Bradshaw, M.J.; Raynes, E.P.; Bunning, J.D.; Faber, T.E. The Frank constants of some nematic liquid crystals. J. Phys. 1985, 46, 1513–1520. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).